User:Jon Awbrey/SEQUENCES

A061396

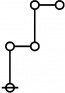
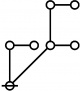
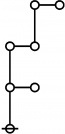
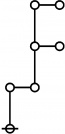
• A061396

Plain Wiki Table

\(\text{Table 1.} ~~ \text{Prime Factorizations, Riffs, and Rotes}\)

\(\text{Integer}\!\)	\(\text{Factorization}\!\)	\(\text{Notation}\!\)	\(\text{Riff Digraph}\!\)	\(\text{Rote Graph}\!\)	\(\text{Traversal}\!\)
\(1\!\)	\(1\!\)
\(2\!\)	\(\text{p}_1^1\!\)	\(\text{p}\!\)			\(((~))\)
\(3\!\)	\(\begin{array}{lll} \text{p}_2^1 & = & \text{p}_{\text{p}_1^1}^1 \end{array}\)	\(\text{p}_\text{p}\!\)	\(\cdots\)		\((((~))(~))\)
\(4\!\)	\(\begin{array}{lll} \text{p}_1^2 & = & \text{p}_1^{\text{p}_1^1} \end{array}\)	\(\text{p}^\text{p}\!\)	\(\cdots\)		\(((((~))))\)
\(5\!\)	\(\begin{array}{lll} \text{p}_3^1 & = & \text{p}_{\text{p}_2^1}^1 \\[6pt] & = & \text{p}_{\text{p}_{\text{p}_1^1}^1}^1 \end{array}\)	\(\text{p}_{\text{p}_{\text{p}}}\!\)	\(\cdots\)		\(((((~))(~))(~))\)
\(6\!\)	\(\begin{array}{lll} \text{p}_1^1 \text{p}_2^1 & = & \text{p}_1^1 \text{p}_{\text{p}_1^1}^1 \end{array}\)	\(\text{p} \text{p}_{\text{p}}\!\)	\(\cdots\)		\(((~))(((~))(~))\)
\(7\!\)	\(\begin{array}{lll} \text{p}_4^1 & = & \text{p}_{\text{p}_1^2}^1 \\[6pt] & = & \text{p}_{\text{p}_1^{\text{p}_1^1}}^1 \end{array}\)	\(\text{p}_{\text{p}^{\text{p}}}\!\)	\(\cdots\)		\((((((~))))(~))\)
\(8\!\)	\(\begin{array}{lll} \text{p}_1^3 & = & \text{p}_1^{\text{p}_2^1} \\[6pt] & = & \text{p}_1^{\text{p}_{\text{p}_1^1}^1} \end{array}\)	\(\text{p}^{\text{p}_{\text{p}}}\!\)	\(\cdots\)		\((((((~))(~))))\)
\(9\!\)	\(\begin{array}{lll} \text{p}_2^2 & = & \text{p}_{\text{p}_1^1}^{\text{p}_1^1} \end{array}\)	\(\text{p}_\text{p}^\text{p}\!\)	\(\cdots\)		\((((~))(((~))))\)
\(16\!\)	\(\begin{array}{lll} \text{p}_1^4 & = & \text{p}_1^{\text{p}_1^2} \\[6pt] & = & \text{p}_1^{\text{p}_1^{\text{p}_1^1}} \end{array}\)	\(\text{p}^{\text{p}^{\text{p}}}\!\)	\(\cdots\)		\(((((((~))))))\)

Nested Wiki Table

\(\text{Table 1.} ~~ \text{Prime Factorizations, Riffs, and Rotes}\)

\(\text{Integer}\!\) \(\text{Factorization}\!\) \(\text{Notation}\!\) \(\text{Riff Digraph}\!\) \(\text{Rote Graph}\!\) \(\text{Traversal}\!\)

\(1\!\) \(1\!\)

\(2\!\) \(\text{p}_1^1\!\) \(\text{p}\!\) \(((~))\)

\(3\!\) \(\begin{array}{lll} \text{p}_2^1 & = & \text{p}_{\text{p}_1^1}^1 \end{array}\) \(\text{p}_\text{p}\!\) \(\cdots\) \((((~))(~))\) \(4\!\) \(\begin{array}{lll} \text{p}_1^2 & = & \text{p}_1^{\text{p}_1^1} \end{array}\) \(\text{p}^\text{p}\!\) \(\cdots\) \(((((~))))\)

\(5\!\) \(\begin{array}{lll} \text{p}_3^1 & = & \text{p}_{\text{p}_2^1}^1 \\[10pt] & = & \text{p}_{\text{p}_{\text{p}_1^1}^1}^1 \end{array}\) \(\text{p}_{\text{p}_{\text{p}}}\!\) \(\cdots\) \(((((~))(~))(~))\) \(6\!\) \(\begin{array}{lll} \text{p}_1^1 \text{p}_2^1 & = & \text{p}_1^1 \text{p}_{\text{p}_1^1}^1 \end{array}\) \(\text{p} \text{p}_{\text{p}}\!\) \(\cdots\) \(((~))(((~))(~))\) \(7\!\) \(\begin{array}{lll} \text{p}_4^1 & = & \text{p}_{\text{p}_1^2}^1 \\[10pt] & = & \text{p}_{\text{p}_1^{\text{p}_1^1}}^1 \end{array}\) \(\text{p}_{\text{p}^{\text{p}}}\!\) \(\cdots\) \((((((~))))(~))\) \(8\!\) \(\begin{array}{lll} \text{p}_1^3 & = & \text{p}_1^{\text{p}_2^1} \\[10pt] & = & \text{p}_1^{\text{p}_{\text{p}_1^1}^1} \end{array}\) \(\text{p}^{\text{p}_{\text{p}}}\!\) \(\cdots\) \((((((~))(~))))\) \(9\!\) \(\begin{array}{lll} \text{p}_2^2 & = & \text{p}_{\text{p}_1^1}^{\text{p}_1^1} \end{array}\) \(\text{p}_\text{p}^\text{p}\!\) \(\cdots\) \((((~))(((~))))\) \(16\!\) \(\begin{array}{lll} \text{p}_1^4 & = & \text{p}_1^{\text{p}_1^2} \\[10pt] & = & \text{p}_1^{\text{p}_1^{\text{p}_1^1}} \end{array}\) \(\text{p}^{\text{p}^{\text{p}}}\!\) \(\cdots\) \(((((((~))))))\)

Old ASCII Version

Illustration of initial terms of A061396
Jon Awbrey (jawbrey(AT)oakland.edu)

o--------------------------------------------------------------------------------
| integer   factorization     riff      r.i.f.f.     rote   -->   in parentheses
|                             k p's     k nodes      2k+1 nodes
o--------------------------------------------------------------------------------
|
| 1         1                 blank     blank        @            blank
|
o--------------------------------------------------------------------------------
|
|                                                    o---o
|                                                    |
| 2         p_1^1             p         @            @            (())
|
o--------------------------------------------------------------------------------
|
|                                                    o---o
|                                                    |
|                                                    o---o
| 3         p_2^1 =                                  |
|           p_(p_1)^1         p_p       @            @            ((())())
|                                        ^
|                                         \
|                                          o
|
|                                                        o---o
|                                          o             |
|                                         ^          o---o
| 4         p_1^2 =                      /           |
|           p_1^p_1           p^p       @            @            (((())))
|
o--------------------------------------------------------------------------------
|
|                                                    o---o
|                                                    |
|                                                    o---o
|                                                    |
| 5         p_3 =                                    o---o
|           p_(p_2) =                                |
|           p_(p_(p_1))       p_(p_p)   @            @            (((())())())
|                                        ^
|                                         \
|                                          o
|                                           ^
|                                            \
|                                             o
|
|                                                        o-o
|                                                       /
|                                                  o-o o-o
| 6         p_1 p_2 =                               \ /
|           p_1 p_(p_1)       p p_p     @ @          @            (())((())())
|                                          ^
|                                           \
|                                            o
|
|                                                        o---o
|                                                        |
|                                                    o---o
|                                                    |
| 7         p_4 =                                    o---o
|           p_(p_1^2) =                              |
|           p_(p_1^p_1)       p_(p^p)   @     o      @            ((((())))())
|                                        ^   ^
|                                         \ /
|                                          o
|
|                                                        o---o
|                                                        |
|                                                        o---o
|                                          o             |
| 8         p_1^3 =                       ^ ^        o---o
|           p_1^p_2 =                    /   \       |
|           p_1^p_(p_1)       p^p_p     @     o      @            ((((())())))
|
|                                                    o-o o-o
|                                          o         |   |
| 9         p_2^2 =                       ^          o---o
|           p_(p_1)^2 =                  /           |
|           p_(p_1)^(p_1)     p_p^p     @            @            ((())((())))
|                                        ^
|                                         \
|                                          o
|
|                                             o              o---o
|                                            ^               |
|                                           /            o---o
|                                          o             |
| 16        p_1^4 =                       ^          o---o
|           p_1^(p_1^2) =                /           |
|           p_1^(p_1^p_1)     p^(p^p)   @            @            (((((())))))
|
o--------------------------------------------------------------------------------

Further Comments:

Here are a couple more pages from my notes,
where it looks like I first arrived at the
generating function, and also carried out
some brute force enumerations of riffs.

I am going to experiment with a different way of
transcribing indices and powers into a plaintext.

|                jj
|              p<
|      j      /  ji
|    p<     p<         etc.
|      i      \  ij
|              p<
|                ii

-------------------------------------------------------

1978-11-06

Generating Function

| R(x) = 1 + x + 2x^2 + ...
|
|      =   1 + x.x^0 (1 + x + 2x^2 + ...)
|        . 1 + x.x^1 (1 + x + 2x^2 + ...)
|        . 1 + x.x^2 (1 + x + 2x^2 + ...)
|        . 1 + x.x^2 (1 + x + 2x^2 + ...)
|        . ...
|
|      = 1 + x + 2x^2 + ...
|
| Product over (i = 0 to infinity) of (1 + x.x^i.R(x))^R_i  =  R(x)

-------------------------------------------------------

1978-11-10

Brute force enumeration of R_n

| 4 p's
|
|       p
|     p<        p_p                 p                    p
|   p<        p<        p p_p     p<_p     p_p_p     p_p<
| p<        p<        p<        p<       p<        p<
|
|
|       p
|     p<        p_p                 p                    p
| p_p<      p_p<      p<        p_p<_p   p_p_p_p   p_p_p<
|                       p p_p
|
|
|     p
|   p<        p_p       p         p        p           p
| p<        p<        p<        p<       p<  p<    p p<
|   p         p         p_p       p^p          p       p
|
|
| p p_p_p   p p<
|               p^p
|

Altogether, 20 riffs of weight 4.

| o---------------------o---------------------o---------------------o
| | 3                   | 4                   | 5                   |
| o---------------------o---------------------o---------------------|
| | // // 2             | 10, 3, 1, 6         | 36, 10, 2, 3, 2, 20 |
| o---------------------o---------------------o---------------------|
| |                     | 0^1 4^1,            |                     |
| |                     | 1^1 3^1,            |                     |
| |                     | 2^2,                |                     |
| |                     | 4^1 0^1             |                     |
| o---------------------o---------------------o---------------------o
| | 6                   | 20                  | 73                  |
| o---------------------o---------------------o---------------------o
|

-------------------------------------------------------

Here are the number values of the riffs on 4 nodes:

o----------------------------------------------------------------------
|
|       p
|     p<        p_p                 p                    p
|   p<        p<        p p_p     p<_p     p_p_p     p_p<
| p<        p<        p<        p<       p<        p<
|
| 2^16      2^8       2^6       2^9      2^5       2^7
| 65536     256       64        512      32        128
o----------------------------------------------------------------------
|
|       p
|     p<        p_p                 p                    p
| p_p<      p_p<      p<        p_p<_p   p_p_p_p   p_p_p<
|                       p p_p
|
| p_16      p_8       p_6       p_9      p_5       p_7
| 53        19        13        23       11        17
o----------------------------------------------------------------------
|
|     p
|   p<        p_p       p         p                    p
| p<        p<        p<        p<       p^p p_p   p p<
|   p         p         p_p       p^p                  p
|
| 3^4       3^3       5^2       7^2
| 81        27        25        49       12        18
o----------------------------------------------------------------------
|
| p p_p_p   p p<
|               p^p
|
| 10        14 
o----------------------------------------------------------------------

For ease of reference, I include the previous table
of smaller riffs and rotes, redone in the new style.

o--------------------------------------------------------------------------------
| integer   factorization     riff      r.i.f.f.     rote   -->   in parentheses
|                             k p's     k nodes      2k+1 nodes
o--------------------------------------------------------------------------------
|
| 1         1                 blank     blank        @            blank
|
o--------------------------------------------------------------------------------
|
|                                                    o---o
|                                                    |
| 2         p_1^1             p         @            @            (())
|
o--------------------------------------------------------------------------------
|
|                                                    o---o
|                                                    |
|                                                    o---o
| 3         p_2^1 =                                  |
|           p_(p_1)^1         p_p       @            @            ((())())
|                                        ^
|                                         \
|                                          o
|
|                                                        o---o
|                                          o             |
|                                         ^          o---o
| 4         p_1^2 =                      /           |
|           p_1^p_1           p^p       @            @            (((())))
|
o--------------------------------------------------------------------------------
|
|                                                    o---o
|                                                    |
|                                                    o---o
|                                                    |
| 5         p_3 =                                    o---o
|           p_(p_2) =                                |
|           p_(p_(p_1))       p_p_p     @            @            (((())())())
|                                        ^
|                                         \
|                                          o
|                                           ^
|                                            \
|                                             o
|
|                                                        o-o
|                                                       /
|                                                  o-o o-o
| 6         p_1 p_2 =                               \ /
|           p_1 p_(p_1)       p p_p     @ @          @            (())((())())
|                                          ^
|                                           \
|                                            o
|
|                                                        o---o
|                                                        |
|                                                    o---o
|                                                    |
| 7         p_4 =                                    o---o
|           p_(p_1^2) =                              |
|           p_(p_1^p_1)       p<        @     o      @            ((((())))())
|                               p^p      ^   ^
|                                         \ /
|                                          o
|
|                                                        o---o
|                                                        |
|                                                        o---o
|                                          o             |
| 8         p_1^3 =                       ^ ^        o---o
|           p_1^p_2 =           p_p      /   \       |
|           p_1^p_(p_1)       p<        @     o      @            ((((())())))
|
|                                                    o-o o-o
|                                          o         |   |
| 9         p_2^2 =                       ^          o---o
|           p_(p_1)^2 =         p        /           |
|           p_(p_1)^(p_1)     p<        @            @            ((())((())))
|                               p        ^
|                                         \
|                                          o
|
|                                             o              o---o
|                                            ^               |
|                                           /            o---o
|                                          o             |
| 16        p_1^4 =               p       ^          o---o
|           p_1^(p_1^2) =       p<       /           |
|           p_1^(p_1^p_1)     p<        @            @            (((((())))))
|
o--------------------------------------------------------------------------------

(later)

Expanded version of first table:

o--------------------------------------------------------------------------------
| integer   factorization     riff      r.i.f.f.     rote   -->   in parentheses
|                             k p's     k nodes      2k+1 nodes
o--------------------------------------------------------------------------------
|
| 1         1                 blank     blank        @            blank
|
o--------------------------------------------------------------------------------
|
|                                                    o---o
|                                                    |
| 2         p_1^1             p         @            @            (())
|
o--------------------------------------------------------------------------------
|
|                                                    o---o
|                                                    |
|                                                    o---o
| 3         p_2^1 =                                  |
|           p_(p_1)^1         p_p       @            @            ((())())
|                                        ^
|                                         \
|                                          o
|
|                                                        o---o
|                                          o             |
|                                         ^          o---o
| 4         p_1^2 =                      /           |
|           p_1^p_1           p^p       @            @            (((())))
|
o--------------------------------------------------------------------------------
|
|                                                    o---o
|                                                    |
|                                                    o---o
|                                                    |
| 5         p_3 =                                    o---o
|           p_(p_2) =                                |
|           p_(p_(p_1))       p_p_p     @            @            (((())())())
|                                        ^
|                                         \
|                                          o
|                                           ^
|                                            \
|                                             o
|
|                                                        o-o
|                                                       /
|                                                  o-o o-o
| 6         p_1 p_2 =                               \ /
|           p_1 p_(p_1)       p p_p     @ @          @            (())((())())
|                                          ^
|                                           \
|                                            o
|
|                                                        o---o
|                                                        |
|                                                    o---o
|                                                    |
| 7         p_4 =                                    o---o
|           p_(p_1^2) =                              |
|           p_(p_1^p_1)       p<        @     o      @            ((((())))())
|                               p^p      ^   ^
|                                         \ /
|                                          o
|
|                                                        o---o
|                                                        |
|                                                        o---o
|                                          o             |
| 8         p_1^3 =                       ^ ^        o---o
|           p_1^p_2 =           p_p      /   \       |
|           p_1^p_(p_1)       p<        @     o      @            ((((())())))
|
|                                                    o-o o-o
|                                          o         |   |
| 9         p_2^2 =                       ^          o---o
|           p_(p_1)^2 =         p        /           |
|           p_(p_1)^(p_1)     p<        @            @            ((())((())))
|                               p        ^
|                                         \
|                                          o
|
|                                             o              o---o
|                                            ^               |
|                                           /            o---o
|                                          o             |
| 16        p_1^4 =               p       ^          o---o
|           p_1^(p_1^2) =       p<       /           |
|           p_1^(p_1^p_1)     p<        @            @            (((((())))))
|
o--------------------------------------------------------------------------------

o================================================================================
|
|       p
|     p<        p          p_p         p
|   p<        p<_p       p<        p_p<      p p_p     p_p_p
| p<        p<         p<        p<        p<        p<
|
| 2^16      2^9        2^8       2^7       2^6       2^5
| 65536     512        256       128       64        32
|
o--------------------------------------------------------------------------------
|
|       p
|     p<        p          p_p         p
| p_p<      p_p<_p     p_p<      p_p_p<    p<        p_p_p_p
|                                            p p_p
|
| p_16      p_9        p_8       p_7       p_6       p_5
| 53        23         19        17        13        11
|
o--------------------------------------------------------------------------------
|
|   p^p       p_p        p         p
| p<        p<         p<        p<
|   p         p          p^p       p_p
|
| 3^4       3^3        7^2       5^2
| 81        27         49        25
|
o--------------------------------------------------------------------------------
|
|     p
| p p<      p p<       p^p p_p   p p_p_p
|     p         p^p
|
| 18        14         12        10
|
o================================================================================

Triangle in which k-th row lists natural number
values for the collection of riffs with k nodes.

k | natural numbers n such that |riff(n)| = k
--o------------------------------------------------
0 | 1;
1 | 2;
2 | 3, 4;
3 | 5, 6, 7, 8, 9, 16;
4 | 10, 11, 12, 13, 14, 17, 18, 19, 23, 25, 27,
  | 32, 49, 53, 64, 81, 128, 256, 512, 65536;

The natural number values for the riffs with
at most 3 pts are as follows (@'s are roots):

|                  o       o  o       o
|                  |       ^  |       ^
|                  v       |  v       |
|            o  o  o    o  o  o  o o  o
|            |  ^  |    |  |  ^  | ^  ^
|            v  |  v    v  v  |  v/   |
| Riff:   @; @, @; @, @ @, @, @, @,   @;
|
| Value:  2; 3, 4; 5,  6 , 7, 8, 9,  16;

---------------------------------------------------

1, 2, 3, 4, 5, 6, 7, 8, 9, 16,
10, 11, 12, 13, 14, 17, 18, 19,
23, 25, 27, 32, 49, 53, 64, 81,
128, 256, 512, 65536,

---------------------------------------------------

1; 2; 3, 4; 5, 6, 7, 8, 9, 16;
10, 11, 12, 13, 14, 17, 18, 19,
23, 25, 27, 32, 49, 53, 64, 81,
128, 256, 512, 65536;

---------------------------------------------------

Example of a Raw HTML Table

\(\text{Table 10.} ~~ \text{Relation of Quantifiers to Higher Order Propositions}\)

\(\text{Mnemonic}\!\)	\(\text{Category}\!\)	\(\text{Classical Form}\!\)	\(\text{Alternate Form}\!\)	\(\text{Symmetric Form}\!\)	\(\text{Operator}\!\)
\(\begin{matrix} \mathrm{E} \\ \mathrm{Exclusive} \end{matrix}\)	\(\begin{matrix} \mathrm{Universal} \\ \mathrm{Negative} \end{matrix}\)	\(\mathrm{All} ~ u ~ \mathrm{is} ~ \texttt{(} v \texttt{)}\)		\(\mathrm{No} ~ u ~ \mathrm{is} ~ v\)	\(\texttt{(} \ell_{11} \texttt{)}\)
\(\begin{matrix} \mathrm{A} \\ \mathrm{Absolute} \end{matrix}\)	\(\begin{matrix} \mathrm{Universal} \\ \mathrm{Affirmative} \end{matrix}\)	\(\mathrm{All} ~ u ~ \mathrm{is} ~ v\)		\(\mathrm{No} ~ u ~ \mathrm{is} ~ \texttt{(} v \texttt{)}\)	\(\texttt{(} \ell_{10} \texttt{)}\)
		\(\mathrm{All} ~ v ~ \mathrm{is} ~ u\)	\(\mathrm{No} ~ v ~ \mathrm{is} ~ \texttt{(} u \texttt{)}\)	\(\mathrm{No} ~ \texttt{(} u \texttt{)} ~ \mathrm{is} ~ v\)	\(\texttt{(} \ell_{01} \texttt{)}\)
		\(\mathrm{All} ~ \texttt{(} v \texttt{)} ~ \mathrm{is} ~ u\)	\(\mathrm{No} ~ \texttt{(} v \texttt{)} ~ \mathrm{is} ~ \texttt{(} u \texttt{)}\)	\(\mathrm{No} ~ \texttt{(} u \texttt{)} ~ \mathrm{is} ~ \texttt{(} v \texttt{)}\)	\(\texttt{(} \ell_{00} \texttt{)}\)
		\(\mathrm{Some} ~ \texttt{(} u \texttt{)} ~ \mathrm{is} ~ \texttt{(} v \texttt{)}\)		\(\mathrm{Some} ~ \texttt{(} u \texttt{)} ~ \mathrm{is} ~ \texttt{(} v \texttt{)}\)	\(\ell_{00}\)
		\(\mathrm{Some} ~ \texttt{(} u \texttt{)} ~ \mathrm{is} ~ v\)		\(\mathrm{Some} ~ \texttt{(} u \texttt{)} ~ \mathrm{is} ~ v\)	\(\ell_{01}\)
\(\begin{matrix} \mathrm{O} \\ \mathrm{Obtrusive} \end{matrix}\)	\(\begin{matrix} \mathrm{Particular} \\ \mathrm{Negative} \end{matrix}\)	\(\mathrm{Some} ~ u ~ \mathrm{is} ~ \texttt{(} v \texttt{)}\)		\(\mathrm{Some} ~ u ~ \mathrm{is} ~ \texttt{(} v \texttt{)}\)	\(\ell_{10}\)
\(\begin{matrix} \mathrm{I} \\ \mathrm{Indefinite} \end{matrix}\)	\(\begin{matrix} \mathrm{Particular} \\ \mathrm{Affirmative} \end{matrix}\)	\(\mathrm{Some} ~ u ~ \mathrm{is} ~ v\)		\(\mathrm{Some} ~ u ~ \mathrm{is} ~ v\)	\(\ell_{11}\)