User:Jon Awbrey/SEQUENCES
A061396
Plain Wiki Table
Large Scale
ASCII
Comment
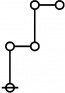
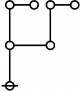
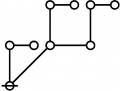
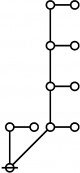
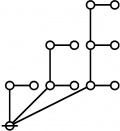
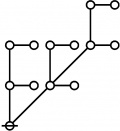
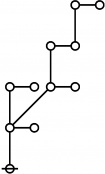
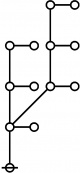
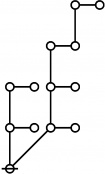
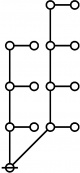
* Table of Rotes and Primal Functions for Positive Integers from 1 to 40
*
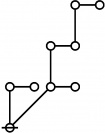
* o-o
* |
* o-o o-o o-o
* | | |
* o-o o-o o-o o-o
* | | | |
* O O O O O
*
* { } 1:1 2:1 1:2 3:1
*
* 1 2 3 4 5
*
*
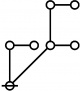
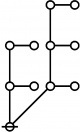
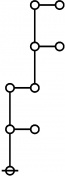
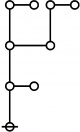
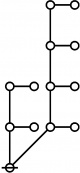
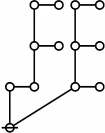
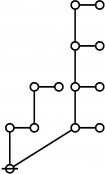
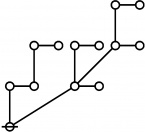
* o-o o-o o-o
* | | |
* o-o o-o o-o o-o o-o o-o
* | | | | | |
* o-o o-o o-o o-o o---o o-o o-o
* | | | | | | |
* O===O O O O O===O
*
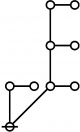
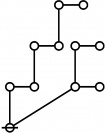
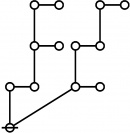
* 1:1 2:1 4:1 1:3 2:2 1:1 3:1
*
* 6 7 8 9 10
*
*
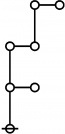
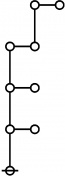
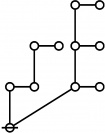
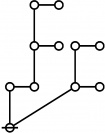
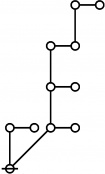
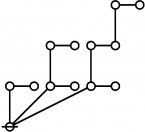
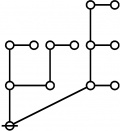
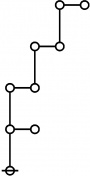
* o-o
* |
* o-o o-o o-o o-o
* | | | |
* o-o o-o o-o o-o o-o o-o o-o o-o
* | | | | | | | |
* o-o o-o o-o o===o-o o-o o-o o-o o-o
* | | | | | | | |
* O O=====O O O===O O===O
*
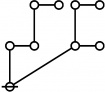
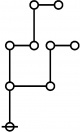
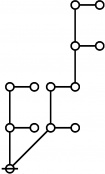
* 5:1 1:2 2:1 6:1 1:1 4:1 2:1 3:1
*
* 11 12 13 14 15
*
*
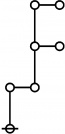
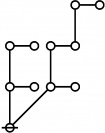
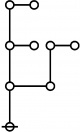
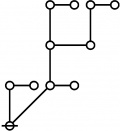
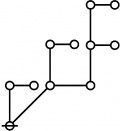
* o-o o-o
* | |
* o-o o-o o-o o-o
* | | | |
* o-o o-o o-o o-o o-o o-o o-o
* | | | | | | |
* o-o o-o o-o o---o o-o o-o o-o
* | | | | | | |
* O O O===O O O=====O
*
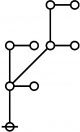
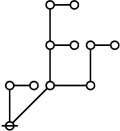
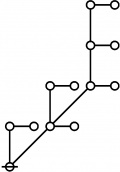
* 1:4 7:1 1:1 2:2 8:1 1:2 3:1
*
* 16 17 18 19 20
*
*
* o-o
* |
* o-o o-o o-o o-o o-o o-o
* | | | | | |
* o-o o-o o-o o---o o-o o-o o-o o-o
* | | | | | | | |
* o-o o-o o-o o-o o-o o-o o-o o---o
* | | | | | | | |
* O===O O===O O O=====O O
*
* 2:1 4:1 1:1 5:1 9:1 1:3 2:1 3:2
*
* 21 22 23 24 25
*
*
* o-o
* |
* o-o o-o o-o o-o o-o
* | | | | |
* o-o o-o o-o o-o o-o o-o o-o o-o o-o o-o
* | | | | | | | | | |
* o-o o===o-o o---o o-o o-o o===o-o o-o o-o o-o
* | | | | | | | | |
* O===O O O=====O O O===O===O
*
* 1:1 6:1 2:3 1:2 4:1 10:1 1:1 2:1 3:1
*
* 26 27 28 29 30
*
*
* o-o
* |
* o-o o-o o-o o-o
* | | | |
* o-o o-o o-o o-o o-o o-o
* | | | | | |
* o-o o-o o-o o-o o-o o-o o-o
* | | | | | | |
* o-o o-o o-o o-o o-o o-o o-o o-o
* | | | | | | | |
* O O O===O O===O O===O
*
* 11:1 1:5 2:1 5:1 1:1 7:1 3:1 4:1
*
* 31 32 33 34 35
*
*
* o-o
* |
* o-o o-o o-o o-o o-o o-o
* | | | | | |
* o-o o-o o-o o-o o-o o-o o-o o-o o-o o-o o-o
* | | | | | | | | | | |
* o-o o---o o=====o-o o-o o-o o-o o===o-o o-o o-o
* | | | | | | | | |
* O=====O O O===O O===O O=====O
*
* 1:2 2:2 12:1 1:1 8:1 2:1 6:1 1:3 3:1
*
* 36 37 38 39 40
*
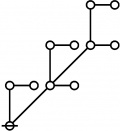
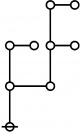
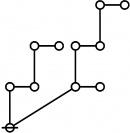
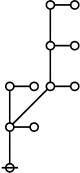
* In these Figures, "extended lines of identity" like o===o
* indicate identified nodes and capital O is the root node.
* The rote height in gammas is found by finding the number
* of graphs of the following shape between the root and one
* of the highest nodes of the tree:
* o--o
* |
* o
* A sequence like this, that can be regarded as a nonnegative integer
* measure on positive integers, may have as many as 3 other sequences
* associated with it. Given that the fiber of a function f at n is all
* the domain elements that map to n, we always have the fiber minimum
* or minimum inverse function and may also have the fiber cardinality
* and the fiber maximum or maximum inverse function. For A109301, the
* minimum inverse is A007097(n) = min {k : A109301(k) = n}, giving the
* first positive integer whose rote height is n, the fiber cardinality
* is A109300, giving the number of positive integers of rote height n,
* while the maximum inverse, g(n) = max {k : A109301(k) = n}, giving
* the last positive integer whose rote height is n, has the following
* initial terms: g(0) = { } = 1, g(1) = 1:1 = 2, g(2) = 1:2 2:2 = 36,
* while g(3) = 1:36 2:36 3:36 4:36 6:36 9:36 12:36 18:36 36:36 =
* (2 3 5 7 13 23 37 61 151)^36 = 21399271530^36 = roughly
* 7.840858554516122655953405327738 x 10^371.
Example
* Writing (prime(i))^j as i:j, we have:
* 802701 = 2:2 8638:1
* 8638 = 1:1 4:1 113:1
* 113 = 30:1
* 30 = 1:1 2:1 3:1
* 4 = 1:2
* 3 = 2:1
* 2 = 1:1
* 1 = { }
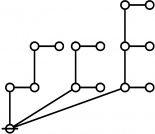
* So rote(802701) is the graph:
*
* o-o
* |
* o-o o-o
* | |
* o-o o-o o-o o-o
* | | | |
* o-o o===o===o-o
* | |
* o-o o-o o-o o-o o---------o
* | | | | |
* o---o o===o=====o---------o
* | |
* O=======O
*
* Therefore rhig(802701) = 6.
A111795
JPEG
|
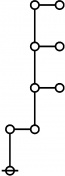
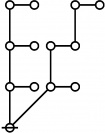
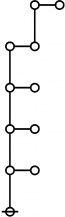
\(\begin{array}{l} \varnothing \\ 1 \end{array}\) |
\(\begin{array}{l} 1\!:\!1 \\ 2 \end{array}\) |
\(\begin{array}{l} 2\!:\!1 \\ 3 \end{array}\) |
\(\begin{array}{l} 1\!:\!2 \\ 4 \end{array}\) |
\(\begin{array}{l} 3\!:\!1 \\ 5 \end{array}\) |
|
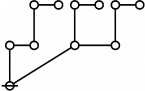
\(\begin{array}{l} 4\!:\!1 \\ 7 \end{array}\) |
\(\begin{array}{l} 1\!:\!3 \\ 8 \end{array}\) |
\(\begin{array}{l} 5\!:\!1 \\ 11 \end{array}\) |
\(\begin{array}{l} 1\!:\!4 \\ 16 \end{array}\) |
\(\begin{array}{l} 7\!:\!1 \\ 17 \end{array}\) |
|
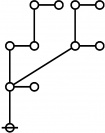
\(\begin{array}{l} 8\!:\!1 \\ 19 \end{array}\) |
\(\begin{array}{l} 11\!:\!1 \\ 31 \end{array}\) |
\(\begin{array}{l} 1\!:\!5 \\ 32 \end{array}\) |
\(\begin{array}{l} 16\!:\!1 \\ 53 \end{array}\) |
\(\begin{array}{l} 17\!:\!1 \\ 59 \end{array}\) |
ASCII
Example
* Tables of Rotes and Primal Codes for a(1) to a(9)
*
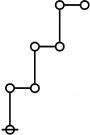
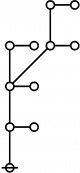
* o-o
* |
* o-o o-o o-o o-o o-o
* | | | | |
* o-o o-o o-o o-o o-o o-o o-o
* | | | | | | |
* o-o o-o o-o o-o o-o o-o o-o o-o
* | | | | | | | |
* O O O O O O O O O
*
* { } 1:1 2:1 1:2 3:1 4:1 1:3 5:1 1:4
*
* 1 2 3 4 5 7 8 11 16
*
A111800
TeX + JPEG
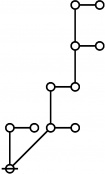
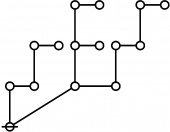
\(\text{Writing}~ \operatorname{prime}(i)^j ~\text{as}~ i\!:\!j, 2500 = 4 \cdot 625 = 2^2 5^4 = 1\!:\!2 ~~ 3\!:\!4 ~\text{has the following rote:}\)
|
\(\text{So}~ a(2500) = a(1\!:\!2 ~~ 3\!:\!4) = a(1) + a(2) + a(3) + a(4) + 1 = 1 + 3 + 5 + 5 + 1 = 15.\)
ASCII
Example
* Writing prime(i)^j as i:j and using equal signs between identified nodes:
* 2500 = 4 * 625 = 2^2 5^4 = 1:2 3:4 has the following rote:
*
* o-o o-o
* | |
* o-o o-o o-o
* | | |
* o-o o---o
* | |
* O=====O
*
* So a(2500) = a(1:2 3:4) = a(1)+a(2)+a(3)+a(4)+1 = 1+3+5+5+1 = 15.