Directory:Punzhu Puzzles/Pathway
Pathway aka Connect-The-Dot
Pathway puzzles, or connect-the-dot puzzles, are variations on a maze game. These puzzles are "simply connected" mazes, meaning these puzzles have no breaks or detached walls to disrupt the Pathway from completely connecting to itself.
Most mazes have parallel sides in which a solver travels until a block is met. The solver must retrace his steps at this point and try another trail until the solver ultimately reaches the end of the maze.
The first mazes, or labyrinths as the Greeks and Romans called them, were blind alleys and passageways that made exiting difficult. Later, mazes were integrated into gardens using high hedges as walls for the pathways. Modern mazes in Japan use movable wooden walls so that the configuration can be easily, and ever so often, changed.
A computer chip, motherboard, software, and other computer devices also work on a maze principle. An electron A travels along path B until it reaches end C or wall D. If it reaches wall D it is diverted to another path until it ultimately reaches end C.
Rush hour traffic and trying to find the quickest, or shortest, route to your destination is another style of maze.
Our Pathway puzzles don't use the typical "walled" maze but instead are based upon the wall-less connect-the-dot puzzle in which a shape is constructed when a solver connects the dots properly.
To direct a solver along the pathway we use the numbers 0 to 3 as guides along a square. Each Pathway puzzle contains a series of squares, like a diagramless crossword puzzle, and a solver chooses one of the four sides as the Pathway using the numbers as guides.
A zero means there are zero points along the square, one means one of the four sides is a pathway, two means two of the four sides are pathways, and three means three of the four sides are pathways.
No Pathway line may cross over another Pathway line, nor may a Pathway line cross back upon itself.
To design a Pathway puzzle we first set the number of squares we want across and down. Then we create the line that becomes the Pathway. Finally, the number guides are entered and the existing line removed so that only the numbers and the squares remain.
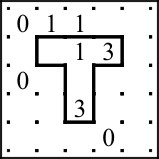
Here is an example of a completed Pathway puzzle with an easy level of difficulty:
Not all corners of the solution Pathway (the letter T in this example) have numbers. As you can see from the example above there is no number three for the left corner of the letter T. This is where your deductive abilities come into play and is a function of designing interesting (and challenging) Pathway puzzles.
Free Puzzle Magazines
Punzhu makes Pathway and other puzzle magazines available for free downloading when you click on the "Free Puzzle Magazines" link on our web site.
Registration is NOT required to access our magazines.
- Directory:Punzhu Puzzles