Directory:Jon Awbrey/MathJax Problems
Variations on a theme of transitivity
The next Example is extremely important, and for reasons that reach well beyond the level of propositional calculus as it is ordinarily conceived. But it's slightly tricky to get all of the details right, so it will be worth taking the trouble to look at it from several different angles and as it appears in diverse frames, genres, or styles of representation.
In discussing this Example, it is useful to observe that the implication relation indicated by the propositional form \(x \Rightarrow y\!\) is equivalent to an order relation \(x \le y\!\) on the boolean values \(0, 1 \in \mathbb{B},\!\) where \(0\!\) is taken to be less than \(1.\!\)
| • | Example 2. Transitivity | ||
| Information Reducing Inference | |||
|
\(\begin{array}{l} ~ p \le q \\ ~ q \le r \\ \overline{~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~} \\ ~ p \le r \end{array}\) | |||
| Information Preserving Inference | |||
|
\(\begin{array}{l} ~ p \le q \\ ~ q \le r \\ \overline{\underline{~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~}} \\ ~ p \le q \le r \end{array}\) | |||
In stating the information-preserving analogue of transitivity, I have taken advantage of a common idiom in the use of order relation symbols, one that represents their logical conjunction by way of a concatenated syntax. Thus, \(p \le q \le r\!\) means \(p \le q ~\mathrm{and}~ q \le r.\!\) The claim that this 3-adic order relation holds among the three propositions \(p, q, r\!\) is a stronger claim — conveys more information — than the claim that the 2-adic relation \(p \le r\!\) holds between the two propositions \(p\!\) and \(r.\!\)
To study the differences between these two versions of transitivity within what is locally a familiar context, let's view the propositional forms involved as if they were elementary cellular automaton rules, resulting in the following Table.
|
\(\mathcal{L}_1\!\) \(\text{Decimal}\!\) |
\(\mathcal{L}_2\!\) \(\text{Binary}\!\) |
\(\mathcal{L}_3\!\) \(\text{Vector}\!\) |
\(\mathcal{L}_4\!\) \(\text{Cactus}\!\) |
\(\mathcal{L}_5\!\) \(\text{Order}\!\) |
| \(p\colon\!\) | \(1~1~1~1~0~0~0~0\!\) | |||
| \(q\colon\!\) | \(1~1~0~0~1~1~0~0\!\) | |||
| \(r\colon\!\) | \(1~0~1~0~1~0~1~0\!\) | |||
|
\(\begin{matrix} f_{207} \\[4pt] f_{187} \\[4pt] f_{175} \\[4pt] f_{139} \end{matrix}\) |
\(\begin{matrix} f_{11001111} \\[4pt] f_{10111011} \\[4pt] f_{10101111} \\[4pt] f_{10001011} \end{matrix}\) |
\(\begin{matrix} 1~1~0~0~1~1~1~1 \\[4pt] 1~0~1~1~1~0~1~1 \\[4pt] 1~0~1~0~1~1~1~1 \\[4pt] 1~0~0~0~1~0~1~1 \end{matrix}\) |
\(\begin{matrix} \texttt{(} p \texttt{ (} q \texttt{))} \\[4pt] \texttt{(} q \texttt{ (} r \texttt{))} \\[4pt] \texttt{(} p \texttt{ (} r \texttt{))} \\[4pt] \texttt{(} p \texttt{ (} q \texttt{)) (} q \texttt{ (} r \texttt{))} \end{matrix}\) |
\(\begin{matrix} p \le q \\[4pt] q \le r \\[4pt] p \le r \\[4pt] p \le q \le r \end{matrix}\) |
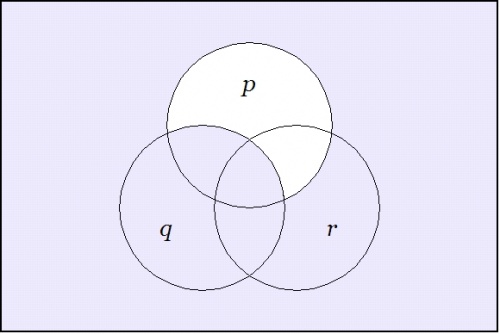
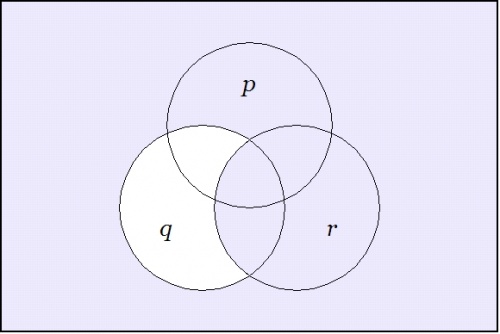
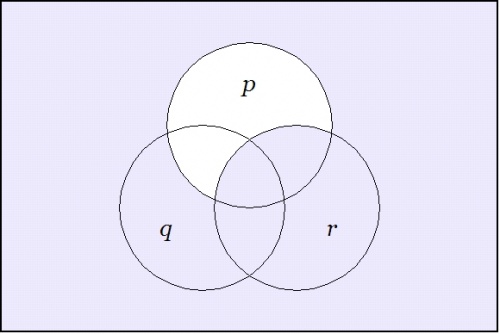
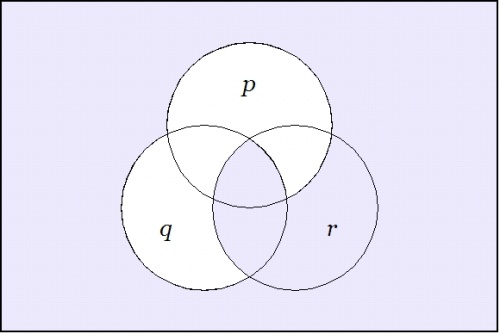
Taking up another angle of incidence by way of extra perspective, let us now reflect on the venn diagrams of our four propositions.
Among other things, these images make it visually obvious that the constraint on the three boolean variables \(p, q, r\!\) that is indicated by asserting either of the forms \(\texttt{(} p \texttt{(} q \texttt{))(} q \texttt{(} r \texttt{))}\!\) or \(p \le q \le r\!\) implies a constraint on the two boolean variables \(p, r\!\) that is indicated by either of the forms \(\texttt{(} p \texttt{(} r \texttt{))}\!\) or \(p \le r,\!\) but that it imposes additional constraints on these variables that are not captured by the illative conclusion.
One way to view a proposition \(f : \mathbb{B}^k \to \mathbb{B}\!\) is to consider its fiber of truth, \(f^{-1}(1) \subseteq \mathbb{B}^k,\!\) and to regard it as a \(k\!\)-adic relation \(L \subseteq \mathbb{B}^k.\!\)
By way of general definition, the fiber of a function \(f : X \to Y\!\) at a given value \(y\!\) of its co-domain \(Y\!\) is the antecedent (also known as the inverse image or pre-image) of \(y\!\) under \(f.\!\) This is a subset, possibly empty, of the domain \(X,\!\) notated as \(f^{-1}(y) \subseteq X.\!\)
In particular, if \(f\!\) is a proposition \(f : X \to \mathbb{B},\!\) then the fiber of truth \(f^{-1}(1)\!\) is the subset of \(X\!\) that is indicated by the proposition \(f.\!\) Whenever we assert a proposition \(f : X \to \mathbb{B},\!\) we are saying that what it indicates is all that happens to be the case in the relevant universe of discourse \(X.\!\) Because the fiber of truth is used so often in logical contexts, it is convenient to define the more compact notation \([| f |] = f^{-1}(1).\!\)
Using this panoply of notions and notations, we may treat the fiber of truth of each proposition \(f : \mathbb{B}^3 \to \mathbb{B}\!\) as if it were a relational data table of the shape \(\{ (p, q, r) \} \subseteq \mathbb{B}^3,\!\) where the triples \((p, q, r)\!\) are bit-tuples indicated by the proposition \(f.\!\)
Thus we obtain the following four relational data tables for the propositions that we are looking at in Example 2.
| \(p\!\) | \(q\!\) | \(r\!\) |
| \(0\!\) | \(0\!\) | \(0\!\) |
| \(0\!\) | \(0\!\) | \(1\!\) |
| \(0\!\) | \(1\!\) | \(0\!\) |
| \(0\!\) | \(1\!\) | \(1\!\) |
| \(1\!\) | \(1\!\) | \(0\!\) |
| \(1\!\) | \(1\!\) | \(1\!\) |
| \(p\!\) | \(q\!\) | \(r\!\) |
| \(0\!\) | \(0\!\) | \(0\!\) |
| \(0\!\) | \(0\!\) | \(1\!\) |
| \(0\!\) | \(1\!\) | \(1\!\) |
| \(1\!\) | \(0\!\) | \(0\!\) |
| \(1\!\) | \(0\!\) | \(1\!\) |
| \(1\!\) | \(1\!\) | \(1\!\) |
| \(p\!\) | \(q\!\) | \(r\!\) |
| \(0\!\) | \(0\!\) | \(0\!\) |
| \(0\!\) | \(0\!\) | \(1\!\) |
| \(0\!\) | \(1\!\) | \(0\!\) |
| \(0\!\) | \(1\!\) | \(1\!\) |
| \(1\!\) | \(0\!\) | \(1\!\) |
| \(1\!\) | \(1\!\) | \(1\!\) |
| \(p\!\) | \(q\!\) | \(r\!\) |
| \(0\!\) | \(0\!\) | \(0\!\) |
| \(0\!\) | \(0\!\) | \(1\!\) |
| \(0\!\) | \(1\!\) | \(1\!\) |
| \(1\!\) | \(1\!\) | \(1\!\) |
In the medium of these unassuming examples, we begin to see the activities of logical inference and methodical inquiry as information clarifying operations.
First, we drew a distinction between information preserving and information reducing processes and we noted the related distinction between equational and implicational inferences. I will use the acronyms EROI and IROI, respectively, for the equational and implicational analogues of the various rules of inference.
For example, we considered the brands of information fusion that are involved in a couple of standard rules of inference, taken in both their equational and their illative variants.
In particular, let us assume that we begin from a state of uncertainty about the universe of discourse \(X = \mathbb{B}^3\!\) that is standardly represented by a uniform distribution \(u : X \to \mathbb{B}\!\) such that \(u(x) = 1\!\) for all \(x\!\) in \(X,\!\) in short, by the constant proposition \(1 : X \to \mathbb{B}.\!\) This amounts to the maximum entropy sign state (MESS). As a measure of uncertainty, let us use either the multiplicative measure given by the cardinality of \(X,\!\) commonly notated as \(|X|,\!\) or else the additive measure given by \({\log_2 |X|}.\!\) In this frame we have \({|X| = 8}\!\) and \({\log_2 |X| = 3},\!\) to wit, 3 bits of doubt.
Let us now consider the various rules of inference for transitivity in the light of their performance as information-developing actions.
| • | Transitive Law (Implicational Inference) | ||
|
\(\begin{array}{l} ~ p \le q \\ ~ q \le r \\ \overline{~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~} \\ ~ p \le r \end{array}\) | |||
| • | By itself, the information \(p \le q\!\) would reduce our uncertainty from \(\log 8\!\) bits to \(\log 6\!\) bits. | ||
| • | By itself, the information \(q \le r\!\) would reduce our uncertainty from \(\log 8\!\) bits to \(\log 6\!\) bits. | ||
| • | By itself, the information \(p \le r\!\) would reduce our uncertainty from \(\log 8\!\) bits to \(\log 6\!\) bits. | ||
In this situation the application of the implicational rule of inference for transitivity to the information \(p \le q\!\) and the information \(q \le r\!\) to get the information \(p \le r\!\) does not increase the measure of information beyond what any one of the three propositions has independently of the other two. In a sense, then, the implicational rule operates only to move the information around without changing its measure in the slightest bit.
| • | Transitive Law (Equational Inference) | ||
|
\(\begin{array}{l} ~ p \le q \\ ~ q \le r \\ \overline{\underline{~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~}} \\ ~ p \le q \le r \end{array}\) | |||
| • | The contents and the measures of information that are associated with the propositions \(p \le q\!\) and \(q \le r\!\) are the same as before. | ||
| • | On its own, the information \(p \le q \le r\!\) would reduce our uncertainty from log(8) = 3 bits to log(4) = 2 bits, a reduction of 1 bit. | ||
These are just some of the initial observations that can be made about the dimensions of information and uncertainty in the conduct of logical inference, and there are many issues to be taken up as we get to the thick of it. In particular, we are taking propositions far too literally at the outset, reading their spots at face value, as it were, without yet considering their species character as fallible signs.
For ease of reference in the rest of this discussion, let us refer to the propositional form \(f : \mathbb{B}^3 \to \mathbb{B}\!\) such that \(f(p, q, r) = f_{139}(p, q, r) = \texttt{(} p \texttt{(} q \texttt{))(} q \texttt{(} r \texttt{))}\!\) as the syllogism map, written as \(\mathrm{syll} : \mathbb{B}^3 \to \mathbb{B},\!\) and let us refer to its fiber of truth \([| \mathrm{syll} |] = \mathrm{syll}^{-1}(1)\!\) as the syllogism relation, written as \(\mathrm{Syll} \subseteq \mathbb{B}^3.\!\) Table 60 shows \(\mathrm{Syll}\!\) as a relational dataset.
| \(p\!\) | \(q\!\) | \(r\!\) |
| \(0\!\) | \(0\!\) | \(0\!\) |
| \(0\!\) | \(0\!\) | \(1\!\) |
| \(0\!\) | \(1\!\) | \(1\!\) |
| \(1\!\) | \(1\!\) | \(1\!\) |
One of the first questions that we might ask about a 3-adic relation, in this case \(\mathrm{Syll},\!\) is whether it is determined by its 2-adic projections. I will illustrate what this means in the present case.
Table 61 repeats the relation \(\mathrm{Syll}\!\) in the first column, listing its 3-tuples in bit-string form, followed by the 2-adic or planar projections of \(\mathrm{Syll}\!\) in the next three columns. For instance, \(\mathrm{Syll}_{pq}\!\) is the 2-adic projection of \(\mathrm{Syll}\!\) on the \(pq\!\) plane that is arrived at by deleting the \(r\!\) column and counting each 2-tuple that results just one time. Likewise, \(\mathrm{Syll}_{pr}\!\) is obtained by deleting the \(q\!\) column and \(\mathrm{Syll}_{qr}\!\) is derived by deleting the \(p\!\) column, ignoring whatever duplicate pairs may result. The final row of the right three columns gives the propositions of the form \(f : \mathbb{B}^2 \to \mathbb{B}\!\) that indicate the 2-adic relations that result from these projections.
| \(\mathrm{Syll}\!\) | \(\mathrm{Syll}_{pq}\!\) | \(\mathrm{Syll}_{pr}\!\) | \(\mathrm{Syll}_{qr}\!\) |
|
\(\begin{matrix} 0~0~0 \\ 0~0~1 \\ 0~1~1 \\ 1~1~1 \end{matrix}\) |
\(\begin{matrix} 0~0 \\ 0~0 \\ 0~1 \\ 1~1 \end{matrix}\) |
\(\begin{matrix} 0~0 \\ 0~1 \\ 0~1 \\ 1~1 \end{matrix}\) |
\(\begin{matrix} 0~0 \\ 0~1 \\ 1~1 \\ 1~1 \end{matrix}\) |
| \(p \le q \le r\!\) | \(\texttt{(} p \texttt{ (} q \texttt{))}\!\) | \(\texttt{(} p \texttt{ (} r \texttt{))}\!\) | \(\texttt{(} q \texttt{ (} r \texttt{))}\!\) |
Let us make the simple observation that taking a projection, in our framework, deleting a column from a relational table, is like taking a derivative in differential calculus. What it means is that our attempt to return to the integral from whence the derivative was derived will in general encounter an indefinite variation on account of the circumstance that real information may have been destroyed by the derivation.
One will find that some relations can be reconstructed from various types of derivatives and projections, others cannot. The reconstuctible relations are said to be reducible to the types of reductive data in question, while the others are said to be irreducible with respect to those means.
The analogies between derivation, differentiation, implication, projection, and others sorts of information reducing operation will undergo extensive development in the remainder and sequel of the present discussion.
We were in the middle of discussing the relationships between information preserving rules of inference and information destroying rules of inference — folks of a 3-basket philosophical bent will no doubt be asking, "And what of information creating rules of inference?", but there I must wait for some signs of enlightenment, desiring not to tread on the rules of that succession.
The contrast between the information destroying and the information preserving versions of the transitive rule of inference led us to examine the relationships among several boolean functions, namely, those that qualify locally as the elementary cellular automata rules \(f_{139}, f_{175}, f_{187}, f_{207}.\!\)
The function \(f_{139} : \mathbb{B}^3 \to \mathbb{B}\!\) and its fiber \([| f_{139} |] \subseteq \mathbb{B}^3\!\) appeared to be key to many structures in this setting, and so I singled them out under the new names of \(\mathrm{syll} : \mathbb{B}^3 \to \mathbb{B}\!\) and \(\mathrm{Syll} \subseteq \mathbb{B}^3,\!\) respectively.
Managing the conceptual complexity of our considerations at this juncture put us in need of some conceptual tools that I broke off to develop in my notes on "Reductions Among Relations". The main items that we need right away from that thread are the definitions of relational projections and their inverses, the tacit extensions.
But the more I survey the problem setting the more it looks like we need better ways to bring our visual intuitions to play on the scene, and so let us next lay out some visual schemata that are designed to facilitate that.
Figure 62 shows the familiar picture of a boolean 3-cube, where the points of \(\mathbb{B}^3\!\) are coordinated as bit strings of length three. Looking at the functions \(f : \mathbb{B}^3 \to \mathbb{B}\!\) and the relations \(L \subseteq \mathbb{B}^3\!\) on this pattern, one views the construction of either type of object as a matter of coloring the nodes of the 3-cube with choices from a pair of colors that stipulate which points are in the relation \({L = [| f |]}\!\) and which points are out of it. Bowing to common convention, we may use the color \(1\!\) for points that are in a given relation and the color \(0\!\) for points that are out of the same relation. However, it will be more convenient here to indicate the former case by writing the coordinates in the place of the node and to indicate the latter case by plotting the point as an unlabeled node "o".
o-------------------------------------------------o | | | 111 | | /|\ | | / | \ | | / | \ | | / | \ | | / | \ | | / | \ | | / | \ | | 110 101 011 | | |\ / \ /| | | | \ / \ / | | | | \ / \ / | | | | \ / | | | | / \ / \ | | | | / \ / \ | | | |/ \ / \| | | 100 010 001 | | \ | / | | \ | / | | \ | / | | \ | / | | \ | / | | \ | / | | \|/ | | 000 | | | o-------------------------------------------------o Figure 62. Boolean 3-Cube B^3 |
(62) |
Table 63 shows the 3-adic relation \(\mathrm{Syll} \subseteq \mathbb{B}^3\!\) again, and Figure 64 shows it plotted on a 3-cube template.
Table 63. Syll c B^3 o-----------------------o | p q r | o-----------------------o | 0 0 0 | | 0 0 1 | | 0 1 1 | | 1 1 1 | o-----------------------o |
(63) |
o-------------------------------------------------o | | | 111 | | /|\ | | / | \ | | / | \ | | / | \ | | / | \ | | / | \ | | / | \ | | o o 011 | | |\ / \ /| | | | \ / \ / | | | | \ / \ / | | | | \ / | | | | / \ / \ | | | | / \ / \ | | | |/ \ / \| | | o o 001 | | \ | / | | \ | / | | \ | / | | \ | / | | \ | / | | \ | / | | \|/ | | 000 | | | o-------------------------------------------------o Figure 64. Triadic Relation Syll c B^3 |
(64) |
We return once more to the plane projections of \(\mathrm{Syll} \subseteq \mathbb{B}^3.\!\)
Table 65. Syll c B^3 o-----------------------o | p q r | o-----------------------o | 0 0 0 | | 0 0 1 | | 0 1 1 | | 1 1 1 | o-----------------------o |
(65) |
Table 66. Dyadic Projections of Syll o-----------o o-----------o o-----------o | Syll_12 | | Syll_13 | | Syll_23 | o-----------o o-----------o o-----------o | p q | | p r | | q r | o-----------o o-----------o o-----------o | 0 0 | | 0 0 | | 0 0 | | 0 1 | | 0 1 | | 0 1 | | 1 1 | | 1 1 | | 1 1 | o-----------o o-----------o o-----------o | (p (q)) | | (p (r)) | | (q (r)) | o-----------o o-----------o o-----------o |
(66) |
In showing the 2-adic projections of a 3-adic relation \(L \subseteq \mathbb{B}^3,\!\) I will translate the coordinates of the points in each relation to the plane of the projection, there dotting out with a dot "." the bit of the bit string that is out of place on that plane.
Figure 67 shows \(\mathrm{Syll}\!\) and its three 2-adic projections:
o-------------------------------------------------o | | | 111 | | /|\ | | / | \ | | / | \ | | / | \ | | / | \ | | / | \ | | / | \ | | o o 011 | | |\ / \ /| | | | \ / \ / | | | | \ / \ / | | | | \ / | | | | / \ / \ | | | | / \ / \ | | | |/ \ / \| | | o o 001 | | \ | / | | 11. \ | / .11 | | |\ \ | / /| | | | \ \ | / / | | | | \ \ | / / | | | | \ \ | / / | | | | \ \|/ / | | | | \ 000 / | | | | \ / | | | o 01. o .01 | | \ | | / | | \ | | / | | \ | | / | | \ | 1.1 | / | | \ | / \ | / | | \ | / \ | / | | \| / \ |/ | | 00. / \ .00 | | / \ | | / \ | | / \ | | o 0.1 | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | 0.0 | | | o-------------------------------------------------o Figure 67. Syll c B^3 and its Dyadic Projections |
(67) |
We now compute the tacit extensions of the 2-adic projections of \(\mathrm{Syll},\!\) alias \(f_{139},\!\) and this makes manifest its relationship to the other functions and fibers, namely, \(f_{175}, f_{187}, f_{207}.\!\)
Table 68. Syll c B^3 o-----------------------o | p q r | o-----------------------o | 0 0 0 | | 0 0 1 | | 0 1 1 | | 1 1 1 | o-----------------------o |
(68) |
Table 69. Dyadic Projections of Syll o-----------o o-----------o o-----------o | Syll_12 | | Syll_13 | | Syll_23 | o-----------o o-----------o o-----------o | p q | | p r | | q r | o-----------o o-----------o o-----------o | 0 0 | | 0 0 | | 0 0 | | 0 1 | | 0 1 | | 0 1 | | 1 1 | | 1 1 | | 1 1 | o-----------o o-----------o o-----------o | (p (q)) | | (p (r)) | | (q (r)) | o-----------o o-----------o o-----------o |
(69) |
Table 70. Tacit Extensions of Projections of Syll o---------------o o---------------o o---------------o | te(Syll_12) | | te(Syll_13) | | te(Syll_23) | o---------------o o---------------o o---------------o | p q r | | p q r | | p q r | o---------------o o---------------o o---------------o | 0 0 0 | | 0 0 0 | | 0 0 0 | | 0 0 1 | | 0 1 0 | | 1 0 0 | | 0 1 0 | | 0 0 1 | | 0 0 1 | | 0 1 1 | | 0 1 1 | | 1 0 1 | | 1 1 0 | | 1 0 1 | | 0 1 1 | | 1 1 1 | | 1 1 1 | | 1 1 1 | o---------------o o---------------o o---------------o | [| (p (q)) |] | | [| (p (r)) |] | | [| (q (r)) |] | o---------------o o---------------o o---------------o | [| f_207 |] | | [| f_175 |] | | [| f_187 |] | o---------------o o---------------o o---------------o |
(70) |
o-------------------------------------------------o | | | 111 | | /|\ | | / | \ | | / | \ | | / | \ | | / | \ | | / | \ | | / | \ | | 110 o 011 | | |\ / \ /| | | | \ / \ / | | | | \ / \ / | | | | \ / | | | | / \ / \ | | | | / \ / \ | | | |/ \ / \| | | o 010 001 | | \ | / | | 11. \ | / | | |\ \ | / | | | \ \ | / | | | \ \ | / | | | \ \ | / | | | \ \|/ | | | \ 000 | | | \ | | o 01. | | \ | | | \ | | | \ | | | \ | | | \ | | | \ | | | \| | | 00. | | | o-------------------------------------------------o Figure 71. Tacit Extension te_12_3 (Syll_12) |
(71) |
o-------------------------------------------------o | | | 111 | | /|\ | | / | \ | | / | \ | | / | \ | | / | \ | | / | \ | | / | \ | | o 101 011 | | |\ / \ /| | | | \ / \ / | | | | \ / \ / | | | | \ / | | | | / \ / \ | | | | / \ / \ | | | |/ \ / \| | | o 010 001 | | \ | / | | \ | / | | \ | / | | \ | / | | \ | / | | \ | / | | \|/ | | 000 | | | | | | 1.1 | | / \ | | / \ | | / \ | | / \ | | / \ | | / \ | | / \ | | o 0.1 | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | 0.0 | | | o-------------------------------------------------o Figure 72. Tacit Extension te_13_2 (Syll_13) |
(72) |
o-------------------------------------------------o | | | 111 | | /|\ | | / | \ | | / | \ | | / | \ | | / | \ | | / | \ | | / | \ | | o 101 011 | | |\ / \ /| | | | \ / \ / | | | | \ / \ / | | | | \ / | | | | / \ / \ | | | | / \ / \ | | | |/ \ / \| | | 100 o 001 | | \ | / | | \ | / .11 | | \ | / /| | | \ | / / | | | \ | / / | | | \ | / / | | | \|/ / | | | 000 / | | | / | | | o .01 | | | / | | | / | | | / | | | / | | | / | | | / | | |/ | | .00 | | | o-------------------------------------------------o Figure 73. Tacit Extension te_23_1 (Syll_23) |
(73) |
The reader may wish to contemplate Figure 74 and use it to verify the following two facts:
|
\(\begin{array}{lcc} \mathrm{Syll} & = & \mathrm{te}(\mathrm{Syll}_{12}) \cap \mathrm{te}(\mathrm{Syll}_{23}) \\[6pt] \mathrm{Syll}_{13} & = & \mathrm{Syll}_{12} \circ \mathrm{Syll}_{23} \end{array}\) |
o-------------------------------------------------o | | | * | | /|\ | | / | \ | | / | \ | | / | \ | | / | \ | | / | \ | | / | \ | | o o * | | /|\ / \ /|\ | | / | \ / \ / | \ | | / | \ / \ / | \ | | / | \ / | \ | | / | / \ / \ | \ | | / | / \ / \ | \ | | / |/ \ / \| \ | | / o o * \ | | / \ /| / \ \ | | * \ / | / \ * | | |\ \ / | / \ /| | | | \ / | / \ / | | | | \ / \ | / \ / | | | | \ / \ | / / | | | | \ / \|/ / \ | | | | \ / * / \ | | | | \ / / \ / \| | | o * / \ o * | | \ | / \ | / | | \ | / \ | / | | \ | / \ | / | | \ | / * \ | / | | \ | / / \ \ | / | | \ | / / \ \ | / | | \|/ / \ \|/ | | * / \ * | | / \ | | / \ | | / \ | | o * | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | * | | | o-------------------------------------------------o Figure 74. Syll = te(Syll_12) |^| te(Syll_23) |
(74) |
I don't know about you, but I am still puzzled by all of thus stuff, that is to say, by the entanglements of composition and projection and their relationship to the information processing properties of logical inference rules. What I lack is a single picture that could show me all of the pieces and make the pattern of their informational relationships clear.
In accord with my experimental way, I will stick with the case of transitive inference until I have pinned it down thoroughly, but of course the real interest is much more general than that.
At first sight, the relationships seem easy enough to write out. Figure 75 shows how the various logical expressions are related to each other: The expressions \({}^{\backprime\backprime} \texttt{(} p \texttt{ (} q \texttt{))} {}^{\prime\prime}\!\) and \({}^{\backprime\backprime} \texttt{(} q \texttt{ (} r \texttt{))} {}^{\prime\prime}\!\) are conjoined in a purely syntactic fashion — much in the way that one might compile a theory from axioms without knowing what either the theory or the axioms were about — and the best way to sum up the state of information implicit in taking them together is just the expression \({}^{\backprime\backprime} \texttt{(} p \texttt{ (} q \texttt{)) (} q \texttt{ (} r \texttt{))}{}^{\prime\prime}\!\) that would the canonical result of an equational or reversible rule of inference. From that equational inference, one might arrive at the implicational inference \({}^{\backprime\backprime} \texttt{(} p \texttt{ (} r \texttt{))} {}^{\prime\prime}\!\) by the most conventional implication.
o-------------------o o-------------------o
| | | |
| q | | r |
| o | | o |
| | | | | |
| p o | | q o |
| | | | | |
| @ | | @ |
| | | |
o-------------------o o-------------------o
| (p (q)) | | (q (r)) |
o-------------------o o-------------------o
| f_207 | | f_187 |
o---------o---------o o---------o---------o
\ /
\ Conjunction /
\ /
v v
o-------------------o
| |
| |
| |
| q r |
| o o |
| | | |
| p o o q |
| \ / |
| @ |
| |
o-------------------o
| (p (q)) (q (r)) |
o-------------------o
| f_139 |
o---------o---------o
|
Implication
|
v
o---------o---------o
| |
| r |
| o |
| | |
| p o |
| | |
| @ |
| |
o-------------------o
| (p (r)) |
o-------------------o
| f_175 |
o-------------------o
Figure 75. Expressive Aspects of Transitive Inference
|
Most of the customary names for this type of process have turned out to have misleading connotations, and so I will experiment with calling it the expressive aspect of the various rules for transitive inference, simply to emphasize the fact that rules can be given for it that operate solely on signs and expressions, without necessarily needing to look at the objects that are denoted by these signs and expressions.
In the way of many experiments, the word expressive does not seem to work for what I wanted to say here, since we too often use it to suggest something that expresses an object or a purpose, and I wanted it to imply what is purely a matter of expression, shorn of consideration for anything objective. Aside from coining a word like ennotative, some other options would be connotative, hermeneutic, semiotic, syntactic — each of which works in some range of interpretation but fails in others. Let's try formulaic.
Despite how simple the formulaic aspects of transitive inference might appear on the surface, there are problems that wait for us just beneath the syntactic surface, as we quickly discover if we turn to considering the kinds of objects, abstract and concrete, that these formulas are meant to denote, and all the more so if we try to do this in a context of computational implementations, where the "interpreters" to be addressed take nothing on faith. Thus we engage the denotative semantics or the model theory of these extremely simple programs that we call propositions.
Figure 76 is an attempt to outline the model-theoretic relationships that are involved in our study of transitive inference. A couple of alternative notations are introduced in this Table:
| The forms \(X:Y:Z\!\) and \(x:y:z\!\) are used as alternative notations for the cartesian product \(X \times Y \times Z\!\) and the tuple \((x, y, z),\!\) respectively. |
| In situations where we have products like \(X:Y:Z\!\) with \(X = Y = Z = \mathbb{B},\!\) and relations like \({L \subseteq X:Y},\!\) \({M \subseteq X:Z},\!\) \({N \subseteq Y:Z},\!\) the forms \({L \subseteq \mathbb{B}:\mathbb{B}:-},\!\) \({M \subseteq \mathbb{B}:-:\mathbb{B}},\!\) \({N \subseteq -:\mathbb{B}:\mathbb{B}}\!\) are used to remind us that we are considering particular ways of situating \({L, M, N}\!\) within the product space \(X:Y:Z.\!\) |
o-------------------o o-------------------o
| | | |
| 0:0:0 | | 0:0:0 |
| 0:0:1 | | 0:0:1 |
| 0:1:0 | | 0:1:1 |
| 0:1:1 | | 1:0:0 |
| 1:1:0 | | 1:0:1 |
| 1:1:1 | | 1:1:1 |
| | | |
o-------------------o o-------------------o
|te(Syll_12) c B:B:B| |te(Syll_23) c B:B:B|
o-------------------o o-------------------o
| [| f_207 |] | | [| f_187 |] |
o----o---------o----o o----o---------o----o
^ \ / ^
| \ Intersection / |
| \ / |
| v v |
| o-------------------o |
| | | |
| | 0:0:0 | |
| | 0:0:1 | |
| | 0:1:1 | |
| | 1:1:1 | |
| | | |
| o-------------------o |
| | Syll c B:B:B | |
| o-------------------o |
| | [| f_139 |] | |
| o---------o---------o |
| | |
| Projection |
| | |
| v |
| o---------o---------o |
| | | |
| | 0:0 | |
| | 0:1 | |
| | 1:1 | |
| | | |
| o-------------------o |
| | Syll_13 c B:~:B | |
| o-------------------o |
| | [| (p (r)) |] | |
| o----o---------o----o |
| ^ ^ |
| / \ |
| / Composition \ |
| / \ |
o----o---------o----o o----o---------o----o
| | | |
| 0:0 | | 0:0 |
| 0:1 | | 0:1 |
| 1:1 | | 1:1 |
| | | |
o-------------------o o-------------------o
| Syll_12 c B:B:~ | | Syll_23 c ~:B:B |
o-------------------o o-------------------o
| [| (p (q)) |] | | [| (q (r)) |] |
o---------o---------o o---------o---------o
Figure 76. Denotative Aspects of Transitive Inference
|
A piece of syntax like \({}^{\backprime\backprime} \texttt{(} p \texttt{(} q \texttt{))} {}^{\prime\prime}\!\) or \({}^{\backprime\backprime} p \Rightarrow q {}^{\prime\prime}\!\) is an abstract description, and abstraction is a process that loses information about the objects described. So when we go to reverse the abstraction, as we do when we look for models of that description, there is a degree of indefiniteness that comes into play.
For example, the proposition \(\texttt{(} p \texttt{(} q \texttt{))}\!\) is typically assigned the functional type \(\mathbb{B}^2 \to \mathbb{B},\!\) but that is only its canonical or its minimal abstract type. No sooner do we use it in a context that invokes additional variables, as we do when we next consider the proposition \(\texttt{(} q \texttt{(} r \texttt{))},\!\) than its type is tacitly adjusted to fit the new context, for instance, acquiring the extended type \({\mathbb{B}^3 \to \mathbb{B}}.\!\) This is one of those things that most people eventually learn to do without blinking an eye, that is to say, unreflectively, and this is precisely what makes the same facility so much trouble to implement properly in computational form.
Both the fibering operation, that takes us from the function \(\texttt{(} p \texttt{(} q \texttt{))}\!\) to the relation \([| \texttt{(} p \texttt{(} q \texttt{))} |],\!\) and the tacit extension operation, that takes us from the relation \([| \texttt{(} p \texttt{(} q \texttt{))} |] \subseteq \mathbb{B}:\mathbb{B}\!\) to the relation \([| q_{207} |] \subseteq \mathbb{B}:\mathbb{B}:\mathbb{B},\!\) have this same character of abstraction-undoing or modelling operations that require us to re-interpret the same pieces of syntax under different types. This accounts for a large part of the apparent ambiguities.
Up till now I've concentrated mostly on the abstract types of domains and propositions, things like \(\mathbb{B}^k\!\) and \(\mathbb{B}^k \to \mathbb{B},\!\) respectively. This is a little like trying to do physics all in dimensionless quantities without keeping track of the qualitative physical units. So much abstraction has its obvious limits, not to mention its hidden dangers.
To remedy this situation I will start to introduce the concrete types of domains and propositions, once again as they pertain to our current collection of examples.
We have been using the lower case letters \(p, q, r\!\) for the basic propositions of abstract type \(\mathbb{B}^3 \to \mathbb{B}\!\) and the upper case letters \(P, Q, R\!\) for the basic regions of the universe of discourse where \(p, q, r,\!\) respectively, hold true.
The set of signs \(\mathcal{X} = \{ {}^{\backprime\backprime} p {}^{\prime\prime}, {}^{\backprime\backprime} q {}^{\prime\prime}, {}^{\backprime\backprime} r {}^{\prime\prime} \}\!\) is the alphabet for the universe of discourse that is notated as \(X^\bullet = [\mathcal{X}] = [p, q, r],\!\) already getting sloppy about quotation marks to single out the signs.
The universe \({X^\bullet}\!\) is composed of two different spaces of objects. The first is the space of positions \(X = \langle p, q, r \rangle = \{ (p, q, r) \}.\!\) The second is the space of propositions \(X^\uparrow = (X \to \mathbb{B}).\!\)
Let us make the following definitions:
|
\(\begin{matrix} P^\ddagger & = & X_p & = & \{ \texttt{(} p \texttt{)}, p \}, \\[4pt] Q^\ddagger & = & X_q & = & \{ \texttt{(} q \texttt{)}, q \}, \\[4pt] R^\ddagger & = & X_r & = & \{ \texttt{(} r \texttt{)}, r \}. \end{matrix}\) |
These are three sets of two abstract signs each, altogether staking out the qualitative dimensions of the universe of discourse \(X^\bullet.\!\)
Given this framework, the concrete type of the space \(X\!\) is \(P^\ddagger \times Q^\ddagger \times R^\ddagger ~\cong~ \mathbb{B}^3\!\) and the concrete type of each proposition in \(X^\uparrow = (X \to \mathbb{B})\!\) is \(P^\ddagger \times Q^\ddagger \times R^\ddagger \to \mathbb{B}.~\!\) Given the length of the type markers, we will often omit the cartesian product symbols and write just \(P^\ddagger Q^\ddagger R^\ddagger.\!\)
An abstract reference to a point of \(X\!\) is a triple in \(\mathbb{B}^3.\!\) A concrete reference to a point of \(X\!\) is a conjunction of signs from the dimensions \(P^\ddagger, Q^\ddagger, R^\ddagger,\!\) picking exactly one sign from each dimension.
To illustrate the use of concrete coordinates for points and concrete types for spaces and propositions, Figure 77 translates the contents of Figure 76 into the new language.
o-------------------o o-------------------o
| | | |
| (p)(q)(r) | | (p)(q)(r) |
| (p)(q) r | | (p)(q) r |
| (p) q (r) | | (p) q r |
| (p) q r | | p (q)(r) |
| p q (r) | | p (q) r |
| p q r | | p q r |
| | | |
o-------------------o o-------------------o
|TE(Syll_12) c B:B:B| |TE(Syll_23) c B:B:B|
o-------------------o o-------------------o
| [| f_207 |] | | [| f_187 |] |
o----o---------o----o o----o---------o----o
^ \ / ^
| \ Intersection / |
| \ / |
| v v |
| o-------------------o |
| | | |
| | (p)(q)(r) | |
| | (p)(q) r | |
| | (p) q r | |
| | p q r | |
| | | |
| o-------------------o |
| | Syll c P‡ Q‡ R‡ | |
| o-------------------o |
| | [| f_139 |] | |
| o---------o---------o |
| | |
| Projection |
| | |
| v |
| o---------o---------o |
| | | |
| | (p) (r) | |
| | (p) r | |
| | p r | |
| | | |
| o-------------------o |
| | Syll_13 c P‡ R‡ | |
| o-------------------o |
| | [| (p (r)) |] | |
| o----o---------o----o |
| ^ ^ |
| / \ |
| / Composition \ |
| / \ |
o----o---------o----o o----o---------o----o
| | | |
| (p) (q) | | (q) (r) |
| (p) q | | (q) r |
| p q | | q r |
| | | |
o-------------------o o-------------------o
| Syll_12 c P‡ Q‡ | | Syll_23 c Q‡ R‡ |
o-------------------o o-------------------o
| [| (p (q)) |] | | [| (q (r)) |] |
o---------o---------o o---------o---------o
Figure 77. Denotative Aspects of Transitive Inference
|