Difference between revisions of "Directory:Jon Awbrey/Papers/Peirce's 1870 Logic Of Relatives"
Jon Awbrey (talk | contribs) (segmenting) |
Jon Awbrey (talk | contribs) |
||
| (540 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{DISPLAYTITLE:Peirce's 1870 Logic Of Relatives}} | {{DISPLAYTITLE:Peirce's 1870 Logic Of Relatives}} | ||
| − | ''' | + | '''Note.''' The MathJax parser is not rendering this page properly.<br>Until it can be fixed please see the [http://intersci.ss.uci.edu/wiki/index.php/Peirce's_1870_Logic_Of_Relatives InterSciWiki version]. |
| − | + | '''Author: [[User:Jon Awbrey|Jon Awbrey]]''' | |
| − | + | Peirce's text employs lower case letters for logical terms of general reference and upper case letters for logical terms of individual reference. General terms fall into types — absolute terms, dyadic relative terms, higher adic relative terms — and Peirce employs different typefaces to distinguish these. The following Tables indicate the typefaces that are used in the text below for Peirce's examples of general terms. | |
| + | |||
| + | <br> | ||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | | | + | |+ <math>\text{Absolute Terms (Monadic Relatives)}\!</math> |
| − | | | ||
| | | | ||
| − | + | <math>\begin{array}{ll} | |
| − | + | \mathrm{a}. & \text{animal} | |
| − | + | \\ | |
| − | | | + | \mathrm{b}. & \text{black} |
| − | | | + | \\ |
| − | | | + | \mathrm{f}. & \text{Frenchman} |
| − | + | \\ | |
| + | \mathrm{h}. & \text{horse} | ||
| + | \\ | ||
| + | \mathrm{m}. & \text{man} | ||
| + | \\ | ||
| + | \mathrm{p}. & \text{President of the United States Senate} | ||
| + | \\ | ||
| + | \mathrm{r}. & \text{rich person} | ||
| + | \\ | ||
| + | \mathrm{u}. & \text{violinist} | ||
| + | \\ | ||
| + | \mathrm{v}. & \text{Vice-President of the United States} | ||
| + | \\ | ||
| + | \mathrm{w}. & \text{woman} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| + | |||
| + | <br> | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| + | |+ <math>\text{Simple Relative Terms (Dyadic Relatives)}\!</math> | ||
| | | | ||
| − | + | <math>\begin{array}{ll} | |
| − | + | \mathit{a}. & \text{enemy} | |
| − | + | \\ | |
| − | + | \mathit{b}. & \text{benefactor} | |
| − | + | \\ | |
| − | + | \mathit{c}. & \text{conqueror} | |
| + | \\ | ||
| + | \mathit{e}. & \text{emperor} | ||
| + | \\ | ||
| + | \mathit{h}. & \text{husband} | ||
| + | \\ | ||
| + | \mathit{l}. & \text{lover} | ||
| + | \\ | ||
| + | \mathit{m}. & \text{mother} | ||
| + | \\ | ||
| + | \mathit{n}. & \text{not} | ||
| + | \\ | ||
| + | \mathit{o}. & \text{owner} | ||
| + | \\ | ||
| + | \mathit{s}. & \text{servant} | ||
| + | \\ | ||
| + | \mathit{w}. & \text{wife} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| + | |||
| + | <br> | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| + | |+ <math>\text{Conjugative Terms (Higher Adic Relatives)}\!</math> | ||
| | | | ||
| − | + | <math>\begin{array}{ll} | |
| − | + | \mathfrak{b}. & \text{betrayer to ------ of ------} | |
| − | + | \\ | |
| − | + | \mathfrak{g}. & \text{giver to ------ of ------} | |
| − | + | \\ | |
| − | + | \mathfrak{t}. & \text{transferrer from ------ to ------} | |
| − | + | \\ | |
| − | + | \mathfrak{w}. & \text{winner over of ------ to ------ from ------} | |
| − | + | \end{array}</math> | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | < | + | <br> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Individual terms are taken to denote individual entities falling under a general term. Peirce uses upper case Roman letters for individual terms, for example, the individual horses <math>\mathrm{H}, \mathrm{H}^{\prime}, \mathrm{H}^{\prime\prime}</math> falling under the general term <math>\mathrm{h}\!</math> for ''horse''. | |
| − | |||
| − | |||
| − | uses | ||
| − | |||
| − | + | The path to understanding Peirce's system and its wider implications for logic can be smoothed by paraphrasing his notations in a variety of contemporary mathematical formalisms, while preserving the semantics as much as possible. Remaining faithful to Peirce's orthography while adding parallel sets of stylistic conventions will, however, demand close attention to typography-in-context. Current style sheets for mathematical texts specify italics for mathematical variables, with upper case letters for sets and lower case letters for individuals. So we need to keep an eye out for the difference between the individual <math>\mathrm{X}\!</math> of the genus <math>\mathrm{x}\!</math> and the element <math>x\!</math> of the set <math>X\!</math> as we pass between the two styles of text. | |
| − | + | __TOC__ | |
| − | + | ==Selection 1== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | ===Use of the Letters=== |
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | + | <p>The letters of the alphabet will denote logical signs.</p> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | + | <p>Now logical terms are of three grand classes.</p> | |
| − | < | + | <p>The first embraces those whose logical form involves only the conception of quality, and which therefore represent a thing simply as “a ——”. These discriminate objects in the most rudimentary way, which does not involve any consciousness of discrimination. They regard an object as it is in itself as ''such'' (''quale''); for example, as horse, tree, or man. These are ''absolute terms''.</p> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <p>The second class embraces terms whose logical form involves the conception of relation, and which require the addition of another term to complete the denotation. These discriminate objects with a distinct consciousness of discrimination. They regard an object as over against another, that is as relative; as father of, lover of, or servant of. These are ''simple relative terms''.</p> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <p>The third class embraces terms whose logical form involves the conception of bringing things into relation, and which require the addition of more than one term to complete the denotation. They discriminate not only with consciousness of discrimination, but with consciousness of its origin. They regard an object as medium or third between two others, that is as conjugative; as giver of —— to ——, or buyer of —— for —— from ——. These may be termed ''conjugative terms''.</p> | |
| − | |||
| − | |||
| − | |||
| − | + | <p>The conjugative term involves the conception of ''third'', the relative that of second or ''other'', the absolute term simply considers ''an'' object. No fourth class of terms exists involving the conception of ''fourth'', because when that of ''third'' is introduced, since it involves the conception of bringing objects into relation, all higher numbers are given at once, inasmuch as the conception of bringing objects into relation is independent of the number of members of the relationship. Whether this ''reason'' for the fact that there is no fourth class of terms fundamentally different from the third is satisfactory or not, the fact itself is made perfectly evident by the study of the logic of relatives.</p> | |
| − | |||
| − | |||
| − | |||
| − | + | <p>(Peirce, CP 3.63).</p> | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | I am going to experiment with an interlacing commentary on Peirce's 1870 “Logic of Relatives” paper, revisiting some critical transitions from several different angles and calling attention to a variety of puzzles, problems, and potentials that are not so often remarked or tapped. | |
| − | |||
| − | |||
| − | + | What strikes me about the initial installment this time around is its use of a certain pattern of argument that I can recognize as invoking a ''closure principle'', and this is a figure of reasoning that Peirce uses in three other places: his discussion of [[continuous predicates]], his definition of [[sign relations]], and in the [[pragmatic maxim]] itself. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | One might also call attention to the following two statements: | |
| − | < | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> |
| − | |||
| | | | ||
| − | + | <p>Now logical terms are of three grand classes.</p> | |
| − | | | + | |- |
| − | |||
| | | | ||
| − | | | + | <p>No fourth class of terms exists involving the conception of ''fourth'', because when that of ''third'' is introduced, since it involves the conception of bringing objects into relation, all higher numbers are given at once, inasmuch as the conception of bringing objects into relation is independent of the number of members of the relationship.</p> |
| + | |} | ||
| + | |||
| + | ==Selection 2== | ||
| + | |||
| + | ===Numbers Corresponding to Letters=== | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | ||
| | | | ||
| − | + | <p>I propose to use the term “universe” to denote that class of individuals ''about'' which alone the whole discourse is understood to run. The universe, therefore, in this sense, as in Mr. De Morgan's, is different on different occasions. In this sense, moreover, discourse may run upon something which is not a subjective part of the universe; for instance, upon the qualities or collections of the individuals it contains.</p> | |
| − | | | + | |
| − | + | <p>I propose to assign to all logical terms, numbers; to an absolute term, the number of individuals it denotes; to a relative term, the average number of things so related to one individual. Thus in a universe of perfect men (''men''), the number of “tooth of” would be 32. The number of a relative with two correlates would be the average number of things so related to a pair of individuals; and so on for relatives of higher numbers of correlates. I propose to denote the number of a logical term by enclosing the term in square brackets, thus <math>[t].\!</math></p> | |
| + | |||
| + | <p>(Peirce, CP 3.65).</p> | ||
| + | |} | ||
| + | |||
| + | Peirce's remarks at CP 3.65 are so replete with remarkable ideas, some of them so taken for granted in mathematical discourse that they usually escape explicit mention, and others so suggestive of things to come in a future remote from his time of writing, and yet so smoothly introduced in passing that it's all too easy to overlook their consequential significance, that I can do no better here than to highlight these ideas in other words, whose main advantage is to be a little more jarring to the mind's sensibilities. | ||
| + | |||
| + | :* This mapping of letters to numbers, or logical terms to mathematical quantities, is the very core of what "quantification theory" is all about, and definitely more to the point than the mere "innovation" of using distinctive symbols for the so-called "quantifiers". We will speak of this more later on. | ||
| + | |||
| + | :* The mapping of logical terms to numerical measures, to express it in current language, would probably be recognizable as some kind of "morphism" or "functor" from a logical domain to a quantitative co-domain. | ||
| + | |||
| + | :* Notice that Peirce follows the mathematician's usual practice, then and now, of making the status of being an "individual" or a "universal" relative to a discourse in progress. I have come to appreciate more and more of late how radically different this "patchwork" or "piecewise" approach to things is from the way of some philosophers who seem to be content with nothing less than many worlds domination, which means that they are never content and rarely get started toward the solution of any real problem. Just my observation, I hope you understand. | ||
| + | |||
| + | :* It is worth noting that Peirce takes the "plural denotation" of terms for granted, or what's the number of a term for, if it could not vary apart from being one or nil? | ||
| + | |||
| + | :* I also observe that Peirce takes the individual objects of a particular universe of discourse in a "generative" way, not a "totalizing" way, and thus they afford us with the basis for talking freely about collections, constructions, properties, qualities, subsets, and "higher types", as the phrase is mint. | ||
| + | |||
| + | ==Selection 3== | ||
| + | |||
| + | ===The Signs of Inclusion, Equality, Etc.=== | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | ||
| | | | ||
| − | | | + | <p>I shall follow Boole in taking the sign of equality to signify identity. Thus, if <math>\mathrm{v}\!</math> denotes the Vice-President of the United States, and <math>\mathrm{p}~\!</math> the President of the Senate of the United States,</p> |
| + | |- | ||
| + | | align="center" | <math>\mathrm{v} = \mathrm{p}\!</math> | ||
| + | |- | ||
| | | | ||
| − | + | <p>means that every Vice-President of the United States is President of the Senate, and every President of the United States Senate is Vice-President.</p> | |
| − | | | + | |
| − | | | + | <p>The sign “less than” is to be so taken that</p> |
| − | | | + | |- |
| + | | align="center" | <math>\mathrm{f} < \mathrm{m}~\!</math> | ||
| + | |- | ||
| | | | ||
| − | | f -< m | + | <p>means that every Frenchman is a man, but there are men besides Frenchmen. Drobisch has used this sign in the same sense. It will follow from these significations of <math>=\!</math> and <math><\!</math> that the sign <math>-\!\!\!<\!</math> (or <math>\leqq</math>, “as small as”) will mean “is”. Thus,</p> |
| + | |- | ||
| + | | align="center" | <math>\mathrm{f} ~-\!\!\!< \mathrm{m}</math> | ||
| + | |- | ||
| | | | ||
| − | + | <p>means “every Frenchman is a man”, without saying whether there are any other men or not. So,</p> | |
| − | + | |- | |
| + | | align="center" | <math>\mathit{m} ~-\!\!\!< \mathit{l}</math> | ||
| + | |- | ||
| | | | ||
| − | | | + | <p>will mean that every mother of anything is a lover of the same thing; although this interpretation in some degree anticipates a convention to be made further on. These significations of <math>=\!</math> and <math><\!</math> plainly conform to the indispensable conditions. Upon the transitive character of these relations the syllogism depends, for by virtue of it, from</p> |
| + | |- | ||
| | | | ||
| − | | | + | {| width="100%" |
| − | | | + | | width="25%" | |
| − | | | + | | align="center" | <math>\mathrm{f} ~-\!\!\!< \mathrm{m}</math> |
| − | | | + | | width="25%" | |
| − | | | + | |- |
| + | | <p>and</p> | ||
| + | | align="center" | <math>\mathrm{m} ~-\!\!\!< \mathrm{a}</math> | ||
| + | | | ||
| + | |- | ||
| + | | <p>we can infer that</p> | ||
| + | | align="center" | <math>\mathrm{f} ~-\!\!\!< \mathrm{a}</math> | ||
| + | | | ||
| + | |} | ||
| + | |- | ||
| | | | ||
| − | + | <p>that is, from every Frenchman being a man and every man being an animal, that every Frenchman is an animal.</p> | |
| − | + | ||
| − | + | <p>But not only do the significations of <math>=\!</math> and <math><\!</math> here adopted fulfill all absolute requirements, but they have the supererogatory virtue of being very nearly the same as the common significations. Equality is, in fact, nothing but the identity of two numbers; numbers that are equal are those which are predicable of the same collections, just as terms that are identical are those which are predicable of the same classes. So, to write <math>5 < 7\!</math> is to say that <math>5\!</math> is part of <math>7\!</math>, just as to write <math>\mathrm{f} < \mathrm{m}~\!</math> is to say that Frenchmen are part of men. Indeed, if <math>\mathrm{f} < \mathrm{m}~\!</math>, then the number of Frenchmen is less than the number of men, and if <math>\mathrm{v} = \mathrm{p}\!</math>, then the number of Vice-Presidents is equal to the number of Presidents of the Senate; so that the numbers may always be substituted for the terms themselves, in case no signs of operation occur in the equations or inequalities.</p> | |
| − | + | ||
| − | + | <p>(Peirce, CP 3.66).</p> | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | + | The quantifier mapping from terms to their numbers that Peirce signifies by means of the square bracket notation <math>[t]\!</math> has one of its principal uses in providing a basis for the computation of frequencies, probabilities, and all of the other statistical measures that can be constructed from these, and thus in affording what may be called a ''principle of correspondence'' between probability theory and its limiting case in the forms of logic. | |
| − | The quantifier mapping from terms to their numbers that Peirce signifies | ||
| − | by means of the square bracket notation has one of its principal uses in | ||
| − | providing a basis for the computation of frequencies, probabilities, and | ||
| − | all of the other statistical measures that can be constructed from these, | ||
| − | and thus in affording what may be called a | ||
| − | between probability theory and its limiting case in the forms of logic. | ||
| − | This brings us once again to the relativity of contingency and necessity, | + | This brings us once again to the relativity of contingency and necessity, as one way of approaching necessity is through the avenue of probability, describing necessity as a probability of 1, but the whole apparatus of probability theory only figures in if it is cast against the backdrop of probability space axioms, the reference class of distributions, and the sample space that we cannot help but to abduce upon the scene of observations. Aye, there's the snake eyes. And with them we can see that there is always an irreducible quantum of facticity to all our necessities. More plainly spoken, it takes a fairly complex conceptual infrastructure just to begin speaking of probabilities, and this setting can only be set up by means of abductive, fallible, hypothetical, and inherently risky mental acts. |
| − | as one way of approaching necessity is through the avenue of probability, | ||
| − | describing necessity as a probability of 1, but the whole apparatus of | ||
| − | probability theory only figures in if it is cast against the backdrop | ||
| − | of probability space axioms, the reference class of distributions, | ||
| − | and the sample space that we cannot help but to | ||
| − | scene of observations. Aye, there's the snake eyes. And with | ||
| − | them we can see that there is always an irreducible quantum | ||
| − | of facticity to all our necessities. More plainly spoken, | ||
| − | it takes a fairly complex conceptual infrastructure just | ||
| − | to begin speaking of probabilities, and this setting | ||
| − | can only be set up by means of abductive, fallible, | ||
| − | hypothetical, and inherently risky mental acts. | ||
| − | Pragmatic thinking is the logic of abduction, which is just another | + | Pragmatic thinking is the logic of abduction, which is just another way of saying that it addresses the question: “What may be hoped?” We have to face the possibility that it may be just as impossible to speak of “absolute identity” with any hope of making practical philosophical sense as it is to speak of “absolute simultaneity” with any hope of making operational physical sense. |
| − | way of saying that it addresses the question: | ||
| − | We have to face the possibility that it may be just as impossible | ||
| − | to speak of | ||
| − | philosophical sense as it is to speak of | ||
| − | with any hope of making operational physical sense. | ||
| − | |||
==Selection 4== | ==Selection 4== | ||
| − | + | ===The Signs for Addition=== | |
| − | + | ||
| + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | ||
| | | | ||
| − | + | <p>The sign of addition is taken by Boole so that</p> | |
| + | |- | ||
| + | | align="center" | <math>x + y\!</math> | ||
| + | |- | ||
| | | | ||
| − | | | + | <p>denotes everything denoted by <math>x\!</math>, and, ''besides'', everything denoted by <math>y\!</math>.</p> |
| + | |||
| + | <p>Thus</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathrm{m} + \mathrm{w}~\!</math> | ||
| + | |- | ||
| | | | ||
| − | + | <p>denotes all men, and, besides, all women.</p> | |
| − | | | + | |
| + | <p>This signification for this sign is needed for connecting the notation of logic with that of the theory of probabilities. But if there is anything which is denoted by both terms of the sum, the latter no longer stands for any logical term on account of its implying that the objects denoted by one term are to be taken ''besides'' the objects denoted by the other.</p> | ||
| + | |||
| + | <p>For example,</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathrm{f} + \mathrm{u}\!</math> | ||
| + | |- | ||
| | | | ||
| − | | | + | <p>means all Frenchmen besides all violinists, and, therefore, considered as a logical term, implies that all French violinists are ''besides themselves''.</p> |
| + | |||
| + | <p>For this reason alone, in a paper which is published in the Proceedings of the Academy for March 17, 1867, I preferred to take as the regular addition of logic a non-invertible process, such that</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathrm{m} ~+\!\!,~ \mathrm{b}</math> | ||
| + | |- | ||
| | | | ||
| − | + | <p>stands for all men and black things, without any implication that the black things are to be taken besides the men; and the study of the logic of relatives has supplied me with other weighty reasons for the same determination.</p> | |
| − | + | ||
| − | + | <p>Since the publication of that paper, I have found that Mr. W. Stanley Jevons, in a tract called ''Pure Logic, or the Logic of Quality'' [1864], had anticipated me in substituting the same operation for Boole's addition, although he rejects Boole's operation entirely and writes the new one with a <math>+\!</math> sign while withholding from it the name of addition.</p> | |
| − | + | ||
| − | + | <p>It is plain that both the regular non-invertible addition and the invertible addition satisfy the absolute conditions. But the notation has other recommendations. The conception of ''taking together'' involved in these processes is strongly analogous to that of summation, the sum of 2 and 5, for example, being the number of a collection which consists of a collection of two and a collection of five. Any logical equation or inequality in which no operation but addition is involved may be converted into a numerical equation or inequality by substituting the numbers of the several terms for the terms themselves — provided all the terms summed are mutually exclusive.</p> | |
| − | + | ||
| − | + | <p>Addition being taken in this sense, ''nothing'' is to be denoted by ''zero'', for then</p> | |
| − | + | |- | |
| − | + | | align="center" | <math>x ~+\!\!,~ 0 ~=~ x</math> | |
| − | + | |- | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| | | | ||
| − | + | <p>whatever is denoted by <math>x\!</math>; and this is the definition of ''zero''. This interpretation is given by Boole, and is very neat, on account of the resemblance between the ordinary conception of ''zero'' and that of nothing, and because we shall thus have</p> | |
| + | |- | ||
| + | | align="center" | <math>[0] ~=~ 0.</math> | ||
| + | |- | ||
| | | | ||
| − | + | <p>(Peirce, CP 3.67).</p> | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | + | A wealth of issues arises here that I hope to take up in depth at a later point, but for the moment I shall be able to mention only the barest sample of them in passing. | |
| − | + | The two papers that precede this one in CP 3 are Peirce's papers of March and September 1867 in the ''Proceedings of the American Academy of Arts and Sciences'', titled “On an Improvement in Boole's Calculus of Logic” and “Upon the Logic of Mathematics”, respectively. Among other things, these two papers provide us with further clues about the motivating considerations that brought Peirce to introduce the “number of a term” function, signified here by square brackets. I have already quoted from the “Logic of Mathematics” paper in a related connection. Here are the links to those excerpts: | |
| − | |||
| − | to | ||
| − | |||
| − | |||
| − | + | <dl style="margin-left:30px;"> | |
| − | + | <dt>Limited Mark Universes | |
| − | + | <dd>[http://web.archive.org/web/20140429004255/http://suo.ieee.org/ontology/msg04349.html (1)] | |
| − | + | <dd>[http://web.archive.org/web/20140429004359/http://suo.ieee.org/ontology/msg04350.html (2)] | |
| − | + | <dd>[http://web.archive.org/web/20140429004130/http://suo.ieee.org/ontology/msg04351.html (3)] | |
| − | + | </dl> | |
| − | |||
| − | |||
| − | |||
| − | + | In setting up a correspondence between “letters” and “numbers”, Peirce constructs a structure-preserving map from a logical domain to a numerical domain. That he does this deliberately is evidenced by the care that he takes with the conditions under which the chosen aspects of structure are preserved, along with his recognition of the critical fact that zeroes are preserved by the mapping. | |
| − | |||
| − | + | Incidentally, Peirce appears to have an inkling of the problems that would later be caused by using the plus sign for inclusive disjunction, but his advice was overridden by the dialects of applied logic that developed in various communities, retarding the exchange of information among engineering, mathematical, and philosophical specialties all throughout the subsequent century. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | his | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ==Selection 5== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | ===The Signs for Multiplication=== |
| − | < | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> |
| − | |||
| | | | ||
| − | + | <p>I shall adopt for the conception of multiplication ''the application of a relation'', in such a way that, for example, <math>\mathit{l}\mathrm{w}~\!</math> shall denote whatever is lover of a woman. This notation is the same as that used by Mr. De Morgan, although he appears not to have had multiplication in his mind.</p> | |
| − | + | ||
| − | + | <p><math>\mathit{s}(\mathrm{m} ~+\!\!,~ \mathrm{w})</math> will, then, denote whatever is servant of anything of the class composed of men and women taken together. So that:</p> | |
| − | + | |- | |
| − | + | | align="center" | <math>\mathit{s}(\mathrm{m} ~+\!\!,~ \mathrm{w}) ~=~ \mathit{s}\mathrm{m} ~+\!\!,~ \mathit{s}\mathrm{w}.</math> | |
| − | + | |- | |
| | | | ||
| − | + | <p><math>(\mathit{l} ~+\!\!,~ \mathit{s})\mathrm{w}</math> will denote whatever is lover or servant to a woman, and:</p> | |
| − | | | + | |- |
| − | | | + | | align="center" | <math>(\mathit{l} ~+\!\!,~ \mathit{s})\mathrm{w} ~=~ \mathit{l}\mathrm{w} ~+\!\!,~ \mathit{s}\mathrm{w}.</math> |
| + | |- | ||
| | | | ||
| − | | | + | <p><math>(\mathit{s}\mathit{l})\mathrm{w}\!</math> will denote whatever stands to a woman in the relation of servant of a lover, and:</p> |
| + | |- | ||
| + | | align="center" | <math>(\mathit{s}\mathit{l})\mathrm{w} ~=~ \mathit{s}(\mathit{l}\mathrm{w}).</math> | ||
| + | |- | ||
| | | | ||
| − | + | <p>Thus all the absolute conditions of multiplication are satisfied.</p> | |
| − | | | + | |
| + | <p>The term “identical with ——” is a unity for this multiplication. That is to say, if we denote “identical with ——” by <math>\mathit{1}\!</math> we have:</p> | ||
| + | |- | ||
| + | | align="center" | <math>x \mathit{1} ~=~ x ~ ,</math> | ||
| + | |- | ||
| | | | ||
| − | + | <p>whatever relative term <math>x\!</math> may be. For what is a lover of something identical with anything, is the same as a lover of that thing.</p> | |
| − | + | ||
| − | + | <p>(Peirce, CP 3.68).</p> | |
| − | + | |} | |
| − | + | ||
| − | + | Peirce in 1870 is five years down the road from the Peirce of 1865–1866 who lectured extensively on the role of sign relations in the logic of scientific inquiry, articulating their involvement in the three types of inference, and inventing the concept of “information” to explain what it is that signs convey in the process. By this time, then, the semiotic or sign relational approach to logic is so implicit in his way of working that he does not always take the trouble to point out its distinctive features at each and every turn. So let's take a moment to draw out a few of these characters. | |
| − | + | ||
| − | + | [[Sign relations]], like any brand of non-trivial [[3-adic relations]], can become overwhelming to think about once the cardinality of the object, sign, and interpretant domains or the complexity of the relation itself ascends beyond the simplest examples. Furthermore, most of the strategies that we would normally use to control the complexity, like neglecting one of the domains, in effect, projecting the 3-adic sign relation onto one of its 2-adic faces, or focusing on a single ordered triple of the form <math>(o, s, i)\!</math> at a time, can result in our receiving a distorted impression of the sign relation's true nature and structure. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | + | I find that it helps me to draw, or at least to imagine drawing, diagrams of the following form, where I can keep tabs on what's an object, what's a sign, and what's an interpretant sign, for a selected set of sign-relational triples. | |
| − | < | + | Here is how I would picture Peirce's example of equivalent terms, <math>\mathrm{v} = \mathrm{p},\!</math> where <math>{}^{\backprime\backprime} \mathrm{v} {}^{\prime\prime}\!</math> denotes the Vice-President of the United States, and <math>{}^{\backprime\backprime} \mathrm{p} {}^{\prime\prime}\!</math> denotes the President of the Senate of the United States. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" border="0" cellspacing="10" style="text-align:center; width:100%" | |
| − | + | | [[Image:LOR 1870 Figure 1.jpg]] | |
| − | + | |- | |
| − | + | | height="20px" valign="top" | <math>\text{Figure 1}~\!</math> | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Depending on whether we interpret the terms <math>{}^{\backprime\backprime} \mathrm{v} {}^{\prime\prime}\!</math> and <math>{}^{\backprime\backprime} \mathrm{p} {}^{\prime\prime}\!</math> as applying to persons who hold these offices at one particular time or as applying to all those persons who have held these offices over an extended period of history, their denotations may be either singular of plural, respectively. | |
| − | |||
| − | |||
| − | |||
| − | + | As a shortcut technique for indicating general denotations or plural referents, I will use the ''elliptic convention'' that represents these by means of figures like “o o o” or “o … o”, placed at the object ends of sign relational triads. | |
| − | |||
| − | |||
| − | + | For a more complex example, here is how I would picture Peirce's example of an equivalence between terms that comes about by applying one of the distributive laws, for relative multiplication over absolute summation. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" border="0" cellspacing="10" style="text-align:center; width:100%" | |
| − | + | | [[Image:LOR 1870 Figure 2.jpg]] | |
| − | + | |- | |
| − | + | | height="20px" valign="top" | <math>\text{Figure 2}\!</math> | |
| + | |} | ||
| − | + | ==Selection 6== | |
| − | |||
| − | |||
| − | + | ===The Signs for Multiplication (cont.)=== | |
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| − | | | + | | |
| − | + | <p>A conjugative term like ''giver'' naturally requires two correlates, one denoting the thing given, the other the recipient of the gift.</p> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | + | <p>We must be able to distinguish, in our notation, the giver of <math>\mathrm{A}\!</math> to <math>\mathrm{B}\!</math> from the giver to <math>\mathrm{A}\!</math> of <math>\mathrm{B}\!</math>, and, therefore, I suppose the signification of the letter equivalent to such a relative to distinguish the correlates as first, second, third, etc., so that “giver of —— to ——” and “giver to —— of ——” will be expressed by different letters.</p> | |
| − | < | + | <p>Let <math>\mathfrak{g}</math> denote the latter of these conjugative terms. Then, the correlates or multiplicands of this multiplier cannot all stand directly after it, as is usual in multiplication, but may be ranged after it in regular order, so that:</p> |
| − | | | + | |- |
| + | | align="center" | <math>\mathfrak{g}\mathit{x}\mathit{y}</math> | ||
| + | |- | ||
| | | | ||
| − | + | <p>will denote a giver to <math>\mathit{x}\!</math> of <math>\mathit{y}\!</math>.</p> | |
| − | | | + | |
| + | <p>But according to the notation, <math>\mathit{x}\!</math> here multiplies <math>\mathit{y}\!</math>, so that if we put for <math>\mathit{x}\!</math> owner (<math>\mathit{o}\!</math>), and for <math>\mathit{y}\!</math> horse (<math>\mathrm{h}\!</math>),</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathfrak{g}\mathit{o}\mathrm{h}</math> | ||
| + | |- | ||
| | | | ||
| − | + | <p>appears to denote the giver of a horse to an owner of a horse. But let the individual horses be <math>\mathrm{H}, \mathrm{H}^{\prime}, \mathrm{H}^{\prime\prime}</math>, etc.</p> | |
| − | + | ||
| − | | | + | <p>Then:</p> |
| − | | | + | |- |
| − | | etc., | + | | align="center" | <math>\mathrm{h} ~=~ \mathrm{H} ~+\!\!,~ \mathrm{H}^{\prime} ~+\!\!,~ \mathrm{H}^{\prime\prime} ~+\!\!,~ \text{etc.}</math> |
| − | | | + | |- |
| + | | align="center" | <math>\mathfrak{g}\mathit{o}\mathrm{h} ~=~ \mathfrak{g}\mathit{o}(\mathrm{H} ~+\!\!,~ \mathrm{H}^{\prime} ~+\!\!,~ \mathrm{H}^{\prime\prime} ~+\!\!,~ \text{etc.}) ~=~ \mathfrak{g}\mathit{o}\mathrm{H} ~+\!\!,~ \mathfrak{g}\mathit{o}\mathrm{H}^{\prime} ~+\!\!,~ \mathfrak{g}\mathit{o}\mathrm{H}^{\prime\prime} ~+\!\!,~ \text{etc.}</math> | ||
| + | |- | ||
| | | | ||
| − | + | <p>Now this last member must be interpreted as a giver of a horse to the owner of ''that'' horse, and this, therefore must be the interpretation of <math>\mathfrak{g}\mathit{o}\mathrm{h}</math>. This is always very important. ''A term multiplied by two relatives shows that the same individual is in the two relations.''</p> | |
| − | + | ||
| − | | | + | <p>If we attempt to express the giver of a horse to a lover of a woman, and for that purpose write:</p> |
| + | |- | ||
| + | | align="center" | <math>\mathfrak{g}\mathit{l}\mathrm{w}\mathrm{h}</math>, | ||
| + | |- | ||
| | | | ||
| − | | | + | <p>we have written giver of a woman to a lover of her, and if we add brackets, thus,</p> |
| + | |- | ||
| + | | align="center" | <math>\mathfrak{g}(\mathit{l}\mathrm{w})\mathrm{h}</math>, | ||
| + | |- | ||
| | | | ||
| − | + | <p>we abandon the associative principle of multiplication.</p> | |
| + | |||
| + | <p>A little reflection will show that the associative principle must in some form or other be abandoned at this point. But while this principle is sometimes falsified, it oftener holds, and a notation must be adopted which will show of itself when it holds. We already see that we cannot express multiplication by writing the multiplicand directly after the multiplier; let us then affix subjacent numbers after letters to show where their correlates are to be found. The first number shall denote how many factors must be counted from left to right to reach the first correlate, the second how many ''more'' must be counted to reach the second, and so on.</p> | ||
| + | |||
| + | <p>Then, the giver of a horse to a lover of a woman may be written:</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathfrak{g}_{12} \mathit{l}_1 \mathrm{w} \mathrm{h} ~=~ \mathfrak{g}_{11} \mathit{l}_2 \mathrm{h} \mathrm{w} ~=~ \mathfrak{g}_{2(-1)} \mathrm{h} \mathit{l}_1 \mathrm{w}</math>. | ||
| + | |- | ||
| | | | ||
| − | + | <p>Of course a negative number indicates that the former correlate follows the latter by the corresponding positive number.</p> | |
| − | | | + | |
| − | | | + | <p>A subjacent ''zero'' makes the term itself the correlate.</p> |
| − | | | + | |
| + | <p>Thus,</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathit{l}_0\!</math> | ||
| + | |- | ||
| | | | ||
| − | + | <p>denotes the lover of ''that'' lover or the lover of himself, just as <math>\mathfrak{g}\mathit{o}\mathrm{h}</math> denotes that the horse is given to the owner of itself, for to make a term doubly a correlate is, by the distributive principle, to make each individual doubly a correlate, so that:</p> | |
| + | |- | ||
| + | | align="center" | <math>\mathit{l}_0 ~=~ \mathit{L}_0 ~+\!\!,~ \mathit{L}_0^{\prime} ~+\!\!,~ \mathit{L}_0^{\prime\prime} ~+\!\!,~ \text{etc.}</math> | ||
| + | |- | ||
| | | | ||
| − | + | <p>A subjacent sign of infinity may indicate that the correlate is indeterminate, so that:</p> | |
| − | | | + | |- |
| − | | | + | | align="center" | <math>\mathit{l}_\infty</math> |
| + | |- | ||
| | | | ||
| − | | | + | <p>will denote a lover of something. We shall have some confirmation of this presently.</p> |
| + | |||
| + | <p>If the last subjacent number is a ''one'' it may be omitted. Thus we shall have:</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathit{l}_1 ~=~ \mathit{l}</math>, | ||
| + | |- | ||
| + | | align="center" | <math>\mathfrak{g}_{11} ~=~ \mathfrak{g}_1 ~=~ \mathfrak{g}</math>. | ||
| + | |- | ||
| | | | ||
| − | + | <p>This enables us to retain our former expressions <math>\mathit{l}\mathrm{w}~\!</math>, <math>\mathfrak{g}\mathit{o}\mathrm{h}</math>, etc.</p> | |
| − | + | ||
| − | + | <p>(Peirce, CP 3.69–70).</p> | |
| − | + | |} | |
| − | + | ||
| − | + | ===Comment : Sets as Logical Sums=== | |
| − | + | ||
| − | + | Peirce's way of representing sets as logical sums may seem archaic, but it is quite often used, and is actually the tool of choice in many branches of algebra, combinatorics, computing, and statistics to this very day. | |
| − | + | ||
| − | | | + | Peirce's application to logic is fairly novel, and the degree of his elaboration of the logic of relative terms is certainly original with him, but this particular genre of representation, commonly going under the handle of ''generating functions'', goes way back, well before anyone thought to stick a flag in set theory as a separate territory or to try to fence off our native possessions of it with expressly decreed axioms. And back in the days when a computer was just a person who computed, before we had the sorts of ''electronic register machines'' that we take so much for granted today, mathematicians were constantly using generating functions as a rough and ready type of addressable memory to sort, store, and keep track of their accounts of a wide variety of formal objects of thought. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Let us look at a few simple examples of generating functions, much as I encountered them during my own first adventures in the Fair Land Of Combinatoria. | |
| − | + | Suppose that we are given a set of three elements, say, <math>\{ a, b, c \},\!</math> and we are asked to find all the ways of choosing a subset from this collection. | |
| − | |||
| − | |||
| − | |||
| − | + | We can represent this problem setup as the problem of computing the following product: | |
| − | |||
| − | |||
| − | the | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | <math>(1 + a)(1 + b)(1 + c).\!</math> | |
| − | + | |} | |
| − | + | The factor <math>(1 + a)\!</math> represents the option that we have, in choosing a subset of <math>\{ a, b, c \},\!</math> to leave the element <math>a\!</math> out (signified by the <math>1\!</math>), or else to include it (signified by the <math>a\!</math>), and likewise for the other elements <math>b\!</math> and <math>c\!</math> in their turns. | |
| − | |||
| − | |||
| − | + | Probably on account of all those years I flippered away playing the oldtime pinball machines, I tend to imagine a product like this being displayed in a vertical array: | |
| − | |||
| − | (1 + a)(1 + b)(1 + c) | + | {| align="center" cellspacing="6" width="90%" |
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | (1 ~+~ a) | ||
| + | \\ | ||
| + | (1 ~+~ b) | ||
| + | \\ | ||
| + | (1 ~+~ c) | ||
| + | \end{matrix}</math> | ||
| + | |} | ||
| − | + | I picture this as a playboard with six bumpers, the ball chuting down the board in such a career that it strikes exactly one of the two bumpers on each and every one of the three levels. | |
| − | a | ||
| − | |||
| − | |||
| − | + | So a trajectory of the ball where it hits the <math>a\!</math> bumper on the 1st level, hits the <math>1\!</math> bumper on the 2nd level, hits the <math>c\!</math> bumper on the 3rd level, and then exits the board, represents a single term in the desired product and corresponds to the subset <math>\{ a, c \}.\!</math> | |
| − | |||
| − | a product | ||
| − | (1 + a) | + | Multiplying out the product <math>(1 + a)(1 + b)(1 + c),\!</math> one obtains: |
| − | (1 + b) | ||
| − | (1 + c) | ||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | | |
| − | + | <math>\begin{array}{*{15}{c}} | |
| − | + | 1 & + & a & + & b & + & c & + & ab & + & ac & + & bc & + & abc. | |
| − | + | \end{array}</math> | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | 1 + a + b + c + ab + ac + bc + abc. | ||
And this informs us that the subsets of choice are: | And this informs us that the subsets of choice are: | ||
| − | {}, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}. | + | {| align="center" cellspacing="6" width="90%" |
| − | </ | + | | |
| + | <math>\begin{matrix} | ||
| + | \varnothing, & \{ a \}, & \{ b \}, & \{ c \}, & \{ a, b \}, & \{ a, c \}, & \{ b, c \}, & \{ a, b, c \}. | ||
| + | \end{matrix}</math> | ||
| + | |} | ||
==Selection 7== | ==Selection 7== | ||
| − | + | ===The Signs for Multiplication (cont.)=== | |
| − | + | ||
| + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | ||
| | | | ||
| − | + | <p>The associative principle does not hold in this counting of factors. Because it does not hold, these subjacent numbers are frequently inconvenient in practice, and I therefore use also another mode of showing where the correlate of a term is to be found. This is by means of the marks of reference, <math>\dagger ~ \ddagger ~ \parallel ~ \S ~ \P</math>, which are placed subjacent to the relative term and before and above the correlate. Thus, giver of a horse to a lover of a woman may be written:</p> | |
| − | + | |- | |
| − | + | | align="center" | <math>\mathfrak{g}_{\dagger\ddagger} \, ^\dagger\mathit{l}_\parallel \, ^\parallel\mathrm{w} \, ^\ddagger\mathrm{h}</math> | |
| − | + | |- | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | + | <p>The asterisk I use exclusively to refer to the last correlate of the last relative of the algebraic term.</p> | |
| − | + | ||
| − | + | <p>Now, considering the order of multiplication to be: — a term, a correlate of it, a correlate of that correlate, etc. — there is no violation of the associative principle. The only violations of it in this mode of notation are that in thus passing from relative to correlate, we skip about among the factors in an irregular manner, and that we cannot substitute in such an expression as <math>\mathfrak{g}\mathit{o}\mathrm{h}</math> a single letter for <math>\mathit{o}\mathrm{h}.\!</math></p> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | + | <p>I would suggest that such a notation may be found useful in treating other cases of non-associative multiplication. By comparing this with what was said above [in CP 3.55] concerning functional multiplication, it appears that multiplication by a conjugative term is functional, and that the letter denoting such a term is a symbol of operation. I am therefore using two alphabets, the Greek and Kennerly, where only one was necessary. But it is convenient to use both.</p> | |
| − | < | + | <p>(Peirce, CP 3.71–72).</p> |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | + | ===Comment : Proto-Graphical Syntax=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | It is clear from our last excerpt that Peirce is already on the verge | + | It is clear from our last excerpt that Peirce is already on the verge of a graphical syntax for the logic of relatives. Indeed, it seems likely that he had already reached this point in his own thinking. |
| − | of a graphical syntax for the logic of relatives. Indeed, it seems | ||
| − | likely that he had already reached this point in his own thinking. | ||
| − | For instance, it seems quite impossible to read his last variation on the | + | For instance, it seems quite impossible to read his last variation on the theme of a “giver of a horse to a lover of a woman” without drawing lines of identity to connect up the corresponding marks of reference, like this: |
| − | theme of a | ||
| − | of identity to connect up the corresponding marks of reference, like this: | ||
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 3.jpg]] || (3) | |
| − | | | + | |} |
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Selection 8== | ==Selection 8== | ||
| − | + | ===The Signs for Multiplication (cont.)=== | |
| − | + | ||
| + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | ||
| | | | ||
| − | + | <p>Thus far, we have considered the multiplication of relative terms only. Since our conception of multiplication is the application of a relation, we can only multiply absolute terms by considering them as relatives.</p> | |
| − | + | ||
| − | + | <p>Now the absolute term “man” is really exactly equivalent to the relative term “man that is ——”, and so with any other. I shall write a comma after any absolute term to show that it is so regarded as a relative term.</p> | |
| + | |||
| + | <p>Then “man that is black” will be written:</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathrm{m},\!\mathrm{b}\!</math> | ||
| + | |- | ||
| | | | ||
| − | + | <p>But not only may any absolute term be thus regarded as a relative term, but any relative term may in the same way be regarded as a relative with one correlate more. It is convenient to take this additional correlate as the first one.</p> | |
| − | + | ||
| − | + | <p>Then:</p> | |
| − | + | |- | |
| + | | align="center" | <math>\mathit{l},\!\mathit{s}\mathrm{w}</math> | ||
| + | |- | ||
| | | | ||
| − | | | + | <p>will denote a lover of a woman that is a servant of that woman.</p> |
| + | |||
| + | <p>The comma here after <math>\mathit{l}\!</math> should not be considered as altering at all the meaning of <math>\mathit{l}\!</math>, but as only a subjacent sign, serving to alter the arrangement of the correlates.</p> | ||
| + | |||
| + | <p>In point of fact, since a comma may be added in this way to any relative term, it may be added to one of these very relatives formed by a comma, and thus by the addition of two commas an absolute term becomes a relative of two correlates.</p> | ||
| + | |||
| + | <p>So:</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathrm{m},\!,\!\mathrm{b},\!\mathrm{r}</math> | ||
| + | |- | ||
| | | | ||
| − | | " | + | <p>interpreted like</p> |
| + | |- | ||
| + | | align="center" | <math>\mathfrak{g}\mathit{o}\mathrm{h}</math> | ||
| + | |- | ||
| | | | ||
| − | | | + | <p>means a man that is a rich individual and is a black that is that rich individual.</p> |
| + | |||
| + | <p>But this has no other meaning than:</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathrm{m},\!\mathrm{b},\!\mathrm{r}</math> | ||
| + | |- | ||
| | | | ||
| − | | | + | <p>or a man that is a black that is rich.</p> |
| + | |||
| + | <p>Thus we see that, after one comma is added, the addition of another does not change the meaning at all, so that whatever has one comma after it must be regarded as having an infinite number.</p> | ||
| + | |||
| + | <p>If, therefore, <math>\mathit{l},\!,\!\mathit{s}\mathrm{w}</math> is not the same as <math>\mathit{l},\!\mathit{s}\mathrm{w}</math> (as it plainly is not, because the latter means a lover and servant of a woman, and the former a lover of and servant of and same as a woman), this is simply because the writing of the comma alters the arrangement of the correlates.</p> | ||
| + | |||
| + | <p>And if we are to suppose that absolute terms are multipliers at all (as mathematical generality demands that we should}, we must regard every term as being a relative requiring an infinite number of correlates to its virtual infinite series “that is —— and is —— and is —— etc.”</p> | ||
| + | |||
| + | <p>Now a relative formed by a comma of course receives its subjacent numbers like any relative, but the question is, What are to be the implied subjacent numbers for these implied correlates?</p> | ||
| + | |||
| + | <p>Any term may be regarded as having an infinite number of factors, those at the end being ''ones'', thus:</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathit{l},\!\mathit{s}\mathrm{w} ~=~ \mathit{l},\!\mathit{s}\mathit{w},\!\mathit{1},\!\mathit{1},\!\mathit{1},\!\mathit{1},\!\mathit{1},\!\mathit{1},\!\mathit{1}, ~\text{etc.}</math> | ||
| + | |- | ||
| | | | ||
| − | + | <p>A subjacent number may therefore be as great as we please.</p> | |
| − | + | ||
| − | + | <p>But all these ''ones'' denote the same identical individual denoted by <math>\mathrm{w}\!</math>; what then can be the subjacent numbers to be applied to <math>\mathit{s}\!</math>, for instance, on account of its infinite “''that is''”'s? What numbers can separate it from being identical with <math>\mathrm{w}\!</math>? There are only two. The first is ''zero'', which plainly neutralizes a comma completely, since</p> | |
| − | | | + | |- |
| + | | align="center" | <math>\mathit{s},_0\!\mathrm{w} ~=~ \mathit{s}\mathrm{w}</math> | ||
| + | |- | ||
| | | | ||
| − | | | + | <p>and the other is infinity; for as <math>1^\infty</math> is indeterminate in ordinary algbra, so it will be shown hereafter to be here, so that to remove the correlate by the product of an infinite series of ''ones'' is to leave it indeterminate.</p> |
| + | |||
| + | <p>Accordingly,</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathrm{m},_\infty</math> | ||
| + | |- | ||
| | | | ||
| − | + | <p>should be regarded as expressing ''some'' man.</p> | |
| + | |||
| + | <p>Any term, then, is properly to be regarded as having an infinite number of commas, all or some of which are neutralized by zeros.</p> | ||
| + | |||
| + | <p>“Something” may then be expressed by:</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathit{1}_\infty\!</math> | ||
| + | |- | ||
| | | | ||
| − | | | + | <p>I shall for brevity frequently express this by an antique figure one <math>(\mathfrak{1}).</math></p> |
| + | |||
| + | <p>“Anything” by:</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathit{1}_0\!</math> | ||
| + | |- | ||
| | | | ||
| − | | | + | <p>I shall often also write a straight <math>1\!</math> for ''anything''.</p> |
| − | + | ||
| − | | | + | <p>(Peirce, CP 3.73).</p> |
| + | |} | ||
| + | |||
| + | ===Commentary Note 8.1=== | ||
| + | |||
| + | To my way of thinking, CP 3.73 is one of the most remarkable passages in the history of logic. In this first pass over its deeper contents I won't be able to accord it much more than a superficial dusting off. | ||
| + | |||
| + | Let us imagine a concrete example that will serve in developing the uses of Peirce's notation. Entertain a discourse whose universe <math>X\!</math> will remind us a little of the cast of characters in Shakespeare's ''Othello''. | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| + | | <math>X ~=~ \{ \mathrm{Bianca}, \mathrm{Cassio}, \mathrm{Clown}, \mathrm{Desdemona}, \mathrm{Emilia}, \mathrm{Iago}, \mathrm{Othello} \}.</math> | ||
| + | |} | ||
| + | |||
| + | The universe <math>X\!</math> is “that class of individuals ''about'' which alone the whole discourse is understood to run” but its marking out for special recognition as a universe of discourse in no way rules out the possibility that “discourse may run upon something which is not a subjective part of the universe; for instance, upon the qualities or collections of the individuals it contains” (CP 3.65). | ||
| + | |||
| + | In order to provide ourselves with the convenience of abbreviated terms, while preserving Peirce's conventions about capitalization, we may use the alternate names <math>^{\backprime\backprime}\mathrm{u}^{\prime\prime}</math> for the universe <math>X\!</math> and <math>^{\backprime\backprime}\mathrm{Jeste}^{\prime\prime}</math> for the character <math>\mathrm{Clown}.~\!</math> This permits the above description of the universe of discourse to be rewritten in the following fashion: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| + | | <math>\mathrm{u} ~=~ \{ \mathrm{B}, \mathrm{C}, \mathrm{D}, \mathrm{E}, \mathrm{I}, \mathrm{J}, \mathrm{O} \}</math> | ||
| + | |} | ||
| + | |||
| + | This specification of the universe of discourse could be summed up in Peirce's notation by the following equation: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | + | <math>\begin{array}{*{15}{c}} | |
| − | + | \mathbf{1} | |
| − | | | + | & = & \mathrm{B} |
| − | | | + | & +\!\!, & \mathrm{C} |
| + | & +\!\!, & \mathrm{D} | ||
| + | & +\!\!, & \mathrm{E} | ||
| + | & +\!\!, & \mathrm{I} | ||
| + | & +\!\!, & \mathrm{J} | ||
| + | & +\!\!, & \mathrm{O} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| + | |||
| + | Within this discussion, then, the ''individual terms'' are as follows: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | | | + | <math>\begin{matrix} |
| + | ^{\backprime\backprime}\mathrm{B}^{\prime\prime}, & | ||
| + | ^{\backprime\backprime}\mathrm{C}^{\prime\prime}, & | ||
| + | ^{\backprime\backprime}\mathrm{D}^{\prime\prime}, & | ||
| + | ^{\backprime\backprime}\mathrm{E}^{\prime\prime}, & | ||
| + | ^{\backprime\backprime}\mathrm{I}^{\prime\prime}, & | ||
| + | ^{\backprime\backprime}\mathrm{J}^{\prime\prime}, & | ||
| + | ^{\backprime\backprime}\mathrm{O}^{\prime\prime} | ||
| + | \end{matrix}</math> | ||
| + | |} | ||
| + | |||
| + | Each of these terms denotes in a singular fashion the corresponding individual in <math>X.\!</math> | ||
| + | |||
| + | By way of ''general terms'' in this discussion, we may begin with the following set: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | | | + | <math>\begin{array}{ccl} |
| + | ^{\backprime\backprime}\mathrm{b}^{\prime\prime} | ||
| + | & = & | ||
| + | ^{\backprime\backprime}\mathrm{black}^{\prime\prime} | ||
| + | \\[6pt] | ||
| + | ^{\backprime\backprime}\mathrm{m}^{\prime\prime} | ||
| + | & = & | ||
| + | ^{\backprime\backprime}\mathrm{man}^{\prime\prime} | ||
| + | \\[6pt] | ||
| + | ^{\backprime\backprime}\mathrm{w}^{\prime\prime} | ||
| + | & = & | ||
| + | ^{\backprime\backprime}\mathrm{woman}^{\prime\prime} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| + | |||
| + | The denotation of a general term may be given by means of an equation between terms: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | | | + | <math>\begin{array}{*{15}{c}} |
| + | \mathrm{b} | ||
| + | & = & \mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{m} | ||
| + | & = & \mathrm{C} | ||
| + | & +\!\!, & \mathrm{I} | ||
| + | & +\!\!, & \mathrm{J} | ||
| + | & +\!\!, & \mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{w} | ||
| + | & = & \mathrm{B} | ||
| + | & +\!\!, & \mathrm{D} | ||
| + | & +\!\!, & \mathrm{E} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| + | |||
| + | ===Commentary Note 8.2=== | ||
| + | |||
| + | I continue with my commentary on CP 3.73, developing the ''Othello'' example as a way of illustrating Peirce's concepts. | ||
| + | |||
| + | In the development of the story so far, we have a universe of discourse that can be characterized by means of the following system of equations: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | | | + | <math>\begin{array}{*{15}{c}} |
| + | \mathbf{1} | ||
| + | & = & \mathrm{B} | ||
| + | & +\!\!, & \mathrm{C} | ||
| + | & +\!\!, & \mathrm{D} | ||
| + | & +\!\!, & \mathrm{E} | ||
| + | & +\!\!, & \mathrm{I} | ||
| + | & +\!\!, & \mathrm{J} | ||
| + | & +\!\!, & \mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{b} | ||
| + | & = & \mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{m} | ||
| + | & = & \mathrm{C} | ||
| + | & +\!\!, & \mathrm{I} | ||
| + | & +\!\!, & \mathrm{J} | ||
| + | & +\!\!, & \mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{w} | ||
| + | & = & \mathrm{B} | ||
| + | & +\!\!, & \mathrm{D} | ||
| + | & +\!\!, & \mathrm{E} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| + | |||
| + | This much provides a basis for collection of absolute terms that I plan to use in this example. Let us now consider how we might represent a sufficiently exemplary collection of relative terms. | ||
| + | |||
| + | Consider the genesis of relative terms, for example: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | | | + | <math>\begin{array}{l} |
| − | | | + | ^{\backprime\backprime}\, \text{lover of}\, \underline{~~ ~~}\, ^{\prime\prime} |
| + | \\[6pt] | ||
| + | ^{\backprime\backprime}\, \text{betrayer to}\, \underline{~~ ~~}\, \text{of}\, \underline{~~ ~~}\, ^{\prime\prime} | ||
| + | \\[6pt] | ||
| + | ^{\backprime\backprime}\, \text{winner over of}\, \underline{~~ ~~}\, \text{to}\, \underline{~~ ~~}\, \text{from}\, \underline{~~ ~~}\, ^{\prime\prime} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| + | |||
| + | We may regard these fill-in-the-blank forms as being derived by a kind of ''rhematic abstraction'' from the corresponding instances of absolute terms. | ||
| + | |||
| + | In other words: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | | | + | <p>The relative term <math>^{\backprime\backprime}\, \text{lover of}\, \underline{~~ ~~}\, ^{\prime\prime}</math></p> |
| + | |||
| + | <p>can be reached by removing the absolute term <math>^{\backprime\backprime}\, \text{Emilia}\, ^{\prime\prime}</math></p> | ||
| + | |||
| + | <p>from the absolute term <math>^{\backprime\backprime}\, \text{lover of Emilia}\, ^{\prime\prime}.</math></p> | ||
| + | |||
| + | <p><math>\text{Iago}</math> is a lover of <math>\text{Emilia},</math> so the relate-correlate pair <math>\mathrm{I}:\mathrm{E}</math></p> | ||
| + | |||
| + | <p>lies in the 2-adic relation associated with the relative term <math>^{\backprime\backprime}\, \text{lover of}\, \underline{~~ ~~}\, ^{\prime\prime}.</math></p> | ||
| + | |- | ||
| | | | ||
| − | + | <p>The relative term <math>^{\backprime\backprime}\, \text{betrayer to}\, \underline{~~ ~~}\, \text{of}\, \underline{~~ ~~}\, ^{\prime\prime}</math></p> | |
| + | |||
| + | <p>can be reached by removing the absolute terms <math>^{\backprime\backprime}\, \text{Othello}\, ^{\prime\prime}</math> and <math>^{\backprime\backprime}\, \text{Desdemona}\, ^{\prime\prime}</math></p> | ||
| + | |||
| + | <p>from the absolute term <math>^{\backprime\backprime}\, \text{betrayer to Othello of Desdemona}\, ^{\prime\prime}.</math></p> | ||
| + | |||
| + | <p><math>\text{Iago}</math> is a betrayer to <math>\text{Othello}</math> of <math>\text{Desdemona},</math> so the relate-correlate-correlate triple <math>\mathrm{I}:\mathrm{O}:\mathrm{D}</math></p> | ||
| + | |||
| + | <p>lies in the 3-adic relation assciated with the relative term <math>^{\backprime\backprime}\, \text{betrayer to}\, \underline{~~ ~~}\, \text{of}\, \underline{~~ ~~}\, ^{\prime\prime}.\!</math></p> | ||
| + | |- | ||
| | | | ||
| − | | | + | <p>The relative term <math>^{\backprime\backprime}\, \text{winner over of}\, \underline{~~ ~~}\, \text{to}\, \underline{~~ ~~}\, \text{from}\, \underline{~~ ~~}\, ^{\prime\prime}</math></p> |
| + | |||
| + | <p>can be reached by removing the absolute terms <math>^{\backprime\backprime}\, \text{Othello}\, ^{\prime\prime},</math> <math>^{\backprime\backprime}\, \text{Iago}\, ^{\prime\prime},</math> and <math>^{\backprime\backprime}\, \text{Cassio}\, ^{\prime\prime}</math></p> | ||
| + | |||
| + | <p>from the absolute term <math>^{\backprime\backprime}\, \text{winner over of Othello to Iago from Cassio}\, ^{\prime\prime}.</math></p> | ||
| + | |||
| + | <p><math>\text{Iago}</math> is a winner over of <math>\text{Othello}</math> to <math>\text{Iago}</math> from <math>\text{Cassio},\!</math> so the elementary relative term <math>\mathrm{I}:\mathrm{O}:\mathrm{I}:\mathrm{C}</math></p> | ||
| + | |||
| + | <p>lies in the 4-adic relation associated with the relative term <math>^{\backprime\backprime}\, \text{winner over of}\, \underline{~~ ~~}\, \text{to}\, \underline{~~ ~~}\, \text{from}\, \underline{~~ ~~}\, ^{\prime\prime}.</math></p> | ||
| + | |} | ||
| + | |||
| + | ===Commentary Note 8.3=== | ||
| + | |||
| + | Speaking very strictly, we need to be careful to distinguish a ''relation'' from a ''relative term''. | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | + | <p>The relation is an ''object'' of thought that may be regarded ''in extension'' as a set of ordered tuples that are known as its ''elementary relations''.</p> | |
| − | + | |- | |
| − | |||
| − | |||
| | | | ||
| − | + | <p>The relative term is a ''sign'' that denotes certain objects, called its ''relates'', as these are determined in relation to certain other objects, called its ''correlates''. Under most circumstances, one may also regard the relative term as denoting the corresponding relation.</p> | |
| − | | | + | |} |
| − | + | ||
| − | + | Returning to the Othello example, let us take up the 2-adic relatives <math>^{\backprime\backprime}\, \text{lover of}\, \underline{~~ ~~}\, ^{\prime\prime}</math> and <math>^{\backprime\backprime}\, \text{servant of}\, \underline{~~ ~~}\, ^{\prime\prime}.</math> | |
| + | |||
| + | Ignoring the many splendored nuances appurtenant to the idea of love, we may regard the relative term <math>\mathit{l}\!</math> for <math>^{\backprime\backprime}\, \text{lover of}\, \underline{~~ ~~}\, ^{\prime\prime}</math> to be given by the following equation: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | + | <math>\begin{array}{*{13}{c}} | |
| − | + | \mathit{l} | |
| − | | | + | & = & |
| − | + | \mathrm{B}:\mathrm{C} | |
| − | | | + | & +\!\!, & |
| + | \mathrm{C}:\mathrm{B} | ||
| + | & +\!\!, & | ||
| + | \mathrm{D}:\mathrm{O} | ||
| + | & +\!\!, & | ||
| + | \mathrm{E}:\mathrm{I} | ||
| + | & +\!\!, & | ||
| + | \mathrm{I}:\mathrm{E} | ||
| + | & +\!\!, & | ||
| + | \mathrm{O}:\mathrm{D} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| + | |||
| + | If for no better reason than to make the example more interesting, let us put aside all distinctions of rank and fealty, collapsing the motley crews of attendant, servant, subordinate, and so on, under the heading of a single service, denoted by the relative term <math>\mathit{s}\!</math> for <math>^{\backprime\backprime}\, \text{servant of}\, \underline{~~ ~~}\, ^{\prime\prime}.</math> The terms of this service are: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | + | <math>\begin{array}{*{11}{c}} | |
| − | + | \mathit{s} | |
| − | + | & = & | |
| − | + | \mathrm{C}:\mathrm{O} | |
| − | + | & +\!\!, & | |
| − | + | \mathrm{E}:\mathrm{D} | |
| − | + | & +\!\!, & | |
| − | + | \mathrm{I}:\mathrm{O} | |
| − | + | & +\!\!, & | |
| − | + | \mathrm{J}:\mathrm{D} | |
| − | + | & +\!\!, & | |
| − | + | \mathrm{J}:\mathrm{O} | |
| − | + | \end{array}</math> | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | + | The term <math>\mathrm{I}:\mathrm{C}\!</math> may also be implied, but, since it is so hotly arguable, I will leave it out of the toll. | |
| − | + | One more thing that we need to be duly wary about: There are many different conventions in the field as to the ordering of terms in their applications, and it happens that different conventions will be more convenient under different circumstances, so there does not appear to be much of a chance that any one of them can be canonized once and for all. | |
| − | |||
| − | |||
| − | |||
| − | + | In the current reading, we are applying relative terms from right to left, and so our conception of relative multiplication, or relational composition, will need to be adjusted accordingly. | |
| − | |||
| − | |||
| − | + | ===Commentary Note 8.4=== | |
| − | + | To familiarize ourselves with the forms of calculation that are available in Peirce's notation, let us compute a few of the simplest products that we find at hand in the Othello case. | |
| − | |||
| − | |||
| − | the | ||
| − | |||
| − | |||
| − | + | Here are the absolute terms: | |
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | | ||
| + | <math>\begin{array}{*{15}{c}} | ||
| + | \mathbf{1} | ||
| + | & = & \mathrm{B} | ||
| + | & +\!\!, & \mathrm{C} | ||
| + | & +\!\!, & \mathrm{D} | ||
| + | & +\!\!, & \mathrm{E} | ||
| + | & +\!\!, & \mathrm{I} | ||
| + | & +\!\!, & \mathrm{J} | ||
| + | & +\!\!, & \mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{b} | ||
| + | & = & \mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{m} | ||
| + | & = & \mathrm{C} | ||
| + | & +\!\!, & \mathrm{I} | ||
| + | & +\!\!, & \mathrm{J} | ||
| + | & +\!\!, & \mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{w} | ||
| + | & = & \mathrm{B} | ||
| + | & +\!\!, & \mathrm{D} | ||
| + | & +\!\!, & \mathrm{E} | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| − | + | Here are the 2-adic relative terms: | |
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | | ||
| + | <math>\begin{array}{*{13}{c}} | ||
| + | \mathit{l} | ||
| + | & = & \mathrm{B}:\mathrm{C} | ||
| + | & +\!\!, & \mathrm{C}:\mathrm{B} | ||
| + | & +\!\!, & \mathrm{D}:\mathrm{O} | ||
| + | & +\!\!, & \mathrm{E}:\mathrm{I} | ||
| + | & +\!\!, & \mathrm{I}:\mathrm{E} | ||
| + | & +\!\!, & \mathrm{O}:\mathrm{D} | ||
| + | \\[6pt] | ||
| + | \mathit{s} | ||
| + | & = & \mathrm{C}:\mathrm{O} | ||
| + | & +\!\!, & \mathrm{E}:\mathrm{D} | ||
| + | & +\!\!, & \mathrm{I}:\mathrm{O} | ||
| + | & +\!\!, & \mathrm{J}:\mathrm{D} | ||
| + | & +\!\!, & \mathrm{J}:\mathrm{O} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | Here are a few of the simplest products among these terms: | |
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | | |
| + | <math>\begin{array}{lll} | ||
| + | \mathit{l}\mathbf{1} | ||
| + | & = & | ||
| + | \text{lover of anything} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | (\mathrm{B}\!:\!\mathrm{C} ~+\!\!,~ \mathrm{C}\!:\!\mathrm{B} ~+\!\!,~ \mathrm{D}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{E}\!:\!\mathrm{I} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{E} ~+\!\!,~ \mathrm{O}\!:\!\mathrm{D}) | ||
| + | \\ | ||
| + | & & | ||
| + | \times | ||
| + | \\ | ||
| + | & & | ||
| + | (\mathrm{B} ~+\!\!,~ \mathrm{C} ~+\!\!,~ \mathrm{D} ~+\!\!,~ \mathrm{E} ~+\!\!,~ \mathrm{I} ~+\!\!,~ \mathrm{J} ~+\!\!,~ \mathrm{O}) | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \mathrm{B} ~+\!\!,~ \mathrm{C} ~+\!\!,~ \mathrm{D} ~+\!\!,~ \mathrm{E} ~+\!\!,~ \mathrm{I} ~+\!\!,~ \mathrm{O} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \text{anything except}~\mathrm{J} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | " | + | {| align="center" cellspacing="6" width="90%" |
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \mathit{l}\mathrm{b} | ||
| + | & = & | ||
| + | \text{lover of a black} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | (\mathrm{B}\!:\!\mathrm{C} ~+\!\!,~ \mathrm{C}\!:\!\mathrm{B} ~+\!\!,~ \mathrm{D}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{E}\!:\!\mathrm{I} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{E} ~+\!\!,~ \mathrm{O}\!:\!\mathrm{D}) | ||
| + | \\ | ||
| + | & & | ||
| + | \times | ||
| + | \\ | ||
| + | & & | ||
| + | \mathrm{O} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \mathrm{D} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | " | + | {| align="center" cellspacing="6" width="90%" |
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \mathit{l}\mathrm{m} | ||
| + | & = & | ||
| + | \text{lover of a man} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | (\mathrm{B}\!:\!\mathrm{C} ~+\!\!,~ \mathrm{C}\!:\!\mathrm{B} ~+\!\!,~ \mathrm{D}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{E}\!:\!\mathrm{I} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{E} ~+\!\!,~ \mathrm{O}\!:\!\mathrm{D}) | ||
| + | \\ | ||
| + | & & | ||
| + | \times | ||
| + | \\ | ||
| + | & & | ||
| + | (\mathrm{C} ~+\!\!,~ \mathrm{I} ~+\!\!,~ \mathrm{J} ~+\!\!,~ \mathrm{O}) | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \mathrm{B} ~+\!\!,~ \mathrm{D} ~+\!\!,~ \mathrm{E} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | " | + | {| align="center" cellspacing="6" width="90%" |
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \mathit{l}\mathrm{w} | ||
| + | & = & | ||
| + | \text{lover of a woman} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | (\mathrm{B}\!:\!\mathrm{C} ~+\!\!,~ \mathrm{C}\!:\!\mathrm{B} ~+\!\!,~ \mathrm{D}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{E}\!:\!\mathrm{I} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{E} ~+\!\!,~ \mathrm{O}\!:\!\mathrm{D}) | ||
| + | \\ | ||
| + | & & | ||
| + | \times | ||
| + | \\ | ||
| + | & & | ||
| + | (\mathrm{B} ~+\!\!,~ \mathrm{D} ~+\!\!,~ \mathrm{E}) | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \mathrm{C} ~+\!\!,~ \mathrm{I} ~+\!\!,~ \mathrm{O} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | | |
| + | <math>\begin{array}{lll} | ||
| + | \mathit{s}\mathbf{1} | ||
| + | & = & | ||
| + | \text{servant of anything} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | (\mathrm{C}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{E}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{O}) | ||
| + | \\ | ||
| + | & & | ||
| + | \times | ||
| + | \\ | ||
| + | & & | ||
| + | (\mathrm{B} ~+\!\!,~ \mathrm{C} ~+\!\!,~ \mathrm{D} ~+\!\!,~ \mathrm{E} ~+\!\!,~ \mathrm{I} ~+\!\!,~ \mathrm{J} ~+\!\!,~ \mathrm{O}) | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \mathrm{C} ~+\!\!,~ \mathrm{E} ~+\!\!,~ \mathrm{I} ~+\!\!,~ \mathrm{J} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | b | + | {| align="center" cellspacing="6" width="90%" |
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \mathit{s}\mathrm{b} | ||
| + | & = & | ||
| + | \text{servant of a black} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | (\mathrm{C}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{E}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{O}) | ||
| + | \\ | ||
| + | & & | ||
| + | \times | ||
| + | \\ | ||
| + | & & | ||
| + | \mathrm{O} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \mathrm{C} ~+\!\!,~ \mathrm{I} ~+\!\!,~ \mathrm{J} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | m | + | {| align="center" cellspacing="6" width="90%" |
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \mathit{s}\mathrm{m} | ||
| + | & = & | ||
| + | \text{servant of a man} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | (\mathrm{C}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{E}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{O}) | ||
| + | \\ | ||
| + | & & | ||
| + | \times | ||
| + | \\ | ||
| + | & & | ||
| + | (\mathrm{C} ~+\!\!,~ \mathrm{I} ~+\!\!,~ \mathrm{J} ~+\!\!,~ \mathrm{O}) | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \mathrm{C} ~+\!\!,~ \mathrm{I} ~+\!\!,~ \mathrm{J} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | w | + | {| align="center" cellspacing="6" width="90%" |
| − | </ | + | | |
| + | <math>\begin{array}{lll} | ||
| + | \mathit{s}\mathrm{w} | ||
| + | & = & | ||
| + | \text{servant of a woman} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | (\mathrm{C}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{E}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{O}) | ||
| + | \\ | ||
| + | & & | ||
| + | \times | ||
| + | \\ | ||
| + | & & | ||
| + | (\mathrm{B} ~+\!\!,~ \mathrm{D} ~+\!\!,~ \mathrm{E}) | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \mathrm{E} ~+\!\!,~ \mathrm{J} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | == | + | {| align="center" cellspacing="6" width="90%" |
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \mathit{l}\mathit{s} | ||
| + | & = & | ||
| + | \text{lover of a servant of}\, \underline{~~ ~~} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | (\mathrm{B}\!:\!\mathrm{C} ~+\!\!,~ \mathrm{C}\!:\!\mathrm{B} ~+\!\!,~ \mathrm{D}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{E}\!:\!\mathrm{I} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{E} ~+\!\!,~ \mathrm{O}\!:\!\mathrm{D}) | ||
| + | \\ | ||
| + | & & | ||
| + | \times | ||
| + | \\ | ||
| + | & & | ||
| + | (\mathrm{C}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{E}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{O}) | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \mathrm{B}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{E}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{D} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | < | + | {| align="center" cellspacing="6" width="90%" |
| − | I | + | | |
| − | + | <math>\begin{array}{lll} | |
| + | \mathit{s}\mathit{l} | ||
| + | & = & | ||
| + | \text{servant of a lover of}\, \underline{~~ ~~} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | (\mathrm{C}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{E}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{O}) | ||
| + | \\ | ||
| + | & & | ||
| + | \times | ||
| + | \\ | ||
| + | & & | ||
| + | (\mathrm{B}\!:\!\mathrm{C} ~+\!\!,~ \mathrm{C}\!:\!\mathrm{B} ~+\!\!,~ \mathrm{D}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{E}\!:\!\mathrm{I} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{E} ~+\!\!,~ \mathrm{O}\!:\!\mathrm{D}) | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \mathrm{C}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{E}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{O} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | Among other things, one observes that the relative terms <math>\mathit{l}\!</math> and <math>\mathit{s}\!</math> do not commute, that is, <math>\mathit{l}\mathit{s}\!</math> is not equal to <math>\mathit{s}\mathit{l}.~\!</math> | |
| − | that | ||
| − | + | ===Commentary Note 8.5=== | |
| − | + | Since multiplication by a 2-adic relative term is a logical analogue of matrix multiplication in linear algebra, all of the products that we computed above can be represented in terms of logical matrices and logical vectors. | |
| − | + | Here are the absolute terms again, followed by their representation as ''coefficient tuples'', otherwise thought of as ''coordinate vectors''. | |
| − | w | + | {| align="center" cellspacing="6" width="90%" |
| + | | | ||
| + | <math>\begin{array}{ccrcccccccccccl} | ||
| + | \mathbf{1} | ||
| + | & = & \mathrm{B} | ||
| + | & +\!\!, & \mathrm{C} | ||
| + | & +\!\!, & \mathrm{D} | ||
| + | & +\!\!, & \mathrm{E} | ||
| + | & +\!\!, & \mathrm{I} | ||
| + | & +\!\!, & \mathrm{J} | ||
| + | & +\!\!, & \mathrm{O} | ||
| + | \\[10pt] | ||
| + | & = & (1 & , & 1 & , & 1 & , & 1 & , & 1 & , & 1 & , & 1) | ||
| + | \\[20pt] | ||
| + | \mathrm{b} | ||
| + | & = & | ||
| + | & & | ||
| + | & & | ||
| + | & & | ||
| + | & & | ||
| + | & & | ||
| + | & & | ||
| + | \mathrm{O} | ||
| + | \\[10pt] | ||
| + | & = & (0 & , & 0 & , & 0 & , & 0 & , & 0 & , & 0 & , & 1) | ||
| + | \\[20pt] | ||
| + | \mathrm{m} | ||
| + | & = & | ||
| + | & & \mathrm{C} | ||
| + | & & | ||
| + | & & | ||
| + | & +\!\!, & \mathrm{I} | ||
| + | & +\!\!, & \mathrm{J} | ||
| + | & +\!\!, & \mathrm{O} | ||
| + | \\[10pt] | ||
| + | & = & (0 & , & 1 & , & 0 & , & 0 & , & 1 & , & 1 & , & 1) | ||
| + | \\[20pt] | ||
| + | \mathrm{w} | ||
| + | & = & \mathrm{B} | ||
| + | & & | ||
| + | & +\!\!, & \mathrm{D} | ||
| + | & +\!\!, & \mathrm{E} | ||
| + | & & | ||
| + | & & | ||
| + | & & | ||
| + | \\[10pt] | ||
| + | & = & (1 & , & 0 & , & 1 & , & 1 & , & 0 & , & 0 & , & 0) | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | Since we are going to be regarding these tuples as ''column vectors'', it is convenient to arrange them into a table of the following form: | |
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | | |
| − | + | <math>\begin{array}{c|cccc} | |
| − | + | \text{ } & \mathbf{1} & \mathrm{b} & \mathrm{m} & \mathrm{w} | |
| + | \\ | ||
| + | \text{---} & \text{---} & \text{---} & \text{---} & \text{---} | ||
| + | \\ | ||
| + | \mathrm{B} & 1 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | \mathrm{C} & 1 & 0 & 1 & 0 | ||
| + | \\ | ||
| + | \mathrm{D} & 1 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | \mathrm{E} & 1 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | \mathrm{I} & 1 & 0 & 1 & 0 | ||
| + | \\ | ||
| + | \mathrm{J} & 1 & 0 & 1 & 0 | ||
| + | \\ | ||
| + | \mathrm{O} & 1 & 1 & 1 & 0 | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | Here are the 2-adic relative terms again, followed by their representation as coefficient matrices, in this case bordered by row and column labels to remind us what the coefficient values are meant to signify. | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | | |
| − | + | <math>\begin{array}{*{13}{c}} | |
| − | + | \mathit{l} | |
| + | & = & \mathrm{B}:\mathrm{C} | ||
| + | & +\!\!, & \mathrm{C}:\mathrm{B} | ||
| + | & +\!\!, & \mathrm{D}:\mathrm{O} | ||
| + | & +\!\!, & \mathrm{E}:\mathrm{I} | ||
| + | & +\!\!, & \mathrm{I}:\mathrm{E} | ||
| + | & +\!\!, & \mathrm{O}:\mathrm{D} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | | |
| − | + | <math>\begin{array}{c|ccccccc} | |
| − | + | \mathit{l} & | |
| − | + | \mathrm{B} & | |
| − | + | \mathrm{C} & | |
| + | \mathrm{D} & | ||
| + | \mathrm{E} & | ||
| + | \mathrm{I} & | ||
| + | \mathrm{J} & | ||
| + | \mathrm{O} | ||
| + | \\ | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} | ||
| + | \\ | ||
| + | \mathrm{B} & 0 & 1 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | \mathrm{C} & 1 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | \mathrm{D} & 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | \mathrm{E} & 0 & 0 & 0 & 0 & 1 & 0 & 0 | ||
| + | \\ | ||
| + | \mathrm{I} & 0 & 0 & 0 & 1 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | \mathrm{J} & 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | \mathrm{O} & 0 & 0 & 1 & 0 & 0 & 0 & 0 | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | | |
| − | + | <math>\begin{array}{*{13}{c}} | |
| − | + | \mathit{s} | |
| − | + | & = & \mathrm{C}:\mathrm{O} | |
| − | </ | + | & +\!\!, & \mathrm{E}:\mathrm{D} |
| + | & +\!\!, & \mathrm{I}:\mathrm{O} | ||
| + | & +\!\!, & \mathrm{J}:\mathrm{D} | ||
| + | & +\!\!, & \mathrm{J}:\mathrm{O} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | == | + | {| align="center" cellspacing="6" width="90%" |
| + | | | ||
| + | <math>\begin{array}{c|ccccccc} | ||
| + | \mathit{s} & | ||
| + | \mathrm{B} & | ||
| + | \mathrm{C} & | ||
| + | \mathrm{D} & | ||
| + | \mathrm{E} & | ||
| + | \mathrm{I} & | ||
| + | \mathrm{J} & | ||
| + | \mathrm{O} | ||
| + | \\ | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} | ||
| + | \\ | ||
| + | \mathrm{B} & 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | \mathrm{C} & 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | \mathrm{D} & 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | \mathrm{E} & 0 & 0 & 1 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | \mathrm{I} & 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | \mathrm{J} & 0 & 0 & 1 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | \mathrm{O} & 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | Here are the matrix representations of the products that we calculated before: | |
| − | |||
| − | |||
| − | 1 | + | {| align="center" cellpadding="6" width="90%" |
| − | + | | | |
| − | + | <math>\begin{matrix} | |
| − | + | \mathit{l}\mathbf{1} & = & \text{lover of anything} & = | |
| + | \end{matrix}</math> | ||
| + | |- | ||
| + | | | ||
| + | <math> | ||
| + | \begin{bmatrix} | ||
| + | 0 & 1 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 1 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 1 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 1 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 0 | ||
| + | \end{bmatrix} | ||
| + | \begin{bmatrix} | ||
| + | 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 | ||
| + | \end{bmatrix} | ||
| + | = | ||
| + | \begin{bmatrix} | ||
| + | 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 0 \\ 1 | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | |} | ||
| − | + | {| align="center" cellpadding="6" width="90%" | |
| − | + | | | |
| − | + | <math>\begin{matrix} | |
| − | + | \mathit{l}\mathrm{b} & = & \text{lover of a black} & = | |
| − | + | \end{matrix}</math> | |
| + | |- | ||
| + | | | ||
| + | <math> | ||
| + | \begin{bmatrix} | ||
| + | 0 & 1 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 1 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 1 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 1 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 0 | ||
| + | \end{bmatrix} | ||
| + | \begin{bmatrix} | ||
| + | 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 1 | ||
| + | \end{bmatrix} | ||
| + | = | ||
| + | \begin{bmatrix} | ||
| + | 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | |} | ||
| − | + | {| align="center" cellpadding="6" width="90%" | |
| − | + | | | |
| + | <math>\begin{matrix} | ||
| + | \mathit{l}\mathrm{m} & = & \text{lover of a man} & = | ||
| + | \end{matrix}</math> | ||
| + | |- | ||
| + | | | ||
| + | <math> | ||
| + | \begin{bmatrix} | ||
| + | 0 & 1 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 1 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 1 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 1 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 0 | ||
| + | \end{bmatrix} | ||
| + | \begin{bmatrix} | ||
| + | 0 \\ 1 \\ 0 \\ 0 \\ 1 \\ 1 \\ 1 | ||
| + | \end{bmatrix} | ||
| + | = | ||
| + | \begin{bmatrix} | ||
| + | 1 \\ 0 \\ 1 \\ 1 \\ 0 \\ 0 \\ 0 | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | |} | ||
| − | + | {| align="center" cellpadding="6" width="90%" | |
| − | + | | | |
| − | + | <math>\begin{matrix} | |
| + | \mathit{l}\mathrm{w} & = & \text{lover of a woman} & = | ||
| + | \end{matrix}</math> | ||
| + | |- | ||
| + | | | ||
| + | <math> | ||
| + | \begin{bmatrix} | ||
| + | 0 & 1 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 1 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 1 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 1 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 0 | ||
| + | \end{bmatrix} | ||
| + | \begin{bmatrix} | ||
| + | 1 \\ 0 \\ 1 \\ 1 \\ 0 \\ 0 \\ 0 | ||
| + | \end{bmatrix} | ||
| + | = | ||
| + | \begin{bmatrix} | ||
| + | 0 \\ 1 \\ 0 \\ 0 \\ 1 \\ 0 \\ 1 | ||
| + | \end{bmatrix}\! | ||
| + | </math> | ||
| + | |} | ||
| − | + | {| align="center" cellpadding="6" width="90%" | |
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \mathit{s}\mathbf{1} & = & \text{servant of anything} & = | ||
| + | \end{matrix}</math> | ||
| + | |- | ||
| + | | | ||
| + | <math> | ||
| + | \begin{bmatrix} | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \end{bmatrix} | ||
| + | \begin{bmatrix} | ||
| + | 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 | ||
| + | \end{bmatrix} | ||
| + | = | ||
| + | \begin{bmatrix} | ||
| + | 0 \\ 1 \\ 0 \\ 1 \\ 1 \\ 1 \\ 0 | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | |} | ||
| − | + | {| align="center" cellpadding="6" width="90%" | |
| − | + | | | |
| − | + | <math>\begin{matrix} | |
| − | + | \mathit{s}\mathrm{b} & = & \text{servant of a black} & = | |
| − | + | \end{matrix}</math> | |
| + | |- | ||
| + | | | ||
| + | <math> | ||
| + | \begin{bmatrix} | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \end{bmatrix} | ||
| + | \begin{bmatrix} | ||
| + | 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 1 | ||
| + | \end{bmatrix} | ||
| + | = | ||
| + | \begin{bmatrix} | ||
| + | 0 \\ 1 \\ 0 \\ 0 \\ 1 \\ 1 \\ 0 | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | |} | ||
| − | + | {| align="center" cellpadding="6" width="90%" | |
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \mathit{s}\mathrm{m} & = & \text{servant of a man} & = | ||
| + | \end{matrix}</math> | ||
| + | |- | ||
| + | | | ||
| + | <math> | ||
| + | \begin{bmatrix} | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \end{bmatrix} | ||
| + | \begin{bmatrix} | ||
| + | 0 \\ 1 \\ 0 \\ 0 \\ 1 \\ 1 \\ 1 | ||
| + | \end{bmatrix} | ||
| + | = | ||
| + | \begin{bmatrix} | ||
| + | 0 \\ 1 \\ 0 \\ 0 \\ 1 \\ 1 \\ 0 | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | |} | ||
| − | + | {| align="center" cellpadding="6" width="90%" | |
| − | + | | | |
| + | <math>\begin{matrix} | ||
| + | \mathit{s}\mathrm{w} & = & \text{servant of a woman} & = | ||
| + | \end{matrix}\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <math> | ||
| + | \begin{bmatrix} | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \end{bmatrix} | ||
| + | \begin{bmatrix} | ||
| + | 1 \\ 0 \\ 1 \\ 1 \\ 0 \\ 0 \\ 0 | ||
| + | \end{bmatrix} | ||
| + | = | ||
| + | \begin{bmatrix} | ||
| + | 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 1 \\ 0 | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | |} | ||
| − | + | {| align="center" cellpadding="6" width="90%" | |
| − | + | | | |
| − | + | <math>\begin{matrix} | |
| − | + | \mathit{l}\mathit{s} & = & \text{lover of a servant of ---} & = | |
| − | + | \end{matrix}</math> | |
| − | + | |- | |
| − | + | | | |
| + | <math> | ||
| + | \begin{bmatrix} | ||
| + | 0 & 1 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 1 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 1 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 1 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 0 | ||
| + | \end{bmatrix} | ||
| + | \begin{bmatrix} | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \end{bmatrix} | ||
| + | = | ||
| + | \begin{bmatrix} | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | |} | ||
| − | + | {| align="center" cellpadding="6" width="90%" | |
| − | + | | | |
| − | + | <math>\begin{matrix} | |
| − | + | \mathit{s}\mathit{l} & = & \text{servant of a lover of ---} & = | |
| − | </ | + | \end{matrix}</math> |
| + | |- | ||
| + | | | ||
| + | <math> | ||
| + | \begin{bmatrix} | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \end{bmatrix} | ||
| + | \begin{bmatrix} | ||
| + | 0 & 1 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 1 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 1 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 1 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 0 | ||
| + | \end{bmatrix} | ||
| + | = | ||
| + | \begin{bmatrix} | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 1 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | |} | ||
| − | ==Commentary Note 8. | + | ===Commentary Note 8.6=== |
| − | + | The foregoing has hopefully filled in enough background that we can begin to make sense of the more mysterious parts of CP 3.73. | |
| − | |||
| − | |||
| − | |||
| − | the | ||
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| + | | | ||
| + | <p>Thus far, we have considered the multiplication of relative terms only. Since our conception of multiplication is the application of a relation, we can only multiply absolute terms by considering them as relatives.</p> | ||
| − | + | <p>Now the absolute term “man” is really exactly equivalent to the relative term “man that is ——”, and so with any other. I shall write a comma after any absolute term to show that it is so regarded as a relative term.</p> | |
| − | b | + | <p>Then “man that is black” will be written:</p> |
| + | |- | ||
| + | | align="center" | <math>\mathrm{m},\!\mathrm{b}</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>(Peirce, CP 3.73).</p> | ||
| + | |} | ||
| − | + | In any system where elements are organized according to types, there tend to be any number of ways in which elements of one type are naturally associated with elements of another type. If the association is anything like a logical equivalence, but with the first type being lower and the second type being higher in some sense, then one may speak of a ''semantic ascent'' from the lower to the higher type. | |
| − | + | For example, it is common in mathematics to associate an element <math>a\!</math> of a set <math>A\!</math> with the constant function <math>f_a : X \to A</math> that has <math>f_a (x) = a\!</math> for all <math>x\!</math> in <math>X,\!</math> where <math>X\!</math> is an arbitrary set. Indeed, the correspondence is so close that one often uses the same name <math>{}^{\backprime\backprime} a {}^{\prime\prime}</math> to denote both the element <math>a\!</math> in <math>A\!</math> and the function <math>a = f_a : X \to A,</math> relying on the context or an explicit type indication to tell them apart. | |
| − | + | For another example, we have the ''tacit extension'' of a <math>k\!</math>-place relation <math>L \subseteq X_1 \times \ldots \times X_k\!</math> to a <math>(k+1)\!</math>-place relation <math>L^\prime \subseteq X_1 \times \ldots \times X_{k+1}\!</math> that we get by letting <math>L^\prime = L \times X_{k+1},</math> that is, by maintaining the constraints of <math>L\!</math> on the first <math>k\!</math> variables and letting the last variable wander freely. | |
| − | ' | + | What we have here, if I understand Peirce correctly, is another such type of natural extension, sometimes called the ''diagonal extension''. This extension associates a <math>k\!</math>-adic relative or a <math>k\!</math>-adic relation, counting the absolute term and the set whose elements it denotes as the cases for <math>k = 0,\!</math> with a series of relatives and relations of higher adicities. |
| − | + | A few examples will suffice to anchor these ideas. | |
| − | + | Absolute terms: | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | | ||
| + | <math>\begin{array}{*{11}{c}} | ||
| + | \mathrm{m} | ||
| + | & = & \text{man} | ||
| + | & = & \mathrm{C} | ||
| + | & +\!\!, & \mathrm{I} | ||
| + | & +\!\!, & \mathrm{J} | ||
| + | & +\!\!, & \mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{n} | ||
| + | & = & \text{noble} | ||
| + | & = & \mathrm{C} | ||
| + | & +\!\!, & \mathrm{D} | ||
| + | & +\!\!, & \mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{w} | ||
| + | & = & \text{woman} | ||
| + | & = & \mathrm{B} | ||
| + | & +\!\!, & \mathrm{D} | ||
| + | & +\!\!, & \mathrm{E} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | Diagonal extensions: | |
| − | = | + | {| align="center" cellspacing="6" width="90%" |
| + | | | ||
| + | <math>\begin{array}{*{11}{c}} | ||
| + | \mathrm{m,} | ||
| + | & = & \text{man that is}\, \underline{~~ ~~} | ||
| + | & = & \mathrm{C}:\mathrm{C} | ||
| + | & +\!\!, & \mathrm{I}:\mathrm{I} | ||
| + | & +\!\!, & \mathrm{J}:\mathrm{J} | ||
| + | & +\!\!, & \mathrm{O}:\mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{n,} | ||
| + | & = & \text{noble that is}\, \underline{~~ ~~} | ||
| + | & = & \mathrm{C}:\mathrm{C} | ||
| + | & +\!\!, & \mathrm{D}:\mathrm{D} | ||
| + | & +\!\!, & \mathrm{O}:\mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{w,} | ||
| + | & = & \text{woman that is}\, \underline{~~ ~~} | ||
| + | & = & \mathrm{B}:\mathrm{B} | ||
| + | & +\!\!, & \mathrm{D}:\mathrm{D} | ||
| + | & +\!\!, & \mathrm{E}:\mathrm{E} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | Sample products: | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \mathrm{m},\!\mathrm{n} | ||
| + | & = & | ||
| + | \text{man that is noble} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | (\mathrm{C}\!:\!\mathrm{C} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{I} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{J} ~+\!\!,~ \mathrm{O}\!:\!\mathrm{O}) | ||
| + | \\ | ||
| + | & & | ||
| + | \times | ||
| + | \\ | ||
| + | & & | ||
| + | (\mathrm{C} ~+\!\!,~ \mathrm{D} ~+\!\!,~ \mathrm{O}) | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \mathrm{C} ~+\!\!,~ \mathrm{O} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \mathrm{n},\!\mathrm{m} | ||
| + | & = & | ||
| + | \text{noble that is a man} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | (\mathrm{C}\!:\!\mathrm{C} ~+\!\!,~ \mathrm{D}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{O}\!:\!\mathrm{O}) | ||
| + | \\ | ||
| + | & & | ||
| + | \times | ||
| + | \\ | ||
| + | & & | ||
| + | (\mathrm{C} ~+\!\!,~ \mathrm{I} ~+\!\!,~ \mathrm{J} ~+\!\!,~ \mathrm{O}) | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \mathrm{C} ~+\!\!,~ \mathrm{O} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \mathrm{w},\!\mathrm{n} | ||
| + | & = & | ||
| + | \text{woman that is noble} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | (\mathrm{B}\!:\!\mathrm{B} ~+\!\!,~ \mathrm{D}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{E}\!:\!\mathrm{E}) | ||
| + | \\ | ||
| + | & & | ||
| + | \times | ||
| + | \\ | ||
| + | & & | ||
| + | (\mathrm{C} ~+\!\!,~ \mathrm{D} ~+\!\!,~ \mathrm{O}) | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \mathrm{D} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \mathrm{n},\!\mathrm{w} | ||
| + | & = & | ||
| + | \text{noble that is a woman} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | (\mathrm{C}\!:\!\mathrm{C} ~+\!\!,~ \mathrm{D}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{O}\!:\!\mathrm{O}) | ||
| + | \\ | ||
| + | & & | ||
| + | \times | ||
| + | \\ | ||
| + | & & | ||
| + | (\mathrm{B} ~+\!\!,~ \mathrm{D} ~+\!\!,~ \mathrm{E}) | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \mathrm{D} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | ==Selection 9== | |
| − | + | ===The Signs for Multiplication (cont.)=== | |
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| + | | | ||
| + | <p>It is obvious that multiplication into a multiplicand indicated by a comma is commutative<sup>1</sup>, that is,</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathit{s},\!\mathit{l} ~=~ \mathit{l},\!\mathit{s}</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>This multiplication is effectively the same as that of Boole in his logical calculus. Boole's unity is my <math>\mathbf{1},</math> that is, it denotes whatever is.</p> | ||
| − | + | #<p>It will often be convenient to speak of the whole operation of affixing a comma and then multiplying as a commutative multiplication, the sign for which is the comma. But though this is allowable, we shall fall into confusion at once if we ever forget that in point of fact it is not a different multiplication, only it is multiplication by a relative whose meaning — or rather whose syntax — has been slightly altered; and that the comma is really the sign of this modification of the foregoing term.</p> | |
| − | + | <p>(Peirce, CP 3.74).</p> | |
| + | |} | ||
| − | + | ===Commentary Note 9.1=== | |
| − | + | Let us backtrack a few years, and consider how George Boole explained his twin conceptions of ''selective operations'' and ''selective symbols''. | |
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| + | | | ||
| + | <p>Let us then suppose that the universe of our discourse is the actual universe, so that words are to be used in the full extent of their meaning, and let us consider the two mental operations implied by the words “white” and “men”. The word “men” implies the operation of selecting in thought from its subject, the universe, all men; and the resulting conception, ''men'', becomes the subject of the next operation. The operation implied by the word “white” is that of selecting from its subject, “men”, all of that class which are white. The final resulting conception is that of “white men”.</p> | ||
| − | ' | + | <p>Now it is perfectly apparent that if the operations above described had been performed in a converse order, the result would have been the same. Whether we begin by forming the conception of “''men''”, and then by a second intellectual act limit that conception to “white men”, or whether we begin by forming the conception of “white objects”, and then limit it to such of that class as are “men”, is perfectly indifferent so far as the result is concerned. It is obvious that the order of the mental processes would be equally indifferent if for the words “white” and “men” we substituted any other descriptive or appellative terms whatever, provided only that their meaning was fixed and absolute. And thus the indifference of the order of two successive acts of the faculty of Conception, the one of which furnishes the subject upon which the other is supposed to operate, is a general condition of the exercise of that faculty. It is a law of the mind, and it is the real origin of that law of the literal symbols of Logic which constitutes its formal expression (1) Chap. II, [ namely, <math>xy = yx~\!</math> ].</p> |
| − | + | <p>It is equally clear that the mental operation above described is of such a nature that its effect is not altered by repetition. Suppose that by a definite act of conception the attention has been fixed upon men, and that by another exercise of the same faculty we limit it to those of the race who are white. Then any further repetition of the latter mental act, by which the attention is limited to white objects, does not in any way modify the conception arrived at, viz., that of white men. This is also an example of a general law of the mind, and it has its formal expression in the law ((2) Chap. II) of the literal symbols [ namely, <math>x^2 = x\!</math> ].</p> | |
| − | + | <p>(Boole, ''Laws of Thought'', 44–45).</p> | |
| + | |} | ||
| − | + | ===Commentary Note 9.2=== | |
| − | + | In setting up his discussion of selective operations and their corresponding selective symbols, Boole writes this: | |
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| + | | | ||
| + | <p>The operation which we really perform is one of ''selection according to a prescribed principle or idea''. To what faculties of the mind such an operation would be referred, according to the received classification of its powers, it is not important to inquire, but I suppose that it would be considered as dependent upon the two faculties of Conception or Imagination, and Attention. To the one of these faculties might be referred the formation of the general conception; to the other the fixing of the mental regard upon those individuals within the prescribed universe of discourse which answer to the conception. If, however, as seems not improbable, the power of Attention is nothing more than the power of continuing the exercise of any other faculty of the mind, we might properly regard the whole of the mental process above described as referrible to the mental faculty of Imagination or Conception, the first step of the process being the conception of the Universe itself, and each succeeding step limiting in a definite manner the conception thus formed. Adopting this view, I shall describe each such step, or any definite combination of such steps, as a ''definite act of conception''.</p> | ||
| − | ' | + | <p>(Boole, ''Laws of Thought'', 43).</p> |
| + | |} | ||
| − | + | ===Commentary Note 9.3=== | |
| − | + | In algebra, an ''idempotent element'' <math>x\!</math> is one that obeys the ''idempotent law'', that is, it satisfies the equation <math>xx = x.\!</math> Under most circumstances, it is usual to write this as <math>x^2 = x.\!</math> | |
| − | + | If the algebraic system in question falls under the additional laws that are necessary to carry out the requisite transformations, then <math>x^2 = x\!</math> is convertible into <math>x - x^2 = 0,\!</math> and this into <math>x(1 - x) = 0.\!</math> | |
| − | + | If the algebraic system in question happens to be a boolean algebra, then the equation <math>x(1 - x) = 0\!</math> says that <math>x \land \lnot x</math> is identically false, in effect, a statement of the classical principle of non-contradiction. | |
| − | + | We have already seen how Boole found rationales for the commutative law and the idempotent law by contemplating the properties of ''selective operations''. | |
| − | ' | + | It is time to bring these threads together, which we can do by considering the so-called ''idempotent representation'' of sets. This will give us one of the best ways to understand the significance that Boole attached to selective operations. It will also link up with the statements that Peirce makes about his adicity-augmenting comma operation. |
| − | + | ===Commentary Note 9.4=== | |
| − | + | Boole rationalized the properties of what we now call ''boolean multiplication'', roughly equivalent to logical conjunction, in terms of the laws that apply to selective operations. Peirce, in his turn, taking a very significant step of analysis that has seldom been recognized for what it would lead to, does not consider this multiplication to be a fundamental operation, but derives it as a by-product of relative multiplication by a comma relative. Thus, Peirce makes logical conjunction a special case of relative composition. | |
| − | + | This opens up a very wide field of investigation, ''the operational significance of logical terms'', one might say, but it will be best to advance bit by bit, and to lean on simple examples. | |
| − | |||
| − | |||
| − | |||
| − | + | Back to Venice, and the close-knit party of absolutes and relatives that we were entertaining when last we were there. | |
| − | + | Here is the list of absolute terms that we were considering before, to which I have thrown in <math>\mathbf{1},</math> the universe of ''anything'', just for good measure: | |
| − | |||
| − | is | ||
| − | in | ||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | | |
| − | + | <math>\begin{array}{*{17}{l}} | |
| + | \mathbf{1} | ||
| + | & = & \text{anything} | ||
| + | & = & \mathrm{B} | ||
| + | & +\!\!, & \mathrm{C} | ||
| + | & +\!\!, & \mathrm{D} | ||
| + | & +\!\!, & \mathrm{E} | ||
| + | & +\!\!, & \mathrm{I} | ||
| + | & +\!\!, & \mathrm{J} | ||
| + | & +\!\!, & \mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{m} | ||
| + | & = & \text{man} | ||
| + | & = & \mathrm{C} | ||
| + | & +\!\!, & \mathrm{I} | ||
| + | & +\!\!, & \mathrm{J} | ||
| + | & +\!\!, & \mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{n} | ||
| + | & = & \text{noble} | ||
| + | & = & \mathrm{C} | ||
| + | & +\!\!, & \mathrm{D} | ||
| + | & +\!\!, & \mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{w} | ||
| + | & = & \text{woman} | ||
| + | & = & \mathrm{B} | ||
| + | & +\!\!, & \mathrm{D} | ||
| + | & +\!\!, & \mathrm{E} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | Here is the list of ''comma inflexions'' or ''diagonal extensions'' of these terms: | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | \mathbf{1,} | ||
| + | & = & \text{anything that is}\, \underline{~~ ~~} | ||
| + | \\[6pt] | ||
| + | & = & \mathrm{B}\!:\!\mathrm{B} ~+\!\!,~ \mathrm{C}\!:\!\mathrm{C} ~+\!\!,~ \mathrm{D}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{E}\!:\!\mathrm{E} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{I} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{J} ~+\!\!,~ \mathrm{O}\!:\!\mathrm{O} | ||
| + | \\[9pt] | ||
| + | \mathrm{m,} | ||
| + | & = & \text{man that is}\, \underline{~~ ~~} | ||
| + | \\[6pt] | ||
| + | & = & \mathrm{C}\!:\!\mathrm{C} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{I} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{J} ~+\!\!,~ \mathrm{O}\!:\!\mathrm{O} | ||
| + | \\[9pt] | ||
| + | \mathrm{n,} | ||
| + | & = & \text{noble that is}\, \underline{~~ ~~} | ||
| + | \\[6pt] | ||
| + | & = & \mathrm{C}\!:\!\mathrm{C} ~+\!\!,~ \mathrm{D}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{O}\!:\!\mathrm{O} | ||
| + | \\[9pt] | ||
| + | \mathrm{w,} | ||
| + | & = & \text{woman that is}\, \underline{~~ ~~} | ||
| + | \\[6pt] | ||
| + | & = & \mathrm{B}\!:\!\mathrm{B} ~+\!\!,~ \mathrm{D}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{E}\!:\!\mathrm{E} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | One observes that the diagonal extension of <math>\mathbf{1}</math> is the same thing as the identity relation <math>\mathit{1}.\!</math> | |
| − | + | Working within our smaller sample of absolute terms, we have already computed the sorts of products that apply the diagonal extension of an absolute term to another absolute term, for instance, these products: | |
| − | m | + | {| align="center" cellspacing="6" width="90%" |
| + | | | ||
| + | <math>\begin{array}{lllll} | ||
| + | \mathrm{m},\!\mathrm{n} | ||
| + | & = & \text{man that is noble} | ||
| + | & = & \mathrm{C} ~+\!\!,~ \mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{n},\!\mathrm{m} | ||
| + | & = & \text{noble that is a man} | ||
| + | & = & \mathrm{C} ~+\!\!,~ \mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{w},\!\mathrm{n} | ||
| + | & = & \text{woman that is noble} | ||
| + | & = & \mathrm{D} | ||
| + | \\[6pt] | ||
| + | \mathrm{n},\!\mathrm{w} | ||
| + | & = & \text{noble that is a woman} | ||
| + | & = & \mathrm{D} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | This exercise gave us a bit of practical insight into why the commutative law holds for logical conjunction. | |
| − | w | + | Further insight into the laws that govern this realm of logic, and the underlying reasons why they apply, might be gained by systematically working through the whole variety of different products that are generated by the operational means in sight, namely, the products indicated by <math>\{\mathbf{1}, \mathrm{m}, \mathrm{n}, \mathrm{w} \} , \{\mathbf{1}, \mathrm{m}, \mathrm{n}, \mathrm{w} \}.</math> |
| − | + | But before we try to explore this territory more systematically, let us equip our intuitions with the forms of graphical and matrical representation that served us so well in our previous adventures. | |
| − | + | ===Commentary Note 9.5=== | |
| − | |||
| − | + | Peirce's comma operation, in its application to an absolute term, is tantamount to the representation of that term's denotation as an idempotent transformation, which is commonly represented as a diagonal matrix. Hence the alternate name, ''diagonal extension''. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | An idempotent element <math>x\!</math> is given by the abstract condition that <math>xx = x,\!</math> but elements like these are commonly encountered in more concrete circumstances, acting as operators or transformations on other sets or spaces, and in that action they will often be represented as matrices of coefficients. | |
| − | |||
| − | |||
| − | |||
| − | ' | + | Let's see how this looks in the matrix and graph pictures of absolute and relative terms: |
| − | + | ====Absolute Terms==== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | | ||
| + | <math>\begin{array}{*{17}{l}} | ||
| + | \mathbf{1} & = & \text{anything} & = & | ||
| + | \mathrm{B} & +\!\!, & | ||
| + | \mathrm{C} & +\!\!, & | ||
| + | \mathrm{D} & +\!\!, & | ||
| + | \mathrm{E} & +\!\!, & | ||
| + | \mathrm{I} & +\!\!, & | ||
| + | \mathrm{J} & +\!\!, & | ||
| + | \mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{m} & = & \text{man} & = & | ||
| + | \mathrm{C} & +\!\!, & | ||
| + | \mathrm{I} & +\!\!, & | ||
| + | \mathrm{J} & +\!\!, & | ||
| + | \mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{n} & = & \text{noble} & = & | ||
| + | \mathrm{C} & +\!\!, & | ||
| + | \mathrm{D} & +\!\!, & | ||
| + | \mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{w} & = & \text{woman} & = & | ||
| + | \mathrm{B} & +\!\!, & | ||
| + | \mathrm{D} & +\!\!, & | ||
| + | \mathrm{E} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | Previously, we represented absolute terms as column arrays. The above four terms are given by the columns of the following table: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | | |
| + | <math>\begin{array}{c|cccc} | ||
| + | \text{ } & \mathbf{1} & \mathrm{m} & \mathrm{n} & \mathrm{w} \\ | ||
| + | \text{---} & \text{---} & \text{---} & \text{---} & \text{---} \\ | ||
| + | \mathrm{B} & 1 & 0 & 0 & 1 \\ | ||
| + | \mathrm{C} & 1 & 1 & 1 & 0 \\ | ||
| + | \mathrm{D} & 1 & 0 & 1 & 1 \\ | ||
| + | \mathrm{E} & 1 & 0 & 0 & 1 \\ | ||
| + | \mathrm{I} & 1 & 1 & 0 & 0 \\ | ||
| + | \mathrm{J} & 1 & 1 & 0 & 0 \\ | ||
| + | \mathrm{O} & 1 & 1 & 1 & 0 | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | ' | + | The types of graphs known as ''bigraphs'' or ''bipartite graphs'' can be used to picture simple relative terms, dyadic relations, and their corresponding logical matrices. One way to bring absolute terms and their corresponding sets of individuals into the bigraph picture is to mark the nodes in some way, for example, hollow nodes for non-members and filled nodes for members of the indicated set, as shown below: |
| − | | | + | {| align="center" cellpadding="10" width="90%" |
| − | | | + | | [[Image:LOR 1870 Figure 4.1.jpg]] || (4.1) |
| − | | | + | |- |
| − | | | + | | [[Image:LOR 1870 Figure 4.2.jpg]] || (4.2) |
| − | | | + | |- |
| − | | | + | | [[Image:LOR 1870 Figure 4.3.jpg]] || (4.3) |
| − | | | + | |- |
| + | | [[Image:LOR 1870 Figure 4.4.jpg]] || (4.4) | ||
| + | |} | ||
| − | + | ====Diagonal Extensions==== | |
| − | | | + | {| align="center" cellspacing="6" width="90%" |
| − | + | | | |
| − | + | <math>\begin{array}{lll} | |
| − | + | \mathbf{1,} | |
| − | | | + | & = & \text{anything that is}\, \underline{~~ ~~} |
| − | + | \\[6pt] | |
| − | + | & = & \mathrm{B}\!:\!\mathrm{B} ~+\!\!,~ \mathrm{C}\!:\!\mathrm{C} ~+\!\!,~ \mathrm{D}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{E}\!:\!\mathrm{E} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{I} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{J} ~+\!\!,~ \mathrm{O}\!:\!\mathrm{O} | |
| + | \\[9pt] | ||
| + | \mathrm{m,} | ||
| + | & = & \text{man that is}\, \underline{~~ ~~} | ||
| + | \\[6pt] | ||
| + | & = & \mathrm{C}\!:\!\mathrm{C} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{I} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{J} ~+\!\!,~ \mathrm{O}\!:\!\mathrm{O} | ||
| + | \\[9pt] | ||
| + | \mathrm{n,} | ||
| + | & = & \text{noble that is}\, \underline{~~ ~~} | ||
| + | \\[6pt] | ||
| + | & = & \mathrm{C}\!:\!\mathrm{C} ~+\!\!,~ \mathrm{D}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{O}\!:\!\mathrm{O} | ||
| + | \\[9pt] | ||
| + | \mathrm{w,} | ||
| + | & = & \text{woman that is}\, \underline{~~ ~~} | ||
| + | \\[6pt] | ||
| + | & = & \mathrm{B}\!:\!\mathrm{B} ~+\!\!,~ \mathrm{D}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{E}\!:\!\mathrm{E} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| + | |||
| + | Naturally enough, the diagonal extensions are represented by diagonal matrices: | ||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{array}{c|ccccccc} | ||
| + | \mathbf{1,} & | ||
| + | \mathrm{B} & | ||
| + | \mathrm{C} & | ||
| + | \mathrm{D} & | ||
| + | \mathrm{E} & | ||
| + | \mathrm{I} & | ||
| + | \mathrm{J} & | ||
| + | \mathrm{O} | ||
| + | \\ | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} | ||
| + | \\ | ||
| + | \mathrm{B} & 1 & & & & & & | ||
| + | \\ | ||
| + | \mathrm{C} & & 1 & & & & & | ||
| + | \\ | ||
| + | \mathrm{D} & & & 1 & & & & | ||
| + | \\ | ||
| + | \mathrm{E} & & & & 1 & & & | ||
| + | \\ | ||
| + | \mathrm{I} & & & & & 1 & & | ||
| + | \\ | ||
| + | \mathrm{J} & & & & & & 1 & | ||
| + | \\ | ||
| + | \mathrm{O} & & & & & & & 1 | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | | | + | {| align="center" cellspacing="6" width="90%" |
| − | + | | | |
| − | + | |- | |
| − | + | | | |
| − | + | <math>\begin{array}{c|ccccccc} | |
| − | + | \mathrm{m,} & | |
| − | + | \mathrm{B} & | |
| + | \mathrm{C} & | ||
| + | \mathrm{D} & | ||
| + | \mathrm{E} & | ||
| + | \mathrm{I} & | ||
| + | \mathrm{J} & | ||
| + | \mathrm{O} | ||
| + | \\ | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} | ||
| + | \\ | ||
| + | \mathrm{B} & 0 & & & & & & | ||
| + | \\ | ||
| + | \mathrm{C} & & 1 & & & & & | ||
| + | \\ | ||
| + | \mathrm{D} & & & 0 & & & & | ||
| + | \\ | ||
| + | \mathrm{E} & & & & 0 & & & | ||
| + | \\ | ||
| + | \mathrm{I} & & & & & 1 & & | ||
| + | \\ | ||
| + | \mathrm{J} & & & & & & 1 & | ||
| + | \\ | ||
| + | \mathrm{O} & & & & & & & 1 | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | | ||
| + | |- | ||
| + | | | ||
| + | <math>\begin{array}{c|ccccccc} | ||
| + | \mathrm{n,} & | ||
| + | \mathrm{B} & | ||
| + | \mathrm{C} & | ||
| + | \mathrm{D} & | ||
| + | \mathrm{E} & | ||
| + | \mathrm{I} & | ||
| + | \mathrm{J} & | ||
| + | \mathrm{O} | ||
| + | \\ | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} | ||
| + | \\ | ||
| + | \mathrm{B} & 0 & & & & & & | ||
| + | \\ | ||
| + | \mathrm{C} & & 1 & & & & & | ||
| + | \\ | ||
| + | \mathrm{D} & & & 1 & & & & | ||
| + | \\ | ||
| + | \mathrm{E} & & & & 0 & & & | ||
| + | \\ | ||
| + | \mathrm{I} & & & & & 0 & & | ||
| + | \\ | ||
| + | \mathrm{J} & & & & & & 0 & | ||
| + | \\ | ||
| + | \mathrm{O} & & & & & & & 1 | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | | | + | {| align="center" cellspacing="6" width="90%" |
| − | + | | | |
| − | + | |- | |
| − | + | | | |
| − | + | <math>\begin{array}{c|ccccccc} | |
| − | + | \mathrm{w,} & | |
| − | | | + | \mathrm{B} & |
| + | \mathrm{C} & | ||
| + | \mathrm{D} & | ||
| + | \mathrm{E} & | ||
| + | \mathrm{I} & | ||
| + | \mathrm{J} & | ||
| + | \mathrm{O} | ||
| + | \\ | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} & | ||
| + | \text{---} | ||
| + | \\ | ||
| + | \mathrm{B} & 1 & & & & & & | ||
| + | \\ | ||
| + | \mathrm{C} & & 0 & & & & & | ||
| + | \\ | ||
| + | \mathrm{D} & & & 1 & & & & | ||
| + | \\ | ||
| + | \mathrm{E} & & & & 1 & & & | ||
| + | \\ | ||
| + | \mathrm{I} & & & & & 0 & & | ||
| + | \\ | ||
| + | \mathrm{J} & & & & & & 0 & | ||
| + | \\ | ||
| + | \mathrm{O} & & & & & & & 0 | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | Cast into the bigraph picture of dyadic relations, the diagonal extension of an absolute term takes on a very distinctive sort of “straight-laced” character: | |
| − | | | + | {| align="center" cellpadding="10" width="90%" |
| − | | | + | | [[Image:LOR 1870 Figure 5.1.jpg]] || (5.1) |
| − | | | + | |- |
| − | | | + | | [[Image:LOR 1870 Figure 5.2.jpg]] || (5.2) |
| − | | | + | |- |
| − | | | + | | [[Image:LOR 1870 Figure 5.3.jpg]] || (5.3) |
| − | | | + | |- |
| + | | [[Image:LOR 1870 Figure 5.4.jpg]] || (5.4) | ||
| + | |} | ||
| − | + | ===Commentary Note 9.6=== | |
| − | + | Just to be doggedly persistent about it, here is what ought to be a sufficient sample of products involving the multiplication of a comma relative onto an absolute term, presented in both matrix and bigraph pictures. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ====Example 1==== | |
| − | | | + | {| align="center" cellpadding="6" width="90%" |
| − | + | | <math>\mathbf{1,}\mathbf{1} ~=~ \mathbf{1}\!</math> | |
| − | + | |- | |
| − | + | | <math>\text{anything that is anything} ~=~ \text{anything}</math> | |
| − | + | |- | |
| − | + | | | |
| − | + | <math> | |
| + | \begin{bmatrix} | ||
| + | 1 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 1 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 1 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 1 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 1 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \end{bmatrix} | ||
| + | \begin{bmatrix} | ||
| + | 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 | ||
| + | \end{bmatrix} | ||
| + | = | ||
| + | \begin{bmatrix} | ||
| + | 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | |} | ||
| − | + | {| align="center" cellpadding="10" width="100%" | |
| + | | width="2%" | | ||
| + | | width="48%" | [[Image:LOR 1870 Figure 6.1.jpg]] | ||
| + | | width="50%" | (6.1) | ||
| + | |} | ||
| − | + | ====Example 2==== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellpadding="6" width="90%" | |
| + | | <math>\mathbf{1,}\mathrm{m} ~=~ \mathrm{m}</math> | ||
| + | |- | ||
| + | | <math>\text{anything that is a man} ~=~ \text{man}</math> | ||
| + | |- | ||
| + | | | ||
| + | <math> | ||
| + | \begin{bmatrix} | ||
| + | 1 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 1 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 1 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 1 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 1 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \end{bmatrix} | ||
| + | \begin{bmatrix} | ||
| + | 0 \\ 1 \\ 0 \\ 0 \\ 1 \\ 1 \\ 1 | ||
| + | \end{bmatrix} | ||
| + | = | ||
| + | \begin{bmatrix} | ||
| + | 0 \\ 1 \\ 0 \\ 0 \\ 1 \\ 1 \\ 1 | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | |} | ||
| − | | | + | {| align="center" cellpadding="10" width="100%" |
| − | | | + | | width="2%" | |
| − | | | + | | width="48%" | [[Image:LOR 1870 Figure 6.2.jpg]] |
| − | | | + | | width="50%" | (6.2) |
| − | + | |} | |
| − | |||
| − | | | ||
| − | + | ====Example 3==== | |
| − | | | + | {| align="center" cellpadding="6" width="90%" |
| − | + | | <math>\mathrm{m,}\mathbf{1} ~=~ \mathrm{m}</math> | |
| − | + | |- | |
| − | + | | <math>\text{man that is anything} ~=~ \text{man}</math> | |
| − | + | |- | |
| − | + | | | |
| − | + | <math> | |
| − | </ | + | \begin{bmatrix} |
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 1 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 1 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 1 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \end{bmatrix} | ||
| + | \begin{bmatrix} | ||
| + | 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 | ||
| + | \end{bmatrix} | ||
| + | = | ||
| + | \begin{bmatrix} | ||
| + | 0 \\ 1 \\ 0 \\ 0 \\ 1 \\ 1 \\ 1 | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | |} | ||
| − | == | + | {| align="center" cellpadding="10" width="100%" |
| + | | width="2%" | | ||
| + | | width="48%" | [[Image:LOR 1870 Figure 6.3.jpg]] | ||
| + | | width="50%" | (6.3) | ||
| + | |} | ||
| − | + | ====Example 4==== | |
| − | |||
| − | |||
| − | | | + | {| align="center" cellpadding="6" width="90%" |
| − | + | | <math>\mathrm{m,}\mathrm{n} ~=~ \text{man that is noble}</math> | |
| − | + | |- | |
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | + | <math> | |
| − | + | \begin{bmatrix} | |
| − | + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | |
| − | + | \\ | |
| − | | | + | 0 & 1 & 0 & 0 & 0 & 0 & 0 |
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 1 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 1 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \end{bmatrix} | ||
| + | \begin{bmatrix} | ||
| + | 0 \\ 1 \\ 1 \\ 0 \\ 0 \\ 0 \\ 1 | ||
| + | \end{bmatrix} | ||
| + | = | ||
| + | \begin{bmatrix} | ||
| + | 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 1 | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | |} | ||
| − | + | {| align="center" cellpadding="10" width="100%" | |
| − | + | | width="2%" | | |
| − | + | | width="48%" | [[Image:LOR 1870 Figure 6.4.jpg]] | |
| − | + | | width="50%" | (6.4) | |
| − | + | |} | |
| − | |||
| − | |||
| − | + | ====Example 5==== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellpadding="6" width="90%" | |
| − | + | | <math>\mathrm{n,}\mathrm{m} ~=~ \text{noble that is a man}</math> | |
| − | + | |- | |
| − | + | | | |
| + | <math> | ||
| + | \begin{bmatrix} | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 1 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 1 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 0 | ||
| + | \\ | ||
| + | 0 & 0 & 0 & 0 & 0 & 0 & 1 | ||
| + | \end{bmatrix} | ||
| + | \begin{bmatrix} | ||
| + | 0 \\ 1 \\ 0 \\ 0 \\ 1 \\ 1 \\ 1 | ||
| + | \end{bmatrix} | ||
| + | = | ||
| + | \begin{bmatrix} | ||
| + | 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 1 | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | |} | ||
| − | + | {| align="center" cellpadding="10" width="100%" | |
| − | + | | width="2%" | | |
| − | + | | width="48%" | [[Image:LOR 1870 Figure 6.5.jpg]] | |
| − | + | | width="50%" | (6.5) | |
| − | + | |} | |
| − | + | ===Commentary Note 9.7=== | |
| − | + | From this point forward we may think of idempotents, selectives, and zero-one diagonal matrices as being roughly equivalent notions. The only reason that I say ''roughly'' is that we are comparing ideas at different levels of abstraction in proposing these connections. | |
| − | + | We have covered the way that Peirce uses his invention of the comma modifier to assimilate boolean multiplication, logical conjunction, and what we may think of as ''serial selection'' under his more general account of relative multiplication. | |
| − | + | But the comma functor has its application to relative terms of any arity, not just the zeroth arity of absolute terms, and so there will be a lot more to explore on this point. But now I must return to the anchorage of Peirce's text and hopefully get a chance to revisit this topic later. | |
| − | + | ==Selection 10== | |
| − | + | ===The Signs for Multiplication (cont.)=== | |
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| + | | | ||
| + | <p>The sum <math>x + x\!</math> generally denotes no logical term. But <math>{x,}_\infty + \, {x,}_\infty</math> may be considered as denoting some two <math>x\!</math>'s.</p> | ||
| − | + | <p>It is natural to write:</p> | |
| − | + | {| align="center" width="100%" | |
| + | | width="20%" | | ||
| + | | width="25%" align="right" | <math>x ~+~ x</math> | ||
| + | | width="10%" align="center"| <math>=\!</math> | ||
| + | | width="25%" align="left" | <math>\mathit{2}.x\!</math> | ||
| + | | width="20%" | | ||
| + | |- | ||
| + | | | ||
| + | |- | ||
| + | | and | ||
| + | | align="right" | <math>{x,}_\infty + \, {x,}_\infty</math> | ||
| + | | align="center" | <math>=\!</math> | ||
| + | | align="left" | <math>\mathit{2}.{x,}_\infty</math> | ||
| + | | | ||
| + | |} | ||
| − | + | <p>where the dot shows that this multiplication is invertible.</p> | |
| − | + | <p>We may also use the antique figures so that:</p> | |
| − | + | {| align="center" width="100%" | |
| + | | width="20%" | | ||
| + | | width="25%" align="right" | <math>\mathit{2}.{x,}_\infty</math> | ||
| + | | width="10%" align="center"| <math>=\!</math> | ||
| + | | width="25%" align="left" | <math>\mathfrak{2}x</math> | ||
| + | | width="20%" | | ||
| + | |- | ||
| + | | | ||
| + | |- | ||
| + | | just as | ||
| + | | align="right" | <math>\mathit{1}_\infty</math> | ||
| + | | align="center" | <math>=\!</math> | ||
| + | | align="left" | <math>\mathfrak{1}</math> | ||
| + | | | ||
| + | |} | ||
| − | + | <p>Then <math>\mathfrak{2}</math> alone will denote some two things.</p> | |
| − | + | <p>But this multiplication is not in general commutative, and only becomes so when it affects a relative which imparts a relation such that a thing only bears it to ''one'' thing, and one thing ''alone'' bears it to a thing.</p> | |
| − | + | <p>For instance, the lovers of two women are not the same as two lovers of women, that is:</p> | |
| − | + | {| align="center" width="100%" | |
| + | | width="20%" | | ||
| + | | width="25%" align="right" | <math>\mathit{l}\mathfrak{2}.\mathrm{w}</math> | ||
| + | | width="10%" align="center"| and | ||
| + | | width="25%" align="left" | <math>\mathfrak{2}.\mathit{l}\mathrm{w}</math> | ||
| + | | width="20%" | | ||
| + | |} | ||
| − | + | <p>are unequal; but the husbands of two women are the same as two husbands of women, that is:</p> | |
| − | + | {| align="center" width="100%" | |
| + | | width="20%" | | ||
| + | | width="25%" align="right" | <math>\mathit{h}\mathfrak{2}.\mathrm{w}</math> | ||
| + | | width="10%" align="center"| <math>=\!</math> | ||
| + | | width="25%" align="left" | <math>\mathfrak{2}.\mathit{h}\mathrm{w}</math> | ||
| + | | width="20%" | | ||
| + | |- | ||
| + | | | ||
| + | |- | ||
| + | | and in general; | ||
| + | | align="right" | <math>x,\!\mathfrak{2}.y</math> | ||
| + | | align="center" | <math>=\!</math> | ||
| + | | align="left" | <math>\mathfrak{2}.x,\!y</math> | ||
| + | | | ||
| + | |} | ||
| − | + | <p>(Peirce, CP 3.75).</p> | |
| + | |} | ||
| − | + | ===Commentary Note 10.1=== | |
| − | + | What Peirce is attempting to do in CP 3.75 is absolutely amazing and I personally did not see anything on par with it again until I began to study the application of mathematical category theory to computation and logic, back in the mid 1980's. To completely evaluate the success of this attempt we would have to return to Peirce's earlier paper “Upon the Logic of Mathematics” (1867) to pick up some of the ideas about arithmetic that he set out there. | |
| − | + | Another branch of the investigation would require that we examine more carefully the entire syntactic mechanics of ''subjacent signs'' that Peirce uses to establish linkages among relational domains. It is important to note that these types of indices constitute a diacritical, interpretive, syntactic category under which Peirce also places the comma functor. | |
| − | |||
| − | + | The way that I would currently approach both of these branches of the investigation would be to open up a wider context for the study of relational compositions, attempting to get at the essence of what is going on when we relate relations, possibly complex, to other relations, possibly simple. | |
| − | + | ===Commentary Note 10.2=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | To say that a relative term “imparts a relation” is to say that it conveys information about the space of tuples in a cartesian product, that is, it determines a particular subset of that space. When we study the combinations of relative terms, from the most elementary forms of composition to the most complex patterns of correlation, we are considering the ways that these constraints, determinations, and informations, as imparted by relative terms, can be compounded in the formation of syntax. | |
| − | + | Let us go back and look more carefully at just how it happens that Peirce's adjacent terms and subjacent indices manage to impart their respective measures of information about relations. I will begin with the two examples illustrated in Figures 7 and 8, where I have drawn in the corresponding lines of identity between the subjacent marks of reference: <math>\dagger, \ddagger, \parallel, \S, \P.\!</math> | |
| − | Let us | ||
| − | |||
| − | + | <br> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | ||
| − | == | + | {| align="center" cellpadding="10" |
| + | | [[Image:LOR 1870 Figure 7.0.jpg]] || (7) | ||
| + | |} | ||
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 8.0.jpg]] || (8) | |
| − | + | |} | |
| − | + | One way to approach the problem of “information fusion” in Peirce's syntax is to soften the distinction between adjacent terms and subjacent signs and to treat the types of constraints that they separately signify more on a par with each other. To that purpose, I will set forth a way of thinking about relational composition that emphasizes the set-theoretic constraints involved in the construction of a composite. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | For example, suppose that we are given the relations <math>L \subseteq X \times Y</math> and <math>M \subseteq Y \times Z.</math> Table 9 and Figure 10 present two ways of picturing the constraints that are involved in constructing the relational composition <math>L \circ M \subseteq X \times Z.</math> | |
| − | < | + | <br> |
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellpadding="10" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center; width:60%" | |
| − | + | |+ style="height:30px" | <math>\text{Table 9.} ~~ \text{Relational Composition}\!</math> | |
| − | + | |- | |
| + | | style="border-right:1px solid black; border-bottom:1px solid black; width:25%" | | ||
| + | | style="border-bottom:1px solid black; width:25%" | <math>\mathit{1}\!</math> | ||
| + | | style="border-bottom:1px solid black; width:25%" | <math>\mathit{1}\!</math> | ||
| + | | style="border-bottom:1px solid black; width:25%" | <math>\mathit{1}\!</math> | ||
| + | |- | ||
| + | | style="border-right:1px solid black" | <math>L\!</math> | ||
| + | | <math>X\!</math> | ||
| + | | <math>Y\!</math> | ||
| + | | | ||
| + | |- | ||
| + | | style="border-right:1px solid black" | <math>M\!</math> | ||
| + | | | ||
| + | | <math>Y\!</math> | ||
| + | | <math>Z\!</math> | ||
| + | |- | ||
| + | | style="border-right:1px solid black" | <math>L \circ M\!</math> | ||
| + | | <math>X\!</math> | ||
| + | | | ||
| + | | <math>Z\!</math> | ||
| + | |} | ||
| − | + | <br> | |
| − | |||
| − | |||
| − | + | The way to read Table 9 is to imagine that you are playing a game that involves placing tokens on the squares of a board that is marked in just this way. The rules are that you have to place a single token on each marked square in the middle of the board in such a way that all of the indicated constraints are satisfied. That is to say, you have to place a token whose denomination is a value in the set <math>X\!</math> on each of the squares marked <math>{}^{\backprime\backprime} X {}^{\prime\prime},</math> and similarly for the squares marked <math>{}^{\backprime\backprime} Y {}^{\prime\prime}</math> and <math>{}^{\backprime\backprime} Z {}^{\prime\prime},</math> meanwhile leaving all of the blank squares empty. Furthermore, the tokens placed in each row and column have to obey the relational constraints that are indicated at the heads of the corresponding row and column. Thus, the two tokens from <math>X\!</math> have to denominate the very same value from <math>X,\!</math> and likewise for <math>Y\!</math> and <math>Z,\!</math> while the pairs of tokens on the rows marked <math>{}^{\backprime\backprime} L {}^{\prime\prime}</math> and <math>{}^{\backprime\backprime} M {}^{\prime\prime}</math> are required to denote elements that are in the relations <math>L\!</math> and <math>M,\!</math> respectively. The upshot is that when just this much is done, that is, when the <math>L,\!</math> <math>M,\!</math> and <math>\mathit{1}\!</math> relations are satisfied, then the row marked <math>{}^{\backprime\backprime} L \circ M {}^{\prime\prime}</math> will automatically bear the tokens of a pair of elements in the composite relation <math>L \circ M.\!</math> | |
| − | the | ||
| − | + | Figure 10 shows a different way of viewing the same situation. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <br> | |
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 10.jpg]] || (10) | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ===Commentary Note 10.3=== | |
| − | |||
| − | |||
| − | |||
| − | + | I will devote some time to drawing out the relationships that exist among the different pictures of relations and relative terms that were shown above, or as redrawn here: | |
| − | of | ||
| − | |||
| − | + | <br> | |
| − | |||
| − | |||
| − | + | {| align="center" cellpadding="10" | |
| + | | [[Image:LOR 1870 Figure 7.0.jpg]] || (11) | ||
| + | |} | ||
| − | + | {| align="center" cellpadding="10" | |
| + | | [[Image:LOR 1870 Figure 8.0.jpg]] || (12) | ||
| + | |} | ||
| − | + | Figures 11 and 12 present examples of relative multiplication in one of the styles of syntax that Peirce used, to which I added lines of identity to connect the corresponding marks of reference. These pictures are adapted to showing the anatomy of relative terms, while the forms of analysis illustrated in Table 13 and Figure 14 are designed to highlight the structures of the objective relations themselves. | |
| − | + | <br> | |
| − | + | {| align="center" cellpadding="10" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center; width:60%" | |
| + | |+ style="height:30px" | <math>\text{Table 13.} ~~ \text{Relational Composition}\!</math> | ||
| + | |- | ||
| + | | style="border-right:1px solid black; border-bottom:1px solid black; width:25%" | | ||
| + | | style="border-bottom:1px solid black; width:25%" | <math>\mathit{1}\!</math> | ||
| + | | style="border-bottom:1px solid black; width:25%" | <math>\mathit{1}\!</math> | ||
| + | | style="border-bottom:1px solid black; width:25%" | <math>\mathit{1}\!</math> | ||
| + | |- | ||
| + | | style="border-right:1px solid black" | <math>L\!</math> | ||
| + | | <math>X\!</math> | ||
| + | | <math>Y\!</math> | ||
| + | | | ||
| + | |- | ||
| + | | style="border-right:1px solid black" | <math>S\!</math> | ||
| + | | | ||
| + | | <math>Y\!</math> | ||
| + | | <math>Z\!</math> | ||
| + | |- | ||
| + | | style="border-right:1px solid black" | <math>L \circ S\!</math> | ||
| + | | <math>X\!</math> | ||
| + | | | ||
| + | | <math>Z\!</math> | ||
| + | |} | ||
| − | + | <br> | |
| − | + | {| align="center" cellpadding="10" | |
| + | | [[Image:LOR 1870 Figure 14.jpg]] || (14) | ||
| + | |} | ||
| − | + | There are many ways that Peirce might have gotten from his 1870 Notation for the Logic of Relatives to his more evolved systems of Logical Graphs. It is interesting to speculate on how the metamorphosis might have been accomplished by way of transformations that act on these nascent forms of syntax and that take place not too far from the pale of its means, that is, as nearly as possible according to the rules and the permissions of the initial system itself. | |
| − | + | In Existential Graphs, a relation is represented by a node whose degree is the adicity of that relation, and which is adjacent via lines of identity to the nodes that represent its correlative relations, including as a special case any of its terminal individual arguments. | |
| − | + | In the 1870 Logic of Relatives, implicit lines of identity are invoked by the subjacent numbers and marks of reference only when a correlate of some relation is the relate of some relation. Thus, the principal relate, which is not a correlate of any explicit relation, is not singled out in this way. | |
| − | is the | ||
| − | + | Remarkably enough, the comma modifier itself provides us with a mechanism to abstract the logic of relations from the logic of relatives, and thus to forge a possible link between the syntax of relative terms and the more graphical depiction of the objective relations themselves. | |
| − | the | ||
| − | |||
| − | |||
| − | + | Figure 15 demonstrates this possibility, posing a transitional case between the style of syntax in Figure 11 and the picture of composition in Figure 14. | |
| − | |||
| − | |||
| − | + | <br> | |
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 15.jpg]] || (15) | |
| − | + | |} | |
| − | |||
| − | This | + | In this composite sketch the diagonal extension <math>\mathit{1}\!</math> of the universe <math>\mathbf{1}\!</math> is invoked up front to anchor an explicit line of identity for the leading relate of the composition, while the terminal argument <math>\mathrm{w}\!</math> has been generalized to the whole universe <math>\mathbf{1},\!</math> in effect, executing an act of abstraction. This type of universal bracketing isolates the composing of the relations <math>L\!</math> and <math>S\!</math> to form the composite <math>L \circ S.\!</math> The three relational domains <math>X, Y, Z\!</math> may be distinguished from one another, or else rolled up into a single universe of discourse, as one prefers. |
| − | |||
| − | + | ===Commentary Note 10.4=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | From now on I will use the forms of analysis exemplified in the last set of Figures and Tables as a routine bridge between the logic of relative terms and the logic of their extended relations. For future reference, we may think of Table 13 as illustrating the ''spreadsheet'' model of relational composition, while Figure 14 may be thought of as making a start toward a ''hypergraph'' model of generalized compositions. I will explain the hypergraph model in some detail at a later point. The transitional form of analysis represented by Figure 15 may be called the ''universal bracketing'' of relatives as relations. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | ==Commentary Note | + | ===Commentary Note 10.5=== |
| − | + | We have sufficiently covered the application of the comma functor, or the diagonal extension, to absolute terms, so let us return to where we were in working our way through CP 3.73 and see whether we can validate Peirce's statements about the “commifications” of 2-adic relative terms that yield their 3-adic diagonal extensions. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| − | + | | | |
| − | + | <p>But not only may any absolute term be thus regarded as a relative term, but any relative term may in the same way be regarded as a relative with one correlate more. It is convenient to take this additional correlate as the first one.</p> | |
| − | |||
| − | + | <p>Then:</p> | |
| + | |- | ||
| + | | align="center" | <math>\mathit{l},\!\mathit{s}\mathrm{w}</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>will denote a lover of a woman that is a servant of that woman.</p> | ||
| − | + | <p>The comma here after <math>\mathit{l}\!</math> should not be considered as altering at all the meaning of <math>\mathit{l}\!</math>, but as only a subjacent sign, serving to alter the arrangement of the correlates.</p> | |
| − | + | <p>(Peirce, CP 3.73).</p> | |
| + | |} | ||
| − | + | Just to plant our feet on a more solid stage, let's apply this idea to the Othello example. For this performance only, just to make the example more interesting, let us assume that <math>\mathrm{Jeste ~ (J)}\!</math> is secretly in love with <math>\mathrm{Desdemona ~ (D)}.\!</math> | |
| − | + | Then we begin with the modified data set: | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | | ||
| + | <math>\begin{array}{*{15}{c}} | ||
| + | \mathrm{w} | ||
| + | & = & \mathrm{B} | ||
| + | & +\!\!, & \mathrm{D} | ||
| + | & +\!\!, & \mathrm{E} | ||
| + | \\[6pt] | ||
| + | \mathit{l} | ||
| + | & = & \mathrm{B}\!:\!\mathrm{C} | ||
| + | & +\!\!, & \mathrm{C}\!:\!\mathrm{B} | ||
| + | & +\!\!, & \mathrm{D}\!:\!\mathrm{O} | ||
| + | & +\!\!, & \mathrm{E}\!:\!\mathrm{I} | ||
| + | & +\!\!, & \mathrm{I}\!:\!\mathrm{E} | ||
| + | & +\!\!, & \mathrm{J}\!:\!\mathrm{D} | ||
| + | & +\!\!, & \mathrm{O}\!:\!\mathrm{D} | ||
| + | \\[6pt] | ||
| + | \mathit{s} | ||
| + | & = & \mathrm{C}\!:\!\mathrm{O} | ||
| + | & +\!\!, & \mathrm{E}\!:\!\mathrm{D} | ||
| + | & +\!\!, & \mathrm{I}\!:\!\mathrm{O} | ||
| + | & +\!\!, & \mathrm{J}\!:\!\mathrm{D} | ||
| + | & +\!\!, & \mathrm{J}\!:\!\mathrm{O} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | And next we derive the following results: | |
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | | |
| − | + | <math>\begin{array}{l} | |
| − | + | \mathit{l}, ~= | |
| − | + | \\[6pt] | |
| − | + | \text{lover that is}\, \underline{~~ ~~}\, \text{of}\, \underline{~~ ~~} ~= | |
| − | + | \\[6pt] | |
| − | + | (\mathrm{B}\!:\!\mathrm{B}\!:\!\mathrm{C} ~+\!\!,~ \mathrm{C}\!:\!\mathrm{C}\!:\!\mathrm{B} ~+\!\!,~ \mathrm{D}\!:\!\mathrm{D}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{E}\!:\!\mathrm{E}\!:\!\mathrm{I} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{I}\!:\!\mathrm{E} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{J}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{O}\!:\!\mathrm{O}\!:\!\mathrm{D}) | |
| − | + | \\[12pt] | |
| + | \mathit{l},\!\mathit{s}\mathrm{w} ~= | ||
| + | \\[6pt] | ||
| + | (\mathrm{B}\!:\!\mathrm{B}\!:\!\mathrm{C} ~+\!\!,~ \mathrm{C}\!:\!\mathrm{C}\!:\!\mathrm{B} ~+\!\!,~ \mathrm{D}\!:\!\mathrm{D}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{E}\!:\!\mathrm{E}\!:\!\mathrm{I} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{I}\!:\!\mathrm{E} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{J}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{O}\!:\!\mathrm{O}\!:\!\mathrm{D}) | ||
| + | \\ | ||
| + | \times | ||
| + | \\ | ||
| + | (\mathrm{C}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{E}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{O} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{O}) | ||
| + | \\ | ||
| + | \times | ||
| + | \\ | ||
| + | (\mathrm{B} ~+\!\!,~ \mathrm{D} ~+\!\!,~ \mathrm{E}) | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | Now what are we to make of that? | |
| − | |||
| − | + | If we operate in accordance with Peirce's example of <math>\mathfrak{g}\mathit{o}\mathrm{h}</math> as the “giver of a horse to an owner of that horse”, then we may assume that the associative law and the distributive law are in force, allowing us to derive this equation: | |
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | | |
| + | <math>\begin{array}{lll} | ||
| + | \mathit{l},\!\mathit{s}\mathrm{w} | ||
| + | & = & | ||
| + | \mathit{l},\!\mathit{s}(\mathrm{B} ~~+\!\!,~~ \mathrm{D} ~~+\!\!,~~ \mathrm{E}) | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \mathit{l},\!\mathit{s}\mathrm{B} ~~+\!\!,~~ \mathit{l},\!\mathit{s}\mathrm{D} ~~+\!\!,~~ \mathit{l},\!\mathit{s}\mathrm{E} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| + | |||
| + | Evidently what Peirce means by the associative principle, as it applies to this type of product, is that a product of elementary relatives having the form <math>(\mathrm{R}\!:\!\mathrm{S}\!:\!\mathrm{T})(\mathrm{S}\!:\!\mathrm{T})(\mathrm{T})\!</math> is equal to <math>\mathrm{R}\!</math> but that no other form of product yields a non-null result. Scanning the implied terms of the triple product tells us that only the case <math>(\mathrm{J}\!:\!\mathrm{J}\!:\!\mathrm{D})(\mathrm{J}\!:\!\mathrm{D})(\mathrm{D}) = \mathrm{J}\!</math> is non-null. | ||
| + | |||
| + | It follows that: | ||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | | |
| + | <math>\begin{array}{lll} | ||
| + | \mathit{l},\!\mathit{s}\mathrm{w} | ||
| + | & = & | ||
| + | \text{lover and servant of a woman} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \text{lover that is a servant of a woman} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \text{lover of a woman that is a servant of that woman} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \mathrm{J} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | And so what Peirce says makes sense in this case. | |
| − | |||
| − | + | ===Commentary Note 10.6=== | |
| − | + | As Peirce observes, it is not possible to work with relations in general without eventually abandoning all of one's algebraic principles, in due time the associative law and maybe even the distributive law, just as we already gave up the commutative law. It cannot be helped, as we cannot reflect on a law if not from a perspective outside it, at any rate, virtually so. | |
| − | + | This could be done from the standpoint of the combinator calculus, and there are places where Peirce verges on systems that are very similar, but here we are making a deliberate effort to stay within the syntactic neighborhood of Peirce's 1870 Logic of Relatives. Not too coincidentally, it is for the sake of making smoother transitions between narrower and wider regimes of algebraic law that we have been developing the paradigm of Figures and Tables indicated above. | |
| − | + | For the next few episodes, then, I will examine the examples that Peirce gives at the next level of complication in the multiplication of relative terms, for example, the three that are repeated below. | |
| − | + | {| align="center" cellpadding="10" | |
| + | | [[Image:LOR 1870 Figure 8.0.jpg]] || (16) | ||
| + | |} | ||
| − | + | {| align="center" cellpadding="10" | |
| + | | [[Image:LOR 1870 Figure 17.0.jpg]] || (17) | ||
| + | |} | ||
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 18.jpg]] || (18) | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ===Commentary Note 10.7=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Here is what I get when I try to analyze Peirce's “giver of a horse to a lover of a woman” example along the same lines as the dyadic compositions. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | We may begin with the mark-up shown in Figure 19. | |
| − | - | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 8.0.jpg]] || (19) | |
| − | + | |} | |
| − | + | If we analyze this in accord with the spreadsheet model of relational composition, the core of it is a particular way of composing a triadic ''giving'' relation <math>G \subseteq T \times U \times V\!</math> with a dyadic ''loving'' relation <math>L \subseteq U \times W\!</math> so as to obtain a specialized sort of triadic relation <math>(G \circ L) \subseteq T \times V \times W.\!</math> The applicable constraints on tuples are shown in Table 20. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <br> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellpadding="10" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center; width:75%" | |
| − | + | |+ style="height:30px" | <math>\text{Table 20.} ~~ \text{Composite of Triadic and Dyadic Relations}\!</math> | |
| − | + | |- | |
| − | + | | style="border-right:1px solid black; border-bottom:1px solid black; width:20%" | | |
| − | + | | style="border-bottom:1px solid black; width:20%" | <math>\mathit{1}\!</math> | |
| − | + | | style="border-bottom:1px solid black; width:20%" | <math>\mathit{1}\!</math> | |
| − | + | | style="border-bottom:1px solid black; width:20%" | <math>\mathit{1}\!</math> | |
| + | | style="border-bottom:1px solid black; width:20%" | <math>\mathit{1}\!</math> | ||
| + | |- | ||
| + | | style="border-right:1px solid black" | <math>G\!</math> | ||
| + | | <math>T\!</math> | ||
| + | | <math>U\!</math> | ||
| + | | <math>V\!</math> | ||
| + | | | ||
| + | |- | ||
| + | | style="border-right:1px solid black" | <math>L\!</math> | ||
| + | | | ||
| + | | <math>U\!</math> | ||
| + | | | ||
| + | | <math>W\!</math> | ||
| + | |- | ||
| + | | style="border-right:1px solid black" | <math>G \circ L</math> | ||
| + | | <math>T\!</math> | ||
| + | | | ||
| + | | <math>V\!</math> | ||
| + | | <math>W\!</math> | ||
| + | |} | ||
| − | + | <br> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | ||
| − | + | The hypergraph picture of the abstract composition is given in Figure 21. | |
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 21.jpg]] || (21) | |
| − | + | |} | |
| − | |||
| − | |||
| − | + | ===Commentary Note 10.8=== | |
| − | + | There's a critical transition point in sight of Peirce's 1870 Logic of Relatives and it's a point that turns on the teridentity relation. | |
| − | + | In taking up the next example of relational composition, let's substitute the relation <math>\mathit{t} = \text{taker of}\, \underline{~~ ~~}\!</math> for Peirce's relation <math>\mathit{o} = \text{owner of}\, \underline{~~ ~~},\!</math> simply for the sake of avoiding conflicts in the symbols we use. In this way, Figure 17 is transformed into Figure 22. | |
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 22.jpg]] || (22) | |
| − | + | |} | |
| − | | | ||
| − | | | ||
| − | |||
| − | + | The hypergraph picture of the abstract composition is given in Figure 23. | |
| − | |||
| − | | | + | {| align="center" cellpadding="10" |
| − | + | | [[Image:LOR 1870 Figure 23.jpg]] || (23) | |
| − | + | |} | |
| − | |||
| − | | | ||
| − | | | ||
| − | |||
| − | + | If we analyze this in accord with the spreadsheet model of relational composition, the core of it is a particular way of composing a triadic “giving” relation <math>G \subseteq X \times Y \times Z\!</math> with a dyadic “taking” relation <math>T \subseteq Y \times Z\!</math> in such a way as to determine a certain dyadic relation <math>(G \circ T) \subseteq X \times Z.\!</math> Table 24 schematizes the associated constraints on tuples. | |
| − | + | <br> | |
| − | " | + | {| align="center" cellpadding="10" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center; width:60%" |
| + | |+ style="height:30px" | <math>\text{Table 24.} ~~ \text{Another Brand of Composition}\!</math> | ||
| + | |- | ||
| + | | style="border-right:1px solid black; border-bottom:1px solid black; width:25%" | | ||
| + | | style="border-bottom:1px solid black; width:25%" | <math>\mathit{1}\!</math> | ||
| + | | style="border-bottom:1px solid black; width:25%" | <math>\mathit{1}\!</math> | ||
| + | | style="border-bottom:1px solid black; width:25%" | <math>\mathit{1}\!</math> | ||
| + | |- | ||
| + | | style="border-right:1px solid black" | <math>G\!</math> | ||
| + | | <math>X\!</math> | ||
| + | | <math>Y\!</math> | ||
| + | | <math>Z\!</math> | ||
| + | |- | ||
| + | | style="border-right:1px solid black" | <math>T\!</math> | ||
| + | | | ||
| + | | <math>Y\!</math> | ||
| + | | <math>Z\!</math> | ||
| + | |- | ||
| + | | style="border-right:1px solid black" | <math>G \circ T</math> | ||
| + | | <math>X\!</math> | ||
| + | | | ||
| + | | <math>Z\!</math> | ||
| + | |} | ||
| − | + | <br> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | So we see that the notorious teridentity relation, which I have left equivocally denoted by the same symbol as the identity relation <math>\mathit{1},\!</math> is already implicit in Peirce's discussion at this point. | |
| − | |||
| − | + | ===Commentary Note 10.9=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The use of the concepts of identity and teridentity is not to identify a thing-in-itself with itself, much less twice or thrice over — there is no need and therefore no utility in that. I can imagine Peirce asking, on Kantian principles if not entirely on Kantian premisses, <i>Where is the manifold to be unified?</i> The manifold that demands unification does not reside in the object but in the phenomena, that is, in the appearances that might have been appearances of different objects but that happen to be constrained by these identities to being just so many aspects, facets, parts, roles, or signs of one and the same object. | |
| − | + | For example, notice how the various identity concepts actually functioned in the last example, where they had the opportunity to show their behavior in something like their natural habitat. | |
| − | + | The use of the teridentity concept in the case of the “giver of a horse to a taker of it” is to say that the thing appearing with respect to its quality under an absolute term, <i>a horse</i>, the thing appearing with respect to its existence as the correlate of a dyadic relative, <i>a potential possession</i>, and the thing appearing with respect to its synthesis as the correlate of a triadic relative, <i>a gift</i>, are one and the same thing. | |
| − | + | ===Commentary Note 10.10=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The last of the three examples involving the composition of triadic relatives with dyadic relatives is shown again in Figure 25. | |
| − | |||
| − | | | + | {| align="center" cellpadding="10" |
| − | + | | [[Image:LOR 1870 Figure 18.jpg]] || (25) | |
| − | + | |} | |
| − | |||
| − | | | ||
| − | | | ||
| − | |||
| − | + | The hypergraph picture of the abstract composition is given in Figure 26. | |
| − | + | {| align="center" cellpadding="10" | |
| + | | [[Image:LOR 1870 Figure 26.jpg]] || (26) | ||
| + | |} | ||
| − | + | This example illustrates the way that Peirce analyzes the logical conjunction, we might even say the ''parallel conjunction'', of a pair of dyadic relatives in terms of the comma extension and the same style of composition that we saw in the last example, that is, according to a pattern of anaphora that invokes the teridentity relation. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | If we lay out this analysis of conjunction on the spreadsheet model of relational composition, the gist of it is the diagonal extension of a dyadic ''loving'' relation <math>L \subseteq X \times Y\!</math> to the corresponding triadic ''being and loving'' relation <math>L \subseteq X \times X \times Y,\!</math> which is then composed in a specific way with a dyadic ''serving'' relation <math>S \subseteq X \times Y\!</math> so as to determine the dyadic relation <math>L,\!S \subseteq X \times Y.\!</math> Table 27 schematizes the associated constraints on tuples. | |
| − | |||
| − | + | <br> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellpadding="10" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center; width:60%" | |
| + | |+ style="height:30px" | <math>\text{Table 27.} ~~ \text{Conjunction Via Composition}\!</math> | ||
| + | |- | ||
| + | | style="border-right:1px solid black; border-bottom:1px solid black; width:25%" | | ||
| + | | style="border-bottom:1px solid black; width:25%" | <math>\mathit{1}\!</math> | ||
| + | | style="border-bottom:1px solid black; width:25%" | <math>\mathit{1}\!</math> | ||
| + | | style="border-bottom:1px solid black; width:25%" | <math>\mathit{1}\!</math> | ||
| + | |- | ||
| + | | style="border-right:1px solid black" | <math>L,\!</math> | ||
| + | | <math>X\!</math> | ||
| + | | <math>X\!</math> | ||
| + | | <math>Y\!</math> | ||
| + | |- | ||
| + | | style="border-right:1px solid black" | <math>S\!</math> | ||
| + | | | ||
| + | | <math>X\!</math> | ||
| + | | <math>Y\!</math> | ||
| + | |- | ||
| + | | style="border-right:1px solid black" | <math>L,\!S</math> | ||
| + | | <math>X\!</math> | ||
| + | | | ||
| + | | <math>Y\!</math> | ||
| + | |} | ||
| − | + | <br> | |
| − | + | ===Commentary Note 10.11=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Let us return to the point where we left off unpacking the contents of CP 3.73. Peirce remarks that the comma operator can be iterated at will: | |
| − | |||
| − | | | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> |
| − | + | | | |
| − | + | <p>In point of fact, since a comma may be added in this way to any relative term, it may be added to one of these very relatives formed by a comma, and thus by the addition of two commas an absolute term becomes a relative of two correlates.</p> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | == | + | <p>So:</p> |
| + | |- | ||
| + | | align="center" | <math>\mathrm{m},\!,\!\mathrm{b},\!\mathrm{r}</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>interpreted like</p> | ||
| + | |- | ||
| + | | align="center" | <math>\mathfrak{g}\mathit{o}\mathrm{h}</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>means a man that is a rich individual and is a black that is that rich individual.</p> | ||
| − | < | + | <p>But this has no other meaning than:</p> |
| − | + | |- | |
| − | + | | align="center" | <math>\mathrm{m},\!\mathrm{b},\!\mathrm{r}</math> | |
| − | + | |- | |
| − | + | | | |
| + | <p>or a man that is a black that is rich.</p> | ||
| − | + | <p>Thus we see that, after one comma is added, the addition of another does not change the meaning at all, so that whatever has one comma after it must be regarded as having an infinite number.</p> | |
| − | comma | ||
| − | |||
| − | |||
| − | + | <p>(Peirce, CP 3.73).</p> | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | + | Again, let us check whether this makes sense on the stage of our small but dramatic model. Let's say that Desdemona and Othello are rich, and, among the persons of the play, only they. With this premiss we obtain a sample of absolute terms that is sufficiently ample to work through our example: | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | | | ||
| | | | ||
| − | + | <math>\begin{array}{*{15}{c}} | |
| − | + | \mathbf{1} | |
| − | | | + | & = & \mathrm{B} |
| + | & +\!\!, & \mathrm{C} | ||
| + | & +\!\!, & \mathrm{D} | ||
| + | & +\!\!, & \mathrm{E} | ||
| + | & +\!\!, & \mathrm{I} | ||
| + | & +\!\!, & \mathrm{J} | ||
| + | & +\!\!, & \mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{b} | ||
| + | & = & \mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{m} | ||
| + | & = & \mathrm{C} | ||
| + | & +\!\!, & \mathrm{I} | ||
| + | & +\!\!, & \mathrm{J} | ||
| + | & +\!\!, & \mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{r} | ||
| + | & = & \mathrm{D} | ||
| + | & +\!\!, & \mathrm{O} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| + | |||
| + | One application of the comma operator yields the following 2-adic relatives: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | | | + | <math>\begin{array}{*{15}{c}} |
| + | \mathbf{1,} | ||
| + | & = & \mathrm{B}\!:\!\mathrm{B} | ||
| + | & +\!\!, & \mathrm{C}\!:\!\mathrm{C} | ||
| + | & +\!\!, & \mathrm{D}\!:\!\mathrm{D} | ||
| + | & +\!\!, & \mathrm{E}\!:\!\mathrm{E} | ||
| + | & +\!\!, & \mathrm{I}\!:\!\mathrm{I} | ||
| + | & +\!\!, & \mathrm{J}\!:\!\mathrm{J} | ||
| + | & +\!\!, & \mathrm{O}\!:\!\mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{b,} | ||
| + | & = & \mathrm{O}\!:\!\mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{m,} | ||
| + | & = & \mathrm{C}\!:\!\mathrm{C} | ||
| + | & +\!\!, & \mathrm{I}\!:\!\mathrm{I} | ||
| + | & +\!\!, & \mathrm{J}\!:\!\mathrm{J} | ||
| + | & +\!\!, & \mathrm{O}\!:\!\mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{r,} | ||
| + | & = & \mathrm{D}\!:\!\mathrm{D} | ||
| + | & +\!\!, & \mathrm{O}\!:\!\mathrm{O} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| + | |||
| + | Another application of the comma operator generates the following 3-adic relatives: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | + | <math>\begin{array}{*{9}{c}} | |
| + | \mathbf{1,\!,} | ||
| + | & = & \mathrm{B}\!:\!\mathrm{B}\!:\!\mathrm{B} | ||
| + | & +\!\!, & \mathrm{C}\!:\!\mathrm{C}\!:\!\mathrm{C} | ||
| + | & +\!\!, & \mathrm{D}\!:\!\mathrm{D}\!:\!\mathrm{D} | ||
| + | & +\!\!, & \mathrm{E}\!:\!\mathrm{E}\!:\!\mathrm{E} | ||
| + | \\ | ||
| + | & & | ||
| + | & +\!\!, & \mathrm{I}\!:\!\mathrm{I}\!:\!\mathrm{I} | ||
| + | & +\!\!, & \mathrm{J}\!:\!\mathrm{J}\!:\!\mathrm{J} | ||
| + | & +\!\!, & \mathrm{O}\!:\!\mathrm{O}\!:\!\mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{b,\!,} | ||
| + | & = & \mathrm{O}\!:\!\mathrm{O}\!:\!\mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{m,\!,} | ||
| + | & = & \mathrm{C}\!:\!\mathrm{C}\!:\!\mathrm{C} | ||
| + | & +\!\!, & \mathrm{I}\!:\!\mathrm{I}\!:\!\mathrm{I} | ||
| + | & +\!\!, & \mathrm{J}\!:\!\mathrm{J}\!:\!\mathrm{J} | ||
| + | & +\!\!, & \mathrm{O}\!:\!\mathrm{O}\!:\!\mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{r,\!,} | ||
| + | & = & \mathrm{D}\!:\!\mathrm{D}\!:\!\mathrm{D} | ||
| + | & +\!\!, & \mathrm{O}\!:\!\mathrm{O}\!:\!\mathrm{O} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| + | |||
| + | Assuming the associativity of multiplication among 2-adic relatives, we may compute the product <math>~\mathrm{m},\mathrm{b},\mathrm{r}~</math> by a brute force method as follows: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | + | <math>\begin{array}{lll} | |
| − | + | \mathrm{m},\mathrm{b},\mathrm{r} | |
| − | + | & = & | |
| − | + | (\mathrm{C}\!:\!\mathrm{C} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{I} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{J} ~+\!\!,~ \mathrm{O}\!:\!\mathrm{O})(\mathrm{O}\!:\!\mathrm{O})(\mathrm{D} ~+\!\!,~ \mathrm{O}) | |
| − | + | \\[6pt] | |
| − | + | & = & | |
| − | + | (\mathrm{C}\!:\!\mathrm{C} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{I} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{J} ~+\!\!,~ \mathrm{O}\!:\!\mathrm{O})(\mathrm{O}) | |
| − | + | \\[6pt] | |
| − | + | & = & | |
| − | + | \mathrm{O} | |
| − | + | \end{array}</math> | |
| − | + | |} | |
| − | + | ||
| − | + | This says that a man that is black that is rich is Othello, which is true on the premisses of our present universe of discourse. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | = | + | Following the standard associative combinations of <math>\mathfrak{g}\mathit{o}\mathrm{h},</math> the product <math>~\mathrm{m},\!,\mathrm{b},\mathrm{r}~</math> is multiplied out along the following lines, where the trinomials of the form <math>\mathrm{(X\!:\!Y\!:\!Z)(Y\!:\!Z)(Z)}\!</math> are the only ones that produce a non-null result, namely, <math>\mathrm{(X\!:\!Y\!:\!Z)(Y\!:\!Z)(Z) = X}.\!</math> |
| − | < | + | {| align="center" cellspacing="6" width="90%" |
| − | + | | | |
| − | + | <math>\begin{array}{lll} | |
| − | I | + | \mathrm{m},\!,\mathrm{b},\mathrm{r} |
| − | + | & = & | |
| − | + | (\mathrm{C}\!:\!\mathrm{C}\!:\!\mathrm{C} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{I}\!:\!\mathrm{I} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{J}\!:\!\mathrm{J} ~+\!\!,~ \mathrm{O}\!:\!\mathrm{O}\!:\!\mathrm{O})(\mathrm{O}\!:\!\mathrm{O})(\mathrm{D} ~+\!\!,~ \mathrm{O}) | |
| − | + | \\[6pt] | |
| − | + | & = & | |
| + | (\mathrm{O}\!:\!\mathrm{O}\!:\!\mathrm{O})(\mathrm{O}\!:\!\mathrm{O})(\mathrm{O}) | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \mathrm{O} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | So we have that <math>\mathrm{m},\!,\mathrm{b},\mathrm{r} ~=~ \mathrm{m},\mathrm{b},\mathrm{r}.</math> | |
| − | |||
| − | that | ||
| − | |||
| − | |||
| − | |||
| − | + | In closing, observe that the teridentity relation has turned up again in this context, as the second comma-ing of the universal term itself: | |
| − | |||
| − | the | ||
| − | the | ||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | | |
| − | </ | + | <math>\begin{array}{l} |
| + | \mathbf{1},\!, ~=~ | ||
| + | \mathrm{B}\!:\!\mathrm{B}\!:\!\mathrm{B} ~+\!\!,~ \mathrm{C}\!:\!\mathrm{C}\!:\!\mathrm{C} ~+\!\!,~ \mathrm{D}\!:\!\mathrm{D}\!:\!\mathrm{D} ~+\!\!,~ \mathrm{E}\!:\!\mathrm{E}\!:\!\mathrm{E} ~+\!\!,~ \mathrm{I}\!:\!\mathrm{I}\!:\!\mathrm{I} ~+\!\!,~ \mathrm{J}\!:\!\mathrm{J}\!:\!\mathrm{J} ~+\!\!,~ \mathrm{O}\!:\!\mathrm{O}\!:\!\mathrm{O} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | ==Commentary Note 10. | + | ===Commentary Note 10.12=== |
| − | + | Potential ambiguities in Peirce's two versions of the “rich black man” example can be resolved by providing them with explicit graphical markups, as shown in Figures 28 and 29. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 28.jpg]] || (28) | |
| − | + | |- | |
| − | + | | [[Image:LOR 1870 Figure 29.jpg]] || (29) | |
| − | + | |} | |
| − | + | On the other hand, as the forms of relational composition become more complex, the corresponding algebraic products of elementary relatives, for example, <math>\mathrm{(x\!:\!y\!:\!z)(y\!:\!z)(z)},\!</math> will not always determine unique results without the addition of more information about the intended linking of terms. | |
| − | |||
| − | |||
| − | + | ==Selection 11== | |
| − | |||
| − | |||
| − | + | ===The Signs for Multiplication (concl.)=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| − | + | | | |
| − | + | <p>The conception of multiplication we have adopted is that of the application of one relation to another. So, a quaternion being the relation of one vector to another, the multiplication of quaternions is the application of one such relation to a second.</p> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <p>Even ordinary numerical multiplication involves the same idea, for <math>~2 \times 3~</math> is a pair of triplets, and <math>~3 \times 2~</math> is a triplet of pairs, where "triplet of" and "pair of" are evidently relatives.</p> | |
| − | |||
| − | |||
| − | of | ||
| − | |||
| − | + | <p>If we have an equation of the form:</p> | |
| − | + | |- | |
| − | + | | align="center" | <math>xy ~=~ z</math> | |
| + | |- | ||
| + | | | ||
| + | <p>and there are just as many <math>x\!</math>'s per <math>y\!</math> as there are, ''per'' things, things of the universe, then we have also the arithmetical equation:</p> | ||
| + | |- | ||
| + | | align="center" | <math>[x][y] ~=~ [z].</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>For instance, if our universe is perfect men, and there are as many teeth to a Frenchman (perfect understood) as there are to any one of the universe, then:</p> | ||
| + | |- | ||
| + | | align="center" | <math>[\mathit{t}][\mathrm{f}] ~=~ [\mathit{t}\mathrm{f}]</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>holds arithmetically.</p> | ||
| − | + | <p>So if men are just as apt to be black as things in general:</p> | |
| − | + | |- | |
| − | + | | align="center" | <math>[\mathrm{m,}][\mathrm{b}] ~=~ [\mathrm{m,}\mathrm{b}]</math> | |
| + | |- | ||
| + | | | ||
| + | <p>where the difference between <math>[\mathrm{m}]\!</math> and <math>[\mathrm{m,}]\!</math> must not be overlooked.</p> | ||
| − | + | <p>It is to be observed that:</p> | |
| − | + | |- | |
| − | | | + | | align="center" | <math>[\mathit{1}] ~=~ \mathfrak{1}.</math> |
| − | + | |- | |
| − | | | + | | |
| − | + | <p>Boole was the first to show this connection between logic and probabilities. He was restricted, however, to absolute terms. I do not remember having seen any extension of probability to relatives, except the ordinary theory of ''expectation''.</p> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <p>Our logical multiplication, then, satisfies the essential conditions of multiplication, has a unity, has a conception similar to that of admitted multiplications, and contains numerical multiplication as a case under it.</p> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | that | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <p>(Peirce, CP 3.76).</p> | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ===Commentary Note 11.1=== | |
| − | |||
| − | + | We have reached a suitable place to pause in our reading of Peirce's text — actually, it's more like a place to run as fast as we can along a parallel track — where I can pay off a few of the expository IOUs I've been using to pave the way to this point. | |
| − | + | The more pressing debts that come to mind are concerned with the matter of Peirce's “number of” function that maps a term <math>t\!</math> into a number <math>[t],\!</math> and with my justification for calling a certain style of illustration the ''hypergraph picture'' of relational composition. As it happens, there is a thematic relation between these topics, and so I can make my way forward by addressing them together. | |
| − | |||
| − | that | ||
| − | |||
| − | + | At this point we have two good pictures of how to compute the relational compositions of arbitrary dyadic relations, namely, the bigraph representation and the matrix representation, each of which has its differential advantages in different types of situations. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | But we do not have a comparable picture of how to compute the richer variety of relational compositions that involve triadic or any higher adicity relations. As a matter of fact, we run into a non-trivial classification problem simply to enumerate the different types of compositions that arise in these cases. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Therefore, let us inaugurate a systematic study of relational composition, general enough to articulate the “generative potency” of Peirce's 1870 Logic of Relatives. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ===Commentary Note 11.2=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Let's bring together the various things that Peirce has said about the “number of function” up to this point in the paper. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | in | ||
| − | |||
| − | + | ====NOF 1==== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| − | + | | | |
| − | + | <p>I propose to assign to all logical terms, numbers; to an absolute term, the number of individuals it denotes; to a relative term, the average number of things so related to one individual. Thus in a universe of perfect men (''men''), the number of “tooth of” would be 32. The number of a relative with two correlates would be the average number of things so related to a pair of individuals; and so on for relatives of higher numbers of correlates. I propose to denote the number of a logical term by enclosing the term in square brackets, thus <math>[t].\!</math></p> | |
| − | |||
| − | |||
| − | + | <p>(Peirce, CP 3.65).</p> | |
| − | + | |} | |
| − | |||
| − | |||
| − | + | ====NOF 2==== | |
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| − | the | + | | |
| + | <p>But not only do the significations of <math>~=~</math> and <math>~<~</math> here adopted fulfill all absolute requirements, but they have the supererogatory virtue of being very nearly the same as the common significations. Equality is, in fact, nothing but the identity of two numbers; numbers that are equal are those which are predicable of the same collections, just as terms that are identical are those which are predicable of the same classes. So, to write <math>~5 < 7~</math> is to say that <math>~5~</math> is part of <math>~7~</math>, just as to write <math>~\mathrm{f} < \mathrm{m}~</math> is to say that Frenchmen are part of men. Indeed, if <math>~\mathrm{f} < \mathrm{m}~</math>, then the number of Frenchmen is less than the number of men, and if <math>~\mathrm{v} = \mathrm{p}~</math>, then the number of Vice-Presidents is equal to the number of Presidents of the Senate; so that the numbers may always be substituted for the terms themselves, in case no signs of operation occur in the equations or inequalities.</p> | ||
| − | + | <p>(Peirce, CP 3.66).</p> | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ====NOF 3==== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> |
| + | | | ||
| + | <p>It is plain that both the regular non-invertible addition and the invertible addition satisfy the absolute conditions. But the notation has other recommendations. The conception of ''taking together'' involved in these processes is strongly analogous to that of summation, the sum of 2 and 5, for example, being the number of a collection which consists of a collection of two and a collection of five. Any logical equation or inequality in which no operation but addition is involved may be converted into a numerical equation or inequality by substituting the numbers of the several terms for the terms themselves — provided all the terms summed are mutually exclusive.</p> | ||
| − | < | + | <p>Addition being taken in this sense, ''nothing'' is to be denoted by ''zero'', for then</p> |
| − | + | |- | |
| − | + | | align="center" | <math>x ~+\!\!,~ 0 ~=~ x</math> | |
| − | and the | + | |- |
| − | + | | | |
| − | of | + | <p>whatever is denoted by <math>~x~</math>; and this is the definition of ''zero''. This interpretation is given by Boole, and is very neat, on account of the resemblance between the ordinary conception of ''zero'' and that of nothing, and because we shall thus have</p> |
| − | + | |- | |
| − | + | | align="center" | <math>[0] ~=~ 0.</math> | |
| − | + | |- | |
| − | + | | | |
| − | </ | + | <p>(Peirce, CP 3.67).</p> |
| + | |} | ||
| + | |||
| + | ====NOF 4==== | ||
| − | == | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> |
| + | | | ||
| + | <p>The conception of multiplication we have adopted is that of the application of one relation to another. …</p> | ||
| − | < | + | <p>Even ordinary numerical multiplication involves the same idea, for <math>~2 \times 3~</math> is a pair of triplets, and <math>~3 \times 2~</math> is a triplet of pairs, where “triplet of” and “pair of” are evidently relatives.</p> |
| − | |||
| − | |||
| − | where | ||
| − | |||
| − | |||
| − | + | <p>If we have an equation of the form:</p> | |
| − | | | + | |- |
| − | | | + | | align="center" | <math>xy ~=~ z</math> |
| − | | | + | |- |
| − | | | ||
| | | | ||
| − | | | + | <p>and there are just as many <math>x\!</math>'s per <math>y\!</math> as there are, ''per'' things, things of the universe, then we have also the arithmetical equation:</p> |
| + | |- | ||
| + | | align="center" | <math>[x][y] ~=~ [z].</math> | ||
| + | |- | ||
| | | | ||
| − | | | + | <p>For instance, if our universe is perfect men, and there are as many teeth to a Frenchman (perfect understood) as there are to any one of the universe, then:</p> |
| + | |- | ||
| + | | align="center" | <math>[\mathit{t}][\mathrm{f}] ~=~ [\mathit{t}\mathrm{f}]</math> | ||
| + | |- | ||
| | | | ||
| − | | | + | <p>holds arithmetically.</p> |
| − | | | + | |
| + | <p>So if men are just as apt to be black as things in general:</p> | ||
| + | |- | ||
| + | | align="center" | <math>[\mathrm{m,}][\mathrm{b}] ~=~ [\mathrm{m,}\mathrm{b}]</math> | ||
| + | |- | ||
| | | | ||
| − | + | <p>where the difference between <math>[\mathrm{m}]\!</math> and <math>[\mathrm{m,}]\!</math> must not be overlooked.</p> | |
| − | | | + | |
| − | | | + | <p>It is to be observed that:</p> |
| − | | | + | |- |
| + | | align="center" | <math>[\mathit{1}] ~=~ \mathfrak{1}.</math> | ||
| + | |- | ||
| | | | ||
| − | + | <p>Boole was the first to show this connection between logic and probabilities. He was restricted, however, to absolute terms. I do not remember having seen any extension of probability to relatives, except the ordinary theory of ''expectation''.</p> | |
| − | + | <p>Our logical multiplication, then, satisfies the essential conditions of multiplication, has a unity, has a conception similar to that of admitted multiplications, and contains numerical multiplication as a case under it.</p> | |
| − | |||
| − | + | <p>(Peirce, CP 3.76).</p> | |
| − | + | |} | |
| − | + | ===Commentary Note 11.3=== | |
| − | + | Before I can discuss Peirce's “number of” function in greater detail I will need to deal with an expositional difficulty that I have been very carefully dancing around all this time, but one that will no longer abide its assigned place under the rug. | |
| − | ' | + | Functions have long been understood, from well before Peirce's time to ours, as special cases of dyadic relations, so the “number of” function itself is already to be numbered among the types of dyadic relatives that we've been explicitly mentioning and implicitly using all this time. But Peirce's way of talking about a dyadic relative term is to list the “relate” first and the “correlate” second, a convention that goes over into functional terms as making the functional value first and the functional argument second, whereas almost anyone brought up in our present time frame has difficulty thinking of a function any other way than as a set of ordered pairs where the order in each pair lists the functional argument first and the functional value second. |
| − | 's | + | All of these syntactic wrinkles can be ironed out in a very smooth way, given a sufficiently general context of flexible enough interpretive conventions, but not without introducing an order of anachronism into Peirce's presentation that I am presently trying to avoid as much as possible. Thus, I will need to experiment with various styles of compromise formation. |
| − | + | The interpretation of Peirce's 1870 “Logic of Relatives” can be facilitated by introducing a few items of background material on relations in general, as regarded from a combinatorial point of view. | |
| − | + | ===Commentary Note 11.4=== | |
| − | + | The task before us is to clarify the relationships among relative terms, relations, and the special cases of relations that are given by equivalence relations, functions, and so on. | |
| − | ' | + | The first obstacle to get past is the order convention that Peirce's orientation to relative terms causes him to use for functions. To focus on a concrete example of immediate use in this discussion, let's take the “number of” function that Peirce denotes by means of square brackets and re-formulate it as a dyadic relative term <math>v\!</math> as follows: |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | <math>v(t) ~:=~ [t] ~=~ \text{the number of the term}~ t.\!</math> | ||
| + | |} | ||
| − | + | To set the dyadic relative term <math>v\!</math> within a suitable context of interpretation, let us suppose that <math>v\!</math> corresponds to a relation <math>V \subseteq \mathbb{R} \times S,\!</math> where <math>\mathbb{R}\!</math> is the set of real numbers and <math>S\!</math> is a suitable syntactic domain, here described as a set of ''terms''. The dyadic relation <math>V\!</math> is at first sight a function from <math>S\!</math> to <math>\mathbb{R}.\!</math> There is, however, a very great likelihood that we cannot always assign numbers to every term in whatever syntactic domain <math>S\!</math> we happen to choose, so we may eventually be forced to treat the dyadic relation <math>V\!</math> as a partial function from <math>S\!</math> to <math>\mathbb{R}.\!</math> All things considered, then, let me try out the following impedimentaria of strategies and compromises. | |
| − | + | First, I adapt the functional arrow notation so that it allows us to detach the functional orientation from the order in which the names of domains are written on the page. Second, I change the notation for ''partial functions'', or ''pre-functions'', to one that is less likely to be confounded. This gives the scheme: | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | <math>q : X \to Y\!</math> means that <math>q\!</math> is functional at <math>X.\!</math> | |
| − | + | |- | |
| − | + | | <math>q : X \leftarrow Y\!</math> means that <math>q\!</math> is functional at <math>Y.\!</math> | |
| + | |- | ||
| + | | <math>q : X \rightharpoonup Y\!</math> means that <math>q\!</math> is pre-functional at <math>X.\!</math> | ||
| + | |- | ||
| + | | <math>q : X \leftharpoonup Y\!</math> means that <math>q\!</math> is pre-functional at <math>Y.\!</math> | ||
| + | |} | ||
| − | + | Until it becomes necessary to stipulate otherwise, let us assume that <math>v\!</math> is a function in <math>\mathbb{R}\!</math> of <math>S,\!</math> written <math>v : \mathbb{R} \leftarrow S,\!</math> amounting to the functional alias of the dyadic relation <math>V \subseteq \mathbb{R} \times S\!</math> and associated with the dyadic relative term <math>v\!</math> whose relate lies in the set <math>\mathbb{R}\!</math> of real numbers and whose correlate lies in the set <math>S\!</math> of syntactic terms. | |
| − | + | '''Note.''' See the article [[Relation Theory]] for the definitions of ''functions'' and ''pre-functions'' used in this section. | |
| − | + | ===Commentary Note 11.5=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The right form of diagram can be a great aid in rendering complex matters comprehensible, so let's extract the overly compressed bits of the “[[Relation Theory]]” article that we need to illuminate Peirce's 1870 “Logic Of Relatives” and draw what icons we can within the current frame. | |
| − | + | For the immediate present, we may start with dyadic relations and describe the customary species of relations and functions in terms of their local and numerical incidence properties. | |
| − | + | Let <math>P \subseteq X \times Y\!</math> be an arbitrary dyadic relation. The following properties of <math>P\!</math> can be defined: | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | P ~\text{is total at}~ X | ||
| + | & \iff & | ||
| + | P ~\text{is}~ (\ge 1)\text{-regular}~ \text{at}~ X. | ||
| + | \\[6pt] | ||
| + | P ~\text{is total at}~ Y | ||
| + | & \iff & | ||
| + | P ~\text{is}~ (\ge 1)\text{-regular}~ \text{at}~ Y. | ||
| + | \\[6pt] | ||
| + | P ~\text{is tubular at}~ X | ||
| + | & \iff & | ||
| + | P ~\text{is}~ (\le 1)\text{-regular}~ \text{at}~ X. | ||
| + | \\[6pt] | ||
| + | P ~\text{is tubular at}~ Y | ||
| + | & \iff & | ||
| + | P ~\text{is}~ (\le 1)\text{-regular}~ \text{at}~ Y. | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | If <math>P \subseteq X \times Y\!</math> is tubular at <math>X,\!</math> then <math>P\!</math> is known as a ''partial function'' or a ''pre-function'' from <math>X\!</math> to <math>Y,\!</math> frequently signalized by renaming <math>P\!</math> with an alternate lower case name, say <math>{}^{\backprime\backprime} p {}^{\prime\prime},~\!</math> and writing <math>p : X \rightharpoonup Y.\!</math> | |
| − | </ | ||
| − | + | Just by way of formalizing the definition: | |
| − | < | + | {| align="center" cellspacing="6" width="90%" |
| − | + | | | |
| − | + | <math>\begin{array}{lll} | |
| − | + | P ~\text{is a pre-function}~ P : X \rightharpoonup Y | |
| − | + | & \iff & | |
| − | + | P ~\text{is tubular at}~ X. | |
| − | + | \\[6pt] | |
| − | a | + | P ~\text{is a pre-function}~ P : X \leftharpoonup Y |
| − | + | & \iff & | |
| + | P ~\text{is tubular at}~ Y. | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| − | + | To illustrate these properties, let us fashion a generic enough example of a dyadic relation, <math>E \subseteq X \times Y,~\!</math> where <math>X = Y = \{ 0, 1, \ldots, 8, 9 \},\!</math> and where the bigraph picture of <math>E\!</math> looks like this: | |
| − | and | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 30.jpg]] || (30) | |
| − | + | |} | |
| − | |||
| − | + | If we scan along the <math>X\!</math> dimension from <math>0\!</math> to <math>9\!</math> we see that the incidence degrees of the <math>X\!</math> nodes with the <math>Y\!</math> domain are <math>0, 1, 2, 3, 1, 1, 1, 2, 0, 0,\!</math> in that order. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | If we scan along the <math>Y\!</math> dimension from <math>0\!</math> to <math>9\!</math> we see that the incidence degrees of the <math>Y\!</math> nodes with the <math>X\!</math> domain are <math>0, 0, 3, 2, 1, 1, 2, 1, 1, 0,\!</math> in that order. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Thus, <math>E\!</math> is not total at either <math>X\!</math> or <math>Y,\!</math> since there are nodes in both <math>X\!</math> and <math>Y\!</math> having incidence degrees less than <math>1.\!</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | + | Also, <math>E\!</math> is not tubular at either <math>X\!</math> or <math>Y,\!</math> since there are nodes in both <math>X\!</math> and <math>Y\!</math> having incidence degrees greater than <math>1.\!</math> | |
| − | < | + | Clearly, then, the relation <math>E\!</math> cannot qualify as a pre-function, much less as a function on either of its relational domains. |
| − | |||
| − | |||
| − | |||
| − | + | ===Commentary Note 11.6=== | |
| − | + | Let's continue working our way through the above definitions, constructing appropriate examples as we go. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <math>E_1\!</math> exemplifies the quality of ''totality at <math>X.\!</math>'' | |
| − | of | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 31.jpg]] || (31) | |
| − | | | + | |} |
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <math>E_2\!</math> exemplifies the quality of ''totality at <math>Y.\!</math>'' | |
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 32.jpg]] || (32) | |
| − | | | + | |} |
| − | |||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <math>E_3\!</math> exemplifies the quality of ''tubularity at <math>X.\!</math>'' | |
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 33.jpg]] || (33) | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | + | <math>E_4\!</math> exemplifies the quality of ''tubularity at <math>Y.\!</math>'' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 34.jpg]] || (34) | |
| − | + | |} | |
| − | 1870 | ||
| − | + | So <math>E_3\!</math> is a pre-function <math>e_3 : X \rightharpoonup Y,\!</math> and <math>E_4\!</math> is a pre-function <math>e_4 : X \leftharpoonup Y.\!</math> | |
| − | + | ===Commentary Note 11.7=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | We come now to the very special cases of dyadic relations that are known as ''functions''. It will serve a dual purpose on behalf of the present exposition if we take the class of functions as a source of object examples to clarify the more abstruse concepts in the [[Relation Theory]] material. | |
| − | of | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | To begin, let's recall the definition of a ''local flag'': | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | <math>L_{x \,\text{at}\, j} = \{ (x_1, \ldots, x_j, \ldots, x_k) \in L : x_j = x \}.\!</math> | |
| − | + | |} | |
| − | |||
| − | </ | ||
| − | = | + | In the case of a dyadic relation <math>L \subseteq X_1 \times X_2 = X \times Y,\!</math> it is possible to simplify the notation for local flags in a couple of ways. First, it is often easier in the dyadic case to refer to <math>L_{u \,\text{at}\, 1}\!</math> as <math>L_{u \,\text{at}\, X}\!</math> and <math>L_{v \,\text{at}\, 2}\!</math> as <math>L_{v \,\text{at}\, Y}.\!</math> Second, the notation may be streamlined even further by writing <math>L_{u \,\text{at}\, 1}\!</math> as <math>u \star L\!</math> and <math>L_{v \,\text{at}\, 2}\!</math> as <math>L \star v.\!</math> |
| − | + | In light of these considerations, the local flags of a dyadic relation <math>L \subseteq X \times Y\!</math> may be formulated as follows: | |
| − | |||
| − | a | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | | |
| − | + | <math>\begin{array}{lll} | |
| + | u \star L | ||
| + | & = & | ||
| + | L_{u \,\text{at}\, X} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \{ (u, y) \in L \} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \text{the ordered pairs in}~ L ~\text{that are incident with}~ u \in X. | ||
| + | \\[9pt] | ||
| + | L \star v | ||
| + | & = & | ||
| + | L_{v \,\text{at}\, Y} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \{ (x, v) \in L \} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \text{the ordered pairs in}~ L ~\text{that are incident with}~ v \in Y. | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| − | The | + | The following definitions are also useful: |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | {| align="center" cellspacing="6" width="90%" |
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | u \cdot L | ||
| + | & = & | ||
| + | \mathrm{proj}_2 (u \star L) | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \{ y \in Y : (u, y) \in L \} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \text{the elements of}~ Y ~\text{that are}~ L\text{-related to}~ u. | ||
| + | \\[9pt] | ||
| + | L \cdot v | ||
| + | & = & | ||
| + | \mathrm{proj}_1 (L \star v) | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \{ x \in X : (x, v) \in L \} | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \text{the elements of}~ X ~\text{that are}~ L\text{-related to}~ v. | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| − | < | + | A sufficient illustration is supplied by the earlier example <math>E.\!</math> |
| − | |||
| − | |||
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 30.jpg]] || (35) | |
| − | | | + | |} |
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | The | + | The local flag <math>E_{3 \,\text{at}\, X}\!</math> is displayed here: |
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 36 ISW.jpg]] || (36) | |
| − | | | + | |} |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The local flag <math>E_{2 \,\text{at}\, Y}\!</math> is displayed here: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 37 ISW.jpg]] || (37) | |
| − | + | |} | |
| − | " | ||
| − | |||
| − | |||
| − | |||
| − | + | ===Commentary Note 11.8=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Next let's re-examine the ''numerical incidence properties'' of relations, concentrating on the definitions of the assorted regularity conditions. | |
| − | < | + | For example, <math>L\!</math> is said to be <math>{}^{\backprime\backprime} c\text{-regular at}~ j \, {}^{\prime\prime}\!</math> if and only if the cardinality of the local flag <math>L_{x \,\text{at}\, j}\!</math> is equal to <math>c\!</math> for all <math>x \in X_j,\!</math> coded in symbols, if and only if <math>|L_{x \,\text{at}\, j}| = c\!</math> for all <math>{x \in X_j}.\!</math> |
| − | |||
| − | |||
| − | + | In a similar fashion, it is possible to define the numerical incidence properties <math>{}^{\backprime\backprime}(< c)\text{-regular at}~ j \, {}^{\prime\prime},\!</math> <math>{}^{\backprime\backprime}(> c)\text{-regular at}~ j \, {}^{\prime\prime},\!</math> and so on. For ease of reference, a few of these definitions are recorded below. | |
| − | + | ||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | |||
| | | | ||
| − | | | + | <math>\begin{array}{lll} |
| − | | | + | L ~\text{is}~ c\text{-regular at}~ j |
| − | | | + | & \iff & |
| − | | | + | |L_{x \,\text{at}\, j}| = c ~\text{for all}~ x \in X_j. |
| − | | | + | \\[6pt] |
| + | L ~\text{is}~ (< c)\text{-regular at}~ j | ||
| + | & \iff & | ||
| + | |L_{x \,\text{at}\, j}| < c ~\text{for all}~ x \in X_j. | ||
| + | \\[6pt] | ||
| + | L ~\text{is}~ (> c)\text{-regular at}~ j | ||
| + | & \iff & | ||
| + | |L_{x \,\text{at}\, j}| > c ~\text{for all}~ x \in X_j. | ||
| + | \\[6pt] | ||
| + | L ~\text{is}~ (\le c)\text{-regular at}~ j | ||
| + | & \iff & | ||
| + | |L_{x \,\text{at}\, j}| \le c ~\text{for all}~ x \in X_j. | ||
| + | \\[6pt] | ||
| + | L ~\text{is}~ (\ge c)\text{-regular at}~ j | ||
| + | & \iff & | ||
| + | |L_{x \,\text{at}\, j}| \ge c ~\text{for all}~ x \in X_j. | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | Clearly, if any relation is <math>(\le c)\text{-regular}\!</math> on one of its domains <math>X_j~\!</math> and also <math>(\ge c)\text{-regular}\!</math> on the same domain, then it must be <math>(= c)\text{-regular}\!</math> on that domain, in effect, <math>c\text{-regular}\!</math> at <math>j.\!</math> | ||
| + | |||
| + | For example, let <math>G = \{ r, s, t \}\!</math> and <math>H = \{ 1, \ldots, 9 \},\!</math> and consider the dyadic relation <math>F \subseteq G \times H\!</math> that is bigraphed here: | ||
| + | |||
| + | {| align="center" cellpadding="10" | ||
| + | | [[Image:LOR 1870 Figure 38.jpg]] || (38) | ||
| + | |} | ||
| + | |||
| + | We observe that <math>F\!</math> is 3-regular at <math>G\!</math> and 1-regular at <math>H.\!</math> | ||
| + | |||
| + | ===Commentary Note 11.9=== | ||
| + | |||
| + | Among the variety of conceivable regularities affecting dyadic relations we pay special attention to the <math>c\!</math>-regularity conditions where <math>c\!</math> is equal to 1. | ||
| + | |||
| + | Let <math>P \subseteq X \times Y\!</math> be an arbitrary dyadic relation. The following properties of <math>P\!</math> can be defined: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | | | + | <math>\begin{array}{lll} |
| + | P ~\text{is total at}~ X | ||
| + | & \iff & | ||
| + | P ~\text{is}~ (\ge 1)\text{-regular}~ \text{at}~ X. | ||
| + | \\[6pt] | ||
| + | P ~\text{is total at}~ Y | ||
| + | & \iff & | ||
| + | P ~\text{is}~ (\ge 1)\text{-regular}~ \text{at}~ Y. | ||
| + | \\[6pt] | ||
| + | P ~\text{is tubular at}~ X | ||
| + | & \iff & | ||
| + | P ~\text{is}~ (\le 1)\text{-regular}~ \text{at}~ X. | ||
| + | \\[6pt] | ||
| + | P ~\text{is tubular at}~ Y | ||
| + | & \iff & | ||
| + | P ~\text{is}~ (\le 1)\text{-regular}~ \text{at}~ Y. | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | We have already looked at dyadic relations that separately exemplify each of these regularities. We also introduced a few bits of additional terminology and special-purpose notations for working with tubular relations: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | + | <math>\begin{array}{lll} | |
| − | + | P ~\text{is a pre-function}~ P : X \rightharpoonup Y | |
| + | & \iff & | ||
| + | P ~\text{is tubular at}~ X. | ||
| + | \\[6pt] | ||
| + | P ~\text{is a pre-function}~ P : X \leftharpoonup Y | ||
| + | & \iff & | ||
| + | P ~\text{is tubular at}~ Y. | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | We arrive by way of this winding stair at the special stamps of dyadic relations <math>P \subseteq X \times Y\!</math> that are variously described as ''1-regular'', ''total and tubular'', or ''total prefunctions'' on specified domains, either <math>X\!</math> or <math>Y\!</math> or both, and that are more often celebrated as ''functions'' on those domains. | ||
| + | |||
| + | If <math>P\!</math> is a pre-function <math>P : X \rightharpoonup Y\!</math> that happens to be total at <math>X,\!</math> then <math>P\!</math> is known as a ''function'' from <math>X\!</math> to <math>Y,\!</math> typically indicated as <math>{P : X \to Y}.\!</math> | ||
| + | |||
| + | To say that a relation <math>P \subseteq X \times Y\!</math> is ''totally tubular'' at <math>X\!</math> is to say that <math>P\!</math> is 1-regular at <math>X.\!</math> Thus, we may formalize the following definitions: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | | | + | <math>\begin{array}{lll} |
| + | P ~\text{is a function}~ P : X \to Y | ||
| + | & \iff & | ||
| + | P ~\text{is}~ 1\text{-regular at}~ X. | ||
| + | \\[6pt] | ||
| + | P ~\text{is a function}~ P : X \leftarrow Y | ||
| + | & \iff & | ||
| + | P ~\text{is}~ 1\text{-regular at}~ Y. | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| + | |||
| + | For example, let <math>X = Y = \{ 0, \ldots, 9 \}\!</math> and let <math>F \subseteq X \times Y\!</math> be the dyadic relation depicted in the bigraph below: | ||
| + | |||
| + | {| align="center" cellpadding="10" | ||
| + | | [[Image:LOR 1870 Figure 39.jpg]] || (39) | ||
| + | |} | ||
| + | |||
| + | We observe that <math>F\!</math> is a function at <math>Y\!</math> and we record this fact in either of the manners <math>F : X \leftarrow Y\!</math> or <math>F : Y \to X.\!</math> | ||
| + | |||
| + | ===Commentary Note 11.10=== | ||
| + | |||
| + | In the case of a dyadic relation <math>F \subseteq X \times Y\!</math> that has the qualifications of a function <math>f : X \to Y,\!</math> there are a number of further differentia that arise: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | + | <math>\begin{array}{lll} | |
| − | + | f ~\text{is surjective} & \iff & f ~\text{is total at}~ Y. | |
| − | + | \\[6pt] | |
| − | + | f ~\text{is injective} & \iff & f ~\text{is tubular at}~ Y. | |
| − | + | \\[6pt] | |
| − | | | + | f ~\text{is bijective} & \iff & f ~\text{is}~ 1\text{-regular at}~ Y. |
| − | + | \end{array}\!</math> | |
| − | + | |} | |
| − | + | ||
| − | + | For example, the function <math>f : X \to Y\!</math> depicted below is neither total at <math>Y\!</math> nor tubular at <math>Y,\!</math> and so it cannot enjoy any of the properties of being surjective, injective, or bijective. | |
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 40.jpg]] || (40) | |
| + | |} | ||
| − | + | An easy way to extract a surjective function from any function is to reset its codomain to its range. For example, the range of the function <math>f\!</math> above is <math>Y^\prime = \{ 0, 2, 5, 6, 7, 8, 9 \}.\!</math> Thus, if we form a new function <math>g : X \to Y^\prime\!</math> that looks just like <math>f\!</math> on the domain <math>X\!</math> but is assigned the codomain <math>Y^\prime,\!</math> then <math>g\!</math> is surjective, and is described as mapping ''onto'' <math>Y^\prime.\!</math> | |
| − | |||
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 41.jpg]] || (41) | |
| + | |} | ||
| − | + | The function <math>h : Y^\prime \to Y\!</math> is injective. | |
| − | + | {| align="center" cellpadding="10" | |
| + | | [[Image:LOR 1870 Figure 42.jpg]] || (42) | ||
| + | |} | ||
| − | m | + | The function <math>m : X \to Y\!</math> is bijective. |
| − | + | {| align="center" cellpadding="10" | |
| + | | [[Image:LOR 1870 Figure 43.jpg]] || (43) | ||
| + | |} | ||
| − | + | ===Commentary Note 11.11=== | |
| − | |||
| − | + | The preceding exercises were intended to beef-up our “functional” literacy skills to the point where we can read our functional alphabets backwards and forwards and recognize the local functionalities that may be immanent in relative terms no matter where they locate themselves within the domains of relations. These skills will serve us in good stead as we work to build a catwalk from Peirce's platform of 1870 to contemporary scenes on the logic of relatives, and back again. | |
| − | + | By way of extending a few very tentative planks, let us experiment with the following definitions: | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | | ||
| + | <p>A relative term <math>p\!</math> and the corresponding relation <math>P \subseteq X \times Y\!</math> are both called ''functional on relates'' if and only if <math>P\!</math> is a function at <math>X,\!</math> in symbols, <math>{P : X \to Y}.\!</math></p> | ||
| + | |- | ||
| + | | | ||
| + | <p>A relative term <math>p\!</math> and the corresponding relation <math>P \subseteq X \times Y\!</math> are both called ''functional on correlates'' if and only if <math>P\!</math> is a function at <math>Y,\!</math> in symbols, <math>P : X \leftarrow Y.\!</math></p> | ||
| + | |} | ||
| − | + | When a relation happens to be a function, it may be excusable to use the same name for it in both applications, writing out explicit type markers like <math>P : X \times Y,\!</math> <math>P : X \to Y,\!</math> <math>P : X \leftarrow Y,\!</math> as the case may be, when and if it serves to clarify matters. | |
| − | + | From this current, perhaps transient, perspective, it appears that our next task is to examine how the known properties of relations are modified when an aspect of functionality is spied in the mix. Let us then return to our various ways of looking at relational composition, and see what changes and what stays the same when the relations in question happen to be functions of various different kinds at some of their domains. Here is one generic picture of relational composition, cast in a style that hews pretty close to the line of potentials inherent in Peirce's syntax of this period. | |
| − | |||
| − | + | <br> | |
| − | + | {| align="center" cellpadding="10" | |
| + | | [[Image:LOR 1870 Figure 44.jpg]] || (44) | ||
| + | |} | ||
| − | + | From this we extract the ''hypergraph picture'' of relational composition: | |
| − | + | <br> | |
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 45.jpg]] || (45) | |
| + | |} | ||
| − | + | All of the relevant information of these Figures can be compressed into the form of a spreadsheet, or constraint satisfaction table: | |
| − | + | <br> | |
| − | + | {| align="center" cellpadding="10" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center; width:60%" | |
| + | |+ style="height:30px" | <math>\text{Table 46.} ~~ \text{Relational Composition}~ P \circ Q\!</math> | ||
| + | |- | ||
| + | | style="border-right:1px solid black; border-bottom:1px solid black; width:25%" | | ||
| + | | style="border-bottom:1px solid black; width:25%" | <math>\mathit{1}\!</math> | ||
| + | | style="border-bottom:1px solid black; width:25%" | <math>\mathit{1}\!</math> | ||
| + | | style="border-bottom:1px solid black; width:25%" | <math>\mathit{1}\!</math> | ||
| + | |- | ||
| + | | style="border-right:1px solid black" | <math>P\!</math> | ||
| + | | <math>X\!</math> | ||
| + | | <math>Y\!</math> | ||
| + | | | ||
| + | |- | ||
| + | | style="border-right:1px solid black" | <math>Q\!</math> | ||
| + | | | ||
| + | | <math>Y\!</math> | ||
| + | | <math>Z\!</math> | ||
| + | |- | ||
| + | | style="border-right:1px solid black" | <math>P \circ Q</math> | ||
| + | | <math>X\!</math> | ||
| + | | | ||
| + | | <math>Z\!</math> | ||
| + | |} | ||
| − | + | <br> | |
| − | |||
| − | + | So the following presents itself as a reasonable plan of study: Let's see how much easy mileage we can get in our exploration of functions by adopting the above templates as a paradigm. | |
| − | |||
| − | of | ||
| − | |||
| − | + | ===Commentary Note 11.12=== | |
| − | + | Since functions are special cases of dyadic relations and since the space of dyadic relations is closed under relational composition — that is, the composition of two dyadic relations is again a dyadic relation — we know that the relational composition of two functions has to be a dyadic relation. If the relational composition of two functions is necessarily a function, too, then we would be justified in speaking of ''functional composition'' and also in saying that the space of functions is closed under this functional form of composition. | |
| − | + | Just for novelty's sake, let's try to prove this for relations that are functional on correlates. | |
| − | + | The task is this — We are given a pair of dyadic relations: | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | <math>P \subseteq X \times Y \quad \text{and} \quad Q \subseteq Y \times Z\!</math> | |
| + | |} | ||
| − | + | <math>P\!</math> and <math>Q\!</math> are assumed to be functional on correlates, a premiss that we express as follows: | |
| − | </ | ||
| − | == | + | {| align="center" cellspacing="6" width="90%" |
| + | | <math>P : X \gets Y \quad \text{and} \quad Q : Y \gets Z\!</math> | ||
| + | |} | ||
| − | < | + | We are charged with deciding whether the relational composition <math>P \circ Q \subseteq X \times Z\!</math> is also functional on correlates, in symbols, whether <math>{P \circ Q : X \gets Z}.\!</math> |
| − | + | ||
| − | + | It always helps to begin by recalling the pertinent definitions. | |
| − | + | ||
| − | + | For a dyadic relation <math>L \subseteq X \times Y,\!</math> we have: | |
| − | + | ||
| − | | | + | {| align="center" cellspacing="6" width="90%" |
| | | | ||
| − | + | <math>\begin{array}{lll} | |
| − | + | L ~\text{is a function}~ L : X \gets Y | |
| − | | " | + | & \iff & |
| + | L ~\text{is}~ 1\text{-regular at}~ Y. | ||
| + | \end{array}</math> | ||
| + | |} | ||
| + | |||
| + | As for the definition of relational composition, it is enough to consider the coefficient of the composite relation on an arbitrary ordered pair, <math>i\!:\!j.</math> For that, we have the following formula, where the summation indicated is logical disjunction: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| + | | <math>(P \circ Q)_{ij} ~=~ \sum_k P_{ik} Q_{kj}\!</math> | ||
| + | |} | ||
| + | |||
| + | So let's begin. | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | + | <p><math>P : X \gets Y,\!</math> or the fact that <math>P ~\text{is}~ 1\text{-regular at}~ Y,\!</math> means that there is exactly one ordered pair <math>i\!:\!k \in P</math> for each <math>k \in Y.\!</math></p> | |
| + | |- | ||
| | | | ||
| − | | | + | <p><math>Q : Y \gets Z,\!</math> or the fact that <math>Q ~\text{is}~ 1\text{-regular at}~ Z,\!</math> means that there is exactly one ordered pair <math>k\!:\!j \in Q</math> for each <math>j \in Z.\!</math></p> |
| + | |- | ||
| | | | ||
| − | + | <p>As a result, there is exactly one ordered pair <math>i\!:\!j \in P \circ Q</math> for each <math>j \in Z,\!</math> which means that <math>P \circ Q ~\text{is}~ 1\text{-regular at}~ Z,\!</math> and so we have the function <math>{P \circ Q : X \gets Z}.\!</math></p> | |
| − | + | |} | |
| − | + | ||
| − | | | + | And we are done. |
| − | + | ||
| − | + | ===Commentary Note 11.13=== | |
| − | + | ||
| − | + | As we make our way toward the foothills of Peirce's 1870 Logic of Relatives, there are several pieces of equipment that we must not leave the plains without, namely, the utilities variously known as ''arrows'', ''morphisms'', ''homomorphisms'', ''structure-preserving maps'', among other names, depending on the altitude of abstraction we happen to be traversing at the moment in question. As a moderate to middling but not too beaten track, let's examine a few ways of defining morphisms that will serve us in the present discussion. | |
| − | + | ||
| + | Suppose we are given three functions <math>J, K, L~\!</math> that satisfy the following conditions: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | + | <math>\begin{array}{lcccl} | |
| + | J & : & X & \gets & Y | ||
| + | \\[6pt] | ||
| + | K & : & X & \gets & X \times X | ||
| + | \\[6pt] | ||
| + | L & : & Y & \gets & Y \times Y | ||
| + | \end{array}</math> | ||
| + | |- | ||
| | | | ||
| − | + | <math>\begin{array}{lll} | |
| − | + | J(L(u, v)) & = & K(Ju, Jv) | |
| − | + | \end{array}</math> | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | + | Our sagittarian leitmotif can be rubricized in the following slogan: | |
| − | < | + | {| align="center" cellspacing="12" width="90%" |
| − | + | | <math>\textit{The~image~of~the~ligature~is~the~compound~of~the~images.}</math> | |
| − | + | |- | |
| − | + | | (Where <math>J\!</math> is the ''image'', <math>K\!</math> is the ''compound'', and <math>L\!</math> is the ''ligature''.) | |
| + | |} | ||
| − | + | Figure 47 presents us with a picture of the situation in question. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <br> | |
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 47.jpg]] || (47) | |
| − | + | |} | |
| − | |||
| − | |||
| − | + | Table 48 gives the constraint matrix version of the same thing. | |
| − | |||
| − | |||
| − | + | <br> | |
| − | < | + | {| align="center" cellpadding="10" cellspacing="0" style="border-left:1px solid black; border-top:1px solid black; border-right:1px solid black; border-bottom:1px solid black; text-align:center; width:60%" |
| − | + | |+ style="height:30px" | <math>\text{Table 48.} ~~ \text{Arrow Equation:} ~~ J(L(u, v)) = K(Ju, Jv)\!</math> | |
| − | + | |- | |
| + | | style="border-right:1px solid black; border-bottom:1px solid black; width:25%" | | ||
| + | | style="border-bottom:1px solid black; width:25%" | <math>J\!</math> | ||
| + | | style="border-bottom:1px solid black; width:25%" | <math>J\!</math> | ||
| + | | style="border-bottom:1px solid black; width:25%" | <math>J\!</math> | ||
| + | |- | ||
| + | | style="border-right:1px solid black" | <math>K\!</math> | ||
| + | | <math>X\!</math> | ||
| + | | <math>X\!</math> | ||
| + | | <math>X\!</math> | ||
| + | |- | ||
| + | | style="border-right:1px solid black" | <math>L\!</math> | ||
| + | | <math>Y\!</math> | ||
| + | | <math>Y\!</math> | ||
| + | | <math>Y\!</math> | ||
| + | |} | ||
| − | + | <br> | |
| − | + | One way to read this Table is in terms of the informational redundancies that it schematizes. In particular, it can be read to say that when one satisfies the constraint in the <math>L\!</math> row, along with all the constraints in the <math>J\!</math> columns, then the constraint in the <math>K\!</math> row is automatically true. That is one way of understanding the equation: <math>J(L(u, v)) ~=~ K(Ju, Jv).</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ===Commentary Note 11.14=== | |
| − | + | Now, as promised, let's look at a more homely example of a morphism, say, any one of the mappings <math>J : \mathbb{R} \to \mathbb{R}\!</math> (roughly speaking) that are commonly known as ''logarithm functions'', where you get to pick your favorite base. In this case, <math>K(r, s) = r + s~\!</math> and <math>L(u, v) = u \cdot v,\!</math> and the defining formula <math>J(L(u, v)) = K(Ju, Jv)\!</math> comes out looking like <math>J(u \cdot v) = J(u) + J(v),\!</math> writing a dot <math>(\cdot)~\!</math> and a plus sign <math>(+)\!</math> for the ordinary binary operations of arithmetical multiplication and arithmetical summation, respectively. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <br> | |
| − | | | + | {| align="center" cellpadding="10" |
| − | | | + | | [[Image:LOR 1870 Figure 49.jpg]] || (49) |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | | | ||
| − | | | ||
| − | + | Thus, where the ''image'' <math>J\!</math> is the logarithm map, the ''compound'' <math>K\!</math> is the numerical sum, and the ''ligature'' <math>L\!</math> is the numerical product, one has the following rule of thumb: | |
| − | | | + | {| align="center" cellspacing="6" width="90%" |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | | | + | <p><math>\textit{The~image~of~the~product~is~the~sum~of~the~images.}</math></p> |
| + | |- | ||
| | | | ||
| − | + | <math>\begin{array}{lll} | |
| − | + | J(u \cdot v) & = & J(u) + J(v) | |
| − | + | \\[12pt] | |
| − | + | J(L(u, v)) & = & K(Ju, Jv) | |
| − | + | \end{array}</math> | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | + | ===Commentary Note 11.15=== | |
| − | |||
| − | |||
| − | |||
| − | + | I'm going to elaborate a little further on the subject of arrows, morphisms, or structure-preserving maps, as a modest amount of extra work at this point will repay ample dividends when it comes time to revisit Peirce's “number of” function on logical terms. | |
| − | |||
| − | |||
| − | |||
| − | of | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The ''structure'' that is preserved by a structure-preserving map is just the structure that we all know and love as a triadic relation. Very typically, it will be the type of triadic relation that defines the type of binary operation that obeys the rules of a mathematical structure that is known as a ''group'', that is, a structure that satisfies the axioms for closure, associativity, identities, and inverses. | |
| − | of | ||
| − | |||
| − | |||
| − | |||
| − | + | For example, in the previous case of the logarithm map <math>J,\!</math> we have the data: | |
| − | < | + | {| align="center" cellspacing="6" width="90%" |
| − | + | | | |
| − | + | <math>\begin{array}{lcccll} | |
| − | + | J & : & \mathbb{R} & \gets & \mathbb{R} | |
| − | + | & \text{(properly restricted)} | |
| − | + | \\[6pt] | |
| − | + | K & : & \mathbb{R} & \gets & \mathbb{R} \times \mathbb{R} | |
| − | + | & \text{where}~ K(r, s) = r + s | |
| − | + | \\[6pt] | |
| − | + | L & : & \mathbb{R} & \gets & \mathbb{R} \times \mathbb{R} | |
| − | + | & \text{where}~ L(u, v) = u \cdot v | |
| − | + | \end{array}</math> | |
| − | + | |} | |
| − | + | Real number addition and real number multiplication (suitably restricted) are examples of group operations. If we write the sign of each operation in braces as a name for the triadic relation that constitutes or defines the corresponding group, then we have the following set-up: | |
| − | |||
| − | as | ||
| − | |||
| − | |||
| − | == | + | {| align="center" cellspacing="6" width="90%" |
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | J | ||
| + | & : & | ||
| + | [+] \gets [\,\cdot\,] | ||
| + | \\[6pt] | ||
| + | [+] | ||
| + | & \subseteq & | ||
| + | \mathbb{R} \times \mathbb{R} \times \mathbb{R} | ||
| + | \\[6pt] | ||
| + | [\,\cdot\,] | ||
| + | & \subseteq & | ||
| + | \mathbb{R} \times \mathbb{R} \times \mathbb{R} | ||
| + | \end{matrix}</math> | ||
| + | |} | ||
| − | < | + | In many cases, one finds that both group operations are indicated by the same sign, typically <math>\cdot\!</math> , <math>*\!</math> , <math>+\!</math> , or simple concatenation, but they remain in general distinct whether considered as operations or as relations, no matter what signs of operation are used. In such a setting, our chiasmatic theme may run a bit like these two variants: |
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | <p><math>\textit{The~image~of~the~sum~is~the~sum~of~the~images.}</math></p> | |
| − | the | + | |- |
| − | + | | <p><math>\textit{The~image~of~the~product~is~the~sum~of~the~images.}</math></p> | |
| − | + | |} | |
| − | |||
| − | |||
| − | + | Figure 50 presents a generic picture for groups <math>G\!</math> and <math>H.\!</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <br> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 50.jpg]] || (50) | |
| − | + | |} | |
| − | |||
| − | |||
| − | + | In a setting where both groups are written with a plus sign, perhaps even constituting the very same group, the defining formula of a morphism, <math>J(L(u, v)) = K(Ju, Jv),\!</math> takes on the shape <math>J(u + v) = Ju + Jv,\!</math> which looks very analogous to the distributive multiplication of a sum <math>(u + v)\!</math> by a factor <math>J.\!</math> Hence another popular name for a morphism: a ''linear'' map. | |
| − | + | ===Commentary Note 11.16=== | |
| − | + | We have enough material on morphisms now to go back and cast a more studied eye on what Peirce is doing with that “number of” function, whose application to a logical term <math>t\!</math> is indicated by writing the term in square brackets, as <math>[t].\!</math> It is convenient to have a prefix notation for the function that maps a term <math>t\!</math> to a number <math>[t]\!</math> but Peirce has previously reserved <math>\mathit{n}\!</math> for the logical <math>\mathrm{not},\!</math> so let's use <math>v(t)\!</math> as a variant for <math>[t].\!</math> | |
| − | + | My plan will be nothing less plodding than to work through the statements that Peirce made in defining and explaining the “number of” function up to our present place in the paper, namely, the budget of points collected in [[Peirce%27s_1870_Logic_Of_Relatives#Commentary_Note_11.2|Section 11.2]]. | |
| − | + | '''NOF 1''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> |
| + | | | ||
| + | <p>I propose to assign to all logical terms, numbers; to an absolute term, the number of individuals it denotes; to a relative term, the average number of things so related to one individual. Thus in a universe of perfect men (''men''), the number of “tooth of” would be 32. The number of a relative with two correlates would be the average number of things so related to a pair of individuals; and so on for relatives of higher numbers of correlates. I propose to denote the number of a logical term by enclosing the term in square brackets, thus <math>[t].\!</math></p> | ||
| − | < | + | <p>(Peirce, CP 3.65).</p> |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The role of the “number of” function may be formalized by assigning it a name and a type as <math>v : S \to \mathbb{R},\!</math> where <math>S\!</math> is a suitable set of signs, a ''>syntactic domain'', containing all the logical terms whose numbers we need to evaluate in a given discussion, and where <math>\mathbb{R}\!</math> is the set of real numbers. | |
| − | and | ||
| − | |||
| − | + | Transcribing Peirce's example: | |
| − | |||
| − | + | {| width="100%" | |
| + | | width="10%" | Let | ||
| + | | <math>\mathrm{m} = \text{man}\!</math> | ||
| + | | width="10%" | | ||
| + | |- | ||
| + | | | ||
| + | |- | ||
| + | | and | ||
| + | | <math>\mathit{t} = \text{tooth of}\,\underline{~~ ~~}.</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |- | ||
| + | | Then | ||
| + | | <math>v(\mathit{t}) ~=~ [\mathit{t}] ~=~ \frac{[\mathit{t}\mathrm{m}]}{[\mathrm{m}]}.\!</math> | ||
| + | | | ||
| + | |} | ||
| − | + | Thus, in a universe of perfect human dentition, the number of the relative term <math>{}^{\backprime\backprime} \text{tooth of}\,\underline{~~ ~~} {}^{\prime\prime}\!</math> is equal to the number of teeth of humans divided by the number of humans, that is, <math>32.\!</math> | |
| − | + | The dyadic relative term <math>t\!</math> determines a dyadic relation <math>T \subseteq X \times Y,</math> where <math>X\!</math> contains all the teeth and <math>Y\!</math> contains all the people that happen to be under discussion. | |
| − | + | A rough indication of the bigraph for <math>T\!</math> might be drawn as follows, showing just the first few items in the toothy part of <math>X\!</math> and the peoply part of <math>Y.\!</math> | |
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 51.jpg]] || (51) | |
| − | + | |} | |
| − | |||
| − | + | Notice that the “number of” function <math>v : S \to \mathbb{R}</math> needs the data that is represented by this entire bigraph for <math>T\!</math> in order to compute the value <math>[t].\!</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Finally, one observes that this component of <math>T\!</math> is a function in the direction <math>T : X \to Y,</math> since we are counting only teeth that occupy exactly one mouth of a tooth-bearing creature. | |
| − | of | ||
| − | + | ===Commentary Note 11.17=== | |
| − | |||
| − | + | I think the reader is beginning to get an inkling of the crucial importance of the “number of” function in Peirce's way of looking at logic. Among other things it is one of the planks in the bridge from logic to the theories of probability, statistics, and information, in which setting logic forms but a limiting case at one scenic turnout on the expanding vista. It is, as a matter of necessity and a matter of fact, practically speaking at any rate, one way that Peirce forges a link between the ''eternal'', logical, or rational realm and the ''secular'', empirical, or real domain. | |
| − | |||
| − | |||
| − | + | With that little bit of encouragement and exhortation, let us return to the nitty gritty details of the text. | |
| − | |||
| − | |||
| − | + | '''NOF 2''' | |
| − | |||
| − | |||
| − | == | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> |
| + | | | ||
| + | <p>But not only do the significations of <math>=\!</math> and <math><\!</math> here adopted fulfill all absolute requirements, but they have the supererogatory virtue of being very nearly the same as the common significations. Equality is, in fact, nothing but the identity of two numbers; numbers that are equal are those which are predicable of the same collections, just as terms that are identical are those which are predicable of the same classes. So, to write <math>5 < 7\!</math> is to say that <math>5\!</math> is part of <math>7\!</math>, just as to write <math>\mathrm{f} < \mathrm{m}~\!</math> is to say that Frenchmen are part of men. Indeed, if <math>\mathrm{f} < \mathrm{m}~\!</math>, then the number of Frenchmen is less than the number of men, and if <math>\mathrm{v} = \mathrm{p}\!</math>, then the number of Vice-Presidents is equal to the number of Presidents of the Senate; so that the numbers may always be substituted for the terms themselves, in case no signs of operation occur in the equations or inequalities.</p> | ||
| − | < | + | <p>(Peirce, CP 3.66).</p> |
| − | + | |} | |
| − | |||
| − | + | Peirce is here remarking on the principle that the measure <math>\mathit{v}\!</math> on terms ''preserves'' or ''respects'' the prevailing implication, inclusion, or subsumption relations that impose an ordering on those terms. In these initiatory passages of the text, Peirce is using a single symbol <math><\!</math> to denote the usual linear ordering on numbers, but also what amounts to the implication ordering on logical terms and the inclusion ordering on classes. Later, of course, he will introduce distinctive symbols for logical orders. The links among terms, sets, and numbers can be pursued in all directions, and Peirce has already indicated in an earlier paper how he would construct the integers from sets, that is, from the aggregate denotations of terms. I will try to get back to that another time. | |
| − | + | ||
| − | + | We have a statement of the following form: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| + | | If <math>\mathrm{f} < \mathrm{m},\!</math> then the number of Frenchmen is less than the number of men. | ||
| + | |} | ||
| − | + | This goes into symbolic form as follows: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{f} < \mathrm{m} & \Rightarrow & [\mathrm{f}] < [\mathrm{m}]. | ||
| + | \end{matrix}</math> | ||
| + | |} | ||
| − | + | In this setting the <math>^{\backprime\backprime}\!\!<\!^{\prime\prime}</math> on the left is a logical ordering on syntactic terms while the <math>^{\backprime\backprime}\!\!<\!^{\prime\prime}</math> on the right is an arithmetic ordering on real numbers. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The question that arises in this case is whether a map between two ordered sets is ''order-preserving''. In order to formulate the question in more general terms, we may begin with the following set-up: | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | Let <math>X_1\!</math> be a set with the ordering <math><_1\!.</math> | |
| − | + | |- | |
| − | + | | Let <math>X_2\!</math> be a set with the ordering <math><_2\!.</math> | |
| − | + | |} | |
| − | |||
| − | |||
| − | + | An order relation is typically defined by a set of axioms that determines its properties. Since we have frequent occasion to view the same set in the light of several different order relations, we often resort to explicit specifications like <math>(X, <_1),\!</math> <math>(X, <_2),\!</math> and so on, to indicate a set with a given ordering. | |
| − | + | A map <math>F : (X_1, <_1) \to (X_2, <_2)</math> is ''order-preserving'' if and only if a statement of a particular form holds for all <math>x\!</math> and <math>y\!</math> in <math>(X_1, <_1),\!</math> namely, the following: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | + | {| align="center" cellspacing="6" width="90%" |
| − | |||
| − | |||
| | | | ||
| − | | | + | <math>\begin{matrix} |
| − | + | x <_1 y & \Rightarrow & F(x) <_2 F(y). | |
| − | | | + | \end{matrix}</math> |
| + | |} | ||
| + | |||
| + | The “number of” map <math>v : (S, <_1) \to (\mathbb{R}, <_2)</math> has just this character, as exemplified in the case at hand: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | | | + | <math>\begin{matrix} |
| + | \mathrm{f} & < & \mathrm{m} & \Rightarrow & [\mathrm{f}] & < & [\mathrm{m}] | ||
| + | \\[6pt] | ||
| + | \mathrm{f} & < & \mathrm{m} & \Rightarrow & v(\mathrm{f}) & < & v(\mathrm{m}) | ||
| + | \end{matrix}</math> | ||
| + | |} | ||
| − | + | Here, the <math>^{\backprime\backprime}\!\!<\!^{\prime\prime}</math> on the left is read as ''proper inclusion'', in other words, ''subset of but not equal to'', while the <math>^{\backprime\backprime}\!\!<\!^{\prime\prime}</math> on the right is read as the ordinary ''less than'' relation. | |
| − | |||
| − | </ | ||
| − | ==Commentary Note 11. | + | ===Commentary Note 11.18=== |
| − | + | An ''order-preserving map'' is a special case of a ''structure preserving map'', and the idea of ''preserving structure'', as used in mathematics, always means preserving ''some'' but not necessarily ''all'' the structure of the source domain in question. People sometimes express this by speaking of ''structure preservation in measure'', the implication being that any property that is amenable to being qualified in manner is potentially amenable to being quantified in degree, perhaps in such a way as to answer questions like “How structure-preserving is it?” | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Let's see how this remark applies to the order-preserving property of the “number of” mapping <math>v : S \to \mathbb{R}.</math> For any pair of absolute terms <math>x\!</math> and <math>y\!</math> in the syntactic domain <math>S,\!</math> we have the following implications, where <math>^{\backprime\backprime}-\!\!\!<\!^{\prime\prime}</math> denotes the logical subsumption relation on terms and <math>^{\backprime\backprime}\!\!\le\!^{\prime\prime}</math> denotes the ''less than or equal to'' relation on the real number domain <math>\mathbb{R}.</math> | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | | ||
| + | <math>\begin{array}{lll} | ||
| + | x ~-\!\!\!< y & \Rightarrow & vx \le vy | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | Equivalently: | |
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | | |
| + | <math>\begin{array}{lll} | ||
| + | x ~-\!\!\!< y & \Rightarrow & [x] \le [y] | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | Nowhere near the number of logical distinctions that exist on the left hand side of the implication arrow can be preserved as one passes to the linear ordering of real numbers on the right hand side of the implication arrow, but that is not required in order to call the map <math>v : S \to \mathbb{R}</math> ''order-preserving'', or what is known as an ''order morphism''. | |
| − | + | ===Commentary Note 11.19=== | |
| − | + | Up to this point in the 1870 Logic of Relatives, Peirce has introduced the “number of” function on logical terms and discussed the extent to which its use as a measure, <math>v : S \to \mathbb{R}\!</math> such that <math>v : s \mapsto [s],\!</math> satisfies the relevant measure-theoretic principles, for starters, these two: | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | valign="top" | 1. | ||
| + | | The “number of” map exhibits a certain type of ''uniformity property'', whereby the value of the measure on a uniformly qualified population is in fact actualized by each member of the population. | ||
| + | |- | ||
| + | | valign="top" | 2. | ||
| + | | The “number of” map satisfies an ''order morphism principle'', whereby the illative partial ordering of logical terms is reflected up to a partial extent by the arithmetical linear ordering of their measures. | ||
| + | |} | ||
| − | + | Peirce next takes up the action of the “number of” map on the two types of, loosely speaking, ''additive'' operations that we normally consider in logic. | |
| − | + | '''NOF 3.1''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| + | | | ||
| + | <p>It is plain that both the regular non-invertible addition and the invertible addition satisfy the absolute conditions.</p> | ||
| − | + | <p>(Peirce, CP 3.67).</p> | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | The | + | The sign <math>^{\backprime\backprime} +\!\!, {}^{\prime\prime}</math> denotes what Peirce calls “the regular non-invertible addition”, corresponding to the inclusive disjunction of logical terms or the union of their extensions as sets. |
| − | + | The sign <math>^{\backprime\backprime} + ^{\prime\prime}</math> denotes what Peirce calls “the invertible addition”, corresponding to the exclusive disjunction of logical terms or the symmetric difference of their extensions as sets. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | + | '''NOF 3.2''' | |
| − | < | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> |
| − | + | | | |
| − | + | <p>But the notation has other recommendations. The conception of ''taking together'' involved in these processes is strongly analogous to that of summation, the sum of <math>2\!</math> and <math>5,\!</math> for example, being the number of a collection which consists of a collection of two and a collection of five.</p> | |
| − | + | <p>(Peirce, CP 3.67).</p> | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | + | A full interpretation of this remark will require us to pick up the precise technical sense in which Peirce is using the word ''collection'', and that will take us back to his logical reconstruction of certain aspects of number theory, all of which I am putting off to another time, but it is still possible to get a rough sense of what he's saying relative to the present frame of discussion. | |
| − | of | ||
| − | |||
| − | |||
| − | + | The “number of” map <math>v : S \to \mathbb{R}</math> evidently induces some sort of morphism with respect to logical sums. If this were straightforwardly true, we could write: | |
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | | |
| − | + | <math>\begin{matrix} | |
| − | + | ? & v(x ~+\!\!,~ y) & = & v(x) ~+~ v(y) & ? | |
| − | + | \end{matrix}</math> | |
| − | + | |} | |
| − | |||
| − | + | Equivalently: | |
| − | |||
| − | == | + | {| align="center" cellspacing="6" width="90%" |
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | ? & [x ~+\!\!,~ y] & = & [x] ~+~ [y] & ? | ||
| + | \end{matrix}</math> | ||
| + | |} | ||
| − | + | Of course, things are not quite that simple when it comes to inclusive disjunctions and set-theoretic unions, so it is usual to introduce the concept of a ''sub-additive measure'' to describe the principle that does hold here, namely, the following: | |
| − | |||
| − | |||
| − | | | + | {| align="center" cellspacing="6" width="90%" |
| − | |||
| | | | ||
| − | | | + | <math>\begin{matrix} |
| + | v(x ~+\!\!,~ y) & \le & v(x) ~+~ v(y) | ||
| + | \end{matrix}</math> | ||
| + | |} | ||
| + | |||
| + | Equivalently: | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" | ||
| | | | ||
| − | + | <math>\begin{matrix} | |
| − | + | [x ~+\!\!,~ y] & \le & [x] ~+~ [y] | |
| − | + | \end{matrix}</math> | |
| − | + | |} | |
| − | | | ||
| − | + | This is why Peirce trims his discussion of this point with the following hedge: | |
| − | |||
| − | + | '''NOF 3.3''' | |
| − | |||
| − | | | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> |
| | | | ||
| − | + | <p>Any logical equation or inequality in which no operation but addition is involved may be converted into a numerical equation or inequality by substituting the numbers of the several terms for the terms themselves — provided all the terms summed are mutually exclusive.</p> | |
| − | + | <p>(Peirce, CP 3.67).</p> | |
| − | + | |} | |
| − | |||
| − | |||
| − | + | Finally, a morphism with respect to addition, even a contingently qualified one, must do the right stuff on behalf of the additive identity: | |
| − | | | + | |
| + | '''NOF 3.4''' | ||
| + | |||
| + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | ||
| | | | ||
| − | + | <p>Addition being taken in this sense, ''nothing'' is to be denoted by ''zero'', for then</p> | |
| − | | | + | |- |
| + | | align="center" | <math>x ~+\!\!,~ 0 ~=~ x</math> | ||
| + | |- | ||
| | | | ||
| − | | | + | <p>whatever is denoted by <math>x\!</math>; and this is the definition of ''zero''. This interpretation is given by Boole, and is very neat, on account of the resemblance between the ordinary conception of ''zero'' and that of nothing, and because we shall thus have</p> |
| + | |- | ||
| + | | align="center" | <math>[0] ~=~ 0.</math> | ||
| + | |- | ||
| | | | ||
| − | + | <p>(Peirce, CP 3.67).</p> | |
| + | |} | ||
| − | + | With respect to the nullity <math>0\!</math> in <math>S\!</math> and the number <math>0\!</math> in <math>\mathbb{R},</math> we have: | |
| − | the | ||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | <math>v0 ~=~ [0] ~=~ 0.</math> | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | In sum, therefore, it can be said: ''It also serves that only preserves a due respect for the function of a vacuum in nature.'' | |
| − | |||
| − | |||
| − | |||
| − | ==Commentary Note 11. | + | ===Commentary Note 11.20=== |
| − | + | We arrive at the last of Peirce's statements about the “number of” map that we singled out above: | |
| − | |||
| − | the | ||
| − | |||
| − | + | '''NOF 4.1''' | |
| − | + | ||
| − | | | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> |
| | | | ||
| − | + | <p>The conception of multiplication we have adopted is that of the application of one relation to another. …</p> | |
| − | + | <p>Even ordinary numerical multiplication involves the same idea, for <math>~2 \times 3~</math> is a pair of triplets, and <math>~3 \times 2~</math> is a triplet of pairs, where “triplet of” and “pair of” are evidently relatives.</p> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <p>If we have an equation of the form:</p> | |
| − | + | |- | |
| − | | | + | | align="center" | <math>xy ~=~ z</math> |
| − | + | |- | |
| − | | | + | | |
| − | + | <p>and there are just as many <math>x\!</math>'s per <math>y\!</math> as there are ''per'' things, things of the universe, then we have also the arithmetical equation:</p> | |
| − | + | |- | |
| + | | align="center" | <math>[x][y] ~=~ [z].</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>(Peirce, CP 3.76).</p> | ||
| + | |} | ||
| − | + | Peirce is here observing what we might call a ''contingent morphism''. Provided that a certain condition, to be named in short order, happens to be satisfied, we would find it holding that the “number of” map <math>v : S \to \mathbb{R}</math> such that <math>v(s) = [s]\!</math> serves to preserve the multiplication of relative terms, that is to say, the composition of relations, in the form: <math>[xy] = [x][y].\!</math> So let us try to uncross Peirce's manifestly chiasmatic encryption of the condition that is called on in support of this preservation. | |
| − | |||
| − | of the | ||
| − | |||
| − | |||
| − | |||
| − | + | The proviso for the equation <math>[xy] = [x][y]\!</math> to hold is this: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| + | | | ||
| + | <p>There are just as many <math>x\!</math>'s per <math>y\!</math> as there are ''per'' things, things of the universe.</p> | ||
| − | + | <p>(Peirce, CP 3.76).</p> | |
| − | + | |} | |
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | + | Returning to the example that Peirce gives: | |
| − | + | '''NOF 4.2''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> |
| + | | | ||
| + | <p>For instance, if our universe is perfect men, and there are as many teeth to a Frenchman (perfect understood) as there are to any one of the universe, then:</p> | ||
| + | |- | ||
| + | | align="center" | <math>[\mathit{t}][\mathrm{f}] ~=~ [\mathit{t}\mathrm{f}]</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>holds arithmetically.</p> | ||
| − | < | + | <p>(Peirce, CP 3.76).</p> |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Peirce | ||
| − | |||
| − | + | Now that is something that we can sink our teeth into and trace the bigraph representation of the situation. It will help to recall our first examination of the “tooth of” relation and to adjust the picture we sketched of it on that occasion. | |
| − | |||
| − | + | Transcribing Peirce's example: | |
| − | |||
| − | |||
| − | + | {| width="100%" | |
| − | + | | width="10%" | Let | |
| − | + | | <math>\mathrm{m} = \text{man}\!</math> | |
| + | | width="10%" | | ||
| + | |- | ||
| + | | | ||
| + | |- | ||
| + | | and | ||
| + | | <math>\mathit{t} = \text{tooth of}\,\underline{~~ ~~}.\!</math> | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |- | ||
| + | | Then | ||
| + | | <math>v(\mathit{t}) ~=~ [\mathit{t}] ~=~ \frac{[\mathit{t}\mathrm{m}]}{[\mathrm{m}]}.\!</math> | ||
| + | | | ||
| + | |} | ||
| − | + | That is to say, the number of the relative term <math>\text{tooth of}\,\underline{~~ ~~}\!</math> is equal to the number of teeth of humans divided by the number of humans. In a universe of perfect human dentition this gives a quotient of <math>32.\!</math> | |
| − | |||
| − | |||
| − | |||
| − | + | The dyadic relative term <math>t\!</math> determines a dyadic relation <math>T \subseteq X \times Y,</math> where <math>X\!</math> contains all the teeth and <math>Y\!</math> contains all the people that happen to be under discussion. | |
| − | |||
| − | |||
| − | + | To make the case as simple as possible and still cover the point, suppose there are just four people in our universe of discourse and just two of them are French. The bigraphical composition below shows the pertinent facts of the case. | |
| − | |||
| − | |||
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:LOR 1870 Figure 52.jpg]] || (52) | |
| − | + | |} | |
| − | + | In this picture the order of relational composition flows down the page. For convenience in composing relations, the absolute term <math>\mathrm{f} = \text{Frenchman}\!</math> is inflected by the comma functor to form the dyadic relative term <math>\mathrm{f,} = \text{Frenchman that is}\,\underline{~~ ~~},\!</math> which in turn determines the idempotent representation of Frenchmen as a subset of mankind, <math>F \subseteq Y \times Y.\!</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | By way of a legend for the figure, we have the following data: | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | | | + | | |
| − | + | <math>\begin{array}{lllr} | |
| − | + | \mathrm{m} | |
| − | + | & = & | |
| − | + | \mathrm{J} ~+\!\!,~ \mathrm{K} ~+\!\!,~ \mathrm{L} ~+\!\!,~ \mathrm{M} \qquad = & | |
| − | + | \mathbf{1} | |
| − | + | \\[6pt] | |
| − | + | \mathrm{f} | |
| − | + | & = & \mathrm{K} ~+\!\!,~ \mathrm{M} | |
| − | + | \\[6pt] | |
| − | + | \mathrm{f,} | |
| − | + | & = & \mathrm{K}\!:\!\mathrm{K} ~+\!\!,~ \mathrm{M}\!:\!\mathrm{M} | |
| − | + | \\[6pt] | |
| − | + | \mathit{t} | |
| − | + | & = & (T_{001} ~+\!\!,~ \dots ~+\!\!,~ T_{032}):J & ~+\!\!, | |
| − | + | \\[6pt] | |
| − | + | & & (T_{033} ~+\!\!,~ \dots ~+\!\!,~ T_{064}):K & ~+\!\!, | |
| − | + | \\[6pt] | |
| + | & & (T_{065} ~+\!\!,~ \dots ~+\!\!,~ T_{096}):L & ~+\!\!, | ||
| + | \\[6pt] | ||
| + | & & (T_{097} ~+\!\!,~ \dots ~+\!\!,~ T_{128}):M | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | Now let's see if we can use this picture to make sense of the following statement: | |
| − | |||
| − | + | '''NOF 4.3''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| − | + | | | |
| − | + | <p>For instance, if our universe is perfect men, and there are as many teeth to a Frenchman (perfect understood) as there are to any one of the universe, then:</p> | |
| − | </ | + | |- |
| + | | align="center" | <math>[\mathit{t}][\mathrm{f}] ~=~ [\mathit{t}\mathrm{f}]</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>holds arithmetically.</p> | ||
| − | + | <p>(Peirce, CP 3.76).</p> | |
| + | |} | ||
| − | + | In statistical terms, Peirce is saying this: If the population of Frenchmen is a ''fair sample'' of the general population with regard to the factor of dentition, then the morphic equation, | |
| − | |||
| − | of | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | <math>[\mathit{t}\mathrm{f}] = [\mathit{t}][\mathrm{f}],\!</math> | |
| + | |} | ||
| − | + | whose transpose gives the equation, | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | <math>[\mathit{t}] = \frac{[\mathit{t}\mathrm{f}]}{[\mathrm{f}]},\!</math> | ||
| + | |} | ||
| − | + | is every bit as true as the defining equation in this circumstance, namely, | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | <math>[\mathit{t}] = \frac{[\mathit{t}\mathrm{m}]}{[\mathrm{m}]}.\!</math> | ||
| + | |} | ||
| − | + | ===Commentary Note 11.21=== | |
| − | |||
| − | |||
| − | + | One more example and one more general observation, and then we will be all caught up with our homework on Peirce's “number of” function. | |
| − | + | '''NOF 4.4''' | |
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| − | + | | | |
| + | <p>So if men are just as apt to be black as things in general,</p> | ||
| + | |- | ||
| + | | align="center" | <math>[\mathrm{m,}][\mathrm{b}] ~=~ [\mathrm{m,}\mathrm{b}],\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>where the difference between <math>[\mathrm{m}]\!</math> and <math>[\mathrm{m,}]\!</math> must not be overlooked.</p> | ||
| − | + | <p>(Peirce, CP 3.76).</p> | |
| − | + | |} | |
| − | + | The protasis, “men are just as apt to be black as things in general”, is elliptic in structure, and presents us with a potential ambiguity. If we had no further clue to its meaning, it might be read as either of the following: | |
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | valign="top" | 1. | ||
| + | | Men are just as apt to be black as things in general are apt to be black. | ||
| + | |- | ||
| + | | valign="top" | 2. | ||
| + | | Men are just as apt to be black as men are apt to be things in general. | ||
| + | |} | ||
| − | + | The second interpretation, if grammatical, is pointless to state, since it equates a proper contingency with an absolute certainty. So I think it is safe to assume this paraphrase of what Peirce intends: | |
| − | |||
| − | == | + | {| align="center" cellspacing="6" width="90%" |
| + | | <p>Men are just as likely to be black as things in general are likely to be black.</p> | ||
| + | |} | ||
| − | + | Stated in terms of the conditional probability: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | <math>\mathrm{P}(\mathrm{b}|\mathrm{m}) ~=~ \mathrm{P}(\mathrm{b}).\!</math> | |
| − | + | |} | |
| − | |||
| − | + | From the definition of conditional probability: | |
| − | |||
| − | |||
| − | | | + | {| align="center" cellspacing="6" width="90%" |
| − | + | | <math>\mathrm{P}(\mathrm{b}|\mathrm{m}) ~=~ {\mathrm{P}(\mathrm{b}\mathrm{m}) \over \mathrm{P}(\mathrm{m})}.\!</math> | |
| − | | | + | |} |
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | + | Equivalently: | |
| − | > | + | {| align="center" cellspacing="6" width="90%" |
| + | | <math>\mathrm{P}(\mathrm{b}\mathrm{m}) ~=~ \mathrm{P}(\mathrm{b}|\mathrm{m})\mathrm{P}(\mathrm{m}).\!</math> | ||
| + | |} | ||
| − | + | Taking everything together, we obtain the following result: | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | <math>\mathrm{P}(\mathrm{b}\mathrm{m}) ~=~ \mathrm{P}(\mathrm{b}|\mathrm{m})\mathrm{P}(\mathrm{m}) ~=~ \mathrm{P}(\mathrm{b})\mathrm{P}(\mathrm{m}).\!</math> | ||
| + | |} | ||
| − | + | This, of course, is the definition of independent events, as applied to the event of being Black and the event of being a Man. It seems to be the most likely guess that this is the meaning of Peirce's statement about frequencies: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | <math>[\mathrm{m,}\mathrm{b}] ~=~ [\mathrm{m,}][\mathrm{b}].\!</math> | |
| + | |} | ||
| − | + | The terms of this equation can be normalized to produce the corresponding statement about probabilities: | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | <math>\mathrm{P}(\mathrm{m}\mathrm{b}) ~=~ \mathrm{P}(\mathrm{m})\mathrm{P}(\mathrm{b}).\!</math> | |
| − | + | |} | |
| − | |||
| − | | | ||
| − | |||
| − | | | ||
| − | |||
| − | + | Let's see if this checks out. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | = | + | Let <math>N\!</math> be the number of things in general. In terms of Peirce's “number of” function, then, we have the equation <math>[\mathbf{1}] = N.</math> On the assumption that <math>\mathrm{m}\!</math> and <math>\mathrm{b}\!</math> are associated with independent events, we obtain the following sequence of equations: |
| − | < | + | {| align="center" cellspacing="6" width="90%" |
| − | + | | | |
| − | + | <math>\begin{array}{lll} | |
| + | [\mathrm{m,}\mathrm{b}] | ||
| + | & = & | ||
| + | \mathrm{P}(\mathrm{m}\mathrm{b}) N | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \mathrm{P}(\mathrm{m})\mathrm{P}(\mathrm{b}) N | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | \mathrm{P}(\mathrm{m})[\mathrm{b}] | ||
| + | \\[6pt] | ||
| + | & = & | ||
| + | [\mathrm{m,}][\mathrm{b}]. | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | As a result, we have to interpret <math>[\mathrm{m,}]\!</math> = “the average number of men per things in general” as <math>\mathrm{P}(\mathrm{m})\!</math> = “the probability of a thing in general being a man”. This seems to make sense. | |
| − | |||
| − | + | ===Commentary Note 11.22=== | |
| − | |||
| − | |||
| − | |||
| − | + | Let's look at that last example from a different angle. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''NOF 4.4''' | |
| − | |||
| − | |||
| − | |||
| − | | | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> |
| | | | ||
| − | | | + | <p>So if men are just as apt to be black as things in general,</p> |
| + | |- | ||
| + | | align="center" | <math>[\mathrm{m,}][\mathrm{b}] ~=~ [\mathrm{m,}\mathrm{b}],\!</math> | ||
| + | |- | ||
| | | | ||
| − | + | <p>where the difference between <math>[\mathrm{m}]\!</math> and <math>[\mathrm{m,}]\!</math> must not be overlooked.</p> | |
| − | </ | ||
| − | + | <p>(Peirce, CP 3.76).</p> | |
| + | |} | ||
| − | < | + | In different lights the formula <math>[\mathrm{m,}\mathrm{b}] = [\mathrm{m,}][\mathrm{b}]\!</math> presents itself as an ''aimed arrow'', ''fair sample'', or ''stochastic independence'' condition. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | The | + | The example apparently assumes a universe of ''things in general'', encompassing among other things the denotations of the absolute terms <math>\mathrm{m} = \text{man}\!</math> and <math>\mathrm{b} = \text{black}.\!</math> That suggests to me that we might well illustrate this case in relief, by returning to our earlier staging of ''Othello'' and seeing how well that universe of dramatic discourse observes the premiss that “men are just as apt to be black as things in general”. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Here are the relevant data: | |
| − | | | + | {| align="center" cellspacing="6" width="90%" |
| − | |||
| − | |||
| | | | ||
| − | + | <math>\begin{array}{*{15}{l}} | |
| + | \mathrm{b} & = & \mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathrm{m} & = & | ||
| + | \mathrm{C} & +\!\!, & | ||
| + | \mathrm{I} & +\!\!, & | ||
| + | \mathrm{J} & +\!\!, & | ||
| + | \mathrm{O} | ||
| + | \\[6pt] | ||
| + | \mathbf{1} & = & | ||
| + | \mathrm{B} & +\!\!, & | ||
| + | \mathrm{C} & +\!\!, & | ||
| + | \mathrm{D} & +\!\!, & | ||
| + | \mathrm{E} & +\!\!, & | ||
| + | \mathrm{I} & +\!\!, & | ||
| + | \mathrm{J} & +\!\!, & | ||
| + | \mathrm{O} | ||
| + | \\[12pt] | ||
| + | \mathrm{b,} & = & \mathrm{O\!:\!O} | ||
| + | \\[6pt] | ||
| + | \mathrm{m,} & = & | ||
| + | \mathrm{C\!:\!C} & +\!\!, & | ||
| + | \mathrm{I\!:\!I} & +\!\!, & | ||
| + | \mathrm{J\!:\!J} & +\!\!, & | ||
| + | \mathrm{O\!:\!O} | ||
| + | \\[6pt] | ||
| + | \mathbf{1,} & = & | ||
| + | \mathrm{B\!:\!B} & +\!\!, & | ||
| + | \mathrm{C\!:\!C} & +\!\!, & | ||
| + | \mathrm{D\!:\!D} & +\!\!, & | ||
| + | \mathrm{E\!:\!E} & +\!\!, & | ||
| + | \mathrm{I\!:\!I} & +\!\!, & | ||
| + | \mathrm{J\!:\!J} & +\!\!, & | ||
| + | \mathrm{O\!:\!O} | ||
| + | \end{array}</math> | ||
| + | |} | ||
| − | + | The ''fair sampling'' condition is tantamount to this: “Men are just as apt to be black as things in general are apt to be black”. In other words, men are a fair sample of things in general with respect to the factor of being black. | |
| − | are | ||
| − | in | ||
| − | |||
| − | + | Should this hold, the consequence would be: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | <math>[\mathrm{m,}\mathrm{b}] ~=~ [\mathrm{m,}][\mathrm{b}].</math> | |
| − | + | |} | |
| − | |||
| − | |||
| − | + | When <math>[\mathrm{b}]\!</math> is not zero, we obtain the result: | |
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | <math>[\mathrm{m,}] ~=~ \frac{[\mathrm{m,}\mathrm{b}]}{[\mathrm{b}]}.</math> | ||
| + | |} | ||
| − | + | As before, it is convenient to represent the absolute term <math>\mathrm{b} = \text{black}\!</math> by means of the corresponding idempotent term <math>\mathrm{b,} = \text{black that is}\,\underline{~~ ~~}.</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Consider the bigraph for the composition: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | {| align="center" cellspacing="6" width="90%" |
| + | | <math>\mathrm{m,}\mathrm{b} ~=~ \text{man that is black}.</math> | ||
| + | |} | ||
| − | + | This is represented below in the equivalent form: | |
| − | |||
| − | |||
| − | is | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | <math>\mathrm{m,}\mathrm{b,} ~=~ \text{man that is black that is}\,\underline{~~ ~~}.</math> | |
| − | + | |} | |
| − | |||
| − | |||
| − | LOR. | + | {| align="center" cellpadding="10" |
| + | | [[Image:LOR 1870 Figure 53.jpg]] || (53) | ||
| + | |} | ||
| − | + | Thus we observe one of the more factitious facts affecting this very special universe of discourse, namely: | |
| − | | | + | {| align="center" cellspacing="6" width="90%" |
| − | + | | <math>\mathrm{m,}\mathrm{b} ~=~ \mathrm{b}.</math> | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | | | ||
| − | |||
| − | + | This is equivalent to the implication <math>\mathrm{b} \Rightarrow \mathrm{m}</math> that Peirce would have written in the form <math>\mathrm{b} ~-\!\!\!<~ \mathrm{m}.</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | That is enough to puncture any notion that <math>\mathrm{b}\!</math> and <math>\mathrm{m}\!</math> are statistically independent, but let us continue to develop the plot a bit more. Putting all the general formulas and particular facts together, we arrive at the following summation of the situation in the ''Othello'' case: | |
| − | |||
| − | |||
| − | the | ||
| − | + | If the fair sampling condition were true, it would have the following consequence: | |
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | <math>[\mathrm{m,}] ~=~ \frac{[\mathrm{m,}\mathrm{b}]}{[\mathrm{b}]} ~=~ \frac{[\mathrm{b}]}{[\mathrm{b}]} ~=~ \mathfrak{1}.</math> | |
| − | + | |} | |
| − | |||
| − | + | On the contrary, we have the following fact: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | <math>[\mathrm{m,}] ~=~ \frac{[\mathrm{m,}\mathbf{1}]}{[\mathbf{1}]} ~=~ \frac{[\mathrm{m}]}{[\mathbf{1}]} ~=~ \frac{4}{7}.\!</math> | |
| − | + | |} | |
| − | + | In sum, it is not the case in the ''Othello'' example that “men are just as apt to be black as things in general”. | |
| − | in the | ||
| − | |||
| − | |||
| − | == | + | Expressed in terms of probabilities: <math>\mathrm{P}(\mathrm{m}) = \frac{4}{7}</math> and <math>\mathrm{P}(\mathrm{b}) = \frac{1}{7}.</math> |
| − | < | + | If these were independent terms we would have: <math>\mathrm{P}(\mathrm{m}\mathrm{b}) = \frac{4}{49}.</math> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | In point of fact, however, we have: <math>\mathrm{P}(\mathrm{m}\mathrm{b}) = \mathrm{P}(\mathrm{b}) = \frac{1}{7}.</math> | |
| − | |||
| − | + | Another way to see it is to observe that: <math>\mathrm{P}(\mathrm{b}|\mathrm{m}) = \frac{1}{4}</math> while <math>\mathrm{P}(\mathrm{b}) = \frac{1}{7}.</math> | |
| − | + | ===Commentary Note 11.23=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Peirce is | + | Peirce's description of logical conjunction and conditional probability via the logic of relatives and the mathematics of relations is critical to understanding the relationship between logic and measurement, in effect, the qualitative and quantitative aspects of inquiry. To ground this connection firmly in mind, I will try to sum up as succinctly as possible, in more current notation, the lesson we ought to take away from Peirce's last “number of” example, since I know the account I have given so far may appear to have wandered widely. |
| − | |||
| − | |||
| − | |||
| − | + | '''NOF 4.4''' | |
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| − | + | | | |
| − | the | + | <p>So if men are just as apt to be black as things in general,</p> |
| + | |- | ||
| + | | align="center" | <math>[\mathrm{m,}][\mathrm{b}] ~=~ [\mathrm{m,}\mathrm{b}],\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>where the difference between <math>[\mathrm{m}]\!</math> and <math>[\mathrm{m,}]\!</math> must not be overlooked.</p> | ||
| − | + | <p>(Peirce, CP 3.76).</p> | |
| + | |} | ||
| − | In the | + | In different lights the formula <math>[\mathrm{m,}\mathrm{b}] = [\mathrm{m,}][\mathrm{b}]\!</math> presents itself as an ''aimed arrow'', ''fair sampling'', or ''statistical independence'' condition. The concept of independence was illustrated above by means of a case where independence fails. The details of that counterexample are summarized below. |
| − | " | + | {| align="center" cellpadding="10" |
| + | | [[Image:LOR 1870 Figure 53.jpg]] || (54) | ||
| + | |} | ||
| − | + | The condition that “men are just as apt to be black as things in general” is expressed in terms of conditional probabilities as <math>\mathrm{P}(\mathrm{b}|\mathrm{m}) = \mathrm{P}(\mathrm{b}),\!</math> which means that the probability of the event <math>\mathrm{b}\!</math> given the event <math>\mathrm{m}\!</math> is equal to the unconditional probability of the event <math>\mathrm{b}.\!</math> | |
| − | + | In the ''Othello'' example, it is enough to observe that <math>\mathrm{P}(\mathrm{b}|\mathrm{m}) = \tfrac{1}{4}\!</math> while <math>\mathrm{P}(\mathrm{b}) = \tfrac{1}{7}\!</math> in order to recognize the bias or dependency of the sampling map. | |
| − | + | The reduction of a conditional probability to an absolute probability, as <math>\mathrm{P}(A|Z) = \mathrm{P}(A),\!</math> is one of the ways we come to recognize the condition of independence, <math>\mathrm{P}(AZ) = \mathrm{P}(A)P(Z),\!</math> via the definition of conditional probability, <math>\mathrm{P}(A|Z) = \displaystyle{\mathrm{P}(AZ) \over \mathrm{P}(Z)}.\!</math> | |
| − | |||
| − | + | To recall the derivation, the definition of conditional probability plus the independence condition yields <math>\mathrm{P}(A|Z) = \displaystyle{\mathrm{P}(AZ) \over P(Z)} = \displaystyle{\mathrm{P}(A)\mathrm{P}(Z) \over \mathrm{P}(Z)},\!</math> in short, <math>\mathrm{P}(A|Z) = \mathrm{P}(A).\!</math> | |
| − | |||
| − | |||
| − | |||
| − | + | As Hamlet discovered, there's a lot to be learned from turning a crank. | |
| − | |||
| − | + | ===Commentary Note 11.24=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | We come to the end of the “number of” examples that we found on our agenda at this point in the text: | |
| − | |||
| − | |||
| − | + | '''NOF 4.5''' | |
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| − | + | | | |
| − | + | <p>It is to be observed that</p> | |
| − | + | |- | |
| − | | | + | | align="center" | <math>[\mathit{1}] ~=~ 1.</math> |
| + | |- | ||
| | | | ||
| − | + | <p>Boole was the first to show this connection between logic and probabilities. He was restricted, however, to absolute terms. I do not remember having seen any extension of probability to relatives, except the ordinary theory of ''expectation''.</p> | |
| − | + | <p>Our logical multiplication, then, satisfies the essential conditions of multiplication, has a unity, has a conception similar to that of admitted multiplications, and contains numerical multiplication as a case under it.</p> | |
| − | |||
| − | |||
| − | </ | ||
| − | + | <p>(Peirce, CP 3.76 and CE 2, 376).</p> | |
| + | |} | ||
| − | + | There are problems with the printing of the text at this point. Let us first recall the conventions we are using in this transcription, in particular, <math>\mathit{1}\!</math> for the italic 1 that signifies the dyadic identity relation and <math>\mathfrak{1}</math> for the “antique figure one” that Peirce defines as <math>\mathit{1}_\infty = \text{something}.</math> | |
| − | There | ||
| − | |||
| − | the | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | this | ||
| − | the | ||
| − | |||
| − | |||
| − | |||
| − | + | CP 3 gives <math>[\mathit{1}] = \mathfrak{1},</math> which I cannot make sense of. CE 2 gives the 1's in different styles of italics, but reading the equation as <math>[\mathit{1}] = 1,\!</math> makes the best sense if the “1” on the right hand side is read as the numeral “1” that denotes the natural number 1, and not as the absolute term “1” that denotes the universe of discourse. Read this way, <math>[\mathit{1}]\!</math> is the average number of things related by the identity relation <math>\mathit{1}\!</math> to one individual, and so it makes sense that <math>[\mathit{1}] = 1 \in \mathbb{N},</math> where <math>\mathbb{N}</math> is the set of non-negative integers <math>\{ 0, 1, 2, \ldots \}.</math> | |
| − | the | ||
| − | |||
| − | where | ||
| − | is the | ||
| − | + | With respect to the relative term <math>^{\backprime\backprime} \mathit{1} ^{\prime\prime}</math> in the syntactic domain <math>S\!</math> and the number <math>1\!</math> in the non-negative integers <math>\mathbb{N} \subset \mathbb{R},</math> we have: | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | <math>v(\mathit{1}) ~=~ [\mathit{1}] ~=~ 1.</math> | ||
| + | |} | ||
| − | + | And so the “number of” mapping <math>v : S \to \mathbb{R}</math> has another one of the properties that would be required of an arrow <math>S \to \mathbb{R}.</math> | |
| − | + | The manner in which these arrows and qualified arrows help us to construct a suspension bridge that unifies logic, semiotics, statistics, stochastics, and information theory will be one of the main themes I aim to elaborate throughout the rest of this inquiry. | |
| − | |||
| − | one | ||
| − | |||
| − | |||
| − | |||
| − | == | + | ==Selection 12== |
| − | + | ===The Sign of Involution=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| − | + | | | |
| − | + | <p>I shall take involution in such a sense that <math>x^y\!</math> will denote everything which is an <math>x\!</math> for every individual of <math>y.\!</math> Thus <math>\mathit{l}^\mathrm{w}\!</math> will be a lover of every woman. Then <math>(\mathit{s}^\mathit{l})^\mathrm{w}\!</math> will denote whatever stands to every woman in the relation of servant of every lover of hers; and <math>\mathit{s}^{(\mathit{l}\mathrm{w})}\!</math> will denote whatever is a servant of everything that is lover of a woman. So that</p> | |
| + | |- | ||
| + | | align="center" | <math>(\mathit{s}^\mathit{l})^\mathrm{w} ~=~ \mathit{s}^{(\mathit{l}\mathrm{w})}.\!</math> | ||
| + | |- | ||
| + | | | ||
| + | <p>(Peirce, CP 3.77).</p> | ||
| + | |} | ||
| − | + | ===Commentary Note 12.1=== | |
| − | |||
| − | |||
| − | + | To get a better sense of why the above formulas mean what they do, and to prepare the ground for understanding more complex relational expressions, it will help to assemble the following materials and definitions: | |
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | height="40" | <math>X\!</math> is a set singled out in a particular discussion as the ''universe of discourse''. | ||
| + | |- | ||
| + | | height="40" | <math>W \subseteq X\!</math> is the 1-adic relation, or set, whose elements fall under the absolute term <math>\mathrm{w} = \text{woman}.\!</math> The elements of <math>W\!</math> are sometimes referred to as the ''denotation'' or the set-theoretic ''extension'' of the term <math>\mathrm{w}.\!</math> | ||
| + | |- | ||
| + | | height="40" | <math>L \subseteq X \times X\!</math> is the 2-adic relation associated with the relative term <math>\mathit{l} = \text{lover of}\,\underline{~~ ~~}.\!</math> | ||
| + | |- | ||
| + | | height="40" | <math>S \subseteq X \times X\!</math> is the 2-adic relation associated with the relative term <math>\mathit{s} = \text{servant of}\,\underline{~~ ~~}.\!</math> | ||
| + | |} | ||
| − | | | + | {| align="center" cellspacing="6" width="90%" |
| − | | | + | | height="40" | <math>\mathsf{W} = (\mathsf{W}_x) = \mathrm{Mat}(W) = \mathrm{Mat}(\mathrm{w})</math> is the 1-dimensional matrix representation of the set <math>W\!</math> and the term <math>\mathrm{w}.\!</math> |
| + | |- | ||
| + | | height="40" | <math>\mathsf{L} = (\mathsf{L}_{xy}) = \mathrm{Mat}(L) = \mathrm{Mat}(\mathit{l})~\!</math> is the 2-dimensional matrix representation of the relation <math>L\!</math> and the relative term <math>\mathit{l}.\!</math> | ||
| + | |- | ||
| + | | height="40" | <math>\mathsf{S} = (\mathsf{S}_{xy}) = \mathrm{Mat}(S) = \mathrm{Mat}(\mathit{s})\!</math> is the 2-dimensional matrix representation of the relation <math>S\!</math> and the relative term <math>\mathit{s}.~\!</math> | ||
| + | |} | ||
| − | + | Recalling a few definitions, the ''local flags'' of the relation <math>L\!</math> are given as follows: | |
| − | |||
| − | of | ||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | | |
| − | + | <math>\begin{array}{lll} | |
| − | + | u \star L | |
| − | + | & = & L_{u \,\text{at}\, 1} | |
| + | \\[6pt] | ||
| + | & = & \{ (u, x) \in L \} | ||
| + | \\[6pt] | ||
| + | & = & \text{the ordered pairs in}~ L ~\text{that have}~ u ~\text{in the 1st place}. | ||
| + | \\[9pt] | ||
| + | L \star v | ||
| + | & = & L_{v \,\text{at}\, 2} | ||
| + | \\[6pt] | ||
| + | & = & \{ (x, v) \in L \} | ||
| + | \\[6pt] | ||
| + | & = & \text{the ordered pairs in}~ L ~\text{that have}~ v ~\text{in the 2nd place}. | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| − | + | The ''applications'' of the relation <math>L\!</math> are defined as follows: | |
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | | |
| − | + | <math>\begin{array}{lll} | |
| − | + | u \cdot L | |
| − | + | & = & \mathrm{proj}_2 (u \star L) | |
| + | \\[6pt] | ||
| + | & = & \{ x \in X : (u, x) \in L \} | ||
| + | \\[6pt] | ||
| + | & = & \text{loved by}~ u. | ||
| + | \\[9pt] | ||
| + | L \cdot v | ||
| + | & = & \mathrm{proj}_1 (L \star v) | ||
| + | \\[6pt] | ||
| + | & = & \{ x \in X : (x, v) \in L \} | ||
| + | \\[6pt] | ||
| + | & = & \text{lover of}~ v. | ||
| + | \end{array}\!</math> | ||
| + | |} | ||
| − | + | ===Commentary Note 12.2=== | |
| − | |||
| − | |||
| − | + | Let us make a few preliminary observations about the operation of ''logical involution'', as Peirce introduces it here: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> | |
| − | + | | | |
| − | + | <p>I shall take involution in such a sense that <math>x^y\!</math> will denote everything which is an <math>x\!</math> for every individual of <math>y.\!</math> Thus <math>\mathit{l}^\mathrm{w}\!</math> will be a lover of every woman.</p> | |
| − | |||
| − | + | <p>(Peirce, CP 3.77).</p> | |
| − | + | |} | |
| − | |||
| − | | | ||
| − | |||
| − | + | In ordinary arithmetic the ''involution'' <math>x^y,\!</math> or the ''exponentiation'' of <math>x\!</math> to the power of <math>y,\!</math> is the repeated application of the multiplier <math>x\!</math> for as many times as there are ones making up the exponent <math>y.\!</math> | |
| − | + | In analogous fashion, the logical involution <math>\mathit{l}^\mathrm{w}\!</math> is the repeated application of the term <math>\mathit{l}\!</math> for as many times as there are individuals under the term <math>\mathrm{w}.\!</math> According to Peirce's interpretive rules, the repeated applications of the base term <math>\mathit{l}\!</math> are distributed across the individuals of the exponent term <math>\mathrm{w}.\!</math> In particular, the base term <math>\mathit{l}\!</math> is not applied successively in the manner that would give something like “a lover of a lover of … a lover of a woman”. | |
| − | |||
| − | |||
| − | |||
| − | + | For example, suppose that a universe of discourse numbers among its contents just three women, <math>\mathrm{W}^{\prime}, \mathrm{W}^{\prime\prime}, \mathrm{W}^{\prime\prime\prime}.</math> This could be expressed in Peirce's notation by writing: | |
| − | |||
| − | |||
| − | | | + | {| align="center" cellspacing="6" width="90%" |
| − | | | + | | height="60" | <math>\mathrm{w} ~=~ \mathrm{W}^{\prime} ~+\!\!,~ \mathrm{W}^{\prime\prime} ~+\!\!,~ \mathrm{W}^{\prime\prime\prime}</math> |
| − | | | + | |} |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | + | Under these circumstances the following equation would hold: | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | height="60" | <math>\mathit{l}^\mathrm{w} ~=~ \mathit{l}^{(\mathrm{W}^{\prime} ~+\!\!,~ \mathrm{W}^{\prime\prime} ~+\!\!,~ \mathrm{W}^{\prime\prime\prime})} ~=~ (\mathit{l}\mathrm{W}^{\prime}), (\mathit{l}\mathrm{W}^{\prime\prime}), (\mathit{l}\mathrm{W}^{\prime\prime\prime}).</math> | ||
| + | |} | ||
| − | + | This says that a lover of every woman in the given universe of discourse is a lover of <math>\mathrm{W}^{\prime}</math> that is a lover of <math>\mathrm{W}^{\prime\prime}</math> that is a lover of <math>\mathrm{W}^{\prime\prime\prime}.</math> In other words, a lover of every woman in this context is a lover of <math>\mathrm{W}^{\prime}</math> and a lover of <math>\mathrm{W}^{\prime\prime}</math> and a lover of <math>\mathrm{W}^{\prime\prime\prime}.</math> | |
| − | a | ||
| − | </ | ||
| − | + | The denotation of the term <math>\mathit{l}^\mathrm{w}\!</math> is a subset of <math>X\!</math> that can be obtained as follows: For each flag of the form <math>L \star x\!</math> with <math>x \in W,\!</math> collect the elements <math>\mathrm{proj}_1 (L \star x)~\!</math> that appear as the first components of these ordered pairs, and then take the intersection of all these subsets. Putting it all together: | |
| − | < | + | {| align="center" cellspacing="6" width="90%" |
| − | + | | height="60" | <math>\mathit{l}^\mathrm{w} ~=~ \bigcap_{x \in W} \mathrm{proj}_1 (L \star x) ~=~ \bigcap_{x \in W} L \cdot x</math> | |
| − | + | |} | |
| − | + | It is very instructive to examine the matrix representation of <math>\mathit{l}^\mathrm{w}\!</math> at this point, not the least because it effectively dispels the mystery of the name ''involution''. First, let us make the following observation. To say that <math>j\!</math> is a lover of every woman is to say that <math>j\!</math> loves <math>k\!</math> if <math>k\!</math> is a woman. This can be rendered in symbols as follows: | |
| − | | | + | {| align="center" cellspacing="6" width="90%" |
| − | + | | height="60" | <math>j ~\text{loves}~ k ~\Leftarrow~ k ~\text{is a woman}</math> | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | | | ||
| − | + | Reading the formula <math>\mathit{l}^\mathrm{w}\!</math> as “<math>j\!</math> loves <math>k\!</math> if <math>k\!</math> is a woman” highlights the operation of converse implication inherent in it, and this in turn reveals the analogy between implication and involution that accounts for the aptness of the latter name. | |
| − | |||
| − | |||
| − | in | ||
| − | |||
| − | |||
| − | |||
| − | + | The operations defined by the formulas <math>x^y = z\!</math> and <math>(x\!\Leftarrow\!y) = z</math> for <math>x, y, z \in \mathbb{B} = \{ 0, 1 \}</math> are tabulated below: | |
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | | ||
| + | <math> | ||
| + | \begin{array}{ccc} | ||
| + | x^y & = & z \\ | ||
| + | \hline | ||
| + | 0^0 & = & 1 \\ | ||
| + | 0^1 & = & 0 \\ | ||
| + | 1^0 & = & 1 \\ | ||
| + | 1^1 & = & 1 | ||
| + | \end{array} | ||
| + | \qquad\qquad\qquad | ||
| + | \begin{array}{ccc} | ||
| + | x\!\Leftarrow\!y & = & z \\ | ||
| + | \hline | ||
| + | 0\!\Leftarrow\!0 & = & 1 \\ | ||
| + | 0\!\Leftarrow\!1 & = & 0 \\ | ||
| + | 1\!\Leftarrow\!0 & = & 1 \\ | ||
| + | 1\!\Leftarrow\!1 & = & 1 | ||
| + | \end{array} | ||
| + | </math> | ||
| + | |} | ||
| − | + | It is clear that these operations are isomorphic, amounting to the same operation of type <math>\mathbb{B} \times \mathbb{B} \to \mathbb{B}.\!</math> All that remains is to see how this operation on coefficient values in <math>\mathbb{B}\!</math> induces the corresponding operations on sets and terms. | |
| − | |||
| − | |||
| − | + | The term <math>\mathit{l}^\mathrm{w}\!</math> determines a selection of individuals from the universe of discourse <math>X\!</math> that may be computed by means of the corresponding operation on coefficient matrices. If the terms <math>\mathit{l}\!</math> and <math>\mathrm{w}\!</math> are represented by the matrices <math>\mathsf{L} = \mathrm{Mat}(\mathit{l})</math> and <math>\mathsf{W} = \mathrm{Mat}(\mathrm{w}),</math> respectively, then the operation on terms that produces the term <math>\mathit{l}^\mathrm{w}\!</math> must be represented by a corresponding operation on matrices, say, <math>\mathsf{L}^\mathsf{W} = \mathrm{Mat}(\mathit{l})^{\mathrm{Mat}(\mathrm{w})},</math> that produces the matrix <math>\mathrm{Mat}(\mathit{l}^\mathrm{w}).</math> In other words, the involution operation on matrices must be defined in such a way that the following equations hold: | |
| − | a | ||
| − | |||
| − | |||
| − | | | + | {| align="center" cellspacing="6" width="90%" |
| − | | | + | | height="60" | <math>\mathsf{L}^\mathsf{W} ~=~ \mathrm{Mat}(\mathit{l})^{\mathrm{Mat}(\mathrm{w})} ~=~ \mathrm{Mat}(\mathit{l}^\mathrm{w})\!</math> |
| − | + | |} | |
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | + | The fact that <math>\mathit{l}^\mathrm{w}\!</math> denotes the elements of a subset of <math>X\!</math> means that the matrix <math>\mathsf{L}^\mathsf{W}\!</math> is a 1-dimensional array of coefficients in <math>\mathbb{B}\!</math> that is indexed by the elements of <math>X.\!</math> The value of the matrix <math>\mathsf{L}^\mathsf{W}\!</math> at the index <math>{u \in X}\!</math> is written <math>(\mathsf{L}^\mathsf{W})_u\!</math> and computed as follows: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | height="60" | <math>(\mathsf{L}^\mathsf{W})_u ~=~ \prod_{v \in X} \mathsf{L}_{uv}^{\mathsf{W}_v}\!</math> | |
| − | + | |} | |
| − | |||
| − | + | ===Commentary Note 12.3=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | We now have two ways of computing a logical involution that raises a dyadic relative term to the power of a monadic absolute term, for example, <math>\mathit{l}^\mathrm{w}\!</math> for “lover of every woman”. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The first method operates in the medium of set theory, expressing the denotation of the term <math>\mathit{l}^\mathrm{w}\!</math> as the intersection of a set of relational applications: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | height="60" | <math>\mathit{l}^\mathrm{w} ~=~ \bigcap_{x \in W} L \cdot x\!</math> | ||
| + | |} | ||
| − | + | The second method operates in the matrix representation, expressing the value of the matrix <math>\mathsf{L}^\mathsf{W}\!</math> with respect to an argument <math>u\!</math> as a product of coefficient powers: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | height="60" | <math>(\mathsf{L}^\mathsf{W})_u ~=~ \prod_{v \in X} \mathsf{L}_{uv}^{\mathsf{W}_v}\!</math> | |
| + | |} | ||
| − | + | Abstract formulas like these are more easily grasped with the aid of a concrete example and a picture of the relations involved. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | ====Example 6==== |
| − | < | + | Consider a universe of discourse <math>X\!</math> that is subject to the following data: |
| − | |||
| − | |||
| − | | | + | {| align="center" cellspacing="6" width="90%" |
| | | | ||
| − | + | <math>\begin{array}{*{15}{c}} | |
| − | + | X & = & \{ & a, & b, & c, & d, & e, & f, & g, & h, & i & \} | |
| − | + | \\[6pt] | |
| − | + | W & = & \{ & d, & f & \} | |
| − | + | \\[6pt] | |
| − | + | L & = & \{ & b\!:\!a, & b\!:\!c, & c\!:\!b, & c\!:\!d, & e\!:\!d, & e\!:\!e, & e\!:\!f, & g\!:\!f, & g\!:\!h, & h\!:\!g, & h\!:\!i & \} | |
| − | + | \end{array}</math> | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Figure 55 shows the placement of <math>W\!</math> within <math>X\!</math> and the placement of <math>L\!</math> within <math>X \times X.\!</math> | |
| − | + | {| align="center" cellpadding="10" width="100%" | |
| + | | width="3%" | | ||
| + | | width="47%" | [[Image:LOR 1870 Figure 55.jpg]] | ||
| + | | width="50%" | (55) | ||
| + | |} | ||
| − | + | To highlight the role of <math>W\!</math> more clearly, the Figure represents the absolute term <math>{}^{\backprime\backprime} \mathrm{w} {}^{\prime\prime}\!</math> by means of the relative term <math>{}^{\backprime\backprime} \mathrm{w}, \! {}^{\prime\prime}\!</math> that conveys the same information. | |
| − | + | Computing the denotation of <math>\mathit{l}^\mathrm{w}\!</math> by way of the set-theoretic formula, we can show our work as follows: | |
| − | 6 | + | {| align="center" cellspacing="6" width="90%" |
| + | | height="60" | <math>\mathit{l}^\mathrm{w} ~=~ \bigcap_{x \in W} L \cdot x ~=~ L \cdot d ~\cap~ L \cdot f ~=~ \{ c, e \} \cap \{ e, g \} ~=~ \{ e \}</math> | ||
| + | |} | ||
| − | + | With the above Figure in mind, we can visualize the computation of <math>(\mathsf{L}^\mathsf{W})_u = \textstyle\prod_{v \in X} \mathsf{L}_{uv}^{\mathsf{W}_v}\!</math> as follows: | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | valign="top" | 1. | ||
| + | | Pick a specific <math>u\!</math> in the bottom row of the Figure. | ||
| + | |- | ||
| + | | valign="top" | 2. | ||
| + | | Pan across the elements <math>v\!</math> in the middle row of the Figure. | ||
| + | |- | ||
| + | | valign="top" | 3. | ||
| + | | If <math>u\!</math> links to <math>v\!</math> then <math>\mathsf{L}_{uv} = 1,\!</math> otherwise <math>{\mathsf{L}_{uv} = 0}.\!</math> | ||
| + | |- | ||
| + | | valign="top" | 4. | ||
| + | | If <math>v\!</math> in the middle row links to <math>v\!</math> in the top row then <math>\mathsf{W}_v = 1,\!</math> otherwise <math>\mathsf{W}_v = 0.\!</math> | ||
| + | |- | ||
| + | | valign="top" | 5. | ||
| + | | Compute the value <math>\mathsf{L}_{uv}^{\mathsf{W}_v} = (\mathsf{L}_{uv} \Leftarrow \mathsf{W}_v)\!</math> for each <math>v\!</math> in the middle row. | ||
| + | |- | ||
| + | | valign="top" | 6. | ||
| + | | If any of the values <math>\mathsf{L}_{uv}^{\mathsf{W}_v}\!</math> is <math>0\!</math> then the product <math>\textstyle\prod_{v \in X} \mathsf{L}_{uv}^{\mathsf{W}_v}\!</math> is <math>0,\!</math> otherwise it is <math>1.\!</math> | ||
| + | |} | ||
| − | + | As a general observation, we know that the value of <math>(\mathsf{L}^\mathsf{W})_u\!</math> goes to <math>0~\!</math> just as soon as we find a <math>v \in X\!</math> such that <math>\mathsf{L}_{uv} = 0\!</math> and <math>\mathsf{W}_v = 1,\!</math> in other words, such that <math>(u, v) \notin L\!</math> but <math>v \in W.\!</math> If there is no such <math>v\!</math> then <math>(\mathsf{L}^\mathsf{W})_u = 1.\!</math> | |
| − | |||
| − | + | Running through the program for each <math>u \in X,\!</math> the only case that produces a non-zero result is <math>(\mathsf{L}^\mathsf{W})_e = 1.\!</math> That portion of the work can be sketched as follows: | |
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | height="60" | <math>(\mathsf{L}^\mathsf{W})_e ~=~ \prod_{v \in X} \mathsf{L}_{ev}^{\mathsf{W}_v} ~=~ 0^0 \cdot 0^0 \cdot 0^0 \cdot 1^1 \cdot 1^0 \cdot 1^1 \cdot 0^0 \cdot 0^0 \cdot 0^0 ~=~ 1\!</math> | ||
| + | |} | ||
| − | + | ===Commentary Note 12.4=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | = | + | Peirce next considers a pair of compound involutions, stating an equation between them that is analogous to a law of exponents in ordinary arithmetic, namely, <math>(a^b)^c = a^{bc}.\!</math> |
| − | < | + | {| align="center" cellspacing="6" width="90%" <!--QUOTE--> |
| − | |||
| − | |||
| − | |||
| | | | ||
| − | | | + | <p>Then <math>(\mathit{s}^\mathit{l})^\mathrm{w}\!</math> will denote whatever stands to every woman in the relation of servant of every lover of hers; and <math>\mathit{s}^{(\mathit{l}\mathrm{w})}\!</math> will denote whatever is a servant of everything that is lover of a woman. So that</p> |
| + | |- | ||
| + | | align="center" | <math>(\mathit{s}^\mathit{l})^\mathrm{w} ~=~ \mathit{s}^{(\mathit{l}\mathrm{w})}.\!</math> | ||
| + | |- | ||
| | | | ||
| − | + | <p>(Peirce, CP 3.77).</p> | |
| − | | | + | |} |
| − | + | ||
| + | Articulating the compound relative term <math>\mathit{s}^{(\mathit{l}\mathrm{w})}\!</math> in set-theoretic terms is fairly immediate: | ||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | height="60" | <math>\mathit{s}^{(\mathit{l}\mathrm{w})} ~=~ \bigcap_{x \in LW} \mathrm{proj}_1 (S \star x) ~=~ \bigcap_{x \in LW} S \cdot x\!</math> | |
| + | |} | ||
| − | + | On the other hand, translating the compound relative term <math>(\mathit{s}^\mathit{l})^\mathrm{w}\!</math> into a set-theoretic equivalent is less immediate, the hang-up being that we have yet to define the case of logical involution that raises a dyadic relative term to the power of a dyadic relative term. As a result, it looks easier to proceed through the matrix representation, drawing once again on the inspection of a concrete example. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ====Example 7==== | |
| − | | | + | {| align="center" cellspacing="6" width="90%" |
| | | | ||
| − | + | <math>\begin{array}{*{15}{c}} | |
| − | + | X & = & \{ & a, & b, & c, & d, & e, & f, & g, & h, & i\ & \} | |
| − | + | \\[6pt] | |
| − | + | L & = & \{ & b\!:\!a, & b\!:\!c, & c\!:\!b, & c\!:\!d, & e\!:\!d, & e\!:\!e, & e\!:\!f, & g\!:\!f, & g\!:\!h, & h\!:\!g, & h\!:\!i & \} | |
| − | + | \\[6pt] | |
| − | + | S & = & \{ & b\!:\!a, & b\!:\!c, & d\!:\!c, & d\!:\!d, & d\!:\!e, & f\!:\!e, & f\!:\!f, & f\!:\!g, & h\!:\!g, & h\!:\!i\ & \} | |
| − | + | \end{array}</math> | |
| − | + | |} | |
| − | |||
| − | + | {| align="center" cellpadding="10" width="100%" | |
| − | " | + | | width="3%" | |
| − | + | | width="47%" | [[Image:LOR 1870 Figure 56.jpg]] | |
| − | + | | width="50%" | (56) | |
| + | |} | ||
| − | + | There is a “servant of every lover of” link between <math>u\!</math> and <math>v\!</math> if and only if <math>u \cdot S ~\supseteq~ L \cdot v.\!</math> But the vacuous inclusions, that is, the cases where <math>L \cdot v = \varnothing,\!</math> have the effect of adding non-intuitive links to the mix. | |
| − | + | The computational requirements are evidently met by the following formula: | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | height="60" | <math>(\mathsf{S}^\mathsf{L})_{xy} ~=~ \prod_{p \in X} \mathsf{S}_{xp}^{\mathsf{L}_{py}}\!</math> | ||
| + | |} | ||
| − | + | In other words, <math>(\mathsf{S}^\mathsf{L})_{xy} = 0\!</math> if and only if there exists a <math>{p \in X}\!</math> such that <math>\mathsf{S}_{xp} = 0\!</math> and <math>\mathsf{L}_{py} = 1.\!</math> | |
| − | + | ===Commentary Note 12.5=== | |
| − | |||
| − | |||
| − | + | The equation <math>(\mathit{s}^\mathit{l})^\mathrm{w} = \mathit{s}^{\mathit{l}\mathrm{w}}\!</math> can be verified by establishing the corresponding equation in matrices: | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | height="60" | <math>(\mathsf{S}^\mathsf{L})^\mathsf{W} ~=~ \mathsf{S}^{\mathsf{L}\mathsf{W}}</math> | ||
| + | |} | ||
| − | + | If <math>\mathsf{A}</math> and <math>\mathsf{B}</math> are two 1-dimensional matrices over the same index set <math>X\!</math> then <math>\mathsf{A} = \mathsf{B}</math> if and only if <math>\mathsf{A}_x = \mathsf{B}_x</math> for every <math>x \in X.</math> Thus, a routine way to check the validity of <math>(\mathsf{S}^\mathsf{L})^\mathsf{W} = \mathsf{S}^{\mathsf{L}\mathsf{W}}</math> is to check whether the following equation holds for arbitrary <math>x \in X.</math> | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| + | | height="60" | <math>((\mathsf{S}^\mathsf{L})^\mathsf{W})_x ~=~ (\mathsf{S}^{\mathsf{L}\mathsf{W}})_x</math> | ||
| + | |} | ||
| − | + | Taking both ends toward the middle, we proceed as follows: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | height="200" | | |
| + | <math> | ||
| + | \begin{array}{*{7}{l}} | ||
| + | ((\mathsf{S}^\mathsf{L})^\mathsf{W})_x | ||
| + | & = & \displaystyle | ||
| + | \prod_{p \in X} (\mathsf{S}^\mathsf{L})_{xp}^{\mathsf{W}_p} | ||
| + | & = & \displaystyle | ||
| + | \prod_{p \in X} (\prod_{q \in X} \mathsf{S}_{xq}^{\mathsf{L}_{qp}})^{\mathsf{W}_p} | ||
| + | & = & \displaystyle | ||
| + | \prod_{p \in X} \prod_{q \in X} \mathsf{S}_{xq}^{\mathsf{L}_{qp}\mathsf{W}_p} | ||
| + | \\[36px] | ||
| + | (\mathsf{S}^{\mathsf{L}\mathsf{W}})_x | ||
| + | & = & \displaystyle | ||
| + | \prod_{q \in X} \mathsf{S}_{xq}^{(\mathsf{L}\mathsf{W})_q} | ||
| + | & = & \displaystyle | ||
| + | \prod_{q \in X} \mathsf{S}_{xq}^{\sum_{p \in X} \mathsf{L}_{qp} \mathsf{W}_p} | ||
| + | & = & \displaystyle | ||
| + | \prod_{q \in X} \prod_{p \in X} \mathsf{S}_{xq}^{\mathsf{L}_{qp} \mathsf{W}_p} | ||
| + | \end{array} | ||
| + | </math> | ||
| + | |} | ||
| − | + | The products commute, so the equation holds. In essence, the matrix identity turns on the fact that the law of exponents <math>(a^b)^c = a^{bc}\!</math> in ordinary arithmetic holds when the values <math>a, b, c\!</math> are restricted to the boolean domain <math>\mathbb{B} = \{ 0, 1 \}.</math> Interpreted as a logical statement, the law of exponents <math>(a^b)^c = a^{bc}\!</math> amounts to a theorem of propositional calculus that is otherwise expressed in the following ways: | |
| − | + | {| align="center" cellspacing="6" width="90%" | |
| − | + | | | |
| − | + | <math>\begin{matrix} | |
| − | + | (a \,\Leftarrow\, b) \,\Leftarrow\, c & = & a \,\Leftarrow\, b \land c | |
| − | + | \\[8pt] | |
| − | + | (a >\!\!\!-~ b) >\!\!\!-~ c & = & a >\!\!\!-~ bc | |
| − | + | \\[8pt] | |
| − | + | c ~-\!\!\!< (b ~-\!\!\!< a) & = & cb ~-\!\!\!< a | |
| − | + | \\[8pt] | |
| − | + | c \,\Rightarrow\, (b \,\Rightarrow\, a) & = & c \land b \,\Rightarrow\, a | |
| − | + | \end{matrix}</math> | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | " | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | = | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | = | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | = | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </ | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | ===Commentary Note 12.6=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | ==References== |
| − | + | * Boole, George (1854), ''An Investigation of the Laws of Thought, On Which are Founded the Mathematical Theories of Logic and Probabilities'', Macmillan, 1854. Reprinted, Dover Publications, New York, NY, 1958. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | * Peirce, C.S. (1870), “Description of a Notation for the Logic of Relatives, Resulting from an Amplification of the Conceptions of Boole's Calculus of Logic”, ''Memoirs of the American Academy of Arts and Sciences'' 9, 317–378, 26 January 1870. Reprinted, ''Collected Papers'' (CP 3.45–149), ''Chronological Edition'' (CE 2, 359–429). Online [http://www.jstor.org/stable/25058006 (1)] [https://archive.org/details/jstor-25058006 (2)] [http://books.google.com/books?id=fFnWmf5oLaoC (3)]. | |
| − | + | * Peirce, C.S., ''Collected Papers of Charles Sanders Peirce'', vols. 1–6, Charles Hartshorne and Paul Weiss (eds.), vols. 7–8, Arthur W. Burks (ed.), Harvard University Press, Cambridge, MA, 1931–1935, 1958. Cited as (CP volume.paragraph). | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | * Peirce, C.S., ''Writings of Charles S. Peirce : A Chronological Edition'', Peirce Edition Project (eds.), Indiana University Press, Bloomington and Indianoplis, IN, 1981–. Cited as (CE volume, page). | |
| − | + | ==Further Reading== | |
| − | |||
| − | |||
| − | + | * [[Charles Sanders Peirce (Bibliography)|Bibliography : Charles Sanders Peirce]]. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | * Brady, G. (2000), ''From Peirce to Skolem : A Neglected Chapter in the History of Logic'', Elsevier, Amsterdam. [http://books.google.com/books?id=ahoH-tLm2S0C Online Preview]. | |
| − | + | * Lambek, J., and Scott, P.J. (1986), ''Introduction to Higher Order Categorical Logic'', Cambridge University Press, Cambridge, UK. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | * Mili, A., Desharnais, J., Mili, F., with Frappier, M. (1994), ''Computer Program Construction'', Oxford University Press, New York, NY. | |
| − | + | * Walsh, A. (2012), ''Relations Between Logic and Mathematics in the Work of Benjamin and Charles S. Peirce'', Docent Press, Boston, MA. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | ==See Also== |
| − | + | {{col-begin}} | |
| − | + | {{col-break}} | |
| − | + | * [[Charles Sanders Peirce]] | |
| − | + | * [[Logic of relatives]] | |
| + | * [[Logic of Relatives (1870)]] | ||
| + | * [[Logic of Relatives (1883)]] | ||
| + | {{col-break}} | ||
| + | * [[Relation (mathematics)|Relation]] | ||
| + | * [[Relation theory]] | ||
| + | * [[Sign relation]] | ||
| + | * [[Triadic relation]] | ||
| + | {{col-end}} | ||
| − | + | [[Category:Artificial Intelligence]] | |
| − | + | [[Category:Charles Sanders Peirce]] | |
| − | + | [[Category:Critical Thinking]] | |
| − | + | [[Category:Cybernetics]] | |
| − | + | [[Category:Education]] | |
| − | + | [[Category:Hermeneutics]] | |
| − | + | [[Category:Information Systems]] | |
| − | + | [[Category:Inquiry]] | |
| − | + | [[Category:Intelligence Amplification]] | |
| − | + | [[Category:Learning Organizations]] | |
| − | + | [[Category:Knowledge Representation]] | |
| − | + | [[Category:Logic]] | |
| − | + | [[Category:Logic Of Relatives]] | |
| − | + | [[Category:Logical Graphs]] | |
| − | + | [[Category:Mathematics]] | |
| − | + | [[Category:Normative Sciences]] | |
| − | + | [[Category:Philosophy]] | |
| − | + | [[Category:Pragmatics]] | |
| − | + | [[Category:Pragmatism]] | |
| − | + | [[Category:Relation Theory]] | |
| − | + | [[Category:Science]] | |
| − | + | [[Category:Semantics]] | |
| − | + | [[Category:Semiotics]] | |
| + | [[Category:Systems Science]] | ||
| + | [[Category:Visualization]] | ||
Latest revision as of 16:22, 29 December 2017
Note. The MathJax parser is not rendering this page properly.
Until it can be fixed please see the InterSciWiki version.
Author: Jon Awbrey
Peirce's text employs lower case letters for logical terms of general reference and upper case letters for logical terms of individual reference. General terms fall into types — absolute terms, dyadic relative terms, higher adic relative terms — and Peirce employs different typefaces to distinguish these. The following Tables indicate the typefaces that are used in the text below for Peirce's examples of general terms.
|
\(\begin{array}{ll} \mathrm{a}. & \text{animal} \\ \mathrm{b}. & \text{black} \\ \mathrm{f}. & \text{Frenchman} \\ \mathrm{h}. & \text{horse} \\ \mathrm{m}. & \text{man} \\ \mathrm{p}. & \text{President of the United States Senate} \\ \mathrm{r}. & \text{rich person} \\ \mathrm{u}. & \text{violinist} \\ \mathrm{v}. & \text{Vice-President of the United States} \\ \mathrm{w}. & \text{woman} \end{array}\) |
|
\(\begin{array}{ll} \mathit{a}. & \text{enemy} \\ \mathit{b}. & \text{benefactor} \\ \mathit{c}. & \text{conqueror} \\ \mathit{e}. & \text{emperor} \\ \mathit{h}. & \text{husband} \\ \mathit{l}. & \text{lover} \\ \mathit{m}. & \text{mother} \\ \mathit{n}. & \text{not} \\ \mathit{o}. & \text{owner} \\ \mathit{s}. & \text{servant} \\ \mathit{w}. & \text{wife} \end{array}\) |
|
\(\begin{array}{ll} \mathfrak{b}. & \text{betrayer to ------ of ------} \\ \mathfrak{g}. & \text{giver to ------ of ------} \\ \mathfrak{t}. & \text{transferrer from ------ to ------} \\ \mathfrak{w}. & \text{winner over of ------ to ------ from ------} \end{array}\) |
Individual terms are taken to denote individual entities falling under a general term. Peirce uses upper case Roman letters for individual terms, for example, the individual horses \(\mathrm{H}, \mathrm{H}^{\prime}, \mathrm{H}^{\prime\prime}\) falling under the general term \(\mathrm{h}\!\) for horse.
The path to understanding Peirce's system and its wider implications for logic can be smoothed by paraphrasing his notations in a variety of contemporary mathematical formalisms, while preserving the semantics as much as possible. Remaining faithful to Peirce's orthography while adding parallel sets of stylistic conventions will, however, demand close attention to typography-in-context. Current style sheets for mathematical texts specify italics for mathematical variables, with upper case letters for sets and lower case letters for individuals. So we need to keep an eye out for the difference between the individual \(\mathrm{X}\!\) of the genus \(\mathrm{x}\!\) and the element \(x\!\) of the set \(X\!\) as we pass between the two styles of text.
Selection 1
Use of the Letters
|
The letters of the alphabet will denote logical signs. Now logical terms are of three grand classes. The first embraces those whose logical form involves only the conception of quality, and which therefore represent a thing simply as “a ——”. These discriminate objects in the most rudimentary way, which does not involve any consciousness of discrimination. They regard an object as it is in itself as such (quale); for example, as horse, tree, or man. These are absolute terms. The second class embraces terms whose logical form involves the conception of relation, and which require the addition of another term to complete the denotation. These discriminate objects with a distinct consciousness of discrimination. They regard an object as over against another, that is as relative; as father of, lover of, or servant of. These are simple relative terms. The third class embraces terms whose logical form involves the conception of bringing things into relation, and which require the addition of more than one term to complete the denotation. They discriminate not only with consciousness of discrimination, but with consciousness of its origin. They regard an object as medium or third between two others, that is as conjugative; as giver of —— to ——, or buyer of —— for —— from ——. These may be termed conjugative terms. The conjugative term involves the conception of third, the relative that of second or other, the absolute term simply considers an object. No fourth class of terms exists involving the conception of fourth, because when that of third is introduced, since it involves the conception of bringing objects into relation, all higher numbers are given at once, inasmuch as the conception of bringing objects into relation is independent of the number of members of the relationship. Whether this reason for the fact that there is no fourth class of terms fundamentally different from the third is satisfactory or not, the fact itself is made perfectly evident by the study of the logic of relatives. (Peirce, CP 3.63). |
I am going to experiment with an interlacing commentary on Peirce's 1870 “Logic of Relatives” paper, revisiting some critical transitions from several different angles and calling attention to a variety of puzzles, problems, and potentials that are not so often remarked or tapped.
What strikes me about the initial installment this time around is its use of a certain pattern of argument that I can recognize as invoking a closure principle, and this is a figure of reasoning that Peirce uses in three other places: his discussion of continuous predicates, his definition of sign relations, and in the pragmatic maxim itself.
One might also call attention to the following two statements:
|
Now logical terms are of three grand classes. |
|
No fourth class of terms exists involving the conception of fourth, because when that of third is introduced, since it involves the conception of bringing objects into relation, all higher numbers are given at once, inasmuch as the conception of bringing objects into relation is independent of the number of members of the relationship. |
Selection 2
Numbers Corresponding to Letters
|
I propose to use the term “universe” to denote that class of individuals about which alone the whole discourse is understood to run. The universe, therefore, in this sense, as in Mr. De Morgan's, is different on different occasions. In this sense, moreover, discourse may run upon something which is not a subjective part of the universe; for instance, upon the qualities or collections of the individuals it contains. I propose to assign to all logical terms, numbers; to an absolute term, the number of individuals it denotes; to a relative term, the average number of things so related to one individual. Thus in a universe of perfect men (men), the number of “tooth of” would be 32. The number of a relative with two correlates would be the average number of things so related to a pair of individuals; and so on for relatives of higher numbers of correlates. I propose to denote the number of a logical term by enclosing the term in square brackets, thus \([t].\!\) (Peirce, CP 3.65). |
Peirce's remarks at CP 3.65 are so replete with remarkable ideas, some of them so taken for granted in mathematical discourse that they usually escape explicit mention, and others so suggestive of things to come in a future remote from his time of writing, and yet so smoothly introduced in passing that it's all too easy to overlook their consequential significance, that I can do no better here than to highlight these ideas in other words, whose main advantage is to be a little more jarring to the mind's sensibilities.
- This mapping of letters to numbers, or logical terms to mathematical quantities, is the very core of what "quantification theory" is all about, and definitely more to the point than the mere "innovation" of using distinctive symbols for the so-called "quantifiers". We will speak of this more later on.
- The mapping of logical terms to numerical measures, to express it in current language, would probably be recognizable as some kind of "morphism" or "functor" from a logical domain to a quantitative co-domain.
- Notice that Peirce follows the mathematician's usual practice, then and now, of making the status of being an "individual" or a "universal" relative to a discourse in progress. I have come to appreciate more and more of late how radically different this "patchwork" or "piecewise" approach to things is from the way of some philosophers who seem to be content with nothing less than many worlds domination, which means that they are never content and rarely get started toward the solution of any real problem. Just my observation, I hope you understand.
- It is worth noting that Peirce takes the "plural denotation" of terms for granted, or what's the number of a term for, if it could not vary apart from being one or nil?
- I also observe that Peirce takes the individual objects of a particular universe of discourse in a "generative" way, not a "totalizing" way, and thus they afford us with the basis for talking freely about collections, constructions, properties, qualities, subsets, and "higher types", as the phrase is mint.
Selection 3
The Signs of Inclusion, Equality, Etc.
|
I shall follow Boole in taking the sign of equality to signify identity. Thus, if \(\mathrm{v}\!\) denotes the Vice-President of the United States, and \(\mathrm{p}~\!\) the President of the Senate of the United States, | |||||||||
| \(\mathrm{v} = \mathrm{p}\!\) | |||||||||
|
means that every Vice-President of the United States is President of the Senate, and every President of the United States Senate is Vice-President. The sign “less than” is to be so taken that | |||||||||
| \(\mathrm{f} < \mathrm{m}~\!\) | |||||||||
|
means that every Frenchman is a man, but there are men besides Frenchmen. Drobisch has used this sign in the same sense. It will follow from these significations of \(=\!\) and \(<\!\) that the sign \(-\!\!\!<\!\) (or \(\leqq\), “as small as”) will mean “is”. Thus, | |||||||||
| \(\mathrm{f} ~-\!\!\!< \mathrm{m}\) | |||||||||
|
means “every Frenchman is a man”, without saying whether there are any other men or not. So, | |||||||||
| \(\mathit{m} ~-\!\!\!< \mathit{l}\) | |||||||||
|
will mean that every mother of anything is a lover of the same thing; although this interpretation in some degree anticipates a convention to be made further on. These significations of \(=\!\) and \(<\!\) plainly conform to the indispensable conditions. Upon the transitive character of these relations the syllogism depends, for by virtue of it, from | |||||||||
| |||||||||
|
that is, from every Frenchman being a man and every man being an animal, that every Frenchman is an animal. But not only do the significations of \(=\!\) and \(<\!\) here adopted fulfill all absolute requirements, but they have the supererogatory virtue of being very nearly the same as the common significations. Equality is, in fact, nothing but the identity of two numbers; numbers that are equal are those which are predicable of the same collections, just as terms that are identical are those which are predicable of the same classes. So, to write \(5 < 7\!\) is to say that \(5\!\) is part of \(7\!\), just as to write \(\mathrm{f} < \mathrm{m}~\!\) is to say that Frenchmen are part of men. Indeed, if \(\mathrm{f} < \mathrm{m}~\!\), then the number of Frenchmen is less than the number of men, and if \(\mathrm{v} = \mathrm{p}\!\), then the number of Vice-Presidents is equal to the number of Presidents of the Senate; so that the numbers may always be substituted for the terms themselves, in case no signs of operation occur in the equations or inequalities. (Peirce, CP 3.66). |
The quantifier mapping from terms to their numbers that Peirce signifies by means of the square bracket notation \([t]\!\) has one of its principal uses in providing a basis for the computation of frequencies, probabilities, and all of the other statistical measures that can be constructed from these, and thus in affording what may be called a principle of correspondence between probability theory and its limiting case in the forms of logic.
This brings us once again to the relativity of contingency and necessity, as one way of approaching necessity is through the avenue of probability, describing necessity as a probability of 1, but the whole apparatus of probability theory only figures in if it is cast against the backdrop of probability space axioms, the reference class of distributions, and the sample space that we cannot help but to abduce upon the scene of observations. Aye, there's the snake eyes. And with them we can see that there is always an irreducible quantum of facticity to all our necessities. More plainly spoken, it takes a fairly complex conceptual infrastructure just to begin speaking of probabilities, and this setting can only be set up by means of abductive, fallible, hypothetical, and inherently risky mental acts.
Pragmatic thinking is the logic of abduction, which is just another way of saying that it addresses the question: “What may be hoped?” We have to face the possibility that it may be just as impossible to speak of “absolute identity” with any hope of making practical philosophical sense as it is to speak of “absolute simultaneity” with any hope of making operational physical sense.
Selection 4
The Signs for Addition
|
The sign of addition is taken by Boole so that |
| \(x + y\!\) |
|
denotes everything denoted by \(x\!\), and, besides, everything denoted by \(y\!\). Thus |
| \(\mathrm{m} + \mathrm{w}~\!\) |
|
denotes all men, and, besides, all women. This signification for this sign is needed for connecting the notation of logic with that of the theory of probabilities. But if there is anything which is denoted by both terms of the sum, the latter no longer stands for any logical term on account of its implying that the objects denoted by one term are to be taken besides the objects denoted by the other. For example, |
| \(\mathrm{f} + \mathrm{u}\!\) |
|
means all Frenchmen besides all violinists, and, therefore, considered as a logical term, implies that all French violinists are besides themselves. For this reason alone, in a paper which is published in the Proceedings of the Academy for March 17, 1867, I preferred to take as the regular addition of logic a non-invertible process, such that |
| \(\mathrm{m} ~+\!\!,~ \mathrm{b}\) |
|
stands for all men and black things, without any implication that the black things are to be taken besides the men; and the study of the logic of relatives has supplied me with other weighty reasons for the same determination. Since the publication of that paper, I have found that Mr. W. Stanley Jevons, in a tract called Pure Logic, or the Logic of Quality [1864], had anticipated me in substituting the same operation for Boole's addition, although he rejects Boole's operation entirely and writes the new one with a \(+\!\) sign while withholding from it the name of addition. It is plain that both the regular non-invertible addition and the invertible addition satisfy the absolute conditions. But the notation has other recommendations. The conception of taking together involved in these processes is strongly analogous to that of summation, the sum of 2 and 5, for example, being the number of a collection which consists of a collection of two and a collection of five. Any logical equation or inequality in which no operation but addition is involved may be converted into a numerical equation or inequality by substituting the numbers of the several terms for the terms themselves — provided all the terms summed are mutually exclusive. Addition being taken in this sense, nothing is to be denoted by zero, for then |
| \(x ~+\!\!,~ 0 ~=~ x\) |
|
whatever is denoted by \(x\!\); and this is the definition of zero. This interpretation is given by Boole, and is very neat, on account of the resemblance between the ordinary conception of zero and that of nothing, and because we shall thus have |
| \([0] ~=~ 0.\) |
|
(Peirce, CP 3.67). |
A wealth of issues arises here that I hope to take up in depth at a later point, but for the moment I shall be able to mention only the barest sample of them in passing.
The two papers that precede this one in CP 3 are Peirce's papers of March and September 1867 in the Proceedings of the American Academy of Arts and Sciences, titled “On an Improvement in Boole's Calculus of Logic” and “Upon the Logic of Mathematics”, respectively. Among other things, these two papers provide us with further clues about the motivating considerations that brought Peirce to introduce the “number of a term” function, signified here by square brackets. I have already quoted from the “Logic of Mathematics” paper in a related connection. Here are the links to those excerpts:
In setting up a correspondence between “letters” and “numbers”, Peirce constructs a structure-preserving map from a logical domain to a numerical domain. That he does this deliberately is evidenced by the care that he takes with the conditions under which the chosen aspects of structure are preserved, along with his recognition of the critical fact that zeroes are preserved by the mapping.
Incidentally, Peirce appears to have an inkling of the problems that would later be caused by using the plus sign for inclusive disjunction, but his advice was overridden by the dialects of applied logic that developed in various communities, retarding the exchange of information among engineering, mathematical, and philosophical specialties all throughout the subsequent century.
Selection 5
The Signs for Multiplication
|
I shall adopt for the conception of multiplication the application of a relation, in such a way that, for example, \(\mathit{l}\mathrm{w}~\!\) shall denote whatever is lover of a woman. This notation is the same as that used by Mr. De Morgan, although he appears not to have had multiplication in his mind. \(\mathit{s}(\mathrm{m} ~+\!\!,~ \mathrm{w})\) will, then, denote whatever is servant of anything of the class composed of men and women taken together. So that: |
| \(\mathit{s}(\mathrm{m} ~+\!\!,~ \mathrm{w}) ~=~ \mathit{s}\mathrm{m} ~+\!\!,~ \mathit{s}\mathrm{w}.\) |
|
\((\mathit{l} ~+\!\!,~ \mathit{s})\mathrm{w}\) will denote whatever is lover or servant to a woman, and: |
| \((\mathit{l} ~+\!\!,~ \mathit{s})\mathrm{w} ~=~ \mathit{l}\mathrm{w} ~+\!\!,~ \mathit{s}\mathrm{w}.\) |
|
\((\mathit{s}\mathit{l})\mathrm{w}\!\) will denote whatever stands to a woman in the relation of servant of a lover, and: |
| \((\mathit{s}\mathit{l})\mathrm{w} ~=~ \mathit{s}(\mathit{l}\mathrm{w}).\) |
|
Thus all the absolute conditions of multiplication are satisfied. The term “identical with ——” is a unity for this multiplication. That is to say, if we denote “identical with ——” by \(\mathit{1}\!\) we have: |
| \(x \mathit{1} ~=~ x ~ ,\) |
|
whatever relative term \(x\!\) may be. For what is a lover of something identical with anything, is the same as a lover of that thing. (Peirce, CP 3.68). |
Peirce in 1870 is five years down the road from the Peirce of 1865–1866 who lectured extensively on the role of sign relations in the logic of scientific inquiry, articulating their involvement in the three types of inference, and inventing the concept of “information” to explain what it is that signs convey in the process. By this time, then, the semiotic or sign relational approach to logic is so implicit in his way of working that he does not always take the trouble to point out its distinctive features at each and every turn. So let's take a moment to draw out a few of these characters.
Sign relations, like any brand of non-trivial 3-adic relations, can become overwhelming to think about once the cardinality of the object, sign, and interpretant domains or the complexity of the relation itself ascends beyond the simplest examples. Furthermore, most of the strategies that we would normally use to control the complexity, like neglecting one of the domains, in effect, projecting the 3-adic sign relation onto one of its 2-adic faces, or focusing on a single ordered triple of the form \((o, s, i)\!\) at a time, can result in our receiving a distorted impression of the sign relation's true nature and structure.
I find that it helps me to draw, or at least to imagine drawing, diagrams of the following form, where I can keep tabs on what's an object, what's a sign, and what's an interpretant sign, for a selected set of sign-relational triples.
Here is how I would picture Peirce's example of equivalent terms, \(\mathrm{v} = \mathrm{p},\!\) where \({}^{\backprime\backprime} \mathrm{v} {}^{\prime\prime}\!\) denotes the Vice-President of the United States, and \({}^{\backprime\backprime} \mathrm{p} {}^{\prime\prime}\!\) denotes the President of the Senate of the United States.
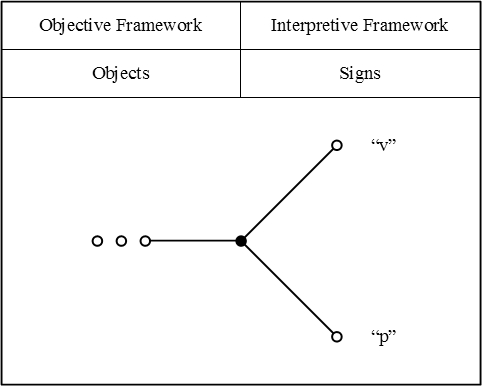
|
| \(\text{Figure 1}~\!\) |
Depending on whether we interpret the terms \({}^{\backprime\backprime} \mathrm{v} {}^{\prime\prime}\!\) and \({}^{\backprime\backprime} \mathrm{p} {}^{\prime\prime}\!\) as applying to persons who hold these offices at one particular time or as applying to all those persons who have held these offices over an extended period of history, their denotations may be either singular of plural, respectively.
As a shortcut technique for indicating general denotations or plural referents, I will use the elliptic convention that represents these by means of figures like “o o o” or “o … o”, placed at the object ends of sign relational triads.
For a more complex example, here is how I would picture Peirce's example of an equivalence between terms that comes about by applying one of the distributive laws, for relative multiplication over absolute summation.
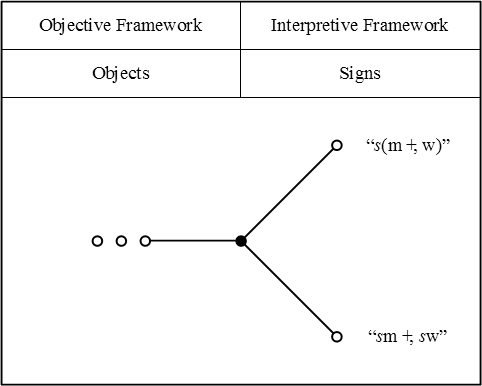
|
| \(\text{Figure 2}\!\) |
Selection 6
The Signs for Multiplication (cont.)
|
A conjugative term like giver naturally requires two correlates, one denoting the thing given, the other the recipient of the gift. We must be able to distinguish, in our notation, the giver of \(\mathrm{A}\!\) to \(\mathrm{B}\!\) from the giver to \(\mathrm{A}\!\) of \(\mathrm{B}\!\), and, therefore, I suppose the signification of the letter equivalent to such a relative to distinguish the correlates as first, second, third, etc., so that “giver of —— to ——” and “giver to —— of ——” will be expressed by different letters. Let \(\mathfrak{g}\) denote the latter of these conjugative terms. Then, the correlates or multiplicands of this multiplier cannot all stand directly after it, as is usual in multiplication, but may be ranged after it in regular order, so that: |
| \(\mathfrak{g}\mathit{x}\mathit{y}\) |
|
will denote a giver to \(\mathit{x}\!\) of \(\mathit{y}\!\). But according to the notation, \(\mathit{x}\!\) here multiplies \(\mathit{y}\!\), so that if we put for \(\mathit{x}\!\) owner (\(\mathit{o}\!\)), and for \(\mathit{y}\!\) horse (\(\mathrm{h}\!\)), |
| \(\mathfrak{g}\mathit{o}\mathrm{h}\) |
|
appears to denote the giver of a horse to an owner of a horse. But let the individual horses be \(\mathrm{H}, \mathrm{H}^{\prime}, \mathrm{H}^{\prime\prime}\), etc. Then: |
| \(\mathrm{h} ~=~ \mathrm{H} ~+\!\!,~ \mathrm{H}^{\prime} ~+\!\!,~ \mathrm{H}^{\prime\prime} ~+\!\!,~ \text{etc.}\) |
| \(\mathfrak{g}\mathit{o}\mathrm{h} ~=~ \mathfrak{g}\mathit{o}(\mathrm{H} ~+\!\!,~ \mathrm{H}^{\prime} ~+\!\!,~ \mathrm{H}^{\prime\prime} ~+\!\!,~ \text{etc.}) ~=~ \mathfrak{g}\mathit{o}\mathrm{H} ~+\!\!,~ \mathfrak{g}\mathit{o}\mathrm{H}^{\prime} ~+\!\!,~ \mathfrak{g}\mathit{o}\mathrm{H}^{\prime\prime} ~+\!\!,~ \text{etc.}\) |
|
Now this last member must be interpreted as a giver of a horse to the owner of that horse, and this, therefore must be the interpretation of \(\mathfrak{g}\mathit{o}\mathrm{h}\). This is always very important. A term multiplied by two relatives shows that the same individual is in the two relations. If we attempt to express the giver of a horse to a lover of a woman, and for that purpose write: |
| \(\mathfrak{g}\mathit{l}\mathrm{w}\mathrm{h}\), |
|
we have written giver of a woman to a lover of her, and if we add brackets, thus, |
| \(\mathfrak{g}(\mathit{l}\mathrm{w})\mathrm{h}\), |
|
we abandon the associative principle of multiplication. A little reflection will show that the associative principle must in some form or other be abandoned at this point. But while this principle is sometimes falsified, it oftener holds, and a notation must be adopted which will show of itself when it holds. We already see that we cannot express multiplication by writing the multiplicand directly after the multiplier; let us then affix subjacent numbers after letters to show where their correlates are to be found. The first number shall denote how many factors must be counted from left to right to reach the first correlate, the second how many more must be counted to reach the second, and so on. Then, the giver of a horse to a lover of a woman may be written: |
| \(\mathfrak{g}_{12} \mathit{l}_1 \mathrm{w} \mathrm{h} ~=~ \mathfrak{g}_{11} \mathit{l}_2 \mathrm{h} \mathrm{w} ~=~ \mathfrak{g}_{2(-1)} \mathrm{h} \mathit{l}_1 \mathrm{w}\). |
|
Of course a negative number indicates that the former correlate follows the latter by the corresponding positive number. A subjacent zero makes the term itself the correlate. Thus, |
| \(\mathit{l}_0\!\) |
|
denotes the lover of that lover or the lover of himself, just as \(\mathfrak{g}\mathit{o}\mathrm{h}\) denotes that the horse is given to the owner of itself, for to make a term doubly a correlate is, by the distributive principle, to make each individual doubly a correlate, so that: |
| \(\mathit{l}_0 ~=~ \mathit{L}_0 ~+\!\!,~ \mathit{L}_0^{\prime} ~+\!\!,~ \mathit{L}_0^{\prime\prime} ~+\!\!,~ \text{etc.}\) |
|
A subjacent sign of infinity may indicate that the correlate is indeterminate, so that: |
| \(\mathit{l}_\infty\) |
|
will denote a lover of something. We shall have some confirmation of this presently. If the last subjacent number is a one it may be omitted. Thus we shall have: |
| \(\mathit{l}_1 ~=~ \mathit{l}\), |
| \(\mathfrak{g}_{11} ~=~ \mathfrak{g}_1 ~=~ \mathfrak{g}\). |
|
This enables us to retain our former expressions \(\mathit{l}\mathrm{w}~\!\), \(\mathfrak{g}\mathit{o}\mathrm{h}\), etc. (Peirce, CP 3.69–70). |
Comment : Sets as Logical Sums
Peirce's way of representing sets as logical sums may seem archaic, but it is quite often used, and is actually the tool of choice in many branches of algebra, combinatorics, computing, and statistics to this very day.
Peirce's application to logic is fairly novel, and the degree of his elaboration of the logic of relative terms is certainly original with him, but this particular genre of representation, commonly going under the handle of generating functions, goes way back, well before anyone thought to stick a flag in set theory as a separate territory or to try to fence off our native possessions of it with expressly decreed axioms. And back in the days when a computer was just a person who computed, before we had the sorts of electronic register machines that we take so much for granted today, mathematicians were constantly using generating functions as a rough and ready type of addressable memory to sort, store, and keep track of their accounts of a wide variety of formal objects of thought.
Let us look at a few simple examples of generating functions, much as I encountered them during my own first adventures in the Fair Land Of Combinatoria.
Suppose that we are given a set of three elements, say, \(\{ a, b, c \},\!\) and we are asked to find all the ways of choosing a subset from this collection.
We can represent this problem setup as the problem of computing the following product:
| \((1 + a)(1 + b)(1 + c).\!\) |
The factor \((1 + a)\!\) represents the option that we have, in choosing a subset of \(\{ a, b, c \},\!\) to leave the element \(a\!\) out (signified by the \(1\!\)), or else to include it (signified by the \(a\!\)), and likewise for the other elements \(b\!\) and \(c\!\) in their turns.
Probably on account of all those years I flippered away playing the oldtime pinball machines, I tend to imagine a product like this being displayed in a vertical array:
|
\(\begin{matrix} (1 ~+~ a) \\ (1 ~+~ b) \\ (1 ~+~ c) \end{matrix}\) |
I picture this as a playboard with six bumpers, the ball chuting down the board in such a career that it strikes exactly one of the two bumpers on each and every one of the three levels.
So a trajectory of the ball where it hits the \(a\!\) bumper on the 1st level, hits the \(1\!\) bumper on the 2nd level, hits the \(c\!\) bumper on the 3rd level, and then exits the board, represents a single term in the desired product and corresponds to the subset \(\{ a, c \}.\!\)
Multiplying out the product \((1 + a)(1 + b)(1 + c),\!\) one obtains:
|
\(\begin{array}{*{15}{c}} 1 & + & a & + & b & + & c & + & ab & + & ac & + & bc & + & abc. \end{array}\) |
And this informs us that the subsets of choice are:
|
\(\begin{matrix} \varnothing, & \{ a \}, & \{ b \}, & \{ c \}, & \{ a, b \}, & \{ a, c \}, & \{ b, c \}, & \{ a, b, c \}. \end{matrix}\) |
Selection 7
The Signs for Multiplication (cont.)
|
The associative principle does not hold in this counting of factors. Because it does not hold, these subjacent numbers are frequently inconvenient in practice, and I therefore use also another mode of showing where the correlate of a term is to be found. This is by means of the marks of reference, \(\dagger ~ \ddagger ~ \parallel ~ \S ~ \P\), which are placed subjacent to the relative term and before and above the correlate. Thus, giver of a horse to a lover of a woman may be written: |
| \(\mathfrak{g}_{\dagger\ddagger} \, ^\dagger\mathit{l}_\parallel \, ^\parallel\mathrm{w} \, ^\ddagger\mathrm{h}\) |
|
The asterisk I use exclusively to refer to the last correlate of the last relative of the algebraic term. Now, considering the order of multiplication to be: — a term, a correlate of it, a correlate of that correlate, etc. — there is no violation of the associative principle. The only violations of it in this mode of notation are that in thus passing from relative to correlate, we skip about among the factors in an irregular manner, and that we cannot substitute in such an expression as \(\mathfrak{g}\mathit{o}\mathrm{h}\) a single letter for \(\mathit{o}\mathrm{h}.\!\) I would suggest that such a notation may be found useful in treating other cases of non-associative multiplication. By comparing this with what was said above [in CP 3.55] concerning functional multiplication, it appears that multiplication by a conjugative term is functional, and that the letter denoting such a term is a symbol of operation. I am therefore using two alphabets, the Greek and Kennerly, where only one was necessary. But it is convenient to use both. (Peirce, CP 3.71–72). |
Comment : Proto-Graphical Syntax
It is clear from our last excerpt that Peirce is already on the verge of a graphical syntax for the logic of relatives. Indeed, it seems likely that he had already reached this point in his own thinking.
For instance, it seems quite impossible to read his last variation on the theme of a “giver of a horse to a lover of a woman” without drawing lines of identity to connect up the corresponding marks of reference, like this:
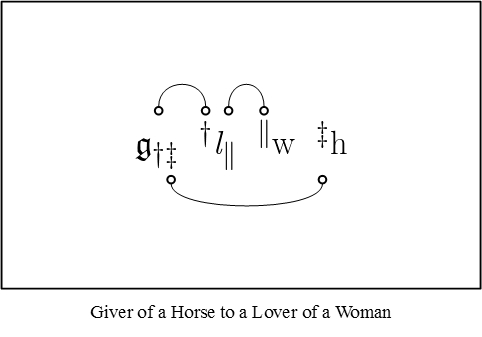 |
(3) |
Selection 8
The Signs for Multiplication (cont.)
|
Thus far, we have considered the multiplication of relative terms only. Since our conception of multiplication is the application of a relation, we can only multiply absolute terms by considering them as relatives. Now the absolute term “man” is really exactly equivalent to the relative term “man that is ——”, and so with any other. I shall write a comma after any absolute term to show that it is so regarded as a relative term. Then “man that is black” will be written: |
| \(\mathrm{m},\!\mathrm{b}\!\) |
|
But not only may any absolute term be thus regarded as a relative term, but any relative term may in the same way be regarded as a relative with one correlate more. It is convenient to take this additional correlate as the first one. Then: |
| \(\mathit{l},\!\mathit{s}\mathrm{w}\) |
|
will denote a lover of a woman that is a servant of that woman. The comma here after \(\mathit{l}\!\) should not be considered as altering at all the meaning of \(\mathit{l}\!\), but as only a subjacent sign, serving to alter the arrangement of the correlates. In point of fact, since a comma may be added in this way to any relative term, it may be added to one of these very relatives formed by a comma, and thus by the addition of two commas an absolute term becomes a relative of two correlates. So: |
| \(\mathrm{m},\!,\!\mathrm{b},\!\mathrm{r}\) |
|
interpreted like |
| \(\mathfrak{g}\mathit{o}\mathrm{h}\) |
|
means a man that is a rich individual and is a black that is that rich individual. But this has no other meaning than: |
| \(\mathrm{m},\!\mathrm{b},\!\mathrm{r}\) |
|
or a man that is a black that is rich. Thus we see that, after one comma is added, the addition of another does not change the meaning at all, so that whatever has one comma after it must be regarded as having an infinite number. If, therefore, \(\mathit{l},\!,\!\mathit{s}\mathrm{w}\) is not the same as \(\mathit{l},\!\mathit{s}\mathrm{w}\) (as it plainly is not, because the latter means a lover and servant of a woman, and the former a lover of and servant of and same as a woman), this is simply because the writing of the comma alters the arrangement of the correlates. And if we are to suppose that absolute terms are multipliers at all (as mathematical generality demands that we should}, we must regard every term as being a relative requiring an infinite number of correlates to its virtual infinite series “that is —— and is —— and is —— etc.” Now a relative formed by a comma of course receives its subjacent numbers like any relative, but the question is, What are to be the implied subjacent numbers for these implied correlates? Any term may be regarded as having an infinite number of factors, those at the end being ones, thus: |
| \(\mathit{l},\!\mathit{s}\mathrm{w} ~=~ \mathit{l},\!\mathit{s}\mathit{w},\!\mathit{1},\!\mathit{1},\!\mathit{1},\!\mathit{1},\!\mathit{1},\!\mathit{1},\!\mathit{1}, ~\text{etc.}\) |
|
A subjacent number may therefore be as great as we please. But all these ones denote the same identical individual denoted by \(\mathrm{w}\!\); what then can be the subjacent numbers to be applied to \(\mathit{s}\!\), for instance, on account of its infinite “that is”'s? What numbers can separate it from being identical with \(\mathrm{w}\!\)? There are only two. The first is zero, which plainly neutralizes a comma completely, since |
| \(\mathit{s},_0\!\mathrm{w} ~=~ \mathit{s}\mathrm{w}\) |
|
and the other is infinity; for as \(1^\infty\) is indeterminate in ordinary algbra, so it will be shown hereafter to be here, so that to remove the correlate by the product of an infinite series of ones is to leave it indeterminate. Accordingly, |
| \(\mathrm{m},_\infty\) |
|
should be regarded as expressing some man. Any term, then, is properly to be regarded as having an infinite number of commas, all or some of which are neutralized by zeros. “Something” may then be expressed by: |
| \(\mathit{1}_\infty\!\) |
|
I shall for brevity frequently express this by an antique figure one \((\mathfrak{1}).\) “Anything” by: |
| \(\mathit{1}_0\!\) |
|
I shall often also write a straight \(1\!\) for anything. (Peirce, CP 3.73). |
Commentary Note 8.1
To my way of thinking, CP 3.73 is one of the most remarkable passages in the history of logic. In this first pass over its deeper contents I won't be able to accord it much more than a superficial dusting off.
Let us imagine a concrete example that will serve in developing the uses of Peirce's notation. Entertain a discourse whose universe \(X\!\) will remind us a little of the cast of characters in Shakespeare's Othello.
| \(X ~=~ \{ \mathrm{Bianca}, \mathrm{Cassio}, \mathrm{Clown}, \mathrm{Desdemona}, \mathrm{Emilia}, \mathrm{Iago}, \mathrm{Othello} \}.\) |
The universe \(X\!\) is “that class of individuals about which alone the whole discourse is understood to run” but its marking out for special recognition as a universe of discourse in no way rules out the possibility that “discourse may run upon something which is not a subjective part of the universe; for instance, upon the qualities or collections of the individuals it contains” (CP 3.65).
In order to provide ourselves with the convenience of abbreviated terms, while preserving Peirce's conventions about capitalization, we may use the alternate names \(^{\backprime\backprime}\mathrm{u}^{\prime\prime}\) for the universe \(X\!\) and \(^{\backprime\backprime}\mathrm{Jeste}^{\prime\prime}\) for the character \(\mathrm{Clown}.~\!\) This permits the above description of the universe of discourse to be rewritten in the following fashion:
| \(\mathrm{u} ~=~ \{ \mathrm{B}, \mathrm{C}, \mathrm{D}, \mathrm{E}, \mathrm{I}, \mathrm{J}, \mathrm{O} \}\) |
This specification of the universe of discourse could be summed up in Peirce's notation by the following equation:
|
\(\begin{array}{*{15}{c}} \mathbf{1} & = & \mathrm{B} & +\!\!, & \mathrm{C} & +\!\!, & \mathrm{D} & +\!\!, & \mathrm{E} & +\!\!, & \mathrm{I} & +\!\!, & \mathrm{J} & +\!\!, & \mathrm{O} \end{array}\) |
Within this discussion, then, the individual terms are as follows:
|
\(\begin{matrix} ^{\backprime\backprime}\mathrm{B}^{\prime\prime}, & ^{\backprime\backprime}\mathrm{C}^{\prime\prime}, & ^{\backprime\backprime}\mathrm{D}^{\prime\prime}, & ^{\backprime\backprime}\mathrm{E}^{\prime\prime}, & ^{\backprime\backprime}\mathrm{I}^{\prime\prime}, & ^{\backprime\backprime}\mathrm{J}^{\prime\prime}, & ^{\backprime\backprime}\mathrm{O}^{\prime\prime} \end{matrix}\) |
Each of these terms denotes in a singular fashion the corresponding individual in \(X.\!\)
By way of general terms in this discussion, we may begin with the following set:
|
\(\begin{array}{ccl} ^{\backprime\backprime}\mathrm{b}^{\prime\prime} & = & ^{\backprime\backprime}\mathrm{black}^{\prime\prime} \'"`UNIQ-MathJax1-QINU`"' <br> {| align="center" cellpadding="10" | [[Image:LOR 1870 Figure 7.0.jpg]] || (7) |} {| align="center" cellpadding="10" | [[Image:LOR 1870 Figure 8.0.jpg]] || (8) |} One way to approach the problem of “information fusion” in Peirce's syntax is to soften the distinction between adjacent terms and subjacent signs and to treat the types of constraints that they separately signify more on a par with each other. To that purpose, I will set forth a way of thinking about relational composition that emphasizes the set-theoretic constraints involved in the construction of a composite. For example, suppose that we are given the relations \(L \subseteq X \times Y\) and \(M \subseteq Y \times Z.\) Table 9 and Figure 10 present two ways of picturing the constraints that are involved in constructing the relational composition \(L \circ M \subseteq X \times Z.\)
The way to read Table 9 is to imagine that you are playing a game that involves placing tokens on the squares of a board that is marked in just this way. The rules are that you have to place a single token on each marked square in the middle of the board in such a way that all of the indicated constraints are satisfied. That is to say, you have to place a token whose denomination is a value in the set \(X\!\) on each of the squares marked \({}^{\backprime\backprime} X {}^{\prime\prime},\) and similarly for the squares marked \({}^{\backprime\backprime} Y {}^{\prime\prime}\) and \({}^{\backprime\backprime} Z {}^{\prime\prime},\) meanwhile leaving all of the blank squares empty. Furthermore, the tokens placed in each row and column have to obey the relational constraints that are indicated at the heads of the corresponding row and column. Thus, the two tokens from \(X\!\) have to denominate the very same value from \(X,\!\) and likewise for \(Y\!\) and \(Z,\!\) while the pairs of tokens on the rows marked \({}^{\backprime\backprime} L {}^{\prime\prime}\) and \({}^{\backprime\backprime} M {}^{\prime\prime}\) are required to denote elements that are in the relations \(L\!\) and \(M,\!\) respectively. The upshot is that when just this much is done, that is, when the \(L,\!\) \(M,\!\) and \(\mathit{1}\!\) relations are satisfied, then the row marked \({}^{\backprime\backprime} L \circ M {}^{\prime\prime}\) will automatically bear the tokens of a pair of elements in the composite relation \(L \circ M.\!\) Figure 10 shows a different way of viewing the same situation.
Commentary Note 10.3I will devote some time to drawing out the relationships that exist among the different pictures of relations and relative terms that were shown above, or as redrawn here:
Figures 11 and 12 present examples of relative multiplication in one of the styles of syntax that Peirce used, to which I added lines of identity to connect the corresponding marks of reference. These pictures are adapted to showing the anatomy of relative terms, while the forms of analysis illustrated in Table 13 and Figure 14 are designed to highlight the structures of the objective relations themselves.
There are many ways that Peirce might have gotten from his 1870 Notation for the Logic of Relatives to his more evolved systems of Logical Graphs. It is interesting to speculate on how the metamorphosis might have been accomplished by way of transformations that act on these nascent forms of syntax and that take place not too far from the pale of its means, that is, as nearly as possible according to the rules and the permissions of the initial system itself. In Existential Graphs, a relation is represented by a node whose degree is the adicity of that relation, and which is adjacent via lines of identity to the nodes that represent its correlative relations, including as a special case any of its terminal individual arguments. In the 1870 Logic of Relatives, implicit lines of identity are invoked by the subjacent numbers and marks of reference only when a correlate of some relation is the relate of some relation. Thus, the principal relate, which is not a correlate of any explicit relation, is not singled out in this way. Remarkably enough, the comma modifier itself provides us with a mechanism to abstract the logic of relations from the logic of relatives, and thus to forge a possible link between the syntax of relative terms and the more graphical depiction of the objective relations themselves. Figure 15 demonstrates this possibility, posing a transitional case between the style of syntax in Figure 11 and the picture of composition in Figure 14.
In this composite sketch the diagonal extension \(\mathit{1}\!\) of the universe \(\mathbf{1}\!\) is invoked up front to anchor an explicit line of identity for the leading relate of the composition, while the terminal argument \(\mathrm{w}\!\) has been generalized to the whole universe \(\mathbf{1},\!\) in effect, executing an act of abstraction. This type of universal bracketing isolates the composing of the relations \(L\!\) and \(S\!\) to form the composite \(L \circ S.\!\) The three relational domains \(X, Y, Z\!\) may be distinguished from one another, or else rolled up into a single universe of discourse, as one prefers. Commentary Note 10.4From now on I will use the forms of analysis exemplified in the last set of Figures and Tables as a routine bridge between the logic of relative terms and the logic of their extended relations. For future reference, we may think of Table 13 as illustrating the spreadsheet model of relational composition, while Figure 14 may be thought of as making a start toward a hypergraph model of generalized compositions. I will explain the hypergraph model in some detail at a later point. The transitional form of analysis represented by Figure 15 may be called the universal bracketing of relatives as relations. Commentary Note 10.5We have sufficiently covered the application of the comma functor, or the diagonal extension, to absolute terms, so let us return to where we were in working our way through CP 3.73 and see whether we can validate Peirce's statements about the “commifications” of 2-adic relative terms that yield their 3-adic diagonal extensions.
Just to plant our feet on a more solid stage, let's apply this idea to the Othello example. For this performance only, just to make the example more interesting, let us assume that \(\mathrm{Jeste ~ (J)}\!\) is secretly in love with \(\mathrm{Desdemona ~ (D)}.\!\) Then we begin with the modified data set:
|
- Pages with broken file links
- Artificial Intelligence
- Charles Sanders Peirce
- Critical Thinking
- Cybernetics
- Education
- Hermeneutics
- Information Systems
- Inquiry
- Intelligence Amplification
- Learning Organizations
- Knowledge Representation
- Logic
- Logic Of Relatives
- Logical Graphs
- Mathematics
- Normative Sciences
- Philosophy
- Pragmatics
- Pragmatism
- Relation Theory
- Science
- Semantics
- Semiotics
- Systems Science
- Visualization