Minimal negation operator
☞ This page belongs to resource collections on Logic and Inquiry.
A minimal negation operator \((\nu)~\!\) is a logical connective that says “just one false” of its logical arguments. The first four cases are described below.
- If the list of arguments is empty, as expressed in the form \(\nu(),~\!\) then it cannot be true that exactly one of the arguments is false, so \(\nu() = \mathrm{false}.~\!\)
-
If \(p~\!\) is the only argument then \(\nu(p)~\!\) says that \(p~\!\) is false, so \(\nu(p)~\!\) expresses the logical negation of the proposition \(p.~\!\) Written in several different notations, we have the following equivalent expressions.
\(\nu(p) ~=~ \mathrm{not}(p) ~=~ \lnot p ~=~ \tilde{p} ~=~ p^{\prime}~\!\)
-
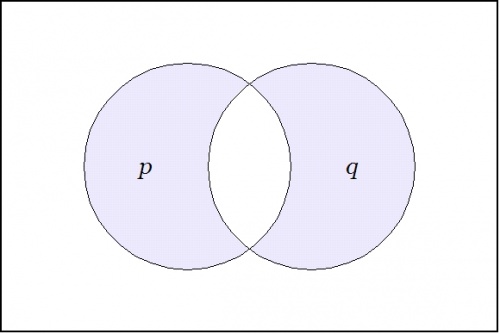
If \(p~\!\) and \(q~\!\) are the only two arguments then \(\nu(p, q)~\!\) says that exactly one of \(p, q~\!\) is false, so \(\nu(p, q)~\!\) says the same thing as \(p \neq q.~\!\) Expressing \(\nu(p, q)~\!\) in terms of ands \((\cdot),~\!\) ors \((\lor),~\!\) and nots \((\tilde{~})~\!\) gives the following form.
\(\nu(p, q) ~=~ \tilde{p} \cdot q ~\lor~ p \cdot \tilde{q}~\!\)
It is permissible to omit the dot \((\cdot)~\!\) in contexts where it is understood, giving the following form.
\(\nu(p, q) ~=~ \tilde{p}q \lor p\tilde{q}~\!\)
The venn diagram for \(\nu(p, q)~\!\) is shown in Figure 1.
\(\text{Figure 1.}~~\nu(p, q)~\!\)
-
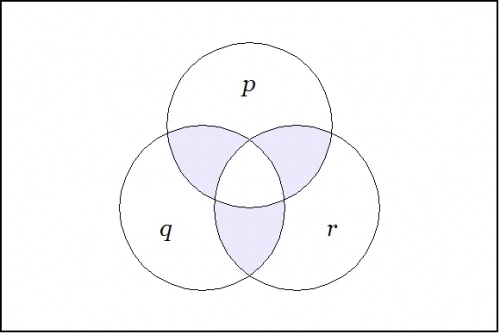
The venn diagram for \(\nu(p, q, r)~\!\) is shown in Figure 2.
\(\text{Figure 2.}~~\nu(p, q, r)~\!\)
The center cell is the region where all three arguments \(p, q, r~\!\) hold true, so \(\nu(p, q, r)~\!\) holds true in just the three neighboring cells. In other words:
\(\nu(p, q, r) ~=~ \tilde{p}qr \lor p\tilde{q}r \lor pq\tilde{r}~\!\)
Initial definition
The minimal negation operator \(\nu~\!\) is a multigrade operator \((\nu_k)_{k \in \mathbb{N}}~\!\) where each \(\nu_k~\!\) is a \(k~\!\)-ary boolean function defined by the rule that \(\nu_k (x_1, \ldots , x_k) = 1~\!\) if and only if exactly one of the arguments \(x_j~\!\) is \(0.~\!\)
In contexts where the initial letter \(\nu~\!\) is understood, the minimal negation operators can be indicated by argument lists in parentheses. In the following text a distinctive typeface will be used for logical expressions based on minimal negation operators, for example, \(\texttt{(x, y, z)} = \nu (x, y, z).~\!\)
The first four members of this family of operators are shown below. The third and fourth columns give paraphrases in two other notations, where tildes and primes, respectively, indicate logical negation.
|
\(\begin{matrix} \texttt{()} & = & \nu_0 & = & 0 & = & \mathrm{false} \\[6pt] \texttt{(x)} & = & \nu_1 (x) & = & \tilde{x} & = & x^\prime \\[6pt] \texttt{(x, y)} & = & \nu_2 (x, y) & = & \tilde{x}y \lor x\tilde{y} & = & x^\prime y \lor x y^\prime \\[6pt] \texttt{(x, y, z)} & = & \nu_3 (x, y, z) & = & \tilde{x}yz \lor x\tilde{y}z \lor xy\tilde{z} & = & x^\prime y z \lor x y^\prime z \lor x y z^\prime \end{matrix}\) |
Formal definition
To express the general case of \(\nu_k~\!\) in terms of familiar operations, it helps to introduce an intermediary concept:
Definition. Let the function \(\lnot_j : \mathbb{B}^k \to \mathbb{B}~\!\) be defined for each integer \(j~\!\) in the interval \([1, k]~\!\) by the following equation:
| \(\lnot_j (x_1, \ldots, x_j, \ldots, x_k) ~=~ x_1 \land \ldots \land x_{j-1} \land \lnot x_j \land x_{j+1} \land \ldots \land x_k.~\!\) |
Then \({\nu_k : \mathbb{B}^k \to \mathbb{B}}~\!\) is defined by the following equation:
| \(\nu_k (x_1, \ldots, x_k) ~=~ \lnot_1 (x_1, \ldots, x_k) \lor \ldots \lor \lnot_j (x_1, \ldots, x_k) \lor \ldots \lor \lnot_k (x_1, \ldots, x_k).~\!\) |
If we take the boolean product \(x_1 \cdot \ldots \cdot x_k~\!\) or the logical conjunction \(x_1 \land \ldots \land x_k~\!\) to indicate the point \(x = (x_1, \ldots, x_k)~\!\) in the space \(\mathbb{B}^k~\!\) then the minimal negation \(\texttt{(} x_1 \texttt{,} \ldots \texttt{,} x_k \texttt{)}~\!\) indicates the set of points in \(\mathbb{B}^k~\!\) that differ from \(x~\!\) in exactly one coordinate. This makes \(\texttt{(} x_1 \texttt{,} \ldots \texttt{,} x_k \texttt{)}~\!\) a discrete functional analogue of a point-omitted neighborhood in ordinary real analysis, more exactly, a point-omitted distance-one neighborhood. In this light, the minimal negation operator can be recognized as a differential construction, an observation that opens a very wide field.
The remainder of this discussion proceeds on the algebraic convention that the plus sign \((+)~\!\) and the summation symbol \((\textstyle\sum)~\!\) both refer to addition mod 2. Unless otherwise noted, the boolean domain \(\mathbb{B} = \{ 0, 1 \}~\!\) is interpreted for logic in such a way that \(0 = \mathrm{false}~\!\) and \(1 = \mathrm{true}.~\!\) This has the following consequences:
| • | The operation \(x + y~\!\) is a function equivalent to the exclusive disjunction of \(x~\!\) and \(y,~\!\) while its fiber of 1 is the relation of inequality between \(x~\!\) and \(y.~\!\) |
| • | The operation \(\textstyle\sum_{j=1}^k x_j~\!\) maps the bit sequence \((x_1, \ldots, x_k)~\!\) to its parity. |
The following properties of the minimal negation operators \({\nu_k : \mathbb{B}^k \to \mathbb{B}}~\!\) may be noted:
| • | The function \(\texttt{(x, y)}~\!\) is the same as that associated with the operation \(x + y~\!\) and the relation \(x \ne y.~\!\) |
| • | In contrast, \(\texttt{(x, y, z)}~\!\) is not identical to \(x + y + z.~\!\) |
| • | More generally, the function \(\nu_k (x_1, \dots, x_k)~\!\) for \(k > 2~\!\) is not identical to the boolean sum \(\textstyle\sum_{j=1}^k x_j.~\!\) |
| • | The inclusive disjunctions indicated for the \(\nu_k~\!\) of more than one argument may be replaced with exclusive disjunctions without affecting the meaning since the terms in disjunction are already disjoint. |
Truth tables
Table 3 is a truth table for the sixteen boolean functions of type \(f : \mathbb{B}^3 \to \mathbb{B}~\!\) whose fibers of 1 are either the boundaries of points in \(\mathbb{B}^3~\!\) or the complements of those boundaries.
| \(\mathcal{L}_1~\!\) | \(\mathcal{L}_2~\!\) | \(\mathcal{L}_3~\!\) | \(\mathcal{L}_4~\!\) |
| \(p\colon~\!\) | \(1~1~1~1~0~0~0~0~\!\) | ||
| \(q\colon~\!\) | \(1~1~0~0~1~1~0~0~\!\) | ||
| \(r\colon~\!\) | \(1~0~1~0~1~0~1~0~\!\) | ||
|
\(\begin{matrix} f_{104} \\[4pt] f_{148} \\[4pt] f_{146} \\[4pt] f_{97} \\[4pt] f_{134} \\[4pt] f_{73} \\[4pt] f_{41} \\[4pt] f_{22} \end{matrix}\) |
\(\begin{matrix} f_{01101000} \\[4pt] f_{10010100} \\[4pt] f_{10010010} \\[4pt] f_{01100001} \\[4pt] f_{10000110} \\[4pt] f_{01001001} \\[4pt] f_{00101001} \\[4pt] f_{00010110} \end{matrix}\) |
\(\begin{matrix} 0~1~1~0~1~0~0~0 \\[4pt] 1~0~0~1~0~1~0~0 \\[4pt] 1~0~0~1~0~0~1~0 \\[4pt] 0~1~1~0~0~0~0~1 \\[4pt] 1~0~0~0~0~1~1~0 \\[4pt] 0~1~0~0~1~0~0~1 \\[4pt] 0~0~1~0~1~0~0~1 \\[4pt] 0~0~0~1~0~1~1~0 \end{matrix}\) |
\(\begin{matrix} \texttt{(~p~,~q~,~r~)} \\[4pt] \texttt{(~p~,~q~,(r))} \\[4pt] \texttt{(~p~,(q),~r~)} \\[4pt] \texttt{(~p~,(q),(r))} \\[4pt] \texttt{((p),~q~,~r~)} \\[4pt] \texttt{((p),~q~,(r))} \\[4pt] \texttt{((p),(q),~r~)} \\[4pt] \texttt{((p),(q),(r))} \end{matrix}\) |
|
\(\begin{matrix} f_{233} \\[4pt] f_{214} \\[4pt] f_{182} \\[4pt] f_{121} \\[4pt] f_{158} \\[4pt] f_{109} \\[4pt] f_{107} \\[4pt] f_{151} \end{matrix}\) |
\(\begin{matrix} f_{11101001} \\[4pt] f_{11010110} \\[4pt] f_{10110110} \\[4pt] f_{01111001} \\[4pt] f_{10011110} \\[4pt] f_{01101101} \\[4pt] f_{01101011} \\[4pt] f_{10010111} \end{matrix}\) |
\(\begin{matrix} 1~1~1~0~1~0~0~1 \\[4pt] 1~1~0~1~0~1~1~0 \\[4pt] 1~0~1~1~0~1~1~0 \\[4pt] 0~1~1~1~1~0~0~1 \\[4pt] 1~0~0~1~1~1~1~0 \\[4pt] 0~1~1~0~1~1~0~1 \\[4pt] 0~1~1~0~1~0~1~1 \\[4pt] 1~0~0~1~0~1~1~1 \end{matrix}\) |
\(\begin{matrix} \texttt{(((p),(q),(r)))} \\[4pt] \texttt{(((p),(q),~r~))} \\[4pt] \texttt{(((p),~q~,(r)))} \\[4pt] \texttt{(((p),~q~,~r~))} \\[4pt] \texttt{((~p~,(q),(r)))} \\[4pt] \texttt{((~p~,(q),~r~))} \\[4pt] \texttt{((~p~,~q~,(r)))} \\[4pt] \texttt{((~p~,~q~,~r~))} \end{matrix}\) |
Charts and graphs
This Section focuses on visual representations of minimal negation operators. A few bits of terminology are useful in describing the pictures, but the formal details are tedious reading, and may be familiar to many readers, so the full definitions of the terms marked in italics are relegated to a Glossary at the end of the article.
Two ways of visualizing the space \(\mathbb{B}^k~\!\) of \(2^k~\!\) points are the hypercube picture and the venn diagram picture. The hypercube picture associates each point of \(\mathbb{B}^k~\!\) with a unique point of the \(k~\!\)-dimensional hypercube. The venn diagram picture associates each point of \(\mathbb{B}^k~\!\) with a unique "cell" of the venn diagram on \(k~\!\) "circles".
In addition, each point of \(\mathbb{B}^k~\!\) is the unique point in the fiber of truth \([|s|]~\!\) of a singular proposition \(s : \mathbb{B}^k \to \mathbb{B},~\!\) and thus it is the unique point where a singular conjunction of \(k~\!\) literals is \(1.~\!\)
For example, consider two cases at opposite vertices of the cube:
| • | The point \((1, 1, \ldots , 1, 1)~\!\) with all 1's as coordinates is the point where the conjunction of all posited variables evaluates to \(1,~\!\) namely, the point where: |
| \(x_1 ~ x_2 ~\ldots~ x_{n-1} ~ x_n ~=~ 1.~\!\) | |
| • | The point \((0, 0, \ldots , 0, 0)~\!\) with all 0's as coordinates is the point where the conjunction of all negated variables evaluates to \(1,~\!\) namely, the point where: |
| \(\texttt{(} x_1 \texttt{)(} x_2 \texttt{)} \ldots \texttt{(} x_{n-1} \texttt{)(} x_n \texttt{)} ~=~ 1.~\!\) |
To pass from these limiting examples to the general case, observe that a singular proposition \(s : \mathbb{B}^k \to \mathbb{B}~\!\) can be given canonical expression as a conjunction of literals, \(s = e_1 e_2 \ldots e_{k-1} e_k~\!\). Then the proposition \(\nu (e_1, e_2, \ldots, e_{k-1}, e_k)~\!\) is \(1~\!\) on the points adjacent to the point where \(s~\!\) is \(1,~\!\) and 0 everywhere else on the cube.
For example, consider the case where \(k = 3.~\!\) Then the minimal negation operation \(\nu (p, q, r)~\!\) — written more simply as \(\texttt{(p, q, r)}~\!\) — has the following venn diagram:
|
\(\text{Figure 4.}~~\texttt{(p, q, r)}~\!\) |
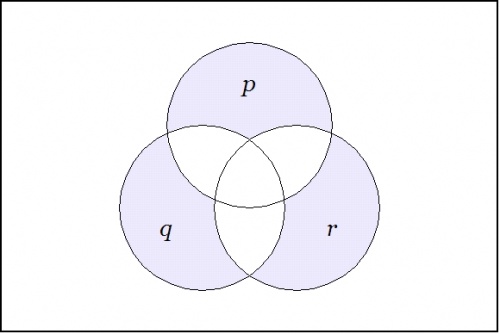
For a contrasting example, the boolean function expressed by the form \(\texttt{((p),(q),(r))}~\!\) has the following venn diagram:
|
\(\text{Figure 5.}~~\texttt{((p),(q),(r))}~\!\) |
Glossary of basic terms
- Boolean domain
- A boolean domain \(\mathbb{B}~\!\) is a generic 2-element set, for example, \(\mathbb{B} = \{ 0, 1 \},~\!\) whose elements are interpreted as logical values, usually but not invariably with \(0 = \mathrm{false}~\!\) and \(1 = \mathrm{true}.~\!\)
- Boolean variable
- A boolean variable \(x~\!\) is a variable that takes its value from a boolean domain, as \(x \in \mathbb{B}.~\!\)
- Proposition
- In situations where boolean values are interpreted as logical values, a boolean-valued function \(f : X \to \mathbb{B}~\!\) or a boolean function \(g : \mathbb{B}^k \to \mathbb{B}~\!\) is frequently called a proposition.
- Basis element, Coordinate projection
- Given a sequence of \(k~\!\) boolean variables, \(x_1, \ldots, x_k,~\!\) each variable \(x_j~\!\) may be treated either as a basis element of the space \(\mathbb{B}^k~\!\) or as a coordinate projection \(x_j : \mathbb{B}^k \to \mathbb{B}.~\!\)
- Basic proposition
- This means that the set of objects \(\{ x_j : 1 \le j \le k \}~\!\) is a set of boolean functions \(\{ x_j : \mathbb{B}^k \to \mathbb{B} \}~\!\) subject to logical interpretation as a set of basic propositions that collectively generate the complete set of \(2^{2^k}~\!\) propositions over \(\mathbb{B}^k.~\!\)
- Literal
- A literal is one of the \(2k~\!\) propositions \(x_1, \ldots, x_k, \texttt{(} x_1 \texttt{)}, \ldots, \texttt{(} x_k \texttt{)},~\!\) in other words, either a posited basic proposition \(x_j~\!\) or a negated basic proposition \(\texttt{(} x_j \texttt{)},~\!\) for some \(j = 1 ~\text{to}~ k.~\!\)
- Fiber
- In mathematics generally, the fiber of a point \(y \in Y~\!\) under a function \(f : X \to Y~\!\) is defined as the inverse image \(f^{-1}(y) \subseteq X.~\!\)
- In the case of a boolean function \(f : \mathbb{B}^k \to \mathbb{B},~\!\) there are just two fibers:
- The fiber of \(0~\!\) under \(f,~\!\) defined as \(f^{-1}(0),~\!\) is the set of points where the value of \(f~\!\) is \(0.~\!\)
- The fiber of \(1~\!\) under \(f,~\!\) defined as \(f^{-1}(1),~\!\) is the set of points where the value of \(f~\!\) is \(1.~\!\)
- Fiber of truth
- When \(1~\!\) is interpreted as the logical value \(\mathrm{true},~\!\) then \(f^{-1}(1)~\!\) is called the fiber of truth in the proposition \(f.~\!\) Frequent mention of this fiber makes it useful to have a shorter way of referring to it. This leads to the definition of the notation \([|f|] = f^{-1}(1)~\!\) for the fiber of truth in the proposition \(f.~\!\)
- Singular boolean function
- A singular boolean function \(s : \mathbb{B}^k \to \mathbb{B}~\!\) is a boolean function whose fiber of \(1~\!\) is a single point of \(\mathbb{B}^k.~\!\)
- Singular proposition
- In the interpretation where \(1~\!\) equals \(\mathrm{true},~\!\) a singular boolean function is called a singular proposition.
- Singular boolean functions and singular propositions serve as functional or logical representatives of the points in \(\mathbb{B}^k.~\!\)
- Singular conjunction
- A singular conjunction in \(\mathbb{B}^k \to \mathbb{B}~\!\) is a conjunction of \(k~\!\) literals that includes just one conjunct of the pair \(\{ x_j, ~\nu(x_j) \}~\!\) for each \(j = 1 ~\text{to}~ k.~\!\)
- A singular proposition \(s : \mathbb{B}^k \to \mathbb{B}~\!\) can be expressed as a singular conjunction:
| \(s ~=~ e_1 e_2 \ldots e_{k-1} e_k~\!\), |
|
\(\begin{array}{llll} \text{where} & e_j & = & x_j \\[6pt] \text{or} & e_j & = & \nu (x_j), \\[6pt] \text{for} & j & = & 1 ~\text{to}~ k. \end{array}\) |
Resources
Syllabus
Focal nodes
Peer nodes
- Minimal Negation Operator @ InterSciWiki
- Minimal Negation Operator @ MyWikiBiz
- Minimal Negation Operator @ Subject Wikis
- Minimal Negation Operator @ Wikiversity
- Minimal Negation Operator @ Wikiversity Beta
Logical operators
Template:Col-breakTemplate:Col-breakTemplate:Col-endRelated topics
- Propositional calculus
- Sole sufficient operator
- Truth table
- Universe of discourse
- Zeroth order logic
Relational concepts
Information, Inquiry
Related articles
- Differential Logic : Introduction
- Differential Propositional Calculus
- Differential Logic and Dynamic Systems
- Prospects for Inquiry Driven Systems
- Introduction to Inquiry Driven Systems
- Inquiry Driven Systems : Inquiry Into Inquiry
Document history
Portions of the above article were adapted from the following sources under the GNU Free Documentation License, under other applicable licenses, or by permission of the copyright holders.
- Minimal Negation Operator, InterSciWiki
- Minimal Negation Operator, MyWikiBiz
- Minimal Negation Operator, PlanetMath
- Minimal Negation Operator, Wikinfo
- Minimal Negation Operator, Wikiversity
- Minimal Negation Operator, Wikiversity Beta
- Minimal Negation Operator, Wikipedia
- Automata Theory
- Boolean Functions
- Charles Sanders Peirce
- Combinatorics
- Computer Science
- Differential Logic
- Equational Reasoning
- Formal Languages
- Formal Sciences
- Formal Systems
- Inquiry
- Linguistics
- Logic
- Logical Graphs
- Minimal Negation Operators
- Mathematics
- Neural Networks
- Philosophy
- Propositional Calculus
- Semiotics
- Visualization