Differential Logic
☆ The MathJax formatter is currently having problems rendering the text below. ☆
☆ Meanwhile, please see the InterSciWiki copy at Differential Logic : Sketch 2. ☆
Author: Jon Awbrey
Note. The present Sketch is largely superseded by the article “Differential Logic : Introduction” but I have preserved it here for the sake of the remaining ideas that have yet to be absorbed elsewhere.
Differential logic is the component of logic whose object is the description of variation — for example, the aspects of change, difference, distribution, and diversity — in universes of discourse that are subject to logical description. In formal logic, differential logic treats the principles that govern the use of a differential logical calculus, that is, a formal system with the expressive capacity to describe change and diversity in logical universes of discourse.
A simple example of a differential logical calculus is furnished by a differential propositional calculus. A differential propositional calculus is a propositional calculus extended by a set of terms for describing aspects of change and difference, for example, processes that take place in a universe of discourse or transformations that map a source universe into a target universe. This augments ordinary propositional calculus in the same way that the differential calculus of Leibniz and Newton augments the analytic geometry of Descartes.
Note 1
One of the first things that you can do, once you have a really decent calculus for boolean functions or propositional logic, whatever you want to call it, is to compute the differentials of these functions or propositions.
Now there are many ways to dance around this idea, and I feel like I have tried them all, before one gets down to acting on it, and there many issues of interpretation and justification that we will have to clear up after the fact, that is, before we can be sure that it all really makes any sense, but I think this time I'll just jump in, and show you the form in which this idea first came to me.
Start with a proposition of the form \(x ~\mathrm{and}~ y,\!\) which is graphed as two labels attached to a root node:
o---------------------------------------o | | | x y | | @ | | | o---------------------------------------o | x and y | o---------------------------------------o |
Written as a string, this is just the concatenation "\(x~y\!\)".
The proposition \(xy\!\) may be taken as a boolean function \(f(x, y)\!\) having the abstract type \(f : \mathbb{B} \times \mathbb{B} \to \mathbb{B},\!\) where \(\mathbb{B} = \{ 0, 1 \}~\!\) is read in such a way that \(0\!\) means \(\mathrm{false}\!\) and \(1\!\) means \(\mathrm{true}.\!\)
In this style of graphical representation, the value \(\mathrm{true}\!\) looks like a blank label and the value \(\mathrm{false}\!\) looks like an edge.
o---------------------------------------o | | | | | @ | | | o---------------------------------------o | true | o---------------------------------------o |
o---------------------------------------o | | | o | | | | | @ | | | o---------------------------------------o | false | o---------------------------------------o |
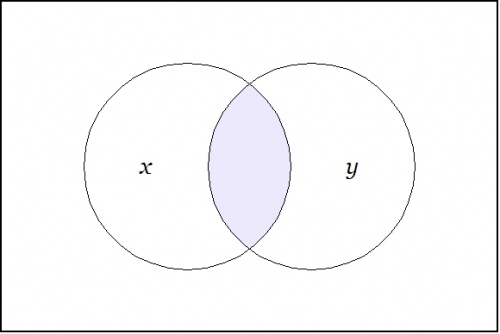
Back to the proposition \(xy.~\!\) Imagine yourself standing in a fixed cell of the corresponding venn diagram, say, the cell where the proposition \(xy\!\) is true, as shown here:
|
Now ask yourself: What is the value of the proposition \(xy\!\) at a distance of \(\mathrm{d}x\!\) and \(\mathrm{d}y\!\) from the cell \(xy\!\) where you are standing?
Don't think about it — just compute:
o---------------------------------------o | | | dx o o dy | | / \ / \ | | x o---@---o y | | | o---------------------------------------o | (x + dx) and (y + dy) | o---------------------------------------o |
To make future graphs easier to draw in ASCII, I will use devices like @=@=@ and o=o=o to identify several nodes into one, as in this next redrawing:
o---------------------------------------o | | | x dx y dy | | o---o o---o | | \ | | / | | \ | | / | | \| |/ | | @=@ | | | o---------------------------------------o | (x + dx) and (y + dy) | o---------------------------------------o |
However you draw it, these expressions follow because the expression \(x + \mathrm{d}x,\!\) where the plus sign indicates addition in \(\mathbb{B},\!\) that is, addition modulo 2, and thus corresponds to the exclusive disjunction operation in logic, parses to a graph of the following form:
o---------------------------------------o | | | x dx | | o---o | | \ / | | @ | | | o---------------------------------------o | x + dx | o---------------------------------------o |
Next question: What is the difference between the value of the proposition \(xy\!\) "over there" and the value of the proposition \(xy\!\) where you are, all expressed as general formula, of course? Here 'tis:
o---------------------------------------o | | | x dx y dy | | o---o o---o | | \ | | / | | \ | | / | | \| |/ x y | | o=o-----------o | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | @ | | | o---------------------------------------o | ((x + dx) & (y + dy)) - xy | o---------------------------------------o |
Oh, I forgot to mention: Computed over \(\mathbb{B},\!\) plus and minus are the very same operation. This will make the relationship between the differential and the integral parts of the resulting calculus slightly stranger than usual, but never mind that now.
Last question, for now: What is the value of this expression from your current standpoint, that is, evaluated at the point where \(xy\!\) is true? Well, substituting \(1\!\) for \(x\!\) and \(1\!\) for \(y\!\) in the graph amounts to the same thing as erasing those labels:
o---------------------------------------o | | | dx dy | | o---o o---o | | \ | | / | | \ | | / | | \| |/ | | o=o-----------o | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | @ | | | o---------------------------------------o | ((1 + dx) & (1 + dy)) - 1·1 | o---------------------------------------o |
And this is equivalent to the following graph:
o---------------------------------------o | | | dx dy | | o o | | \ / | | o | | | | | @ | | | o---------------------------------------o | dx or dy | o---------------------------------------o |
Note 2
We have just met with the fact that the differential of the and is the or of the differentials.
|
\(x ~\mathrm{and}~ y \quad \xrightarrow{~\mathrm{Diff}~} \quad \mathrm{d}x ~\mathrm{or}~ \mathrm{d}y\!\) |
o---------------------------------------o | | | dx dy | | o o | | \ / | | o | | x y | | | @ --Diff--> @ | | | o---------------------------------------o | x y --Diff--> ((dx)(dy)) | o---------------------------------------o |
It will be necessary to develop a more refined analysis of that statement directly, but that is roughly the nub of it.
If the form of the above statement reminds you of De Morgan's rule, it is no accident, as differentiation and negation turn out to be closely related operations. Indeed, one can find discussions of logical difference calculus in the Boole–De Morgan correspondence and Peirce also made use of differential operators in a logical context, but the exploration of these ideas has been hampered by a number of factors, not the least of which being a syntax adequate to handle the complexity of expressions that evolve.
For my part, it was definitely a case of the calculus being smarter than the calculator thereof. The graphical pictures were catalytic in their power over my thinking process, leading me so quickly past so many obstructions that I did not have time to think about all of the difficulties that would otherwise have inhibited the derivation. It did eventually became necessary to write all this up in a linear script, and to deal with the various problems of interpretation and justification that I could imagine, but that took another 120 pages, and so, if you don't like this intuitive approach, then let that be your sufficient notice.
Let us run through the initial example again, this time attempting to interpret the formulas that develop at each stage along the way.
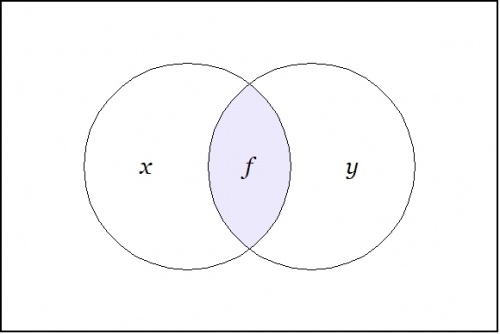
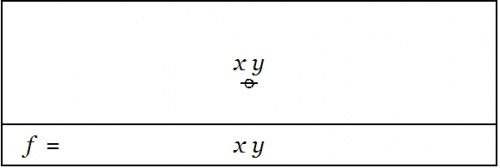
We begin with a proposition or a boolean function \(f(x, y) = xy.\!\)
|
|
A function like this has an abstract type and a concrete type. The abstract type is what we invoke when we write things like \(f : \mathbb{B} \times \mathbb{B} \to \mathbb{B}\!\) or \(f : \mathbb{B}^2 \to \mathbb{B}.\!\) The concrete type takes into account the qualitative dimensions or the "units" of the case, which can be explained as follows.
| Let \(X\!\) be the set of values \(\{ \texttt{(} x \texttt{)},~ x \} ~=~ \{ \mathrm{not}~ x,~ x \}.\!\) |
| Let \(Y\!\) be the set of values \(\{ \texttt{(} y \texttt{)},~ y \} ~=~ \{ \mathrm{not}~ y,~ y \}.\!\) |
Then interpret the usual propositions about \(x, y\!\) as functions of the concrete type \(f : X \times Y \to \mathbb{B}.\!\)
We are going to consider various operators on these functions. Here, an operator \(\mathrm{F}\!\) is a function that takes one function \(f\!\) into another function \(\mathrm{F}f.\!\)
The first couple of operators that we need to consider are logical analogues of those that occur in the classical finite difference calculus, namely:
| The difference operator \(\Delta,\!\) written here as \(\mathrm{D}.\!\) |
| The enlargement" operator \(\Epsilon,\!\) written here as \(\mathrm{E}.\!\) |
These days, \(\mathrm{E}\!\) is more often called the shift operator.
In order to describe the universe in which these operators operate, it is necessary to enlarge the original universe of discourse, passing from the space \(U = X \times Y\!\) to its differential extension, \(\mathrm{E}U,\!\) that has the following description:
| \(\mathrm{E}U ~=~ U \times \mathrm{d}U ~=~ X \times Y \times \mathrm{d}X \times \mathrm{d}Y,\!\) |
with
| \(\mathrm{d}X = \{ \texttt{(} \mathrm{d}x \texttt{)}, \mathrm{d}x \}\!\) and \(\mathrm{d}Y = \{ \texttt{(} \mathrm{d}y \texttt{)}, \mathrm{d}y \}.\!\) |
The interpretations of these new symbols can be diverse, but the easiest option for now is just to say that \(\mathrm{d}x\!\) means "change \(x\!\)" and \(\mathrm{d}y\!\) means "change \(y\!\)". To draw the differential extension \(\mathrm{E}U~\!\) of our present universe \(U = X \times Y\!\) as a venn diagram, it would take us four logical dimensions \(X, Y, \mathrm{d}X, \mathrm{d}Y,\!\) but we can project a suggestion of what it's about on the universe \(X \times Y\!\) by drawing arrows that cross designated borders, labeling the arrows as \(\mathrm{d}x\!\) when crossing the border between \(x\!\) and \(\texttt{(} x \texttt{)}\!\) and as \(\mathrm{d}y\!\) when crossing the border between \(y\!\) and \(\texttt{(} y \texttt{)},\!\) in either direction, in either case.
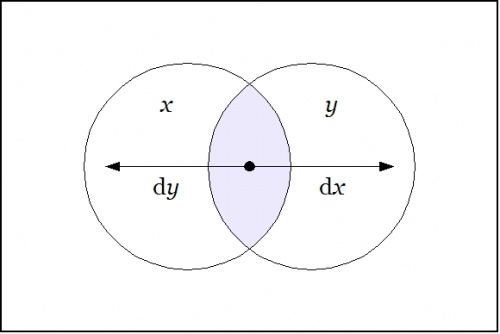
|
Propositions can be formed on differential variables, or any combination of ordinary logical variables and differential logical variables, in all the same ways that propositions can be formed on ordinary logical variables alone. For instance, the proposition \(\texttt{(} \mathrm{d}x \texttt{(} \mathrm{d}y \texttt{))}\!\) may be read to say that \(\mathrm{d}x \Rightarrow \mathrm{d}y,\!\) in other words, there is "no change in \(x\!\) without a change in \(y\!\)".
Given the proposition \(f(x, y)\!\) in \(U = X \times Y,\!\) the (first order) enlargement of \(f\!\) is the proposition \(\mathrm{E}f\!\) in \(\mathrm{E}U~\!\) that is defined by the formula \(\mathrm{E}f(x, y, \mathrm{d}x, \mathrm{d}y) = f(x + \mathrm{d}x, y + \mathrm{d}y).\!\)
Applying the enlargement operator \(\mathrm{E}\!\) to the present example, \(f(x, y) = xy,\!\) we may compute the result as follows:
|
\(\mathrm{E}f(x, y, \mathrm{d}x, \mathrm{d}y) \quad = \quad (x + \mathrm{d}x)(y + \mathrm{d}y).\!\) |
o---------------------------------------o | | | x dx y dy | | o---o o---o | | \ | | / | | \ | | / | | \| |/ | | @=@ | | | o---------------------------------------o | Ef = (x, dx) (y, dy) | o---------------------------------------o |
Given the proposition \(f(x, y)\!\) in \(U = X \times Y,\!\) the (first order) difference of \(f\!\) is the proposition \(\mathrm{D}f~\!\) in \(\mathrm{E}U~\!\) that is defined by the formula \(\mathrm{D}f = \mathrm{E}f - f,\!\) that is, \(\mathrm{D}f(x, y, \mathrm{d}x, \mathrm{d}y) = f(x + \mathrm{d}x, y + \mathrm{d}y) - f(x, y).\!\)
In the example \(f(x, y) = xy,\!\) the result is:
|
\(\mathrm{D}f(x, y, \mathrm{d}x, \mathrm{d}y) \quad = \quad (x + \mathrm{d}x)(y + \mathrm{d}y) - xy.\!\) |
o---------------------------------------o | | | x dx y dy | | o---o o---o | | \ | | / | | \ | | / | | \| |/ x y | | o=o-----------o | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | @ | | | o---------------------------------------o | Df = ((x, dx)(y, dy), xy) | o---------------------------------------o |
We did not yet go through the trouble to interpret this (first order) difference of conjunction fully, but were happy simply to evaluate it with respect to a single location in the universe of discourse, namely, at the point picked out by the singular proposition \(xy,\!\) that is, at the place where \(x = 1\!\) and \(y = 1.\!\) This evaluation is written in the form \(\mathrm{D}f|_{xy}\!\) or \(\mathrm{D}f|_{(1, 1)},\!\) and we arrived at the locally applicable law that is stated and illustrated as follows:
|
\(f(x, y) ~=~ xy ~=~ x ~\mathrm{and}~ y \quad \Rightarrow \quad \mathrm{D}f|_{xy} ~=~ \texttt{((} \mathrm{dx} \texttt{)(} \mathrm{d}y \texttt{))} ~=~ \mathrm{d}x ~\mathrm{or}~ \mathrm{d}y.\!\) |
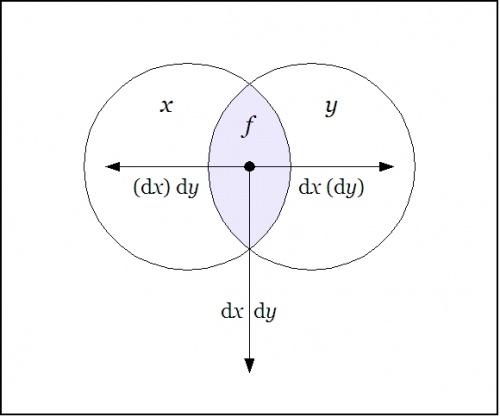
|
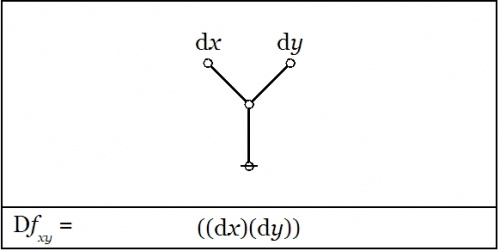
|
The picture shows the analysis of the inclusive disjunction \(\texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))}\!\) into the following exclusive disjunction:
| \(\mathrm{d}x ~\texttt{(} \mathrm{d}y \texttt{)} ~+~ \mathrm{d}y ~\texttt{(} \mathrm{d}x \texttt{)} ~+~ \mathrm{d}x ~\mathrm{d}y.\!\) |
This resulting differential proposition may be interpreted to say "change \(x\!\) or change \(y\!\) or both". And this can be recognized as just what you need to do if you happen to find yourself in the center cell and desire a detailed description of ways to depart it.
Note 3
Last time we computed what will variously be called the difference map, the difference proposition, or the local proposition \(\mathrm{D}f_p\!\) for the proposition \(f(x, y) = xy\!\) at the point \(p\!\) where \(x = 1\!\) and \(y = 1.\!\)
In the universe \(U = X \times Y,\!\) the four propositions \(xy,~ x\texttt{(}y\texttt{)},~ \texttt{(}x\texttt{)}y,~ \texttt{(}x\texttt{)(}y\texttt{)}\!\) that indicate the "cells", or the smallest regions of the venn diagram, are called singular propositions. These serve as an alternative notation for naming the points \((1, 1),~ (1, 0),~ (0, 1),~ (0, 0),\!\) respectively.
Thus we can write \(\mathrm{D}f_p = \mathrm{D}f|p = \mathrm{D}f|(1, 1) = \mathrm{D}f|xy,\!\) so long as we know the frame of reference in force.
Sticking with the example \(f(x, y) = xy,\!\) let us compute the value of the difference proposition \(\mathrm{D}f~\!\) at all 4 points.
o---------------------------------------o | | | x dx y dy | | o---o o---o | | \ | | / | | \ | | / | | \| |/ x y | | o=o-----------o | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | @ | | | o---------------------------------------o | Df = ((x, dx)(y, dy), xy) | o---------------------------------------o |
o---------------------------------------o | | | dx dy | | o---o o---o | | \ | | / | | \ | | / | | \| |/ | | o=o-----------o | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | @ | | | o---------------------------------------o | Df|xy = ((dx)(dy)) | o---------------------------------------o |
o---------------------------------------o | | | o | | dx | dy | | o---o o---o | | \ | | / | | \ | | / o | | \| |/ | | | o=o-----------o | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | @ | | | o---------------------------------------o | Df|x(y) = (dx) dy | o---------------------------------------o |
o---------------------------------------o | | | o | | | dx dy | | o---o o---o | | \ | | / | | \ | | / o | | \| |/ | | | o=o-----------o | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | @ | | | o---------------------------------------o | Df|(x)y = dx (dy) | o---------------------------------------o |
o---------------------------------------o | | | o o | | | dx | dy | | o---o o---o | | \ | | / | | \ | | / o o | | \| |/ \ / | | o=o-----------o | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | @ | | | o---------------------------------------o | Df|(x)(y) = dx dy | o---------------------------------------o |
The easy way to visualize the values of these graphical expressions is just to notice the following equivalents:
o---------------------------------------o | | | x | | o-o-o-...-o-o-o | | \ / | | \ / | | \ / | | \ / x | | \ / o | | \ / | | | @ = @ | | | o---------------------------------------o | (x, , ... , , ) = (x) | o---------------------------------------o |
o---------------------------------------o | | | o | | x_1 x_2 x_k | | | o---o-...-o---o | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / x_1 ... x_k | | @ = @ | | | o---------------------------------------o | (x_1, ..., x_k, ()) = x_1 · ... · x_k | o---------------------------------------o |
Laying out the arrows on the augmented venn diagram, one gets a picture of a differential vector field.
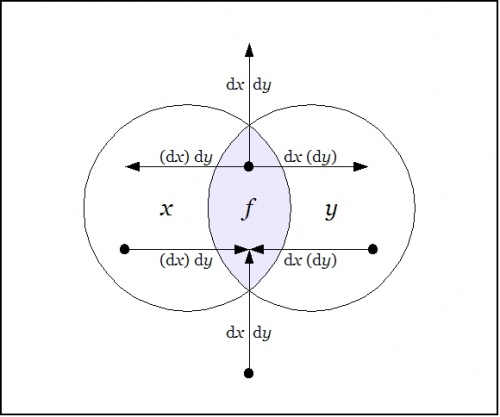
|
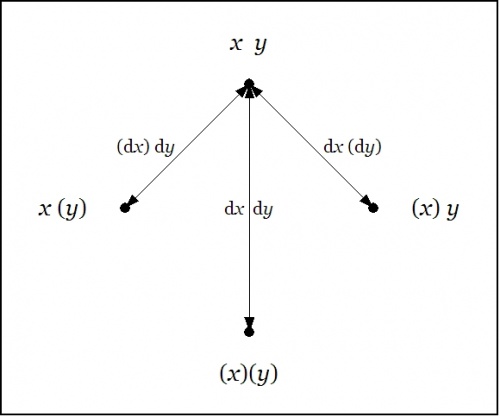
The Figure shows the points of the extended universe \(\mathrm{E}U = X \times Y \times \mathrm{d}X \times \mathrm{d}Y\!\) that satisfy the difference proposition \(\mathrm{D}f,\!\) namely, these:
|
\(\begin{array}{rcccc} 1. & x & y & \mathrm{d}x & \mathrm{d}y \\ 2. & x & y & \mathrm{d}x & (\mathrm{d}y) \\ 3. & x & y & (\mathrm{d}x) & \mathrm{d}y \\ 4. & x & (y) & (\mathrm{d}x) & \mathrm{d}y \\ 5. & (x) & y & \mathrm{d}x & (\mathrm{d}y) \\ 6. & (x) & (y) & \mathrm{d}x & \mathrm{d}y \end{array}\!\) |
An inspection of these six points should make it easy to understand \(\mathrm{D}f~\!\) as telling you what you have to do from each point of \(U\!\) in order to change the value borne by the proposition \(f(x, y).\!\)
Note 4
We have been studying the action of the difference operator \(\mathrm{D},\!\) also known as the localization operator, on the proposition \(f : X \times Y \to \mathbb{B}\!\) that is commonly known as the conjunction \(x \cdot y.\!\) We described \(\mathrm{D}f~\!\) as a (first order) differential proposition, that is, a proposition of the type \(\mathrm{D}f : X \times Y \times \mathrm{d}X \times \mathrm{d}Y \to \mathbb{B}.\!\) Abstracting from the augmented venn diagram that illustrates how the models or satisfying interpretations of \(\mathrm{D}f~\!\) distribute within the extended universe \(\mathrm{E}U = X \times Y \times \mathrm{d}X \times \mathrm{d}Y,\!\) we can depict \(\mathrm{D}f~\!\) in the form of a digraph or directed graph, one whose points are labeled with the elements of \(U = X \times Y\!\) and whose arrows are labeled with the elements of \(\mathrm{d}U = \mathrm{d}X \times \mathrm{d}Y.\!\)
|
|
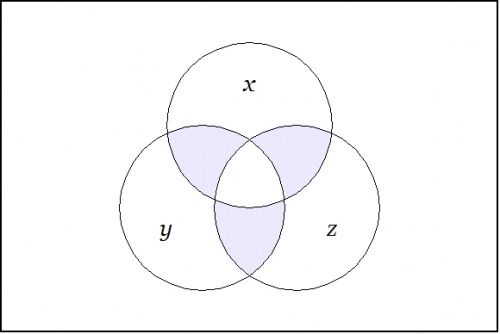
\(\begin{array}{rcccccc} f & = & x & \cdot & y \'"`UNIQ-MathJax1-QINU`"' Amazing! =='"`UNIQ--h-7--QINU`"'Note 8== We have been contemplating functions of the type \(f : U \to \mathbb{B}\!\) and studying the action of the operators \(\mathrm{E}\!\) and \(\mathrm{D}\!\) on this family. These functions, that we may identify for our present aims with propositions, inasmuch as they capture their abstract forms, are logical analogues of scalar potential fields. These are the sorts of fields that are so picturesquely presented in elementary calculus and physics textbooks by images of snow-covered hills and parties of skiers who trek down their slopes like least action heroes. The analogous scene in propositional logic presents us with forms more reminiscent of plateaunic idylls, being all plains at one of two levels, the mesas of verity and falsity, as it were, with nary a niche to inhabit between them, restricting our options for a sporting gradient of downhill dynamics to just one of two: standing still on level ground or falling off a bluff. We are still working well within the logical analogue of the classical finite difference calculus, taking in the novelties that the logical transmutation of familiar elements is able to bring to light. Soon we will take up several different notions of approximation relationships that may be seen to organize the space of propositions, and these will allow us to define several different forms of differential analysis applying to propositions. In time we will find reason to consider more general types of maps, having concrete types of the form \(X_1 \times \ldots \times X_k \to Y_1 \times \ldots \times Y_n\!\) and abstract types \(\mathbb{B}^k \to \mathbb{B}^n.\!\) We will think of these mappings as transforming universes of discourse into themselves or into others, in short, as transformations of discourse. Before we continue with this intinerary, however, I would like to highlight another sort of differential aspect that concerns the boundary operator or the marked connective that serves as one of the two basic connectives in the cactus language for ZOL. For example, consider the proposition \(f\!\) of concrete type \(f : X \times Y \times Z \to \mathbb{B}\!\) and abstract type \(f : \mathbb{B}^3 \to \mathbb{B}\!\) that is written \(\texttt{(} x, y, z \texttt{)}\!\) in cactus syntax. Taken as an assertion in what Peirce called the existential interpretation, \(\texttt{(} x, y, z \texttt{)}\!\) says that just one of \(x, y, z\!\) is false. It is useful to consider this assertion in relation to the conjunction \(xyz\!\) of the features that are engaged as its arguments. A venn diagram of \(\texttt{(} x, y, z \texttt{)}\!\) looks like this:
In relation to the center cell indicated by the conjunction \(xyz,\!\) the region indicated by \(\texttt{(} x, y, z \texttt{)}\!\) is comprised of the adjacent or bordering cells. Thus they are the cells that are just across the boundary of the center cell, as if reached by way of Leibniz's minimal changes from the point of origin, here, \(xyz.\!\) The same sort of boundary relationship holds for any cell of origin that one chooses to indicate. One way to indicate a cell is by forming a logical conjunction of positive and negative basis features, that is, by constructing an expression of the form \(e_1 \cdot \ldots \cdot e_k,\!\) where \(e_j = x_j ~\text{or}~ e_j = \texttt{(} x_j \texttt{)},\!\) for \(j = 1 ~\text{to}~ k.\!\) The proposition \(\texttt{(} e_1, \ldots, e_k \texttt{)}\!\) indicates the disjunctive region consisting of the cells that are just next door to \(e_1 \cdot \ldots \cdot e_k.\!\) Note 9
One other subject that it would be opportune to mention at this point, while we have an object example of a mathematical group fresh in mind, is the relationship between the pragmatic maxim and what are commonly known in mathematics as representation principles. As it turns out, with regard to its formal characteristics, the pragmatic maxim unites the aspects of a representation principle with the attributes of what would ordinarily be known as a closure principle. We will consider the form of closure that is invoked by the pragmatic maxim on another occasion, focusing here and now on the topic of group representations. Let us return to the example of the four-group \(V_4.\!\) We encountered this group in one of its concrete representations, namely, as a transformation group that acts on a set of objects, in this case a set of sixteen functions or propositions. Forgetting about the set of objects that the group transforms among themselves, we may take the abstract view of the group's operational structure, for example, in the form of the group operation table copied here:
This operation table is abstractly the same as, or isomorphic to, the versions with the \(\mathrm{E}_{ij}\!\) operators and the \(\mathrm{T}_{ij}\!\) transformations that we discussed earlier. That is to say, the story is the same — only the names have been changed. An abstract group can have a multitude of significantly and superficially different representations. Even after we have long forgotten the details of the particular representation that we may have come in with, there are species of concrete representations, called the regular representations, that are always readily available, as they can be generated from the mere data of the abstract operation table itself. To see how a regular representation is constructed from the abstract operation table, pick a group element at the top of the table and "consider its effects" on each of the group elements listed on the left. These effects may be recorded in one of the ways that Peirce often used, as a logical aggregate of elementary dyadic relatives, that is, as a logical disjunction or sum whose terms represent the \(\mathrm{input} : \mathrm{output}\!\) pairs that are produced by each group element in turn. This forms one of the two possible regular representations of the group, specifically, the one that is called the post-regular representation or the right regular representation. It has long been conventional to organize the terms of this logical sum in the form of a matrix: Reading "\(+\!\)" as a logical disjunction:
And so, by expanding effects, we get:
|
- Artificial Intelligence
- Boolean Algebra
- Boolean Functions
- Charles Sanders Peirce
- Combinatorics
- Computational Complexity
- Computer Science
- Cybernetics
- Differential Logic
- Equational Reasoning
- Formal Languages
- Formal Systems
- Graph Theory
- Inquiry
- Inquiry Driven Systems
- Knowledge Representation
- Logic
- Logical Graphs
- Mathematics
- Philosophy
- Propositional Calculus
- Semiotics
- Visualization