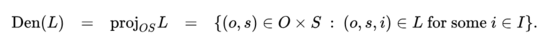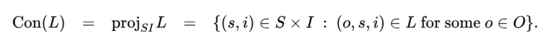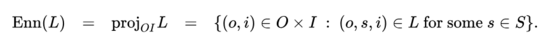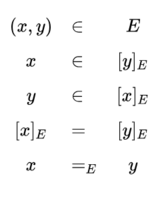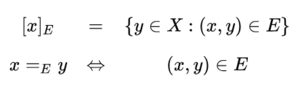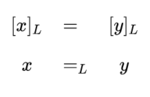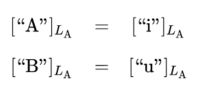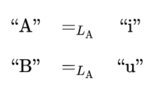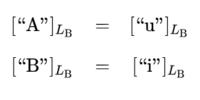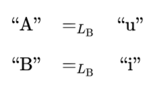Difference between revisions of "Sign relation"
Jon Awbrey (talk | contribs) |
Jon Awbrey (talk | contribs) (update) |
||
| Line 45: | Line 45: | ||
Tracing the passage of inquiry through the medium of signs calls for an active, intricate form of cooperation between the converging modes of investigation. Its proper character is best understood by realizing the theory of inquiry is adapted to study the developmental aspects of sign relations, a subject the theory of signs is specialized to treat from comparative and structural points of view. | Tracing the passage of inquiry through the medium of signs calls for an active, intricate form of cooperation between the converging modes of investigation. Its proper character is best understood by realizing the theory of inquiry is adapted to study the developmental aspects of sign relations, a subject the theory of signs is specialized to treat from comparative and structural points of view. | ||
| − | ==Examples of sign relations== | + | =={{anchor|Examples}}Examples of sign relations== |
Despite their simplicity, the examples to follow have subtleties of their own and their careful treatment serves to illustrate important issues in the general theory of signs. | Despite their simplicity, the examples to follow have subtleties of their own and their careful treatment serves to illustrate important issues in the general theory of signs. | ||
| Line 87: | Line 87: | ||
Already in this elementary context, there are several different meanings that might attach to the project of a <i>formal semiotics</i>, or a formal theory of meaning for signs. In the process of discussing these alternatives, it is useful to introduce a few terms that are occasionally used in the philosophy of language to point out the needed distinctions. | Already in this elementary context, there are several different meanings that might attach to the project of a <i>formal semiotics</i>, or a formal theory of meaning for signs. In the process of discussing these alternatives, it is useful to introduce a few terms that are occasionally used in the philosophy of language to point out the needed distinctions. | ||
| − | ==Dyadic aspects of sign relations== | + | =={{anchor|Dyadic Aspects}}Dyadic aspects of sign relations== |
| − | For an arbitrary triadic relation <math>L \subseteq O \times S \times I,</math> whether it happens to be a sign relation or not, there are six dyadic relations obtained by <i>projecting</i> <math>L</math> on one of the planes of the <math>OSI</math> | + | For an arbitrary triadic relation <math>L \subseteq O \times S \times I,</math> whether it happens to be a sign relation or not, there are six dyadic relations obtained by <i>projecting</i> <math>L</math> on one of the planes of the <math>OSI</math>‑space <math>O \times S \times I.</math> The six dyadic projections of a triadic relation <math>L</math> are defined and notated as shown in Table 2. |
{| align="center" cellpadding="0" cellspacing="0" style="text-align:center" | {| align="center" cellpadding="0" cellspacing="0" style="text-align:center" | ||
| Line 101: | Line 101: | ||
{| align="center" cellpadding="6" width="90%" | {| align="center" cellpadding="6" width="90%" | ||
| | | | ||
| − | <p>The dyadic relation resulting from the projection of <math>L</math> on the <math>OS</math> | + | <p>The dyadic relation resulting from the projection of <math>L</math> on the <math>OS</math>‑plane <math>O \times S</math> is written briefly as <math>L_{OS}</math> or written more fully as <math>\mathrm{proj}_{OS}(L)</math> and is defined as the set of all ordered pairs <math>(o, s)</math> in the cartesian product <math>O \times S</math> for which there exists an ordered triple <math>(o, s, i)</math> in <math>L</math> for some element <math>i</math> in the set <math>I.</math></p> |
|} | |} | ||
| Line 110: | Line 110: | ||
One aspect of a sign's complete meaning concerns the reference a sign has to its objects, which objects are collectively known as the <i>denotation</i> of the sign. In the pragmatic theory of sign relations, denotative references fall within the projection of the sign relation on the plane spanned by its object domain and its sign domain. | One aspect of a sign's complete meaning concerns the reference a sign has to its objects, which objects are collectively known as the <i>denotation</i> of the sign. In the pragmatic theory of sign relations, denotative references fall within the projection of the sign relation on the plane spanned by its object domain and its sign domain. | ||
| − | The dyadic relation making up the <i>denotative</i>, <i>referent</i>, or <i>semantic</i> aspect of a sign relation <math>L</math> is notated as <math>\mathrm{Den}(L).</math> Information about the denotative aspect of meaning is obtained from <math>L</math> by taking its <i>projection</i> on the object | + | The dyadic relation making up the <i>denotative</i>, <i>referent</i>, or <i>semantic</i> aspect of a sign relation <math>L</math> is notated as <math>\mathrm{Den}(L).</math> Information about the denotative aspect of meaning is obtained from <math>L</math> by taking its <i>projection</i> on the object‑sign plane. The result may be visualized as the “shadow” <math>L</math> casts on the 2‑dimensional space whose axes are the object domain <math>O</math> and the sign domain <math>S.</math> The denotative component of a sign relation <math>L,</math> variously written as <math>\mathrm{proj}_{OS} L,</math> <math>L_{OS},</math> <math>\mathrm{proj}_{12} L,</math> or <math>L_{12},</math> is defined as follows. |
<p align="center">[[File:Sign Relation Display 3.png|550px]]</p> | <p align="center">[[File:Sign Relation Display 3.png|550px]]</p> | ||
| Line 126: | Line 126: | ||
Another aspect of a sign's complete meaning concerns the reference a sign has to its interpretants, which interpretants are collectively known as the <i>connotation</i> of the sign. In the pragmatic theory of sign relations, connotative references fall within the projection of the sign relation on the plane spanned by its sign domain and its interpretant domain. | Another aspect of a sign's complete meaning concerns the reference a sign has to its interpretants, which interpretants are collectively known as the <i>connotation</i> of the sign. In the pragmatic theory of sign relations, connotative references fall within the projection of the sign relation on the plane spanned by its sign domain and its interpretant domain. | ||
| − | In the full theory of sign relations the connotative aspect of meaning includes the links a | + | In the full theory of sign relations the connotative aspect of meaning includes the links a sign has to affects, concepts, ideas, impressions, intentions, and the whole realm of an interpretive agent's mental states and allied activities, broadly encompassing intellectual associations, emotional impressions, motivational impulses, and real conduct. Taken at the full, in the natural setting of semiotic phenomena, this complex system of references is unlikely ever to find itself mapped in much detail, much less completely formalized, but the tangible warp of its accumulated mass is commonly alluded to as the connotative import of language. |
| − | Formally speaking, however, the connotative aspect of meaning presents no additional difficulty. The dyadic relation making up the <i>connotative</i> aspect of a sign relation <math>L</math> is notated as <math>\mathrm{Con}(L).</math> Information about the connotative aspect of meaning is obtained from <math>L</math> by taking its <i>projection</i> on the sign | + | Formally speaking, however, the connotative aspect of meaning presents no additional difficulty. The dyadic relation making up the <i>connotative</i> aspect of a sign relation <math>L</math> is notated as <math>\mathrm{Con}(L).</math> Information about the connotative aspect of meaning is obtained from <math>L</math> by taking its <i>projection</i> on the sign‑interpretant plane and visualized as the “shadow” <math>L</math> casts on the 2‑dimensional space whose axes are the sign domain <math>S</math> and the interpretant domain <math>I.</math> The connotative component of a sign relation <math>L,</math> variously written as <math>\mathrm{proj}_{SI} L,</math> <math>L_{SI},</math> <math>\mathrm{proj}_{23} L,</math> or <math>L_{23},</math> is defined as follows. |
<p align="center">[[File:Sign Relation Display 4.png|550px]]</p> | <p align="center">[[File:Sign Relation Display 4.png|550px]]</p> | ||
| Line 140: | Line 140: | ||
===Ennotation=== | ===Ennotation=== | ||
| − | A third aspect of a sign's complete meaning concerns the reference its objects have to its interpretants, which has no standard name in semiotics. It would be called an <i>induced relation</i> in graph theory or the result of <i>relational composition</i> in relation theory. If an interpretant is recognized as a sign in its own right then its independent reference to an object can be taken as belonging to another moment of denotation, but this neglects the mediational character of the whole transaction in which this occurs. Denotation and connotation have to do with dyadic relations in which the sign plays an active role but here | + | A third aspect of a sign's complete meaning concerns the reference its objects have to its interpretants, which has no standard name in semiotics. It would be called an <i>induced relation</i> in graph theory or the result of <i>relational composition</i> in relation theory. If an interpretant is recognized as a sign in its own right then its independent reference to an object can be taken as belonging to another moment of denotation, but this neglects the mediational character of the whole transaction in which this occurs. Denotation and connotation have to do with dyadic relations in which the sign plays an active role but here we are dealing with a dyadic relation between objects and interpretants mediated by the sign from an off‑stage position, as it were. |
| − | As a relation between objects and interpretants mediated by a sign, this third aspect of meaning may be referred to as the <i>ennotation</i> of a sign and the dyadic relation making up the <i>ennotative aspect</i> of a sign relation <math>L</math> may be notated as <math>\mathrm{Enn}(L).</math> Information about the ennotative aspect of meaning is obtained from <math>L</math> by taking its <i>projection</i> on the object | + | As a relation between objects and interpretants mediated by a sign, this third aspect of meaning may be referred to as the <i>ennotation</i> of a sign and the dyadic relation making up the <i>ennotative aspect</i> of a sign relation <math>L</math> may be notated as <math>\mathrm{Enn}(L).</math> Information about the ennotative aspect of meaning is obtained from <math>L</math> by taking its <i>projection</i> on the object‑interpretant plane and visualized as the “shadow” <math>L</math> casts on the 2‑dimensional space whose axes are the object domain <math>O</math> and the interpretant domain <math>I.</math> The ennotative component of a sign relation <math>L,</math> variously written as <math>\mathrm{proj}_{OI} L,</math> <math>L_{OI},</math> <math>\mathrm{proj}_{13} L,</math> or <math>L_{13},</math> is defined as follows. |
<p align="center">[[File:Sign Relation Display 5.png|550px]]</p> | <p align="center">[[File:Sign Relation Display 5.png|550px]]</p> | ||
| Line 154: | Line 154: | ||
|} | |} | ||
| − | ==Semiotic equivalence relations== | + | =={{anchor|Semiotic Equivalence Relations 1}}Semiotic equivalence relations== |
A <i>semiotic equivalence relation</i> (SER) is a special type of equivalence relation arising in the analysis of sign relations. As a general rule, any equivalence relation is closely associated with a family of equivalence classes which partition the underlying set of elements, frequently called the <i>domain</i> or <i>space</i> of the relation. In the case of a SER, the equivalence classes are called <i>semiotic equivalence classes</i> (SECs) and the partition is called a <i>semiotic partition</i> (SEP). | A <i>semiotic equivalence relation</i> (SER) is a special type of equivalence relation arising in the analysis of sign relations. As a general rule, any equivalence relation is closely associated with a family of equivalence classes which partition the underlying set of elements, frequently called the <i>domain</i> or <i>space</i> of the relation. In the case of a SER, the equivalence classes are called <i>semiotic equivalence classes</i> (SECs) and the partition is called a <i>semiotic partition</i> (SEP). | ||
| Line 172: | Line 172: | ||
|} | |} | ||
| + | {{anchor|Semiotic Equivalence Relations 2}} | ||
A few items of notation are useful in discussing equivalence relations in general and semiotic equivalence relations in particular. | A few items of notation are useful in discussing equivalence relations in general and semiotic equivalence relations in particular. | ||
| Line 348: | Line 349: | ||
[[Category:Cognitive science]] | [[Category:Cognitive science]] | ||
[[Category:Computer science]] | [[Category:Computer science]] | ||
| + | [[Category:Differential logic]] | ||
[[Category:Graph theory]] | [[Category:Graph theory]] | ||
| + | [[Category:Hermeneutics]] | ||
| + | [[Category:Information systems]] | ||
| + | [[Category:Information theory]] | ||
[[Category:Inquiry]] | [[Category:Inquiry]] | ||
[[Category:Intelligent systems]] | [[Category:Intelligent systems]] | ||
| + | [[Category:Knowledge representation]] | ||
[[Category:Logic]] | [[Category:Logic]] | ||
[[Category:Logical graphs]] | [[Category:Logical graphs]] | ||
Revision as of 17:00, 7 January 2026
☞ This page belongs to resource collections on Logic and Inquiry.
A sign relation is the basic construct in the theory of signs, also known as semeiotic or semiotics, as developed by Charles Sanders Peirce.
Anthesis
Thus, if a sunflower, in turning towards the sun, becomes by that very act fully capable, without further condition, of reproducing a sunflower which turns in precisely corresponding ways toward the sun, and of doing so with the same reproductive power, the sunflower would become a Representamen of the sun.
— C.S. Peirce, Collected Papers, CP 2.274
In his picturesque illustration of a sign relation, along with his tracing of a corresponding sign process, or semiosis, Peirce uses the technical term representamen for his concept of a sign, but the shorter word is precise enough, so long as one recognizes its meaning in a particular theory of signs is given by a specific definition of what it means to be a sign.
Definition
One of Peirce's clearest and most complete definitions of a sign is one he gives in the context of providing a definition for logic, and so it is informative to view it in that setting.
Logic will here be defined as formal semiotic. A definition of a sign will be given which no more refers to human thought than does the definition of a line as the place which a particle occupies, part by part, during a lapse of time. Namely, a sign is something, A, which brings something, B, its interpretant sign determined or created by it, into the same sort of correspondence with something, C, its object, as that in which itself stands to C.
It is from this definition, together with a definition of “formal”, that I deduce mathematically the principles of logic. I also make a historical review of all the definitions and conceptions of logic, and show, not merely that my definition is no novelty, but that my non‑psychological conception of logic has virtually been quite generally held, though not generally recognized.
— C.S. Peirce, New Elements of Mathematics, vol. 4, 20–21
In the general discussion of diverse theories of signs, the question arises whether signhood is an absolute, essential, indelible, or ontological property of a thing, or whether it is a relational, interpretive, and mutable role a thing may be said to have only within a particular context of relationships.
Peirce's definition of a sign defines it in relation to its objects and its interpretant signs, and thus defines signhood in relative terms, by means of a predicate with three places. In that definition, signhood is a role in a triadic relation, a role a thing bears or plays in a determinate context of relationships — it is not an absolute or non‑relative property of a thing‑in‑itself, one it possesses independently of all relationships to other things.
Some of the terms Peirce uses in his definition of a sign may need to be elaborated for the contemporary reader.
- Correspondence. From the way Peirce uses the term throughout his work, it is clear he means what he elsewhere calls a “triple correspondence”, and thus this is just another way of referring to the whole triadic sign relation itself. In particular, his use of the term should not be taken to imply a dyadic correspondence, like the kinds of “mirror image” correspondence between realities and representations bandied about in contemporary controversies about “correspondence theories of truth”.
- Determination. Peirce's concept of determination is broader in several directions than the sense of the word referring to strictly deterministic causal‑temporal processes. First, and especially in this context, he is invoking a more general concept of determination, what is called a formal or informational determination, as in saying “two points determine a line”, rather than the more special cases of causal and temporal determinisms. Second, he characteristically allows for what is called determination in measure, that is, an order of determinism admitting a full spectrum of more and less determined relationships.
- Non‑psychological. Peirce's “non‑psychological conception of logic” must be distinguished from any variety of anti‑psychologism. He was quite interested in matters of psychology and had much of import to say about them. But logic and psychology operate on different planes of study even when they have occasion to view the same data, as logic is a normative science where psychology is a descriptive science, and so they have very different aims, methods, and rationales.
Signs and inquiry
- Main article : Inquiry
There is a close relationship between the pragmatic theory of signs and the pragmatic theory of inquiry. In fact, the correspondence between the two studies exhibits so many congruences and parallels it is often best to treat them as integral parts of one and the same subject. In a very real sense, inquiry is the process by which sign relations come to be established and continue to evolve. In other words, inquiry, “thinking” in its best sense, “is a term denoting the various ways in which things acquire significance” (Dewey, 38).
Tracing the passage of inquiry through the medium of signs calls for an active, intricate form of cooperation between the converging modes of investigation. Its proper character is best understood by realizing the theory of inquiry is adapted to study the developmental aspects of sign relations, a subject the theory of signs is specialized to treat from comparative and structural points of view.
Template:AnchorExamples of sign relations
Despite their simplicity, the examples to follow have subtleties of their own and their careful treatment serves to illustrate important issues in the general theory of signs.
Imagine a discussion between two people, Ann and Bob, and attend only to that aspect of their interpretive practice that involves the use of the following nouns and pronouns: “Ann”, “Bob”, “I”, “you”.
- The object domain of this discussion fragment is the set of two people \(\{ \text{Ann}, \text{Bob} \}.\)
- The syntactic domain or the sign system of their discussion is limited to the set of four signs \(\{ \text{“Ann”}, \text{“Bob”}, \text{“I”}, \text{“you”} \}.\)
In their discussion, Ann and Bob are not only the passive objects of nominative and accusative references but also the active interpreters of the language that they use. The system of interpretation (SOI) associated with each language user can be represented in the form of an individual three-place relation called the sign relation of that interpreter.
Understood in terms of its set‑theoretic extension, a sign relation \(L\) is a subset of a cartesian product \(O \times S \times I.\) Here, \(O, S, I\) are three sets that are known as the object domain, the sign domain, and the interpretant domain, respectively, of the sign relation \(L \subseteq O \times S \times I.\)
Broadly speaking, the three domains of a sign relation can be any sets whatsoever, but the kinds of sign relations typically contemplated in formal settings are usually constrained to having \(I \subseteq S\). In this case interpretants are just a special variety of signs and this makes it convenient to lump signs and interpretants together into a single class called the syntactic domain. In the forthcoming examples \(S\) and \(I\) are identical as sets, so the same elements manifest themselves in two different roles of the sign relations in question. When it is necessary to refer to the whole set of objects and signs in the union of the domains \(O, S, I\) for a given sign relation \(L,\) one may refer to this set as the World of \(L\) and write \(W = W_L = O \cup S \cup I.\)
To facilitate an interest in the abstract structures of sign relations, and to keep the notations as brief as possible as the examples become more complicated, it serves to introduce the following general notations.

|
Introducing a few abbreviations for use in considering the present Example, we have the following data.
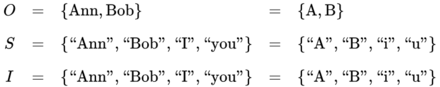
|
In the present example, \(S = I = \text{Syntactic Domain}\).
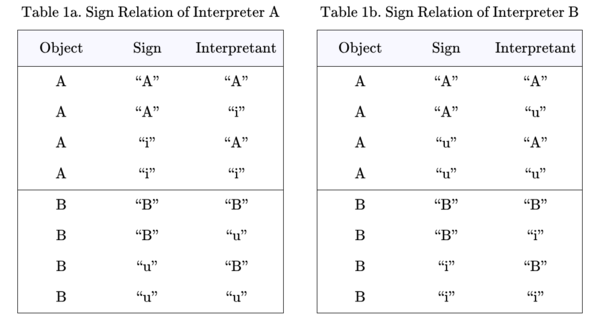
The next two Tables show the sign relations associated with the interpreters \(\mathrm{A}\) and \(\mathrm{B},\) respectively, putting them in the form of relational databases. Thus, the rows of each Table list the ordered triples of the form \((o, s, i)\) belonging to the corresponding sign relations, \(L_\mathrm{A}, L_\mathrm{B} \subseteq O \times S \times I.\)
|
These Tables codify a rudimentary level of interpretive practice for the agents \(\mathrm{A}\) and \(\mathrm{B}\) and provide a basis for formalizing the initial semantics that is appropriate to their common syntactic domain. Each row of a Table names an object and two co‑referent signs, making up an ordered triple of the form \((o, s, i)\) called an elementary relation, that is, one element of the relation's set-theoretic extension.
Already in this elementary context, there are several different meanings that might attach to the project of a formal semiotics, or a formal theory of meaning for signs. In the process of discussing these alternatives, it is useful to introduce a few terms that are occasionally used in the philosophy of language to point out the needed distinctions.
Template:AnchorDyadic aspects of sign relations
For an arbitrary triadic relation \(L \subseteq O \times S \times I,\) whether it happens to be a sign relation or not, there are six dyadic relations obtained by projecting \(L\) on one of the planes of the \(OSI\)‑space \(O \times S \times I.\) The six dyadic projections of a triadic relation \(L\) are defined and notated as shown in Table 2.
| \(\text{Table 2. Dyadic Projections of Triadic Relations}\) |

|
By way of unpacking the set‑theoretic notation, here is what the first definition says in ordinary language.
|
The dyadic relation resulting from the projection of \(L\) on the \(OS\)‑plane \(O \times S\) is written briefly as \(L_{OS}\) or written more fully as \(\mathrm{proj}_{OS}(L)\) and is defined as the set of all ordered pairs \((o, s)\) in the cartesian product \(O \times S\) for which there exists an ordered triple \((o, s, i)\) in \(L\) for some element \(i\) in the set \(I.\) |
In the case where \(L\) is a sign relation, which it becomes by satisfying one of the definitions of a sign relation, some of the dyadic aspects of \(L\) can be recognized as formalizing aspects of sign meaning which have received their share of attention from students of signs over the centuries, and thus they can be associated with traditional concepts and terminology. Of course, traditions vary with respect to the precise formation and usage of such concepts and terms. Other aspects of meaning have not received their fair share of attention and thus remain innominate in current anatomies of sign relations.
Denotation
One aspect of a sign's complete meaning concerns the reference a sign has to its objects, which objects are collectively known as the denotation of the sign. In the pragmatic theory of sign relations, denotative references fall within the projection of the sign relation on the plane spanned by its object domain and its sign domain.
The dyadic relation making up the denotative, referent, or semantic aspect of a sign relation \(L\) is notated as \(\mathrm{Den}(L).\) Information about the denotative aspect of meaning is obtained from \(L\) by taking its projection on the object‑sign plane. The result may be visualized as the “shadow” \(L\) casts on the 2‑dimensional space whose axes are the object domain \(O\) and the sign domain \(S.\) The denotative component of a sign relation \(L,\) variously written as \(\mathrm{proj}_{OS} L,\) \(L_{OS},\) \(\mathrm{proj}_{12} L,\) or \(L_{12},\) is defined as follows.
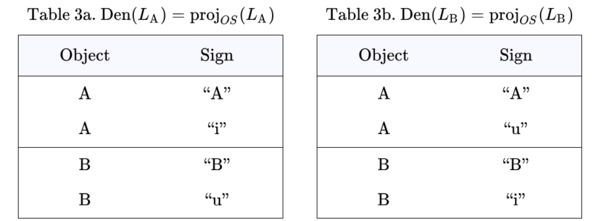
Tables 3a and 3b show the denotative components of the sign relations associated with the interpreters \(\mathrm{A}\) and \(\mathrm{B},\) respectively. The rows of each Table list the ordered pairs \((o, s)\) in the corresponding projections, \(\mathrm{Den}(L_\mathrm{A}), \mathrm{Den}(L_\mathrm{B}) \subseteq O \times S.\)
|
Looking to the denotative aspects of \(L_\mathrm{A}\) and \(L_\mathrm{B},\) various rows of the Tables specify, for example, that \(\mathrm{A}\) uses \(\text{“i”}\) to denote \(\mathrm{A}\) and \(\text{“u”}\) to denote \(\mathrm{B},\) while \(\mathrm{B}\) uses \(\text{“i”}\) to denote \(\mathrm{B}\) and \(\text{“u”}\) to denote \(\mathrm{A}.\)
Connotation
Another aspect of a sign's complete meaning concerns the reference a sign has to its interpretants, which interpretants are collectively known as the connotation of the sign. In the pragmatic theory of sign relations, connotative references fall within the projection of the sign relation on the plane spanned by its sign domain and its interpretant domain.
In the full theory of sign relations the connotative aspect of meaning includes the links a sign has to affects, concepts, ideas, impressions, intentions, and the whole realm of an interpretive agent's mental states and allied activities, broadly encompassing intellectual associations, emotional impressions, motivational impulses, and real conduct. Taken at the full, in the natural setting of semiotic phenomena, this complex system of references is unlikely ever to find itself mapped in much detail, much less completely formalized, but the tangible warp of its accumulated mass is commonly alluded to as the connotative import of language.
Formally speaking, however, the connotative aspect of meaning presents no additional difficulty. The dyadic relation making up the connotative aspect of a sign relation \(L\) is notated as \(\mathrm{Con}(L).\) Information about the connotative aspect of meaning is obtained from \(L\) by taking its projection on the sign‑interpretant plane and visualized as the “shadow” \(L\) casts on the 2‑dimensional space whose axes are the sign domain \(S\) and the interpretant domain \(I.\) The connotative component of a sign relation \(L,\) variously written as \(\mathrm{proj}_{SI} L,\) \(L_{SI},\) \(\mathrm{proj}_{23} L,\) or \(L_{23},\) is defined as follows.
Tables 4a and 4b show the connotative components of the sign relations associated with the interpreters \(\mathrm{A}\) and \(\mathrm{B},\) respectively. The rows of each Table list the ordered pairs \((s, i)\) in the corresponding projections, \(\mathrm{Con}(L_\mathrm{A}), \mathrm{Con}(L_\mathrm{B}) \subseteq S \times I.\)

|
Ennotation
A third aspect of a sign's complete meaning concerns the reference its objects have to its interpretants, which has no standard name in semiotics. It would be called an induced relation in graph theory or the result of relational composition in relation theory. If an interpretant is recognized as a sign in its own right then its independent reference to an object can be taken as belonging to another moment of denotation, but this neglects the mediational character of the whole transaction in which this occurs. Denotation and connotation have to do with dyadic relations in which the sign plays an active role but here we are dealing with a dyadic relation between objects and interpretants mediated by the sign from an off‑stage position, as it were.
As a relation between objects and interpretants mediated by a sign, this third aspect of meaning may be referred to as the ennotation of a sign and the dyadic relation making up the ennotative aspect of a sign relation \(L\) may be notated as \(\mathrm{Enn}(L).\) Information about the ennotative aspect of meaning is obtained from \(L\) by taking its projection on the object‑interpretant plane and visualized as the “shadow” \(L\) casts on the 2‑dimensional space whose axes are the object domain \(O\) and the interpretant domain \(I.\) The ennotative component of a sign relation \(L,\) variously written as \(\mathrm{proj}_{OI} L,\) \(L_{OI},\) \(\mathrm{proj}_{13} L,\) or \(L_{13},\) is defined as follows.
As it happens, the sign relations \(L_\mathrm{A}\) and \(L_\mathrm{B}\) are fully symmetric with respect to exchanging signs and interpretants, so all the data of \(\mathrm{proj}_{OS} L_\mathrm{A}\) is echoed unchanged in \(\mathrm{proj}_{OI} L_\mathrm{A}\) and all the data of \(\mathrm{proj}_{OS} L_\mathrm{B}\) is echoed unchanged in \(\mathrm{proj}_{OI} L_\mathrm{B}.\)
Tables 5a and 5b show the ennotative components of the sign relations associated with the interpreters \(\mathrm{A}\) and \(\mathrm{B},\) respectively. The rows of each Table list the ordered pairs \((o, i)\) in the corresponding projections, \(\mathrm{Enn}(L_\mathrm{A}), \mathrm{Enn}(L_\mathrm{B}) \subseteq O \times I.\)

|
Template:AnchorSemiotic equivalence relations
A semiotic equivalence relation (SER) is a special type of equivalence relation arising in the analysis of sign relations. As a general rule, any equivalence relation is closely associated with a family of equivalence classes which partition the underlying set of elements, frequently called the domain or space of the relation. In the case of a SER, the equivalence classes are called semiotic equivalence classes (SECs) and the partition is called a semiotic partition (SEP).
The sign relations \(L_\mathrm{A}\) and \(L_\mathrm{B}\) have many interesting properties which are not possessed by sign relations in general. Some of these properties have to do with the relation between signs and their interpretant signs, as reflected in the projections of \(L_\mathrm{A}\) and \(L_\mathrm{B}\) on the \(SI\)-plane, notated as \(\mathrm{proj}_{SI} L_\mathrm{A}\) and \(\mathrm{proj}_{SI} L_\mathrm{B},\) respectively. The 2-adic relations on \(S \times I\) induced by these projections are also referred to as the connotative components of the corresponding sign relations, notated as \(\mathrm{Con}(L_\mathrm{A})\) and \(\mathrm{Con}(L_\mathrm{B}),\) respectively. Tables 6a and 6b show the corresponding connotative components.

|
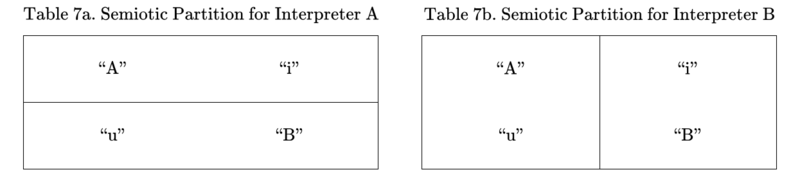
One nice property possessed by the sign relations \(L_\mathrm{A}\) and \(L_\mathrm{B}\) is that their connotative components \(\mathrm{Con}(L_\mathrm{A})\) and \(\mathrm{Con}(L_\mathrm{B})\) form a pair of equivalence relations on their common syntactic domain \(S = I.\) It is convenient to refer to such a structure as a semiotic equivalence relation (SER) since it equates signs that mean the same thing to some interpreter. Each of the SERs, \(\mathrm{Con}(L_\mathrm{A}), \mathrm{Con}(L_\mathrm{B}) \subseteq S \times I \cong S \times S\) partitions the whole collection of signs into semiotic equivalence classes (SECs). This makes for a strong form of representation in that the structure of the interpreters' common object domain \(\{ \mathrm{A}, \mathrm{B} \}\) is reflected or reconstructed, part for part, in the structure of each of their semiotic partitions (SEPs) of the syntactic domain \(\{ \text{“A”}, \text{“B”}, \text{“i”}, \text{“u”} \}.\) But it needs to be observed that the semiotic partitions for interpreters \(\mathrm{A}\) and \(\mathrm{B}\) are not the same, indeed, they are orthogonal to each other. This makes it difficult to interpret either one of the partitions or equivalence relations on the syntactic domain as corresponding to any sort of objective structure or invariant reality, independent of the individual interpreter's point of view.
Information about the contrasting patterns of semiotic equivalence induced by the interpreters \(\mathrm{A}\) and \(\mathrm{B}\) is summarized in Tables 7a and 7b. The form of these Tables should suffice to explain what is meant by saying that the SEPs for \(\mathrm{A}\) and \(\mathrm{B}\) are orthogonal to each other.
|
Template:Anchor A few items of notation are useful in discussing equivalence relations in general and semiotic equivalence relations in particular.
As a general consideration, if \(E\) is an equivalence relation on a set \(X,\) then every element \(x\) of \(X\) belongs to a unique equivalence class under \(E\) called the equivalence class of \(x\) under \(E\). Convention provides the square bracket notation for denoting this equivalence class, either in the subscripted form \([x]_E\) or in the simpler form \([x]\) when the subscript \(E\) is understood. A statement that the elements \(x\) and \(y\) are equivalent under \(E\) is called an equation or an equivalence and may be expressed in any of the following ways.
Thus we have the following definitions.
In the application to sign relations it is useful to extend the square bracket notation in the following ways. If \(L\) is a sign relation whose connotative component or syntactic projection \(L_{SI}\) is an equivalence relation on \(S = I,\) let \([s]_L\) be the equivalence class of \(s\) under \(L_{SI}.\) That is to say, \([s]_L = [s]_{L_{SI}}.\) A statement that the signs \(x\) and \(y\) are equivalent under a semiotic equivalence relation \(L_{SI}\) is called a semiotic equation (SEQ) and may be written in either of the following equivalent forms.
In many situations there is one further adaptation of the square bracket notation for semiotic equivalence classes that can be useful. Namely, when there is known to exist a particular triple \((o, s, i)\) in a sign relation \(L,\) it is permissible to let \([o]_L\) be defined as \([s]_L.\) These modifications are designed to make the notation for semiotic equivalence classes harmonize as well as possible with the frequent use of similar devices for the denotations of signs and expressions.
The semiotic equivalence relation for interpreter \(\mathrm{A}\) yields the following semiotic equations.
or
Thus it induces the semiotic partition.
The semiotic equivalence relation for interpreter \(\mathrm{B}\) yields the following semiotic equations.
or
Thus it induces the semiotic partition.
Graphical representations
The dyadic components of sign relations have graph-theoretic representations, as digraphs (or directed graphs), which provide concise pictures of their structural and potential dynamic properties.
By way of terminology, a directed edge \((x, y)\) is called an arc from point \(x\) to point \(y,\) and a self-loop \((x, x)\) is called a sling at \(x.\)
The denotative components \(\mathrm{Den}(L_\mathrm{A})\) and \(\mathrm{Den}(L_\mathrm{B})\) can be represented as digraphs on the six points of their common world set \(W = O \cup S \cup I =\) \(\{ \mathrm{A}, \mathrm{B}, \text{“A”}, \text{“B”}, \text{“i”}, \text{“u”} \}.\) The arcs are given as follows:
|
\(\mathrm{Den}(L_\mathrm{A})\) has an arc from each point of \(\{ \text{“A”}, \text{“i”} \}\) to \(\mathrm{A}\) and an arc from each point of \(\{ \text{“B”}, \text{“u”} \}\) to \(\mathrm{B}.\) |
|
\(\mathrm{Den}(L_\mathrm{B})\) has an arc from each point of \(\{ \text{“A”}, \text{“u”} \}\) to \(\mathrm{A}\) and an arc from each point of \(\{ \text{“B”}, \text{“i”} \}\) to \(\mathrm{B}.\) |
\(\mathrm{Den}(L_\mathrm{A})\) and \(\mathrm{Den}(L_\mathrm{B})\) can be interpreted as transition digraphs which chart the succession of steps or the connection of states in a computational process. If the graphs are read this way, the denotational arcs summarize the upshots of the computations involved when the interpreters \(\mathrm{A}\) and \(\mathrm{B}\) evaluate the signs in \(S\) according to their own frames of reference.
The connotative components \(\mathrm{Con}(L_\mathrm{A})\) and \(\mathrm{Con}(L_\mathrm{B})\) can be represented as digraphs on the four points of their common syntactic domain \(S = I =\) \(\{ \text{“A”}, \text{“B”}, \text{“i”}, \text{“u”} \}.\) Since \(\mathrm{Con}(L_\mathrm{A})\) and \(\mathrm{Con}(L_\mathrm{B})\) are semiotic equivalence relations, their digraphs conform to the pattern manifested by all digraphs of equivalence relations. In general, a digraph of an equivalence relation falls into connected components that correspond to the parts of the associated partition, with a complete digraph on the points of each part, and no other arcs. In the present case, the arcs are given as follows:
|
\(\mathrm{Con}(L_\mathrm{A})\) has the structure of a semiotic equivalence relation on \(S,\) with a sling at each point of \(S,\) arcs in both directions between the points of \(\{ \text{“A”}, \text{“i”} \},\) and arcs in both directions between the points of \(\{ \text{“B”}, \text{“u”} \}.\) |
|
\(\mathrm{Con}(L_\mathrm{B})\) has the structure of a semiotic equivalence relation on \(S,\) with a sling at each point of \(S,\) arcs in both directions between the points of \(\{ \text{“A”}, \text{“u”} \},\) and arcs in both directions between the points of \(\{ \text{“B”}, \text{“i”} \}.\) |
Taken as transition digraphs, \(\mathrm{Con}(L_\mathrm{A})\) and \(\mathrm{Con}(L_\mathrm{B})\) highlight the associations permitted between equivalent signs, as this equivalence is judged by the interpreters \(\mathrm{A}\) and \(\mathrm{B},\) respectively.
Six ways of looking at a sign relation
In the context of 3-adic relations in general, Peirce provides the following illustration of the six converses of a 3-adic relation, that is, the six differently ordered ways of stating what is logically the same 3-adic relation:
- So in a triadic fact, say, for example
| A gives B to C |
- we make no distinction in the ordinary logic of relations between the subject nominative, the direct object, and the indirect object. We say that the proposition has three logical subjects. We regard it as a mere affair of English grammar that there are six ways of expressing this:
| A gives B to C | A benefits C with B |
| B enriches C at expense of A | C receives B from A |
| C thanks A for B | B leaves A for C |
- These six sentences express one and the same indivisible phenomenon. (C.S. Peirce, “The Categories Defended”, MS 308 (1903), EP 2, 170–171).
IOS
(Text in Progress)
ISO
(Text in Progress)
OIS
|
Words spoken are symbols or signs (σύμβολα) of affections or impressions (παθήματα) of the soul (ψυχή); written words are the signs of words spoken. As writing, so also is speech not the same for all races of men. But the mental affections themselves, of which these words are primarily signs (σημεια), are the same for the whole of mankind, as are also the objects (πράγματα) of which those affections are representations or likenesses, images, copies (ομοιώματα). (Aristotle, De Interpretatione, 1.16a4). |
OSI
(Text in Progress)
SIO
|
Logic will here be defined as formal semiotic. A definition of a sign will be given which no more refers to human thought than does the definition of a line as the place which a particle occupies, part by part, during a lapse of time. Namely, a sign is something, A, which brings something, B, its interpretant sign determined or created by it, into the same sort of correspondence with something, C, its object, as that in which itself stands to C. It is from this definition, together with a definition of “formal”, that I deduce mathematically the principles of logic. I also make a historical review of all the definitions and conceptions of logic, and show, not merely that my definition is no novelty, but that my non-psychological conception of logic has virtually been quite generally held, though not generally recognized. (C.S. Peirce, “Application to the Carnegie Institution”, L75 (1902), NEM 4, 20–21). |
SOI
|
A Sign is anything which is related to a Second thing, its Object, in respect to a Quality, in such a way as to bring a Third thing, its Interpretant, into relation to the same Object, and that in such a way as to bring a Fourth into relation to that Object in the same form, ad infinitum. (CP 2.92, quoted in Fisch 1986, p. 274) |
References
- Awbrey, J.L., and Awbrey, S.M. (Autumn 1995), “Interpretation as Action : The Risk of Inquiry”, Inquiry : Critical Thinking Across the Disciplines 15(1), pp. 40–52. Archive. Journal. Online (doc) (pdf).
- Deledalle, Gérard (2000), C.S. Peirce's Philosophy of Signs, Indiana University Press, Bloomington, IN.
- Dewey, John. (1910), How We Think, D.C. Heath, Boston, MA. Reprinted (1991), Prometheus Books, Buffalo, NY. Online.
- Eisele, Carolyn (1979), in Studies in the Scientific and Mathematical Philosophy of C.S. Peirce, Richard Milton Martin (ed.), Mouton, The Hague.
- Esposito, Joseph (1980), Evolutionary Metaphysics : The Development of Peirce's Theory of Categories, Ohio University Press (?).
- Fisch, Max (1986), Peirce, Semeiotic, and Pragmatism, Indiana University Press, Bloomington, IN.
- Houser, N., Roberts, D.D., and Van Evra, J. (eds., 1997), Studies in the Logic of C.S. Peirce, Indiana University Press, Bloomington, IN.
- Liszka, J.J. (1996), A General Introduction to the Semeiotic of C.S. Peirce, Indiana University Press, Bloomington, IN.
- Misak, C. (ed., 2004), Cambridge Companion to C.S. Peirce, Cambridge University Press.
- Moore, E., and Robin, R. (1964), Studies in the Philosophy of C.S. Peirce, Second Series, University of Massachusetts Press, Amherst, MA.
- Murphey, M. (1961), The Development of Peirce's Thought. Reprinted, Hackett, Indianapolis, IN, 1993.
- Peirce, C.S. (1902), “Parts of Carnegie Application” (L 75), in Carolyn Eisele (ed., 1976), The New Elements of Mathematics by Charles S. Peirce, vol. 4, 13–73. Online.
- Percy, Walker (2000), pp. 271–291 in Signposts in a Strange Land, P. Samway (ed.), Saint Martin's Press.
Resources
Document history
Portions of the above article were adapted from the following sources under the GNU Free Documentation License, under other applicable licenses, or by permission of the copyright holders.
- Charles Sanders Peirce
- Cognitive science
- Computer science
- Differential logic
- Graph theory
- Hermeneutics
- Information systems
- Information theory
- Inquiry
- Intelligent systems
- Knowledge representation
- Logic
- Logical graphs
- Mathematics
- Peirce, Charles Sanders
- Peircean semiotics
- Pragmatics
- Relation theory
- Semantics
- Semiotics
- Syntax