Difference between revisions of "Directory:Jon Awbrey/Papers/Differential Logic and Dynamic Systems 2.0"
Jon Awbrey (talk | contribs) (restore original appendices ... with a slight permutation ...) |
Jon Awbrey (talk | contribs) (update) |
||
| Line 8,908: | Line 8,908: | ||
<br> | <br> | ||
| + | |||
| + | ====Differential Forms==== | ||
| + | |||
| + | The actions of the difference operator <math>\mathrm{D}\!</math> and the tangent operator <math>\mathrm{d}\!</math> on the 16 bivariate propositions are shown in Tables A7 and A8. | ||
| + | |||
| + | Table A7 expands the differential forms that result over a ''logical basis'': | ||
| + | |||
| + | {| align="center" cellpadding="6" style="text-align:center" | ||
| + | | | ||
| + | <math>\{~ \texttt{(}\mathrm{d}x\texttt{)(}\mathrm{d}y\texttt{)}, ~\mathrm{d}x~\texttt{(}\mathrm{d}y\texttt{)}, ~\texttt{(}\mathrm{d}x\texttt{)}~\mathrm{d}y, ~\mathrm{d}x~\mathrm{d}y ~\}.\!</math> | ||
| + | |} | ||
| + | |||
| + | This set consists of the singular propositions in the first order differential variables, indicating mutually exclusive and exhaustive ''cells'' of the tangent universe of discourse. Accordingly, this set of differential propositions may also be referred to as the cell-basis, point-basis, or singular differential basis. In this setting it is frequently convenient to use the following abbreviations: | ||
| + | |||
| + | {| align="center" cellpadding="6" style="text-align:center" | ||
| + | | | ||
| + | <math>\partial x ~=~ \mathrm{d}x~\texttt{(}\mathrm{d}y\texttt{)}\!</math> and <math>\partial y ~=~ \texttt{(}\mathrm{d}x\texttt{)}~\mathrm{d}y.\!</math> | ||
| + | |} | ||
| + | |||
| + | Table A8 expands the differential forms that result over an ''algebraic basis'': | ||
| + | |||
| + | {| align="center" cellpadding="6" style="text-align:center" | ||
| + | | <math>\{~ 1, ~\mathrm{d}x, ~\mathrm{d}y, ~\mathrm{d}x~\mathrm{d}y ~\}.\!</math> | ||
| + | |} | ||
| + | |||
| + | This set consists of the ''positive propositions'' in the first order differential variables, indicating overlapping positive regions of the tangent universe of discourse. Accordingly, this set of differential propositions may also be referred to as the ''positive differential basis''. | ||
| + | |||
| + | ====Table A7. Differential Forms Expanded on a Logical Basis==== | ||
| + | |||
| + | <br> | ||
| + | |||
| + | {| align="center" border="1" cellpadding="10" cellspacing="0" style="text-align:center; width:90%" | ||
| + | |+ style="height:30px" | <math>\text{Table A7.} ~~ \text{Differential Forms Expanded on a Logical Basis}\!</math> | ||
| + | |- style="background:ghostwhite; height:40px" | ||
| + | | | ||
| + | | style="border-right:none" | <math>f\!</math> | ||
| + | | style="border-left:4px double black" | <math>\mathrm{D}f</math> | ||
| + | | <math>\mathrm{d}f</math> | ||
| + | |- | ||
| + | | <math>f_{0}\!</math> | ||
| + | | style="border-right:none" | <math>\texttt{(~)}\!</math> | ||
| + | | style="border-left:4px double black" | <math>0\!</math> | ||
| + | | <math>0\!</math> | ||
| + | |- | ||
| + | | <math>\begin{matrix}f_{1}\\f_{2}\\f_{4}\\f_{8}\end{matrix}</math> | ||
| + | | style="border-right:none" | | ||
| + | <math>\begin{matrix} | ||
| + | \texttt{(} x \texttt{)(} y \texttt{)} | ||
| + | \\ | ||
| + | \texttt{(} x \texttt{)~} y \texttt{~} | ||
| + | \\ | ||
| + | \texttt{~} x \texttt{~(} y \texttt{)} | ||
| + | \\ | ||
| + | \texttt{~} x \texttt{~~} y \texttt{~} | ||
| + | \end{matrix}</math> | ||
| + | | style="border-left:4px double black" | | ||
| + | <math>\begin{matrix} | ||
| + | \texttt{(} y \texttt{)} & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} | ||
| + | & + & | ||
| + | \texttt{(} x \texttt{)} & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y | ||
| + | & + & | ||
| + | \texttt{((} x \texttt{,~} y \texttt{))} & \mathrm{d}x ~ \mathrm{d}y | ||
| + | \\ | ||
| + | y & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} | ||
| + | & + & | ||
| + | \texttt{(} x \texttt{)} & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y | ||
| + | & + & | ||
| + | \texttt{(} x \texttt{,~} y \texttt{)} & \mathrm{d}x ~ \mathrm{d}y | ||
| + | \\ | ||
| + | \texttt{(} y \texttt{)} & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} | ||
| + | & + & | ||
| + | x & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y | ||
| + | & + & | ||
| + | \texttt{(} x \texttt{,~} y \texttt{)} & \mathrm{d}x ~ \mathrm{d}y | ||
| + | \\ | ||
| + | y & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} | ||
| + | & + & | ||
| + | x & \texttt{(} \mathrm{d}x) ~ \mathrm{d}y | ||
| + | & + & | ||
| + | \texttt{((} x \texttt{,~} y \texttt{))} & \mathrm{d}x ~ \mathrm{d}y | ||
| + | \end{matrix}</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \texttt{(} y \texttt{)} ~\partial x | ||
| + | & + & | ||
| + | \texttt{(} x \texttt{)} ~\partial y | ||
| + | \\ | ||
| + | \texttt{~} y \texttt{~} ~\partial x | ||
| + | & + & | ||
| + | \texttt{(} x \texttt{)} ~\partial y | ||
| + | \\ | ||
| + | \texttt{(} y \texttt{)} ~\partial x | ||
| + | & + & | ||
| + | \texttt{~} x \texttt{~} ~\partial y | ||
| + | \\ | ||
| + | \texttt{~} y \texttt{~} ~\partial x | ||
| + | & + & | ||
| + | \texttt{~} x \texttt{~} ~\partial y | ||
| + | \end{matrix}</math> | ||
| + | |- | ||
| + | | <math>\begin{matrix}f_{3}\\f_{12}\end{matrix}</math> | ||
| + | | style="border-right:none" | | ||
| + | <math>\begin{matrix} | ||
| + | \texttt{(} x \texttt{)} | ||
| + | \\ | ||
| + | \texttt{~} x \texttt{~} | ||
| + | \end{matrix}</math> | ||
| + | | style="border-left:4px double black" | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \mathrm{d}x ~ \mathrm{d}y | ||
| + | \\ | ||
| + | \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \mathrm{d}x ~ \mathrm{d}y | ||
| + | \end{matrix}\!</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \partial x | ||
| + | \\ | ||
| + | \partial x | ||
| + | \end{matrix}</math> | ||
| + | |- | ||
| + | | <math>\begin{matrix}f_{6}\\f_{9}\end{matrix}</math> | ||
| + | | style="border-right:none" | | ||
| + | <math>\begin{matrix} | ||
| + | \texttt{~(} x \texttt{,~} y \texttt{)~} | ||
| + | \\ | ||
| + | \texttt{((} x \texttt{,~} y \texttt{))} | ||
| + | \end{matrix}</math> | ||
| + | | style="border-left:4px double black" | | ||
| + | <math>\begin{matrix} | ||
| + | \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y | ||
| + | \\ | ||
| + | \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y | ||
| + | \end{matrix}</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \partial x & + & \partial y | ||
| + | \\ | ||
| + | \partial x & + & \partial y | ||
| + | \end{matrix}</math> | ||
| + | |- | ||
| + | | <math>\begin{matrix}f_{5}\\f_{10}\end{matrix}</math> | ||
| + | | style="border-right:none" | | ||
| + | <math>\begin{matrix} | ||
| + | \texttt{(} y \texttt{)} | ||
| + | \\ | ||
| + | \texttt{~} y \texttt{~} | ||
| + | \end{matrix}</math> | ||
| + | | style="border-left:4px double black" | | ||
| + | <math>\begin{matrix} | ||
| + | \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y & + & \mathrm{d}x ~ \mathrm{d}y | ||
| + | \\ | ||
| + | \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y & + & \mathrm{d}x ~ \mathrm{d}y | ||
| + | \end{matrix}</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \partial y | ||
| + | \\ | ||
| + | \partial y | ||
| + | \end{matrix}</math> | ||
| + | |- | ||
| + | | <math>\begin{matrix}f_{7}\\f_{11}\\f_{13}\\f_{14}\end{matrix}</math> | ||
| + | | style="border-right:none" | | ||
| + | <math>\begin{matrix} | ||
| + | \texttt{(~} x \texttt{~~} y \texttt{~)} | ||
| + | \\ | ||
| + | \texttt{(~} x \texttt{~(} y \texttt{))} | ||
| + | \\ | ||
| + | \texttt{((} x \texttt{)~} y \texttt{~)} | ||
| + | \\ | ||
| + | \texttt{((} x \texttt{)(} y \texttt{))} | ||
| + | \end{matrix}</math> | ||
| + | | style="border-left:4px double black" | | ||
| + | <math>\begin{matrix} | ||
| + | y & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} | ||
| + | & + & | ||
| + | x & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y | ||
| + | & + & | ||
| + | \texttt{((} x \texttt{,~} y \texttt{))} & \mathrm{d}x ~ \mathrm{d}y | ||
| + | \\ | ||
| + | \texttt{(} y \texttt{)} & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} | ||
| + | & + & | ||
| + | x & \texttt{(} \mathrm{d}x) ~ \mathrm{d}y | ||
| + | & + & | ||
| + | \texttt{(} x \texttt{,~} y \texttt{)} & \mathrm{d}x ~ \mathrm{d}y | ||
| + | \\ | ||
| + | y & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} | ||
| + | & + & | ||
| + | \texttt{(} x \texttt{)} & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y | ||
| + | & + & | ||
| + | \texttt{(} x \texttt{,~} y \texttt{)} & \mathrm{d}x ~ \mathrm{d}y | ||
| + | \\ | ||
| + | \texttt{(} y \texttt{)} & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} | ||
| + | & + & | ||
| + | \texttt{(} x \texttt{)} & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y | ||
| + | & + & | ||
| + | \texttt{((} x \texttt{,~} y \texttt{))} & \mathrm{d}x ~ \mathrm{d}y | ||
| + | \end{matrix}</math> | ||
| + | | | ||
| + | <math>\begin{matrix} | ||
| + | \texttt{~} y \texttt{~} ~\partial x | ||
| + | & + & | ||
| + | \texttt{~} x \texttt{~} ~\partial y | ||
| + | \\ | ||
| + | \texttt{(} y \texttt{)} ~\partial x | ||
| + | & + & | ||
| + | \texttt{~} x \texttt{~} ~\partial y | ||
| + | \\ | ||
| + | \texttt{~} y \texttt{~} ~\partial x | ||
| + | & + & | ||
| + | \texttt{(} x \texttt{)} ~\partial y | ||
| + | \\ | ||
| + | \texttt{(} y \texttt{)} ~\partial x | ||
| + | & + & | ||
| + | \texttt{(} x \texttt{)} ~\partial y | ||
| + | \end{matrix}</math> | ||
| + | |- | ||
| + | | <math>f_{15}\!</math> | ||
| + | | style="border-right:none" | <math>\texttt{((~))}\!</math> | ||
| + | | style="border-left:4px double black" | <math>0\!</math> | ||
| + | | <math>0\!</math> | ||
| + | |} | ||
| + | |||
| + | <br> | ||
| + | |||
| + | ====Table A8. Differential Forms Expanded on an Algebraic Basis==== | ||
====Table A12. Detail of Calculation for the Difference Map==== | ====Table A12. Detail of Calculation for the Difference Map==== | ||
Revision as of 14:24, 16 September 2013
Author: Jon Awbrey
|
| Stand and unfold yourself. | Hamlet: Francsico—1.1.2 |
This article develops a differential extension of propositional calculus and applies it to a context of problems arising in dynamic systems. The work pursued here is coordinated with a parallel application that focuses on neural network systems, but the dependencies are arranged to make the present article the main and the more self-contained work, to serve as a conceptual frame and a technical background for the network project.
Review and Transition
This note continues a previous discussion on the problem of dealing with change and diversity in logic-based intelligent systems. It is useful to begin by summarizing essential material from previous reports.
Table 1 outlines a notation for propositional calculus based on two types of logical connectives, both of variable \(k\!\)-ary scope.
- A bracketed list of propositional expressions in the form \(\texttt{(} e_1, e_2, \ldots, e_{k-1}, e_k \texttt{)}\!\) indicates that exactly one of the propositions \(e_1, e_2, \ldots, e_{k-1}, e_k\) is false.
- A concatenation of propositional expressions in the form \(e_1 ~ e_2 ~ \ldots ~ e_{k-1} ~ e_k\) indicates that all of the propositions \(e_1, e_2, \ldots, e_{k-1}, e_k\) are true, in other words, that their logical conjunction is true.
All other propositional connectives can be obtained in a very efficient style of representation through combinations of these two forms. Strictly speaking, the concatenation form is dispensable in light of the bracketed form, but it is convenient to maintain it as an abbreviation of more complicated bracket expressions.
This treatment of propositional logic is derived from the work of C.S. Peirce [P1, P2], who gave this approach an extensive development in his graphical systems of predicate, relational, and modal logic [Rob]. More recently, these ideas were revived and supplemented in an alternative interpretation by George Spencer-Brown [SpB]. Both of these authors used other forms of enclosure where I use parentheses, but the structural topologies of expression and the functional varieties of interpretation are fundamentally the same.
While working with expressions solely in propositional calculus, it is easiest to use plain parentheses for logical connectives. In contexts where parentheses are needed for other purposes “teletype” parentheses \(\texttt{(} \ldots \texttt{)}\!\) or barred parentheses \((\!| \ldots |\!)\) may be used for logical operators.
The briefest expression for logical truth is the empty word, usually denoted by \({}^{\backprime\backprime} \boldsymbol\varepsilon {}^{\prime\prime}\!\) or \({}^{\backprime\backprime} \boldsymbol\lambda {}^{\prime\prime}\!\) in formal languages, where it forms the identity element for concatenation. To make it visible in this text, it may be denoted by the equivalent expression \({}^{\backprime\backprime} \texttt{((~))} {}^{\prime\prime},\!\) or, especially if operating in an algebraic context, by a simple \({}^{\backprime\backprime} 1 {}^{\prime\prime}.\!\) Also when working in an algebraic mode, the plus sign \({}^{\backprime\backprime} + {}^{\prime\prime}\!\) may be used for exclusive disjunction. For example, we have the following paraphrases of algebraic expressions by bracket expressions:
|
\(\begin{matrix} x + y ~=~ \texttt{(} x, y \texttt{)} \\[6pt] x + y + z ~=~ \texttt{((} x, y \texttt{)}, z \texttt{)} ~=~ \texttt{(} x, \texttt{(} y, z \texttt{))} \end{matrix}\) |
It is important to note that the last expressions are not equivalent to the triple bracket \(\texttt{(} x, y, z \texttt{)}.\!\)
| \(\text{Expression}~\!\) | \(\text{Interpretation}\!\) | \(\text{Other Notations}\!\) |
| \(\text{True}\!\) | \(1\!\) | |
| \(\texttt{(~)}\!\) | \(\text{False}\!\) | \(0\!\) |
| \(x\!\) | \(x\!\) | \(x\!\) |
| \(\texttt{(} x \texttt{)}\!\) | \(\text{Not}~ x\!\) |
\(\begin{matrix} x' \\ \tilde{x} \\ \lnot x \end{matrix}\!\) |
| \(x~y~z\!\) | \(x ~\text{and}~ y ~\text{and}~ z\!\) | \(x \land y \land z\!\) |
| \(\texttt{((} x \texttt{)(} y \texttt{)(} z \texttt{))}\!\) | \(x ~\text{or}~ y ~\text{or}~ z\!\) | \(x \lor y \lor z\!\) |
| \(\texttt{(} x ~ \texttt{(} y \texttt{))}\!\) |
\(\begin{matrix} x ~\text{implies}~ y \\ \mathrm{If}~ x ~\text{then}~ y \end{matrix}\) |
\(x \Rightarrow y\!\) |
| \(\texttt{(} x \texttt{,} y \texttt{)}\!\) |
\(\begin{matrix} x ~\text{not equal to}~ y \\ x ~\text{exclusive or}~ y \end{matrix}\) |
\(\begin{matrix} x \ne y \\ x + y \end{matrix}\) |
| \(\texttt{((} x \texttt{,} y \texttt{))}\!\) |
\(\begin{matrix} x ~\text{is equal to}~ y \\ x ~\text{if and only if}~ y \end{matrix}\) |
\(\begin{matrix} x = y \\ x \Leftrightarrow y \end{matrix}\) |
| \(\texttt{(} x \texttt{,} y \texttt{,} z \texttt{)}\!\) |
\(\begin{matrix} \text{Just one of} \\ x, y, z \\ \text{is false}. \end{matrix}\) |
\(\begin{matrix} x'y~z~ & \lor \\ x~y'z~ & \lor \\ x~y~z' & \end{matrix}\) |
| \(\texttt{((} x \texttt{),(} y \texttt{),(} z \texttt{))}\!\) |
\(\begin{matrix} \text{Just one of} \\ x, y, z \\ \text{is true}. \\ & \\ \text{Partition all} \\ \text{into}~ x, y, z. \end{matrix}\) |
\(\begin{matrix} x~y'z' & \lor \\ x'y~z' & \lor \\ x'y'z~ & \end{matrix}\) |
|
\(\begin{matrix} \texttt{((} x \texttt{,} y \texttt{),} z \texttt{)} \\ & \\ \texttt{(} x \texttt{,(} y \texttt{,} z \texttt{))} \end{matrix}\!\) |
\(\begin{matrix} \text{Oddly many of} \\ x, y, z \\ \text{are true}. \end{matrix}\!\) |
\(x + y + z\!\)
\(\begin{matrix} x~y~z~ & \lor \\ x~y'z' & \lor \\ x'y~z' & \lor \\ x'y'z~ & \end{matrix}\!\) |
| \(\texttt{(} w \texttt{,(} x \texttt{),(} y \texttt{),(} z \texttt{))}\!\) |
\(\begin{matrix} \text{Partition}~ w \\ \text{into}~ x, y, z. \\ & \\ \text{Genus}~ w ~\text{comprises} \\ \text{species}~ x, y, z. \end{matrix}\) |
\(\begin{matrix} w'x'y'z' & \lor \\ w~x~y'z' & \lor \\ w~x'y~z' & \lor \\ w~x'y'z~ & \end{matrix}\) |
Note. The usage that one often sees, of a plus sign "\(+\!\)" to represent inclusive disjunction, and the reference to this operation as boolean addition, is a misnomer on at least two counts. Boole used the plus sign to represent exclusive disjunction (at any rate, an operation of aggregation restricted in its logical interpretation to cases where the represented sets are disjoint (Boole, 32)), as any mathematician with a sensitivity to the ring and field properties of algebra would do:
The expression \(x + y\!\) seems indeed uninterpretable, unless it be assumed that the things represented by \(x\!\) and the things represented by \(y\!\) are entirely separate; that they embrace no individuals in common. (Boole, 66).
It was only later that Peirce and Jevons treated inclusive disjunction as a fundamental operation, but these authors, with a respect for the algebraic properties that were already associated with the plus sign, used a variety of other symbols for inclusive disjunction (Sty, 177, 189). It seems to have been Schröder who later reassigned the plus sign to inclusive disjunction (Sty, 208). Additional information, discussion, and references can be found in (Boole) and (Sty, 177–263). Aside from these historical points, which never really count against a current practice that has gained a life of its own, this usage does have a further disadvantage of cutting or confounding the lines of communication between algebra and logic. For this reason, it will be avoided here.
A Functional Conception of Propositional Calculus
|
Out of the dimness opposite equals advance . . . . | |
| — Walt Whitman, Leaves of Grass, [Whi, 28] |
In the general case, we start with a set of logical features \(\{a_1, \ldots, a_n\}\) that represent properties of objects or propositions about the world. In concrete examples the features \(\{a_i\!\}\) commonly appear as capital letters from an alphabet like \(\{A, B, C, \ldots\}\) or as meaningful words from a linguistic vocabulary of codes. This language can be drawn from any sources, whether natural, technical, or artificial in character and interpretation. In the application to dynamic systems we tend to use the letters \(\{x_1, \ldots, x_n\}\) as our coordinate propositions, and to interpret them as denoting properties of a system's state, that is, as propositions about its location in configuration space. Because I have to consider non-deterministic systems from the outset, I often use the word state in a loose sense, to denote the position or configuration component of a contemplated state vector, whether or not it ever gets a deterministic completion.
The set of logical features \(\{a_1, \ldots, a_n\}\) provides a basis for generating an \(n\!\)-dimensional universe of discourse that I denote as \([a_1, \ldots, a_n].\) It is useful to consider each universe of discourse as a unified categorical object that incorporates both the set of points \(\langle a_1, \ldots, a_n \rangle\) and the set of propositions \(f : \langle a_1, \ldots, a_n \rangle \to \mathbb{B}\) that are implicit with the ordinary picture of a venn diagram on \(n\!\) features. Thus, we may regard the universe of discourse \([a_1, \ldots, a_n]\) as an ordered pair having the type \((\mathbb{B}^n, (\mathbb{B}^n \to \mathbb{B}),\) and we may abbreviate this last type designation as \(\mathbb{B}^n\ +\!\to \mathbb{B},\) or even more succinctly as \([\mathbb{B}^n].\) (Used this way, the angle brackets \(\langle\ldots\rangle\) are referred to as generator brackets.)
Table 2 exhibits the scheme of notation I use to formalize the domain of propositional calculus, corresponding to the logical content of truth tables and venn diagrams. Although it overworks the square brackets a bit, I also use either one of the equivalent notations \([n]\!\) or \(\mathbf{n}\) to denote the data type of a finite set on \(n\!\) elements.
| \(\text{Symbol}\!\) | \(\text{Notation}\!\) | \(\text{Description}\!\) | \(\text{Type}\!\) |
| \(\mathfrak{A}\!\) | \(\{ {}^{\backprime\backprime} a_1 {}^{\prime\prime}, \ldots, {}^{\backprime\backprime} a_n {}^{\prime\prime} \}\!\) | \(\text{Alphabet}\!\) | \([n] = \mathbf{n}\!\) |
| \(\mathcal{A}\!\) | \(\{ a_1, \ldots, a_n \}\!\) | \(\text{Basis}\!\) | \([n] = \mathbf{n}\!\) |
| \(A_i\!\) | \(\{ (a_i), a_i \}\!\) | \(\text{Dimension}~ i\!\) | \(\mathbb{B}\!\) |
| \(A\!\) |
\(\begin{matrix} \langle \mathcal{A} \rangle \\[2pt] \langle a_1, \ldots, a_n \rangle \\[2pt] \{ (a_1, \ldots, a_n) \} \\[2pt] A_1 \times \ldots \times A_n \\[2pt] \textstyle \prod_{i=1}^n A_i \end{matrix}\) |
\(\begin{matrix} \text{Set of cells}, \\[2pt] \text{coordinate tuples}, \\[2pt] \text{points, or vectors} \\[2pt] \text{in the universe} \\[2pt] \text{of discourse} \end{matrix}\) |
\(\mathbb{B}^n\!\) |
| \(A^*\!\) | \((\mathrm{hom} : A \to \mathbb{B})\!\) | \(\text{Linear functions}\!\) | \((\mathbb{B}^n)^* \cong \mathbb{B}^n\!\) |
| \(A^\uparrow\!\) | \((A \to \mathbb{B})\!\) | \(\text{Boolean functions}\!\) | \(\mathbb{B}^n \to \mathbb{B}\!\) |
| \(A^\bullet\!\) |
\(\begin{matrix} [\mathcal{A}] \\[2pt] (A, A^\uparrow) \\[2pt] (A ~+\!\to \mathbb{B}) \\[2pt] (A, (A \to \mathbb{B})) \\[2pt] [a_1, \ldots, a_n] \end{matrix}\) |
\(\begin{matrix} \text{Universe of discourse} \\[2pt] \text{based on the features} \\[2pt] \{ a_1, \ldots, a_n \} \end{matrix}\) |
\(\begin{matrix} (\mathbb{B}^n, (\mathbb{B}^n \to \mathbb{B})) \\[2pt] (\mathbb{B}^n ~+\!\to \mathbb{B}) \\[2pt] [\mathbb{B}^n] \end{matrix}\) |
Qualitative Logic and Quantitative Analogy
|
Logical, however, is used in a third sense, which is at once more vital and more practical; to denote, namely, the systematic care, negative and positive, taken to safeguard reflection so that it may yield the best results under the given conditions. |
||
| — John Dewey, How We Think, [Dew, 56] | ||
These concepts and notations may now be explained in greater detail. In order to begin as simply as possible, let us distinguish two levels of analysis and set out initially on the easier path. On the first level of analysis we take spaces like \(\mathbb{B},\) \(\mathbb{B}^n,\) and \((\mathbb{B}^n \to \mathbb{B})\) at face value and treat them as the primary objects of interest. On the second level of analysis we use these spaces as coordinate charts for talking about points and functions in more fundamental spaces.
A pair of spaces, of types \(\mathbb{B}^n\) and \((\mathbb{B}^n \to \mathbb{B}),\) give typical expression to everything that we commonly associate with the ordinary picture of a venn diagram. The dimension, \(n,\!\) counts the number of "circles" or simple closed curves that are inscribed in the universe of discourse, corresponding to its relevant logical features or basic propositions. Elements of type \(\mathbb{B}^n\) correspond to what are often called propositional interpretations in logic, that is, the different assignments of truth values to sentence letters. Relative to a given universe of discourse, these interpretations are visualized as its cells, in other words, the smallest enclosed areas or undivided regions of the venn diagram. The functions \(f : \mathbb{B}^n \to \mathbb{B}\) correspond to the different ways of shading the venn diagram to indicate arbitrary propositions, regions, or sets. Regions included under a shading indicate the models, and regions excluded represent the non-models of a proposition. To recognize and formalize the natural cohesion of these two layers of concepts into a single universe of discourse, we introduce the type notations \([\mathbb{B}^n] = \mathbb{B}^n\ +\!\to \mathbb{B}\) to stand for the pair of types \((\mathbb{B}^n, (\mathbb{B}^n \to \mathbb{B})).\) The resulting "stereotype" serves to frame the universe of discourse as a unified categorical object, and makes it subject to prescribed sets of evaluations and transformations (categorical morphisms or arrows) that affect the universe of discourse as an integrated whole.
Most of the time we can serve the algebraic, geometric, and logical interests of our study without worrying about their occasional conflicts and incidental divergences. The conventions and definitions already set down will continue to cover most of the algebraic and functional aspects of our discussion, but to handle the logical and qualitative aspects we will need to add a few more. In general, abstract sets may be denoted by gothic, greek, or script capital variants of \(A, B, C,\!\) and so on, with their elements being denoted by a corresponding set of subscripted letters in plain lower case, for example, \(\mathcal{A} = \{a_i\}.\) Most of the time, a set such as \(\mathcal{A} = \{a_i\}\!\) will be employed as the alphabet of a formal language. These alphabet letters serve to name the logical features (properties or propositions) that generate a particular universe of discourse. When we want to discuss the particular features of a universe of discourse, beyond the abstract designation of a type like \((\mathbb{B}^n\ +\!\to \mathbb{B}),\) then we may use the following notations. If \(\mathcal{A} = \{a_1, \ldots, a_n\}\) is an alphabet of logical features, then \(A = \langle \mathcal{A} \rangle = \langle a_1, \ldots, a_n \rangle\) is the set of interpretations, \(A^\uparrow = (A \to \mathbb{B})\) is the set of propositions, and \(A^\bullet = [\mathcal{A}] = [a_1, \ldots, a_n]\) is the combination of these interpretations and propositions into the universe of discourse that is based on the features \(\{a_1, \ldots, a_n\}.\)
As always, especially in concrete examples, these rules may be dropped whenever necessary, reverting to a free assortment of feature labels. However, when we need to talk about the logical aspects of a space that is already named as a vector space, it will be necessary to make special provisions. At any rate, these elaborations can be deferred until actually needed.
Philosophy of Notation : Formal Terms and Flexible Types
|
Where number is irrelevant, regimented mathematical technique has hitherto tended to be lacking. Thus it is that the progress of natural science has depended so largely upon the discernment of measurable quantity of one sort or another. |
||
| — W.V. Quine, Mathematical Logic, [Qui, 7] | ||
For much of our discussion propositions and boolean functions are treated as the same formal objects, or as different interpretations of the same formal calculus. This rule of interpretation has exceptions, though. There is a distinctively logical interest in the use of propositional calculus that is not exhausted by its functional interpretation. It is part of our task in this study to deal with these uniquely logical characteristics as they present themselves both in our subject matter and in our formal calculus. Just to provide a hint of what's at stake: In logic, as opposed to the more imaginative realms of mathematics, we consider it a good thing to always know what we are talking about. Where mathematics encourages tolerance for uninterpreted symbols as intermediate terms, logic exerts a keener effort to interpret directly each oblique carrier of meaning, no matter how slight, and to unfold the complicities of every indirection in the flow of information. Translated into functional terms, this means that we want to maintain a continual, immediate, and persistent sense of both the converse relation \(f^{-1} \subseteq \mathbb{B} \times \mathbb{B}^n,\) or what is the same thing, \(f^{-1} : \mathbb{B} \to \mathcal{P}(\mathbb{B}^n),\) and the fibers or inverse images \(f^{-1}(0)\!\) and \(f^{-1}(1),\!\) associated with each boolean function \(f : \mathbb{B}^n \to \mathbb{B}\) that we use. In practical terms, the desired implementation of a propositional interpreter should incorporate our intuitive recognition that the induced partition of the functional domain into level sets \(f^{-1}(b),\!\) for \(b \in \mathbb{B},\) is part and parcel of understanding the denotative uses of each propositional function \(f.\!\)
Special Classes of Propositions
It is important to remember that the coordinate propositions \(\{a_i\},\!\) besides being projection maps \(a_i : \mathbb{B}^n \to \mathbb{B},\) are propositions on an equal footing with all others, even though employed as a basis in a particular moment. This set of \(n\!\) propositions may sometimes be referred to as the basic propositions, the coordinate propositions, or the simple propositions that found a universe of discourse. Either one of the equivalent notations, \(\{a_i : \mathbb{B}^n \to \mathbb{B}\}\) or \((\mathbb{B}^n \xrightarrow{i} \mathbb{B}),\) may be used to indicate the adoption of the propositions \(a_i\!\) as a basis for describing a universe of discourse.
Among the \(2^{2^n}\) propositions in \([a_1, \ldots, a_n]\) are several families of \(2^n\!\) propositions each that take on special forms with respect to the basis \(\{ a_1, \ldots, a_n \}.\) Three of these families are especially prominent in the present context, the linear, the positive, and the singular propositions. Each family is naturally parameterized by the coordinate \(n\!\)-tuples in \(\mathbb{B}^n\) and falls into \(n + 1\!\) ranks, with a binomial coefficient \(\tbinom{n}{k}\) giving the number of propositions that have rank or weight \(k.\!\)
-
The linear propositions, \(\{ \ell : \mathbb{B}^n \to \mathbb{B} \} = (\mathbb{B}^n \xrightarrow{\ell} \mathbb{B}),\!\) may be written as sums:
\(\sum_{i=1}^n e_i ~=~ e_1 + \ldots + e_n ~\text{where}~ \left\{\begin{matrix} e_i = a_i \\ \text{or} \\ e_i = 0 \end{matrix}\right\} ~\text{for}~ i = 1 ~\text{to}~ n.\!\)
-
The positive propositions, \(\{ p : \mathbb{B}^n \to \mathbb{B} \} = (\mathbb{B}^n \xrightarrow{p} \mathbb{B}),\!\) may be written as products:
\(\prod_{i=1}^n e_i ~=~ e_1 \cdot \ldots \cdot e_n ~\text{where}~ \left\{\begin{matrix} e_i = a_i \\ \text{or} \\ e_i = 1 \end{matrix}\right\} ~\text{for}~ i = 1 ~\text{to}~ n.\!\)
-
The singular propositions, \(\{ \mathbf{x} : \mathbb{B}^n \to \mathbb{B} \} = (\mathbb{B}^n \xrightarrow{s} \mathbb{B}),\!\) may be written as products:
\(\prod_{i=1}^n e_i ~=~ e_1 \cdot \ldots \cdot e_n ~\text{where}~ \left\{\begin{matrix} e_i = a_i \\ \text{or} \\ e_i = \texttt{(} a_i \texttt{)} \end{matrix}\right\} ~\text{for}~ i = 1 ~\text{to}~ n.\!\)
In each case the rank \(k\!\) ranges from \(0\!\) to \(n\!\) and counts the number of positive appearances of the coordinate propositions \(a_1, \ldots, a_n\!\) in the resulting expression. For example, for \({n = 3},\!\) the linear proposition of rank \(0\!\) is \(0,\!\) the positive proposition of rank \(0\!\) is \(1,\!\) and the singular proposition of rank \(0\!\) is \(\texttt{(} a_1 \texttt{)(} a_2 \texttt{)(} a_3\texttt{)}.\!\)
The basic propositions \(a_i : \mathbb{B}^n \to \mathbb{B}\) are both linear and positive. So these two kinds of propositions, the linear and the positive, may be viewed as two different ways of generalizing the class of basic propositions.
Linear propositions and positive propositions are generated by taking boolean sums and products, respectively, over selected subsets of basic propositions, so both families of propositions are parameterized by the powerset \(\mathcal{P}(\mathcal{I}),\) that is, the set of all subsets \(J\!\) of the basic index set \(\mathcal{I} = \{1, \ldots, n\}.\!\)
Let us define \(\mathcal{A}_J\) as the subset of \(\mathcal{A}\) that is given by \(\{a_i : i \in J\}.\!\) Then we may comprehend the action of the linear and the positive propositions in the following terms:
- The linear proposition \(\ell_J : \mathbb{B}^n \to \mathbb{B}\) evaluates each cell \(\mathbf{x}\) of \(\mathbb{B}^n\) by looking at the coefficients of \(\mathbf{x}\) with respect to the features that \(\ell_J\) "likes", namely those in \(\mathcal{A}_J,\) and then adds them up in \(\mathbb{B}.\) Thus, \(\ell_J(\mathbf{x})\) computes the parity of the number of features that \(\mathbf{x}\) has in \(\mathcal{A}_J,\) yielding one for odd and zero for even. Expressed in this idiom, \(\ell_J(\mathbf{x}) = 1\) says that \(\mathbf{x}\) seems odd (or oddly true) to \(\mathcal{A}_J,\) whereas \(\ell_J(\mathbf{x}) = 0\) says that \(\mathbf{x}\) seems even (or evenly true) to \(\mathcal{A}_J,\) so long as we recall that zero times is evenly often, too.
- The positive proposition \(p_J : \mathbb{B}^n \to \mathbb{B}\) evaluates each cell \(\mathbf{x}\) of \(\mathbb{B}^n\) by looking at the coefficients of \(\mathbf{x}\) with regard to the features that \(p_J\!\) "likes", namely those in \(\mathcal{A}_J,\) and then takes their product in \(\mathbb{B}.\) Thus, \(p_J(\mathbf{x})\) assesses the unanimity of the multitude of features that \(\mathbf{x}\) has in \(\mathcal{A}_J,\) yielding one for all and aught for else. In these consensual or contractual terms, \(p_J(\mathbf{x}) = 1\) means that \(\mathbf{x}\) is AOK or congruent with all of the conditions of \(\mathcal{A}_J,\) while \(p_J(\mathbf{x}) = 0\) means that \(\mathbf{x}\) defaults or dissents from some condition of \(\mathcal{A}_J.\)
Basis Relativity and Type Ambiguity
Finally, two things are important to keep in mind with regard to the simplicity, linearity, positivity, and singularity of propositions.
First, all of these properties are relative to a particular basis. For example, a singular proposition with respect to a basis \(\mathcal{A}\) will not remain singular if \(\mathcal{A}\) is extended by a number of new and independent features. Even if we stick to the original set of pairwise options \(\{a_i\} \cup \{ \texttt{(} a_i \texttt{)} \}\!\) to select a new basis, the sets of linear and positive propositions are determined by the choice of simple propositions, and this determination is tantamount to the conventional choice of a cell as origin.
Second, the singular propositions \(\mathbb{B}^n \xrightarrow{\mathbf{x}} \mathbb{B},\) picking out as they do a single cell or a coordinate tuple \(\mathbf{x}\) of \(\mathbb{B}^n,\) become the carriers or the vehicles of a certain type-ambiguity that vacillates between the dual forms \(\mathbb{B}^n\) and \((\mathbb{B}^n \xrightarrow{\mathbf{x}} \mathbb{B})\) and infects the whole hierarchy of types built on them. In other words, the terms that signify the interpretations \(\mathbf{x} : \mathbb{B}^n\) and the singular propositions \(\mathbf{x} : \mathbb{B}^n \xrightarrow{\mathbf{x}} \mathbb{B}\) are fully equivalent in information, and this means that every token of the type \(\mathbb{B}^n\) can be reinterpreted as an appearance of the subtype \(\mathbb{B}^n \xrightarrow{\mathbf{x}} \mathbb{B}.\) And vice versa, the two types can be exchanged with each other everywhere that they turn up. In practical terms, this allows the use of singular propositions as a way of denoting points, forming an alternative to coordinate tuples.
For example, relative to the universe of discourse \([a_1, a_2, a_3]\!\) the singular proposition \(a_1 a_2 a_3 : \mathbb{B}^3 \xrightarrow{s} \mathbb{B}\) could be explicitly retyped as \(a_1 a_2 a_3 : \mathbb{B}^3\) to indicate the point \((1, 1, 1)\!\) but in most cases the proper interpretation could be gathered from context. Both notations remain dependent on a particular basis, but the code that is generated under the singular option has the advantage in its self-commenting features, in other words, it constantly reminds us of its basis in the process of denoting points. When the time comes to put a multiplicity of different bases into play, and to search for objects and properties that remain invariant under the transformations between them, this infinitesimal potential advantage may well evolve into an overwhelming practical necessity.
The Analogy Between Real and Boolean Types
|
Measurement consists in correlating our subject matter with the series of real numbers; and such correlations are desirable because, once they are set up, all the well-worked theory of numerical mathematics lies ready at hand as a tool for our further reasoning. |
||
| — W.V. Quine, Mathematical Logic, [Qui, 7] | ||
There are two further reasons why it useful to spend time on a careful treatment of types, and they both have to do with our being able to take full computational advantage of certain dimensions of flexibility in the types that apply to terms. First, the domains of differential geometry and logic programming are connected by analogies between real and boolean types of the same pattern. Second, the types involved in these patterns have important isomorphisms connecting them that apply on both the real and the boolean sides of the picture.
Amazingly enough, these isomorphisms are themselves schematized by the axioms and theorems of propositional logic. This fact is known as the propositions as types analogy or the Curry–Howard isomorphism [How]. In another formulation it says that terms are to types as proofs are to propositions. See [LaS, 42–46] and [SeH] for a good discussion and further references. To anticipate the bearing of these issues on our immediate topic, Table 3 sketches a partial overview of the Real to Boolean analogy that may serve to illustrate the paradigm in question.
| \(\text{Real Domain} ~ \mathbb{R}\!\) | \(\longleftrightarrow\!\) | \(\text{Boolean Domain} ~ \mathbb{B}\!\) |
| \(\mathbb{R}^n\!\) | \(\text{Basic Space}\!\) | \(\mathbb{B}^n\!\) |
| \(\mathbb{R}^n \to \mathbb{R}\!\) | \(\text{Function Space}\!\) | \(\mathbb{B}^n \to \mathbb{B}\!\) |
| \((\mathbb{R}^n \to \mathbb{R}) \to \mathbb{R}\!\) | \(\text{Tangent Vector}\!\) | \((\mathbb{B}^n \to \mathbb{B}) \to \mathbb{B}\!\) |
| \(\mathbb{R}^n \to ((\mathbb{R}^n \to \mathbb{R}) \to \mathbb{R})\!\) | \(\text{Vector Field}\!\) | \(\mathbb{B}^n \to ((\mathbb{B}^n \to \mathbb{B}) \to \mathbb{B})\!\) |
| \((\mathbb{R}^n \times (\mathbb{R}^n \to \mathbb{R})) \to \mathbb{R}\!\) | " | \((\mathbb{B}^n \times (\mathbb{B}^n \to \mathbb{B})) \to \mathbb{B}\!\) |
| \(((\mathbb{R}^n \to \mathbb{R}) \times \mathbb{R}^n) \to \mathbb{R}\!\) | " | \(((\mathbb{B}^n \to \mathbb{B}) \times \mathbb{B}^n) \to \mathbb{B}\!\) |
| \((\mathbb{R}^n \to \mathbb{R}) \to (\mathbb{R}^n \to \mathbb{R})~\!\) | \(\text{Derivation}\!\) | \((\mathbb{B}^n \to \mathbb{B}) \to (\mathbb{B}^n \to \mathbb{B})\!\) |
| \(\mathbb{R}^n \to \mathbb{R}^m\!\) | \(\begin{matrix}\text{Basic}\\[2pt]\text{Transformation}\end{matrix}\) | \(\mathbb{B}^n \to \mathbb{B}^m\!\) |
| \((\mathbb{R}^n \to \mathbb{R}) \to (\mathbb{R}^m \to \mathbb{R})\!\) | \(\begin{matrix}\text{Function}\\[2pt]\text{Transformation}\end{matrix}\) | \((\mathbb{B}^n \to \mathbb{B}) \to (\mathbb{B}^m \to \mathbb{B})\!\) |
The Table exhibits a sample of likely parallels between the real and boolean domains. The central column gives a selection of terminology that is borrowed from differential geometry and extended in its meaning to the logical side of the Table. These are the varieties of spaces that come up when we turn to analyzing the dynamics of processes that pursue their courses through the states of an arbitrary space \(X.\!\) Moreover, when it becomes necessary to approach situations of overwhelming dynamic complexity in a succession of qualitative reaches, then the methods of logic that are afforded by the boolean domains, with their declarative means of synthesis and deductive modes of analysis, supply a natural battery of tools for the task.
It is usually expedient to take these spaces two at a time, in dual pairs of the form \(X\!\) and \((X \to \mathbb{K}).\) In general, one creates pairs of type schemas by replacing any space \(X\!\) with its dual \((X \to \mathbb{K}),\) for example, pairing the type \(X \to Y\) with the type \((X \to \mathbb{K}) \to (Y \to \mathbb{K}),\) and \(X \times Y\) with \((X \to \mathbb{K}) \times (Y \to \mathbb{K}).\) The word dual is used here in its broader sense to mean all of the functionals, not just the linear ones. Given any function \(f : X \to \mathbb{K},\) the converse or inverse relation corresponding to \(f\!\) is denoted \(f^{-1},\!\) and the subsets of \(X\!\) that are defined by \(f^{-1}(k),\!\) taken over \(k\!\) in \(\mathbb{K},\) are called the fibers or the level sets of the function \(f.\!\)
Theory of Control and Control of Theory
|
You will hardly know who I am or what I mean, | |
| — Walt Whitman, Leaves of Grass, [Whi, 88] |
In the boolean context a function \(f : X \to \mathbb{B}\) is tantamount to a proposition about elements of \(X,\!\) and the elements of \(X\!\) constitute the interpretations of that proposition. The fiber \(f^{-1}(1)\!\) comprises the set of models of \(f,\!\) or examples of elements in \(X\!\) satisfying the proposition \(f.\!\) The fiber \(f^{-1}(0)\!\) collects the complementary set of anti-models, or the exceptions to the proposition \(f\!\) that exist in \(X.\!\) Of course, the space of functions \((X \to \mathbb{B})\!\) is isomorphic to the set of all subsets of \(X,\!\) called the power set of \(X,\!\) and often denoted \(\mathcal{P}(X)\) or \(2^X.\!\)
The operation of replacing \(X\!\) by \((X \to \mathbb{B})\!\) in a type schema corresponds to a certain shift of attitude towards the space \(X,\!\) in which one passes from a focus on the ostensibly individual elements of \(X\!\) to a concern with the states of information and uncertainty that one possesses about objects and situations in \(X.\!\) The conceptual obstacles in the path of this transition can be smoothed over by using singular functions \((\mathbb{B}^n \xrightarrow{\mathbf{x}} \mathbb{B})\) as stepping stones. First of all, it's an easy step from an element \(\mathbf{x}\) of type \(\mathbb{B}^n\) to the equivalent information of a singular proposition \(\mathbf{x} : X \xrightarrow{s} \mathbb{B}, \) and then only a small jump of generalization remains to reach the type of an arbitrary proposition \(f : X \to \mathbb{B},\) perhaps understood to indicate a relaxed constraint on the singularity of points or a neighborhood circumscribing the original \(\mathbf{x}.\) This is frequently a useful transformation, communicating between the objective and the intentional perspectives, in spite perhaps of the open objection that this distinction is transient in the mean time and ultimately superficial.
It is hoped that this measure of flexibility, allowing us to stretch a point into a proposition, can be useful in the examination of inquiry driven systems, where the differences between empirical, intentional, and theoretical propositions constitute the discrepancies and the distributions that drive experimental activity. I can give this model of inquiry a cybernetic cast by realizing that theory change and theory evolution, as well as the choice and the evaluation of experiments, are actions that are taken by a system or its agent in response to the differences that are detected between observational contents and theoretical coverage.
All of the above notwithstanding, there are several points that distinguish these two tasks, namely, the theory of control and the control of theory, features that are often obscured by too much precipitation in the quickness with which we understand their similarities. In the control of uncertainty through inquiry, some of the actuators that we need to be concerned with are axiom changers and theory modifiers, operators with the power to compile and to revise the theories that generate expectations and predictions, effectors that form and edit our grammars for the languages of observational data, and agencies that rework the proposed model to fit the actual sequences of events and the realized relationships of values that are observed in the environment. Moreover, when steps must be taken to carry out an experimental action, there must be something about the particular shape of our uncertainty that guides us in choosing what directions to explore, and this impression is more than likely influenced by previous accumulations of experience. Thus it must be anticipated that much of what goes into scientific progress, or any sustainable effort toward a goal of knowledge, is necessarily predicated on long term observation and modal expectations, not only on the more local or short term prediction and correction.
Propositions as Types and Higher Order Types
The types collected in Table 3 (repeated below) serve to illustrate the themes of higher order propositional expressions and the propositions as types (PAT) analogy.
| \(\text{Real Domain} ~ \mathbb{R}\!\) | \(\longleftrightarrow\!\) | \(\text{Boolean Domain} ~ \mathbb{B}\!\) |
| \(\mathbb{R}^n\!\) | \(\text{Basic Space}\!\) | \(\mathbb{B}^n\!\) |
| \(\mathbb{R}^n \to \mathbb{R}\!\) | \(\text{Function Space}\!\) | \(\mathbb{B}^n \to \mathbb{B}\!\) |
| \((\mathbb{R}^n \to \mathbb{R}) \to \mathbb{R}\!\) | \(\text{Tangent Vector}\!\) | \((\mathbb{B}^n \to \mathbb{B}) \to \mathbb{B}\!\) |
| \(\mathbb{R}^n \to ((\mathbb{R}^n \to \mathbb{R}) \to \mathbb{R})\!\) | \(\text{Vector Field}\!\) | \(\mathbb{B}^n \to ((\mathbb{B}^n \to \mathbb{B}) \to \mathbb{B})\!\) |
| \((\mathbb{R}^n \times (\mathbb{R}^n \to \mathbb{R})) \to \mathbb{R}\!\) | " | \((\mathbb{B}^n \times (\mathbb{B}^n \to \mathbb{B})) \to \mathbb{B}\!\) |
| \(((\mathbb{R}^n \to \mathbb{R}) \times \mathbb{R}^n) \to \mathbb{R}\!\) | " | \(((\mathbb{B}^n \to \mathbb{B}) \times \mathbb{B}^n) \to \mathbb{B}\!\) |
| \((\mathbb{R}^n \to \mathbb{R}) \to (\mathbb{R}^n \to \mathbb{R})~\!\) | \(\text{Derivation}\!\) | \((\mathbb{B}^n \to \mathbb{B}) \to (\mathbb{B}^n \to \mathbb{B})\!\) |
| \(\mathbb{R}^n \to \mathbb{R}^m\!\) | \(\begin{matrix}\text{Basic}\\[2pt]\text{Transformation}\end{matrix}\) | \(\mathbb{B}^n \to \mathbb{B}^m\!\) |
| \((\mathbb{R}^n \to \mathbb{R}) \to (\mathbb{R}^m \to \mathbb{R})\!\) | \(\begin{matrix}\text{Function}\\[2pt]\text{Transformation}\end{matrix}\) | \((\mathbb{B}^n \to \mathbb{B}) \to (\mathbb{B}^m \to \mathbb{B})\!\) |
First, observe that the type of a tangent vector at a point, also known as a directional derivative at that point, has the form \((\mathbb{K}^n \to \mathbb{K}) \to \mathbb{K},\) where \(\mathbb{K}\) is the chosen ground field, in the present case either \(\mathbb{R}\) or \(\mathbb{B}.\) At a point in a space of type \(\mathbb{K}^n,\) a directional derivative operator \(\vartheta\!\) takes a function on that space, an \(f\!\) of type \((\mathbb{K}^n \to \mathbb{K}),\) and maps it to a ground field value of type \(\mathbb{K}.\) This value is known as the derivative of \(f\!\) in the direction \(\vartheta\!\) [Che46, 76–77]. In the boolean case \(\vartheta : (\mathbb{B}^n \to \mathbb{B}) \to \mathbb{B}\) has the form of a proposition about propositions, in other words, a proposition of the next higher type.
Next, by way of illustrating the propositions as types idea, consider a proposition of the form \(X \Rightarrow (Y \Rightarrow Z).\) One knows from propositional calculus that this is logically equivalent to a proposition of the form \((X \land Y) \Rightarrow Z.\) But this equivalence should remind us of the functional isomorphism that exists between a construction of the type \(X \to (Y \to Z)\) and a construction of the type \((X \times Y) \to Z.\) The propositions as types analogy permits us to take a functional type like this and, under the right conditions, replace the functional arrows “\(\to~\!\)” and products “\(\times\!\)” with the respective logical arrows “\(\Rightarrow\!\)” and products “\(\land\!\)”. Accordingly, viewing the result as a proposition, we can employ axioms and theorems of propositional calculus to suggest appropriate isomorphisms among the categorical and functional constructions.
Finally, examine the middle four rows of Table 3. These display a series of isomorphic types that stretch from the categories that are labeled Vector Field to those that are labeled Derivation. A vector field, also known as an infinitesimal transformation, associates a tangent vector at a point with each point of a space. In symbols, a vector field is a function of the form \(\textstyle \xi : X \to \bigcup_{x \in X} \xi_x\!\) that assigns to each point \(x\!\) of the space \(X\!\) a tangent vector to \(X\!\) at that point, namely, the tangent vector \(\xi_x\!\) [Che46, 82–83]. If \(X\!\) is of the type \(\mathbb{K}^n,\) then \(\xi\!\) is of the type \(\mathbb{K}^n \to ((\mathbb{K}^n \to \mathbb{K}) \to \mathbb{K}).\) This has the pattern \(X \to (Y \to Z),\) with \(X = \mathbb{K}^n,\) \(Y = (\mathbb{K}^n \to \mathbb{K}),\) and \(Z = \mathbb{K}.\)
Applying the propositions as types analogy, one can follow this pattern through a series of metamorphoses from the type of a vector field to the type of a derivation, as traced out in Table 4. Observe how the function \(f : X \to \mathbb{K},\) associated with the place of \(Y\!\) in the pattern, moves through its paces from the second to the first position. In this way, the vector field \(\xi,\!\) initially viewed as attaching each tangent vector \(\xi_x\!\) to the site \(x\!\) where it acts in \(X,\!\) now comes to be seen as acting on each scalar potential \(f : X \to \mathbb{K}\) like a generalized species of differentiation, producing another function \(\xi f : X \to \mathbb{K}\) of the same type.
| \(\text{Pattern}\!\) | \(\text{Construct}\!\) | \(\text{Instance}\!\) |
| \(X \to (Y \to Z)\!\) | \(\text{Vector Field}\!\) | \(\mathbb{K}^n \to ((\mathbb{K}^n \to \mathbb{K}) \to \mathbb{K})\!\) |
| \((X \times Y) \to Z\!\) | \(\Uparrow\!\) | \((\mathbb{K}^n \times (\mathbb{K}^n \to \mathbb{K})) \to \mathbb{K}\!\) |
| \((Y \times X) \to Z\!\) | \(\Downarrow\!\) | \(((\mathbb{K}^n \to \mathbb{K}) \times \mathbb{K}^n) \to \mathbb{K}\!\) |
| \(Y \to (X \to Z)\!\) | \(\text{Derivation}\!\) | \((\mathbb{K}^n \to \mathbb{K}) \to (\mathbb{K}^n \to \mathbb{K})\!\) |
Reality at the Threshold of Logic
|
But no science can rest entirely on measurement, and many scientific investigations are quite out of reach of that device. To the scientist longing for non-quantitative techniques, then, mathematical logic brings hope. |
||
| — W.V. Quine, Mathematical Logic, [Qui, 7] | ||
Table 5 accumulates an array of notation that I hope will not be too distracting. Some of it is rarely needed, but has been filled in for the sake of completeness. Its purpose is simple, to give literal expression to the visual intuitions that come with venn diagrams, and to help build a bridge between our qualitative and quantitative outlooks on dynamic systems.
| \(\text{Linear Space}\!\) | \(\text{Liminal Space}\!\) | \(\text{Logical Space}\!\) |
| \(\begin{matrix}\mathcal{X} & = & \{ x_1, \ldots, x_n \}\end{matrix}\) | \(\begin{matrix}\underline\mathcal{X} & = & \{ \underline{x}_1, \ldots, \underline{x}_n \}\end{matrix}\) | \(\begin{matrix}\mathcal{A} & = & \{ a_1, \ldots, a_n \}\end{matrix}\) |
|
\(\begin{matrix} X_i & = & \langle x_i \rangle \\ & \cong & \mathbb{K} \end{matrix}\) |
\(\begin{matrix} \underline{X}_i & = & \{ (\underline{x}_i), \underline{x}_i \} \\ & \cong & \mathbb{B} \end{matrix}\) |
\(\begin{matrix} A_i & = & \{ (a_i), a_i \} \\ & \cong & \mathbb{B} \end{matrix}\) |
|
\(\begin{matrix} X \\ = & \langle \mathcal{X} \rangle \\ = & \langle x_1, \ldots, x_n \rangle \\ = & X_1 \times \ldots \times X_n \\ = & \prod_{i=1}^n X_i \\ \cong & \mathbb{K}^n \end{matrix}\) |
\(\begin{matrix} \underline{X} \\ = & \langle \underline\mathcal{X} \rangle \\ = & \langle \underline{x}_1, \ldots, \underline{x}_n \rangle \\ = & \underline{X}_1 \times \ldots \times \underline{X}_n \\ = & \prod_{i=1}^n \underline{X}_i \\ \cong & \mathbb{B}^n \end{matrix}\) |
\(\begin{matrix} A \\ = & \langle \mathcal{A} \rangle \\ = & \langle a_1, \ldots, a_n \rangle \\ = & A_1 \times \ldots \times A_n \\ = & \prod_{i=1}^n A_i \\ \cong & \mathbb{B}^n \end{matrix}\) |
|
\(\begin{matrix} X^* & = & (\ell : X \to \mathbb{K}) \\ & \cong & \mathbb{K}^n \end{matrix}\) |
\(\begin{matrix} \underline{X}^* & = & (\ell : \underline{X} \to \mathbb{B}) \\ & \cong & \mathbb{B}^n \end{matrix}\) |
\(\begin{matrix} A^* & = & (\ell : A \to \mathbb{B}) \\ & \cong & \mathbb{B}^n \end{matrix}\) |
|
\(\begin{matrix} X^\uparrow & = & (X \to \mathbb{K}) \\ & \cong & (\mathbb{K}^n \to \mathbb{K}) \end{matrix}\) |
\(\begin{matrix} \underline{X}^\uparrow & = & (\underline{X} \to \mathbb{B}) \\ & \cong & (\mathbb{B}^n \to \mathbb{B}) \end{matrix}\) |
\(\begin{matrix} A^\uparrow & = & (A \to \mathbb{B}) \\ & \cong & (\mathbb{B}^n \to \mathbb{B}) \end{matrix}\) |
|
\(\begin{matrix} X^\bullet \\ = & [\mathcal{X}] \\ = & [x_1, \ldots, x_n] \\ = & (X, X^\uparrow) \\ = & (X ~+\!\to \mathbb{K}) \\ = & (X, (X \to \mathbb{K})) \\ \cong & (\mathbb{K}^n, (\mathbb{K}^n \to \mathbb{K})) \\ = & (\mathbb{K}^n ~+\!\to \mathbb{K}) \\ = & [\mathbb{K}^n] \end{matrix}\) |
\(\begin{matrix} \underline{X}^\bullet \\ = & [\underline\mathcal{X}] \\ = & [\underline{x}_1, \ldots, \underline{x}_n] \\ = & (\underline{X}, \underline{X}^\uparrow) \\ = & (\underline{X} ~+\!\to \mathbb{B}) \\ = & (\underline{X}, (\underline{X} \to \mathbb{B})) \\ \cong & (\mathbb{B}^n, (\mathbb{B}^n \to \mathbb{B})) \\ = & (\mathbb{B}^n ~+\!\to \mathbb{B}) \\ = & [\mathbb{B}^n] \end{matrix}\) |
\(\begin{matrix} A^\bullet \\ = & [\mathcal{A}] \\ = & [a_1, \ldots, a_n] \\ = & (A, A^\uparrow) \\ = & (A ~+\!\to \mathbb{B}) \\ = & (A, (A \to \mathbb{B})) \\ \cong & (\mathbb{B}^n, (\mathbb{B}^n \to \mathbb{B})) \\ = & (\mathbb{B}^n ~+\!\to \mathbb{B}) \\ = & [\mathbb{B}^n] \end{matrix}\) |
The left side of the Table collects mostly standard notation for an \(n\!\)-dimensional vector space over a field \(\mathbb{K}.\) The right side of the table repeats the first elements of a notation that I sketched above, to be used in further developments of propositional calculus. (I plan to use this notation in the logical analysis of neural network systems.) The middle column of the table is designed as a transitional step from the case of an arbitrary field \(\mathbb{K},\) with a special interest in the continuous line \(\mathbb{R},\) to the qualitative and discrete situations that are instanced and typified by \(\mathbb{B}.\)
I now proceed to explain these concepts in more detail. The most important ideas developed in Table 5 are these:
- The idea of a universe of discourse, which includes both a space of points and a space of maps on those points.
- The idea of passing from a more complex universe to a simpler universe by a process of thresholding each dimension of variation down to a single bit of information.
For the sake of concreteness, let us suppose that we start with a continuous \(n\!\)-dimensional vector space like \(X = \langle x_1, \ldots, x_n \rangle \cong \mathbb{R}^n.\) The coordinate system \(\mathcal{X} = \{x_i\}\) is a set of maps \(x_i : \mathbb{R}^n \to \mathbb{R},\) also known as the coordinate projections. Given a "dataset" of points \(\mathbf{x}\) in \(\mathbb{R}^n,\) there are numerous ways of sensibly reducing the data down to one bit for each dimension. One strategy that is general enough for our present purposes is as follows. For each \(i\!\) we choose an \(n\!\)-ary relation \(L_i\!\) on \(\mathbb{R}^n,\) that is, a subset of \(\mathbb{R}^n,\) and then we define the \(i^\mathrm{th}\!\) threshold map, or limen \(\underline{x}_i\) as follows:
| \(\underline{x}_i : \mathbb{R}^n \to \mathbb{B}\ \text{such that:}\!\) |
|
\(\begin{matrix} \underline{x}_i(\mathbf{x}) = 1 & \text{if} & \mathbf{x} \in L_i, \\[4pt] \underline{x}_i(\mathbf{x}) = 0 & \text{if} & \mathbf{x} \not\in L_i. \end{matrix}\) |
In other notations that are sometimes used, the operator \(\chi (\ldots)\) or the corner brackets \(\lceil\ldots\rceil\) can be used to denote a characteristic function, that is, a mapping from statements to their truth values in \(\mathbb{B}.\) Finally, it is not uncommon to use the name of the relation itself as a predicate that maps \(n\!\)-tuples into truth values. Thus we have the following notational variants of the above definition:
|
\(\begin{matrix} \underline{x}_i (\mathbf{x}) & = & \chi (\mathbf{x} \in L_i) & = & \lceil \mathbf{x} \in L_i \rceil & = & L_i (\mathbf{x}). \end{matrix}\) |
Notice that, as defined here, there need be no actual relation between the \(n\!\)-dimensional subsets \(\{L_i\}\!\) and the coordinate axes corresponding to \(\{x_i\},\!\) aside from the circumstance that the two sets have the same cardinality. In concrete cases, though, one usually has some reason for associating these "volumes" with these "lines", for instance, \(L_i\!\) is bounded by some hyperplane that intersects the \(i^\text{th}\!\) axis at a unique threshold value \(r_i \in \mathbb{R}.\!\) Often, the hyperplane is chosen normal to the axis. In recognition of this motive, let us make the following convention. When the set \(L_i\!\) has points on the \(i^\text{th}\!\) axis, that is, points of the form \((0, \ldots, 0, r_i, 0, \ldots, 0)\) where only the \(x_i\!\) coordinate is possibly non-zero, we may pick any one of these coordinate values as a parametric index of the relation. In this case we say that the indexing is real, otherwise the indexing is imaginary. For a knowledge based system \(X,\!\) this should serve once again to mark the distinction between acquaintance and opinion.
States of knowledge about the location of a system or about the distribution of a population of systems in a state space \(X = \mathbb{R}^n\) can now be expressed by taking the set \(\underline\mathcal{X} = \{\underline{x}_i\}\) as a basis of logical features. In picturesque terms, one may think of the underscore and the subscript as combining to form a subtextual spelling for the \(i^\text{th}\!\) threshold map. This can help to remind us that the threshold operator \((\underline{~})_i\) acts on \(\mathbf{x}\) by setting up a kind of a “hurdle” for it. In this interpretation the coordinate proposition \(\underline{x}_i\) asserts that the representative point \(\mathbf{x}\) resides above the \(i^\mathrm{th}\!\) threshold.
Primitive assertions of the form \(\underline{x}_i (\mathbf{x})\) may then be negated and joined by means of propositional connectives in the usual ways to provide information about the state \(\mathbf{x}\) of a contemplated system or a statistical ensemble of systems. Parentheses \(\texttt{(} \ldots \texttt{)}\!\) may be used to indicate logical negation. Eventually one discovers the usefulness of the \(k\!\)-ary just one false operators of the form \(\texttt{(} a_1 \texttt{,} \ldots \texttt{,} a_k \texttt{)},\!\) as treated in earlier reports. This much tackle generates a space of points (cells, interpretations), \(\underline{X} \cong \mathbb{B}^n,\) and a space of functions (regions, propositions), \(\underline{X}^\uparrow \cong (\mathbb{B}^n \to \mathbb{B}).\) Together these form a new universe of discourse \(\underline{X}^\bullet\) of the type \((\mathbb{B}^n, (\mathbb{B}^n \to \mathbb{B})),\) which we may abbreviate as \(\mathbb{B}^n\ +\!\to \mathbb{B}\) or most succinctly as \([\mathbb{B}^n].\)
The square brackets have been chosen to recall the rectangular frame of a venn diagram. In thinking about a universe of discourse it is a good idea to keep this picture in mind, graphically illustrating the links among the elementary cells \(\underline\mathbf{x},\) the defining features \(\underline{x}_i,\) and the potential shadings \(f : \underline{X} \to \mathbb{B}\) all at the same time, not to mention the arbitrariness of the way we choose to inscribe our distinctions in the medium of a continuous space.
Finally, let \(X^*\!\) denote the space of linear functions, \((\ell : X \to \mathbb{K}),\) which has in the finite case the same dimensionality as \(X,\!\) and let the same notation be extended across the Table.
We have just gone through a lot of work, apparently doing nothing more substantial than spinning a complex spell of notational devices through a labyrinth of baffled spaces and baffling maps. The reason for doing this was to bind together and to constitute the intuitive concept of a universe of discourse into a coherent categorical object, the kind of thing, once grasped, that can be turned over in the mind and considered in all its manifold changes and facets. The effort invested in these preliminary measures is intended to pay off later, when we need to consider the state transformations and the time evolution of neural network systems.
Tables of Propositional Forms
|
To the scientist longing for non-quantitative techniques, then, mathematical logic brings hope. It provides explicit techniques for manipulating the most basic ingredients of discourse. |
||
| — W.V. Quine, Mathematical Logic, [Qui, 7–8] | ||
To prepare for the next phase of discussion, Tables 6 and 7 collect and summarize all of the propositional forms on one and two variables. These propositional forms are represented over bases of boolean variables as complete sets of boolean-valued functions. Adjacent to their names and specifications are listed what are roughly the simplest expressions in the cactus language, the particular syntax for propositional calculus that I use in formal and computational contexts. For the sake of orientation, the English paraphrases and the more common notations are listed in the last two columns. As simple and circumscribed as these low-dimensional universes may appear to be, a careful exploration of their differential extensions will involve us in complexities sufficient to demand our attention for some time to come.
Propositional forms on one variable correspond to boolean functions \(f : \mathbb{B}^1 \to \mathbb{B}.\) In Table 6 these functions are listed in a variant form of truth table, one in which the axes of the usual arrangement are rotated through a right angle. Each function \(f_i\!\) is indexed by the string of values that it takes on the points of the universe \(X^\bullet = [x] \cong \mathbb{B}^1.\) The binary index generated in this way is converted to its decimal equivalent and these are used as conventional names for the \(f_i,\!\) as shown in the first column of the Table. In their own right the \(2^1\!\) points of the universe \(X^\bullet\) are coordinated as a space of type \(\mathbb{B}^1,\) this in light of the universe \(X^\bullet\) being a functional domain where the coordinate projection \(x\!\) takes on its values in \(\mathbb{B}.\)
| \(\begin{matrix}\mathcal{L}_1 \\ \text{Decimal}\end{matrix}\) | \(\begin{matrix}\mathcal{L}_2 \\ \text{Binary}\end{matrix}\) | \(\begin{matrix}\mathcal{L}_3 \\ \text{Vector}\end{matrix}\) | \(\begin{matrix}\mathcal{L}_4 \\ \text{Cactus}\end{matrix}\) | \(\begin{matrix}\mathcal{L}_5 \\ \text{English}\end{matrix}\) | \(\begin{matrix}\mathcal{L}_6 \\ \text{Ordinary}\end{matrix}\) |
| \(x\colon\!\) | \(1~0\!\) | ||||
| \(f_0\!\) | \(f_{00}\!\) | \(0~0\!\) | \(\texttt{(~)}\!\) | \(\text{false}\!\) | \(0\!\) |
| \(f_1\!\) | \(f_{01}\!\) | \(0~1\!\) | \(\texttt{(} x \texttt{)}\!\) | \(\text{not}~ x\!\) | \(\lnot x\!\) |
| \(f_2\!\) | \(f_{10}\!\) | \(1~0\!\) | \(x\!\) | \(x\!\) | \(x\!\) |
| \(f_3\!\) | \(f_{11}\!\) | \(1~1\!\) | \(\texttt{((~))}\!\) | \(\text{true}\!\) | \(1\!\) |
Propositional forms on two variables correspond to boolean functions \(f : \mathbb{B}^2 \to \mathbb{B}.\) In Table 7 each function \(f_i\!\) is indexed by the values that it takes on the points of the universe \(X^\bullet = [x, y] \cong \mathbb{B}^2.\) Converting the binary index thus generated to a decimal equivalent, we obtain the functional nicknames that are listed in the first column. The \(2^2\!\) points of the universe \(X^\bullet\) are coordinated as a space of type \(\mathbb{B}^2,\) as indicated under the heading of the Table, where the coordinate projections \(x\!\) and \(y\!\) run through the various combinations of their values in \(\mathbb{B}.\)
| \(\begin{matrix}\mathcal{L}_1 \\ \text{Decimal}\end{matrix}\!\) | \(\begin{matrix}\mathcal{L}_2 \\ \text{Binary}\end{matrix}\!\) | \(\begin{matrix}\mathcal{L}_3 \\ \text{Vector}\end{matrix}\!\) | \(\begin{matrix}\mathcal{L}_4 \\ \text{Cactus}\end{matrix}\!\) | \(\begin{matrix}\mathcal{L}_5 \\ \text{English}\end{matrix}\!\) | \(\begin{matrix}\mathcal{L}_6 \\ \text{Ordinary}\end{matrix}\!\) |
| \(x\colon\!\) | \(1~1~0~0\!\) | ||||
| \(y\colon\!\) | \(1~0~1~0\!\) | ||||
|
\(\begin{matrix} f_{0} \\[4pt] f_{1} \\[4pt] f_{2} \\[4pt] f_{3} \\[4pt] f_{4} \\[4pt] f_{5} \\[4pt] f_{6} \\[4pt] f_{7} \end{matrix}\!\) |
\(\begin{matrix} f_{0000} \\[4pt] f_{0001} \\[4pt] f_{0010} \\[4pt] f_{0011} \\[4pt] f_{0100} \\[4pt] f_{0101} \\[4pt] f_{0110} \\[4pt] f_{0111} \end{matrix}\!\) |
\(\begin{matrix} 0~0~0~0 \\[4pt] 0~0~0~1 \\[4pt] 0~0~1~0 \\[4pt] 0~0~1~1 \\[4pt] 0~1~0~0 \\[4pt] 0~1~0~1 \\[4pt] 0~1~1~0 \\[4pt] 0~1~1~1 \end{matrix}\!\) |
\(\begin{matrix} \texttt{(~)} \\[4pt] \texttt{(} x \texttt{)(} y \texttt{)} \\[4pt] \texttt{(} x \texttt{)} ~ y ~ \\[4pt] \texttt{(} x \texttt{)} \\[4pt] ~ x ~ \texttt{(} y \texttt{)} \\[4pt] \texttt{(} y \texttt{)} \\[4pt] \texttt{(} x \texttt{,} ~ y \texttt{)} \\[4pt] \texttt{(} x ~ y \texttt{)} \end{matrix}\!\) |
\(\begin{matrix} \text{false} \\[4pt] \text{neither}~ x ~\text{nor}~ y \\[4pt] y ~\text{without}~ x \\[4pt] \text{not}~ x \\[4pt] x ~\text{without}~ y \\[4pt] \text{not}~ y \\[4pt] x ~\text{not equal to}~ y \\[4pt] \text{not both}~ x ~\text{and}~ y \end{matrix}\!\) |
\(\begin{matrix} 0 \\[4pt] \lnot x \land \lnot y \\[4pt] \lnot x \land y \\[4pt] \lnot x \\[4pt] x \land \lnot y \\[4pt] \lnot y \\[4pt] x \ne y \\[4pt] \lnot x \lor \lnot y \end{matrix}\!\) |
|
\(\begin{matrix} f_{8} \\[4pt] f_{9} \\[4pt] f_{10} \\[4pt] f_{11} \\[4pt] f_{12} \\[4pt] f_{13} \\[4pt] f_{14} \\[4pt] f_{15} \end{matrix}\!\) |
\(\begin{matrix} f_{1000} \\[4pt] f_{1001} \\[4pt] f_{1010} \\[4pt] f_{1011} \\[4pt] f_{1100} \\[4pt] f_{1101} \\[4pt] f_{1110} \\[4pt] f_{1111} \end{matrix}\!\) |
\(\begin{matrix} 1~0~0~0 \\[4pt] 1~0~0~1 \\[4pt] 1~0~1~0 \\[4pt] 1~0~1~1 \\[4pt] 1~1~0~0 \\[4pt] 1~1~0~1 \\[4pt] 1~1~1~0 \\[4pt] 1~1~1~1 \end{matrix}\!\) |
\(\begin{matrix} x ~ y \\[4pt] \texttt{((} x \texttt{,} ~ y \texttt{))} \\[4pt] y \\[4pt] \texttt{(} x ~ \texttt{(} y \texttt{))} \\[4pt] x \\[4pt] \texttt{((} x \texttt{)} ~ y \texttt{)} \\[4pt] \texttt{((} x \texttt{)(} y \texttt{))} \\[4pt] \texttt{((~))} \end{matrix}\!\) |
\(\begin{matrix} x ~\text{and}~ y \\[4pt] x ~\text{equal to}~ y \\[4pt] y \\[4pt] \text{not}~ x ~\text{without}~ y \\[4pt] x \\[4pt] \text{not}~ y ~\text{without}~ x \\[4pt] x ~\text{or}~ y \\[4pt] \text{true} \end{matrix}\!\) |
\(\begin{matrix} x \land y \\[4pt] x = y \\[4pt] y \\[4pt] x \Rightarrow y \\[4pt] x \\[4pt] x \Leftarrow y \\[4pt] x \lor y \\[4pt] 1 \end{matrix}\!\) |
| \(\begin{matrix}\mathcal{L}_1 \\ \text{Decimal}\end{matrix}\) | \(\begin{matrix}\mathcal{L}_2 \\ \text{Binary}\end{matrix}\) | \(\begin{matrix}\mathcal{L}_3 \\ \text{Vector}\end{matrix}\) | \(\begin{matrix}\mathcal{L}_4 \\ \text{Cactus}\end{matrix}\) | \(\begin{matrix}\mathcal{L}_5 \\ \text{English}\end{matrix}\) | \(\begin{matrix}\mathcal{L}_6 \\ \text{Ordinary}\end{matrix}\) |
| \(x\colon\!\) | \(1~1~0~0\!\) | ||||
| \(y\colon\!\) | \(1~0~1~0\!\) | ||||
| \(f_{0}\!\) | \(f_{0000}\!\) | \(0~0~0~0\!\) | \(\texttt{(~)}\!\) | \(\text{false}\!\) | \(0\!\) |
|
\(\begin{matrix} f_{1} \\[4pt] f_{2} \\[4pt] f_{4} \\[4pt] f_{8} \end{matrix}\!\) |
\(\begin{matrix} f_{0001} \\[4pt] f_{0010} \\[4pt] f_{0100} \\[4pt] f_{1000} \end{matrix}\!\) |
\(\begin{matrix} 0~0~0~1 \\[4pt] 0~0~1~0 \\[4pt] 0~1~0~0 \\[4pt] 1~0~0~0 \end{matrix}\!\) |
\(\begin{matrix} \texttt{(} x \texttt{)(} y \texttt{)} \\[4pt] \texttt{(} x \texttt{)} ~ y ~ \\[4pt] ~ x ~ \texttt{(} y \texttt{)} \\[4pt] ~ x ~~ y ~ \end{matrix}\!\) |
\(\begin{matrix} \text{neither}~ x ~\text{nor}~ y \\[4pt] y ~\text{without}~ x \\[4pt] x ~\text{without}~ y \\[4pt] x ~\text{and}~ y \end{matrix}\!\) |
\(\begin{matrix} \lnot x \land \lnot y \\[4pt] \lnot x \land y \\[4pt] x \land \lnot y \\[4pt] x \land y \end{matrix}\!\) |
|
\(\begin{matrix} f_{3} \\[4pt] f_{12} \end{matrix}\!\) |
\(\begin{matrix} f_{0011} \\[4pt] f_{1100} \end{matrix}\!\) |
\(\begin{matrix} 0~0~1~1 \\[4pt] 1~1~0~0 \end{matrix}\!\) |
\(\begin{matrix} \texttt{(} x \texttt{)} \\[4pt] x \end{matrix}\!\) |
\(\begin{matrix} \text{not}~ x \\[4pt] x \end{matrix}\!\) |
\(\begin{matrix} \lnot x \\[4pt] x \end{matrix}\!\) |
|
\(\begin{matrix} f_{6} \\[4pt] f_{9} \end{matrix}\!\) |
\(\begin{matrix} f_{0110} \\[4pt] f_{1001} \end{matrix}\!\) |
\(\begin{matrix} 0~1~1~0 \\[4pt] 1~0~0~1 \end{matrix}\!\) |
\(\begin{matrix} \texttt{(} x \texttt{,} y \texttt{)} \\[4pt] \texttt{((} x \texttt{,} y \texttt{))} \end{matrix}\!\) |
\(\begin{matrix} x ~\text{not equal to}~ y \\[4pt] x ~\text{equal to}~ y \end{matrix}\!\) |
\(\begin{matrix} x \ne y \\[4pt] x = y \end{matrix}\!\) |
|
\(\begin{matrix} f_{5} \\[4pt] f_{10} \end{matrix}\!\) |
\(\begin{matrix} f_{0101} \\[4pt] f_{1010} \end{matrix}\!\) |
\(\begin{matrix} 0~1~0~1 \\[4pt] 1~0~1~0 \end{matrix}\!\) |
\(\begin{matrix} \texttt{(} y \texttt{)} \\[4pt] y \end{matrix}\!\) |
\(\begin{matrix} \text{not}~ y \\[4pt] y \end{matrix}\) |
\(\begin{matrix} \lnot y \\[4pt] y \end{matrix}\!\) |
|
\(\begin{matrix} f_{7} \\[4pt] f_{11} \\[4pt] f_{13} \\[4pt] f_{14} \end{matrix}\!\) |
\(\begin{matrix} f_{0111} \\[4pt] f_{1011} \\[4pt] f_{1101} \\[4pt] f_{1110} \end{matrix}\!\) |
\(\begin{matrix} 0~1~1~1 \\[4pt] 1~0~1~1 \\[4pt] 1~1~0~1 \\[4pt] 1~1~1~0 \end{matrix}\!\) |
\(\begin{matrix} \texttt{(} ~ x ~~ y ~ \texttt{)} \\[4pt] \texttt{(} ~ x ~ \texttt{(} y \texttt{))} \\[4pt] \texttt{((} x \texttt{)} ~ y ~ \texttt{)} \\[4pt] \texttt{((} x \texttt{)(} y \texttt{))} \end{matrix}\!\) |
\(\begin{matrix} \text{not both}~ x ~\text{and}~ y \\[4pt] \text{not}~ x ~\text{without}~ y \\[4pt] \text{not}~ y ~\text{without}~ x \\[4pt] x ~\text{or}~ y \end{matrix}\) |
\(\begin{matrix} \lnot x \lor \lnot y \\[4pt] x \Rightarrow y \\[4pt] x \Leftarrow y \\[4pt] x \lor y \end{matrix}\!\) |
| \(f_{15}\!\) | \(f_{1111}\!\) | \(1~1~1~1\!\) | \(\texttt{((~))}\!\) | \(\text{true}\!\) | \(1\!\) |
A Differential Extension of Propositional Calculus
|
Fire over water: | |
| — I Ching, Hexagram 64, [Wil, 249] |
This much preparation is enough to begin introducing my subject, if I excuse myself from giving full arguments for my definitional choices until some later stage. I am trying to develop a differential theory of qualitative equations that parallels the application of differential geometry to dynamic systems. The idea of a tangent vector is key to this work and a major goal is to find the right logical analogues of tangent spaces, bundles, and functors. The strategy is taken of looking for the simplest versions of these constructions that can be discovered within the realm of propositional calculus, so long as they serve to fill out the general theme.
Differential Propositions : The Qualitative Analogues of Differential Equations
In order to define the differential extension of a universe of discourse \([\mathcal{A}],\) the initial alphabet \(\mathcal{A}\) must be extended to include a collection of symbols for differential features, or basic changes that are capable of occurring in \([\mathcal{A}].\) Intuitively, these symbols may be construed as denoting primitive features of change, qualitative attributes of motion, or propositions about how things or points in the universe may be changing or moving with respect to the features that are noted in the initial alphabet.
Therefore, let us define the corresponding differential alphabet or tangent alphabet as \(\mathrm{d}\mathcal{A}\!\) \(=\!\) \(\{\mathrm{d}a_1, \ldots, \mathrm{d}a_n\},\) in principle just an arbitrary alphabet of symbols, disjoint from the initial alphabet \(\mathcal{A}\!\) \(=\!\) \(\{ a_1, \ldots, a_n \},\!\) that is intended to be interpreted in the way just indicated. It only remains to be understood that the precise interpretation of the symbols in \(\mathrm{d}\mathcal{A}\!\) is often conceived to be changeable from point to point of the underlying space \(A.\!\) Indeed, for all we know, the state space \(A\!\) might well be the state space of a language interpreter, one that is concerned, among other things, with the idiomatic meanings of the dialect generated by \(\mathcal{A}\) and \(\mathrm{d}\mathcal{A}.\!\)
The tangent space to \(A\!\) at one of its points \(x,\!\) sometimes written \(\mathrm{T}_x(A),\) takes the form \(\mathrm{d}A\) \(=\!\) \(\langle \mathrm{d}\mathcal{A} \rangle\) \(=\!\) \(\langle \mathrm{d}a_1, \ldots, \mathrm{d}a_n \rangle.\!\) Strictly speaking, the name cotangent space is probably more correct for this construction, but the fact that we take up spaces and their duals in pairs to form our universes of discourse allows our language to be pliable here.
Proceeding as we did with the base space \(A,\!\) the tangent space \(\mathrm{d}A\) at a point of \(A\!\) can be analyzed as a product of distinct and independent factors:
| \(\mathrm{d}A ~=~ \prod_{i=1}^n \mathrm{d}A_i ~=~ \mathrm{d}A_1 \times \ldots \times \mathrm{d}A_n.\!\) |
Here, \(\mathrm{d}A_i\!\) is a set of two differential propositions, \(\mathrm{d}A_i = \{ (\mathrm{d}a_i), \mathrm{d}a_i \},\!\) where \(\texttt{(} \mathrm{d}a_i \texttt{)}\!\) is a proposition with the logical value of \(\text{not} ~ \mathrm{d}a_i.\!\) Each component \(\mathrm{d}A_i\!\) has the type \(\mathbb{B},\!\) operating under the ordered correspondence \(\{ \texttt{(} \mathrm{d}a_i \texttt{)}, \mathrm{d}a_i \} \cong \{ 0, 1 \}.\!\) However, clarity is often served by acknowledging this differential usage with a superficially distinct type \(\mathbb{D},\!\) whose intension may be indicated as follows:
| \(\mathbb{D} = \{ \texttt{(} \mathrm{d}a_i \texttt{)}, \mathrm{d}a_i \} = \{ \text{same}, \text{different} \} = \{ \text{stay}, \text{change} \} = \{ \text{stop}, \text{step} \}.\!\) |
Viewed within a coordinate representation, spaces of type \(\mathbb{B}^n\!\) and \(\mathbb{D}^n\!\) may appear to be identical sets of binary vectors, but taking a view at this level of abstraction would be like ignoring the qualitative units and the diverse dimensions that distinguish position and momentum, or the different roles of quantity and impulse.
An Interlude on the Path
|
There would have been no beginnings: instead, speech would proceed from me, while I stood in its path – a slender gap – the point of its possible disappearance. |
||
| — Michel Foucault, The Discourse on Language, [Fou, 215] | ||
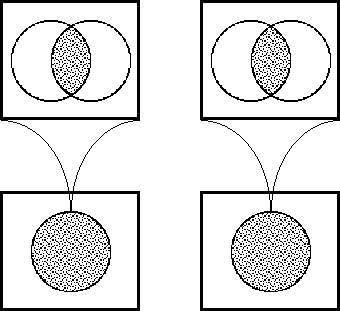
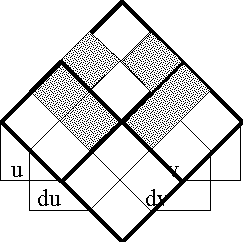
A sense of the relation between \(\mathbb{B}\) and \(\mathbb{D}\) may be obtained by considering the path classifier (or the equivalence class of curves) approach to tangent vectors. Consider a universe \([\mathcal{X}].\!\) Given the boolean value system, a path in the space \(X = \langle \mathcal{X} \rangle\) is a map \(q : \mathbb{B} \to X.\) In this context the set of paths \((\mathbb{B} \to X)\) is isomorphic to the cartesian square \(X^2 = X \times X,\) or the set of ordered pairs chosen from \(X.\!\)
We may analyze \(X^2 = \{ (u, v) : u, v \in X \}\) into two parts, specifically, the ordered pairs \((u, v)\!\) that lie on and off the diagonal:
| \(\begin{matrix}X^2 & = & \{ (u, v) : u = v \} & \cup & \{ (u, v) : u \ne v \}.\end{matrix}\) |
This partition may also be expressed in the following symbolic form:
| \(\begin{matrix}X^2 & \cong & \operatorname{diag} (X) & + & 2 \binom{X}{2}.\end{matrix}\) |
The separate terms of this formula are defined as follows:
| \(\begin{matrix}\operatorname{diag} (X) & = & \{ (x, x) : x \in X \}.\end{matrix}\!\) |
| \(\begin{matrix}\binom{X}{k} & = & X ~\text{choose}~ k & = & \{ k\text{-sets from}~ X \}.\end{matrix}\!\) |
Thus we have:
| \(\begin{matrix}\binom{X}{2} & = & \{ \{ u, v \} : u, v \in X \}.\end{matrix}\) |
We may now use the features in \(\mathrm{d}\mathcal{X} = \{ \mathrm{d}x_i \} = \{ \mathrm{d}x_1, \ldots, \mathrm{d}x_n \}\) to classify the paths of \((\mathbb{B} \to X)\) by way of the pairs in \(X^2.\!\) If \(X \cong \mathbb{B}^n,\) then a path \(q\!\) in \(X\!\) has the following form:
|
\(\begin{matrix} q : (\mathbb{B} \to \mathbb{B}^n) & \cong & \mathbb{B}^n \times \mathbb{B}^n & \cong & \mathbb{B}^{2n} & \cong & (\mathbb{B}^2)^n. \end{matrix}\) |
Intuitively, we want to map this \((\mathbb{B}^2)^n\) onto \(\mathbb{D}^n\) by mapping each component \(\mathbb{B}^2\) onto a copy of \(\mathbb{D}.\) But in the presenting context \({}^{\backprime\backprime} \mathbb{D} {}^{\prime\prime}\) is just a name associated with, or an incidental quality attributed to, coefficient values in \(\mathbb{B}\) when they are attached to features in \(\mathrm{d}\mathcal{X}.\)
Taking these intentions into account, define \(\mathrm{d}x_i : X^2 \to \mathbb{B}\) in the following manner:
|
\(\begin{array}{lcrcl} \mathrm{d}x_i(u, v) & = & \texttt{(} ~ x_i(u) & \texttt{,} & x_i(v) ~ \texttt{)} \\ & = & x_i(u) & + & x_i(v) \\ & = & x_i(v) & - & x_i(u). \end{array}\) |
In the above transcription, the operator bracket of the form \(\texttt{(} \ldots \texttt{,} \ldots \texttt{)}\!\) is a cactus lobe, in general signifying that just one of the arguments listed is false. In the case of two arguments this is the same thing as saying that the arguments are not equal. The plus sign signifies boolean addition, in the sense of addition in \(\mathrm{GF}(2),\) and thus means the same thing in this context as the minus sign, in the sense of adding the additive inverse.
The above definition of \(\mathrm{d}x_i : X^2 \to \mathbb{B}\) is equivalent to defining \(\mathrm{d}x_i : (\mathbb{B} \to X) \to \mathbb{B}\!\) in the following way:
|
\(\begin{array}{lcrcl} \mathrm{d}x_i (q) & = & \texttt{(} ~ x_i(q_0) & \texttt{,} & x_i(q_1) ~ \texttt{)} \\ & = & x_i(q_0) & + & x_i(q_1) \\ & = & x_i(q_1) & - & x_i(q_0). \end{array}\) |
In this definition \(q_b = q(b),\!\) for each \(b\!\) in \(\mathbb{B}.\) Thus, the proposition \(\mathrm{d}x_i\) is true of the path \(q = (u, v)\!\) exactly if the terms of \(q,\!\) the endpoints \(u\!\) and \(v,\!\) lie on different sides of the question \(x_i.\!\)
The language of features in \(\langle \mathrm{d}\mathcal{X} \rangle,\) indeed the whole calculus of propositions in \([\mathrm{d}\mathcal{X}],\) may now be used to classify paths and sets of paths. In other words, the paths can be taken as models of the propositions \(g : \mathrm{d}X \to \mathbb{B}.\) For example, the paths corresponding to \(\mathrm{diag}(X)\) fall under the description \(\texttt{(} \mathrm{d}x_1 \texttt{)} \cdots \texttt{(} \mathrm{d}x_n \texttt{)},\!\) which says that nothing changes against the backdrop of the coordinate frame \(\{ x_1, \ldots, x_n \}.\!\)
Finally, a few words of explanation may be in order. If this concept of a path appears to be described in a roundabout fashion, it is because I am trying to avoid using any assumption of vector space properties for the space \(X\!\) that contains its range. In many ways the treatment is still unsatisfactory, but improvements will have to wait for the introduction of substitution operators acting on singular propositions.
The Extended Universe of Discourse
|
At the moment of speaking, I would like to have perceived a nameless voice, long preceding me, leaving me merely to enmesh myself in it, taking up its cadence, and to lodge myself, when no one was looking, in its interstices as if it had paused an instant, in suspense, to beckon to me. |
||
| — Michel Foucault, The Discourse on Language, [Fou, 215] | ||
Next we define the extended alphabet or bundled alphabet \(\mathrm{E}\mathcal{A}\) as follows:
|
\(\begin{array}{lclcl} \mathrm{E}\mathcal{A} & = & \mathcal{A} \cup \mathrm{d}\mathcal{A} & = & \{ a_1, \ldots, a_n, \mathrm{d}a_1, \ldots, \mathrm{d}a_n \}. \end{array}\) |
This supplies enough material to construct the differential extension \(\mathrm{E}A,\) or the tangent bundle over the initial space \(A,\!\) in the following fashion:
|
\(\begin{array}{lcl} \mathrm{E}A & = & \langle \mathrm{E}\mathcal{A} \rangle \\[4pt] & = & \langle \mathcal{A} \cup \mathrm{d}\mathcal{A} \rangle \\[4pt] & = & \langle a_1, \ldots, a_n, \mathrm{d}a_1, \ldots, \mathrm{d}a_n \rangle, \end{array}\) |
and also:
|
\(\begin{array}{lcl} \mathrm{E}A & = & A \times \mathrm{d}A \\[4pt] & = & A_1 \times \ldots \times A_n \times \mathrm{d}A_1 \times \ldots \times \mathrm{d}A_n. \end{array}\) |
This gives \(\mathrm{E}A\) the type \(\mathbb{B}^n \times \mathbb{D}^n.\)
Finally, the tangent universe \(\mathrm{E}A^\bullet = [\mathrm{E}\mathcal{A}]\!\) is constituted from the totality of points and maps, or interpretations and propositions, that are based on the extended set of features \(\mathrm{E}\mathcal{A},\) and this fact is summed up in the following notation:
|
\(\begin{array}{lclcl} \mathrm{E}A^\bullet & = & [\mathrm{E}\mathcal{A}] & = & [a_1, \ldots, a_n, \mathrm{d}a_1, \ldots, \mathrm{d}a_n]. \end{array}\) |
This gives the tangent universe \(\mathrm{E}A^\bullet\!\) the type:
|
\(\begin{array}{lcl} (\mathbb{B}^n \times \mathbb{D}^n\ +\!\to \mathbb{B}) & = & (\mathbb{B}^n \times \mathbb{D}^n, (\mathbb{B}^n \times \mathbb{D}^n \to \mathbb{B})). \end{array}\) |
A proposition in the tangent universe \([\mathrm{E}\mathcal{A}]\) is called a differential proposition and forms the analogue of a system of differential equations, constraints, or relations in ordinary calculus.
With these constructions, the differential extension \(\mathrm{E}A\) and the space of differential propositions \((\mathrm{E}A \to \mathbb{B}),\!\) we have arrived, in main outline, at one of the major subgoals of this study. Table 8 summarizes the concepts that have been introduced for working with differentially extended universes of discourse.
| \(\text{Symbol}\!\) | \(\text{Notation}\!\) | \(\text{Description}\!\) | \(\text{Type}\!\) |
| \(\mathrm{d}\mathfrak{A}\!\) | \(\{ {}^{\backprime\backprime} \mathrm{d}a_1 {}^{\prime\prime}, \ldots, {}^{\backprime\backprime} \mathrm{d}a_n {}^{\prime\prime} \}\!\) |
\(\begin{matrix} \text{Alphabet of} \\[2pt] \text{differential symbols} \end{matrix}\) |
\([n] = \mathbf{n}\!\) |
| \(\mathrm{d}\mathcal{A}\!\) | \(\{ \mathrm{d}a_1, \ldots, \mathrm{d}a_n \}\!\) |
\(\begin{matrix} \text{Basis of} \\[2pt] \text{differential features} \end{matrix}\) |
\([n] = \mathbf{n}\!\) |
| \(\mathrm{d}A_i\!\) | \(\{ (\mathrm{d}a_i), \mathrm{d}a_i \}~\!\) | \(\text{Differential dimension}~ i\!\) | \(\mathbb{D}\!\) |
| \(\mathrm{d}A\!\) |
\(\begin{matrix} \langle \mathrm{d}\mathcal{A} \rangle \\[2pt] \langle \mathrm{d}a_1, \ldots, \mathrm{d}a_n \rangle \\[2pt] \{ (\mathrm{d}a_1, \ldots, \mathrm{d}a_n) \} \\[2pt] \mathrm{d}A_1 \times \ldots \times \mathrm{d}A_n \\[2pt] \textstyle \prod_i \mathrm{d}A_i \end{matrix}\) |
\(\begin{matrix} \text{Tangent space at a point:} \\[2pt] \text{Set of changes, motions,} \\[2pt] \text{steps, tangent vectors} \\[2pt] \text{at a point} \end{matrix}\) |
\(\mathbb{D}^n\!\) |
| \(\mathrm{d}A^*\!\) | \((\mathrm{hom} : \mathrm{d}A \to \mathbb{B})\!\) | \(\text{Linear functions on}~ \mathrm{d}A\!\) | \((\mathbb{D}^n)^* \cong \mathbb{D}^n\!\) |
| \(\mathrm{d}A^\uparrow\!\) | \((\mathrm{d}A \to \mathbb{B})\!\) | \(\text{Boolean functions on}~ \mathrm{d}A\!\) | \(\mathbb{D}^n \to \mathbb{B}\!\) |
| \(\mathrm{d}A^\bullet\!\) |
\(\begin{matrix} [\mathrm{d}\mathcal{A}] \\[2pt] (\mathrm{d}A, \mathrm{d}A^\uparrow) \\[2pt] (\mathrm{d}A ~+\!\to \mathbb{B}) \\[2pt] (\mathrm{d}A, (\mathrm{d}A \to \mathbb{B})) \\[2pt] [\mathrm{d}a_1, \ldots, \mathrm{d}a_n] \end{matrix}\) |
\(\begin{matrix} \text{Tangent universe at a point of}~ A^\bullet, \\[2pt] \text{based on the tangent features} \\[2pt] \{ \mathrm{d}a_1, \ldots, \mathrm{d}a_n \} \end{matrix}\) |
\(\begin{matrix} (\mathbb{D}^n, (\mathbb{D}^n \to \mathbb{B})) \\[2pt] (\mathbb{D}^n ~+\!\to \mathbb{B}) \\[2pt] [\mathbb{D}^n] \end{matrix}\) |
The adjectives differential or tangent are systematically attached to every construct based on the differential alphabet \(\mathrm{d}\mathfrak{A},\) taken by itself. Strictly speaking, we probably ought to call \(\mathrm{d}\mathcal{A}\) the set of cotangent features derived from \(\mathcal{A},\) but the only time this distinction really seems to matter is when we need to distinguish the tangent vectors as maps of type \((\mathbb{B}^n \to \mathbb{B}) \to \mathbb{B}\) from cotangent vectors as elements of type \(\mathbb{D}^n.\) In like fashion, having defined \(\mathrm{E}\mathcal{A} = \mathcal{A} \cup \mathrm{d}\mathcal{A},\) we can systematically attach the adjective extended or the substantive bundle to all of the constructs associated with this full complement of \({2n}\!\) features.
It eventually becomes necessary to extend the initial alphabet even further, to allow for the discussion of higher order differential expressions. Table 9 provides a suggestion of how these further extensions can be carried out.
|
\(\begin{array}{lllll} \mathrm{d}^0 \mathcal{A} & = & \{ a_1, \ldots, a_n \} & = & \mathcal{A} \\ \mathrm{d}^1 \mathcal{A} & = & \{ \mathrm{d}a_1, \ldots, \mathrm{d}a_n \} & = & \mathrm{d}\mathcal{A} \end{array}\) \(\begin{array}{lll} \mathrm{d}^k \mathcal{A} & = & \{ \mathrm{d}^k a_1, \ldots, \mathrm{d}^k a_n \} \\ \mathrm{d}^* \mathcal{A} & = & \{ \mathrm{d}^0 \mathcal{A}, \ldots, \mathrm{d}^k \mathcal{A}, \ldots \} \end{array}\) |
\(\begin{array}{lll} \mathrm{E}^0 \mathcal{A} & = & \mathrm{d}^0 \mathcal{A} \\ \mathrm{E}^1 \mathcal{A} & = & \mathrm{d}^0 \mathcal{A} ~\cup~ \mathrm{d}^1 \mathcal{A} \\ \mathrm{E}^k \mathcal{A} & = & \mathrm{d}^0 \mathcal{A} ~\cup~ \ldots ~\cup~ \mathrm{d}^k \mathcal{A} \\ \mathrm{E}^\infty \mathcal{A} & = & \bigcup~ \mathrm{d}^* \mathcal{A} \end{array}\) |
Intentional Propositions
|
Do you guess I have some intricate purpose? | |
| — Walt Whitman, Leaves of Grass, [Whi, 45] |
In order to analyze the behavior of a system at successive moments in time, while staying within the limitations of propositional logic, it is necessary to create independent alphabets of logical features for each moment of time that we contemplate using in our discussion. These moments have reference to typical instances and relative intervals, not actual or absolute times. For example, to discuss velocities (first order rates of change) we need to consider points of time in pairs. There are a number of natural ways of doing this. Given an initial alphabet, we could use its symbols as a lexical basis to generate successive alphabets of compound symbols, say, with temporal markers appended as suffixes.
As a standard way of dealing with these situations, the following scheme of notation suggests a way of extending any alphabet of logical features through as many temporal moments as a particular order of analysis may demand. The lexical operators \(\mathrm{p}^k\) and \(\mathrm{Q}^k\) are convenient in many contexts where the accumulation of prime symbols and union symbols would otherwise be cumbersome.
|
\(\begin{array}{lllll} \mathrm{p}^0 \mathcal{A} & = & \{ a_1, \ldots, a_n \} & = & \mathcal{A} \\ \mathrm{p}^1 \mathcal{A} & = & \{ a_1^\prime, \ldots, a_n^\prime \} & = & \mathcal{A}^\prime \\ \mathrm{p}^2 \mathcal{A} & = & \{ a_1^{\prime\prime}, \ldots, a_n^{\prime\prime} \} & = & \mathcal{A}^{\prime\prime} \\ \cdots & & \cdots & \end{array}\) \(\begin{array}{lll} \mathrm{p}^k \mathcal{A} & = & \{ \mathrm{p}^k a_1, \ldots, \mathrm{p}^k a_n \} \end{array}\) |
\(\begin{array}{lll} \mathrm{Q}^0 \mathcal{A} & = & \mathcal{A} \\ \mathrm{Q}^1 \mathcal{A} & = & \mathcal{A} \cup \mathcal{A}' \\ \mathrm{Q}^2 \mathcal{A} & = & \mathcal{A} \cup \mathcal{A}' \cup \mathcal{A}'' \\ \cdots & & \cdots \\ \mathrm{Q}^k \mathcal{A} & = & \mathcal{A} \cup \mathcal{A}' \cup \ldots \cup \mathrm{p}^k \mathcal{A} \end{array}\) |
The resulting augmentations of our logical basis determine a series of discursive universes that may be called the intentional extension of propositional calculus. This extension follows a pattern analogous to the differential extension, which was developed in terms of the operators \(\mathrm{d}^k\) and \(\mathrm{E}^k,\) and there is a natural relation between these two extensions that bears further examination. In contexts displaying this pattern, where a sequence of domains stretches from an anchoring domain \(X\!\) through an indefinite number of higher reaches, a particular collection of domains based on \(X\!\) will be referred to as a realm of \(X,\!\) and when the succession exhibits a temporal aspect, as a reign of \(X.\!\)
For the purposes of this discussion, an intentional proposition is defined as a proposition in the universe of discourse \(\mathrm{Q}X^\bullet = [\mathrm{Q}\mathcal{X}],\) in other words, a map \(q : \mathrm{Q}X \to \mathbb{B}.\) The sense of this definition may be seen if we consider the following facts. First, the equivalence \(\mathrm{Q}X = X \times X'\) motivates the following chain of isomorphisms between spaces:
|
\(\begin{array}{lllcl} (\mathrm{Q}X \to \mathbb{B}) & \cong & (X & \times & ~X' \to \mathbb{B}) \\[4pt] & \cong & (X & \to & (X' \to \mathbb{B})) \\[4pt] & \cong & (X' & \to & (X~ \to \mathbb{B})). \end{array}\) |
Viewed in this light, an intentional proposition \(q\!\) may be rephrased as a map \(q : X \times X' \to \mathbb{B},\) which judges the juxtaposition of states in \(X\!\) from one moment to the next. Alternatively, \(q\!\) may be parsed in two stages in two different ways, as \(q : X \to (X' \to \mathbb{B})\) and as \(q : X' \to (X \to \mathbb{B}),\) which associate to each point of \(X\!\) or \(X'\!\) a proposition about states in \(X'\!\) or \(X,\!\) respectively. In this way, an intentional proposition embodies a type of value system, in effect, a proposal that places a value on a collection of ends-in-view, or a project that evaluates a set of goals as regarded from each point of view in the state space of a system.
In sum, the intentional proposition \(q\!\) indicates a method for the systematic selection of local goals. As a general form of description, a map of the type \(q : \mathrm{Q}^i X \to \mathbb{B}\!\) may be referred to as an "\(i^\text{th}\) order intentional proposition". Naturally, when we speak of intentional propositions without qualification, we usually mean first order intentions.
Many different realms of discourse have the same structure as the extensions that have been indicated here. From a strictly logical point of view, each new layer of terms is composed of independent logical variables that are no different in kind from those that go before, and each further course of logical atoms is treated like so many individual, but otherwise indifferent bricks by the prototype computer program that I use as a propositional interpreter. Thus, the names that I use to single out the differential and the intentional extensions, and the lexical paradigms that I follow to construct them, are meant to suggest the interpretations that I have in mind, but they can only hint at the extra meanings that human communicators may pack into their terms and inflections.
As applied here, the word intentional is drawn from common use and may have little bearing on its technical use in other, more properly philosophical, contexts. I am merely using the complex of intentional concepts — aims, ends, goals, objectives, purposes, and so on — metaphorically to flesh out and vividly to represent any situation where one needs to contemplate a system in multiple aspects of state and destination, that is, its being in certain states and at the same time acting as if headed through certain states. If confusion arises, more neutral words like conative, contingent, discretionary, experimental, kinetic, progressive, tentative, or trial would probably serve as well.
Life on Easy Street
|
Failing to fetch me at first keep encouraged, | |
| — Walt Whitman, Leaves of Grass, [Whi, 88] |
The finite character of the extended universe \([\mathrm{E}\mathcal{A}]\) makes the problem of solving differential propositions relatively straightforward, at least, in principle. The solution set of the differential proposition \(q : \mathrm{E}A \to \mathbb{B}\) is the set of models \(q^{-1}(1)\!\) in \(\mathrm{E}A.\) Finding all the models of \(q,\!\) the extended interpretations in \(\mathrm{E}A\) that satisfy \(q,\!\) can be carried out by a finite search. Being in possession of complete algorithms for propositional calculus modeling, theorem checking, or theorem proving makes the analytic task fairly simple in principle, though the question of efficiency in the face of arbitrary complexity may always remain another matter entirely. While the fact that propositional satisfiability is NP-complete may be discouraging for the prospects of a single efficient algorithm that covers the whole space \([\mathrm{E}\mathcal{A}]\) with equal facility, there appears to be much room for improvement in classifying special forms and in developing algorithms that are tailored to their practical processing.
In view of these constraints and contingencies, our focus shifts to the tasks of approximation and interpretation that support intuition, especially in dealing with the natural kinds of differential propositions that arise in applications, and in the effort to understand, in succinct and adaptive forms, their dynamic implications. In the absence of direct insights, these tasks are partially carried out by forging analogies with the familiar situations and customary routines of ordinary calculus. But the indirect approach, going by way of specious analogy and intuitive habit, forces us to remain on guard against the circumstance that occurs when the word forging takes on its shadier nuance, indicting the constant risk of a counterfeit in the proportion.
Back to the Beginning : Exemplary Universes
|
I would have preferred to be enveloped in words, borne way beyond all possible beginnings. |
||
| — Michel Foucault, The Discourse on Language, [Fou, 215] | ||
To anchor our understanding of differential logic, let us look at how the various concepts apply in the simplest possible concrete cases, where the initial dimension is only 1 or 2. In spite of the obvious simplicity of these cases, it is possible to observe how central difficulties of the subject begin to arise already at this stage.
A One-Dimensional Universe
|
There was never any more inception than there is now, | |
| — Walt Whitman, Leaves of Grass, [Whi, 28] |
Let \(\mathcal{X} = \{ x_1 \} = \{ A \}\) be an alphabet that represents one boolean variable or a single logical feature. In this example the capital letter \({}^{\backprime\backprime} A {}^{\prime\prime}\!\) is used usual informally, to name a feature and not a space, in departure from our formerly stated formal conventions. At any rate, the basis element \(A = x_1\!\) may be interpreted as a simple proposition or a coordinate projection \(A = x_1 : \mathbb{B} \xrightarrow{i} \mathbb{B}.\) The space \(X = \langle A \rangle = \{ \texttt{(} A \texttt{)}, A \}\) of points (cells, vectors, interpretations) has cardinality \(2^n = 2^1 = 2\!\) and is isomorphic to \(\mathbb{B} = \{ 0, 1 \}.\) Moreover, \(X\!\) may be identified with the set of singular propositions \(\{ x : \mathbb{B} \xrightarrow{s} \mathbb{B} \}.\) The space of linear propositions \(X^* = \{ \mathrm{hom} : \mathbb{B} \xrightarrow{\ell} \mathbb{B} \} = \{ 0, A \}\) is algebraically dual to \(X\!\) and also has cardinality \(2.\!\) Here, \({}^{\backprime\backprime} 0 {}^{\prime\prime}\!\) is interpreted as denoting the constant function \(0 : \mathbb{B} \to \mathbb{B},\) amounting to the linear proposition of rank \(0,\!\) while \(A\!\) is the linear proposition of rank \(1.\!\) Last but not least we have the positive propositions \(\{ \mathrm{pos} : \mathbb{B} \xrightarrow{p} \mathbb{B} \} = \{ A, 1 \},\!\) of rank \(1\!\) and \(0,\!\) respectively, where \({}^{\backprime\backprime} 1 {}^{\prime\prime}\!\) is understood as denoting the constant function \(1 : \mathbb{B} \to \mathbb{B}.\) In sum, there are \(2^{2^n} = 2^{2^1} = 4\) propositions altogether in the universe of discourse, comprising the set \(X^\uparrow = \{ f : X \to \mathbb{B} \} = \{ 0, \texttt{(} A \texttt{)}, A, 1 \} \cong (\mathbb{B} \to \mathbb{B}).\)
The first order differential extension of \(\mathcal{X}\) is \(\mathrm{E}\mathcal{X} = \{ x_1, \mathrm{d}x_1 \} = \{ A, \mathrm{d}A \}.\) If the feature \(A\!\) is understood as applying to some object or state, then the feature \(\mathrm{d}A\) may be interpreted as an attribute of the same object or state that says that it is changing significantly with respect to the property \(A,\!\) or that it has an escape velocity with respect to the state \(A.\!\) In practice, differential features acquire their logical meaning through a class of temporal inference rules.
For example, relative to a frame of observation that is left implicit for now, one is permitted to make the following sorts of inference: From the fact that \(A\!\) and \(\mathrm{d}A\) are true at a given moment one may infer that \(\texttt{(} A \texttt{)}\!\) will be true in the next moment of observation. Altogether in the present instance, there is the fourfold scheme of inference that is shown below:
|
\(\begin{matrix} \text{From} & \texttt{(} A \texttt{)} & \text{and} & \texttt{(} \mathrm{d}A \texttt{)} & \text{infer} & \texttt{(} A \texttt{)} & \text{next.} \\[8pt] \text{From} & \texttt{(} A \texttt{)} & \text{and} & \mathrm{d}A & \text{infer} & A & \text{next.} \\[8pt] \text{From} & A & \text{and} & \texttt{(} \mathrm{d}A \texttt{)} & \text{infer} & A & \text{next.} \\[8pt] \text{From} & A & \text{and} & \mathrm{d}A & \text{infer} & \texttt{(} A \texttt{)} & \text{next.} \end{matrix}\) |
It might be thought that an independent time variable needs to be brought in at this point, but it is an insight of fundamental importance that the idea of process is logically prior to the notion of time. A time variable is a reference to a clock — a canonical, conventional process that is accepted or established as a standard of measurement, but in essence no different than any other process. This raises the question of how different subsystems in a more global process can be brought into comparison, and what it means for one process to serve the function of a local standard for others. But these inquiries only wrap up puzzles in further riddles, and are obviously too involved to be handled at our current level of approximation.
|
The clock indicates the moment . . . . but what does | |
| — Walt Whitman, Leaves of Grass, [Whi, 79] |
Observe that the secular inference rules, used by themselves, involve a loss of information, since nothing in them can tell us whether the momenta \(\{ \texttt{(} \mathrm{d}A \texttt{)}, \mathrm{d}A \}\!\) are changed or unchanged in the next instance. In order to know this, one would have to determine \(\mathrm{d}^2 A,\!\) and so on, pursuing an infinite regress. Ultimately, in order to rest with a finitely determinate system, it is necessary to make an infinite assumption, for example, that \(\mathrm{d}^k A = 0\!\) for all \(k\!\) greater than some fixed value \(M.\!\) Another way to escape the regress is through the provision of a dynamic law, in typical form making higher order differentials dependent on lower degrees and estates.
Example 1. A Square Rigging
|
Urge and urge and urge, | |
| — Walt Whitman, Leaves of Grass, [Whi, 28] |
By way of example, suppose that we are given the initial condition \(A = \mathrm{d}A\!\) and the law \(\mathrm{d}^2 A = \texttt{(} A \texttt{)}.\!\) Since the equation \(A = \mathrm{d}A\!\) is logically equivalent to the disjunction \(A ~ \mathrm{d}A ~\text{or}~ \texttt{(} A \texttt{)(} \mathrm{d}A \texttt{)},\!\) we may infer two possible trajectories, as displayed in Table 11. In either case the state \(A ~ \texttt{(} \mathrm{d}A \texttt{)(} \mathrm{d}^2 A \texttt{)}\!\) is a stable attractor or a terminal condition for both starting points.
| \(\text{Time}\!\) | \(\text{Trajectory 1}\!\) | \(\text{Trajectory 2}\!\) |
|
\(\begin{matrix} 0 \\[4pt] 1 \\[4pt] 2 \\[4pt] 3 \\[4pt] 4 \end{matrix}\) |
\(\begin{matrix} A & \mathrm{d}A & \texttt{(} \mathrm{d}^2 A \texttt{)} \\[4pt] \texttt{(} A \texttt{)} & \mathrm{d}A & \mathrm{d}^2 A \\[4pt] A & \texttt{(} \mathrm{d}A \texttt{)} & \texttt{(} \mathrm{d}^2 A \texttt{)} \\[4pt] A & \texttt{(} \mathrm{d}A \texttt{)} & \texttt{(} \mathrm{d}^2 A \texttt{)} \\[4pt] {}^{\shortparallel} & {}^{\shortparallel} & {}^{\shortparallel} \end{matrix}\) |
\(\begin{matrix} \texttt{(} A \texttt{)} & \texttt{(} \mathrm{d}A \texttt{)} & \mathrm{d}^2 A \\[4pt] \texttt{(} A \texttt{)} & \mathrm{d}A & \mathrm{d}^2 A \\[4pt] A & \texttt{(} \mathrm{d}A \texttt{)} & \texttt{(} \mathrm{d}^2 A \texttt{)} \\[4pt] A & \texttt{(} \mathrm{d}A \texttt{)} & \texttt{(} \mathrm{d}^2 A \texttt{)} \\[4pt] {}^{\shortparallel} & {}^{\shortparallel} & {}^{\shortparallel} \end{matrix}\!\) |
Because the initial space \(X = \langle A \rangle\!\) is one-dimensional, we can easily fit the second order extension \(\mathrm{E}^2 X = \langle A, \mathrm{d}A, \mathrm{d}^2 A \rangle\!\) within the compass of a single venn diagram, charting the couple of converging trajectories as shown in Figure 12.
| \(\text{Figure 12.} ~~ \text{The Anchor}\!\) |
If we eliminate from view the regions of \(\mathrm{E}^2 X\!\) that are ruled out by the dynamic law \(\mathrm{d}^2 A = \texttt{(} A \texttt{)},\!\) then what remains is the quotient structure that is shown in Figure 13. This picture makes it easy to see that the dynamically allowable portion of the universe is partitioned between the properties \(A\!\) and \(\mathrm{d}^2 A\!.\) As it happens, this fact might have been expressed “right off the bat” by an equivalent formulation of the differential law, one that uses the exclusive disjunction to state the law as \(\texttt{(} A \texttt{,} \mathrm{d}^2 A \texttt{)}\!.\)
| \(\text{Figure 13.} ~~ \text{The Tiller}\!\) |
What we have achieved in this example is to give a differential description of a simple dynamic process. In effect, we did this by embedding a directed graph, which can be taken to represent the state transitions of a finite automaton, in a dynamically allotted quotient structure that is created from a boolean lattice or an \(n\!\)-cube by nullifying all of the regions that the dynamics outlaws. With growth in the dimensions of our contemplated universes, it becomes essential, both for human comprehension and for computer implementation, that the dynamic structures of interest to us be represented not actually, by acquaintance, but virtually, by description. In our present study, we are using the language of propositional calculus to express the relevant descriptions, and to comprehend the structure that is implicit in the subsets of a \(n\!\)-cube without necessarily being forced to actualize all of its points.
One of the reasons for engaging in this kind of extremely reduced, but explicitly controlled case study is to throw light on the general study of languages, formal and natural, in their full array of syntactic, semantic, and pragmatic aspects. Propositional calculus is one of the last points of departure where we can view these three aspects interacting in a non-trivial way without being immediately and totally overwhelmed by the complexity they generate. Often this complexity causes investigators of formal and natural languages to adopt the strategy of focusing on a single aspect and to abandon all hope of understanding the whole, whether it's the still living natural language or the dynamics of inquiry that lies crystallized in formal logic.
From the perspective that I find most useful here, a language is a syntactic system that is designed or evolved in part to express a set of descriptions. When the explicit symbols of a language have extensions in its object world that are actually infinite, or when the implicit categories and generative devices of a linguistic theory have extensions in its subject matter that are potentially infinite, then the finite characters of terms, statements, arguments, grammars, logics, and rhetorics force an excess of intension to reside in all these symbols and functions, across the spectrum from the object language to the metalinguistic uses. In the aphorism from W. von Humboldt that Chomsky often cites, for example, in [Cho86, 30] and [Cho93, 49], language requires “the infinite use of finite means”. This is necessarily true when the extensions are infinite, when the referential symbols and grammatical categories of a language possess infinite sets of models and instances. But it also voices a practical truth when the extensions, though finite at every stage, tend to grow at exponential rates.
This consequence of dealing with extensions that are “practically infinite” becomes crucial when one tries to build neural network systems that learn, since the learning competence of any intelligent system is limited to the objects and domains that it is able to represent. If we want to design systems that operate intelligently with the full deck of propositions dealt by intact universes of discourse, then we must supply them with succinct representations and efficient transformations in this domain. Furthermore, in the project of constructing inquiry driven systems, we find ourselves forced to contemplate the level of generality that is embodied in propositions, because the dynamic evolution of these systems is driven by the measurable discrepancies that occur among their expectations, intentions, and observations, and because each of these subsystems or components of knowledge constitutes a propositional modality that can take on the fully generic character of an empirical summary or an axiomatic theory.
A compression scheme by any other name is a symbolic representation, and this is what the differential extension of propositional calculus, through all of its many universes of discourse, is intended to supply. Why is this particular program of mental calisthenics worth carrying out in general? By providing a uniform logical medium for describing dynamic systems we can make the task of understanding complex systems much easier, both in looking for invariant representations of individual cases and in finding points of comparison among diverse structures that would otherwise appear as isolated systems. All of this goes to facilitate the search for compact knowledge and to adapt what is learned from individual cases to the general realm.
Back to the Feature
|
I guess it must be the flag of my disposition, out of hopeful | |
| — Walt Whitman, Leaves of Grass, [Whi, 31] |
Let us assume that the sense intended for differential features is well enough established in the intuition, for now, that we may continue with outlining the structure of the differential extension \([\mathrm{E}\mathcal{X}] = [A, \mathrm{d}A].\!\) Over the extended alphabet \(\mathrm{E}\mathcal{X} = \{ x_1, \mathrm{d}x_1 \} = \{ A, \mathrm{d}A \}\!\) of cardinality \(2^n = 2\!\) we generate the set of points \(\mathrm{E}X\!\) of cardinality \(2^{2n} = 4\!\) that bears the following chain of equivalent descriptions:
|
\(\begin{array}{lll} \mathrm{E}X & = & \langle A, \mathrm{d}A \rangle \\[4pt] & = & \{ \texttt{(} A \texttt{)}, A \} ~\times~ \{ \texttt{(} \mathrm{d}A \texttt{)}, \mathrm{d}A \} \\[4pt] & = & \{ \texttt{(} A \texttt{)(} \mathrm{d}A \texttt{)},~ \texttt{(} A \texttt{)} \mathrm{d}A,~ A \texttt{(} \mathrm{d}A \texttt{)},~ A ~ \mathrm{d}A \}. \end{array}\) |
The space \(\mathrm{E}X\!\) may be assigned the mnemonic type \(\mathbb{B} \times \mathbb{D},\!\) which is really no different than \(\mathbb{B} \times \mathbb{B} = \mathbb{B}^2.\!\) An individual element of \(\mathrm{E}X\!\) may be regarded as a disposition at a point or a situated direction, in effect, a singular mode of change occurring at a single point in the universe of discourse. In applications, the modality of this change can be interpreted in various ways, for example, as an expectation, an intention, or an observation with respect to the behavior of a system.
To complete the construction of the extended universe of discourse \(\mathrm{E}X^\bullet = [x_1, \mathrm{d}x_1] = [A, \mathrm{d}A]\!\) one must add the set of differential propositions \(\mathrm{E}X^\uparrow = \{ g : \mathrm{E}X \to \mathbb{B} \} \cong (\mathbb{B} \times \mathbb{D} \to \mathbb{B})\!\) to the set of dispositions in \(\mathrm{E}X.\!\) There are \(2^{2^{2n}} = 16\!\) propositions in \(\mathrm{E}X^\uparrow,\!\) as detailed in Table 14.
| \(A\colon\!\) | \(1~1~0~0\!\) | ||||
| \(\mathrm{d}A\colon\!\) | \(1~0~1~0\!\) | ||||
| \(f_{0}\!\) | \(g_{0}\!\) | \(0~0~0~0\!\) | \(\texttt{(~)}\!\) | \(\text{false}\!\) | \(0\!\) |
|
\(\begin{matrix} g_{1} \\[4pt] g_{2} \\[4pt] g_{4} \\[4pt] g_{8} \end{matrix}\!\) |
\(\begin{matrix} 0~0~0~1 \\[4pt] 0~0~1~0 \\[4pt] 0~1~0~0 \\[4pt] 1~0~0~0 \end{matrix}\!\) |
\(\begin{matrix} \texttt{(} A \texttt{)(} \mathrm{d}A \texttt{)} \\[4pt] \texttt{(} A \texttt{)} ~ \mathrm{d}A ~ \\[4pt] ~ A ~ \texttt{(} \mathrm{d}A \texttt{)} \\[4pt] ~ A ~~ \mathrm{d}A ~ \end{matrix}\!\) |
\(\begin{matrix} \text{neither}~ A ~\text{nor}~ \mathrm{d}A \\[4pt] \mathrm{d}A ~\text{and not}~ A \\[4pt] A ~\text{and not}~ \mathrm{d}A \\[4pt] A ~\text{and}~ \mathrm{d}A \end{matrix}\!\) |
\(\begin{matrix} \lnot A \land \lnot \mathrm{d}A \\[4pt] \lnot A \land \mathrm{d}A \\[4pt] A \land \lnot \mathrm{d}A \\[4pt] A \land \mathrm{d}A \end{matrix}\!\) | |
|
\(\begin{matrix} f_{1} \\[4pt] f_{2} \end{matrix}\!\) |
\(\begin{matrix} g_{3} \\[4pt] g_{12} \end{matrix}\!\) |
\(\begin{matrix} 0~0~1~1 \\[4pt] 1~1~0~0 \end{matrix}\!\) |
\(\begin{matrix} \texttt{(} A \texttt{)} \\[4pt] A \end{matrix}\!\) |
\(\begin{matrix} \text{not}~ A \\[4pt] A \end{matrix}\!\) |
\(\begin{matrix} \lnot A \\[4pt] A \end{matrix}\!\) |
|
\(\begin{matrix} g_{6} \\[4pt] g_{9} \end{matrix}\!\) |
\(\begin{matrix} 0~1~1~0 \\[4pt] 1~0~0~1 \end{matrix}\!\) |
\(\begin{matrix} \texttt{(} A \texttt{,} \mathrm{d}A \texttt{)} \\[4pt] \texttt{((} A \texttt{,} \mathrm{d}A \texttt{))} \end{matrix}\!\) |
\(\begin{matrix} A ~\text{not equal to}~ \mathrm{d}A \\[4pt] A ~\text{equal to}~ \mathrm{d}A \end{matrix}\!\) |
\(\begin{matrix} A \ne \mathrm{d}A \\[4pt] A = \mathrm{d}A \end{matrix}\!\) | |
|
\(\begin{matrix} g_{5} \\[4pt] g_{10} \end{matrix}\!\) |
\(\begin{matrix} 0~1~0~1 \\[4pt] 1~0~1~0 \end{matrix}\!\) |
\(\begin{matrix} \texttt{(} \mathrm{d}A \texttt{)} \\[4pt] \mathrm{d}A \end{matrix}\!\) |
\(\begin{matrix} \text{not}~ \mathrm{d}A \\[4pt] \mathrm{d}A \end{matrix}\!\) |
\(\begin{matrix} \lnot \mathrm{d}A \\[4pt] \mathrm{d}A \end{matrix}\!\) | |
|
\(\begin{matrix} g_{7} \\[4pt] g_{11} \\[4pt] g_{13} \\[4pt] g_{14} \end{matrix}\!\) |
\(\begin{matrix} 0~1~1~1 \\[4pt] 1~0~1~1 \\[4pt] 1~1~0~1 \\[4pt] 1~1~1~0 \end{matrix}\!\) |
\(\begin{matrix} \texttt{(} ~ A ~~ \mathrm{d}A ~ \texttt{)} \\[4pt] \texttt{(} ~ A ~ \texttt{(} \mathrm{d}A \texttt{))} \\[4pt] \texttt{((} A \texttt{)} ~ \mathrm{d}A ~ \texttt{)} \\[4pt] \texttt{((} A \texttt{)(} \mathrm{d}A \texttt{))} \end{matrix}\!\) |
\(\begin{matrix} \text{not both}~ A ~\text{and}~ \mathrm{d}A \\[4pt] \text{not}~ A ~\text{without}~ \mathrm{d}A \\[4pt] \text{not}~ \mathrm{d}A ~\text{without}~ A \\[4pt] A ~\text{or}~ \mathrm{d}A \end{matrix}\!\) |
\(\begin{matrix} \lnot A \lor \lnot \mathrm{d}A \\[4pt] A \Rightarrow \mathrm{d}A \\[4pt] A \Leftarrow \mathrm{d}A \\[4pt] A \lor \mathrm{d}A \end{matrix}\!\) | |
| \(f_{3}\!\) | \(g_{15}\!\) | \(1~1~1~1\!\) | \(\texttt{((~))}\!\) | \(\text{true}\!\) | \(1\!\) |
Aside from changing the names of variables and shuffling the order of rows, this Table follows the format that was used previously for boolean functions of two variables. The rows are grouped to reflect natural similarity classes among the propositions. In a future discussion, these classes will be given additional explanation and motivation as the orbits of a certain transformation group acting on the set of 16 propositions. Notice that four of the propositions, in their logical expressions, resemble those given in the table for \(X^\uparrow.\!\) Thus the first set of propositions \(\{ f_i \}\!\) is automatically embedded in the present set \(\{ g_j \}\!\) and the corresponding inclusions are indicated at the far left margin of the Table.
Tacit Extensions
|
I would really like to have slipped imperceptibly into this lecture, as into all the others I shall be delivering, perhaps over the years ahead. |
||
| — Michel Foucault, The Discourse on Language, [Fou, 215] | ||
Strictly speaking, however, there is a subtle distinction in type between the function \(f_i : X \to \mathbb{B}\) and the corresponding function \(g_j : \mathrm{E}X \to \mathbb{B},\) even though they share the same logical expression. Naturally, we want to maintain the logical equivalence of expressions that represent the same proposition while appreciating the full diversity of that proposition's functional and typical representatives. Both perspectives, and all the levels of abstraction extending through them, have their reasons, as will develop in time.
Because this special circumstance points up an important general theme, it is a good idea to discuss it more carefully. Whenever there arises a situation like this, where one alphabet \(\mathcal{X}\) is a subset of another alphabet \(\mathcal{Y},\) then we say that any proposition \(f : \langle \mathcal{X} \rangle \to \mathbb{B}\) has a tacit extension to a proposition \(\boldsymbol\varepsilon f : \langle \mathcal{Y} \rangle \to \mathbb{B},\!\) and that the space \((\langle \mathcal{X} \rangle \to \mathbb{B})\) has an automatic embedding within the space \((\langle \mathcal{Y} \rangle \to \mathbb{B}).\) The extension is defined in such a way that \(\boldsymbol\varepsilon f\!\) puts the same constraint on the variables of \(\mathcal{X}\) that are contained in \(\mathcal{Y}\) as the proposition \(f\!\) initially did, while it puts no constraint on the variables of \(\mathcal{Y}\) outside of \(\mathcal{X},\) in effect, conjoining the two constraints.
If the variables in question are indexed as \(\mathcal{X} = \{ x_1, \ldots, x_n \}\) and \(\mathcal{Y} = \{ x_1, \ldots, x_n, \ldots, x_{n+k} \},\) then the definition of the tacit extension from \(\mathcal{X}\) to \(\mathcal{Y}\) may be expressed in the form of an equation:
| \(\boldsymbol\varepsilon f(x_1, \ldots, x_n, \ldots, x_{n+k}) ~=~ f(x_1, \ldots, x_n).\!\) |
On formal occasions, such as the present context of definition, the tacit extension from \(\mathcal{X}\) to \(\mathcal{Y}\) is explicitly symbolized by the operator \(\boldsymbol\varepsilon : (\langle \mathcal{X} \rangle \to \mathbb{B}) \to (\langle \mathcal{Y} \rangle \to \mathbb{B}),\) where the appropriate alphabets \(\mathcal{X}\) and \(\mathcal{Y}\) are understood from context, but normally one may leave the "\(\boldsymbol\varepsilon\!\)" silent.
Let's explore what this means for the present Example. Here, \(\mathcal{X} = \{ A \}\) and \(\mathcal{Y} = \mathrm{E}\mathcal{X} = \{ A, \mathrm{d}A \}.\) For each of the propositions \(f_i\!\) over \(X\!,\) specifically, those whose expression \(e_i\!\) lies in the collection \(\{ 0, \texttt{(} A \texttt{)}, A, 1 \},\!\) the tacit extension \(\boldsymbol\varepsilon f\!\) of \(f\!\) to \(\mathrm{E}X\) can be phrased as a logical conjunction of two factors, \(f_i = e_i \cdot \tau ~ ,\!\) where \(\tau\!\) is a logical tautology that uses all the variables of \(\mathcal{Y} - \mathcal{X}.\) Working in these terms, the tacit extensions \(\boldsymbol\varepsilon f\!\) of \(f\!\) to \(\mathrm{E}X\) may be explicated as shown in Table 15.
|
\(\begin{matrix} 0 & = & 0 & \cdot & \texttt{(} \mathrm{d}A \texttt{,(} \mathrm{d}A \texttt{))} & = & & 0 \\[8pt] \texttt{(} A \texttt{)} & = & \texttt{(} A \texttt{)} & \cdot & \texttt{(} \mathrm{d}A \texttt{,(} \mathrm{d}A \texttt{))} & = & \texttt{(} A \texttt{)} \, \mathrm{d}A ~ & + & \texttt{(} A \texttt{)(} \mathrm{d}A \texttt{)} \\[8pt] A & = & ~A~ & \cdot & \texttt{(} \mathrm{d}A \texttt{,(} \mathrm{d}A \texttt{))} & = & ~A~ ~\mathrm{d}A~ & + & ~A~ \texttt{(} \mathrm{d}A \texttt{)} \\[8pt] 1 & = & 1 & \cdot & \texttt{(} \mathrm{d}A \texttt{,(} \mathrm{d}A \texttt{))} & = & & 1 \end{matrix}\) |
In its effect on the singular propositions over \(X,\!\) this analysis has an interesting interpretation. The tacit extension takes us from thinking about a particular state, like \(A\!\) or \(\texttt{(} A \texttt{)},\!\) to considering the collection of outcomes, the outgoing changes or the singular dispositions, that spring from that state.
Example 2. Drives and Their Vicissitudes
|
I open my scuttle at night and see the far-sprinkled systems, | |
| — Walt Whitman, Leaves of Grass, [Whi, 81] |
Before we leave the one-feature case let's look at a more substantial example, one that illustrates a general class of curves that can be charted through the extended feature spaces and that provides an opportunity to discuss a number of important themes concerning their structure and dynamics.
Again, let \(\mathcal{X} = \{ x_1 \} = \{ A \}.\!\) In the discussion that follows we will consider a class of trajectories having the property that \(\mathrm{d}^k A = 0\!\) for all \(k\!\) greater than some fixed \(m\!\) and we may indulge in the use of some picturesque terms that describe salient classes of such curves. Given the finite order condition, there is a highest order non-zero difference \(\mathrm{d}^m A\!\) exhibited at each point in the course of any determinate trajectory that one may wish to consider. With respect to any point of the corresponding orbit or curve let us call this highest order differential feature \(\mathrm{d}^m A\!\) the drive at that point. Curves of constant drive \(\mathrm{d}^m A\!\) are then referred to as \(m^\text{th}\!\)-gear curves.
- Scholium. The fact that a difference calculus can be developed for boolean functions is well known [Fuji], [Koh, § 8-4] and was probably familiar to Boole, who was an expert in difference equations before he turned to logic. And of course there is the strange but true story of how the Turin machines of the 1840s prefigured the Turing machines of the 1940s [Men, 225-297]. At the very outset of general purpose, mechanized computing we find that the motive power driving the Analytical Engine of Babbage, the kernel of an idea behind all of his wheels, was exactly his notion that difference operations, suitably trained, can serve as universal joints for any conceivable computation [M&M], [Mel, ch. 4].
Given this language, the Example we take up here can be described as the family of \(4^\text{th}\!\)-gear curves through \(\mathrm{E}^4 X\!\) \(=\!\) \(\langle A, ~\mathrm{d}A, ~\mathrm{d}^2\!A, ~\mathrm{d}^3\!A, ~\mathrm{d}^4\!A \rangle.\) These are the trajectories generated subject to the dynamic law \(\mathrm{d}^4 A = 1,\!\) where it is understood in such a statement that all higher order differences are equal to \(0.\!\) Since \(\mathrm{d}^4 A\!\) and all higher \(\mathrm{d}^k A\!\) are fixed, the temporal or transitional conditions (initial, mediate, terminal — transient or stable states) vary only with respect to their projections as points of \(\mathrm{E}^3 X = \langle A, ~\mathrm{d}A, ~\mathrm{d}^2\!A, ~\mathrm{d}^3\!A \rangle.\) Thus, there is just enough space in a planar venn diagram to plot all of these orbits and to show how they partition the points of \(\mathrm{E}^3 X.\!\) It turns out that there are exactly two possible orbits, of eight points each, as illustrated in Figure 16.
| \(\text{Figure 16.} ~~ \text{A Couple of Fourth Gear Orbits}\!\) |
With a little thought it is possible to devise an indexing scheme for the general run of dynamic states that allows for comparing universes of discourse that weigh in on different scales of observation. With this end in sight, let us index the states \(q \in \mathrm{E}^m X\!\) with the dyadic rationals (or the binary fractions) in the half-open interval \([0, 2).\!\) Formally and canonically, a state \(q_r\!\) is indexed by a fraction \(r = \tfrac{s}{t}\!\) whose denominator is the power of two \(t = 2^m\!\) and whose numerator is a binary numeral formed from the coefficients of state in a manner to be described next. The differential coefficients of the state \(q\!\) are just the values \(\mathrm{d}^k\!A(q)\) for \(k = 0 ~\text{to}~ m,\!\) where \(\mathrm{d}^0\!A\) is defined as being identical to \(A.\!\) To form the binary index \(d_0.d_1 \ldots d_m\!\) of the state \(q\!\) the coefficient \(\mathrm{d}^k\!A(q)\) is read off as the binary digit \(d_k\!\) associated with the place value \(2^{-k}.\!\) Expressed by way of algebraic formulas, the rational index \(r\!\) of the state \(q\!\) can be given by the following equivalent formulations:
|
\(\begin{matrix} r(q) & = & \displaystyle\sum_k d_k \cdot 2^{-k} & = & \displaystyle\sum_k \text{d}^k A(q) \cdot 2^{-k} \\[8pt] = \\[8pt] \displaystyle\frac{s(q)}{t} & = & \displaystyle\frac{\sum_k d_k \cdot 2^{(m-k)}}{2^m} & = & \displaystyle\frac{\sum_k \text{d}^k A(q) \cdot 2^{(m-k)}}{2^m} \end{matrix}\) |
Applied to the example of \(4^\text{th}\!\)-gear curves, this scheme results in the data of Tables 17-a and 17-b, which exhibit one period for each orbit. The states in each orbit are listed as ordered pairs \((p_i, q_j),\!\) where \(p_i\!\) may be read as a temporal parameter that indicates the present time of the state and where \(j\!\) is the decimal equivalent of the binary numeral \(s.\!\) Informally and more casually, the Tables exhibit the states \(q_s\!\) as subscripted with the numerators of their rational indices, taking for granted the constant denominators of \(2^m\! = 2^4 = 16.\!\) In this set-up the temporal successions of states can be reckoned as given by a kind of parallel round-up rule. That is, if \((d_k, d_{k+1})\!\) is any pair of adjacent digits in the state index \(r,\!\) then the value of \(d_k\!\) in the next state is \({d_k}' = d_k + d_{k+1}.\!\)
| \(\text{Time}\!\) | \(\text{State}\!\) | \(A\!\) | \(\mathrm{d}A\!\) | ||||||||
| \(p_i\!\) | \(q_j\!\) | \(\mathrm{d}^0\!A\) | \(\mathrm{d}^1\!A\) | \(\mathrm{d}^2\!A\) | \(\mathrm{d}^3\!A\) | \(\mathrm{d}^4\!A\) | |||||
|
\(\begin{matrix} p_0 \\[4pt] p_1 \\[4pt] p_2 \\[4pt] p_3 \\[4pt] p_4 \\[4pt] p_5 \\[4pt] p_6 \\[4pt] p_7 \end{matrix}\!\) |
\(\begin{matrix} q_{01} \\[4pt] q_{03} \\[4pt] q_{05} \\[4pt] q_{15} \\[4pt] q_{17} \\[4pt] q_{19} \\[4pt] q_{21} \\[4pt] q_{31} \end{matrix}\!\) |
| |||||||||
| \(\text{Time}\!\) | \(\text{State}\!\) | \(A\!\) | \(\mathrm{d}A\!\) | ||||||||
| \(p_i\!\) | \(q_j\!\) | \(\mathrm{d}^0\!A\) | \(\mathrm{d}^1\!A\) | \(\mathrm{d}^2\!A\) | \(\mathrm{d}^3\!A\) | \(\mathrm{d}^4\!A\) | |||||
|
\(\begin{matrix} p_0 \\[4pt] p_1 \\[4pt] p_2 \\[4pt] p_3 \\[4pt] p_4 \\[4pt] p_5 \\[4pt] p_6 \\[4pt] p_7 \end{matrix}\!\) |
\(\begin{matrix} q_{25} \\[4pt] q_{11} \\[4pt] q_{29} \\[4pt] q_{07} \\[4pt] q_{09} \\[4pt] q_{27} \\[4pt] q_{13} \\[4pt] q_{23} \end{matrix}\!\) |
| |||||||||
Transformations of Discourse
|
It is understandable that an engineer should be completely absorbed in his speciality, instead of pouring himself out into the freedom and vastness of the world of thought, even though his machines are being sent off to the ends of the earth; for he no more needs to be capable of applying to his own personal soul what is daring and new in the soul of his subject than a machine is in fact capable of applying to itself the differential calculus on which it is based. The same thing cannot, however, be said about mathematics; for here we have the new method of thought, pure intellect, the very well-spring of the times, the fons et origo of an unfathomable transformation. |
||
| — Robert Musil, The Man Without Qualities, [Mus, 39] | ||
In this section we take up the general study of logical transformations, or maps that relate one universe of discourse to another. In many ways, and especially as applied to the subject of intelligent dynamic systems, my argument develops the antithesis of the statement just quoted. Along the way, if incidental to my ends, I hope this essay can pose a fittingly irenic epitaph to the frankly ironic epigraph inscribed at its head.
My goal in this section is to answer a single question: What is a propositional tangent functor? In other words, my aim is to develop a clear conception of what manner of thing would pass in the logical realm for a genuine analogue of the tangent functor, an object conceived to generalize as far as possible in the abstract terms of category theory the ordinary notions of functional differentiation and the all too familiar operations of taking derivatives.
As a first step I discuss the kinds of transformations that we already know as extensions and projections, and I use these special cases to illustrate several different styles of logical and visual representation that will figure heavily in the sequel.
Foreshadowing Transformations : Extensions and Projections of Discourse
|
And, despite the care which she took to look behind her at every moment, she failed to see a shadow which followed her like her own shadow, which stopped when she stopped, which started again when she did, and which made no more noise than a well-conducted shadow should. |
||
| — Gaston Leroux, The Phantom of the Opera, [Ler, 126] | ||
Many times in our discussion we have occasion to place one universe of discourse in the context of a larger universe of discourse. An embedding of the general type \([\mathcal{X}] \to [\mathcal{Y}]\!\) is implied any time that we make use of one alphabet \([\mathcal{X}]\!\) that happens to be included in another alphabet \([\mathcal{Y}].\!\) When we are discussing differential issues we usually have in mind that the extended alphabet \([\mathcal{Y}]\!\) has a special construction or a specific lexical relation with respect to the initial alphabet \([\mathcal{X}],\!\) one that is marked by characteristic types of accents, indices, or inflected forms.
Extension from 1 to 2 Dimensions
Figure 18-a lays out the angular form of venn diagram for universes of 1 and 2 dimensions, indicating the embedding map of type \(\mathbb{B}^1 \to \mathbb{B}^2\!\) and detailing the coordinates that are associated with individual cells. Because all points, cells, or logical interpretations are represented as connected geometric areas, we can say that these pictures provide us with an areal view of each universe of discourse.
| \(\text{Figure 18-a.} ~~ \text{Extension from 1 to 2 Dimensions : Areal}\!\) |
Figure 18-b shows the differential extension from \(X^\bullet = [x]\!\) to \(\mathrm{E}X^\bullet = [x, \mathrm{d}x]\!\) in a bundle of boxes form of venn diagram. As awkward as it may seem at first, this type of picture is often the most natural and the most easily available representation when we want to conceptualize the localized information or momentary knowledge of an intelligent dynamic system. It gives a ready picture of a proposition at a point, in the present instance, of a proposition about changing states which is itself associated with a particular dynamic state of a system. It is easy to see how this application might be extended to conceive of more general types of instantaneous knowledge that are possessed by a system.
| \(\text{Figure 18-b.} ~~ \text{Extension from 1 to 2 Dimensions : Bundle}\!\) |
Figure 18-c shows the same extension in a compact style of venn diagram, where the differential features at each position are represented by arrows extending from that position that cross or do not cross, as the case may be, the corresponding feature boundaries.
| \(\text{Figure 18-c.} ~~ \text{Extension from 1 to 2 Dimensions : Compact}\!\) |
Figure 18-d compresses the picture of the differential extension even further, yielding a directed graph or digraph form of representation. (Notice that my definition of a digraph allows for loops or slings at individual points, in addition to arcs or arrows between the points.)
| \(\text{Figure 18-d.} ~~ \text{Extension from 1 to 2 Dimensions : Digraph}\!\) |
Extension from 2 to 4 Dimensions
Figure 19-a lays out the areal view or the angular form of venn diagram for universes of 2 and 4 dimensions, indicating the embedding map of type \(\mathbb{B}^2 \to \mathbb{B}^4.\!\) In many ways these pictures are the best kind there is, giving full canvass to an ideal vista. Their style allows the clearest, the fairest, and the plainest view that we can form of a universe of discourse, affording equal representation to all dispositions and maintaining a balance with respect to ordinary and differential features. If only we could extend this view! Unluckily, an obvious difficulty beclouds this prospect, and that is how precipitately we run into the limits of our plane and visual intuitions. Even within the scope of the spare few dimensions that we have scanned up to this point subtle discrepancies have crept in already. The circumstances that bind us and the frameworks that block us, the flat distortion of the planar projection and the inevitable ineffability that precludes us from wrapping its rhomb figure into rings around a torus, all of these factors disguise the underlying but true connectivity of the universe of discourse.
| \(\text{Figure 19-a.} ~~ \text{Extension from 2 to 4 Dimensions : Areal}\!\) |
Figure 19-b shows the differential extension from \(U^\bullet = [u, v]\!\) to \(\mathrm{E}U^\bullet = [u, v, \mathrm{d}u, \mathrm{d}v]\!\) in the bundle of boxes form of venn diagram.
| \(\text{Figure 19-b.} ~~ \text{Extension from 2 to 4 Dimensions : Bundle}\!\) |
As dimensions increase, this factorization of the extended universe along the lines that are marked out by the bundle picture begins to look more and more like a practical necessity. But whenever we use a propositional model to address a real situation in the context of nature we need to remain aware that this articulation into factors, affecting our description, may be wholly artificial in nature and cleave to nothing, no joint in nature, nor any juncture in time to be in or out of joint.
Figure 19-c illustrates the extension from 2 to 4 dimensions in the compact style of venn diagram. Here, just the changes with respect to the center cell are shown.
| \(\text{Figure 19-c.} ~~ \text{Extension from 2 to 4 Dimensions : Compact}\!\) |
Figure 19-d gives the digraph form of representation for the differential extension \(U^\bullet \to \mathrm{E}U^\bullet,\!\) where the 4 nodes marked with a circle \({}^{\bigcirc}\!\) are the cells \(uv,\, u \texttt{(} v \texttt{)},\, \texttt{(} u \texttt{)} v,\, \texttt{(} u \texttt{)(} v \texttt{)},\!\) respectively, and where a 2-headed arc counts as 2 arcs of the differential digraph.
| \(\text{Figure 19-d.} ~~ \text{Extension from 2 to 4 Dimensions : Digraph}\!\) |
Thematization of Functions : And a Declaration of Independence for Variables
|
And as imagination bodies forth |
A Midsummer Night's Dream, 5.1.18 |
In the representation of propositions as functions it is possible to notice different degrees of explicitness in the way their functional character is symbolized. To indicate what I mean by this, the next series of Figures illustrates a set of graphic conventions that will be put to frequent use in the remainder of this discussion, both to mark the relevant distinctions and to help us convert between related expressions at different levels of explicitness in their functionality.
Thematization : Venn Diagrams
|
The known universe has one complete lover and that is the greatest poet. He consumes an eternal passion and is indifferent which chance happens and which possible contingency of fortune or misfortune and persuades daily and hourly his delicious pay. |
||
| — Walt Whitman, Leaves of Grass, [Whi, 11–12] | ||
Figure 20-i traces the first couple of steps in this order of thematic progression, that will gradually run the gamut through a complete series of degrees of functional explicitness in the expression of logical propositions. The first venn diagram represents a situation where the function is indicated by a shaded figure and a logical expression. At this stage one may be thinking of the proposition only as expressed by a formula in a particular language and its content only as a subset of the universe of discourse, as when considering the proposition \(u\!\cdot\!v\) in the universe \([u, v].\!\) The second venn diagram depicts a situation in which two significant steps have been taken. First, one has taken the trouble to give the proposition \(u\!\cdot\!v\) a distinctive functional name \({}^{\backprime\backprime} J {}^{\prime\prime}.\!\) Second, one has come to think explicitly about the target domain that contains the functional values of \(J,\!\) as when writing \(J : \langle u, v \rangle \to \mathbb{B}.\!\)
| \(\text{Figure 20-i.} ~~ \text{Thematization of Conjunction (Stage 1)}\!\) |
In Figure 20-ii the proposition \(J\!\) is viewed explicitly as a transformation from one universe of discourse to another.
| \(\text{Figure 20-ii.} ~~ \text{Thematization of Conjunction (Stage 2)}\!\) |
o-------------------------------o o-------------------------------o
| | | |
| o-----o o-----o | | o-----o o-----o |
| / \ / \ | | / \ / \ |
| / o \ | | / o \ |
| / /`\ \ | | / /`\ \ |
| o o```o o | | o o```o o |
| | u |```| v | | | | u |```| v | |
| o o```o o | | o o```o o |
| \ \`/ / | | \ \`/ / |
| \ o / | | \ o / |
| \ / \ / | | \ / \ / |
| o-----o o-----o | | o-----o o-----o |
| | | |
o-------------------------------o o-------------------------------o
\ / \ /
\ / \ /
\ / \ J /
\ / \ /
\ / \ /
o----------\---------/----------o o----------\---------/----------o
| \ / | | \ / |
| \ / | | \ / |
| o-----@-----o | | o-----@-----o |
| /`````````````\ | | /`````````````\ |
| /```````````````\ | | /```````````````\ |
| /`````````````````\ | | /`````````````````\ |
| o```````````````````o | | o```````````````````o |
| |```````````````````| | | |```````````````````| |
| |```````` J ````````| | | |```````` x ````````| |
| |```````````````````| | | |```````````````````| |
| o```````````````````o | | o```````````````````o |
| \`````````````````/ | | \`````````````````/ |
| \```````````````/ | | \```````````````/ |
| \`````````````/ | | \`````````````/ |
| o-----------o | | o-----------o |
| | | |
| | | |
o-------------------------------o o-------------------------------o
J = u v x = J<u, v>
Figure 20-ii. Thematization of Conjunction (Stage 2)
|
In the first venn diagram the name that is assigned to a composite proposition, function, or region in the source universe is delegated to a simple feature in the target universe. This can result in a single character or term exceeding the responsibilities it can carry off well. Allowing the name of a function \(J : \langle u, v \rangle \to \mathbb{B}\!\) to serve as the name of its dependent variable \(J : \mathbb{B}\!\) does not mean that one has to confuse a function with any of its values, but it does put one at risk for a number of obvious problems, and we should not be surprised, on numerous and limiting occasions, when quibbling arises from the attempts of a too original syntax to serve these two masters.
The second venn diagram circumvents these difficulties by introducing a new variable name for each basic feature of the target universe, as when writing \(J : \langle u, v \rangle \to \langle x \rangle,\!\) and thereby assigns a concrete type \(\langle x \rangle\) to the abstract codomain \(\mathbb{B}.\!\) To make this induction of variables more formal one can append subscripts, as in \(x_J,\!\) to indicate the origin or derivation of the new characters. Or we may use a lexical modifier to convert function names into variable names, for example, associating the function name \(J\!\) with the variable name \(\check{J}.\!\) Thus we may think of \(x = x_J = \check{J}\!\) as the cache variable corresponding to the function \(J\!\) or the symbol \({}^{\backprime\backprime} J {}^{\prime\prime}\) considered as a contingent variable.
In Figure 20-iii we arrive at a stage where the functional equations \(J = u\!\cdot\!v\) and \(x = u\!\cdot\!v\) are regarded as propositions in their own right, reigning in and ruling over the 3-feature universes of discourse \([u, v, J]~\!\) and \([u, v, x],\!\) respectively. Subject to the cautions already noted, the function name \({}^{\backprime\backprime} J {}^{\prime\prime}\) can be reinterpreted as the name of a feature \(\check{J}\) and the equation \(J = u\!\cdot\!v\) can be read as the logical equivalence \(\texttt{((} J, u ~ v \texttt{))}.\!\) To give it a generic name let us call this newly expressed, collateral proposition the thematization or the thematic extension of the original proposition \(J.\!\)
| \(\text{Figure 20-iii.} ~~ \text{Thematization of Conjunction (Stage 3)}\!\) |
The first venn diagram represents the thematization of the conjunction \(J\!\) with shading in the appropriate regions of the universe \([u, v, J].\!\) Also, it illustrates a quick way of constructing a thematic extension. First, draw a line, in practice or the imagination, that bisects every cell of the original universe, placing half of each cell under the aegis of the thematized proposition and the other half under its antithesis. Next, on the scene where the theme applies leave the shade wherever it lies, and off the stage, where it plays otherwise, stagger the pattern in a harlequin guise.
In the final venn diagram of this sequence the thematic progression comes full circle and completes one round of its development. The ambiguities that were occasioned by the changing role of the name \({}^{\backprime\backprime} J {}^{\prime\prime}\) are resolved by introducing a new variable name \({}^{\backprime\backprime} x {}^{\prime\prime}\) to take the place of \(\check{J},\!\) and the region that represents this fresh featured \(x\!\) is circumscribed in a more conventional symmetry of form and placement. Just as we once gave the name \({}^{\backprime\backprime} J {}^{\prime\prime}\) to the proposition \(u\!\cdot\!v,\) we now give the name \({}^{\backprime\backprime} \iota {}^{\prime\prime}\) to its thematization \(\texttt{((} x, u ~ v \texttt{))}.\!\) Already, again, at this culminating stage of reflection, we begin to think of the newly named proposition as a distinctive individual, a particular function \(\iota : \langle u, v, x \rangle \to \mathbb{B}.\!\)
From now on, the terms thematic extension and thematization will be used to describe both the process and degree of explication that progresses through this series of pictures, both the operation of increasingly explicit symbolization and the dimension of variation that is swept out by it. To speak of this change in general, that takes us in our current example from \(J\!\) to \(\iota,\!\) we introduce a class of operators symbolized by the Greek letter \(\theta,\!\) writing \(\iota = \theta J\!\) in the present instance. The operator \(\theta,\!\) in the present situation bearing the type \(\theta : [u, v] \to [u, v, x],\!\) provides us with a convenient way of recapitulating and summarizing the complete cycle of thematic developments.
Figure 21 shows how the thematic extension operator \(\theta\!\) acts on two further examples, the disjunction \(\texttt{((} u \texttt{)(} v \texttt{))}\!\) and the equality \(\texttt{((} u, v \texttt{))}.\!\) Referring to the disjunction as \(f(u, v)\!\) and the equality as \(f(u, v),\!\) we may express the thematic extensions as \(\varphi = \theta f\!\) and \(\gamma = \theta g.\!\)
| \(\text{Figure 21.} ~~ \text{Thematization of Disjunction and Equality}\!\) |
Thematization : Truth Tables
|
That which distorts honest shapes or which creates unearthly beings or places or contingencies is a nuisance and a revolt. |
||
| — Walt Whitman, Leaves of Grass, [Whi, 19] | ||
Tables 22 through 25 outline a method for computing the thematic extensions of propositions in terms of their coordinate values.
A preliminary step, as illustrated in Table 22, is to write out the truth table representations of the propositional forms whose thematic extensions one wants to compute, in the present instance, the functions \(f(u, v) = \texttt{((} u \texttt{)(} v \texttt{))}\!\) and \(g(u, v) = \texttt{((} u, v \texttt{))}.\!\)
| \(u\!\) | \(v\!\) | \(f\!\) | \(g\!\) |
|
\(\begin{matrix} 0 \\[4pt] 0 \\[4pt] 1 \\[4pt] 1 \end{matrix}\!\) |
\(\begin{matrix} 0 \\[4pt] 1 \\[4pt] 0 \\[4pt] 1 \end{matrix}\!\) |
\(\begin{matrix} 0 \\[4pt] 1 \\[4pt] 1 \\[4pt] 1 \end{matrix}\!\) |
\(\begin{matrix} 1 \\[4pt] 0 \\[4pt] 0 \\[4pt] 1 \end{matrix}\!\) |
Next, each propositional form is individually represented in the fashion shown in Tables 23-i and 23-ii, using \({}^{\backprime\backprime} f {}^{\prime\prime}\!\) and \({}^{\backprime\backprime} g {}^{\prime\prime}\!\) as function names and creating new variables \(x\!\) and \(y\!\) to hold the associated functional values. This pair of Tables outlines the first stage in the transition from the \(2\!\)-dimensional universes of \(f\!\) and \(g\!\) to the \(3\!\)-dimensional universes of \(\theta f\!\) and \(\theta g.\!\) The top halves of the Tables replicate the truth table patterns for \(f\!\) and \(g\!\) in the form \(f : [u, v] \to [x]\!\) and \(g : [u, v] \to [y].\!\) The bottom halves of the tables print the negatives of these pictures, as it were, and paste the truth tables for \(\texttt{(} f \texttt{)}\!\) and \(\texttt{(} g \texttt{)}\!\) under the copies for \(f\!\) and \(g.\!\) At this stage, the columns for \(\theta f\!\) and \(\theta g\!\) are appended almost as afterthoughts, amounting to indicator functions for the sets of ordered triples that make up the functions \(f\!\) and \(g.\!\)
|
|
All the data are now in place to give the truth tables for \(\theta f\!\) and \(\theta g.\!\) All that remains to be done is to permute the rows and change the roles of \(x\!\) and \(y\!\) from dependent to independent variables. In Tables 24-i and 24-ii the rows are arranged in such a way as to put the 3-tuples \((u, v, x)\!\) and \((u, v, y)\!\) in binary numerical order, suitable for viewing as the arguments of the maps \(\theta f = \varphi : [u, v, x] \to \mathbb{B}\!\) and \(\theta g = \gamma : [u, v, y] \to \mathbb{B}.\!\) Moreover, the structure of the tables is altered slightly, allowing the now vestigial functions \(\theta f\!\) and \(\theta g\!\) to be passed over without further attention and shifting the heavy vertical bars a notch to the right. In effect, this clinches the fact that the thematic variables \(x := \check{f}\!\) and \(y := \check{g}\!\) are now treated as independent variables.
|
|
An optional reshuffling of the rows brings additional features of the thematic extensions to light. Leaving the columns in place for the sake of comparison, Tables 25-i and 25-ii sort the rows in a different order, in effect treating \(x\!\) and \(y\!\) as the primary variables in their respective 3-tuples. Regarding the thematic extensions in the form \(\varphi : [x, u, v] \to \mathbb{B}\!\) and \(\gamma : [y, u, v] \to \mathbb{B}\!\) makes it easier to see in this tabular setting a property that was graphically obvious in the venn diagrams above. Specifically, when the thematic variable \(\check{F}\!\) is true then \(\theta F\!\) exhibits the pattern of the original \(F,\!\) and when \(\check{F}\!\) is false then \(\theta F\!\) exhibits the pattern of its negation \(\texttt{(} F \texttt{)}.\!\)
|
|
Finally, Tables 26-i and 26-ii compare the tacit extensions \(\boldsymbol\varepsilon : [u, v] \to [u, v, x]\!\) and \(\boldsymbol\varepsilon : [u, v] \to [u, v, y]\!\) with the thematic extensions of the same types, as applied to the propositions \(f\!\) and \(g,\!\) respectively.
|
|
Table 27 summarizes the thematic extensions of all propositions on two variables. Column 4 lists the equations of form \(\texttt{((} \check{f_i}, f_i (u, v) \texttt{))}\!\) and Column 5 simplifies these equations into the form of algebraic expressions. As always, \({}^{\backprime\backprime} + {}^{\prime\prime}\!\) refers to exclusive disjunction and each \({}^{\backprime\backprime} \check{f} {}^{\prime\prime}\!\) appearing in the last two Columns refers to the corresponding variable name \({}^{\backprime\backprime} \check{f_i} {}^{\prime\prime}.~\!\)
| \({f}\!\) | \(\theta f\!\) | \(\theta f\!\) | ||
| \(u\colon\!\) | \(1~1~0~0\!\) | |||
| \(v\colon\!\) | \(1~0~1~0\!\) | |||
| \(f_{0}\!\) | \(0~0~0~0\!\) | \(\texttt{(~)}\!\) | \(\texttt{((} \check{f} \texttt{,~(~)~))}\!\) | \(\check{f} + 1\!\) |
|
\(\begin{matrix} f_{1} \\[4pt] f_{2} \\[4pt] f_{4} \\[4pt] f_{8} \end{matrix}\!\) |
\(\begin{matrix} 0~0~0~1 \\[4pt] 0~0~1~0 \\[4pt] 0~1~0~0 \\[4pt] 1~0~0~0 \end{matrix}\!\) |
\(\begin{matrix} \texttt{(} u \texttt{)(} v \texttt{)} \\[4pt] \texttt{(} u \texttt{)~} v \texttt{~} \\[4pt] \texttt{~} u \texttt{~(} v \texttt{)} \\[4pt] \texttt{~} u \texttt{~~} v \texttt{~} \end{matrix}\!\) |
\(\begin{array}{l} \texttt{((} \check{f} \texttt{,~(u)(v)~))} \\[4pt] \texttt{((} \check{f} \texttt{,~(u)~v~~))} \\[4pt] \texttt{((} \check{f} \texttt{,~~u~(v)~))} \\[4pt] \texttt{((} \check{f} \texttt{,~~u~~v~~))} \end{array}\) |
\(\begin{array}{l} \check{f} + u + v + uv \\[4pt] \check{f} + v + uv + 1 \\[4pt] \check{f} + u + uv + 1 \\[4pt] \check{f} + uv + 1 \end{array}\!\) |
|
\(\begin{matrix} f_{3} \\[4pt] f_{12} \end{matrix}\!\) |
\(\begin{matrix} 0~0~1~1 \\[4pt] 1~1~0~0 \end{matrix}\!\) |
\(\begin{matrix} \texttt{(} u \texttt{)} \\[4pt] \texttt{~} u \texttt{~} \end{matrix}\!\) |
\(\begin{array}{l} \texttt{((} \check{f} \texttt{,~(u)~))} \\[4pt] \texttt{((} \check{f} \texttt{,~~u~~))} \end{array}\!\) |
\(\begin{array}{l} \check{f} + u \\[4pt] \check{f} + u + 1 \end{array}\!\) |
|
\(\begin{matrix} f_{6} \\[4pt] f_{9} \end{matrix}\!\) |
\(\begin{matrix} 0~1~1~0 \\[4pt] 1~0~0~1 \end{matrix}\!\) |
\(\begin{matrix} \texttt{(} u \texttt{,} v \texttt{)} \\[4pt] \texttt{((} u \texttt{,} v \texttt{))} \end{matrix}\!\) |
\(\begin{array}{l} \texttt{((} \check{f} \texttt{,~~(} u \texttt{,} v \texttt{)~~))} \\[4pt] \texttt{((} \check{f} \texttt{,~((} u \texttt{,} v \texttt{))~))} \end{array}\!\) |
\(\begin{array}{l} \check{f} + u + v + 1 \\[4pt] \check{f} + u + v \end{array}\!\) |
|
\(\begin{matrix} f_{5} \\[4pt] f_{10} \end{matrix}\!\) |
\(\begin{matrix} 0~1~0~1 \\[4pt] 1~0~1~0 \end{matrix}\!\) |
\(\begin{matrix} \texttt{(} v \texttt{)} \\[4pt] \texttt{~} v \texttt{~} \end{matrix}\) |
\(\begin{array}{l} \texttt{((} \check{f} \texttt{,~(} v \texttt{)~))} \\[4pt] \texttt{((} \check{f} \texttt{,~~} v \texttt{~~))} \end{array}\!\) |
\(\begin{array}{l} \check{f} + v \\[4pt] \check{f} + v + 1 \end{array}\!\) |
|
\(\begin{matrix} f_{7} \\[4pt] f_{11} \\[4pt] f_{13} \\[4pt] f_{14} \end{matrix}\!\) |
\(\begin{matrix} 0~1~1~1 \\[4pt] 1~0~1~1 \\[4pt] 1~1~0~1 \\[4pt] 1~1~1~0 \end{matrix}\!\) |
\(\begin{matrix} \texttt{(~} u \texttt{~~} v \texttt{~)} \\[4pt] \texttt{(~} u \texttt{~(} v \texttt{))} \\[4pt] \texttt{((} u \texttt{)~} v \texttt{~)} \\[4pt] \texttt{((} u \texttt{)(} v \texttt{))} \end{matrix}\!\) |
\(\begin{array}{l} \texttt{((} \check{f} \texttt{,~(~} u \texttt{~~} v \texttt{~)~))} \\[4pt] \texttt{((} \check{f} \texttt{,~(~} u \texttt{~(} v \texttt{))~))} \\[4pt] \texttt{((} \check{f} \texttt{,~((} u \texttt{)~} v \texttt{~)~))} \\[4pt] \texttt{((} \check{f} \texttt{,~((} u \texttt{)(} v \texttt{))~))} \end{array}\!\) |
\(\begin{array}{l} \check{f} + uv \\[4pt] \check{f} + u + uv \\[4pt] \check{f} + v + uv \\[4pt] \check{f} + u + v + uv + 1 \end{array}\!\) |
| \(f_{15}\!\) | \(1~1~1~1\!\) | \(\texttt{((~))}\!\) | \(\texttt{((} \check{f} \texttt{,~((~))~))}\!\) | \(\check{f}\!\) |
In order to show what all of the thematic extensions from two dimensions to three dimensions look like in terms of coordinates, Tables 28 and 29 present ordinary truth tables for the functions \(f_i : \mathbb{B}^2 \to \mathbb{B}\!\) and for the corresponding thematizations \(\theta f_i = \varphi_i : \mathbb{B}^3 \to \mathbb{B}.\!\)
| \(u\!\) | \(v\!\) | \(f_{0}\!\) | \(f_{1}\!\) | \(f_{2}\!\) | \(f_{3}\!\) | \(f_{4}\!\) | \(f_{5}\!\) | \(f_{6}\!\) | \(f_{7}\!\) | \(f_{8}\!\) | \(f_{9}\!\) | \(f_{10}\!\) | \(f_{11}\!\) | \(f_{12}\!\) | \(f_{13}\!\) | \(f_{14}\!\) | \(f_{15}\!\) |
| \(0\!\) | \(0\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | ||||||||
| \(0\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | ||||||||
| \(1\!\) | \(0\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | ||||||||
| \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) |
| \(u\!\) | \(v\!\) | \(\check{f}\!\) | \(\varphi_{0}\!\) | \(\varphi_{1}\!\) | \(\varphi_{2}\!\) | \(\varphi_{3}\!\) | \(\varphi_{4}\!\) | \(\varphi_{5}\!\) | \(\varphi_{6}\!\) | \(\varphi_{7}\!\) | \(\varphi_{8}\!\) | \(\varphi_{9}\!\) | \(\varphi_{10}\!\) | \(\varphi_{11}\!\) | \(\varphi_{12}\!\) | \(\varphi_{13}\!\) | \(\varphi_{14}\!\) | \(\varphi_{15}\!\) |
| \(0\!\) | \(0\!\) | \(0\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | ||||||||
| \(0\!\) | \(0\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | ||||||||
| \(0\!\) | \(1\!\) | \(0\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | ||||||||
| \(0\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | ||||||||
| \(1\!\) | \(0\!\) | \(0\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | ||||||||
| \(1\!\) | \(0\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | ||||||||
| \(1\!\) | \(1\!\) | \(0\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | ||||||||
| \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) |
Propositional Transformations
|
If only the word ‘artificial’ were associated with the idea of art, or expert skill gained through voluntary apprenticeship (instead of suggesting the factitious and unreal), we might say that logical refers to artificial thought. |
||
| — John Dewey, How We Think, [Dew, 56–57] | ||
In this section we develop a comprehensive set of concepts for dealing with transformations between universes of discourse. In this most general setting the source and target universes of a transformation are allowed to be different, but may be the same. When we apply these concepts to dynamic systems we focus on the important special case of transformations that map a universe into itself, regarding them as the state transitions of a discrete dynamical process and placing them among the myriad ways that a universe of discourse might change, and by that change turn into itself.
Alias and Alibi Transformations
There are customarily two modes of understanding a transformation, at least, when we try to interpret its relevance to something in reality. A transformation always refers to a changing prospect, to say it in a unified but equivocal way, but this can be taken to mean either a subjective change in the interpreting observer's point of view or an objective change in the systematic subject of discussion. In practice these variant uses of the transformation concept are distinguished in the following terms:
- A perspectival or alias transformation refers to a shift in perspective or a change in language that takes place in the observer's frame of reference.
- A transitional or alibi transformation refers to a change of position or an alteration of state that occurs in the object system as it falls under study.
(For a recent discussion of the alias vs. alibi issue, as it relates to linear transformations in vector spaces and to other issues of an algebraic nature, see [MaB, 256, 582-4].)
Naturally, when we are concerned with the dynamical properties of a system, the transitional aspect of transformation is the factor that comes to the fore, and this involves us in contemplating all of the ways of changing a universe into itself while remaining under the rule of established dynamical laws. In the prospective application to dynamic systems, and to neural networks viewed in this light, our interest lies chiefly with the transformations of a state space into itself that constitute the state transitions of a discrete dynamic process. Nevertheless, many important properties of these transformations, and some constructions that we need to see most clearly, are independent of the transitional interpretation and are likely to be confounded with irrelevant features if presented first and only in that association.
In addition, and in partial contrast, intelligent systems are exactly that species of dynamic agents that have the capacity to have a point of view, and we cannot do justice to their peculiar properties without examining their ability to form and transform their own frames of reference in exposure to the elements of their own experience. In this setting, the perspectival aspect of transformation is the facet that shines most brightly, perhaps too often leaving us fascinated with mere glimmerings of its actual potential. It needs to be emphasized that nothing of the ordinary sort needs be moved in carrying out a transformation under the alias interpretation, that it may only involve a change in the forms of address, an amendment of the terms which are customed to approach and fashioned to describe the very same things in the very same world. But again, working within a discipline of realistic computation, we know how formidably complex and resource-consuming such transformations of perspective can be to implement in practice, much less to endow in the self-governed form of a nascently intelligent dynamical system.
Transformations of General Type
|
Es ist passiert, “it just sort of happened”, people said there when other people in other places thought heaven knows what had occurred. It was a peculiar phrase, not known in this sense to the Germans and with no equivalent in other languages, the very breath of it transforming facts and the bludgeonings of fate into something light as eiderdown, as thought itself. |
||
| — Robert Musil, The Man Without Qualities, [Mus, 34] | ||
Consider the situation illustrated in Figure 30, where the alphabets \(\mathcal{U} = \{ u, v \}\!\) and \(\mathcal{X} = \{ x, y, z \}\!\) are used to label basic features in two different logical universes, \(U^\bullet = [u, v]\!\) and \(X^\bullet = [x, y, z].\!\)
o-------------------------------------------------------o
| U |
| |
| o-----------o o-----------o |
| / \ / \ |
| / o \ |
| / / \ \ |
| / / \ \ |
| o o o o |
| | | | | |
| | u | | v | |
| | | | | |
| o o o o |
| \ \ / / |
| \ \ / / |
| \ o / |
| \ / \ / |
| o-----------o o-----------o |
| |
| |
o---------------------------o---------------------------o
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
o-------------------------o o-------------------------o o-------------------------o
| U | | U | | U |
| o---o o---o | | o---o o---o | | o---o o---o |
| / \ / \ | | / \ / \ | | / \ / \ |
| / o \ | | / o \ | | / o \ |
| / / \ \ | | / / \ \ | | / / \ \ |
| o o o o | | o o o o | | o o o o |
| | u | | v | | | | u | | v | | | | u | | v | |
| o o o o | | o o o o | | o o o o |
| \ \ / / | | \ \ / / | | \ \ / / |
| \ o / | | \ o / | | \ o / |
| \ / \ / | | \ / \ / | | \ / \ / |
| o---o o---o | | o---o o---o | | o---o o---o |
| | | | | |
o-------------------------o o-------------------------o o-------------------------o
\ | \ / | /
\ | \ / | /
\ | \ / | /
\ | \ / | /
\ g | \ f / | h /
\ | \ / | /
\ | \ / | /
\ | \ / | /
\ | \ / | /
\ o----------|-----------\-----/-----------|----------o /
\ | X | \ / | | /
\ | | \ / | | /
\ | | o-----o-----o | | /
\| | / \ | |/
\ | / \ | /
|\ | / \ | /|
| \ | / \ | / |
| \ | / \ | / |
| \ | o x o | / |
| \ | | | | / |
| \ | | | | / |
| \ | | | | / |
| \ | | | | / |
| \ | | | | / |
| \| | | |/ |
| o--o--------o o--------o--o |
| / \ \ / / \ |
| / \ \ / / \ |
| / \ o / \ |
| / \ / \ / \ |
| / \ / \ / \ |
| o o--o-----o--o o |
| | | | | |
| | | | | |
| | | | | |
| | y | | z | |
| | | | | |
| | | | | |
| o o o o |
| \ \ / / |
| \ \ / / |
| \ o / |
| \ / \ / |
| \ / \ / |
| o-----------o o-----------o |
| |
| |
o---------------------------------------------------o
\ /
\ /
\ /
\ /
\ /
\ p , q /
\ /
\ /
\ /
\ /
\ /
\ /
\ /
o
Figure 30. Generic Frame of a Logical Transformation
|
Enter the picture, as we usually do, in the middle of things, with features like \(x, y , z\!\) that present themselves to be simple enough in their own right and that form a satisfactory, if temporary foundation to provide a basis for discussion. In this universe and on these terms we find expression for various propositions and questions of principal interest to ourselves, as indicated by the maps \(p, q : X \to \mathbb{B}.\!\) Then we discover that the simple features \(\{ x, y, z \}\!\) are really more complex than we thought at first, and it becomes useful to regard them as functions \(\{ f, g, h \}\!\) of other features \(\{ u, v \}\!\) that we place in a preface to our original discourse, or suppose as topics of a preliminary universe of discourse \(U^\bullet = [u, v].\!\) It may happen that these late-blooming but pre-ambling features are found to lie closer, in a sense that may be our job to determine, to the central nature of the situation of interest, in which case they earn our regard as being more fundamental, but these functions and features are only required to supply a critical stance on the universe of discourse or an alternate perspective on the nature of things in order to be preserved as useful.
A particular transformation \(F : [u, v] \to [x, y, z]\!\) may be expressed by a system of equations, as shown below. Here, \(F\!\) is defined by its component maps \(F = (F_1, F_2, F_3) = (f, g, h),\!\) where each component map in \(\{ f, g, h \}\!\) is a proposition of type \(\mathbb{B}^n \to \mathbb{B}^1.\!\)
|
\(\begin{matrix} x & = & f(u, v) \\[10pt] y & = & g(u, v) \\[10pt] z & = & h(u, v) \end{matrix}\) |
Regarded as a logical statement, this system of equations expresses a relation between a collection of freely chosen propositions \(\{ f, g, h \}\!\) in one universe of discourse and the special collection of simple propositions \(\{ x, y, z \}\!\) on which is founded another universe of discourse. Growing familiarity with a particular transformation of discourse, and the desire to achieve a ready understanding of its implications, requires that we be able to convert this information about generals and simples into information about all the main subtypes of propositions, including the linear and singular propositions.
Analytic Expansions : Operators and Functors
|
Consider what effects that might conceivably have practical bearings you conceive the objects of your conception to have. Then, your conception of those effects is the whole of your conception of the object. |
||
| — C.S. Peirce, “The Maxim of Pragmatism”, CP 5.438 | ||
Given the barest idea of a logical transformation, as suggested by the sketch in Figure 30, and having conceptualized the universe of discourse, with all of its points and propositions, as a beginning object of discussion, we are ready to enter the next phase of our investigation.
Operators on Propositions and Transformations
The next step is naturally inclined toward objects of the next higher order, namely, with operators that take in argument lists of logical transformations and that give back specified types of logical transformations as their results. For our present aims, we do not need to consider the most general class of such operators, nor any one of them for its own sake. Rather, we are interested in the special sorts of operators that arise in the study and analysis of logical transformations. Figuratively speaking, these operators serve as instruments for the live tomography (and hopefully not the vivisection) of the forms of change under view. Beyond that, they open up ways to implement the changes of view that we need to grasp all the variations on a transformational theme, or to appreciate enough of its significant features to “get the drift” of the change occurring, to form a passing acquaintance or a synthetic comprehension of its general character and disposition.
The simplest type of operator is one that takes a single transformation as an argument and returns a single transformation as a result, and most of the operators explicitly considered in our discussion will be of this kind. Figure 31 illustrates the typical situation.
o---------------------------------------o | | | | | U% F X% | | o------------------>o | | | | | | | | | | | | | | | | | | !W! | | !W! | | | | | | | | | | | | | | v v | | o------------------>o | | !W!U% !W!F !W!X% | | | | | o---------------------------------------o Figure 31. Operator Diagram (1) |
In this Figure \({}^{\backprime\backprime} \mathsf{W} {}^{\prime\prime}\!\) stands for a generic operator \(\mathsf{W},\!\) in this case one that takes a logical transformation \(F\!\) of type \((U^\bullet \to X^\bullet)\!\) into a logical transformation \(\mathsf{W}F\!\) of type \((\mathsf{W}U^\bullet \to \mathsf{W}X^\bullet).\!\) Thus, the operator \(\mathsf{W}\!\) must be viewed as making assignments for both families of objects we have previously considered, that is, for universes of discourse like \({U^\bullet}\!\) and \({X^\bullet}\!\) and for logical transformations like \(F.\!\)
Note. Strictly speaking, an operator like \(\mathsf{W}\!\) works between two whole categories of universes and transformations, which we call the source and the target categories of \(\mathsf{W}.\!\) Given this setting, \(\mathsf{W}\!\) specifies for each universe \(U^\bullet\!\) in its source category a definite universe \(\mathsf{W}U^\bullet\!\) in its target category, and to each transformation \(F\!\) in its source category it assigns a unique transformation \(\mathsf{W}F\!\) in its target category. Naturally, this only works if \(\mathsf{W}\!\) takes the source \(U^\bullet\) and the target \(X^\bullet\) of the map \(F\!\) over to the source \(\mathsf{W}U^\bullet\!\) and the target \(\mathsf{W}X^\bullet\!\) of the map \(\mathsf{W}F.\!\) With luck or care enough, we can avoid ever having to put anything like that in words again, letting diagrams do the work. In the situations of present concern we are usually focused on a single transformation \(F,\!\) and thus we can take it for granted that the assignment of universes under \(\mathsf{W}\!\) is defined appropriately at the source and target ends of \(F.\!\) It is not always the case, though, that we need to use the particular names (like \({}^{\backprime\backprime} \mathsf{W}U^\bullet {}^{\prime\prime}\!\) and \({}^{\backprime\backprime} \mathsf{W}X^\bullet {}^{\prime\prime}\!\)) that \(\mathsf{W}\!\) assigns by default to its operative image universes. In most contexts we will usually have a prior acquaintance with these universes under other names and it is necessary only that we can tell from the information associated with an operator \(\mathsf{W}\!\) what universes they are.
In Figure 31 the maps \(F\!\) and \(\mathsf{W}F\!\) are displayed horizontally, the way one normally orients functional arrows in a written text, and \(\mathsf{W}\!\) rolls the map \(F\!\) downward into the images that are associated with \(\mathsf{W}F.\!\) In Figure 32 the same information is redrawn so that the maps \(F\!\) and \(\mathsf{W}F\!\) flow down the page, and \(\mathsf{W}\!\) unfurls the map \(F\!\) rightward into domains that are the eminent purview of \(\mathsf{W}F.\!\)
o---------------------------------------o | | | | | U% !W! !W!U% | | o------------------>o | | | | | | | | | | | | | | | | | | F | | !W!F | | | | | | | | | | | | | | v v | | o------------------>o | | X% !W! !W!X% | | | | | o---------------------------------------o Figure 32. Operator Diagram (2) |
The latter arrangement, as exhibited in Figure 32, is more congruent with the thinking about operators that we shall do in the rest of this discussion, since all logical transformations from here on out will be pictured vertically, after the fashion of Figure 30.
Differential Analysis of Propositions and Transformations
| The resultant metaphysical problem now is this: Does the man go round the squirrel or not? | ||
| — William James, Pragmatism, [Jam, 43] | ||
The approach to the differential analysis of logical propositions and transformations of discourse to be pursued here is carried out in terms of particular operators \(\mathsf{W}\!\) that act on propositions \(F\!\) or on transformations \(F\!\) to yield the corresponding operator maps \(\mathsf{W}F.\!\) The operator results then become the subject of a series of further stages of analysis, which take them apart into their propositional components, rendering them as a set of purely logical constituents. After this is done, all the parts are then re-integrated to reconstruct the original object in the light of a more complete understanding, at least in ways that enable one to appreciate certain aspects of it with fresh insight.
- Remark on Strategy. At this point we run into a set of conceptual difficulties that force us to make a strategic choice in how we proceed. Part of the problem can be remedied by extending our discussion of tacit extensions to the transformational context. But the troubles that remain are much more obstinate and lead us to try two different types of solution. The approach that we develop first makes use of a variant type of extension operator, the trope extension, to be defined below. This method is more conservative and requires less preparation, but has features which make it seem unsatisfactory in the long run. A more radical approach, but one with a better hope of long term success, makes use of the notion of contingency spaces. These are an even more generous type of extended universe than the kind we currently use, but are defined subject to certain internal constraints. The extra work needed to set up this method forces us to put it off to a later stage. However, as a compromise, and to prepare the ground for the next pass, we call attention to the various conceptual difficulties as they arise along the way and try to give an honest estimate of how well our first approach deals with them.
We now describe in general terms the particular operators that are instrumental to this form of analysis. The main series of operators all have the form:
|
\(\begin{matrix} \mathsf{W} & : & ( U^\bullet \to X^\bullet ) & \to & ( \mathrm{E}U^\bullet \to \mathrm{E}X^\bullet ) \end{matrix}\!\) |
If we assume that the source universe \(U^\bullet\) and the target universe \(X^\bullet\) have finite dimensions \(n\!\) and \(k,\!\) respectively, then each operator \(\mathsf{W}\!\) is encompassed by the same abstract type:
|
\(\begin{matrix} \mathsf{W} & : & ( [\mathbb{B}^n] \to [\mathbb{B}^k] ) & \to & ( [\mathbb{B}^n \times \mathbb{D}^n] \to [\mathbb{B}^k \times \mathbb{D}^k] ) \end{matrix}\!\) |
Since the range features of the operator result \(\mathsf{W}F : [\mathbb{B}^n \times \mathbb{D}^n] \to [\mathbb{B}^k \times \mathbb{D}^k]\) can be sorted by their ordinary versus differential qualities and the component maps can be examined independently, the complete operator \(\mathsf{W}\!\) can be separated accordingly into two components, in the form \(\mathsf{W} = (\boldsymbol\varepsilon, \mathrm{W}).\!\) Given a fixed context of source and target universes, \(\boldsymbol\varepsilon\!\) is always the same type of operator, a multiple component version of the tacit extension operators that were described earlier. In this context \(\boldsymbol\varepsilon\!\) has the form:
|
\(\begin{array}{lccccc} \text{Concrete type} & \boldsymbol\varepsilon & : & ( U^\bullet \to X^\bullet ) & \to & ( \mathrm{E}U^\bullet \to X^\bullet ) \\[10pt] \text{Abstract type} & \boldsymbol\varepsilon & : & ( [\mathbb{B}^n] \to [\mathbb{B}^k] ) & \to & ( [\mathbb{B}^n \times \mathbb{D}^n] \to [\mathbb{B}^k] ) \end{array}\) |
On the other hand, the operator \(\mathrm{W}\!\) is specific to each \(\mathsf{W}.\!\) In this context \(\mathrm{W}\!\) always has the form:
|
\(\begin{array}{lccccc} \text{Concrete type} & W & : & ( U^\bullet \to X^\bullet ) & \to & ( \mathrm{E}U^\bullet \to \mathrm{d}X^\bullet ) \\[10pt] \text{Abstract type} & W & : & ( [\mathbb{B}^n] \to [\mathbb{B}^k] ) & \to & ( [\mathbb{B}^n \times \mathbb{D}^n] \to [\mathbb{D}^k] ) \end{array}\) |
In the types just assigned to \(\boldsymbol\varepsilon\!\) and \(\mathrm{W}\!\) and by implication to their results \(\boldsymbol\varepsilon F\!\) and \(\mathrm{W}F,\!\) we have listed the most restrictive ranges defined for them rather than the more expansive target spaces that subsume these ranges. When there is need to recognize both, we may use type indications like the following:
|
\(\begin{matrix} \boldsymbol\varepsilon F & : & ( \mathrm{E}U^\bullet \to X^\bullet \subseteq \mathrm{E}X^\bullet ) & \cong & ( [\mathbb{B}^n \times \mathbb{D}^n] \to [\mathbb{B}^k] \subseteq [\mathbb{B}^k \times \mathbb{D}^k] ) \\[10pt] WF & : & ( \mathrm{E}U^\bullet \to \mathrm{d}X^\bullet \subseteq \mathrm{E}X^\bullet ) & \cong & ( [\mathbb{B}^n \times \mathbb{D}^n] \to [\mathbb{D}^k] \subseteq [\mathbb{B}^k \times \mathbb{D}^k] ) \end{matrix}\) |
Hopefully, though, a general appreciation of these subsumptions will prevent us from having to make such declarations more often than absolutely necessary.
In giving names to these operators we try to preserve as much of the traditional nomenclature and as many of the classical associations as possible. The chief difficulty in doing this is occasioned by the distinction between the “sans serif” operators \(\mathsf{W}\!\) and their “serified” components \(\mathrm{W},\!\) which forces us to find two distinct but parallel sets of terminology. Here is a plan to that purpose. First, the component operators \(\mathrm{W}\!\) are named by analogy with the corresponding operators in the classical difference calculus. Next, the complete operators \(\mathsf{W} = (\boldsymbol\varepsilon, \mathrm{W})\) are assigned titles according to their roles in a geometric or trigonometric allegory, if only to ensure that the tangent functor, that belongs to this family and whose exposition we are still working toward, comes out fit with its customary name. Finally, the operator results \(\mathsf{W}F\!\) and \(\mathrm{W}F\!\) can be fixed in our frame of reference by tethering the operative adjective for \(\mathsf{W}\!\) or \(\mathrm{W}\!\) to the anchoring epithet “map”, in conformity with an already standard practice.
The Secant Operator : E
|
Mr. Peirce, after pointing out that our beliefs are really rules for action, said that, to develop a thought's meaning, we need only determine what conduct it is fitted to produce: that conduct is for us its sole significance. |
||
| — William James, Pragmatism, [Jam, 46] | ||
Figures 33-i and 33-ii depict two stages in the form of analysis that will be applied to transformations throughout the remainder of this study. From now on our interest is staked on an operator denoted \({}^{\backprime\backprime} \mathsf{E} {}^{\prime\prime},\!\) which receives the principal investment of analytic attention, and on the constituent parts of \(\mathsf{E},\!\) which derive their shares of significance as developed by the analysis. In the sequel, we refer to \(\mathsf{E}\!\) as the secant operator, taking it for granted that a context has been chosen that defines its type. The secant operator has the component description \(\mathsf{E} = (\boldsymbol\varepsilon, \mathrm{E}),\!\) and its active ingredient \(\mathrm{E}\!\) is known as the enlargement operator. (Here, we name \(\mathrm{E}\!\) after the literal ancestor of the shift operator in the calculus of finite differences, defined so that \(\mathrm{E}f(x) = f(x+1)\!\) for any suitable function \(f,\!\) though of course the logical analogue that we take up here must have a rather different definition.)
U% $E$ $E$U% $E$U% $E$U% o------------------>o============o============o | | | | | | | | | | | | | | | | F | | $E$F = | $d$^0.F + | $r$^0.F | | | | | | | | | | | | v v v v o------------------>o============o============o X% $E$ $E$X% $E$X% $E$X% Figure 33-i. Analytic Diagram (1) |
U% $E$ $E$U% $E$U% $E$U% $E$U% o------------------>o============o============o============o | | | | | | | | | | | | | | | | | | | | F | | $E$F = | $d$^0.F + | $d$^1.F + | $r$^1.F | | | | | | | | | | | | | | | v v v v v o------------------>o============o============o============o X% $E$ $E$X% $E$X% $E$X% $E$X% Figure 33-ii. Analytic Diagram (2) |
In its action on universes \(\mathsf{E}\!\) yields the same result as \(\mathrm{E},\!\) a fact that can be expressed in equational form by writing \(\mathsf{E}U^\bullet = \mathrm{E}U^\bullet\!\) for any universe \(U^\bullet.\!\) Notice that the extended universes across the top and bottom of the diagram are indicated to be strictly identical, rather than requiring a corresponding decomposition for them. In a certain sense, the functional parts of \(\mathsf{E}F\!\) are partitioned into separate contexts that have to be re-integrated again, but the best image to use is that of making transparent copies of each universe and then overlapping their functional contents once more at the conclusion of the analysis, as suggested by the graphic conventions that are used at the top of Figure 30.
Acting on a transformation \(F\!\) from universe \(U^\bullet\!\) to universe \(X^\bullet,\!\) the operator \(\mathsf{E}\!\) determines a transformation \(\mathsf{E}F\!\) from \(\mathsf{E}U^\bullet\!\) to \(\mathsf{E}X^\bullet.\!\) The map \(\mathsf{E}F\!\) forms the main body of evidence to be investigated in performing a differential analysis of \(F.\!\) Because we shall frequently be focusing on small pieces of this map for considerable lengths of time, and consequently lose sight of the “big picture”, it is critically important to emphasize that the map \(\mathsf{E}F\!\) is a transformation that determines a relation from one extended universe into another. This means that we should not be satisfied with our understanding of a transformation \(F\!\) until we can lay out the full “parts diagram” of \(\mathsf{E}F\!\) along the lines of the generic frame in Figure 30.
Working within the confines of propositional calculus, it is possible to give an elementary definition of \(\mathsf{E}F\!\) by means of a system of propositional equations, as we now describe.
Given a transformation
| \(F = (F_1, \ldots, F_k) : \mathbb{B}^n \to \mathbb{B}^k\!\) |
of concrete type
| \(F : [u_1, \ldots, u_n] \to [x_1, \ldots, x_k],\!\) |
the transformation
| \(\mathsf{E}F = (F_1, \ldots, F_k, \mathrm{E}F_1, \ldots, \mathrm{E}F_k) : \mathbb{B}^n \times \mathbb{D}^n \to \mathbb{B}^k \times \mathbb{D}^k\!\) |
of concrete type
| \(\mathsf{E}F : [u_1, \dots, u_n, \mathrm{d}u_1, \dots, \mathrm{d}u_n] \to [x_1, \ldots, x_k, \mathrm{d}x_1, \ldots, \mathrm{d}x_k]\!\) |
is defined by means of the following system of logical equations:
|
\(\begin{matrix} x_1 & = & \boldsymbol\varepsilon F_1 (u_1, \ldots, u_n, \mathrm{d}u_1, \ldots, \mathrm{d}u_n) & = & F_1 (u_1, \ldots, u_n) \\[4pt] \cdots && \cdots && \cdots \\[4pt] x_k & = & \boldsymbol\varepsilon F_k (u_1, \ldots, u_n, \mathrm{d}u_1, \ldots, \mathrm{d}u_n) & = & F_k (u_1, \ldots, u_n) \\[16pt] \mathrm{d}x_1 & = & \mathrm{E}F_1 (u_1, \ldots, u_n, \mathrm{d}u_1, \ldots, \mathrm{d}u_n) & = & F_1 (u_1 + \mathrm{d}u_1, \ldots, u_n + \mathrm{d}u_n) \\[4pt] \cdots && \cdots && \cdots \\[4pt] \mathrm{d}x_k & = & \mathrm{E}F_k (u_1, \ldots, u_n, \mathrm{d}u_1, \ldots, \mathrm{d}u_n) & = & F_k (u_1 + \mathrm{d}u_1, \ldots, u_n + \mathrm{d}u_n) \end{matrix}\) |
It is important to note that this system of equations can be read as a conjunction of equational propositions, in effect, as a single proposition in the universe of discourse generated by all the named variables. Specifically, this is the universe of discourse over \(2(n+k)\!\) variables denoted by:
|
\(\begin{matrix} \mathrm{E}[\mathcal{U} \cup \mathcal{X}] & = & [u_1, \ldots, u_n, ~ x_1, \ldots, x_k, ~ \mathrm{d}u_1, \ldots, \mathrm{d}u_n, ~ \mathrm{d}x_1, \ldots, \mathrm{d}x_k]. \end{matrix}\) |
In this light, it should be clear that the system of equations defining \(\mathsf{E}F\!\) embodies, in a higher rank and differentially extended version, an analogy with the process of thematization that we treated earlier for propositions of type \(F : \mathbb{B}^n \to \mathbb{B}.\!\)
The entire collection of constraints that is represented in the above system of equations may be abbreviated by writing \(\mathsf{E}F = (\boldsymbol\varepsilon F, \mathrm{E}F),\!\) for any map \(F.\!\) This is tantamount to regarding \(\mathsf{E}\!\) as a complex operator, \(\mathsf{E} = (\boldsymbol\varepsilon, \mathrm{E}),\!\) with a form of application that distributes each component of the operator to work on each component of the operand, as follows:
|
\(\begin{matrix} \mathsf{E}F & = & (\boldsymbol\varepsilon, \mathrm{E})F & = & (\boldsymbol\varepsilon F, \mathrm{E}F) & = & (\boldsymbol\varepsilon F_1, \ldots, \boldsymbol\varepsilon F_k, ~ \mathrm{E}F_1, \ldots, \mathrm{E}F_k). \end{matrix}\) |
Quite a lot of “thematic infrastructure” or interpretive information is being swept under the rug in the use of such abbreviations. When confusion arises about the meaning of such constructions, one always has recourse to the defining system of equations, in its totality a purely propositional expression. This means that the parenthesized argument lists, that were used in this context to build an image of multi-component transformations, should not be expected to determine a well-defined product in themselves but only to serve as reminders of the prior thematic decisions (choices of variable names, etc.) that have to be made in order to determine one. Accordingly, the argument list notation can be regarded as a kind of thematic frame, an interpretive storage device that preserves the proper associations of concrete logical features between the extended universes at the source and target of \(\mathsf{E}F.\!\)
The generic notations \(\mathsf{d}^0\!F, \mathsf{d}^1\!F, \ldots, \mathsf{d}^m\!F\!\) in Figure 33 refer to the increasing orders of differentials that are extracted in the course of analyzing \(F.\!\) When the analysis is halted at a partial stage of development, notations like \(\mathsf{r}^0\!F, \mathsf{r}^1\!F, \ldots, \mathsf{r}^m\!F\!\) may be used to summarize the contributions to \(\mathsf{E}F\!\) that remain to be analyzed. The Figure illustrates a convention that makes \(\mathsf{r}^m\!F,\!\) in effect, the sum of all differentials of order strictly greater than \(m.\!\)
We next discuss the operators that figure into this form of analysis, describing their effects on transformations. In simplified or specialized contexts these operators tend to take on a variety of different names and notations, some of whose number we introduce along the way.
The Radius Operator : e
|
And the tangible fact at the root of all our thought-distinctions, however subtle, is that there is no one of them so fine as to consist in anything but a possible difference of practice. |
||
| — William James, Pragmatism, [Jam, 46] | ||
The operator identified as \(\mathrm{d}^0\!\) in the analytic diagram (Figure 33) has the sole purpose of creating a proxy for \(F\!\) in the appropriately extended context. Construed in terms of its broadest components, \(\mathrm{d}^0\!\) is equivalent to the doubly tacit extension operator \((\boldsymbol\varepsilon, \boldsymbol\varepsilon),\!\) in recognition of which let us redub it as \({}^{\backprime\backprime} \mathsf{e} {}^{\prime\prime}.\!\) Pursuing a geometric analogy, we may refer to \(\mathsf{e} =(\boldsymbol\varepsilon, \boldsymbol\varepsilon) = \mathrm{d}^0\!\) as the radius operator. The operation intended by all of these forms is defined by the following equation:
|
\(\begin{array}{lll} \mathsf{e}F & = & (\boldsymbol\varepsilon, \boldsymbol\varepsilon)F \\[4pt] & = & (\boldsymbol\varepsilon F, ~ \boldsymbol\varepsilon F) \\[4pt] & = & (\boldsymbol\varepsilon F_1, \ldots, \boldsymbol\varepsilon F_k, ~ \boldsymbol\varepsilon F_1, \ldots, \boldsymbol\varepsilon F_k). \end{array}\) |
which is tantamount to the system of equations below.
|
\(\begin{matrix} x_1 & = & \boldsymbol\varepsilon F_1 (u_1, \ldots, u_n, \mathrm{d}u_1, \ldots, \mathrm{d}u_n) & = & F_1 (u_1, \ldots, u_n) \\[4pt] \cdots && \cdots && \cdots \\[4pt] x_k & = & \boldsymbol\varepsilon F_k (u_1, \ldots, u_n, \mathrm{d}u_1, \ldots, \mathrm{d}u_n) & = & F_k (u_1, \ldots, u_n) \\[16pt] \mathrm{d}x_1 & = & \boldsymbol\varepsilon F_1 (u_1, \ldots, u_n, \mathrm{d}u_1, \ldots, \mathrm{d}u_n) & = & F_1 (u_1, \ldots, u_n) \\[4pt] \cdots && \cdots && \cdots \\[4pt] \mathrm{d}x_k & = & \boldsymbol\varepsilon F_k (u_1, \ldots, u_n, \mathrm{d}u_1, \ldots, \mathrm{d}u_n) & = & F_k (u_1, \ldots, u_n) \end{matrix}\) |
The Phantom of the Operators : η
|
I was wondering what the reason could be, when I myself raised my head and everything within me seemed drawn towards the Unseen, which was playing the most perfect music! |
||
| — Gaston Leroux, The Phantom of the Opera, [Ler, 81] | ||
We now describe an operator whose persistent but elusive action behind the scenes, whose slightly twisted and ambivalent character, and whose fugitive disposition, caught somewhere in flight between the arrantly negative and the positive but errant intent, has cost us some painstaking trouble to detect. In the end we shall place it among the other extensions and projections, as a shade among shadows, of muted tones and motley hue, that adumbrates its own thematic frame and paradoxically lights the way toward a whole new spectrum of values.
Given a transformation \(F : [u_1, \ldots, u_n] \to [x_1, \dots, x_k],\!\) we often have call to consider a family of related transformations, all having the form:
| \(F^\dagger : [u_1, \ldots, u_n, \mathrm{d}u_1, \ldots, \mathrm{d}u_n] \to [\mathrm{d}x_1, \dots, \mathrm{d}x_k].\!\) |
The operator \(\eta\) is introduced to deal with the simplest one of these maps:
| \(\eta F : [u_1, \ldots, u_n, \mathrm{d}u_1, \ldots, \mathrm{d}u_n] \to [\mathrm{d}x_1, \ldots \mathrm{d}x_k],\!\) |
which is defined by the following equations:
|
\(\begin{matrix} \mathrm{d}x_1 & = & \boldsymbol\varepsilon F_1 (u_1, \ldots, u_n, ~ \mathrm{d}u_1, \ldots, \mathrm{d}u_n) & = & F_1 (u_1, \ldots, u_n) \\[4pt] \cdots && \cdots && \cdots \\[4pt] \mathrm{d}x_k & = & \boldsymbol\varepsilon F_k (u_1, \ldots, u_n, ~ \mathrm{d}u_1, \ldots, \mathrm{d}u_n) & = & F_k (u_1, \ldots, u_n) \end{matrix}\) |
In effect, the operator \(\eta\!\) is nothing but the stand-alone version of a procedure that is otherwise invoked subordinate to the work of the radius operator \(\mathsf{e}.\!\) Operating independently, \(\eta\!\) achieves precisely the same results that the second \(\boldsymbol\varepsilon\!\) in \((\boldsymbol\varepsilon, \boldsymbol\varepsilon)\!\) accomplishes by working within the context of its ordered pair thematic frame. From this point on, because the use of \(\boldsymbol\varepsilon\!\) and \(\eta\!\) in this setting combines the aims of both the tacit and the thematic extensions, and because \(\eta\!\) reflects in regard to \(\boldsymbol\varepsilon\!\) little more than the application of a differential twist, a mere turn of phrase, we refer to \(\eta\!\) as the trope extension operator.
The Chord Operator : D
|
What difference would it practically make to any one if this notion rather than that notion were true? If no practical difference whatever can be traced, then the alternatives mean practically the same thing, and all dispute is idle. |
||
| — William James, Pragmatism, [Jam, 45] | ||
Next we discuss an operator that is always immanent in this form of analysis, and remains implicitly present in the entire proceeding. It may appear once as a record: a relic or revenant that reprises the reminders of an earlier stage of development. Or it may appear always as a resource: a reserve or redoubt that caches in advance an echo of what remains to be played out, cleared up, and requited in full at a future stage. And all of this remains true whether or not we recall the key at any time, and whether or not the subtending theme is recited explicitly at any stage of play.
This is the operator that is referred to as \(\mathsf{r}^0\!\) in the initial stage of analysis (Figure 33-i) and that is expanded as \(\mathsf{d}^1 + \mathsf{r}^1\!\) in the subsequent step (Figure 33-ii). In congruence, but not quite harmony with our allusions of analogy that are not quite geometry, we call this the chord operator and denote it \(\mathsf{D}.\!\) In the more casual terms that are here introduced, \(\mathsf{D}\) is defined as the remainder of \(\mathsf{E}\!\) and \(\mathsf{e}\!\) and it assigns a due measure to each undertone of accord or discord that is struck between the note of enterprise \(\mathsf{E}\!\) and the bar of exigency \(\mathsf{e}.\!\)
The tension between these counterposed notions, in balance transient but regular in stridence, may be refracted along familiar lines, though never by any such fraction resolved. In this style we write \(\mathsf{D} = (\boldsymbol\varepsilon, \mathrm{D}),\!\) calling \(\mathrm{D}\!\) the difference operator and noting that it plays a role in this realm of mutable and diverse discourse that is analogous to the part taken by the discrete difference operator in the ordinary difference calculus. Finally, we should note that the chord \(\mathsf{D}\!\) is not one that need be lost at any stage of development. At the \(m^\text{th}\!\) stage of play it can always be reconstituted in the following form:
|
\(\begin{array}{lll} \mathsf{D} & = & \mathsf{E} - \mathsf{e} \\[6pt] & = & \mathsf{r}^0 \\[6pt] & = & \mathsf{d}^1 + \mathsf{r}^1 \\[6pt] & = & \mathsf{d}^1 + \ldots + \mathsf{d}^m + \mathsf{r}^m \\[6pt] & = & \displaystyle \sum_{i=1}^m \mathsf{d}^i + \mathsf{r}^m \end{array}\) |
The Tangent Operator : T
|
They take part in scenes of whose significance they have no inkling. They are merely tangent to curves of history the beginnings and ends and forms of which pass wholly beyond their ken. So we are tangent to the wider life of things. |
||
| — William James, Pragmatism, [Jam, 300] | ||
The operator tagged as \(\mathsf{d}^1\!\) in the analytic diagram (Figure 33) is called the tangent operator and is usually denoted in this text as \(\mathsf{d}\!\) or \(\mathsf{T}.\!\) Because it has the properties required to qualify as a functor, namely, preserving the identity element of the composition operation and the articulated form of every composition of transformations, it also earns the title of a tangent functor. According to the custom adopted here, we dissect it as \(\mathsf{T} = \mathsf{d} = (\boldsymbol\varepsilon, \mathrm{d}),\!\) where \(\mathrm{d}\!\) is the operator that yields the first order differential \(\mathrm{d}F\!\) when applied to a transformation \(F,\!\) and whose name is legion.
Figure 34 illustrates a stage of analysis where we ignore everything but the tangent functor \(\mathsf{T}\!\) and attend to it chiefly as it bears on the first order differential \(\mathrm{d}F\!\) in the analytic expansion of \(F.\!\) In this situation we often refer to the extended universes \(\mathrm{E}U^\bullet\!\) and \(\mathrm{E}X^\bullet\!\) under the equivalent designations \(\mathsf{T}U^\bullet\!\) and \(\mathsf{T}X^\bullet,\!\) respectively. The purpose of the tangent functor \(\mathsf{T}\!\) is to extract the tangent map \(\mathsf{T}F\!\) at each point of \(U^\bullet,\!\) and the tangent map \(\mathsf{T}F = (\boldsymbol\varepsilon, \mathrm{d})F\!\) tells us not only what the transformation \(F\!\) is doing at each point of the universe \(U^\bullet\!\) but also what \(F\!\) is doing to states in the neighborhood of that point, approximately, linearly, and relatively speaking.
U% $T$ $T$U% $T$U% o------------------>o============o | | | | | | | | | | | | F | | $T$F = | <!e!, d> F | | | | | | | | | v v v o------------------>o============o X% $T$ $T$X% $T$X% Figure 34. Tangent Functor Diagram |
- NB. There is one aspect of the preceding construction that remains especially problematic. Why did we define the operators \(\mathrm{W}\!\) in \(\{ \eta, \mathrm{E}, \mathrm{D}, \mathrm{d}, \mathrm{r} \}\!\) so that the ranges of their resulting maps all fall within the realms of differential quality, even fabricating a variant of the tacit extension operator to have that character? Clearly, not all of the operator maps \(\mathrm{W}F\!\) have equally good reasons for placing their values in differential stocks. The reason for it appears to be that, without doing this, we cannot justify the comparison and combination of their functional values in the various analytic steps. By default, only those values in the same functional component can be brought into algebraic modes of interaction. Up till now the only mechanism provided for their broader association has been a purely logical one, their common placement in a target universe of discourse, but the task of converting this logical circumstance into algebraic forms of application has not yet been taken up.
Transformations of Type B2 → B1
To study the effects of these analytic operators in the simplest possible setting, let us revert to a still more primitive case. Consider the singular proposition \(J(u, v)= u\!\cdot\!v,\!\) regarded either as the functional product of the maps \(u\!\) and \(v\!\) or as the logical conjunction of the features \(u\!\) and \(v,\!\) a map whose fiber of truth \(J^{-1}(1)\!\) picks out the single cell of that logical description in the universe of discourse \(U^\bullet.\!\) Thus \(J,\!\) or \(u\!\cdot\!v,\!\) may be treated as another name for the point whose coordinates are \((1, 1)\!\) in \(U^\bullet.\!\)
Analytic Expansion of Conjunction
|
In her sufferings she read a great deal and discovered that she had lost something, the possession of which she had previously not been much aware of: a soul. What is that? It is easily defined negatively: it is simply what curls up and hides when there is any mention of algebraic series. |
||
| — Robert Musil, The Man Without Qualities, [Mus, 118] | ||
Figure 35 pictures the form of conjunction \(J : \mathbb{B}^2 \to \mathbb{B}\!\) as a transformation from the \(2\!\)-dimensional universe \([u, v]\!\) to the \(1\!\)-dimensional universe \([x].\!\) This is a subtle but significant change of viewpoint on the proposition, attaching an arbitrary but concrete quality to its functional value. Using the language introduced earlier, we can express this change by saying that the proposition \(J : \langle u, v \rangle \to \mathbb{B}\!\) is being recast into the thematized role of a transformation \(J : [u, v] \to [x],\!\) where the new variable \(x\!\) takes the part of a thematic variable \(\check{J}.\!\)
| \(\text{Figure 35.} ~~ \text{Conjunction as Transformation}\!\) |
Tacit Extension of Conjunction
|
I teach straying from me, yet who can stray from me? | |
| — Walt Whitman, Leaves of Grass, [Whi, 83] |
Earlier we defined the tacit extension operators \(\boldsymbol\varepsilon : X^\bullet \to Y^\bullet\!\) as maps embedding each proposition of a given universe \(X^\bullet~\!\) in a more generously given universe \(Y^\bullet \supset X^\bullet.\!\) Of immediate interest are the tacit extensions \(\boldsymbol\epsilon : U^\bullet \to \mathrm{E}U^\bullet,\!\) that locate each proposition of \(U^\bullet\!\) in the enlarged context of \(\mathrm{E}U^\bullet.\!\) In its application to the propositional conjunction \(J = u\!\cdot\!v\) in \([u, v],\!\) the tacit extension operator \(\boldsymbol\varepsilon\!\) yields the proposition \(\boldsymbol\varepsilon J\!\) in \(\mathrm{E}U^\bullet = [u, v, \mathrm{d}u, \mathrm{d}v].\!\) The extended proposition \(\boldsymbol\varepsilon J\!\) may be computed according to the scheme in Table 36, in effect doing nothing more that conjoining a tautology of \([\mathrm{d}u, \mathrm{d}v]\!\) to \(J\!\) in \(U^\bullet.\!\)
|
\(\begin{array}{*{9}{l}} \boldsymbol\varepsilon J & = & J {}_{^\langle} u, v {}_{^\rangle} \\[4pt] & = & u \cdot v \\[4pt] & = & u \cdot v \cdot \texttt{(} \mathrm{d}u \texttt{)} \cdot \texttt{(} \mathrm{d}v \texttt{)} & + & u \cdot v \cdot \texttt{(} \mathrm{d}u \texttt{)} \cdot \texttt{ } \mathrm{d}v \texttt{ } & + & u \cdot v \cdot \texttt{ } \mathrm{d}u \texttt{ } \cdot \texttt{(} \mathrm{d}v \texttt{)} & + & u \cdot v \cdot \texttt{ } \mathrm{d}u \texttt{ } \cdot \texttt{ } \mathrm{d}v \texttt{ } \end{array}\!\) |
|
\(\begin{array}{*{4}{l}} \boldsymbol\varepsilon J & = && u \cdot v \cdot \texttt{(} \mathrm{d}u \texttt{)} \cdot \texttt{(} \mathrm{d}v \texttt{)} \\[4pt] && + & u \cdot v \cdot \texttt{(} \mathrm{d}u \texttt{)} \cdot \texttt{~} \mathrm{d}v \texttt{~} \\[4pt] && + & u \cdot v \cdot \texttt{~} \mathrm{d}u \texttt{~} \cdot \texttt{(} \mathrm{d}v \texttt{)} \\[4pt] && + & u \cdot v \cdot \texttt{~} \mathrm{d}u \texttt{~} \cdot \texttt{~} \mathrm{d}v \texttt{~} \end{array}\!\) |
The lower portion of the Table contains the dispositional features of \(\boldsymbol\varepsilon J\!\) arranged in such a way that the variety of ordinary features spreads across the rows and the variety of differential features runs through the columns. This organization serves to facilitate pattern matching in the remainder of our computations. Again, the tacit extension is usually so trivial a concern that we do not always bother to make an explicit note of it, taking it for granted that any function \(F\!\) being employed in a differential context is equivalent to \(\boldsymbol\varepsilon F\!\) for a suitable \(\boldsymbol\varepsilon.\!\)
Figures 37-a through 37-d present several pictures of the proposition \(J\!\) and its tacit extension \(\boldsymbol\varepsilon J.\!\) Notice in these Figures how \(\boldsymbol\varepsilon J\!\) in \(\mathrm{E}U^\bullet\!\) visibly extends \(J\!\) in \(U^\bullet\!\) by annexing to the indicated cells of \(J\!\) all the arcs that exit from or flow out of them. In effect, this extension attaches to these cells all the dispositions that spring from them, in other words, it attributes to these cells all the conceivable changes that are their issue.
| \(\text{Figure 37-a.} ~~ \text{Tacit Extension of}~ J ~\text{(Areal)}\!\) |
| \(\text{Figure 37-b.} ~~ \text{Tacit Extension of}~ J ~\text{(Bundle)}\!\) |
| \(\text{Figure 37-c.} ~~ \text{Tacit Extension of}~ J ~\text{(Compact)}\!\) |
| \(\text{Figure 37-d.} ~~ \text{Tacit Extension of}~ J ~\text{(Digraph)}\!\) |
The computational scheme shown in Table 36 treated \(J\!\) as a proposition in \(U^\bullet\!\) and formed \(\boldsymbol\varepsilon J\!\) as a proposition in \(\mathrm{E}U^\bullet.\!\) When \(J\!\) is regarded as a mapping \(J : U^\bullet \to X^\bullet\!\) then \(\boldsymbol\varepsilon J\!\) must be obtained as a mapping \(\boldsymbol\varepsilon J : \mathrm{E}U^\bullet \to X^\bullet.\!\) By default, the tacit extension of the map \(J : [u, v] \to [x]\!\) is naturally taken to be a particular map,
| \(\boldsymbol\varepsilon J : [u, v, \mathrm{d}u, \mathrm{d}v] \to [x] \subseteq [x, \mathrm{d}x],\!\) |
namely, the one that looks like \(J\!\) when painted in the frame of the extended source universe and that takes the same thematic variable in the extended target universe as the one that \(J\!\) already takes.
But the choice of a particular thematic variable, for example \(x\!\) for \(\check{J},\!\) is a shade more arbitrary than the choice of original variable names \(\{ u, v \},\!\) so the map we are calling the trope extension,
| \(\eta J : [u, v, \mathrm{d}u, \mathrm{d}v] \to [\mathrm{d}x] \subseteq [x, \mathrm{d}x],\!\) |
since it looks just the same as \(\boldsymbol\varepsilon J\!\) in the way its fibers paint the source domain, belongs just as fully to the family of tacit extensions, generically considered.
These considerations have the practical consequence that all of our computations and illustrations of \(\boldsymbol\varepsilon J\!\) perform the double duty of capturing \(\eta J\!\) as well. In other words, we are saved the work of carrying out calculations and drawing figures for the trope extension \(\eta J,\!\) because it would be identical to the work already done for \(\boldsymbol\varepsilon J.\!\) Since the computations given for \(\boldsymbol\varepsilon J\!\) are expressed solely in terms of the variables \(\{ u, v, \mathrm{d}u, \mathrm{d}v \},\!\) they work equally well for finding \(\eta J.\!\) Further, since each of the above Figures shows only how the level sets of \(\boldsymbol\varepsilon J\!\) partition the extended source universe \(\mathrm{E}U^\bullet = [u, v, \mathrm{d}u, \mathrm{d}v],\!\) all of them serve equally well as portraits of \(\eta J.\!\)
Enlargement Map of Conjunction
|
No one could have established the existence of any details that might not just as well have existed in earlier times too; but all the relations between things had shifted slightly. Ideas that had once been of lean account grew fat. |
||
| — Robert Musil, The Man Without Qualities, [Mus, 62] | ||
The enlargement map \(\mathrm{E}J\!\) is computed from the proposition \(J\!\) by making a particular class of formal substitutions for its variables, in this case \(u + \mathrm{d}u\!\) for \(u\!\) and \(v + \mathrm{d}v\!\) for \(v,\!\) and afterwards expanding the result in whatever way is found convenient.
Table 38 shows a typical scheme of computation, following a systematic method of exploiting boolean expansions over selected variables and ultimately developing \(\mathrm{E}J\!\) over the cells of \([u, v].\!\) The critical step of this procedure uses the facts that \(\texttt{(} 0, x \texttt{)} = 0 + x = x\!\) and \(\texttt{(} 1, x \texttt{)} = 1 + x = \texttt{(} x \texttt{)}\!\) for any boolean variable \(x.\!\)
|
\(\begin{array}{*{9}{l}} \mathrm{E}J & = & J_{(u + \mathrm{d}u, v + \mathrm{d}v)} \\[4pt] & = & \texttt{(} u \texttt{,} \mathrm{d}u \texttt{)} \cdot \texttt{(} v \texttt{,} \mathrm{d}v \texttt{)} \\[4pt] & = & \texttt{ } u \texttt{ } \texttt{ } v \texttt{ } \cdot J_{(1 + \mathrm{d}u, 1 + \mathrm{d}v)} & + & \texttt{ } u \texttt{ } \texttt{(} v \texttt{)} \cdot J_{(1 + \mathrm{d}u, \mathrm{d}v)} & + & \texttt{(} u \texttt{)} \texttt{ } v \texttt{ } \cdot J_{(\mathrm{d}u, 1 + \mathrm{d}v)} & + & \texttt{(} u \texttt{)} \texttt{(} v \texttt{)} \cdot J_{(\mathrm{d}u, \mathrm{d}v)} \\[4pt] & = & \texttt{ } u \texttt{ } \texttt{ } v \texttt{ } \cdot J_{(\texttt{(} \mathrm{d}u \texttt{)}, \texttt{(} \mathrm{d}v \texttt{)})} & + & \texttt{ } u \texttt{ } \texttt{(} v \texttt{)} \cdot J_{(\texttt{(} \mathrm{d}u \texttt{)}, \mathrm{d}v)} & + & \texttt{(} u \texttt{)} \texttt{ } v \texttt{ } \cdot J_{(\mathrm{d}u, \texttt{(} \mathrm{d}v \texttt{)})} & + & \texttt{(} u \texttt{)} \texttt{(} v \texttt{)} \cdot J_{(\mathrm{d}u, \mathrm{d}v)} \end{array}\!\) |
|
\(\begin{array}{*{9}{l}} \mathrm{E}J & = & \texttt{ } u \texttt{ } \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)} \texttt{(} \mathrm{d}v \texttt{)} \\[4pt] &&& + & \texttt{ } u \texttt{ } \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} \texttt{ } \mathrm{d}v \texttt{ } \\[4pt] &&&&& + & \texttt{(} u \texttt{)} \texttt{ } v \texttt{ } \cdot \texttt{ } \mathrm{d}u \texttt{ } \texttt{(} \mathrm{d}v \texttt{)} \\[4pt] &&&&&&& + & \texttt{(} u \texttt{)} \texttt{(} v \texttt{)} \cdot \texttt{ } \mathrm{d}u \texttt{ }~\texttt{ } \mathrm{d}v \texttt{ } \end{array}\) |
Table 39 exhibits another method that happens to work quickly in this particular case, using distributive laws to multiply things out in an algebraic manner, arranging the notations of feature and fluxion according to a scale of simple character and degree. Proceeding this way leads through an intermediate step which, in chiming the changes of ordinary calculus, should take on a familiar ring. Consequential properties of exclusive disjunction then carry us on to the concluding line.
|
\(\begin{array}{*{9}{c}} \mathrm{E}J & = & (u + \mathrm{d}u) \cdot (v + \mathrm{d}v) \\[6pt] & = & u \cdot v & + & u \cdot \mathrm{d}v & + & v \cdot \mathrm{d}u & + & \mathrm{d}u \cdot \mathrm{d}v \\[6pt] \mathrm{E}J & = & \texttt{ } u \texttt{ } \texttt{ } v \texttt{ } \cdot \texttt{(} \mathrm{d}u \texttt{)} \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{ } u \texttt{ } \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} \texttt{ } \mathrm{d}v \texttt{ } & + & \texttt{(} u \texttt{)} \texttt{ } v \texttt{ } \cdot \texttt{ } \mathrm{d}u \texttt{ } \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} \texttt{(} v \texttt{)} \cdot \texttt{ } \mathrm{d}u \texttt{ }~\texttt{ } \mathrm{d}v \texttt{ } \end{array}\!\) |
Figures 40-a through 40-d present several views of the enlarged proposition \(\mathrm{E}J.\!\)
| \(\text{Figure 40-a.} ~~ \text{Enlargement of}~ J ~\text{(Areal)}\!\) |
| \(\text{Figure 40-b.} ~~ \text{Enlargement of}~ J ~\text{(Bundle)}\!\) |
| \(\text{Figure 40-c.} ~~ \text{Enlargement of}~ J ~\text{(Compact)}\!\) |
| \(\text{Figure 40-d.} ~~ \text{Enlargement of}~ J ~\text{(Digraph)}\!\) |
An intuitive reading of the proposition \(\mathrm{E}J\!\) becomes available at this point. Recall that propositions in the extended universe \(\mathrm{E}U^\bullet\!\) express the dispositions of a system and the constraints that are placed on them. In other words, a differential proposition in \(\mathrm{E}U^\bullet\!\) can be read as referring to various changes that a system might undergo in and from its various states. In particular, we can understand \(\mathrm{E}J\!\) as a statement that tells us what changes need to be made with regard to each state in the universe of discourse in order to reach the truth of \(J,\!\) that is, the region of the universe where \(J\!\) is true. This interpretation is visibly clear in the Figures above and appeals to the imagination in a satisfying way but it has the added benefit of giving fresh meaning to the original name of the shift operator \(\mathrm{E}.\!\) Namely, \(\mathrm{E}J\!\) can be read as a proposition that enlarges on the meaning of \(J,\!\) in the sense of explaining its practical bearings and clarifying what it means in terms of actions and effects — the available options for differential action and the consequential effects that result from each choice.
Read this way, the enlargement \(\mathrm{E}J\!\) has strong ties to the normal use of \(J,\!\) no matter whether it is understood as a proposition or a function, namely, to act as a figurative device for indicating the models of \(J,\!\) in effect, pointing to the interpretive elements in its fiber of truth \(J^{-1}(1).\!\) It is this kind of “use” that is often contrasted with the “mention” of a proposition, and thereby hangs a tale.
Digression : Reflection on Use and Mention
|
Reflection is turning a topic over in various aspects and in various lights so that nothing significant about it shall be overlooked — almost as one might turn a stone over to see what its hidden side is like or what is covered by it. |
||
| — John Dewey, How We Think, [Dew, 57] | ||
The contrast drawn in logic between the use and the mention of a proposition corresponds to the difference that we observe in functional terms between using \({}^{\backprime\backprime} J \, {}^{\prime\prime}\!\) to indicate the region \(J^{-1}(1)\!\) and using \({}^{\backprime\backprime} J \, {}^{\prime\prime}\!\) to indicate the function \(J.\!\) You may think that one of these uses ought to be proscribed, and logicians are quick to prescribe against their confusion. But there seems to be no likelihood in practice that their interactions can be avoided. If the name \({}^{\backprime\backprime} J \, {}^{\prime\prime}\!\) is used as a sign of the function \(J,\!\) and if the function \(J\!\) has its use in signifying something else, as would constantly be the case when some future theory of signs has given a functional meaning to every sign whatsoever, then is not \(J,\!\) by transitivity a sign of the thing itself? There are, of course, two answers to this question. Not every act of signifying or referring need be transitive. Not every warrant or guarantee or certificate is automatically transferable, indeed, not many. Not every feature of a feature is a feature of the featuree. Otherwise, if a buffalo is white, and white is a color, then a buffalo would be a color.
The logical or pragmatic distinction between use and mention is cogent and necessary, and so is the analogous functional distinction between determining a value and determining what determines that value, but so are the normal techniques that we use to make these distinctions apply flexibly in practice. The way that the hue and cry about use and mention is raised in logical discussions, you might be led to think that this single dimension of choices embraces the only kinds of use worth mentioning and the only kinds of mention worth using. It will constitute the expeditionary and taxonomic tasks of that future theory of signs to explore and to classify the many other constellations and dimensions of use and mention that are yet to be opened up by the generative potential of full-fledged sign relations.
|
The well-known capacity that thoughts have — as doctors have discovered — for dissolving and dispersing those hard lumps of deep, ingrowing, morbidly entangled conflict that arise out of gloomy regions of the self probably rests on nothing other than their social and worldly nature, which links the individual being with other people and things; but unfortunately what gives them their power of healing seems to be the same as what diminishes the quality of personal experience in them. |
||
| — Robert Musil, The Man Without Qualities, [Mus, 130] | ||
Difference Map of Conjunction
|
“It doesn't matter what one does,” the Man Without Qualities said to himself, shrugging his shoulders. “In a tangle of forces like this it doesn't make a scrap of difference.” He turned away like a man who has learned renunciation, almost indeed like a sick man who shrinks from any intensity of contact. And then, striding through his adjacent dressing-room, he passed a punching-ball that hung there; he gave it a blow far swifter and harder than is usual in moods of resignation or states of weakness. |
||
| — Robert Musil, The Man Without Qualities, [Mus, 8] | ||
With the tacit extension map \(\boldsymbol\varepsilon J\!\) and the enlargement map \(\mathrm{E}J\!\) well in place, the difference map \(\mathrm{D}J\!\) can be computed along the lines displayed in Table 41, ending up with an expansion of \(\mathrm{D}J\!\) over the cells of \([u, v].\!\)
|
\(\begin{array}{*{9}{l}} \mathrm{D}J & = & \mathrm{E}J & + & \boldsymbol\varepsilon J \\[6pt] & = & J_{(u + \mathrm{d}u, v + \mathrm{d}v)} & + & J_{(u, v)} \\[6pt] & = & \texttt{(} u \texttt{,} \mathrm{d}u \texttt{)} \cdot \texttt{(} v \texttt{,} \mathrm{d}v \texttt{)} & + & u \cdot v \end{array}\) |
|
\(\begin{array}{*{9}{l}} \mathrm{D}J & = & u \cdot v \cdot \qquad 0 \\[6pt] & + & u \cdot v \cdot \texttt{(} \mathrm{d}u \texttt{)} \cdot \mathrm{d}v & + & u \cdot \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} \cdot \mathrm{d}v \\[6pt] & + & u \cdot v \cdot \texttt{~} \mathrm{d}u \cdot \texttt{(} \mathrm{d}v \texttt{)} &&& + & \texttt{(} u \texttt{)} \cdot v \cdot \mathrm{d}u \cdot \texttt{(} \mathrm{d}v \texttt{)} \\[6pt] & + & u \cdot v \cdot \texttt{~} \mathrm{d}u \;\cdot\; \mathrm{d}v \texttt{~} &&&&& + & \texttt{(} u \texttt{)} \cdot \texttt{(} v \texttt{)} \cdot \mathrm{d}u \cdot \mathrm{d}v \texttt{~} \end{array}\) |
|
\(\begin{array}{*{9}{l}} \mathrm{D}J & = & u \cdot v \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} & + & u \cdot \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} \cdot \mathrm{d}v & + & \texttt{(} u \texttt{)} \cdot v \cdot \mathrm{d}u \cdot \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} \cdot \texttt{(} v \texttt{)} \cdot \mathrm{d}u \cdot \mathrm{d}v \texttt{~} \end{array}\) |
Alternatively, the difference map \(\mathrm{D}J\!\) can be expanded over the cells of \([\mathrm{d}u, \mathrm{d}v]\!\) to arrive at the formulation shown in Table 42. The same development would be obtained from the previous Table by collecting terms in an alternate manner, along the rows rather than the columns in the middle portion of the Table.
|
\(\begin{array}{*{9}{l}} \mathrm{D}J & = & \boldsymbol\varepsilon J & + & \mathrm{E}J \\[6pt] & = & J_{(u, v)} & + & J_{(u + \mathrm{d}u, v + \mathrm{d}v)} \\[6pt] & = & u \cdot v & + & \texttt{(} u \texttt{,} \mathrm{d}u \texttt{)} \cdot \texttt{(} v \texttt{,} \mathrm{d}v \texttt{)} \\[6pt] & = & 0 & + & u \cdot \mathrm{d}v & + & v \cdot \mathrm{d}u & + & \mathrm{d}u \cdot \mathrm{d}v \\[6pt] \mathrm{D}J & = & 0 & + & u \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & v \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{((} u \texttt{,} v \texttt{))} \cdot \mathrm{d}u \cdot \mathrm{d}v \end{array}\) |
Even more simply, the same result is reached by matching up the propositional coefficients of \(\boldsymbol\varepsilon J\) and \(\mathrm{E}J\!\) along the cells of \([\mathrm{d}u, \mathrm{d}v]\!\) and adding the pairs under boolean addition, that is, “mod 2”, where 1 + 1 = 0, as shown in Table 43.
|
\(\begin{array}{*{5}{l}} \mathrm{D}J & = & \boldsymbol\varepsilon J & + & \mathrm{E}J \end{array}\) |
|
\(\begin{array}{*{9}{l}} \boldsymbol\varepsilon J & = & u \,\cdot\, v \,\cdot\, \texttt{(} \mathrm{d}u \texttt{)} \texttt{(} \mathrm{d}v \texttt{)} & + & u \,\cdot\, v \,\cdot\, \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & ~ u \,\cdot\, v \,\cdot\, \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} & + & ~ u \;\cdot\; v \;\cdot\; \mathrm{d}u ~ \mathrm{d}v \\[6pt] \mathrm{E}J & = & u \,\cdot\, v \,\cdot\, \texttt{(} \mathrm{d}u \texttt{)} \texttt{(} \mathrm{d}v \texttt{)} & + & u ~ \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & \texttt{(} u \texttt{)} ~ v \,\cdot\, \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} \texttt{(} v \texttt{)} \cdot\, \mathrm{d}u ~ \mathrm{d}v \end{array}\) |
|
\(\begin{array}{*{9}{l}} \mathrm{D}J & = & ~~ 0 ~~ \,\cdot\, ~ \texttt{(} \mathrm{d}u \texttt{)} \texttt{(} \mathrm{d}v \texttt{)} & + & ~~ u ~ \,\cdot\, ~~ \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & ~~~ v ~~ \,\cdot\, \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{((} u \texttt{,} v \texttt{))} \cdot \mathrm{d}u ~ \mathrm{d}v \end{array}\!\) |
The difference map \(\mathrm{D}J\!\) can also be given a dispositional interpretation. First, recall that \(\boldsymbol\varepsilon J\!\) exhibits the dispositions to change from anywhere in \(J\!\) to anywhere at all in the universe of discourse and \(\mathrm{E}J\!\) exhibits the dispositions to change from anywhere in the universe to anywhere in \(J.\!\) Next, observe that each of these classes of dispositions may be divided in accordance with the case of \(J\!\) versus \(\texttt{(} J \texttt{)}\!\) that applies to their points of departure and destination, as shown below. Then, since the dispositions corresponding to \(\boldsymbol\varepsilon J\) and \(\mathrm{E}J\!\) have in common the dispositions to preserve \(J,\!\) their symmetric difference \(\texttt{(} \boldsymbol\varepsilon J, \mathrm{E}J \texttt{)}\!\) is made up of all the remaining dispositions, which are in fact disposed to cross the boundary of \(J\!\) in one direction or the other. In other words, we may conclude that \(\mathrm{D}J\!\) expresses the collective disposition to make a definite change with respect to \(J,\!\) no matter what value it holds in the current state of affairs.
|
\(\begin{array}{lllll} \boldsymbol\varepsilon J & = & \{ \text{Dispositions from}~ J ~\text{to}~ J \} & + & \{ \text{Dispositions from}~ J ~\text{to}~ \texttt{(} J \texttt{)} \} \\[6pt] \mathrm{E}J & = & \{ \text{Dispositions from}~ J ~\text{to}~ J \} & + & \{ \text{Dispositions from}~ \texttt{(} J \texttt{)} ~\text{to}~ J \} \\[6pt] \mathrm{D}J & = & \{ \text{Dispositions from}~ J ~\text{to}~ \texttt{(} J \texttt{)} \} & + & \{ \text{Dispositions from}~ \texttt{(} J \texttt{)} ~\text{to}~ J \} \end{array}\) |
Figures 44-a through 44-d illustrate the difference proposition \(\mathrm{D}J.\!\)
| \(\text{Figure 44-a.} ~~ \text{Difference Map of}~ J ~\text{(Areal)}\!\) |
| \(\text{Figure 44-b.} ~~ \text{Difference Map of}~ J ~\text{(Bundle)}\!\) |
| \(\text{Figure 44-c.} ~~ \text{Difference Map of}~ J ~\text{(Compact)}\!\) |
| \(\text{Figure 44-d.} ~~ \text{Difference Map of}~ J ~\text{(Digraph)}\!\) |
Differential of Conjunction
|
By deploying discourse throughout a calendar, and by giving a date to each of its elements, one does not obtain a definitive hierarchy of precessions and originalities; this hierarchy is never more than relative to the systems of discourse that it sets out to evaluate. |
||
| — Michel Foucault, The Archaeology of Knowledge, [Fou, 143] | ||
Finally, at long last, the differential proposition \(\mathrm{d}J\!\) can be gleaned from the difference proposition \(\mathrm{D}J\!\) by ranging over the cells of \([u, v]\!\) and picking out the linear proposition of \([\mathrm{d}u, \mathrm{d}v]\!\) that is “closest” to the portion of \(\mathrm{D}J\!\) that touches on each point. The idea of distance that would give this definition unequivocal sense has been referred to in cautionary quotes, the kind we use to distance ourselves from taking a final position. There are obvious notions of approximation that suggest themselves, but finding one that can be justified as ultimately correct is not as straightforward as it seems.
|
He had drifted into the very heart of the world. From him to the distant beloved was as far as to the next tree. |
||
| — Robert Musil, The Man Without Qualities, [Mus, 144] | ||
Let us venture a guess as to where these developments might be heading. From the present vantage point it appears that the ultimate answer to the quandary of distances and the question of a fitting measure may be that, rather than having the constitution of an analytic series depend on our familiar notions of approach, proximity, and approximation, it will be found preferable, and perhaps unavoidable, to turn the tables and let the orders of approximation be defined in terms of our favored and operative notions of formal analysis. Only the aftermath of this conversion, if it does converge, could be hoped to prove whether this hortatory form of analysis and the cohort idea of an analytic form — the limitary concept of a self-corrective process and the coefficient concept of a completable product — are truly (in practical reality) the more inceptive and persistent of principles and really (for all practical purposes) the more effective and regulative of ideas.
Awaiting that determination, I proceed with what seems like the obvious course, and compute \(\mathrm{d}J\!\) according to the pattern in Table 45.
|
\(\begin{array}{c*{8}{l}} \mathrm{D}J & = & u\!\cdot\!v \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} & + & u \, \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} \, \mathrm{d}v & + & \texttt{(} u \texttt{)} \, v \cdot \mathrm{d}u \, \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u \!\cdot\! \mathrm{d}v \texttt{~} \\[6pt] \Downarrow \\[6pt] \mathrm{d}J & = & u\!\cdot\!v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & u \, \texttt{(} v \texttt{)} \cdot \mathrm{d}v & + & \texttt{(} u \texttt{)} \, v \cdot \mathrm{d}u & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 0 \end{array}\) |
Figures 46-a through 46-d illustrate the proposition \({\mathrm{d}J},\!\) rounded out in our usual array of prospects. This proposition of \(\mathrm{E}U^\bullet\!\) is what we refer to as the (first order) differential of \(J,\!\) and normally regard as the differential proposition corresponding to \(J.\!\)
| \(\text{Figure 46-a.} ~~ \text{Differential of}~ J ~\text{(Areal)}\!\) |
| \(\text{Figure 46-b.} ~~ \text{Differential of}~ J ~\text{(Bundle)}\!\) |
| \(\text{Figure 46-c.} ~~ \text{Differential of}~ J ~\text{(Compact)}\!\) |
| \(\text{Figure 46-d.} ~~ \text{Differential of}~ J ~\text{(Digraph)}\!\) |
Remainder of Conjunction
|
I bequeath myself to the dirt to grow from the grass I love, You will hardly know who I am or what I mean, Failing to fetch me at first keep encouraged, | |
| — Walt Whitman, Leaves of Grass, [Whi, 88] |
Let us recapitulate the story so far. We have in effect been carrying out a decomposition of the enlarged proposition \(\mathrm{E}J\!\) in a series of stages. First, we considered the equation \(\mathrm{E}J = \boldsymbol\varepsilon J + \mathrm{D}J,\!\) which was involved in the definition of \(\mathrm{D}J\!\) as the difference \(\mathrm{E}J - \boldsymbol\varepsilon J.\!\) Next, we contemplated the equation \(\mathrm{D}J = \mathrm{d}J + \mathrm{r}J,\!\) which expresses \(\mathrm{D}J\!\) in terms of two components, the differential \(\mathrm{d}J\!\) that was just extracted and the residual component \(\mathrm{r}J = \mathrm{D}J - \mathrm{d}J.~\!\) This remaining proposition \(\mathrm{r}J\!\) can be computed as shown in Table 47.
|
\(\begin{array}{*{5}{l}} \mathrm{r}J & = & \mathrm{D}J & + & \mathrm{d}J \end{array}\!\) |
|
\(\begin{array}{*{9}{l}} \mathrm{D}J & = & u \!\cdot\! v \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} \texttt{(} v \texttt{)} \cdot \mathrm{d}u \cdot \mathrm{d}v \\[6pt] \mathrm{d}J & = & u \!\cdot\! v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}v & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u & + & \texttt{(} u \texttt{)} \texttt{(} v \texttt{)} \cdot 0 \end{array}\) |
|
\(\begin{array}{*{9}{l}} \mathrm{r}J ~ & = & u \!\cdot\! v \cdot ~ \mathrm{d}u \cdot \mathrm{d}v ~~~~~~ & + & u \texttt{(} v \texttt{)} \cdot \, \mathrm{d}u \cdot \mathrm{d}v \, & + & \texttt{(} u \texttt{)} v \cdot \, \mathrm{d}u \cdot \mathrm{d}v \, & + & \texttt{(} u \texttt{)} \texttt{(} v \texttt{)} \cdot \, \mathrm{d}u \cdot \mathrm{d}v \end{array}\!\) |
As it happens, the remainder \(\mathrm{r}J\!\) falls under the description of a second order differential \(\mathrm{r}J = \mathrm{d}^2 J.\!\) This means that the expansion of \(\mathrm{E}J\!\) in the form:
|
\(\begin{array}{*{7}{l}} \mathrm{E}J & = & \boldsymbol\varepsilon J & + & \mathrm{D}J \\[6pt] & = & \boldsymbol\varepsilon J & + & \mathrm{d}J & + & \mathrm{r}J \\[6pt] & = & \mathrm{d}^0 J & + & \mathrm{d}^1 J & + & \mathrm{d}^2 J \end{array}\) |
which is nothing other than the propositional analogue of a Taylor series, is a decomposition that terminates in a finite number of steps.
Figures 48-a through 48-d illustrate the proposition \(\mathrm{r}J = \mathrm{d}^2 J,\!\) which forms the remainder map of \(J\!\) and also, in this instance, the second order differential of \(J.\!\)
| \(\text{Figure 48-a.} ~~ \text{Remainder of}~ J ~\text{(Areal)}\!\) |
| \(\text{Figure 48-b.} ~~ \text{Remainder of}~ J ~\text{(Bundle)}\!\) |
| \(\text{Figure 48-c.} ~~ \text{Remainder of}~ J ~\text{(Compact)}\!\) |
| \(\text{Figure 48-d.} ~~ \text{Remainder of}~ J ~\text{(Digraph)}\!\) |
Summary of Conjunction
To establish a convenient reference point for further discussion, Table 49 summarizes the operator actions that have been computed for the form of conjunction, as exemplified by the proposition \(J.\!\)
|
\(\begin{array}{c*{8}{l}} \boldsymbol\varepsilon J & = & u \!\cdot\! v \cdot 1 & + & u \texttt{(} v \texttt{)} \cdot 0 & + & \texttt{(} u \texttt{)} v \cdot 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 0 \\[6pt] \mathrm{E}J & = & u \!\cdot\! v \cdot \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u \cdot \mathrm{d}v \\[6pt] \mathrm{D}J & = & u \!\cdot\! v \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u \cdot \mathrm{d}v \\[6pt] \mathrm{d}J & = & u \!\cdot\! v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}v & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 0 \\[6pt] \mathrm{r}J & = & u \!\cdot\! v \cdot \mathrm{d}u \cdot \mathrm{d}v & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u \cdot \mathrm{d}v & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u \cdot \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u \cdot \mathrm{d}v \end{array}\) |
Analytic Series : Coordinate Method
|
And if he is told that something is the way it is, then he thinks: Well, it could probably just as easily be some other way. So the sense of possibility might be defined outright as the capacity to think how everything could “just as easily” be, and to attach no more importance to what is than to what is not. |
||
| — Robert Musil, The Man Without Qualities, [Mus, 12] | ||
Table 50 exhibits a truth table method for computing the analytic series (or the differential expansion) of a proposition in terms of coordinates.
| \(u\!\) | \(v\!\) | \(\mathrm{d}u\!\) | \(\mathrm{d}v\!\) | \(u'\!\) | \(v'\!\) | \(\boldsymbol\varepsilon J\!\) | \(\mathrm{E}J\!\) | \(\mathrm{D}J\!\) | \(\mathrm{d}J\!\) | \(\mathrm{d}^2\!J\!\) |
| \(0\!\) | \(0\!\) |
\(\begin{matrix}0\\0\\1\\1\end{matrix}\!\) |
\(\begin{matrix}0\\1\\0\\1\end{matrix}\!\) |
\(\begin{matrix}0\\0\\1\\1\end{matrix}\!\) |
\(\begin{matrix}0\\1\\0\\1\end{matrix}\!\) |
\(0\!\) |
\(\begin{matrix}0\\0\\0\\1\end{matrix}\!\) |
\(\begin{matrix}0\\0\\0\\1\end{matrix}\!\) |
\(\begin{matrix}0\\0\\0\\0\end{matrix}\!\) |
\(\begin{matrix}0\\0\\0\\1\end{matrix}\!\) |
| \(0\!\) | \(1\!\) |
\(\begin{matrix}0\\0\\1\\1\end{matrix}\!\) |
\(\begin{matrix}0\\1\\0\\1\end{matrix}\!\) |
\(\begin{matrix}0\\0\\1\\1\end{matrix}\!\) |
\(\begin{matrix}1\\0\\1\\0\end{matrix}\!\) |
\(0\!\) |
\(\begin{matrix}0\\0\\1\\0\end{matrix}\!\) |
\(\begin{matrix}0\\0\\1\\0\end{matrix}\!\) |
\(\begin{matrix}0\\0\\1\\1\end{matrix}\!\) |
\(\begin{matrix}0\\0\\0\\1\end{matrix}\!\) |
| \(1\!\) | \(0\!\) |
\(\begin{matrix}0\\0\\1\\1\end{matrix}\!\) |
\(\begin{matrix}0\\1\\0\\1\end{matrix}\!\) |
\(\begin{matrix}1\\1\\0\\0\end{matrix}\!\) |
\(\begin{matrix}0\\1\\0\\1\end{matrix}\!\) |
\(0\!\) |
\(\begin{matrix}0\\1\\0\\0\end{matrix}\!\) |
\(\begin{matrix}0\\1\\0\\0\end{matrix}\!\) |
\(\begin{matrix}0\\1\\0\\1\end{matrix}\!\) |
\(\begin{matrix}0\\0\\0\\1\end{matrix}\!\) |
| \(1\!\) | \(1\!\) |
\(\begin{matrix}0\\0\\1\\1\end{matrix}\!\) |
\(\begin{matrix}0\\1\\0\\1\end{matrix}\!\) |
\(\begin{matrix}1\\1\\0\\0\end{matrix}\!\) |
\(\begin{matrix}1\\0\\1\\0\end{matrix}\!\) |
\(1\!\) |
\(\begin{matrix}1\\0\\0\\0\end{matrix}\!\) |
\(\begin{matrix}0\\1\\1\\1\end{matrix}\!\) |
\(\begin{matrix}0\\1\\1\\0\end{matrix}\!\) |
\(\begin{matrix}0\\0\\0\\1\end{matrix}\!\) |
The first six columns of the Table, taken as a whole, represent the variables of a construct called the contingent universe \([u, v, \mathrm{d}u, \mathrm{d}v, u', v'],\!\) or the bundle of contingency spaces \([\mathrm{d}u, \mathrm{d}v, u', v']\!\) over the universe \([u, v].\!\) Their placement to the left of the double bar indicates that all of them amount to independent variables, but there is a co-dependency among them, as described by the following equations:
|
\(\begin{matrix} u' & = & u + \mathrm{d}u & = & \texttt{(} u \texttt{,} \mathrm{d}u \texttt{)} \\[8pt] v' & = & v + \mathrm{d}v & = & \texttt{(} v \texttt{,} \mathrm{d}v \texttt{)} \end{matrix}\) |
These relations correspond to the formal substitutions that are made in defining \(\mathrm{E}J\!\) and \(\mathrm{D}J.\!\) For now, the whole rigamarole of contingency spaces can be regarded as a technical device for achieving the effect of these substitutions, adapted to a setting where functional compositions and other symbolic manipulations are difficult to contemplate and execute.
The five columns to the right of the double bar in Table 50 contain the values of the dependent variables \(\{ \boldsymbol\varepsilon J, ~\mathrm{E}J, ~\mathrm{D}J, ~\mathrm{d}J, ~\mathrm{d}^2\!J \}.\!\) These are normally interpreted as values of functions \(\mathrm{W}J : \mathrm{E}U \to \mathbb{B}\!\) or as values of propositions in the extended universe \([u, v, \mathrm{d}u, \mathrm{d}v]\!\) but the dependencies prevailing in the contingent universe make it possible to regard these same final values as arising via functions on alternative lists of arguments, for example, the set \(\{ u, v, u', v' \}.\!\)
The column for \(\boldsymbol\varepsilon J\!\) is computed as \(J(u, v) = uv\!\) and together with the columns for \(u\!\) and \(v\!\) illustrates how we “share structure” in the Table by listing only the first entries of each constant block.
The column for \(\mathrm{E}J\!\) is computed by means of the following chain of identities, where the contingent variables \(u'\!\) and \(v'\!\) are defined as \(u' = u + \mathrm{d}u\!\) and \(v' = v + \mathrm{d}v.\!\)
|
\(\begin{matrix} \mathrm{E}J(u, v, \mathrm{d}u, \mathrm{d}v) & = & J(u + \mathrm{d}u, v + \mathrm{d}v) & = & J(u', v') \end{matrix}\) |
This makes it easy to determine \(\mathrm{E}J\!\) by inspection, computing the conjunction \(J(u', v') = u'v'\!\) from the columns headed \(u'\!\) and \(v'.\!\) Since each of these forms expresses the same proposition \(\mathrm{E}J\!\) in \(\mathrm{E}U^\bullet,\!\) the dependence on \(\mathrm{d}u\!\) and \(\mathrm{d}v\!\) is still present but merely left implicit in the final variant \(J(u', v').\!\)
- Note. On occasion, it is tempting to use the further notation \(J'(u, v) = J(u', v'),\!\) especially to suggest a transformation that acts on whole propositions, for example, taking the proposition \(J\!\) into the proposition \(J' = \mathrm{E}J.\!\) The prime \(( {}^{\prime} )\!\) then signifies an action that is mediated by a field of choices, namely, the values that are picked out for the contingent variables in sweeping through the initial universe. But this heaps an unwieldy lot of construed intentions on a rather slight character and puts too high a premium on the constant correctness of its interpretation. In practice, therefore, it is best to avoid this usage.
Given the values of \(\boldsymbol\varepsilon J\!\) and \(\mathrm{E}J,\!\) the columns for the remaining functions can be filled in quickly. The difference map is computed according to the relation \(\mathrm{D}J = \boldsymbol\varepsilon J + \mathrm{E}J.\!\) The first order differential \(\mathrm{d}J\!\) is found by looking in each block of constant argument pairs \(u, v\!\) and choosing the linear function of \(\mathrm{d}u, \mathrm{d}v\!\) that best approximates \(\mathrm{D}J\!\) in that block. Finally, the remainder is computed as \(\mathrm{r}J = \mathrm{D}J + \mathrm{d}J,\!\) in this case yielding the second order differential \(\mathrm{d}^2\!J.\!\)
Analytic Series : Recap
Let us now summarize the results of Table 50 by writing down for each column and for each block of constant argument pairs \(u, v\!\) a reasonably canonical symbolic expression for the function of \(\mathrm{d}u, \mathrm{d}v\!\) that appears there. The synopsis formed in this way is presented in Table 51. As one has a right to expect, it confirms the results that were obtained previously by operating solely in terms of the formal calculus.
| \(u\!\) | \(v\!\) | \(J\!\) | \(\mathrm{E}J\!\) | \(\mathrm{D}J\!\) | \(\mathrm{d}J\!\) | \(\mathrm{d}^2\!J\!\) |
|
\(\begin{matrix} 0 \\[4pt] 0 \\[4pt] 1 \\[4pt] 1 \end{matrix}\) |
\(\begin{matrix} 0 \\[4pt] 1 \\[4pt] 0 \\[4pt] 1 \end{matrix}\) |
\(\begin{matrix} 0 \\[4pt] 0 \\[4pt] 0 \\[4pt] 1 \end{matrix}\) |
\(\begin{matrix} \texttt{~} \mathrm{d}u \!\;\cdot\;\! \mathrm{d}v \texttt{~} \\[4pt] \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} \\[4pt] \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} \\[4pt] \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)} \end{matrix}\) |
\(\begin{matrix} \texttt{~} \mathrm{d}u \!\;\cdot\;\! \mathrm{d}v \texttt{~} \\[4pt] \texttt{~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)} \\[4pt] \texttt{(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~} \\[4pt] \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} \end{matrix}\) |
\(\begin{matrix} 0 \\[4pt] \mathrm{d}u \\[4pt] \mathrm{d}v \\[4pt] \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \end{matrix}\!\) |
\(\begin{matrix} \mathrm{d}u \cdot \mathrm{d}v \\[4pt] \mathrm{d}u \cdot \mathrm{d}v \\[4pt] \mathrm{d}u \cdot \mathrm{d}v \\[4pt] \mathrm{d}u \cdot \mathrm{d}v \end{matrix}\) |
Figures 52 and 53 provide a quick overview of the analysis performed so far, giving the successive decompositions of \(\mathrm{E}J = J + \mathrm{D}J\!\) and \(\mathrm{D}J = \mathrm{d}J + \mathrm{r}J\!\) in two different styles of diagram.
| \(\text{Figure 52.} ~~ \text{Decomposition of}~ \mathrm{E}J\!\) |
| \(\text{Figure 53.} ~~ \text{Decomposition of}~ \mathrm{D}J\!\) |
Terminological Interlude
|
Lastly, my attention was especially attracted, not so much to the scene, as to the mirrors that produced it. These mirrors were broken in parts. Yes, they were marked and scratched; they had been “starred”, in spite of their solidity … |
||
| — Gaston Leroux, The Phantom of the Opera, [Ler, 230] | ||
At this point several issues of terminology have accrued enough substance to intrude on our discussion. The remarks of this Subsection are intended to accomplish two goals. First, we call attention to significant aspects of the previous series of Figures, translating into literal terms what they depict in iconic forms, and we re-stress the most important structural elements they indicate. Next, we prepare the way for taking on more complex examples of transformations, those whose target universes have more than one dimension.
In talking about the actions of operators it is important to keep in mind the distinctions between the operators per se, their operands, and their results. Furthermore, in working with composite forms of operators \(\mathrm{W} = (\mathrm{W}_1, \ldots, \mathrm{W}_n),\!\) transformations \(\mathrm{F} = (\mathrm{F}_1, \ldots, \mathrm{F}_n),\!\) and target domains \(X^\bullet = [x_1, \ldots, x_n],\!\) we need to preserve a clear distinction between the compound entity of each given type and any one of its separate components. It is curious, given the usefulness of the concepts operator and operand, that we seem to lack a generic term, formed on the same root, for the corresponding result of an operation. Following the obvious paradigm would lead to words like opus, opera, and operant, but these words are too affected with clang associations to work well at present, though they might be adapted in time. One current usage gets around this problem by using the substantive map as a systematic epithet to express the result of each operator's action. We will follow this practice as far as possible, for example, using the phrase tangent map to denote the end product of the tangent functor acting on its operand map.
- Scholium. See [JGH, 6-9] for a good account of tangent functors and tangent maps in ordinary analysis and for examples of their use in mechanics. This work as a whole is a model of clarity in applying functorial principles to problems in physical dynamics.
Whenever we focus on isolated propositions, on single components of composite operators, or on the portions of transformations that have \(1\!\)-dimensional ranges, we are free to shift between the native form of a proposition \(J : U \to \mathbb{B}\!\) and the thematized form of a mapping \(J : U^\bullet \to [x]\!\) without much trouble. In these cases we are able to tolerate a higher degree of ambiguity about the precise nature of an operator's input and output domains than we otherwise might. For example, in the preceding treatment of the example \(J,\!\) and for each operator \(\mathrm{W}\!\) in the set \(\{ \boldsymbol\varepsilon, \eta, \mathrm{E}, \mathrm{D}, \mathrm{d}, \mathrm{r} \},\!\) both the operand \(J\!\) and the result \(\mathrm{W}J\!\) could be viewed in either one of two ways. On one hand we may treat them as propositions \(J : U \to \mathbb{B}\!\) and \(\mathrm{W}J : \mathrm{E}U \to \mathbb{B},\!\) ignoring the distinction between the range \([x] \cong \mathbb{B}\!\) of \(\boldsymbol\varepsilon J\!\) and the range \([\mathrm{d}x] \cong \mathbb{D}\!\) of the other types of \(\mathrm{W}J.\!\) This is what we usually do when we content ourselves with simply coloring in regions of venn diagrams. On the other hand we may view these entities as maps \(J : U^\bullet \to [x] = X^\bullet\!\) and \(\boldsymbol\varepsilon J : \mathrm{E}U^\bullet \to [x] \subseteq \mathrm{E}X^\bullet\!\) or \(\mathrm{W}J : \mathrm{E}U^\bullet \to [\mathrm{d}x] \subseteq \mathrm{E}X^\bullet,\!\) in which case the qualitative characters of the output features are not ignored.
At the beginning of this Section we recast the natural form of a proposition \(J : U \to \mathbb{B}\!\) into the thematic role of a transformation \(J : U^\bullet \to [x],\!\) where \(x\!\) was a variable recruited to express the newly independent \(\check{J}.\!\) However, in our computations and representations of operator actions we immediately lapsed back to viewing the results as native elements of the extended universe \(\mathrm{E}U^\bullet,\!\) in other words, as propositions \(\mathrm{W}J : \mathrm{E}U \to \mathbb{B},\!\) where \(\mathrm{W}\!\) ranged over the set \(\{ \boldsymbol\varepsilon, \mathrm{E}, \mathrm{D}, \mathrm{d}, \mathrm{r} \}.\!\) That is as it should be. We have worked hard to devise a language that gives us these advantages — the flexibility to exchange terms and types of equal information value and the capacity to reflect as quickly and as wittingly as a controlled reflex on the fibers of our propositions, independently of whether they express amusements, beliefs, or conjectures.
As we take on target spaces of increasing dimension, however, these types of confusions (and confusions of types) become less and less permissible. For this reason, Tables 54 and 55 present a rather detailed summary of the notation and the terminology we are using, as applied to the case \(J = uv.\!\) The rationale of these Tables is not so much to train more elephant guns on this poor drosophila of a concrete example but to invest our paradigm with enough solidity to bear the weight of abstraction to come.
Table 54 provides basic notation and descriptive information for the objects and operators used in this Example, giving the generic type (or broadest defined type) for each entity. Here, the sans serif operators \(\mathsf{W} \in \{ \mathsf{e}, \mathsf{E}, \mathsf{D}, \mathsf{d}, \mathsf{r} \}\!\) and their components \(\mathrm{W} \in \{ \boldsymbol\varepsilon, \eta, \mathrm{E}, \mathrm{D}, \mathrm{d}, \mathrm{r} \}\!\) both have the same broad type \(\mathsf{W}, \mathrm{W} : (U^\bullet \to X^\bullet) \to (\mathrm{E}U^\bullet \to \mathrm{E}X^\bullet),\!\) as appropriate to operators that map transformations \(J : U^\bullet \to X^\bullet\!\) to extended transformations \(\mathsf{W}J, \mathrm{W}J : \mathrm{E}U^\bullet \to \mathrm{E}X^\bullet.\!\)
| \(\text{Symbol}\!\) | \(\text{Notation}\!\) | \(\text{Description}\!\) | \(\text{Type}\!\) |
| \(U^\bullet\!\) | \(= [u, v]\!\) | \(\text{Source universe}\!\) | \([\mathbb{B}^2]\!\) |
| \(X^\bullet~\!\) | \(= [x]\!\) | \(\text{Target universe}\!\) | \([\mathbb{B}^1]~\!\) |
| \(\mathrm{E}U^\bullet\!\) | \(= [u, v, \mathrm{d}u, \mathrm{d}v]\!\) | \(\text{Extended source universe}\!\) | \([\mathbb{B}^2 \!\times\! \mathbb{D}^2]\) |
| \(\mathrm{E}X^\bullet\!\) | \(= [x, \mathrm{d}x]~\!\) | \(\text{Extended target universe}\!\) | \([\mathbb{B}^1 \!\times\! \mathbb{D}^1]\) |
| \(J\!\) | \(J : U \!\to\! \mathbb{B}\!\) | \(\text{Proposition}\!\) | \((\mathbb{B}^2 \!\to\! \mathbb{B}) \in [\mathbb{B}^2]\!\) |
| \(J\!\) | \(J : U^\bullet \!\to\! X^\bullet\!\) | \(\text{Transformation or Map}\!\) | \([\mathbb{B}^2] \!\to\! [\mathbb{B}^1]\!\) |
|
\(\begin{matrix} \boldsymbol\varepsilon \\ \eta \\ \mathrm{E} \\ \mathrm{D} \\ \mathrm{d} \end{matrix}\) |
\(\begin{array}{l} \mathrm{W} : U^\bullet \!\to\! \mathrm{E}U^\bullet, \\ \mathrm{W} : X^\bullet \!\to\! \mathrm{E}X^\bullet, \\ \mathrm{W} : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathrm{E}U^\bullet \!\to\! \mathrm{E}X^\bullet) \\ \text{for each}~ \mathrm{W} ~\text{in the set:} \\ \{ \boldsymbol\varepsilon, \eta, \mathrm{E}, \mathrm{D}, \mathrm{d} \} \end{array}\) |
\(\begin{array}{ll} \text{Tacit extension operator} & \boldsymbol\varepsilon \\ \text{Trope extension operator} & \eta \\ \text{Enlargement operator} & \mathrm{E} \\ \text{Difference operator} & \mathrm{D} \\ \text{Differential operator} & \mathrm{d} \end{array}\) |
\(\begin{array}{l} {[\mathbb{B}^2] \!\to\! [\mathbb{B}^2 \!\times\! \mathbb{D}^2]}, \\ {[\mathbb{B}^1] \!\to\! [\mathbb{B}^1 \!\times\! \mathbb{D}^1]}, \\\\ ([\mathbb{B}^2] \!\to\! [\mathbb{B}^1]) \!\to\! \\ ([\mathbb{B}^2 \!\times\! \mathbb{D}^2] \!\to\! [\mathbb{B}^1 \!\times\! \mathbb{D}^1]) \end{array}\) |
|
\(\begin{matrix} \mathsf{e} \\ \mathsf{E} \\ \mathsf{D} \\ \mathsf{T} \end{matrix}\) |
\(\begin{array}{l} \mathsf{W} : U^\bullet \!\to\! \mathsf{T}U^\bullet = \mathrm{E}U^\bullet, \\ \mathsf{W} : X^\bullet \!\to\! \mathsf{T}X^\bullet = \mathrm{E}X^\bullet, \\ \mathsf{W} : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathsf{T}U^\bullet \!\to\! \mathsf{T}X^\bullet) \\ \text{for each}~ \mathsf{W} ~\text{in the set:} \\ \{ \mathsf{e}, \mathsf{E}, \mathsf{D}, \mathsf{T} \} \end{array}\) |
\(\begin{array}{lll} \text{Radius operator} & \mathsf{e} & = (\boldsymbol\varepsilon, \eta) \\ \text{Secant operator} & \mathsf{E} & = (\boldsymbol\varepsilon, \mathrm{E}) \\ \text{Chord operator} & \mathsf{D} & = (\boldsymbol\varepsilon, \mathrm{D}) \\ \text{Tangent functor} & \mathsf{T} & = (\boldsymbol\varepsilon, \mathrm{d}) \end{array}\) |
\(\begin{array}{l} {[\mathbb{B}^2] \!\to\! [\mathbb{B}^2 \!\times\! \mathbb{D}^2]}, \\ {[\mathbb{B}^1] \!\to\! [\mathbb{B}^1 \!\times\! \mathbb{D}^1]}, \\\\ ([\mathbb{B}^2] \!\to\! [\mathbb{B}^1]) \!\to\! \\ ([\mathbb{B}^2 \!\times\! \mathbb{D}^2] \!\to\! [\mathbb{B}^1 \!\times\! \mathbb{D}^1]) \end{array}\) |
Table 55 supplies a more detailed outline of terminology for operators and their results. Here, we list the restrictive subtype (or narrowest defined subtype) that applies to each entity and we indicate across the span of the Table the whole spectrum of alternative types that color the interpretation of each symbol. For example, all the component operator maps \(\mathrm{W}J\!\) have \(1\!\)-dimensional ranges, either \(\mathbb{B}^1\!\) or \(\mathbb{D}^1,\!\) and so they can be viewed either as propositions \(\mathrm{W}J : \mathrm{E}U \to \mathbb{B}\!\) or as logical transformations \(\mathrm{W}J : \mathrm{E}U^\bullet \to X^\bullet.\!\) As a rule, the plan of the Table allows us to name each entry by detaching the underlined adjective at the left of its row and prefixing it to the generic noun at the top of its column. In one case, however, it is customary to depart from this scheme. Because the phrase differential proposition, applied to the result \(\mathrm{d}J : \mathrm{E}U \to \mathbb{D},\!\) does not distinguish it from the general run of differential propositions \(\mathrm{G}: \mathrm{E}U \to \mathbb{B},\!\) it is usual to single out \(\mathrm{d}J\!\) as the tangent proposition of \(J.\!\)
| \(\text{Operator}\!\) | \(\text{Proposition}\!\) | \(\text{Map}\!\) | |
| \(\begin{matrix}\underline\text{Tacit}\\\text{extension}\end{matrix}\) |
\(\begin{array}{l} \boldsymbol\varepsilon : U^\bullet \!\to\! \mathrm{E}U^\bullet,~ \boldsymbol\varepsilon : X^\bullet \!\to\! \mathrm{E}X^\bullet \\ \boldsymbol\varepsilon : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathrm{E}U^\bullet \!\to\! X^\bullet) \end{array}\) |
\(\begin{array}{l} \boldsymbol\varepsilon J : \langle u, v, \mathrm{d}u, \mathrm{d}v \rangle \!\to\! \mathbb{B} \\ \boldsymbol\varepsilon J : \mathbb{B}^2 \!\times\! \mathbb{D}^2 \!\to\! \mathbb{B} \end{array}\) |
\(\begin{array}{l} \boldsymbol\varepsilon J : [u, v, \mathrm{d}u, \mathrm{d}v] \!\to\! [x] \\ \boldsymbol\varepsilon J : [\mathbb{B}^2 \!\times\! \mathbb{D}^2] \!\to\! [\mathbb{B}^1] \end{array}\) |
| \(\begin{matrix}\underline\text{Trope}\\\text{extension}\end{matrix}\) |
\(\begin{array}{l} \eta : U^\bullet \!\to\! \mathrm{E}U^\bullet,~ \eta : X^\bullet \!\to\! \mathrm{E}X^\bullet \\ \eta : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathrm{E}U^\bullet \!\to\! \mathrm{d}X^\bullet) \end{array}\) |
\(\begin{array}{l} \eta J : \langle u, v, \mathrm{d}u, \mathrm{d}v \rangle \!\to\! \mathbb{D} \\ \eta J : \mathbb{B}^2 \!\times\! \mathbb{D}^2 \!\to\! \mathbb{D} \end{array}\) |
\(\begin{array}{l} \eta J : [u, v, \mathrm{d}u, \mathrm{d}v] \!\to\! [\mathrm{d}x] \\ \eta J : [\mathbb{B}^2 \!\times\! \mathbb{D}^2] \!\to\! [\mathbb{D}^1] \end{array}\) |
| \(\begin{matrix}\underline\text{Enlargement}\\\text{operator}\end{matrix}\) |
\(\begin{array}{l} \mathrm{E} : U^\bullet \!\to\! \mathrm{E}U^\bullet,~ \mathrm{E} : X^\bullet \!\to\! \mathrm{E}X^\bullet \\ \mathrm{E} : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathrm{E}U^\bullet \!\to\! \mathrm{d}X^\bullet) \end{array}\) |
\(\begin{array}{l} \mathrm{E}J : \langle u, v, \mathrm{d}u, \mathrm{d}v \rangle \!\to\! \mathbb{D} \\ \mathrm{E}J : \mathbb{B}^2 \!\times\! \mathbb{D}^2 \!\to\! \mathbb{D} \end{array}\) |
\(\begin{array}{l} \mathrm{E}J : [u, v, \mathrm{d}u, \mathrm{d}v] \!\to\! [\mathrm{d}x] \\ \mathrm{E}J : [\mathbb{B}^2 \!\times\! \mathbb{D}^2] \!\to\! [\mathbb{D}^1] \end{array}\) |
| \(\begin{matrix}\underline\text{Difference}\\\text{operator}\end{matrix}\) |
\(\begin{array}{l} \mathrm{D} : U^\bullet \!\to\! \mathrm{E}U^\bullet,~ \mathrm{D} : X^\bullet \!\to\! \mathrm{E}X^\bullet \\ \mathrm{D} : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathrm{E}U^\bullet \!\to\! \mathrm{d}X^\bullet) \end{array}\) |
\(\begin{array}{l} \mathrm{D}J : \langle u, v, \mathrm{d}u, \mathrm{d}v \rangle \!\to\! \mathbb{D} \\ \mathrm{D}J : \mathbb{B}^2 \!\times\! \mathbb{D}^2 \!\to\! \mathbb{D} \end{array}\) |
\(\begin{array}{l} \mathrm{D}J : [u, v, \mathrm{d}u, \mathrm{d}v] \!\to\! [\mathrm{d}x] \\ \mathrm{D}J : [\mathbb{B}^2 \!\times\! \mathbb{D}^2] \!\to\! [\mathbb{D}^1] \end{array}\) |
| \(\begin{matrix}\underline\text{Differential}\\\text{operator}\end{matrix}\) |
\(\begin{array}{l} \mathrm{d} : U^\bullet \!\to\! \mathrm{E}U^\bullet,~ \mathrm{d} : X^\bullet \!\to\! \mathrm{E}X^\bullet \\ \mathrm{d} : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathrm{E}U^\bullet \!\to\! \mathrm{d}X^\bullet) \end{array}\) |
\(\begin{array}{l} \mathrm{d}J : \langle u, v, \mathrm{d}u, \mathrm{d}v \rangle \!\to\! \mathbb{D} \\ \mathrm{d}J : \mathbb{B}^2 \!\times\! \mathbb{D}^2 \!\to\! \mathbb{D} \end{array}\) |
\(\begin{array}{l} \mathrm{d}J : [u, v, \mathrm{d}u, \mathrm{d}v] \!\to\! [\mathrm{d}x] \\ \mathrm{d}J : [\mathbb{B}^2 \!\times\! \mathbb{D}^2] \!\to\! [\mathbb{D}^1] \end{array}\!\) |
| \(\begin{matrix}\underline\text{Remainder}\\\text{operator}\end{matrix}\!\) |
\(\begin{array}{l} \mathrm{r} : U^\bullet \!\to\! \mathrm{E}U^\bullet,~ \mathrm{r} : X^\bullet \!\to\! \mathrm{E}X^\bullet \\ \mathrm{r} : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathrm{E}U^\bullet \!\to\! \mathrm{d}X^\bullet) \end{array}\) |
\(\begin{array}{l} \mathrm{r}J : \langle u, v, \mathrm{d}u, \mathrm{d}v \rangle \!\to\! \mathbb{D} \\ \mathrm{r}J : \mathbb{B}^2 \!\times\! \mathbb{D}^2 \!\to\! \mathbb{D} \end{array}\) |
\(\begin{array}{l} \mathrm{r}J : [u, v, \mathrm{d}u, \mathrm{d}v] \!\to\! [\mathrm{d}x] \\ \mathrm{r}J : [\mathbb{B}^2 \!\times\! \mathbb{D}^2] \!\to\! [\mathbb{D}^1] \end{array}\) |
| \(\begin{matrix}\underline\text{Radius}\\\text{operator}\end{matrix}\) |
\(\begin{array}{l} \mathsf{e} = (\boldsymbol\varepsilon, \eta) \\ \mathsf{e} : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathrm{E}U^\bullet \!\to\! \mathrm{E}X^\bullet) \end{array}\) |
\(\begin{array}{l} \mathsf{e}J : [u, v, \mathrm{d}u, \mathrm{d}v] \!\to\! [x, \mathrm{d}x] \\ \mathsf{e}J : [\mathbb{B}^2 \!\times\! \mathbb{D}^2] \!\to\! [\mathbb{B}^1 \!\times\! \mathbb{D}^1] \end{array}\) | |
| \(\begin{matrix}\underline\text{Secant}\\\text{operator}\end{matrix}\) |
\(\begin{array}{l} \mathsf{E} = (\boldsymbol\varepsilon, \mathrm{E}) \\ \mathsf{E} : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathrm{E}U^\bullet \!\to\! \mathrm{E}X^\bullet) \end{array}\) |
\(\begin{array}{l} \mathsf{E}J : [u, v, \mathrm{d}u, \mathrm{d}v] \!\to\! [x, \mathrm{d}x] \\ \mathsf{E}J : [\mathbb{B}^2 \!\times\! \mathbb{D}^2] \!\to\! [\mathbb{B}^1 \!\times\! \mathbb{D}^1] \end{array}\) | |
| \(\begin{matrix}\underline\text{Chord}\\\text{operator}\end{matrix}\) |
\(\begin{array}{l} \mathsf{D} = (\boldsymbol\varepsilon, \mathrm{D}) \\ \mathsf{D} : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathrm{E}U^\bullet \!\to\! \mathrm{E}X^\bullet) \end{array}\) |
\(\begin{array}{l} \mathsf{D}J : [u, v, \mathrm{d}u, \mathrm{d}v] \!\to\! [x, \mathrm{d}x] \\ \mathsf{D}J : [\mathbb{B}^2 \!\times\! \mathbb{D}^2] \!\to\! [\mathbb{B}^1 \!\times\! \mathbb{D}^1] \end{array}\) | |
| \(\begin{matrix}\underline\text{Tangent}\\\text{functor}\end{matrix}\) |
\(\begin{array}{l} \mathsf{T} = (\boldsymbol\varepsilon, \mathrm{d}) \\ \mathsf{T} : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathrm{E}U^\bullet \!\to\! \mathrm{E}X^\bullet) \end{array}\) |
\(\begin{array}{l} \mathrm{d}J : \langle u, v, \mathrm{d}u, \mathrm{d}v \rangle \!\to\! \mathbb{D} \\ \mathrm{d}J : \mathbb{B}^2 \!\times\! \mathbb{D}^2 \!\to\! \mathbb{D} \end{array}\) |
\(\begin{array}{l} \mathsf{T}J : [u, v, \mathrm{d}u, \mathrm{d}v] \!\to\! [x, \mathrm{d}x] \\ \mathsf{T}J : [\mathbb{B}^2 \!\times\! \mathbb{D}^2] \!\to\! [\mathbb{B}^1 \!\times\! \mathbb{D}^1] \end{array}\) |
End of Perfunctory Chatter : Time to Roll the Clip!
Two steps remain to finish the analysis of \(J\!\) that we began so long ago. First, we need to paste our accumulated heap of flat pictures into the frames of transformations, filling out the shapes of the operator maps \(\mathsf{W}J : \mathrm{E}U^\bullet \to \mathrm{E}X^\bullet.~\!\) This scheme is executed in two styles, using the areal views in Figures 56-a and the box views in Figures 56-b. Finally, in Figures 57-1 to 57-4 we put all the pieces together to construct the full operator diagrams for \(\mathsf{W} : J \to \mathsf{W}J.\!\) There is a considerable amount of redundancy among the following three series of Figures but that will hopefully provide a fuller picture of the operations under review, enabling these snapshots to serve as successive frames in the animation of logic they are meant to become.
Operator Maps : Areal Views
| \(\text{Figure 56-a1.} ~~ \text{Radius Map of the Conjunction}~ J = uv\!\) |
| \(\text{Figure 56-a2.} ~~ \text{Secant Map of the Conjunction}~ J = uv\!\) |
| \(\text{Figure 56-a3.} ~~ \text{Chord Map of the Conjunction}~ J = uv\!\) |
| \(\text{Figure 56-a4.} ~~ \text{Tangent Map of the Conjunction}~ J = uv\!\) |
Operator Maps : Box Views
| \(\text{Figure 56-b1.} ~~ \text{Radius Map of the Conjunction}~ J = uv\!\) |
| \(\text{Figure 56-b2.} ~~ \text{Secant Map of the Conjunction}~ J = uv\!\) |
| \(\text{Figure 56-b3.} ~~ \text{Chord Map of the Conjunction}~ J = uv\!\) |
| \(\text{Figure 56-b4.} ~~ \text{Tangent Map of the Conjunction}~ J = uv\!\) |
Operator Diagrams for the Conjunction J = uv
| \(\text{Figure 57-1.} ~~ \text{Radius Operator Diagram for the Conjunction}~ J = uv\!\) |
| \(\text{Figure 57-2.} ~~ \text{Secant Operator Diagram for the Conjunction}~ J = uv~\!\) |
| \(\text{Figure 57-3.} ~~ \text{Chord Operator Diagram for the Conjunction}~ J = uv\!\) |
| \(\text{Figure 57-4.} ~~ \text{Tangent Functor Diagram for the Conjunction}~ J = uv\!\) |
Taking Aim at Higher Dimensional Targets
|
The past and present wilt . . . . I have filled them and | |
| — Walt Whitman, Leaves of Grass, [Whi, 87] |
In the next Section we consider a transformation \(F\!\) of concrete type \(F : [u, v] \to [x, y]\!\) and abstract type \(F : [\mathbb{B}^2] \to [\mathbb{B}^2].\!\) From the standpoint of propositional calculus we naturally approach the task of understanding such a transformation by parsing it into component maps with \(1\!\)-dimensional ranges, as follows:
|
\(\begin{array}{ccccccl} F & = & (F_1, F_2) & = & (f, g) & : & [u, v] \to [x, y], \\[6pt] && F_1 & = & f & : & [u, v] \to [x], \\[6pt] && F_2 & = & g & : & [u, v] \to [y]. \end{array}\) |
Then we tackle the separate components, now viewed as propositions \(F_i : U \to \mathbb{B},\!\) one at a time. At the completion of this analytic phase, we return to the task of synthesizing these partial and transient impressions into an agile form of integrity, a solidly coordinated and deeply integrated comprehension of the ongoing transformation. (Very often, of course, in tangling with refractory cases, we never get as far as the beginning again.)
Let us now refer to the dimension of the target space or codomain as the toll (or tole) of a transformation, as distinguished from the dimension of the range or image that is customarily called the rank. When we keep to transformations with a toll of \(1,\!\) as \(J : [u, v] \to [x],\!\) we tend to get lazy about distinguishing a logical transformation from its component propositions. However, if we deal with transformations of a higher toll, this form of indolence can no longer be tolerated.
Well, perhaps we can carry it a little further. After all, the operator result \(\mathrm{W}J : \mathrm{E}U^\bullet \to \mathrm{E}X^\bullet\!\) is a map of toll \(2,\!\) and cannot be unfolded in one piece as a proposition. But when a map has rank \(1,\!\) like \(\boldsymbol\varepsilon J : \mathrm{E}U \to X \subseteq \mathrm{E}X\!\) or \(\mathrm{d}J : \mathrm{E}U \to \mathrm{d}X \subseteq \mathrm{E}X,\!\) we naturally choose to concentrate on the \(1\!\)-dimensional range of the operator result \(\mathrm{W}J,\!\) ignoring the final difference in quality between the spaces \(X\!\) and \(\mathrm{d}X,\!\) and view \(\mathrm{W}J\!\) as a proposition about \(\mathrm{E}U.\!\)
In this way, an initial ambivalence about the role of the operand \(J\!\) conveys a double duty to the result \(\mathrm{W}J.\!\) The pivot that is formed by our focus of attention is essential to the linkage that transfers this double moment, as the whole process takes its bearing and wheels around the precise measure of a narrow bead that we can draw on the range of \(\mathrm{W}J.\!\) This is the escapement that it takes to get away with what may otherwise seem to be a simple duplicity, and this is the tolerance that is needed to counterbalance a certain arrogance of equivocation, by all of which machinations we make ourselves free to indicate the operator results \(\mathrm{W}J\!\) as propositions or as transformations, indifferently.
But that's it, and no further. Neglect of these distinctions in range and target universes of higher dimensions is bound to cause a hopeless confusion. To guard against these adverse prospects, Tables 58 and 59 lay the groundwork for discussing a typical map \(F : [\mathbb{B}^2] \to [\mathbb{B}^2],\!\) and begin to pave the way to some extent for discussing any transformation of the form \(F : [\mathbb{B}^n] \to [\mathbb{B}^k].\!\)
| \(\text{Symbol}\!\) | \(\text{Notation}\!\) | \(\text{Description}\!\) | \(\text{Type}\!\) |
| \(U^\bullet\!\) | \(= [u, v]\!\) | \(\text{Source universe}\!\) | \([\mathbb{B}^n]\!\) |
| \(X^\bullet~\!\) | \(\begin{array}{l} = [x, y] \\ = [f, g] \end{array}\) | \(\text{Target universe}\!\) | \([\mathbb{B}^k]\!\) |
| \(\mathrm{E}U^\bullet\!\) | \(= [u, v, \mathrm{d}u, \mathrm{d}v]\!\) | \(\text{Extended source universe}\!\) | \([\mathbb{B}^n \!\times\! \mathbb{D}^n]\!\) |
| \(\mathrm{E}X^\bullet\!\) | \(\begin{array}{l} = [x, y, \mathrm{d}x, \mathrm{d}y] \\ = [f, g, \mathrm{d}f, \mathrm{d}g] \end{array}\) | \(\text{Extended target universe}\!\) | \([\mathbb{B}^k \!\times\! \mathbb{D}^k]\!\) |
|
\(\begin{matrix} f \\ g \end{matrix}\) |
\(\begin{array}{ll} f : U \!\to\! [x] \cong \mathbb{B} \\ g : U \!\to\! [y] \cong \mathbb{B} \end{array}\) |
\(\text{Proposition}\!\) |
\(\begin{array}{l} \mathbb{B}^n \!\to\! \mathbb{B} \\ \in (\mathbb{B}^n, \mathbb{B}^n \!\to\! \mathbb{B}) = [\mathbb{B}^n] \end{array}\) |
| \(F\!\) | \(F = (f, g) : U^\bullet \!\to\! X^\bullet\!\) | \(\text{Transformation of Map}\!\) | \([\mathbb{B}^n] \!\to\! [\mathbb{B}^k]\) |
|
\(\begin{matrix} \boldsymbol\varepsilon \\ \eta \\ \mathrm{E} \\ \mathrm{D} \\ \mathrm{d} \end{matrix}\) |
\(\begin{array}{l} \mathrm{W} : U^\bullet \!\to\! \mathrm{E}U^\bullet, \\ \mathrm{W} : X^\bullet \!\to\! \mathrm{E}X^\bullet, \\ \mathrm{W} : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathrm{E}U^\bullet \!\to\! \mathrm{E}X^\bullet) \\ \text{for each}~ \mathrm{W} ~\text{in the set:} \\ \{ \boldsymbol\varepsilon, \eta, \mathrm{E}, \mathrm{D}, \mathrm{d} \} \end{array}\) |
\(\begin{array}{ll} \text{Tacit extension operator} & \boldsymbol\varepsilon \\ \text{Trope extension operator} & \eta \\ \text{Enlargement operator} & \mathrm{E} \\ \text{Difference operator} & \mathrm{D} \\ \text{Differential operator} & \mathrm{d} \end{array}\) |
\(\begin{array}{l} {[\mathbb{B}^n] \!\to\! [\mathbb{B}^n \!\times\! \mathbb{D}^n]}, \\ {[\mathbb{B}^k] \!\to\! [\mathbb{B}^k \!\times\! \mathbb{D}^k]}, \\\\ ([\mathbb{B}^n] \!\to\! [\mathbb{B}^k]) \!\to\! \\ ([\mathbb{B}^n \!\times\! \mathbb{D}^n] \!\to\! [\mathbb{B}^k \!\times\! \mathbb{D}^k]) \end{array}\) |
|
\(\begin{matrix} \mathsf{e} \\ \mathsf{E} \\ \mathsf{D} \\ \mathsf{T} \end{matrix}\) |
\(\begin{array}{l} \mathsf{W} : U^\bullet \!\to\! \mathsf{T}U^\bullet = \mathrm{E}U^\bullet, \\ \mathsf{W} : X^\bullet \!\to\! \mathsf{T}X^\bullet = \mathrm{E}X^\bullet, \\ \mathsf{W} : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathsf{T}U^\bullet \!\to\! \mathsf{T}X^\bullet) \\ \text{for each}~ \mathsf{W} ~\text{in the set:} \\ \{ \mathsf{e}, \mathsf{E}, \mathsf{D}, \mathsf{T} \} \end{array}\) |
\(\begin{array}{lll} \text{Radius operator} & \mathsf{e} & = (\boldsymbol\varepsilon, \eta) \\ \text{Secant operator} & \mathsf{E} & = (\boldsymbol\varepsilon, \mathrm{E}) \\ \text{Chord operator} & \mathsf{D} & = (\boldsymbol\varepsilon, \mathrm{D}) \\ \text{Tangent functor} & \mathsf{T} & = (\boldsymbol\varepsilon, \mathrm{d}) \end{array}\) |
\(\begin{array}{l} {[\mathbb{B}^n] \!\to\! [\mathbb{B}^n \!\times\! \mathbb{D}^n]}, \\ {[\mathbb{B}^k] \!\to\! [\mathbb{B}^k \!\times\! \mathbb{D}^k]}, \\\\ ([\mathbb{B}^n] \!\to\! [\mathbb{B}^k]) \!\to\! \\ ([\mathbb{B}^n \!\times\! \mathbb{D}^n] \!\to\! [\mathbb{B}^k \!\times\! \mathbb{D}^k]) \end{array}\) |
| \(\begin{matrix}\text{Operator}\\\text{or}\\\text{Operand}\end{matrix}\) | \(\begin{matrix}\text{Proposition}\\\text{or}\\\text{Component}\end{matrix}\) | \(\begin{matrix}\text{Transformation}\\\text{or}\\\text{Map}\end{matrix}\) | |
| \(\underline\text{Operand}\!\) |
\(\begin{array}{l} F = (F_1, F_2) \\ F = (f, g) : U \!\to\! X \end{array}\) |
\(\begin{array}{l} F_i : \langle u, v \rangle \!\to\! \mathbb{B} \\ F_i : \mathbb{B}^n \!\to\! \mathbb{B} \end{array}\) |
\(\begin{array}{l} F : [u, v] \!\to\! [x, y] \\ F : [\mathbb{B}^n] \!\to\! [\mathbb{B}^k] \end{array}\) |
| \(\begin{matrix}\underline\text{Tacit}\\\text{extension}\end{matrix}\) |
\(\begin{array}{l} \boldsymbol\varepsilon : U^\bullet \!\to\! \mathrm{E}U^\bullet,~ \boldsymbol\varepsilon : X^\bullet \!\to\! \mathrm{E}X^\bullet \\ \boldsymbol\varepsilon : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathrm{E}U^\bullet \!\to\! X^\bullet) \end{array}\) |
\(\begin{array}{l} \boldsymbol\varepsilon F_i : \langle u, v, \mathrm{d}u, \mathrm{d}v \rangle \!\to\! \mathbb{B} \\ \boldsymbol\varepsilon F_i : \mathbb{B}^n \!\times\! \mathbb{D}^n \!\to\! \mathbb{B} \end{array}\) |
\(\begin{array}{l} \boldsymbol\varepsilon F : [u, v, \mathrm{d}u, \mathrm{d}v] \!\to\! [x, y] \\ \boldsymbol\varepsilon F : [\mathbb{B}^n \!\times\! \mathbb{D}^n] \!\to\! [\mathbb{B}^k] \end{array}\) |
| \(\begin{matrix}\underline\text{Trope}\\\text{extension}\end{matrix}\) |
\(\begin{array}{l} \eta : U^\bullet \!\to\! \mathrm{E}U^\bullet,~ \eta : X^\bullet \!\to\! \mathrm{E}X^\bullet \\ \eta : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathrm{E}U^\bullet \!\to\! \mathrm{d}X^\bullet) \end{array}\) |
\(\begin{array}{l} \eta F_i : \langle u, v, \mathrm{d}u, \mathrm{d}v \rangle \!\to\! \mathbb{D} \\ \eta F_i : \mathbb{B}^n \!\times\! \mathbb{D}^n \!\to\! \mathbb{D} \end{array}\) |
\(\begin{array}{l} \eta F : [u, v, \mathrm{d}u, \mathrm{d}v] \!\to\! [\mathrm{d}x, \mathrm{d}y] \\ \eta F : [\mathbb{B}^n \!\times\! \mathbb{D}^n] \!\to\! [\mathbb{D}^k] \end{array}\) |
| \(\begin{matrix}\underline\text{Enlargement}\\\text{operator}\end{matrix}\) |
\(\begin{array}{l} \mathrm{E} : U^\bullet \!\to\! \mathrm{E}U^\bullet,~ \mathrm{E} : X^\bullet \!\to\! \mathrm{E}X^\bullet \\ \mathrm{E} : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathrm{E}U^\bullet \!\to\! \mathrm{d}X^\bullet) \end{array}\) |
\(\begin{array}{l} \mathrm{E}F_i : \langle u, v, \mathrm{d}u, \mathrm{d}v \rangle \!\to\! \mathbb{D} \\ \mathrm{E}F_i : \mathbb{B}^n \!\times\! \mathbb{D}^n \!\to\! \mathbb{D} \end{array}\) |
\(\begin{array}{l} \mathrm{E}F : [u, v, \mathrm{d}u, \mathrm{d}v] \!\to\! [\mathrm{d}x, \mathrm{d}y] \\ \mathrm{E}F : [\mathbb{B}^n \!\times\! \mathbb{D}^n] \!\to\! [\mathbb{D}^k] \end{array}\) |
| \(\begin{matrix}\underline\text{Difference}\\\text{operator}\end{matrix}\) |
\(\begin{array}{l} \mathrm{D} : U^\bullet \!\to\! \mathrm{E}U^\bullet,~ \mathrm{D} : X^\bullet \!\to\! \mathrm{E}X^\bullet \\ \mathrm{D} : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathrm{E}U^\bullet \!\to\! \mathrm{d}X^\bullet) \end{array}\) |
\(\begin{array}{l} \mathrm{D}F_i : \langle u, v, \mathrm{d}u, \mathrm{d}v \rangle \!\to\! \mathbb{D} \\ \mathrm{D}F_i : \mathbb{B}^n \!\times\! \mathbb{D}^n \!\to\! \mathbb{D} \end{array}\) |
\(\begin{array}{l} \mathrm{D}F : [u, v, \mathrm{d}u, \mathrm{d}v] \!\to\! [\mathrm{d}x, \mathrm{d}y] \\ \mathrm{D}F : [\mathbb{B}^n \!\times\! \mathbb{D}^n] \!\to\! [\mathbb{D}^k] \end{array}\) |
| \(\begin{matrix}\underline\text{Differential}\\\text{operator}\end{matrix}\) |
\(\begin{array}{l} \mathrm{d} : U^\bullet \!\to\! \mathrm{E}U^\bullet,~ \mathrm{d} : X^\bullet \!\to\! \mathrm{E}X^\bullet \\ \mathrm{d} : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathrm{E}U^\bullet \!\to\! \mathrm{d}X^\bullet) \end{array}\) |
\(\begin{array}{l} \mathrm{d}F_i : \langle u, v, \mathrm{d}u, \mathrm{d}v \rangle \!\to\! \mathbb{D} \\ \mathrm{d}F_i : \mathbb{B}^n \!\times\! \mathbb{D}^n \!\to\! \mathbb{D} \end{array}\) |
\(\begin{array}{l} \mathrm{d}F : [u, v, \mathrm{d}u, \mathrm{d}v] \!\to\! [\mathrm{d}x, \mathrm{d}y] \\ \mathrm{d}F : [\mathbb{B}^n \!\times\! \mathbb{D}^n] \!\to\! [\mathbb{D}^k] \end{array}\!\) |
| \(\begin{matrix}\underline\text{Remainder}\\\text{operator}\end{matrix}\!\) |
\(\begin{array}{l} \mathrm{r} : U^\bullet \!\to\! \mathrm{E}U^\bullet,~ \mathrm{r} : X^\bullet \!\to\! \mathrm{E}X^\bullet \\ \mathrm{r} : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathrm{E}U^\bullet \!\to\! \mathrm{d}X^\bullet) \end{array}\) |
\(\begin{array}{l} \mathrm{r}F_i : \langle u, v, \mathrm{d}u, \mathrm{d}v \rangle \!\to\! \mathbb{D} \\ \mathrm{r}F_i : \mathbb{B}^n \!\times\! \mathbb{D}^n \!\to\! \mathbb{D} \end{array}\) |
\(\begin{array}{l} \mathrm{r}F : [u, v, \mathrm{d}u, \mathrm{d}v] \!\to\! [\mathrm{d}x, \mathrm{d}y] \\ \mathrm{r}F : [\mathbb{B}^n \!\times\! \mathbb{D}^n] \!\to\! [\mathbb{D}^k] \end{array}\) |
| \(\begin{matrix}\underline\text{Radius}\\\text{operator}\end{matrix}\) |
\(\begin{array}{l} \mathsf{e} = (\boldsymbol\varepsilon, \eta) \\ \mathsf{e} : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathrm{E}U^\bullet \!\to\! \mathrm{E}X^\bullet) \end{array}\) |
\(\begin{array}{l} \mathsf{e}F : [u, v, \mathrm{d}u, \mathrm{d}v] \!\to\! [x, y, \mathrm{d}x, \mathrm{d}y] \\ \mathsf{e}F : [\mathbb{B}^n \!\times\! \mathbb{D}^n] \!\to\! [\mathbb{B}^k \!\times\! \mathbb{D}^k] \end{array}\) | |
| \(\begin{matrix}\underline\text{Secant}\\\text{operator}\end{matrix}\) |
\(\begin{array}{l} \mathsf{E} = (\boldsymbol\varepsilon, \mathrm{E}) \\ \mathsf{E} : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathrm{E}U^\bullet \!\to\! \mathrm{E}X^\bullet) \end{array}\) |
\(\begin{array}{l} \mathsf{E}F : [u, v, \mathrm{d}u, \mathrm{d}v] \!\to\! [x, y, \mathrm{d}x, \mathrm{d}y] \\ \mathsf{E}F : [\mathbb{B}^n \!\times\! \mathbb{D}^n] \!\to\! [\mathbb{B}^k \!\times\! \mathbb{D}^k] \end{array}\) | |
| \(\begin{matrix}\underline\text{Chord}\\\text{operator}\end{matrix}\) |
\(\begin{array}{l} \mathsf{D} = (\boldsymbol\varepsilon, \mathrm{D}) \\ \mathsf{D} : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathrm{E}U^\bullet \!\to\! \mathrm{E}X^\bullet) \end{array}\) |
\(\begin{array}{l} \mathsf{D}F : [u, v, \mathrm{d}u, \mathrm{d}v] \!\to\! [x, y, \mathrm{d}x, \mathrm{d}y] \\ \mathsf{D}F : [\mathbb{B}^n \!\times\! \mathbb{D}^n] \!\to\! [\mathbb{B}^k \!\times\! \mathbb{D}^k] \end{array}\) | |
| \(\begin{matrix}\underline\text{Tangent}\\\text{functor}\end{matrix}\) |
\(\begin{array}{l} \mathsf{T} = (\boldsymbol\varepsilon, \mathrm{d}) \\ \mathsf{T} : (U^\bullet \!\to\! X^\bullet) \!\to\! (\mathrm{E}U^\bullet \!\to\! \mathrm{E}X^\bullet) \end{array}\) |
\(\begin{array}{l} \mathrm{d}F_i : \langle u, v, \mathrm{d}u, \mathrm{d}v \rangle \!\to\! \mathbb{D} \\ \mathrm{d}F_i : \mathbb{B}^n \!\times\! \mathbb{D}^n \!\to\! \mathbb{D} \end{array}\) |
\(\begin{array}{l} \mathsf{T}F : [u, v, \mathrm{d}u, \mathrm{d}v] \!\to\! [x, y, \mathrm{d}x, \mathrm{d}y] \\ \mathsf{T}F : [\mathbb{B}^n \!\times\! \mathbb{D}^n] \!\to\! [\mathbb{B}^k \!\times\! \mathbb{D}^k] \end{array}\) |
Transformations of Type B2 → B2
To take up a slightly more complex example, but one that remains simple enough to pursue through a complete series of developments, consider the transformation from \(U^\bullet = [u, v]\!\) to \(X^\bullet = [x, y]\!\) that is defined by the following system of equations:
|
\(\begin{array}{lllll} x & = & f(u, v) & = & \texttt{((} u \texttt{)(} v \texttt{))} \\[8pt] y & = & g(u, v) & = & \texttt{((} u \texttt{,} v \texttt{))} \end{array}\) |
The component notation \(F = (F_1, F_2) = (f, g) : U^\bullet \to X^\bullet\!\) allows us to give a name and a type to this transformation and permits defining it by the compact description that follows:
|
\(\begin{array}{lllll} (x, y) & = & F(u, v) & = & (\; \texttt{((} u \texttt{)(} v \texttt{))} \;,\; \texttt{((} u \texttt{,} v \texttt{))} \;) \end{array}\) |
Logical Transformations
The information that defines the logical transformation \(F\!\) can be represented in the form of a truth table, as shown in Table 60. To cut down on subscripts in this example we continue to use plain letter equivalents for all components of spaces and maps.
| \(u\!\) | \(v\!\) | \(f\!\) | \(g\!\) |
|
\(\begin{matrix} 0 \\[4pt] 0 \\[4pt] 1 \\[4pt] 1 \end{matrix}\) |
\(\begin{matrix} 0 \\[4pt] 1 \\[4pt] 0 \\[4pt] 1 \end{matrix}\) |
\(\begin{matrix} 0 \\[4pt] 1 \\[4pt] 1 \\[4pt] 1 \end{matrix}\) |
\(\begin{matrix} 1 \\[4pt] 0 \\[4pt] 0 \\[4pt] 1 \end{matrix}\) |
| \(u\!\) | \(v\!\) |
\(\texttt{((} u \texttt{)(} v \texttt{))}\!\) |
\(\texttt{((} u \texttt{,} v \texttt{))}\!\) |
Figure 61 shows how we might paint a picture of the transformation \(F\!\) in the manner of Figure 30.
| \(\text{Figure 61.} ~~ \text{A Propositional Transformation}\!\) |
Figure 62 extracts the gist of Figure 61, exhibiting a style of diagram that is adequate for most purposes.
| \(\text{Figure 62.} ~~ \text{A Propositional Transformation (Short Form)}\!\) |
Local Transformations
Figure 63 gives a more complete picture of the transformation \(F,\!\) showing how the points of \(U^\bullet\!\) are transformed into points of \(X^\bullet.\!\) The bold lines crossing from one universe to the other trace the action that \(F\!\) induces on points, in other words, they show how the transformation acts as a mapping from points to points and chart its effects on the elements that are variously called cells, points, positions, or singular propositions.
| \(\text{Figure 63.} ~~ \text{A Transformation of Positions}\!\) |
Table 64 shows how the action of \(F\!\) on cells or points can be computed in terms of coordinates.
| \(u\!\) | \(v\!\) | \(x\!\) | \(y\!\) | \(x~y\!\) | \(x \texttt{(} y \texttt{)}\!\) | \(\texttt{(} x \texttt{)} y\!\) | \(\texttt{(} x \texttt{)(} y \texttt{)}\!\) | \(X^\bullet = [x, y]\!\) |
|
\(\begin{matrix} 0 \\[4pt] 0 \\[4pt] 1 \\[4pt] 1 \end{matrix}\) |
\(\begin{matrix} 0 \\[4pt] 1 \\[4pt] 0 \\[4pt] 1 \end{matrix}\) |
\(\begin{matrix} 0 \\[4pt] 1 \\[4pt] 1 \\[4pt] 1 \end{matrix}\) |
\(\begin{matrix} 1 \\[4pt] 0 \\[4pt] 0 \\[4pt] 1 \end{matrix}\) |
\(\begin{matrix} 0 \\[4pt] 0 \\[4pt] 0 \\[4pt] 1 \end{matrix}\) |
\(\begin{matrix} 0 \\[4pt] 1 \\[4pt] 1 \\[4pt] 0 \end{matrix}\) |
\(\begin{matrix} 1 \\[4pt] 0 \\[4pt] 0 \\[4pt] 0 \end{matrix}\) |
\(\begin{matrix} 0 \\[4pt] 0 \\[4pt] 0 \\[4pt] 0 \end{matrix}\) |
\(\begin{matrix} \uparrow \\[4pt] F = \\[4pt] (f, g) \\[4pt] \uparrow \end{matrix}\) |
| \(u\!\) | \(v\!\) | \(\texttt{((} u \texttt{)(} v \texttt{))}\!\) | \(\texttt{((} u \texttt{,} v \texttt{))}\!\) | \(u~v\!\) | \(\texttt{(} u \texttt{,} v \texttt{)}\!\) | \(\texttt{(} u \texttt{)(} v \texttt{)}\!\) | \(0\!\) | \(U^\bullet = [u, v]\!\) |
Table 65 extends this scheme from single cells to arbitrary regions, showing how we might compute the action of a logical transformation on arbitrary propositions in the universe of discourse. The effect of a point-transformation on arbitrary propositions, or any other structures erected on points, is referred to as the induced action of the transformation on the structures in question.
| \(X^\bullet~\!\) | \(\longleftarrow\!\) | \(F = (f, g)\!\) | \(\longleftarrow\!\) | \(U^\bullet~\!\) |
| \(f_i (x, y)\!\) | \(\begin{matrix}u = \\ v =\end{matrix}\) | \(\begin{matrix}1~1~0~0\\1~0~1~0\end{matrix}\) | \(\begin{matrix}= u \\ = v\end{matrix}\) | \(f_j (u, v)\!\) |
| \(\begin{matrix}x = \\ y =\end{matrix}\) | \(\begin{matrix}1~1~1~0\\1~0~0~1\end{matrix}\) | \(\begin{matrix}= f(u, v) \\ = g(u, v)\end{matrix}\) | ||
|
\(\begin{matrix} f_{0} \\[2pt] f_{1} \\[2pt] f_{2} \\[2pt] f_{3} \\[2pt] f_{4} \\[2pt] f_{5} \\[2pt] f_{6} \\[2pt] f_{7} \end{matrix}\) |
\(\begin{matrix} \texttt{(~)} \\[2pt] \texttt{(} x \texttt{)(} y \texttt{)} \\[2pt] \texttt{(} x \texttt{)~} y \texttt{~} \\[2pt] \texttt{(} x \texttt{)~~~} \\[2pt] \texttt{~} x \texttt{~(} y \texttt{)} \\[2pt] \texttt{~~~(} y \texttt{)} \\[2pt] \texttt{(} x \texttt{,~} y \texttt{)} \\[2pt] \texttt{(} x \texttt{~~} y \texttt{)} \end{matrix}\) |
\(\begin{matrix} 0~0~0~0 \\[2pt] 0~0~0~0 \\[2pt] 0~0~0~1 \\[2pt] 0~0~0~1 \\[2pt] 0~1~1~0 \\[2pt] 0~1~1~0 \\[2pt] 0~1~1~1 \\[2pt] 0~1~1~1 \end{matrix}\) |
\(\begin{matrix} \texttt{(~)} \\[2pt] \texttt{(~)} \\[2pt] \texttt{(} u \texttt{)(} v \texttt{)} \\[2pt] \texttt{(} u \texttt{)(} v \texttt{)} \\[2pt] \texttt{(} u \texttt{,~} v \texttt{)} \\[2pt] \texttt{(} u \texttt{,~} v \texttt{)} \\[2pt] \texttt{(} u \texttt{~~} v \texttt{)} \\[2pt] \texttt{(} u \texttt{~~} v \texttt{)} \end{matrix}\!\) |
\(\begin{matrix} f_{0} \\[2pt] f_{0} \\[2pt] f_{1} \\[2pt] f_{1} \\[2pt] f_{6} \\[2pt] f_{6} \\[2pt] f_{7} \\[2pt] f_{7} \end{matrix}\) |
|
\(\begin{matrix} f_{8} \\[2pt] f_{9} \\[2pt] f_{10} \\[2pt] f_{11} \\[2pt] f_{12} \\[2pt] f_{13} \\[2pt] f_{14} \\[2pt] f_{15} \end{matrix}\) |
\(\begin{matrix} \texttt{~~} x \texttt{~~} y \texttt{~~} \\[2pt] \texttt{((} x \texttt{,~} y \texttt{))} \\[2pt] \texttt{~~~~~} y \texttt{~~} \\[2pt] \texttt{~(} x \texttt{~(} y \texttt{))} \\[2pt] \texttt{~~} x \texttt{~~~~~} \\[2pt] \texttt{((} x \texttt{)~} y \texttt{)~} \\[2pt] \texttt{((} x \texttt{)(} y \texttt{))} \\[2pt] \texttt{((~))} \end{matrix}\) |
\(\begin{matrix} 1~0~0~0 \\[2pt] 1~0~0~0 \\[2pt] 1~0~0~1 \\[2pt] 1~0~0~1 \\[2pt] 1~1~1~0 \\[2pt] 1~1~1~0 \\[2pt] 1~1~1~1 \\[2pt] 1~1~1~1 \end{matrix}\) |
\(\begin{matrix} \texttt{~~} u \texttt{~~} v \texttt{~~} \\[2pt] \texttt{~~} u \texttt{~~} v \texttt{~~} \\[2pt] \texttt{((} u \texttt{,~} v \texttt{))} \\[2pt] \texttt{((} u \texttt{,~} v \texttt{))} \\[2pt] \texttt{((} u \texttt{)(} v \texttt{))} \\[2pt] \texttt{((} u \texttt{)(} v \texttt{))} \\[2pt] \texttt{((~))} \\[2pt] \texttt{((~))} \end{matrix}\) |
\(\begin{matrix} f_{8} \\[2pt] f_{8} \\[2pt] f_{9} \\[2pt] f_{9} \\[2pt] f_{14} \\[2pt] f_{14} \\[2pt] f_{15} \\[2pt] f_{15} \end{matrix}\) |
| \(X^\bullet~\!\) | \(\longleftarrow\!\) | \(F = (f, g)\!\) | \(\longleftarrow\!\) | \(U^\bullet~\!\) |
| \(f_i (x, y)\!\) | \(\begin{matrix}u = \\ v =\end{matrix}\) | \(\begin{matrix}1~1~0~0\\1~0~1~0\end{matrix}\) | \(\begin{matrix}= u \\ = v\end{matrix}\) | \(f_j (u, v)\!\) |
| \(\begin{matrix}x = \\ y =\end{matrix}\) | \(\begin{matrix}1~1~1~0\\1~0~0~1\end{matrix}\) | \(\begin{matrix}= f(u, v) \\ = g(u, v)\end{matrix}\) | ||
| \(f_{0}\!\) | \(\texttt{(~)}\!\) | \(0~0~0~0\!\) | \(\texttt{(~)}\!\) | \(f_{0}\!\) |
|
\(\begin{matrix} f_{1} \\[2pt] f_{2} \\[2pt] f_{4} \\[2pt] f_{8} \end{matrix}\) |
\(\begin{matrix} \texttt{(} x \texttt{)(} y \texttt{)} \\[2pt] \texttt{(} x \texttt{)~} y \texttt{~} \\[2pt] \texttt{~} x \texttt{~(} y \texttt{)} \\[2pt] \texttt{~} x \texttt{~~} y \texttt{~} \end{matrix}\) |
\(\begin{matrix} 0~0~0~0 \\[2pt] 0~0~0~1 \\[2pt] 0~1~1~0 \\[2pt] 1~0~0~0 \end{matrix}\) |
\(\begin{matrix} \texttt{(~)} \\[2pt] \texttt{(} u \texttt{)(} v \texttt{)} \\[2pt] \texttt{(} u \texttt{,~} v \texttt{)} \\[2pt] \texttt{~} u \texttt{~~} v \texttt{~} \end{matrix}\) |
\(\begin{matrix} f_{0} \\[2pt] f_{1} \\[2pt] f_{6} \\[2pt] f_{8} \end{matrix}\) |
|
\(\begin{matrix} f_{3} \\[2pt] f_{12} \end{matrix}\) |
\(\begin{matrix} \texttt{(} x \texttt{)} \\[2pt] \texttt{~} x \texttt{~} \end{matrix}\) |
\(\begin{matrix} 0~0~0~1 \\[2pt] 1~1~1~0 \end{matrix}\) |
\(\begin{matrix} \texttt{~(} u \texttt{)(} v \texttt{)~} \\[2pt] \texttt{((} u \texttt{)(} v \texttt{))} \end{matrix}\) |
\(\begin{matrix} f_{1} \\[2pt] f_{14} \end{matrix}\) |
|
\(\begin{matrix} f_{6} \\[2pt] f_{9} \end{matrix}\) |
\(\begin{matrix} \texttt{~(} x \texttt{,~} y \texttt{)~} \\[2pt] \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\) |
\(\begin{matrix} 0~1~1~1 \\[2pt] 1~0~0~0 \end{matrix}\) |
\(\begin{matrix} \texttt{(} u \texttt{~~} v \texttt{)} \\[2pt] \texttt{~} u \texttt{~~} v \texttt{~} \end{matrix}\) |
\(\begin{matrix} f_{7} \\[2pt] f_{8} \end{matrix}\) |
|
\(\begin{matrix} f_{5} \\[2pt] f_{10} \end{matrix}\) |
\(\begin{matrix} \texttt{(} y \texttt{)} \\[2pt] \texttt{~} y \texttt{~} \end{matrix}\) |
\(\begin{matrix} 0~1~1~0 \\[2pt] 1~0~0~1 \end{matrix}~\!\) |
\(\begin{matrix} \texttt{~(} u \texttt{,~} v \texttt{)~} \\[2pt] \texttt{((} u \texttt{,~} v \texttt{))} \end{matrix}\) |
\(\begin{matrix} f_{6} \\[2pt] f_{9} \end{matrix}\) |
|
\(\begin{matrix} f_{7} \\[2pt] f_{11} \\[2pt] f_{13} \\[2pt] f_{14} \end{matrix}\) |
\(\begin{matrix} \texttt{~(} x \texttt{~~} y \texttt{)~} \\[2pt] \texttt{~(} x \texttt{~(} y \texttt{))} \\[2pt] \texttt{((} x \texttt{)~} y \texttt{)~} \\[2pt] \texttt{((} x \texttt{)(} y \texttt{))} \end{matrix}\) |
\(\begin{matrix} 0~1~1~1 \\[2pt] 1~0~0~1 \\[2pt] 1~1~1~0 \\[2pt] 1~1~1~1 \end{matrix}\) |
\(\begin{matrix} \texttt{~(} u \texttt{~~} v \texttt{)~} \\[2pt] \texttt{((} u \texttt{,~} v \texttt{))} \\[2pt] \texttt{((} u \texttt{)(} v \texttt{))} \\[2pt] \texttt{((~))} \end{matrix}\!\) |
\(\begin{matrix} f_{7} \\[2pt] f_{9} \\[2pt] f_{14} \\[2pt] f_{15} \end{matrix}\) |
| \(f_{15}\!\) | \(\texttt{((~))}\!\) | \(1~1~1~1\!\) | \(\texttt{((~))}\!\) | \(f_{15}\!\) |
Difference Operators and Tangent Functors
Given the alphabets \(\mathcal{U} = \{ u, v \}\!\) and \(\mathcal{X} = \{ x, y \},\!\) along with the corresponding universes of discourse \(U^\bullet, X^\bullet \cong [\mathbb{B}^2],\!\) how many logical transformations of the general form \(G = (G_1, G_2) : U^\bullet \to X^\bullet\!\) are there? Since \(G_1\!\) and \(G_2\!\) can be any propositions of the type \(\mathbb{B}^2 \to \mathbb{B},\!\) there are \(2^4 = 16\!\) choices for each of the maps \(G_1\!\) and \(G_2\!\) and thus there are \(2^4 \cdot 2^4 = 2^8 = 256\!\) different mappings altogether of the form \(G : U^\bullet \to X^\bullet.\!\) The set of functions of a given type is denoted by placing its type indicator in parentheses, in the present instance writing \((U^\bullet \to X^\bullet) = \{ G : U^\bullet \to X^\bullet \},\!\) and so the cardinality of the function space \((U^\bullet \to X^\bullet)\!\) is summed up by writing \(|(U^\bullet \to X^\bullet)| = |(\mathbb{B}^2 \to \mathbb{B}^2)| = 4^4 = 256.\!\)
Given a transformation \(G = (G_1, G_2) : U^\bullet \to X^\bullet\!\) of this type, we proceed to define a pair of further transformations, related to \(G,\!\) that operate between the extended universes, \(\mathrm{E}U^\bullet\!\) and \(\mathrm{E}X^\bullet,\!\) of its source and target domains.
First, the enlargement map (or secant transformation) \(\mathrm{E}G = (\mathrm{E}G_1, \mathrm{E}G_2) : \mathrm{E}U^\bullet \to \mathrm{E}X^\bullet\!\) is defined by the following set of component equations:
|
\(\begin{array}{lll} \mathrm{E}G_i & = & G_i (u + \mathrm{d}u, v + \mathrm{d}v) \end{array}\) |
Next, the difference map (or chordal transformation) \(\mathrm{D}G = (\mathrm{D}G_1, \mathrm{D}G_2) : \mathrm{E}U^\bullet \to \mathrm{E}X^\bullet~\!\) is defined in component-wise fashion as the boolean sum of the initial proposition \(G_i\!\) and the enlarged proposition \(\mathrm{E}G_i,\!\) for \(i = 1, 2,\!\) according to the following set of equations:
|
\(\begin{array}{lllll} \mathrm{D}G_i & = & G_i (u, v) & + & \mathrm{E}G_i (u, v, \mathrm{d}u, \mathrm{d}v) \\[8pt] & = & G_i (u, v) & + & G_i (u + \mathrm{d}u, v + \mathrm{d}v) \end{array}\) |
Maintaining a strict analogy with ordinary difference calculus would perhaps have us write \(\mathrm{D}G_i = \mathrm{E}G_i - G_i,\!\) but the sum and difference operations are the same thing in boolean arithmetic. It is more often natural in the logical context to consider an initial proposition \(q,\!\) then to compute the enlargement \(\mathrm{E}q,\!\) and finally to determine the difference \(\mathrm{D}q = q + \mathrm{E}q,\!\) so we let the variant order of terms reflect this sequence of considerations.
Viewed in this light the difference operator \(\mathrm{D}\!\) is imagined to be a function of very wide scope and polymorphic application, one that is able to realize the association between each transformation \(G\!\) and its difference map \(\mathrm{D}G,\!\) for example, taking the function space \((U^\bullet \to X^\bullet)\!\) into \((\mathrm{E}U^\bullet \to \mathrm{E}X^\bullet).\!\) When we consider the variety of interpretations permitted to propositions over the contexts in which we put them to use, it should be clear that an operator of this scope is not at all a trivial matter to define in general and that it may take some trouble to work out. For the moment we content ourselves with returning to particular cases.
Acting on the logical transformation \(F = (f, g) = (\; \texttt{((} u \texttt{)(} v \texttt{))} \;,\; \texttt{((} u \texttt{,} v \texttt{))} \;),\!\) the operators \(\mathrm{E}\!\) and \(\mathrm{D}\!\) yield the enlarged map \(\mathrm{E}F = (\mathrm{E}f, \mathrm{E}g)\!\) and the difference map \(\mathrm{D}F = (\mathrm{D}f, \mathrm{D}g),\!\) respectively, whose components are given as follows.
|
\(\begin{array}{lll} \mathrm{E}f & = & \texttt{((} u + \mathrm{d}u \texttt{)(} v + \mathrm{d}v \texttt{))} \\[8pt] \mathrm{E}g & = & \texttt{((} u + \mathrm{d}u \texttt{,~} v + \mathrm{d}v \texttt{))} \end{array}\) |
|
\(\begin{array}{lllll} \mathrm{D}f & = & \texttt{((} u \texttt{)(} v \texttt{))} & + & \texttt{((} u + \mathrm{d}u \texttt{)(} v + \mathrm{d}v \texttt{))} \\[8pt] \mathrm{D}g & = & \texttt{((} u \texttt{,~} v \texttt{))} & + & \texttt{((} u + \mathrm{d}u \texttt{,~} v + \mathrm{d}v \texttt{))} \end{array}\) |
But these initial formulas are purely definitional, and help us little in understanding either the purpose of the operators or the meaning of their results. Working symbolically, let us apply the same method to the separate components \(f\!\) and \(g\!\) that we earlier used on \(J.\!\) This work is recorded in Appendix 1 and a summary of the results is presented in Tables 66-i and 66-ii.
|
\(\begin{array}{c*{8}{l}} \boldsymbol\varepsilon f & = & u \!\cdot\! v \cdot 1 & + & u \texttt{(} v \texttt{)} \cdot 1 & + & \texttt{(} u \texttt{)} v \cdot 1 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 0 \\[6pt] \mathrm{E}f & = & u \!\cdot\! v \cdot \texttt{(} \mathrm{d}u \cdot \mathrm{d}v \texttt{)} & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{))} & + & \texttt{(} u \texttt{)} v \cdot \texttt{((} \mathrm{d}u \texttt{)} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} \\[6pt] \mathrm{D}f & = & u \!\cdot\! v \cdot \mathrm{d}u \cdot \mathrm{d}v & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} \\[6pt] \mathrm{d}f & = & u \!\cdot\! v \cdot 0 & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \\[6pt] \mathrm{r}f & = & u \!\cdot\! v \cdot \mathrm{d}u \cdot \mathrm{d}v & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u \cdot \mathrm{d}v & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u \cdot \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u \cdot \mathrm{d}v \end{array}\) |
|
\(\begin{array}{c*{8}{l}} \boldsymbol\varepsilon g & = & u \!\cdot\! v \cdot 1 & + & u \texttt{(} v \texttt{)} \cdot 0 & + & \texttt{(} u \texttt{)} v \cdot 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 1 \\[6pt] \mathrm{E}g & = & u \!\cdot\! v \cdot \texttt{((} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{))} & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{))} \\[6pt] \mathrm{D}g & = & u \!\cdot\! v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \\[6pt] \mathrm{d}g & = & u \!\cdot\! v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \\[6pt] \mathrm{r}g & = & u \!\cdot\! v \cdot 0 & + & u \texttt{(} v \texttt{)} \cdot 0 & + & \texttt{(} u \texttt{)} v \cdot 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 0 \end{array}\) |
Table 67 shows how to compute the analytic series for \(F = (f, g) = (\; \texttt{((} u \texttt{)(} v \texttt{))} \;,\; \texttt{((} u \texttt{,} v \texttt{))} \;)\) in terms of coordinates, and Table 68 recaps these results in symbolic terms, agreeing with earlier derivations.
| \(u\!\) | \(v\!\) | \(\mathrm{d}u\!\) | \(\mathrm{d}v\!\) | \(u'\!\) | \(v'\!\) | \(f\!\) | \(g\!\) | \({\mathrm{E}f}\!\) | \({\mathrm{E}g}\!\) | \({\mathrm{D}f}\!\) | \({\mathrm{D}g}\!\) | \({\mathrm{d}f}\!\) | \({\mathrm{d}g}\!\) | \({\mathrm{d}^2\!f}\!\) | \({\mathrm{d}^2\!g}\!\) |
| \(0\!\) | \(0\!\) |
\(\begin{matrix}0\\0\\1\\1\end{matrix}\!\) |
\(\begin{matrix}0\\1\\0\\1\end{matrix}\!\) |
\(\begin{matrix}0\\0\\1\\1\end{matrix}\!\) |
\(\begin{matrix}0\\1\\0\\1\end{matrix}\!\) |
\(0\!\) | \(1\!\) |
\(\begin{matrix}0\\1\\1\\1\end{matrix}\!\) |
\(\begin{matrix}1\\0\\0\\1\end{matrix}\!\) |
\(\begin{matrix}0\\1\\1\\1\end{matrix}\!\) |
\(\begin{matrix}0\\1\\1\\0\end{matrix}\!\) |
\(\begin{matrix}0\\1\\1\\0\end{matrix}\!\) |
\(\begin{matrix}0\\1\\1\\0\end{matrix}\!\) |
\(\begin{matrix}0\\0\\0\\1\end{matrix}\!\) |
\(\begin{matrix}0\\0\\0\\0\end{matrix}\!\) |
| \(0\!\) | \(1\!\) |
\(\begin{matrix}0\\0\\1\\1\end{matrix}\!\) |
\(\begin{matrix}0\\1\\0\\1\end{matrix}\!\) |
\(\begin{matrix}0\\0\\1\\1\end{matrix}\!\) |
\(\begin{matrix}1\\0\\1\\0\end{matrix}\!\) |
\(1\!\) | \(0\!\) |
\(\begin{matrix}1\\0\\1\\1\end{matrix}\!\) |
\(\begin{matrix}0\\1\\1\\0\end{matrix}\!\) |
\(\begin{matrix}0\\1\\0\\0\end{matrix}\!\) |
\(\begin{matrix}0\\1\\1\\0\end{matrix}\!\) |
\(\begin{matrix}0\\1\\0\\1\end{matrix}\!\) |
\(\begin{matrix}0\\1\\1\\0\end{matrix}\!\) |
\(\begin{matrix}0\\0\\0\\1\end{matrix}\!\) |
\(\begin{matrix}0\\0\\0\\0\end{matrix}\!\) |
| \(1\!\) | \(0\!\) |
\(\begin{matrix}0\\0\\1\\1\end{matrix}\!\) |
\(\begin{matrix}0\\1\\0\\1\end{matrix}\!\) |
\(\begin{matrix}1\\1\\0\\0\end{matrix}\!\) |
\(\begin{matrix}0\\1\\0\\1\end{matrix}\!\) |
\(1\!\) | \(0\!\) |
\(\begin{matrix}1\\1\\0\\1\end{matrix}\!\) |
\(\begin{matrix}0\\1\\1\\0\end{matrix}\!\) |
\(\begin{matrix}0\\0\\1\\0\end{matrix}\!\) |
\(\begin{matrix}0\\1\\1\\0\end{matrix}\!\) |
\(\begin{matrix}0\\0\\1\\1\end{matrix}\!\) |
\(\begin{matrix}0\\1\\1\\0\end{matrix}\!\) |
\(\begin{matrix}0\\0\\0\\1\end{matrix}\!\) |
\(\begin{matrix}0\\0\\0\\0\end{matrix}\!\) |
| \(1\!\) | \(1\!\) |
\(\begin{matrix}0\\0\\1\\1\end{matrix}\!\) |
\(\begin{matrix}0\\1\\0\\1\end{matrix}\!\) |
\(\begin{matrix}1\\1\\0\\0\end{matrix}\!\) |
\(\begin{matrix}1\\0\\1\\0\end{matrix}\!\) |
\(1\!\) | \(1\!\) |
\(\begin{matrix}1\\1\\1\\0\end{matrix}\!\) |
\(\begin{matrix}1\\0\\0\\1\end{matrix}\!\) |
\(\begin{matrix}0\\0\\0\\1\end{matrix}\!\) |
\(\begin{matrix}0\\1\\1\\0\end{matrix}\!\) |
\(\begin{matrix}0\\0\\0\\0\end{matrix}\!\) |
\(\begin{matrix}0\\1\\1\\0\end{matrix}\!\) |
\(\begin{matrix}0\\0\\0\\1\end{matrix}\!\) |
\(\begin{matrix}0\\0\\0\\0\end{matrix}\!\) |
| \(u\!\) | \(v\!\) | \(f\!\) | \(g\!\) | \({\mathrm{D}f}\!\) | \({\mathrm{D}g}\!\) | \({\mathrm{d}f}\!\) | \({\mathrm{d}g}\!\) | \({\mathrm{d}^2\!f}\!\) | \({\mathrm{d}^2\!g}\!\) |
|
\(\begin{matrix} 0 \\[4pt] 0 \\[4pt] 1 \\[4pt] 1 \end{matrix}\) |
\(\begin{matrix} 0 \\[4pt] 1 \\[4pt] 0 \\[4pt] 1 \end{matrix}\) |
\(\begin{matrix} 0 \\[4pt] 1 \\[4pt] 1 \\[4pt] 1 \end{matrix}\) |
\(\begin{matrix} 1 \\[4pt] 0 \\[4pt] 0 \\[4pt] 1 \end{matrix}\) |
\(\begin{matrix} \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} \\[4pt] \texttt{~(} \mathrm{d}u \texttt{)~} \mathrm{d}v \texttt{~~} \\[4pt] \texttt{~~} \mathrm{d}u \texttt{~(} \mathrm{d}v \texttt{)~} \\[4pt] \texttt{~~} \mathrm{d}u \texttt{~~} \mathrm{d}v \texttt{~~} \end{matrix}\) |
\(\begin{matrix} \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \\[4pt] \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \\[4pt] \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \\[4pt] \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \end{matrix}\) |
\(\begin{matrix} \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \\[4pt] \mathrm{d}v \\[4pt] \mathrm{d}u \\[4pt] 0 \end{matrix}\) |
\(\begin{matrix} \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \\[4pt] \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \\[4pt] \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \\[4pt] \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \end{matrix}\) |
\(\begin{matrix} \mathrm{d}u \cdot \mathrm{d}v \\[4pt] \mathrm{d}u \cdot \mathrm{d}v \\[4pt] \mathrm{d}u \cdot \mathrm{d}v \\[4pt] \mathrm{d}u \cdot \mathrm{d}v \end{matrix}\!\) |
\(\begin{matrix} 0 \\[4pt] 0 \\[4pt] 0 \\[4pt] 0 \end{matrix}\) |
Figure 69 gives a graphical picture of the difference map \(\mathrm{D}F = (\mathrm{D}f, \mathrm{D}g)\!\) for the transformation \(F = (f, g) = (\; \texttt{((} u \texttt{)(} v \texttt{))} \;,\; \texttt{((} u \texttt{,} v \texttt{))} \;).\!\) This represents the same information about \(\mathrm{D}f~\!\) and \(\mathrm{D}g~\!\) that was given in the corresponding rows of Tables 66-i and 66-ii, for ease of reference repeated below.
|
\(\begin{array}{c*{8}{l}} \mathrm{D}f & = & u \!\cdot\! v \cdot \mathrm{d}u \cdot \mathrm{d}v & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} \\[8pt] \mathrm{D}g & = & u \!\cdot\! v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \end{array}\) |
| \(\text{Figure 69.} ~~ \text{Difference Map of}~ F(u, v) = (\; \texttt{((} u \texttt{)(} v \texttt{))} \;,\; \texttt{((} u \texttt{,} v \texttt{))} \;)\) |
Figure 70-a shows a way of visualizing the tangent functor map \(\mathrm{d}F = (\mathrm{d}f, \mathrm{d}g)\!\) for the transformation \(F = (f, g) = (\; \texttt{((} u \texttt{)(} v \texttt{))} \;,\; \texttt{((} u \texttt{,} v \texttt{))} \;).\!\) This amounts to the same information about \(\mathrm{d}f~\!\) and \(\mathrm{d}g~\!\) that was given in Tables 66-i and 66-ii, the corresponding rows of which are repeated below.
|
\(\begin{array}{c*{8}{l}} \mathrm{d}f & = & u \!\cdot\! v \cdot 0 & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \\[8pt] \mathrm{d}g & = & u \!\cdot\! v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \end{array}\) |
| \(\text{Figure 70-a.} ~~ \text{Tangent Functor Diagram for}~ F(u, v) = (\; \texttt{((} u \texttt{)(} v \texttt{))} \;,\; \texttt{((} u \texttt{,} v \texttt{))} \;)\) |
Figure 70-b shows another way to picture the action of the tangent functor on the logical transformation \(F(u, v) = (\; \texttt{((} u \texttt{)(} v \texttt{))} \;,\; \texttt{((} u \texttt{,} v \texttt{))} \;).\!\)
| \(\text{Figure 70-b.} ~~ \text{Tangent Functor Ferris Wheel for}~ F(u, v) = (\; \texttt{((} u \texttt{)(} v \texttt{))} \;,\; \texttt{((} u \texttt{,} v \texttt{))} \;)\) |
- Note. The original Figure 70-b lost some of its labeling in a succession of platform metamorphoses over the years, so we have included an ASCII version below to indicate where the missing labels go.
o-----------------------o o-----------------------o o-----------------------o
| dU | | dU | | dU |
| o--o o--o | | o--o o--o | | o--o o--o |
| /////\ /////\ | | /XXXX\ /XXXX\ | | /\\\\\ /\\\\\ |
| ///////o//////\ | | /XXXXXXoXXXXXX\ | | /\\\\\\o\\\\\\\ |
| //////// \//////\ | | /XXXXXX/ \XXXXXX\ | | /\\\\\\/ \\\\\\\\ |
| o/////// \//////o | | oXXXXXX/ \XXXXXXo | | o\\\\\\/ \\\\\\\o |
| |/////o o/////| | | |XXXXXo oXXXXX| | | |\\\\\o o\\\\\| |
| |/du//| |//dv/| | | |XXXXX| |XXXXX| | | |\du\\| |\\dv\| |
| |/////o o/////| | | |XXXXXo oXXXXX| | | |\\\\\o o\\\\\| |
| o//////\ ///////o | | oXXXXXX\ /XXXXXXo | | o\\\\\\\ /\\\\\\o |
| \//////\ //////// | | \XXXXXX\ /XXXXXX/ | | \\\\\\\\ /\\\\\\/ |
| \//////o/////// | | \XXXXXXoXXXXXX/ | | \\\\\\\o\\\\\\/ |
| \///// \///// | | \XXXX/ \XXXX/ | | \\\\\/ \\\\\/ |
| o--o o--o | | o--o o--o | | o--o o--o |
| | | | | |
o-----------------------o o-----------------------o o-----------------------o
= du' @ (u)(v) o-----------------------o dv' @ (u)(v) =
= | dU' | =
= | o--o o--o | =
= | /////\ /\\\\\ | =
= | ///////o\\\\\\\ | =
= | ////////X\\\\\\\\ | =
= | o///////XXX\\\\\\\o | =
= | |/////oXXXXXo\\\\\| | =
= = = = = = = = = = =|/du'/|XXXXX|\dv'\|= = = = = = = = = = =
| |/////oXXXXXo\\\\\| |
| o//////\XXX/\\\\\\o |
| \//////\X/\\\\\\/ |
| \//////o\\\\\\/ |
| \///// \\\\\/ |
| o--o o--o |
| |
o-----------------------o
o-----------------------o o-----------------------o o-----------------------o
| dU | | dU | | dU |
| o--o o--o | | o--o o--o | | o--o o--o |
| / \ /////\ | | /\\\\\ /XXXX\ | | /\\\\\ /\\\\\ |
| / o//////\ | | /\\\\\\oXXXXXX\ | | /\\\\\\o\\\\\\\ |
| / //\//////\ | | /\\\\\\//\XXXXXX\ | | /\\\\\\/ \\\\\\\\ |
| o ////\//////o | | o\\\\\\////\XXXXXXo | | o\\\\\\/ \\\\\\\o |
| | o/////o/////| | | |\\\\\o/////oXXXXX| | | |\\\\\o o\\\\\| |
| | du |/////|//dv/| | | |\\\\\|/////|XXXXX| | | |\du\\| |\\dv\| |
| | o/////o/////| | | |\\\\\o/////oXXXXX| | | |\\\\\o o\\\\\| |
| o \//////////o | | o\\\\\\\////XXXXXXo | | o\\\\\\\ /\\\\\\o |
| \ \///////// | | \\\\\\\\//XXXXXX/ | | \\\\\\\\ /\\\\\\/ |
| \ o/////// | | \\\\\\\oXXXXXX/ | | \\\\\\\o\\\\\\/ |
| \ / \///// | | \\\\\/ \XXXX/ | | \\\\\/ \\\\\/ |
| o--o o--o | | o--o o--o | | o--o o--o |
| | | | | |
o-----------------------o o-----------------------o o-----------------------o
= du' @ (u) v o-----------------------o dv' @ (u) v =
= | dU' | =
= | o--o o--o | =
= | /////\ /\\\\\ | =
= | ///////o\\\\\\\ | =
= | ////////X\\\\\\\\ | =
= | o///////XXX\\\\\\\o | =
= | |/////oXXXXXo\\\\\| | =
= = = = = = = = = = =|/du'/|XXXXX|\dv'\|= = = = = = = = = = =
| |/////oXXXXXo\\\\\| |
| o//////\XXX/\\\\\\o |
| \//////\X/\\\\\\/ |
| \//////o\\\\\\/ |
| \///// \\\\\/ |
| o--o o--o |
| |
o-----------------------o
o-----------------------o o-----------------------o o-----------------------o
| dU | | dU | | dU |
| o--o o--o | | o--o o--o | | o--o o--o |
| /////\ / \ | | /XXXX\ /\\\\\ | | /\\\\\ /\\\\\ |
| ///////o \ | | /XXXXXXo\\\\\\\ | | /\\\\\\o\\\\\\\ |
| /////////\ \ | | /XXXXXX//\\\\\\\\ | | /\\\\\\/ \\\\\\\\ |
| o//////////\ o | | oXXXXXX////\\\\\\\o | | o\\\\\\/ \\\\\\\o |
| |/////o/////o | | | |XXXXXo/////o\\\\\| | | |\\\\\o o\\\\\| |
| |/du//|/////| dv | | | |XXXXX|/////|\\\\\| | | |\du\\| |\\dv\| |
| |/////o/////o | | | |XXXXXo/////o\\\\\| | | |\\\\\o o\\\\\| |
| o//////\//// o | | oXXXXXX\////\\\\\\o | | o\\\\\\\ /\\\\\\o |
| \//////\// / | | \XXXXXX\//\\\\\\/ | | \\\\\\\\ /\\\\\\/ |
| \//////o / | | \XXXXXXo\\\\\\/ | | \\\\\\\o\\\\\\/ |
| \///// \ / | | \XXXX/ \\\\\/ | | \\\\\/ \\\\\/ |
| o--o o--o | | o--o o--o | | o--o o--o |
| | | | | |
o-----------------------o o-----------------------o o-----------------------o
= du' @ u (v) o-----------------------o dv' @ u (v) =
= | dU' | =
= | o--o o--o | =
= | /////\ /\\\\\ | =
= | ///////o\\\\\\\ | =
= | ////////X\\\\\\\\ | =
= | o///////XXX\\\\\\\o | =
= | |/////oXXXXXo\\\\\| | =
= = = = = = = = = = =|/du'/|XXXXX|\dv'\|= = = = = = = = = = =
| |/////oXXXXXo\\\\\| |
| o//////\XXX/\\\\\\o |
| \//////\X/\\\\\\/ |
| \//////o\\\\\\/ |
| \///// \\\\\/ |
| o--o o--o |
| |
o-----------------------o
o-----------------------o o-----------------------o o-----------------------o
| dU | | dU | | dU |
| o--o o--o | | o--o o--o | | o--o o--o |
| / \ / \ | | /\\\\\ /\\\\\ | | /\\\\\ /\\\\\ |
| / o \ | | /\\\\\\o\\\\\\\ | | /\\\\\\o\\\\\\\ |
| / / \ \ | | /\\\\\\/ \\\\\\\\ | | /\\\\\\/ \\\\\\\\ |
| o / \ o | | o\\\\\\/ \\\\\\\o | | o\\\\\\/ \\\\\\\o |
| | o o | | | |\\\\\o o\\\\\| | | |\\\\\o o\\\\\| |
| | du | | dv | | | |\\\\\| |\\\\\| | | |\du\\| |\\dv\| |
| | o o | | | |\\\\\o o\\\\\| | | |\\\\\o o\\\\\| |
| o \ / o | | o\\\\\\\ /\\\\\\o | | o\\\\\\\ /\\\\\\o |
| \ \ / / | | \\\\\\\\ /\\\\\\/ | | \\\\\\\\ /\\\\\\/ |
| \ o / | | \\\\\\\o\\\\\\/ | | \\\\\\\o\\\\\\/ |
| \ / \ / | | \\\\\/ \\\\\/ | | \\\\\/ \\\\\/ |
| o--o o--o | | o--o o--o | | o--o o--o |
| | | | | |
o-----------------------o o-----------------------o o-----------------------o
= du' @ u v o-----------------------o dv' @ u v =
= | dU' | =
= | o--o o--o | =
= | /////\ /\\\\\ | =
= | ///////o\\\\\\\ | =
= | ////////X\\\\\\\\ | =
= | o///////XXX\\\\\\\o | =
= | |/////oXXXXXo\\\\\| | =
= = = = = = = = = = =|/du'/|XXXXX|\dv'\|= = = = = = = = = = =
| |/////oXXXXXo\\\\\| |
| o//////\XXX/\\\\\\o |
| \//////\X/\\\\\\/ |
| \//////o\\\\\\/ |
| \///// \\\\\/ |
| o--o o--o |
| |
o-----------------------o
o-----------------------o o-----------------------o o-----------------------o
| U | |\U\\\\\\\\\\\\\\\\\\\\\| |\U\\\\\\\\\\\\\\\\\\\\\|
| o--o o--o | |\\\\\\o--o\\\o--o\\\\\\| |\\\\\\o--o\\\o--o\\\\\\|
| /////\ /////\ | |\\\\\/////\\/////\\\\\\| |\\\\\/ \\/ \\\\\\|
| ///////o//////\ | |\\\\///////o//////\\\\\| |\\\\/ o \\\\\|
| /////////\//////\ | |\\\////////X\//////\\\\| |\\\/ /\\ \\\\|
| o//////////\//////o | |\\o///////XXX\//////o\\| |\\o /\\\\ o\\|
| |/////o/////o/////| | |\\|/////oXXXXXo/////|\\| |\\| o\\\\\o |\\|
| |//u//|/////|//v//| | |\\|//u//|XXXXX|//v//|\\| |\\| u |\\\\\| v |\\|
| |/////o/////o/////| | |\\|/////oXXXXXo/////|\\| |\\| o\\\\\o |\\|
| o//////\//////////o | |\\o//////\XXX///////o\\| |\\o \\\\/ o\\|
| \//////\///////// | |\\\\//////\X////////\\\| |\\\\ \\/ /\\\|
| \//////o/////// | |\\\\\//////o///////\\\\| |\\\\\ o /\\\\|
| \///// \///// | |\\\\\\/////\\/////\\\\\| |\\\\\\ /\\ /\\\\\|
| o--o o--o | |\\\\\\o--o\\\o--o\\\\\\| |\\\\\\o--o\\\o--o\\\\\\|
| | |\\\\\\\\\\\\\\\\\\\\\\\| |\\\\\\\\\\\\\\\\\\\\\\\|
o-----------------------o o-----------------------o o-----------------------o
= u' o-----------------------o v' =
= | U' | =
= | o--o o--o | =
= | /////\ /\\\\\ | =
= | ///////o\\\\\\\ | =
= | ////////X\\\\\\\\ | =
= | o///////XXX\\\\\\\o | =
= | |/////oXXXXXo\\\\\| | =
= = = = = = = = = = =|/u'//|XXXXX|\\v'\|= = = = = = = = = = =
| |/////oXXXXXo\\\\\| |
| o//////\XXX/\\\\\\o |
| \//////\X/\\\\\\/ |
| \//////o\\\\\\/ |
| \///// \\\\\/ |
| o--o o--o |
| |
o-----------------------o
Figure 70-b. Tangent Functor Ferris Wheel for F<u, v> = <((u)(v)), ((u, v))>
|
Epilogue, Enchoiry, Exodus
|
It is time to explain myself . . . . let us stand up. |
||
| — Walt Whitman, Leaves of Grass, [Whi, 79] | ||
Appendices
Appendix 1. Propositional Forms and Differential Expansions
Table A1. Propositional Forms on Two Variables
| \(\begin{matrix}\mathcal{L}_1\\\text{Decimal}\\\text{Index}\end{matrix}\) | \(\begin{matrix}\mathcal{L}_2\\\text{Binary}\\\text{Index}\end{matrix}\) | \(\begin{matrix}\mathcal{L}_3\\\text{Truth}\\\text{Table}\end{matrix}\) | \(\begin{matrix}\mathcal{L}_4\\\text{Cactus}\\\text{Language}\end{matrix}\) | \(\begin{matrix}\mathcal{L}_5\\\text{English}\\\text{Paraphrase}\end{matrix}\) | \(\begin{matrix}\mathcal{L}_6\\\text{Conventional}\\\text{Formula}\end{matrix}\) |
| \(x\colon\!\) | \(1~1~0~0\!\) | ||||
| \(y\colon\!\) | \(1~0~1~0\!\) | ||||
|
\(\begin{matrix} f_{0}\\f_{1}\\f_{2}\\f_{3}\\f_{4}\\f_{5}\\f_{6}\\f_{7} \end{matrix}\) |
\(\begin{matrix} f_{0000}\\f_{0001}\\f_{0010}\\f_{0011}\\f_{0100}\\f_{0101}\\f_{0110}\\f_{0111} \end{matrix}\) |
\(\begin{matrix} 0~0~0~0\\0~0~0~1\\0~0~1~0\\0~0~1~1\\0~1~0~0\\0~1~0~1\\0~1~1~0\\0~1~1~1 \end{matrix}\!\) |
\(\begin{matrix} \texttt{(~)} \\ \texttt{(} x \texttt{)(} y \texttt{)} \\ \texttt{(} x \texttt{)~} y \texttt{~} \\ \texttt{(} x \texttt{)~~~} \\ \texttt{~} x \texttt{~(} y \texttt{)} \\ \texttt{~~~(} y \texttt{)} \\ \texttt{(} x \texttt{,~} y \texttt{)} \\ \texttt{(} x \texttt{~~} y \texttt{)} \end{matrix}\) |
\(\begin{matrix} \text{false} \\ \text{neither}~ x ~\text{nor}~ y \\ y ~\text{without}~ x \\ \text{not}~ x \\ x ~\text{without}~ y \\ \text{not}~ y \\ x ~\text{not equal to}~ y \\ \text{not both}~ x ~\text{and}~ y \end{matrix}\) |
\(\begin{matrix} 0 \\ \lnot x \land \lnot y \\ \lnot x \land y \\ \lnot x \\ x \land \lnot y \\ \lnot y \\ x \ne y \\ \lnot x \lor \lnot y \end{matrix}\) |
|
\(\begin{matrix} f_{8}\\f_{9}\\f_{10}\\f_{11}\\f_{12}\\f_{13}\\f_{14}\\f_{15} \end{matrix}\) |
\(\begin{matrix} f_{1000}\\f_{1001}\\f_{1010}\\f_{1011}\\f_{1100}\\f_{1101}\\f_{1110}\\f_{1111} \end{matrix}\!\) |
\(\begin{matrix} 1~0~0~0\\1~0~0~1\\1~0~1~0\\1~0~1~1\\1~1~0~0\\1~1~0~1\\1~1~1~0\\1~1~1~1 \end{matrix}\) |
\(\begin{matrix} \texttt{~~} x \texttt{~~} y \texttt{~~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \\ \texttt{~~~~~} y \texttt{~~} \\ \texttt{~(} x \texttt{~(} y \texttt{))} \\ \texttt{~~} x \texttt{~~~~~} \\ \texttt{((} x \texttt{)~} y \texttt{)~} \\ \texttt{((} x \texttt{)(} y \texttt{))} \\ \texttt{((~))} \end{matrix}\) |
\(\begin{matrix} x ~\text{and}~ y \\ x ~\text{equal to}~ y \\ y \\ \text{not}~ x ~\text{without}~ y \\ x \\ \text{not}~ y ~\text{without}~ x \\ x ~\text{or}~ y \\ \text{true} \end{matrix}\) |
\(\begin{matrix} x \land y \\ x = y \\ y \\ x \Rightarrow y \\ x \\ x \Leftarrow y \\ x \lor y \\ 1 \end{matrix}\) |
Table A2. Propositional Forms on Two Variables
| \(\begin{matrix}\mathcal{L}_1\\\text{Decimal}\\\text{Index}\end{matrix}\) | \(\begin{matrix}\mathcal{L}_2\\\text{Binary}\\\text{Index}\end{matrix}\) | \(\begin{matrix}\mathcal{L}_3\\\text{Truth}\\\text{Table}\end{matrix}\) | \(\begin{matrix}\mathcal{L}_4\\\text{Cactus}\\\text{Language}\end{matrix}\) | \(\begin{matrix}\mathcal{L}_5\\\text{English}\\\text{Paraphrase}\end{matrix}\) | \(\begin{matrix}\mathcal{L}_6\\\text{Conventional}\\\text{Formula}\end{matrix}\) |
| \(x\colon\!\) | \(1~1~0~0\!\) | ||||
| \(y\colon\!\) | \(1~0~1~0\!\) | ||||
| \(f_{0}\!\) | \(f_{0000}\!\) | \(0~0~0~0\) | \(\texttt{(~)}\!\) | \(\text{false}\!\) | \(0\!\) |
|
\(\begin{matrix} f_{1}\\f_{2}\\f_{4}\\f_{8} \end{matrix}\) |
\(\begin{matrix} f_{0001}\\f_{0010}\\f_{0100}\\f_{1000} \end{matrix}\) |
\(\begin{matrix} 0~0~0~1\\0~0~1~0\\0~1~0~0\\1~0~0~0 \end{matrix}\) |
\(\begin{matrix} \texttt{(} x \texttt{)(} y \texttt{)} \\ \texttt{(} x \texttt{)~} y \texttt{~} \\ \texttt{~} x \texttt{~(} y \texttt{)} \\ \texttt{~} x \texttt{~~} y \texttt{~} \end{matrix}\) |
\(\begin{matrix} \text{neither}~ x ~\text{nor}~ y \\ y ~\text{without}~ x \\ x ~\text{without}~ y \\ x ~\text{and}~ y \end{matrix}\) |
\(\begin{matrix} \lnot x \land \lnot y \\ \lnot x \land y \\ x \land \lnot y \\ x \land y \end{matrix}\) |
|
\(\begin{matrix} f_{3}\\f_{12} \end{matrix}\) |
\(\begin{matrix} f_{0011}\\f_{1100} \end{matrix}\) |
\(\begin{matrix} 0~0~1~1\\1~1~0~0 \end{matrix}\) |
\(\begin{matrix} \texttt{(} x \texttt{)} \\ \texttt{~} x \texttt{~} \end{matrix}\) |
\(\begin{matrix} \text{not}~ x \\ x \end{matrix}\!\) |
\(\begin{matrix} \lnot x \\ x \end{matrix}\) |
|
\(\begin{matrix} f_{6}\\f_{9} \end{matrix}\) |
\(\begin{matrix} f_{0110}\\f_{1001} \end{matrix}\!\) |
\(\begin{matrix} 0~1~1~0\\1~0~0~1 \end{matrix}\) |
\(\begin{matrix} \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\) |
\(\begin{matrix} x ~\text{not equal to}~ y \\ x ~\text{equal to}~ y \end{matrix}\) |
\(\begin{matrix} x \ne y \\ x = y \end{matrix}\) |
|
\(\begin{matrix} f_{5}\\f_{10} \end{matrix}\) |
\(\begin{matrix} f_{0101}\\f_{1010} \end{matrix}\) |
\(\begin{matrix} 0~1~0~1\\1~0~1~0 \end{matrix}\) |
\(\begin{matrix} \texttt{(} y \texttt{)} \\ \texttt{~} y \texttt{~} \end{matrix}\) |
\(\begin{matrix} \text{not}~ y \\ y \end{matrix}\) |
\(\begin{matrix} \lnot y \\ y \end{matrix}\) |
|
\(\begin{matrix} f_{7}\\f_{11}\\f_{13}\\f_{14} \end{matrix}\) |
\(\begin{matrix} f_{0111}\\f_{1011}\\f_{1101}\\f_{1110} \end{matrix}\) |
\(\begin{matrix} 0~1~1~1\\1~0~1~1\\1~1~0~1\\1~1~1~0 \end{matrix}\) |
\(\begin{matrix} \texttt{~(} x \texttt{~~} y \texttt{)~} \\ \texttt{~(} x \texttt{~(} y \texttt{))} \\ \texttt{((} x \texttt{)~} y \texttt{)~} \\ \texttt{((} x \texttt{)(} y \texttt{))} \end{matrix}\) |
\(\begin{matrix} \text{not both}~ x ~\text{and}~ y \\ \text{not}~ x ~\text{without}~ y \\ \text{not}~ y ~\text{without}~ x \\ x ~\text{or}~ y \end{matrix}\) |
\(\begin{matrix} \lnot x \lor \lnot y \\ x \Rightarrow y \\ x \Leftarrow y \\ x \lor y \end{matrix}\) |
| \(f_{15}\!\) | \(f_{1111}\!\) | \(1~1~1~1\!\) | \(\texttt{((~))}\!\) | \(\text{true}\!\) | \(1\!\) |
Table A3. Ef Expanded Over Differential Features
| \(f\!\) |
\(\begin{matrix}\mathrm{T}_{11}f\\\mathrm{E}f|_{\mathrm{d}x ~ \mathrm{d}y}\end{matrix}\) |
\(\begin{matrix}\mathrm{T}_{10}f\\\mathrm{E}f|_{\mathrm{d}x \texttt{(} \mathrm{d}y \texttt{)}}\end{matrix}\) |
\(\begin{matrix}\mathrm{T}_{01}f\\\mathrm{E}f|_{\texttt{(} \mathrm{d}x \texttt{)} \mathrm{d}y}\end{matrix}\) |
\(\begin{matrix}\mathrm{T}_{00}f\\\mathrm{E}f|_{\texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)}}\end{matrix}\) | |
| \(f_{0}\!\) | \(0\!\) | \(0\!\) | \(0\!\) | \(0\!\) | \(0\!\) |
|
\(\begin{matrix} f_{1}\\f_{2}\\f_{4}\\f_{8} \end{matrix}\) |
\(\begin{matrix} \texttt{(} x \texttt{)(} y \texttt{)} \\ \texttt{(} x \texttt{)~} y \texttt{~} \\ \texttt{~} x \texttt{~(} y \texttt{)} \\ \texttt{~} x \texttt{~~} y \texttt{~} \end{matrix}\) |
\(\begin{matrix} \texttt{~} x \texttt{~~} y \texttt{~} \\ \texttt{~} x \texttt{~(} y \texttt{)} \\ \texttt{(} x \texttt{)~} y \texttt{~} \\ \texttt{(} x \texttt{)(} y \texttt{)} \end{matrix}\) |
\(\begin{matrix} \texttt{~} x \texttt{~(} y \texttt{)} \\ \texttt{~} x \texttt{~~} y \texttt{~} \\ \texttt{(} x \texttt{)(} y \texttt{)} \\ \texttt{(} x \texttt{)~} y \texttt{~} \end{matrix}\!\) |
\(\begin{matrix} \texttt{(} x \texttt{)~} y \texttt{~} \\ \texttt{(} x \texttt{)(} y \texttt{)} \\ \texttt{~} x \texttt{~~} y \texttt{~} \\ \texttt{~} x \texttt{~(} y \texttt{)} \end{matrix}\) |
\(\begin{matrix} \texttt{(} x \texttt{)(} y \texttt{)} \\ \texttt{(} x \texttt{)~} y \texttt{~} \\ \texttt{~} x \texttt{~(} y \texttt{)} \\ \texttt{~} x \texttt{~~} y \texttt{~} \end{matrix}\) |
|
\(\begin{matrix} f_{3}\\f_{12} \end{matrix}\) |
\(\begin{matrix} \texttt{(} x \texttt{)} \\ \texttt{~} x \texttt{~} \end{matrix}\) |
\(\begin{matrix} \texttt{~} x \texttt{~} \\ \texttt{(} x \texttt{)} \end{matrix}\) |
\(\begin{matrix} \texttt{~} x \texttt{~} \\ \texttt{(} x \texttt{)} \end{matrix}\) |
\(\begin{matrix} \texttt{(} x \texttt{)} \\ \texttt{~} x \texttt{~} \end{matrix}\) |
\(\begin{matrix} \texttt{(} x \texttt{)} \\ \texttt{~} x \texttt{~} \end{matrix}\) |
|
\(\begin{matrix} f_{6}\\f_{9} \end{matrix}\) |
\(\begin{matrix} \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\) |
\(\begin{matrix} \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\) |
\(\begin{matrix} \texttt{((} x \texttt{,~} y \texttt{))} \\ \texttt{~(} x \texttt{,~} y \texttt{)~} \end{matrix}\) |
\(\begin{matrix} \texttt{((} x \texttt{,~} y \texttt{))} \\ \texttt{~(} x \texttt{,~} y \texttt{)~} \end{matrix}\) |
\(\begin{matrix} \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\) |
|
\(\begin{matrix} f_{5}\\f_{10} \end{matrix}\) |
\(\begin{matrix} \texttt{(} y \texttt{)} \\ \texttt{~} y \texttt{~} \end{matrix}\) |
\(\begin{matrix} \texttt{~} y \texttt{~} \\ \texttt{(} y \texttt{)} \end{matrix}\) |
\(\begin{matrix} \texttt{(} y \texttt{)} \\ \texttt{~} y \texttt{~} \end{matrix}\) |
\(\begin{matrix} \texttt{~} y \texttt{~} \\ \texttt{(} y \texttt{)} \end{matrix}\) |
\(\begin{matrix} \texttt{(} y \texttt{)} \\ \texttt{~} y \texttt{~} \end{matrix}\) |
|
\(\begin{matrix} f_{7}\\f_{11}\\f_{13}\\f_{14} \end{matrix}\) |
\(\begin{matrix} \texttt{(~} x \texttt{~~} y \texttt{~)} \\ \texttt{(~} x \texttt{~(} y \texttt{))} \\ \texttt{((} x \texttt{)~} y \texttt{~)} \\ \texttt{((} x \texttt{)(} y \texttt{))} \end{matrix}\) |
\(\begin{matrix} \texttt{((} x \texttt{)(} y \texttt{))} \\ \texttt{((} x \texttt{)~} y \texttt{~)} \\ \texttt{(~} x \texttt{~(} y \texttt{))} \\ \texttt{(~} x \texttt{~~} y \texttt{~)} \end{matrix}\) |
\(\begin{matrix} \texttt{((} x \texttt{)~} y \texttt{~)} \\ \texttt{((} x \texttt{)(} y \texttt{))} \\ \texttt{(~} x \texttt{~~} y \texttt{~)} \\ \texttt{(~} x \texttt{~(} y \texttt{))} \end{matrix}\) |
\(\begin{matrix} \texttt{(~} x \texttt{~(} y \texttt{))} \\ \texttt{(~} x \texttt{~~} y \texttt{~)} \\ \texttt{((} x \texttt{)(} y \texttt{))} \\ \texttt{((} x \texttt{)~} y \texttt{~)} \end{matrix}\!\) |
\(\begin{matrix} \texttt{(~} x \texttt{~~} y \texttt{~)} \\ \texttt{(~} x \texttt{~(} y \texttt{))} \\ \texttt{((} x \texttt{)~} y \texttt{~)} \\ \texttt{((} x \texttt{)(} y \texttt{))} \end{matrix}\) |
| \(f_{15}\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) |
| \(\text{Fixed Point Total}\!\) | \(4\!\) | \(4\!\) | \(4\!\) | \(16\!\) | |
Table A4. Df Expanded Over Differential Features
| \(f\!\) |
\(\mathrm{D}f|_{\mathrm{d}x ~ \mathrm{d}y}\!\) |
\(\mathrm{D}f|_{\mathrm{d}x \texttt{(} \mathrm{d}y \texttt{)}}\!\) |
\(\mathrm{D}f|_{\texttt{(} \mathrm{d}x \texttt{)} \mathrm{d}y}~\!\) |
\(\mathrm{D}f|_{\texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)}}\!\) | |
| \(f_{0}\!\) | \(0\!\) | \(0\!\) | \(0\!\) | \(0\!\) | \(0\!\) |
|
\(\begin{matrix} f_{1}\\f_{2}\\f_{4}\\f_{8} \end{matrix}\) |
\(\begin{matrix} \texttt{(} x \texttt{)(} y \texttt{)} \\ \texttt{(} x \texttt{)~} y \texttt{~} \\ \texttt{~} x \texttt{~(} y \texttt{)} \\ \texttt{~} x \texttt{~~} y \texttt{~} \end{matrix}\) |
\(\begin{matrix} \texttt{((} x \texttt{,~} y \texttt{))} \\ \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\) |
\(\begin{matrix} \texttt{(} y \texttt{)} \\ y \\ \texttt{(} y \texttt{)} \\ y \end{matrix}\!\) |
\(\begin{matrix} \texttt{(} x \texttt{)} \\ \texttt{(} x \texttt{)} \\ x \\ x \end{matrix}\) |
\(\begin{matrix}0\\0\\0\\0\end{matrix}\) |
|
\(\begin{matrix}f_{3}\\f_{12}\end{matrix}\) |
\(\begin{matrix} \texttt{(} x \texttt{)} \\ x \end{matrix}\) |
\(\begin{matrix}1\\1\end{matrix}\) |
\(\begin{matrix}1\\1\end{matrix}\) |
\(\begin{matrix}0\\0\end{matrix}\) |
\(\begin{matrix}0\\0\end{matrix}\) |
|
\(\begin{matrix}f_{6}\\f_{9}\end{matrix}\) |
\(\begin{matrix} \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\) |
\(\begin{matrix}0\\0\end{matrix}\) |
\(\begin{matrix}1\\1\end{matrix}\) |
\(\begin{matrix}1\\1\end{matrix}\) |
\(\begin{matrix}0\\0\end{matrix}\) |
|
\(\begin{matrix}f_{5}\\f_{10}\end{matrix}\) |
\(\begin{matrix} \texttt{(} y \texttt{)} \\ \texttt{~} y \texttt{~} \end{matrix}\) |
\(\begin{matrix}1\\1\end{matrix}\) |
\(\begin{matrix}0\\0\end{matrix}\) |
\(\begin{matrix}1\\1\end{matrix}\) |
\(\begin{matrix}0\\0\end{matrix}\) |
|
\(\begin{matrix}f_{7}\\f_{11}\\f_{13}\\f_{14}\end{matrix}\) |
\(\begin{matrix} \texttt{(~} x \texttt{~~} y \texttt{~)} \\ \texttt{(~} x \texttt{~(} y \texttt{))} \\ \texttt{((} x \texttt{)~} y \texttt{~)} \\ \texttt{((} x \texttt{)(} y \texttt{))} \end{matrix}\) |
\(\begin{matrix} \texttt{((} x \texttt{,~} y \texttt{))} \\ \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\) |
\(\begin{matrix} y \\ \texttt{(} y \texttt{)} \\ y \\ \texttt{(} y \texttt{)} \end{matrix}\) |
\(\begin{matrix} x \\ x \\ \texttt{(} x \texttt{)} \\ \texttt{(} x \texttt{)} \end{matrix}\) |
\(\begin{matrix}0\\0\\0\\0\end{matrix}\) |
| \(f_{15}\!\) | \(1\!\) | \(0\!\) | \(0\!\) | \(0\!\) | \(0\!\) |
Table A5. Ef Expanded Over Ordinary Features
| \(f\!\) |
\(\mathrm{E}f|_{xy}\!\) |
\(\mathrm{E}f|_{x \texttt{(} y \texttt{)}}\!\) |
\(\mathrm{E}f|_{\texttt{(} x \texttt{)} y}\!\) |
\(\mathrm{E}f|_{\texttt{(} x \texttt{)(} y \texttt{)}}\!\) | |
| \(f_{0}\!\) | \(0\!\) | \(0\!\) | \(0\!\) | \(0\!\) | \(0\!\) |
|
\(\begin{matrix} f_{1}\\f_{2}\\f_{4}\\f_{8} \end{matrix}\) |
\(\begin{matrix} \texttt{(} x \texttt{)(} y \texttt{)} \\ \texttt{(} x \texttt{)~} y \texttt{~} \\ \texttt{~} x \texttt{~(} y \texttt{)} \\ \texttt{~} x \texttt{~~} y \texttt{~} \end{matrix}\) |
\(\begin{matrix} \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \\ \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \\ \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \\ \texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)} \end{matrix}\) |
\(\begin{matrix} \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \\ \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \\ \texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)} \\ \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \end{matrix}\!\) |
\(\begin{matrix} \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \\ \texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)} \\ \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \\ \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \end{matrix}\) |
\(\begin{matrix} \texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)} \\ \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \\ \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \\ \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \end{matrix}\) |
|
\(\begin{matrix} f_{3}\\f_{12} \end{matrix}\) |
\(\begin{matrix} \texttt{(} x \texttt{)} \\ \texttt{~} x \texttt{~} \end{matrix}\) |
\(\begin{matrix} \texttt{~} \mathrm{d}x \texttt{~} \\ \texttt{(} \mathrm{d}x \texttt{)} \end{matrix}\) |
\(\begin{matrix} \texttt{~} \mathrm{d}x \texttt{~} \\ \texttt{(} \mathrm{d}x \texttt{)} \end{matrix}\) |
\(\begin{matrix} \texttt{(} \mathrm{d}x \texttt{)} \\ \texttt{~} \mathrm{d}x \texttt{~} \end{matrix}\) |
\(\begin{matrix} \texttt{(} \mathrm{d}x \texttt{)} \\ \texttt{~} \mathrm{d}x \texttt{~} \end{matrix}\) |
|
\(\begin{matrix} f_{6}\\f_{9} \end{matrix}\) |
\(\begin{matrix} \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\) |
\(\begin{matrix} \texttt{~(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)~} \\ \texttt{((} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{))} \end{matrix}\) |
\(\begin{matrix} \texttt{((} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{))} \\ \texttt{~(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)~} \end{matrix}\) |
\(\begin{matrix} \texttt{((} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{))} \\ \texttt{~(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)~} \end{matrix}\) |
\(\begin{matrix} \texttt{~(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)~} \\ \texttt{((} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{))} \end{matrix}\) |
|
\(\begin{matrix} f_{5}\\f_{10} \end{matrix}\) |
\(\begin{matrix} \texttt{(} y \texttt{)} \\ \texttt{~} y \texttt{~} \end{matrix}\) |
\(\begin{matrix} \texttt{~} \mathrm{d}y \texttt{~} \\ \texttt{(} \mathrm{d}y \texttt{)} \end{matrix}\) |
\(\begin{matrix} \texttt{(} \mathrm{d}y \texttt{)} \\ \texttt{~} \mathrm{d}y \texttt{~} \end{matrix}\) |
\(\begin{matrix} \texttt{~} \mathrm{d}y \texttt{~} \\ \texttt{(} \mathrm{d}y \texttt{)} \end{matrix}\) |
\(\begin{matrix} \texttt{(} \mathrm{d}y \texttt{)} \\ \texttt{~} \mathrm{d}y \texttt{~} \end{matrix}\) |
|
\(\begin{matrix} f_{7}\\f_{11}\\f_{13}\\f_{14} \end{matrix}\) |
\(\begin{matrix} \texttt{(~} x \texttt{~~} y \texttt{~)} \\ \texttt{(~} x \texttt{~(} y \texttt{))} \\ \texttt{((} x \texttt{)~} y \texttt{~)} \\ \texttt{((} x \texttt{)(} y \texttt{))} \end{matrix}\) |
\(\begin{matrix} \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \\ \texttt{((} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~)} \\ \texttt{(~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{))} \\ \texttt{(~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~)} \end{matrix}\) |
\(\begin{matrix} \texttt{((} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~)} \\ \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \\ \texttt{(~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~)} \\ \texttt{(~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{))} \end{matrix}\) |
\(\begin{matrix} \texttt{(~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{))} \\ \texttt{(~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~)} \\ \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \\ \texttt{((} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~)} \end{matrix}\!\) |
\(\begin{matrix} \texttt{(~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~)} \\ \texttt{(~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{))} \\ \texttt{((} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~)} \\ \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \end{matrix}\) |
| \(f_{15}\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) | \(1\!\) |
Table A6. Df Expanded Over Ordinary Features
| \(f\!\) |
\(\mathrm{D}f|_{xy}\!\) |
\(\mathrm{D}f|_{x \texttt{(} y \texttt{)}}\!\) |
\(\mathrm{D}f|_{\texttt{(} x \texttt{)} y}\!\) |
\(\mathrm{D}f|_{\texttt{(} x \texttt{)(} y \texttt{)}}\!\) | |
| \(f_{0}\!\) | \(0\!\) | \(0\!\) | \(0\!\) | \(0\!\) | \(0\!\) |
| \(\begin{matrix}f_{1}\\f_{2}\\f_{4}\\f_{8}\end{matrix}\) |
\(\begin{matrix} \texttt{(} x \texttt{)(} y \texttt{)} \\ \texttt{(} x \texttt{)~} y \texttt{~} \\ \texttt{~} x \texttt{~(} y \texttt{)} \\ \texttt{~} x \texttt{~~} y \texttt{~} \end{matrix}\) |
\(\begin{matrix} \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \\ \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \\ \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \\ \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \end{matrix}\) |
\(\begin{matrix} \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \\ \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \\ \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \\ \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \end{matrix}\!\) |
\(\begin{matrix} \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \\ \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \\ \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \\ \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \end{matrix}\) |
\(\begin{matrix} \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \\ \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \\ \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \\ \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \end{matrix}\) |
| \(\begin{matrix}f_{3}\\f_{12}\end{matrix}\) |
\(\begin{matrix}\texttt{(} x \texttt{)}\\\texttt{~} x \texttt{~}\end{matrix}\) |
\(\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}\) |
\(\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}\) |
\(\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}\) |
\(\begin{matrix}\mathrm{d}x\\\mathrm{d}x\end{matrix}\) |
| \(\begin{matrix}f_{6}\\f_{9}\end{matrix}\) |
\(\begin{matrix} \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\) |
\(\begin{matrix} \texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)} \\ \texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)} \end{matrix}\) |
\(\begin{matrix} \texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)} \\ \texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)} \end{matrix}\) |
\(\begin{matrix} \texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)} \\ \texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)} \end{matrix}\) |
\(\begin{matrix} \texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)} \\ \texttt{(} \mathrm{d}x \texttt{,~} \mathrm{d}y \texttt{)} \end{matrix}\) |
| \(\begin{matrix}f_{5}\\f_{10}\end{matrix}\) |
\(\begin{matrix} \texttt{(} y \texttt{)} \\ \texttt{~} y \texttt{~} \end{matrix}\) |
\(\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}\) |
\(\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}\) |
\(\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}\) |
\(\begin{matrix}\mathrm{d}y\\\mathrm{d}y\end{matrix}\) |
| \(\begin{matrix}f_{7}\\f_{11}\\f_{13}\\f_{14}\end{matrix}\) |
\(\begin{matrix} \texttt{(~} x \texttt{~~} y \texttt{~)} \\ \texttt{(~} x \texttt{~(} y \texttt{))} \\ \texttt{((} x \texttt{)~} y \texttt{~)} \\ \texttt{((} x \texttt{)(} y \texttt{))} \end{matrix}\) |
\(\begin{matrix} \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \\ \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \\ \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \\ \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \end{matrix}\) |
\(\begin{matrix} \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \\ \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \\ \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \\ \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \end{matrix}\) |
\(\begin{matrix} \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \\ \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \\ \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \\ \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \end{matrix}\!\) |
\(\begin{matrix} \texttt{~} \mathrm{d}x \texttt{~~} \mathrm{d}y \texttt{~} \\ \texttt{~} \mathrm{d}x \texttt{~(} \mathrm{d}y \texttt{)} \\ \texttt{(} \mathrm{d}x \texttt{)~} \mathrm{d}y \texttt{~} \\ \texttt{((} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{))} \end{matrix}\) |
| \(f_{15}\!\) | \(1\!\) | \(0\!\) | \(0\!\) | \(0\!\) | \(0\!\) |
Differential Forms
The actions of the difference operator \(\mathrm{D}\!\) and the tangent operator \(\mathrm{d}\!\) on the 16 bivariate propositions are shown in Tables A7 and A8.
Table A7 expands the differential forms that result over a logical basis:
|
\(\{~ \texttt{(}\mathrm{d}x\texttt{)(}\mathrm{d}y\texttt{)}, ~\mathrm{d}x~\texttt{(}\mathrm{d}y\texttt{)}, ~\texttt{(}\mathrm{d}x\texttt{)}~\mathrm{d}y, ~\mathrm{d}x~\mathrm{d}y ~\}.\!\) |
This set consists of the singular propositions in the first order differential variables, indicating mutually exclusive and exhaustive cells of the tangent universe of discourse. Accordingly, this set of differential propositions may also be referred to as the cell-basis, point-basis, or singular differential basis. In this setting it is frequently convenient to use the following abbreviations:
|
\(\partial x ~=~ \mathrm{d}x~\texttt{(}\mathrm{d}y\texttt{)}\!\) and \(\partial y ~=~ \texttt{(}\mathrm{d}x\texttt{)}~\mathrm{d}y.\!\) |
Table A8 expands the differential forms that result over an algebraic basis:
| \(\{~ 1, ~\mathrm{d}x, ~\mathrm{d}y, ~\mathrm{d}x~\mathrm{d}y ~\}.\!\) |
This set consists of the positive propositions in the first order differential variables, indicating overlapping positive regions of the tangent universe of discourse. Accordingly, this set of differential propositions may also be referred to as the positive differential basis.
Table A7. Differential Forms Expanded on a Logical Basis
| \(f\!\) | \(\mathrm{D}f\) | \(\mathrm{d}f\) | |
| \(f_{0}\!\) | \(\texttt{(~)}\!\) | \(0\!\) | \(0\!\) |
| \(\begin{matrix}f_{1}\\f_{2}\\f_{4}\\f_{8}\end{matrix}\) |
\(\begin{matrix} \texttt{(} x \texttt{)(} y \texttt{)} \\ \texttt{(} x \texttt{)~} y \texttt{~} \\ \texttt{~} x \texttt{~(} y \texttt{)} \\ \texttt{~} x \texttt{~~} y \texttt{~} \end{matrix}\) |
\(\begin{matrix} \texttt{(} y \texttt{)} & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \texttt{(} x \texttt{)} & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y & + & \texttt{((} x \texttt{,~} y \texttt{))} & \mathrm{d}x ~ \mathrm{d}y \\ y & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \texttt{(} x \texttt{)} & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y & + & \texttt{(} x \texttt{,~} y \texttt{)} & \mathrm{d}x ~ \mathrm{d}y \\ \texttt{(} y \texttt{)} & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & x & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y & + & \texttt{(} x \texttt{,~} y \texttt{)} & \mathrm{d}x ~ \mathrm{d}y \\ y & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & x & \texttt{(} \mathrm{d}x) ~ \mathrm{d}y & + & \texttt{((} x \texttt{,~} y \texttt{))} & \mathrm{d}x ~ \mathrm{d}y \end{matrix}\) |
\(\begin{matrix} \texttt{(} y \texttt{)} ~\partial x & + & \texttt{(} x \texttt{)} ~\partial y \\ \texttt{~} y \texttt{~} ~\partial x & + & \texttt{(} x \texttt{)} ~\partial y \\ \texttt{(} y \texttt{)} ~\partial x & + & \texttt{~} x \texttt{~} ~\partial y \\ \texttt{~} y \texttt{~} ~\partial x & + & \texttt{~} x \texttt{~} ~\partial y \end{matrix}\) |
| \(\begin{matrix}f_{3}\\f_{12}\end{matrix}\) |
\(\begin{matrix} \texttt{(} x \texttt{)} \\ \texttt{~} x \texttt{~} \end{matrix}\) |
\(\begin{matrix} \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \mathrm{d}x ~ \mathrm{d}y \\ \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \mathrm{d}x ~ \mathrm{d}y \end{matrix}\!\) |
\(\begin{matrix} \partial x \\ \partial x \end{matrix}\) |
| \(\begin{matrix}f_{6}\\f_{9}\end{matrix}\) |
\(\begin{matrix} \texttt{~(} x \texttt{,~} y \texttt{)~} \\ \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\) |
\(\begin{matrix} \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y \\ \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y \end{matrix}\) |
\(\begin{matrix} \partial x & + & \partial y \\ \partial x & + & \partial y \end{matrix}\) |
| \(\begin{matrix}f_{5}\\f_{10}\end{matrix}\) |
\(\begin{matrix} \texttt{(} y \texttt{)} \\ \texttt{~} y \texttt{~} \end{matrix}\) |
\(\begin{matrix} \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y & + & \mathrm{d}x ~ \mathrm{d}y \\ \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y & + & \mathrm{d}x ~ \mathrm{d}y \end{matrix}\) |
\(\begin{matrix} \partial y \\ \partial y \end{matrix}\) |
| \(\begin{matrix}f_{7}\\f_{11}\\f_{13}\\f_{14}\end{matrix}\) |
\(\begin{matrix} \texttt{(~} x \texttt{~~} y \texttt{~)} \\ \texttt{(~} x \texttt{~(} y \texttt{))} \\ \texttt{((} x \texttt{)~} y \texttt{~)} \\ \texttt{((} x \texttt{)(} y \texttt{))} \end{matrix}\) |
\(\begin{matrix} y & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & x & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y & + & \texttt{((} x \texttt{,~} y \texttt{))} & \mathrm{d}x ~ \mathrm{d}y \\ \texttt{(} y \texttt{)} & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & x & \texttt{(} \mathrm{d}x) ~ \mathrm{d}y & + & \texttt{(} x \texttt{,~} y \texttt{)} & \mathrm{d}x ~ \mathrm{d}y \\ y & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \texttt{(} x \texttt{)} & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y & + & \texttt{(} x \texttt{,~} y \texttt{)} & \mathrm{d}x ~ \mathrm{d}y \\ \texttt{(} y \texttt{)} & \mathrm{d}x ~ \texttt{(} \mathrm{d}y \texttt{)} & + & \texttt{(} x \texttt{)} & \texttt{(} \mathrm{d}x \texttt{)} ~ \mathrm{d}y & + & \texttt{((} x \texttt{,~} y \texttt{))} & \mathrm{d}x ~ \mathrm{d}y \end{matrix}\) |
\(\begin{matrix} \texttt{~} y \texttt{~} ~\partial x & + & \texttt{~} x \texttt{~} ~\partial y \\ \texttt{(} y \texttt{)} ~\partial x & + & \texttt{~} x \texttt{~} ~\partial y \\ \texttt{~} y \texttt{~} ~\partial x & + & \texttt{(} x \texttt{)} ~\partial y \\ \texttt{(} y \texttt{)} ~\partial x & + & \texttt{(} x \texttt{)} ~\partial y \end{matrix}\) |
| \(f_{15}\!\) | \(\texttt{((~))}\!\) | \(0\!\) | \(0\!\) |
Table A8. Differential Forms Expanded on an Algebraic Basis
Table A12. Detail of Calculation for the Difference Map
| \(f\!\) |
\(\begin{array}{cr} ~ & \mathrm{E}f|_{\mathrm{d}x ~ \mathrm{d}y} \\[4pt] + & f|_{\mathrm{d}x ~ \mathrm{d}y} \\[4pt] = & \mathrm{D}f|_{\mathrm{d}x ~ \mathrm{d}y} \end{array}\) |
\(\begin{array}{cr} ~ & \mathrm{E}f|_{\texttt{(} \mathrm{d}x \texttt{)} \mathrm{d}y} \\[4pt] + & f|_{\texttt{(} \mathrm{d}x \texttt{)} \mathrm{d}y} \\[4pt] = & \mathrm{D}f|_{\texttt{(} \mathrm{d}x \texttt{)} \mathrm{d}y} \end{array}\) |
\(\begin{array}{cr} ~ & \mathrm{E}f|_{\mathrm{d}x \texttt{(} \mathrm{d}y \texttt{)}} \\[4pt] + & f|_{\mathrm{d}x \texttt{(} \mathrm{d}y \texttt{)}} \\[4pt] = & \mathrm{D}f|_{\mathrm{d}x \texttt{(} \mathrm{d}y \texttt{)}} \end{array}\) |
\(\begin{array}{cr} ~ & \mathrm{E}f|_{\texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)}} \\[4pt] + & f|_{\texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)}} \\[4pt] = & \mathrm{D}f|_{\texttt{(} \mathrm{d}x \texttt{)(} \mathrm{d}y \texttt{)}} \end{array}\) | |
| \(f_{0}\!\) | \(0\!\) | \(0 ~+~ 0 ~=~ 0\!\) | \(0 ~+~ 0 ~=~ 0\!\) | \(0 ~+~ 0 ~=~ 0\!\) | \(0 ~+~ 0 ~=~ 0\!\) |
| \(f_{1}\!\) |
\(\texttt{~(} x \texttt{)(} y \texttt{)~}\!\) |
\(\begin{matrix} ~ & \texttt{~~} x \texttt{~~} y \texttt{~~} \\[4pt] + & \texttt{~(} x \texttt{)(} y \texttt{)~} \\[4pt] = & \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{~~} x \texttt{~(} y \texttt{)~} \\[4pt] + & \texttt{~(} x \texttt{)(} y \texttt{)~} \\[4pt] = & \texttt{~~} ~ \texttt{~(} y \texttt{)~} \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{~(} x \texttt{)~} y \texttt{~~} \\[4pt] + & \texttt{~(} x \texttt{)(} y \texttt{)~} \\[4pt] = & \texttt{~(} x \texttt{)~} ~ \texttt{~~} \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{~(} x \texttt{)(} y \texttt{)~} \\[4pt] + & \texttt{~(} x \texttt{)(} y \texttt{)~} \\[4pt] = & 0 \end{matrix}\) |
| \(f_{2}\!\) |
\(\texttt{~(} x \texttt{)~} y \texttt{~~}\!\) |
\(\begin{matrix} ~ & \texttt{~~} x \texttt{~(} y \texttt{)~} \\[4pt] + & \texttt{~(} x \texttt{)~} y \texttt{~~} \\[4pt] = & \texttt{~(} x \texttt{,~} y \texttt{)~} \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{~~} x \texttt{~~} y \texttt{~~} \\[4pt] + & \texttt{~(} x \texttt{)~} y \texttt{~~} \\[4pt] = & \texttt{~~} ~ \texttt{~~} y \texttt{~~} \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{~(} x \texttt{)(} y \texttt{)~} \\[4pt] + & \texttt{~(} x \texttt{)~} y \texttt{~~} \\[4pt] = & \texttt{~(} x \texttt{)~} ~ \texttt{~~} \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{~(} x \texttt{)~} y \texttt{~~} \\[4pt] + & \texttt{~(} x \texttt{)~} y \texttt{~~} \\[4pt] = & 0 \end{matrix}\) |
| \(f_{4}\!\) |
\(\texttt{~~} x \texttt{~(} y \texttt{)~}\!\) |
\(\begin{matrix} ~ & \texttt{~(} x \texttt{)~} y \texttt{~~} \\[4pt] + & \texttt{~~} x \texttt{~(} y \texttt{)~} \\[4pt] = & \texttt{~(} x \texttt{,~} y \texttt{)~} \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{~(} x \texttt{)(} y \texttt{)~} \\[4pt] + & \texttt{~~} x \texttt{~(} y \texttt{)~} \\[4pt] = & \texttt{~~} ~ \texttt{~(} y \texttt{)~} \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{~~} x \texttt{~~} y \texttt{~~} \\[4pt] + & \texttt{~~} x \texttt{~(} y \texttt{)~} \\[4pt] = & \texttt{~~} x \texttt{~~} ~ \texttt{~~} \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{~~} x \texttt{~(} y \texttt{)~} \\[4pt] + & \texttt{~~} x \texttt{~(} y \texttt{)~} \\[4pt] = & 0 \end{matrix}\) |
| \(f_{8}\!\) |
\(\texttt{~~} x \texttt{~~} y \texttt{~~}\!\) |
\(\begin{matrix} ~ & \texttt{~(} x \texttt{)(} y \texttt{)~} \\[4pt] + & \texttt{~~} x \texttt{~~} y \texttt{~~} \\[4pt] = & \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{~(} x \texttt{)~} y \texttt{~~} \\[4pt] + & \texttt{~~} x \texttt{~~} y \texttt{~~} \\[4pt] = & \texttt{~~} ~ \texttt{~~} y \texttt{~~} \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{~~} x \texttt{~(} y \texttt{)~} \\[4pt] + & \texttt{~~} x \texttt{~~} y \texttt{~~} \\[4pt] = & \texttt{~~} x \texttt{~~} ~ \texttt{~~} \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{~~} x \texttt{~~} y \texttt{~~} \\[4pt] + & \texttt{~~} x \texttt{~~} y \texttt{~~} \\[4pt] = & 0 \end{matrix}\) |
| \(f_{3}\!\) |
\(\texttt{(} x \texttt{)}\!\) |
\(\begin{matrix} ~ & x \\[4pt] + & \texttt{(} x \texttt{)} \\[4pt] = & 1 \end{matrix}\) |
\(\begin{matrix} ~ & x \\[4pt] + & \texttt{(} x \texttt{)} \\[4pt] = & 1 \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{(} x \texttt{)} \\[4pt] + & \texttt{(} x \texttt{)} \\[4pt] = & 0 \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{(} x \texttt{)} \\[4pt] + & \texttt{(} x \texttt{)} \\[4pt] = & 0 \end{matrix}\) |
| \(f_{12}\!\) |
\(x\!\) |
\(\begin{matrix} ~ & \texttt{(} x \texttt{)} \\[4pt] + & x \\[4pt] = & 1 \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{(} x \texttt{)} \\[4pt] + & x \\[4pt] = & 1 \end{matrix}\) |
\(\begin{matrix} ~ & x \\[4pt] + & x \\[4pt] = & 0 \end{matrix}\) |
\(\begin{matrix} ~ & x \\[4pt] + & x \\[4pt] = & 0 \end{matrix}\) |
| \(f_{6}\!\) |
\(\texttt{~(} x \texttt{,~} y \texttt{)~}\!\) |
\(\begin{matrix} ~ & \texttt{~(} x \texttt{,~} y \texttt{)~} \\[4pt] + & \texttt{~(} x \texttt{,~} y \texttt{)~} \\[4pt] = & 0 \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{((} x \texttt{,~} y \texttt{))} \\[4pt] + & \texttt{~(} x \texttt{,~} y \texttt{)~} \\[4pt] = & 1 \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{((} x \texttt{,~} y \texttt{))} \\[4pt] + & \texttt{~(} x \texttt{,~} y \texttt{)~} \\[4pt] = & 1 \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{~(} x \texttt{,~} y \texttt{)~} \\[4pt] + & \texttt{~(} x \texttt{,~} y \texttt{)~} \\[4pt] = & 0 \end{matrix}\) |
| \(f_{9}\!\) |
\(\texttt{((} x \texttt{,~} y \texttt{))}\!\) |
\(\begin{matrix} ~ & \texttt{((} x \texttt{,~} y \texttt{))} \\[4pt] + & \texttt{((} x \texttt{,~} y \texttt{))} \\[4pt] = & 0 \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{~(} x \texttt{,~} y \texttt{)~} \\[4pt] + & \texttt{((} x \texttt{,~} y \texttt{))} \\[4pt] = & 1 \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{~(} x \texttt{,~} y \texttt{)~} \\[4pt] + & \texttt{((} x \texttt{,~} y \texttt{))} \\[4pt] = & 1 \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{((} x \texttt{,~} y \texttt{))} \\[4pt] + & \texttt{((} x \texttt{,~} y \texttt{))} \\[4pt] = & 0 \end{matrix}\) |
| \(f_{5}\!\) |
\(\texttt{(} y \texttt{)}\!\) |
\(\begin{matrix} ~ & y \\[4pt] + & \texttt{(} y \texttt{)} \\[4pt] = & 1 \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{(} y \texttt{)} \\[4pt] + & \texttt{(} y \texttt{)} \\[4pt] = & 0 \end{matrix}\) |
\(\begin{matrix} ~ & y \\[4pt] + & \texttt{(} y \texttt{)} \\[4pt] = & 1 \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{(} y \texttt{)} \\[4pt] + & \texttt{(} y \texttt{)} \\[4pt] = & 0 \end{matrix}\) |
| \(f_{10}\!\) |
\(y\!\) |
\(\begin{matrix} ~ & \texttt{(} y \texttt{)} \\[4pt] + & y \\[4pt] = & 1 \end{matrix}\) |
\(\begin{matrix} ~ & y \\[4pt] + & y \\[4pt] = & 0 \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{(} y \texttt{)} \\[4pt] + & y \\[4pt] = & 1 \end{matrix}\) |
\(\begin{matrix} ~ & y \\[4pt] + & y \\[4pt] = & 0 \end{matrix}\) |
| \(f_{7}\!\) |
\(\texttt{~(} x \texttt{~~} y \texttt{)~}\!\) |
\(\begin{matrix} ~ & \texttt{((} x \texttt{)(} y \texttt{))} \\[4pt] + & \texttt{~(} x \texttt{~~} y \texttt{)~} \\[4pt] = & \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{((} x \texttt{)~} y \texttt{)~} \\[4pt] + & \texttt{~(} x \texttt{~~} y \texttt{)~} \\[4pt] = & \texttt{~~} ~ \texttt{~~} y \texttt{~~} \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{~(} x \texttt{~(} y \texttt{))} \\[4pt] + & \texttt{~(} x \texttt{~~} y \texttt{)~} \\[4pt] = & \texttt{~~} x \texttt{~~} ~ \texttt{~~} \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{~(} x \texttt{~~} y \texttt{)~} \\[4pt] + & \texttt{~(} x \texttt{~~} y \texttt{)~} \\[4pt] = & 0 \end{matrix}\) |
| \(f_{11}\!\) |
\(\texttt{~(} x \texttt{~(} y \texttt{))}\!\) |
\(\begin{matrix} ~ & \texttt{((} x \texttt{)~} y \texttt{)~} \\[4pt] + & \texttt{~(} x \texttt{~(} y \texttt{))} \\[4pt] = & \texttt{~(} x \texttt{,~} y \texttt{)~} \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{((} x \texttt{)(} y \texttt{))} \\[4pt] + & \texttt{~(} x \texttt{~(} y \texttt{))} \\[4pt] = & \texttt{~~} ~ \texttt{~(} y \texttt{)~} \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{~(} x \texttt{~~} y \texttt{)~} \\[4pt] + & \texttt{~(} x \texttt{~(} y \texttt{))} \\[4pt] = & \texttt{~~} x \texttt{~~} ~ \texttt{~~} \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{~(} x \texttt{~(} y \texttt{))} \\[4pt] + & \texttt{~(} x \texttt{~(} y \texttt{))} \\[4pt] = & 0 \end{matrix}\) |
| \(f_{13}\!\) |
\(\texttt{((} x \texttt{)~} y \texttt{)~}\!\) |
\(\begin{matrix} ~ & \texttt{~(} x \texttt{~(} y \texttt{))} \\[4pt] + & \texttt{((} x \texttt{)~} y \texttt{)~} \\[4pt] = & \texttt{~(} x \texttt{,~} y \texttt{)~} \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{~(} x \texttt{~~} y \texttt{)~} \\[4pt] + & \texttt{((} x \texttt{)~} y \texttt{)~} \\[4pt] = & \texttt{~~} ~ \texttt{~~} y \texttt{~~} \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{((} x \texttt{)(} y \texttt{))} \\[4pt] + & \texttt{((} x \texttt{)~} y \texttt{)~} \\[4pt] = & \texttt{~(} x \texttt{)~} ~ \texttt{~~} \end{matrix}\!\) |
\(\begin{matrix} ~ & \texttt{((} x \texttt{)~} y \texttt{)~} \\[4pt] + & \texttt{((} x \texttt{)~} y \texttt{)~} \\[4pt] = & 0 \end{matrix}\) |
| \(f_{14}\!\) |
\(\texttt{((} x \texttt{)(} y \texttt{))}\!\) |
\(\begin{matrix} ~ & \texttt{~(} x \texttt{~~} y \texttt{)~} \\[4pt] + & \texttt{((} x \texttt{)(} y \texttt{))} \\[4pt] = & \texttt{((} x \texttt{,~} y \texttt{))} \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{~(} x \texttt{~(} y \texttt{))} \\[4pt] + & \texttt{((} x \texttt{)(} y \texttt{))} \\[4pt] = & \texttt{~~} ~ \texttt{~(} y \texttt{)~} \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{((} x \texttt{)~} y \texttt{)~} \\[4pt] + & \texttt{((} x \texttt{)(} y \texttt{))} \\[4pt] = & \texttt{~(} x \texttt{)~} ~ \texttt{~~} \end{matrix}\) |
\(\begin{matrix} ~ & \texttt{((} x \texttt{)(} y \texttt{))} \\[4pt] + & \texttt{((} x \texttt{)(} y \texttt{))} \\[4pt] = & 0 \end{matrix}\) |
| \(f_{15}\!\) | \(1\!\) | \(1 ~+~ 1 ~=~ 0\!\) | \(1 ~+~ 1 ~=~ 0\!\) | \(1 ~+~ 1 ~=~ 0\!\) | \(1 ~+~ 1 ~=~ 0\!\) |
Appendix 2. Computational Details
Operator Maps for the Logical Disjunction f(u, v)
Computation of “εf”
Computation of “Ef”
Computation of “Df” (1)
Computation of “Df” (2)
Computation of “df”
Computation of “rf”
Computation Summary for Disjunction
|
\(\begin{array}{c*{8}{l}} \boldsymbol\varepsilon f & = & u \!\cdot\! v \cdot 1 & + & u \texttt{(} v \texttt{)} \cdot 1 & + & \texttt{(} u \texttt{)} v \cdot 1 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 0 \\[6pt] \mathrm{E}f & = & u \!\cdot\! v \cdot \texttt{(} \mathrm{d}u \cdot \mathrm{d}v \texttt{)} & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{))} & + & \texttt{(} u \texttt{)} v \cdot \texttt{((} \mathrm{d}u \texttt{)} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} \\[6pt] \mathrm{D}f & = & u \!\cdot\! v \cdot \mathrm{d}u \cdot \mathrm{d}v & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} \\[6pt] \mathrm{d}f & = & u \!\cdot\! v \cdot 0 & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \\[6pt] \mathrm{r}f & = & u \!\cdot\! v \cdot \mathrm{d}u \cdot \mathrm{d}v & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u \cdot \mathrm{d}v & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u \cdot \mathrm{d}v & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u \cdot \mathrm{d}v \end{array}\) |
Operator Maps for the Logical Equality g(u, v)
Computation of “εg”
Computation of “Eg”
Computation of “Dg” (1)
Computation of “Dg” (2)
Computation of “dg”
Computation of “rg”
Computation Summary for Equality
|
\(\begin{array}{c*{8}{l}} \boldsymbol\varepsilon g & = & u \!\cdot\! v \cdot 1 & + & u \texttt{(} v \texttt{)} \cdot 0 & + & \texttt{(} u \texttt{)} v \cdot 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 1 \\[6pt] \mathrm{E}g & = & u \!\cdot\! v \cdot \texttt{((} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{))} & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{))} \\[6pt] \mathrm{D}g & = & u \!\cdot\! v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \\[6pt] \mathrm{d}g & = & u \!\cdot\! v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} \\[6pt] \mathrm{r}g & = & u \!\cdot\! v \cdot 0 & + & u \texttt{(} v \texttt{)} \cdot 0 & + & \texttt{(} u \texttt{)} v \cdot 0 & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 0 \end{array}\) |
Appendix 3. Source Materials
Appendix 4. Various Definitions of the Tangent Vector
References
Works Cited
| [AuM] | Auslander, L., and MacKenzie, R.E., Introduction to Differentiable Manifolds, McGraw-Hill, 1963. Reprinted, Dover, New York, NY, 1977. |
| [BiG] | Bishop, R.L., and Goldberg, S.I., Tensor Analysis on Manifolds, Macmillan, 1968. Reprinted, Dover, New York, NY, 1980. |
| [Boo] | Boole, G., An Investigation of The Laws of Thought, Macmillan, 1854. Reprinted, Dover, New York, NY, 1958. |
| [BoT] | Bott, R., and Tu, L.W., Differential Forms in Algebraic Topology, Springer-Verlag, New York, NY, 1982. |
| [dCa] | do Carmo, M.P., Riemannian Geometry. Originally published in Portuguese, 1st editiom 1979, 2nd edition 1988. Translated by F. Flaherty, Birkhäuser, Boston, MA, 1992. |
| [Che46] | Chevalley, C., Theory of Lie Groups, Princeton University Press, Princeton, NJ, 1946. |
| [Che56] | Chevalley, C., Fundamental Concepts of Algebra, Academic Press, 1956. |
| [Cho86] | Chomsky, N., Knowledge of Language : Its Nature, Origin, and Use, Praeger, New York, NY, 1986. |
| [Cho93] | Chomsky, N., Language and Thought, Moyer Bell, Wakefield, RI, 1993. |
| [DoM] | Doolin, B.F., and Martin, C.F., Introduction to Differential Geometry for Engineers, Marcel Dekker, New York, NY, 1990. |
| [Fuji] | Fujiwara, H., Logic Testing and Design for Testability, MIT Press, Cambridge, MA, 1985. |
| [Hic] | Hicks, N.J., Notes on Differential Geometry, Van Nostrand, Princeton, NJ, 1965. |
| [Hir] | Hirsch, M.W., Differential Topology, Springer-Verlag, New York, NY, 1976. |
| [How] | Howard, W.A., "The Formulae-as-Types Notion of Construction", Notes circulated from 1969. Reprinted in [SeH, 479-490]. |
| [JGH] | Jones, A., Gray, A., and Hutton, R., Manifolds and Mechanics, Cambridge University Press, Cambridge, UK, 1987. |
| [KoA] | Kosinski, A.A., Differential Manifolds, Academic Press, San Diego, CA, 1993. |
| [Koh] | Kohavi, Z., Switching and Finite Automata Theory, 2nd edition, McGraw-Hill, New York, NY, 1978. |
| [LaS] | Lambek, J., and Scott, P.J., Introduction to Higher Order Categorical Logic, Cambridge University Press, Cambridge, UK, 1986. |
| [La83] | Lang, S., Real Analysis, 2nd edition, Addison-Wesley, Reading, MA, 1983. |
| [La84] | Lang, S., Algebra, 2nd edition, Addison-Wesley, Menlo Park, CA, 1984. |
| [La85] | Lang, S., Differential Manifolds, Springer-Verlag, New York, NY, 1985. |
| [La93] | Lang, S., Real and Functional Analysis, 3rd edition, Springer-Verlag, New York, NY, 1993. |
| [Lie80] | Lie, S., "Sophus Lie's 1880 Transformation Group Paper", in Lie Groups : History, Frontiers, and Applications, Volume 1, translated by M. Ackerman, comments by R. Hermann, Math Sci Press, Brookline, MA, 1975. Original paper 1880. |
| [Lie84] | Lie, S., "Sophus Lie's 1884 Differential Invariant Paper", in Lie Groups : History, Frontiers, and Applications, Volume 3, translated by M. Ackerman, comments by R. Hermann, Math Sci Press, Brookline, MA, 1976. Original paper 1884. |
| [LoS] | Loomis, L.H., and Sternberg, S., Advanced Calculus, Addison-Wesley, Reading, MA, 1968. |
| [Mel] | Melzak, Z.A., Companion to Concrete Mathematics, Volume 2 : Mathematical Ideas, Modeling, and Applications, John Wiley amd Sons, New York, NY, 1976. |
| [Men] | Menabrea, L.F., "Sketch of the Analytical Engine Invented by Charles Babbage" with Notes by the Translator, Ada Augusta (Byron), Countess of Lovelace, in [M&M, 225–297]. Originally published 1842. |
| [M&M] | Morrison, P., and Morrison, E. (eds.), Charles Babbage on the Principles and Development of the Calculator, and Other Seminal Writings by Charles Babbage and Others, With an Introduction by the Editors, Dover, Mineola, NY, 1961. |
| [P1] | Peirce, C.S., Collected Papers of Charles Sanders Peirce, vols. 1–8, C. Hartshorne, P. Weiss, and A.W. Burks (eds.), Harvard University Press, Cambridge, MA, 1931–1960. Cited as CP [volume].[paragraph]. |
| [P2] | Peirce, C.S., "Qualitative Logic", in The New Elements of Mathematics, Volume 4, C. Eisele (ed.), Mouton, The Hague, 1976. Cited as NE [volume], [page]. |
| [Rob] | Roberts, D.D., The Existential Graphs of Charles S. Peirce, Mouton, The Hague, 1973. |
| [SeH] | Seldin, J.P., and Hindley, J.R. (eds.), To H.B. Curry : Essays on Combinatory Logic, Lambda Calculus, and Formalism, Academic Press, London, UK, 1980. |
| [SpB] | Spencer-Brown, G., Laws of Form, George Allen and Unwin, London, UK, 1969. |
| [Sp65] | Spivak, M., Calculus on Manifolds : A Modern Approach to Classical Theorems of Advanced Calculus, W.A. Benjamin, New York, NY, 1965. |
| [Sp79] | Spivak, M., A Comprehensive Introduction to Differential Geometry, vols. 1–2. 1st edition 1970. 2nd edition, Publish or Perish Inc., Houston, TX, 1979. |
| [Sty] | Styazhkin, N.I., History of Mathematical Logic from Leibniz to Peano, 1st published in Russian, Nauka, Moscow, 1964. MIT Press, Cambridge, MA, 1969. |
| [Wie] | Wiener, N., Cybernetics : or Control and Communication in the Animal and the Machine, 1st edition 1948. 2nd edition, MIT Press, Cambridge, MA, 1961. |
Works Consulted
| [Ami] | Amit, D.J., Modeling Brain Function : The World of Attractor Neural Networks, Cambridge University Press, Cambridge, UK, 1989. |
| [Ed87] | Edelman, G.M., Neural Darwinism : The Theory of Neuronal Group Selection, Basic Books, New York, NY, 1987. |
| [Ed88] | Edelman, G.M., Topobiology : An Introduction to Molecular Embryology, Basic Books, New York, NY, 1988. |
| [Fla] | Flanders, H., Differential Forms with Applications to the Physical Sciences, Academic Press, 1963. Reprinted, Dover, Mineola, NY, 1989. |
| [Has] | Hassoun, M.H. (ed.), Associative Neural Memories : Theory and Implementation, Oxford University Press, New York, NY, 1993. |
| [KoB] | Kosko, B., Neural Networks and Fuzzy Systems : A Dynamical Systems Approach to Machine Intelligence, Prentice-Hall, Englewood Cliffs, NJ, 1992. |
| [MaB] | Mac Lane, S., and Birkhoff, G., Algebra, 3rd edition, Chelsea, New York, NY, 1993. |
| [Mac] | Mac Lane, S., Categories for the Working Mathematician, Springer-Verlag, New York, NY, 1971. |
| [McC] | McCulloch, W.S., Embodiments of Mind, MIT Press, Cambridge, MA, 1965. |
| [Mc1] | McCulloch, W.S., "A Heterarchy of Values Determined by the Topology of Nervous Nets", Bulletin of Mathematical Biophysics, vol. 7 (1945), pp. 89–93. Reprinted in [McC]. |
| [MiP] | Minsky, M.L., and Papert, S.A., Perceptrons : An Introduction to Computational Geometry, MIT Press, Cambridge, MA, 1969. 2nd printing 1972. Expanded edition 1988. |
| [Rum] | Rumelhart, D.E., Hinton, G.E., and McClelland, J.L., "A General Framework for Parallel Distributed Processing" = Chapter 2 in Rumelhart, McClelland, and the PDP Research Group, Parallel Distributed Processing, Explorations in the Microstructure of Cognition, Volume 1 : Foundations, MIT Press, Cambridge, MA, 1986. |
Incidental Works
| [Dew] | Dewey, John, How We Think, D.C. Heath, Lexington, MA, 1910. Reprinted, Prometheus Books, Buffalo, NY, 1991. |
| [Fou] | Foucault, Michel, The Archaeology of Knowledge and The Discourse on Language, A.M. Sheridan-Smith and Rupert Swyer (trans.), Pantheon, New York, NY, 1972. Originally published as L´Archéologie du Savoir et L´ordre du discours, Editions Gallimard, 1969 & 1971. |
| [Hom] | Homer, The Odyssey, with an English translation by A.T. Murray, Loeb Classical Library, Harvard University Press, Cambridge, MA, 1980. First printed 1919. |
| [Jam] | James, William, Pragmatism : A New Name for Some Old Ways of Thinking, Longmans, Green, and Company, New York, NY, 1907. |
| [Ler] | Leroux, Gaston, The Phantom of the Opera, foreword by P. Haining, Dorset Press, New York, NY, 1988. Originally published in French, 1911. |
| [Mus] | Musil, Robert, The Man Without Qualities, 3 volumes, translated with a foreword by Eithne Wilkins and Ernst Kaiser, Pan Books, London, UK, 1979. English edition first published by Secker and Warburg, 1954. Originally published in German, Der Mann ohne Eigenschaften, 1930 & 1932. |
| [PlaR] | Plato, The Republic, with an English translation by Paul Shorey, Loeb Classical Library, Harvard University Press, Cambridge, MA, 1980. First printed 1930 & 1935. |
| [PlaS] | Plato, The Sophist, Loeb Classical Library, William Heinemann, London, 1921, 1987. |
| [Qui] | Quine, W.V., Mathematical Logic, 1st edition, 1940. Revised edition, 1951. Harvard University Press, Cambridge, MA, 1981. |
| [SaD] | de Santillana, Giorgio, and von Dechend, Hertha, Hamlet's Mill : An Essay on Myth and the Frame of Time, David R. Godine, Publisher, Boston, MA, 1977. 1st published 1969. |
| [Sha] | Shakespeare, William, William Shakespeare : The Complete Works, Compact Edition, S. Wells and G. Taylor (eds.), Oxford University Press, Oxford, UK, 1988. |
| [Sh1] | Shakespeare, William, A Midsummer Night's Dream, Washington Square Press, New York, NY, 1958. |
| [Sh2] | Shakespeare, William, The Tragedy of Hamlet, Prince of Denmark, In [Sha], pp. 654–690. |
| [Sh3] | Shakespeare, William, Measure for Measure, Washington Square Press, New York, NY, 1965. |
| [Web] | Webster's Ninth New Collegiate Dictionary, Merriam-Webster, Springfield, MA, 1983. |
| [Whi] | Whitman, Walt, Leaves of Grass, Vintage Books / The Library of America, New York, NY, 1992. Originally published in numerous editions, 1855–1892. |
| [Wil] | Wilhelm, R., and Baynes, C.F. (trans.), The I Ching, or Book of Changes, foreword by C.G. Jung, preface by H. Wilhelm, 3rd edition, Bollingen Series XIX, Princeton University Press, Princeton, NJ, 1967. |
Document History
Author: Jon Awbrey Created: 16 Dec 1993 Relayed: 31 Oct 1994 Revised: 03 Jun 2003 Recoded: 03 Jun 2007
- Pages with broken file links
- Adaptive Systems
- Artificial Intelligence
- Combinatorics
- Computer Science
- Cybernetics
- Differential Logic
- Discrete Systems
- Dynamical Systems
- Formal Languages
- Formal Sciences
- Formal Systems
- Functional Logic
- Graph Theory
- Group Theory
- Inquiry
- Knowledge Representation
- Linguistics
- Logic
- Logical Graphs
- Mathematics
- Mathematical Systems Theory
- Science
- Semiotics
- Philosophy
- Systems Science
- Visualization