Difference between revisions of "Directory:Jon Awbrey/Papers/Functional Logic : Inquiry and Analogy"
Jon Awbrey (talk | contribs) (→Extending the Existential Interpretation to Quantificational Logic: convert graphic to PNG) |
Jon Awbrey (talk | contribs) (→Abstract: + note on notation) |
||
| Line 3: | Line 3: | ||
This report discusses C.S. Peirce's treatment of analogy, placing it in relation to his overall theory of inquiry. The first order of business is to introduce the three fundamental types of reasoning that Peirce adopted from classical logic. In Peirce's analysis both inquiry and analogy are complex programs of reasoning that develop through stages of these three types, although normally in different orders. | This report discusses C.S. Peirce's treatment of analogy, placing it in relation to his overall theory of inquiry. The first order of business is to introduce the three fundamental types of reasoning that Peirce adopted from classical logic. In Peirce's analysis both inquiry and analogy are complex programs of reasoning that develop through stages of these three types, although normally in different orders. | ||
| + | |||
| + | '''Note on notation.''' The discussion that follows uses [[minimal negation operations]], expressed as bracketed tuples of the form <math>\texttt{(} e_1 \texttt{,} \ldots \texttt{,} e_k \texttt{)},</math> and logical conjunctions, expressed as concatenated tuples of the form <math>e_1 ~\ldots~ e_k,</math> as the sole expression-forming operations of a calculus for [[boolean-valued functions]] or "propositions". The expressions of this calculus parse into data structures whose underlying graphs are called ''cacti'' by graph theorists. Hence the name ''[[cactus language]]'' for this dialect of propositional calculus. | ||
<div class="nonumtoc">__TOC__</div> | <div class="nonumtoc">__TOC__</div> | ||
Revision as of 18:34, 30 October 2009
Abstract
This report discusses C.S. Peirce's treatment of analogy, placing it in relation to his overall theory of inquiry. The first order of business is to introduce the three fundamental types of reasoning that Peirce adopted from classical logic. In Peirce's analysis both inquiry and analogy are complex programs of reasoning that develop through stages of these three types, although normally in different orders.
Note on notation. The discussion that follows uses minimal negation operations, expressed as bracketed tuples of the form \(\texttt{(} e_1 \texttt{,} \ldots \texttt{,} e_k \texttt{)},\) and logical conjunctions, expressed as concatenated tuples of the form \(e_1 ~\ldots~ e_k,\) as the sole expression-forming operations of a calculus for boolean-valued functions or "propositions". The expressions of this calculus parse into data structures whose underlying graphs are called cacti by graph theorists. Hence the name cactus language for this dialect of propositional calculus.
1. Three Types of Reasoning
(This section has been omitted from the present copy.)
1.1. Types of Reasoning in Aristotle
1.2. Types of Reasoning in C.S. Peirce
1.3. Comparison of the Analyses
1.4. Aristotle's "Apagogy" : Abductive Reasoning as Problem Reduction
1.5. Aristotle's "Paradigm" : Reasoning by Analogy or Example
1.6. Peirce's Formulation of Analogy
1.7. Dewey's "Sign of Rain" : An Example of Inquiry
2. Functional Conception of Quantification Theory
Up till now quantification theory has been based on the assumption of individual variables ranging over universal collections of perfectly determinate elements. Merely to write down quantified formulas like \(\forall_{x \in X} f(x)\) and \(\exists_{x \in X} f(x)\) involves a subscription to such notions, as shown by the membership relations invoked in their indices. Reflected on pragmatic and constructive principles, however, these ideas begin to appear as problematic hypotheses whose warrants are not beyond question, projects of exhaustive determination that overreach the powers of finite information and control to manage. Therefore, it is worth considering how we might shift the scene of quantification theory closer to familiar ground, toward the predicates themselves that represent our continuing acquaintance with phenomena.
Higher Order Propositional Expressions
By way of equipping this inquiry with a bit of concrete material, I begin with a consideration of higher order propositional expressions, in particular, those that stem from the propositions on 1 and 2 variables.
Higher Order Propositions and Logical Operators (n = 1)
A higher order proposition is, very roughly speaking, a proposition about propositions. If the original order of propositions is a class of indicator functions \(f : X \to \mathbb{B},\) then the next higher order of propositions consists of maps of the type \(m : (X \to \mathbb{B}) \to \mathbb{B}.\)
For example, consider the case where \(X = \mathbb{B}.\) Then there are exactly four propositions \(f : \mathbb{B} \to \mathbb{B},\) and exactly sixteen higher order propositions that are based on this set, all bearing the type \(m : (\mathbb{B} \to \mathbb{B}) \to \mathbb{B}.\)
Table 10 lists the sixteen higher order propositions about propositions on one boolean variable, organized in the following fashion: Columns 1 and 2 form a truth table for the four \(f : \mathbb{B} \to \mathbb{B},\) turned on its side from the way that one is most likely accustomed to see truth tables, with the row leaders in Column 1 displaying the names of the functions \(f_i,\!\) for \(i\!\) = 1 to 4, while the entries in Column 2 give the values of each function for the argument values that are listed in the corresponding column head. Column 3 displays one of the more usual expressions for the proposition in question. The last sixteen columns are topped by a collection of conventional names for the higher order propositions, also known as the measures \(m_j,\!\) for \(j\!\) = 0 to 15, where the entries in the body of the Table record the values that each \(m_j\!\) assigns to each \(f_i.\!\)
| \(x:\) | 1 0 | \(f\!\) | \(m_0\) | \(m_1\) | \(m_2\) | \(m_3\) | \(m_4\) | \(m_5\) | \(m_6\) | \(m_7\) | \(m_8\) | \(m_9\) | \(m_{10}\) | \(m_{11}\) | \(m_{12}\) | \(m_{13}\) | \(m_{14}\) | \(m_{15}\) |
| \(f_0\) | 0 0 | \(0\!\) | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| \(f_1\) | 0 1 | \((x)\!\) | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| \(f_2\) | 1 0 | \(x\!\) | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| \(f_3\) | 1 1 | \(1\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
I am going to put off explaining Table 11, that presents a sample of what I call interpretive categories for higher order propositions, until after we get beyond the 1-dimensional case, since these lower dimensional cases tend to be a bit condensed or degenerate in their structures, and a lot of what is going on here will almost automatically become clearer as soon as we get even two logical variables into the mix.
| Measure | Happening | Exactness | Existence | Linearity | Uniformity | Information |
| \(m_0\!\) | Nothing happens | |||||
| \(m_1\!\) | Just false | Nothing exists | ||||
| \(m_2\!\) | Just not \(x\!\) | |||||
| \(m_3\!\) | Nothing is \(x\!\) | |||||
| \(m_4\!\) | Just \(x\!\) | |||||
| \(m_5\!\) | Everything is \(x\!\) | \(f\!\) is linear | ||||
| \(m_6\!\) | \(f\!\) is not uniform | \(f\!\) is informed | ||||
| \(m_7\!\) | Not just true | |||||
| \(m_8\!\) | Just true | |||||
| \(m_9\!\) | \(f\!\) is uniform | \(f\!\) is not informed | ||||
| \(m_{10}\!\) | Something is not \(x\!\) | \(f\!\) is not linear | ||||
| \(m_{11}\!\) | Not just \(x\!\) | |||||
| \(m_{12}\!\) | Something is \(x\!\) | |||||
| \(m_{13}\!\) | Not just not \(x\!\) | |||||
| \(m_{14}\!\) | Not just false | Something exists | ||||
| \(m_{15}\!\) | Anything happens |
Higher Order Propositions and Logical Operators (n = 2)
By way of reviewing notation and preparing to extend it to higher order universes of discourse, let us first consider the universe of discourse \(X^\circ = [\mathcal{X}] = [x_1, x_2] = [u, v],\) based on two logical features or boolean variables \(u\!\) and \(v.\!\)
The universe of discourse \(X^\circ\!\) consists of two parts, a set of points and a set of propositions.
The points of \(X^\circ\) form the space:
| \(X \quad = \quad \langle \mathcal{X} \rangle \quad = \quad \langle u, v \rangle \quad = \quad \{ (u, v) \} \quad \cong \quad \mathbb{B}^2.\) |
Each point in \(X\!\) may be indicated by means of a singular proposition, that is, a proposition that describes it uniquely. This form of representation leads to the following enumeration of points, presented in two different styles of typography that are used in this text:
| \(X\!\) | \(=\!\) | \(\{\!\) (u)(v), (u)v, u(v), uv \(\}\!\)
|
\(\cong\!\) | \(\mathbb{B}^2,\) |
| \(X\!\) | \(=\!\) | \(\{\ \underline{(u)(v)},\ \underline{(u)v},\ \underline{u(v)},\ \underline{uv}\ \}\) | \(\cong\!\) | \(\mathbb{B}^2.\) |
Each point in \(X\!\) may also be described by means of its coordinates, that is, by the ordered pair of values in \(\mathbb{B}\) that the coordinate propositions \(u\!\) and \(v\!\) take on that point. This form of representation leads to the following enumeration of points:
| \(X\!\) | \(=\!\) | \(\{\ (0, 0),\ (0, 1),\ (1, 0),\ (1, 1)\ \}\) | \(\cong\!\) | \(\mathbb{B}^2.\) |
The propositions of \(X^\circ\) form the space:
| \(X^\uparrow \quad = \quad (X \to \mathbb{B}) \quad = \quad \{ f : X \to \mathbb{B} \} \quad \cong \quad (\mathbb{B}^2 \to \mathbb{B}).\) |
As always, it is frequently convenient to omit a few of the finer markings of distinctions among isomorphic structures, so long as one is aware of their presence and knows when it is crucial to call upon them again.
The next higher order universe of discourse that is built on \(X^\circ\) is \(X^{\circ 2} = [X^\circ] = [[u, v]],\) which may be developed in the following way. The propositions of \(X^\circ\) become the points of \(X^{\circ 2},\) and the mappings of the type \(m : (X \to \mathbb{B}) \to \mathbb{B}\) become the propositions of \(X^{\circ 2}.\) In addition, it is convenient to equip the discussion with a selected set of higher order operators on propositions, all of which have the form \(w : (\mathbb{B}^2 \to \mathbb{B})^k \to \mathbb{B}.\)
To save a few words in the remainder of this discussion, I will use the terms measure and qualifier to refer to all types of higher order propositions and operators. To describe the present setting in picturesque terms, the propositions of \([u, v]\!\) may be regarded as a gallery of sixteen venn diagrams, while the measures \(m : (X \to \mathbb{B}) \to \mathbb{B}\) are analogous to a body of judges or a panel of critical viewers, each of whom evaluates each of the pictures as a whole and reports the ones that find favor or not. In this way, each judge \(m_j\!\) partitions the gallery of pictures into two aesthetic portions, the pictures \(m_j^{-1}(1)\!\) that \(m_j\!\) likes and the pictures \(m_j^{-1}(0)\!\) that \(m_j\!\) dislikes.
There are \(2^{16} = 65536\!\) measures of the type \(m : (\mathbb{B}^2 \to \mathbb{B}) \to \mathbb{B}.\) Table 12 introduces the first 24 of these measures in the fashion of the higher order truth table that I used before. The column headed \(m_j\!\) shows the values of the measure \(m_j\!\) on each of the propositions \(f_i : \mathbb{B}^2 \to \mathbb{B},\) for \(i\!\) = 0 to 23, with blank entries in the Table being optional for values of zero. The arrangement of measures that continues according to the plan indicated here is referred to as the standard ordering of these measures. In this scheme of things, the index \(j\!\) of the measure \(m_j\!\) is the decimal equivalent of the bit string that is associated with \(m_j\!\)'s functional values, which can be obtained in turn by reading the \(j^\mathrm{th}\!\) column of binary digits in the Table as the corresponding range of boolean values, taking them up in the order from bottom to top.
| \(u:\) \(v:\) |
1100 1010 |
\(f\!\) | \(m_0\) | \(m_1\) | \(m_2\) | \(m_3\) | \(m_4\) | \(m_5\) | \(m_6\) | \(m_7\) | \(m_8\) | \(m_9\) | \(m_{10}\) | \(m_{11}\) | \(m_{12}\) | \(m_{13}\) | \(m_{14}\) | \(m_{15}\) | \(m_{16}\) | \(m_{17}\) | \(m_{18}\) | \(m_{19}\) | \(m_{20}\) | \(m_{21}\) | \(m_{22}\) | \(m_{23}\) |
| \(f_0\) | 0000 | \((~)\) | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| \(f_1\) | 0001 | \((u)(v)\!\) | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| \(f_2\) | 0010 | \((u) v\!\) | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| \(f_3\) | 0011 | \((u)\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_4\) | 0100 | \(u (v)\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| \(f_5\) | 0101 | \((v)\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_6\) | 0110 | \((u, v)\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_7\) | 0111 | \((u v)\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_8\) | 1000 | \(u v\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_9\) | 1001 | \(((u, v))\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_{10}\) | 1010 | \(v\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_{11}\) | 1011 | \((u (v))\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_{12}\) | 1100 | \(u\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_{13}\) | 1101 | \(((u) v)\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_{14}\) | 1110 | \(((u)(v))\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_{15}\) | 1111 | \(((~))\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Umpire Operators
We now examine measures at the high end of the standard ordering. Instrumental to this purpose we define a couple of higher order operators, \(\Upsilon_1 : (\langle u, v \rangle \to \mathbb{B}) \to \mathbb{B}\) and \(\Upsilon : (\langle u, v \rangle \to \mathbb{B})^2 \to \mathbb{B},\) both symbolized by cursive upsilon characters and referred to as the absolute and relative umpire operators, respectively. If either one of these operators is defined in terms of more primitive notions then the remaining operator can be defined in terms of the one first established.
Given an ordered pair of propositions \(e, f : \langle u, v \rangle \to \mathbb{B}\) as arguments, the relative operator reports the value 1 if the first implies the second, otherwise 0.
| \(\Upsilon (e, f) = 1\!\) | \(\operatorname{if~and~only~if}\) | \(e \Rightarrow f.\!\) |
Expressing it another way, we may also write:
| \(\Upsilon (e, f) = 1\!\) | \(\Leftrightarrow\) | \(\underline{(e (f))} = \underline{1}.\) |
In writing this, however, it is important to notice that the 1's appearing on the left and right have different meanings. Filling in the details, we have:
| \(\Upsilon (e, f) = 1 \in \mathbb{B}\) | \(\Leftrightarrow\) | \(\underline{(e (f))} = 1 : \langle u, v \rangle \to \mathbb{B}.\) |
Writing types as subscripts and using the fact that \(X = \langle u, v \rangle,\) it is possible to express this a little more succinctly as follows:
| \(\Upsilon (e, f) = 1_\mathbb{B}\) | \(\Leftrightarrow\) | \(\underline{(e (f))} = 1_{X \to \mathbb{B}}.\) |
Finally, it is often convenient to write the first argument as a subscript, hence \(\Upsilon_e (f) = \Upsilon (e, f).\!\)
As a special application of this operator, we next define the absolute umpire operator, also called the umpire measure. This is a higher order proposition \(\Upsilon_1 : (\mathbb{B}^2 \to \mathbb{B}) \to \mathbb{B}\) which is given by the relation \(\Upsilon_1 (f) = \Upsilon (1, f).\!\) Here, the subscript 1 on the left and the argument 1 on the right both refer to the constant proposition \(1 : \mathbb{B}^2 \to \mathbb{B}.\) In most contexts where \(\Upsilon_1\!\) is actually applied the subscript 1 is safely omitted, since the number of arguments indicates which type of operator is intended. Thus, we have the following identities and equivalents:
| \(\Upsilon f = \Upsilon_1 (f) = 1 \in \mathbb{B}\) | \(\Leftrightarrow\) | \(\underline{(1~(f))} = \underline{1}\) | \(\Leftrightarrow\) | \(f = 1 : \mathbb{B}^2 \to \mathbb{B}.\) |
The umpire measure is defined at the level of truth functions, but can also be understood in terms of its implied judgments at the syntactic level. Interpreted this way, \(\Upsilon_1\!\) recognizes theorems of the propositional calculus over \([u, v],\!\) giving a score of "1" to tautologies and a score of "0" to everything else, regarding all contingent statements as no better than falsehoods.
One remark in passing for those who might prefer an alternative definition. If we had originally taken \(\Upsilon\!\) to mean the absolute measure, then the relative version could have been defined as \(\Upsilon_e f = \Upsilon \underline{(e (f))}.\!\)
Measure for Measure
Define two families of measures:
| \(\alpha_i, \beta_i : (\mathbb{B}^2 \to \mathbb{B}) \to \mathbb{B}, i = 0 \ldots 15,\) |
by means of the following formulas:
| \(\alpha_i f = \Upsilon (f_i, f) = \Upsilon (f_i \Rightarrow f),\) |
| \(\beta_i f = \Upsilon (f, f_i) = \Upsilon (f \Rightarrow f_i).\) |
The values of the sixteen \(\alpha_i\!\) on each of the sixteen boolean functions \(f : \mathbb{B}^2 \to \mathbb{B}\) are shown in Table 13. Expressed in terms of the implication ordering on the sixteen functions, \(\alpha_i f = 1\!\) says that \(f\!\) is above or identical to \(f_i\!\) in the implication lattice, that is, \(\ge f_i\!\) in the implication ordering.
| \(u:\) \(v:\) |
1100 1010 |
\(f\!\) | \(\alpha_0\) | \(\alpha_1\) | \(\alpha_2\) | \(\alpha_3\) | \(\alpha_4\) | \(\alpha_5\) | \(\alpha_6\) | \(\alpha_7\) | \(\alpha_8\) | \(\alpha_9\) | \(\alpha_{10}\) | \(\alpha_{11}\) | \(\alpha_{12}\) | \(\alpha_{13}\) | \(\alpha_{14}\) | \(\alpha_{15}\) |
| \(f_0\) | 0000 | \((~)\) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_1\) | 0001 | \((u)(v)\!\) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_2\) | 0010 | \((u) v\!\) | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_3\) | 0011 | \((u)\!\) | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_4\) | 0100 | \(u (v)\!\) | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_5\) | 0101 | \((v)\!\) | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_6\) | 0110 | \((u, v)\!\) | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_7\) | 0111 | \((u v)\!\) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_8\) | 1000 | \(u v\!\) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_9\) | 1001 | \(((u, v))\!\) | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| \(f_{10}\) | 1010 | \(v\!\) | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| \(f_{11}\) | 1011 | \((u (v))\!\) | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| \(f_{12}\) | 1100 | \(u\!\) | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| \(f_{13}\) | 1101 | \(((u) v)\!\) | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| \(f_{14}\) | 1110 | \(((u)(v))\!\) | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| \(f_{15}\) | 1111 | \(((~))\) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
The values of the sixteen \(\beta_i\!\) on each of the sixteen boolean functions \(f : \mathbb{B}^2 \to \mathbb{B}\) are shown in Table 14. Expressed in terms of the implication ordering on the sixteen functions, \(\beta_i f = 1\!\) says that \(f\!\) is below or identical to \(f_i\!\) in the implication lattice, that is, \(\le f_i\!\) in the implication ordering.
| \(u:\) \(v:\) |
1100 1010 |
\(f\!\) | \(\beta_0\) | \(\beta_1\) | \(\beta_2\) | \(\beta_3\) | \(\beta_4\) | \(\beta_5\) | \(\beta_6\) | \(\beta_7\) | \(\beta_8\) | \(\beta_9\) | \(\beta_{10}\) | \(\beta_{11}\) | \(\beta_{12}\) | \(\beta_{13}\) | \(\beta_{14}\) | \(\beta_{15}\) |
| \(f_0\) | 0000 | \((~)\) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| \(f_1\) | 0001 | \((u)(v)\!\) | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| \(f_2\) | 0010 | \((u) v\!\) | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| \(f_3\) | 0011 | \((u)\!\) | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| \(f_4\) | 0100 | \(u (v)\!\) | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| \(f_5\) | 0101 | \((v)\!\) | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| \(f_6\) | 0110 | \((u, v)\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| \(f_7\) | 0111 | \((u v)\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| \(f_8\) | 1000 | \(u v\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| \(f_9\) | 1001 | \(((u, v))\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| \(f_{10}\) | 1010 | \(v\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| \(f_{11}\) | 1011 | \((u (v))\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| \(f_{12}\) | 1100 | \(u\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| \(f_{13}\) | 1101 | \(((u) v)\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| \(f_{14}\) | 1110 | \(((u)(v))\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| \(f_{15}\) | 1111 | \(((~))\!\) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Applied to a given proposition \(f,\!\) the qualifiers \(\alpha_i\!\) and \(\beta_i\!\) tell whether \(f\!\) rests \(\operatorname{above}\ f_i\) or \(\operatorname{below}\ f_i,\) respectively, in the implication ordering. By way of example, let us trace the effects of several such measures, namely, those that occupy the limiting positions of the Tables.
Thus, \(\alpha_0 = \beta_{15}\!\) is a totally indiscriminate measure, one that accepts all propositions \(f : \mathbb{B}^2 \to \mathbb{B},\) whereas \(\alpha_{15}\!\) and \(\beta_0\!\) are measures that value the constant propositions \(1 : \mathbb{B}^2 \to \mathbb{B}\) and \(0 : \mathbb{B}^2 \to \mathbb{B},\) respectively, above all others.
Finally, in conformity with the use of the fiber notation to indicate sets of models, it is natural to use notations like:
| \([| \alpha_i |]\!\) | \(=\!\) | \((\alpha_i)^{-1}(1),\!\) |
| \([| \beta_i |]\!\) | \(=\!\) | \((\beta_i)^{-1}(1),\!\) |
| \([| \Upsilon_p |]\!\) | \(=\!\) | \((\Upsilon_p)^{-1}(1),\!\) |
to denote sets of propositions that satisfy the umpires in question.
Extending the Existential Interpretation to Quantificational Logic
Previously I introduced a calculus for propositional logic, fixing its meaning according to what C.S. Peirce called the existential interpretation. As far as it concerns propositional calculus this interpretation settles the meanings that are associated with merely the most basic symbols and logical connectives. Now we must extend and refine the existential interpretation to comprehend the analysis of quantifications, that is, quantified propositions. In doing so we recognize two additional aspects of logic that need to be developed, over and above the material of propositional logic. At the formal extreme there is the aspect of higher order functional types, into which we have already ventured a little above. At the level of the fundamental content of the available propositions we have to introduce a different interpretation for what we may call elemental or singular propositions.
Let us return to the 2-dimensional case \(X^\circ = [u, v].\) In order to provide a bridge between propositions and quantifications it serves to define a set of qualifiers \(\ell_{ij} : (\mathbb{B}^2 \to \mathbb{B}) \to \mathbb{B}\) that have the following characters:
Intuitively, the \(\ell_{ij}\!\) operators may be thought of as qualifying propositions according to the elements of the universe of discourse that each proposition positively values. Taken together, these measures provide us with the means to express many useful observations about the propositions in \(X^\circ = [u, v],\) and so they mediate a subtext \([\ell_{00}, \ell_{01}, \ell_{10}, \ell_{11}]\!\) that takes place within the higher order universe of discourse \(X^{\circ 2} = [X^\circ] = [[u, v]].\!\) Figure 15 summarizes the action of the \(\ell_{ij}\!\) operators on the \(f_i\!\) within \(X^{\circ 2}.\!\)
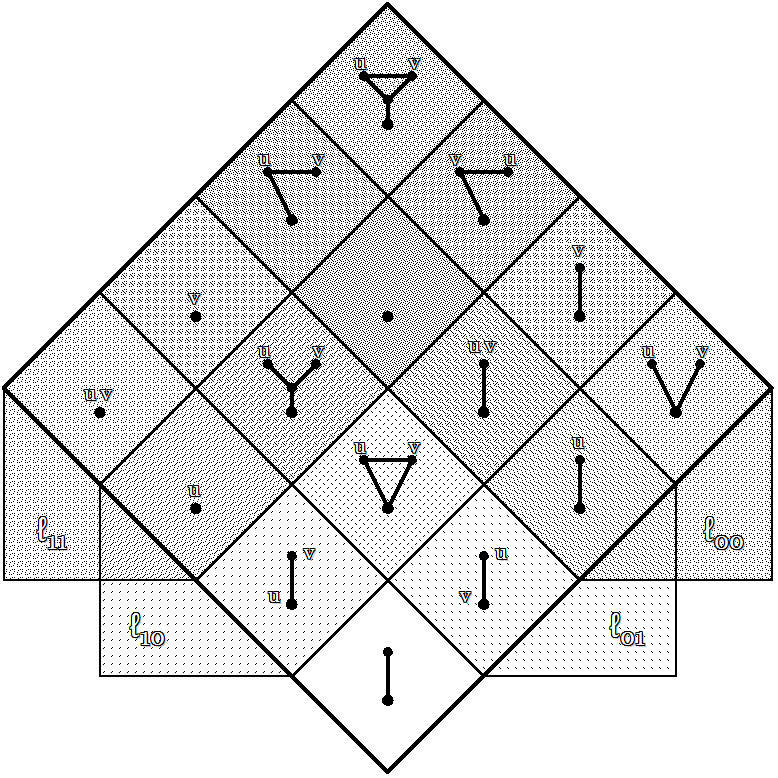
|
| \(\text{Figure 6.} ~~ \text{Higher Order Universe of Discourse} ~ \left[ \ell_{00}, \ell_{01}, \ell_{10}, \ell_{11} \right] \subseteq \left[\left[ u, v \right]\right]\) |
Application of Higher Order Propositions to Quantification Theory
Our excursion into the vastening landscape of higher order propositions has finally come round to the stage where we can bring its returns to bear on opening up new perspectives for quantificational logic.
There is a question arising next that is still experimental in my mind. Whether it makes much difference from a purely formal point of view is not a question I can answer yet, but it does seem to aid the intuition to invent a slightly different interpretation for the two-valued space that we use as the target of our basic indicator functions. Therefore, let us declare a type of existential-valued functions \(f : \mathbb{B}^k \to \mathbb{E},\) where \(\mathbb{E} = \{ -e, +e \} = \{ \operatorname{empty}, \operatorname{exist} \}\) is a couple of values that we interpret as indicating whether of not anything exists in the cells of the underlying universe of discourse, venn diagram, or other domain. As usual, let us not be too strict about the coding of these functions, reverting to binary codes whenever the interpretation is clear enough.
With this interpretation in mind we note the following correspondences between classical quantifications and higher order indicator functions:
|
\(\begin{array}{clcl} \mathrm{A} & \mathrm{Universal~Affirmative} & \mathrm{All}\ u\ \mathrm{is}\ v & \mathrm{Indicator~of}\ u (v) = 0 \\ \mathrm{E} & \mathrm{Universal~Negative} & \mathrm{All}\ u\ \mathrm{is}\ (v) & \mathrm{Indicator~of}\ u \cdot v = 0 \\ \mathrm{I} & \mathrm{Particular~Affirmative} & \mathrm{Some}\ u\ \mathrm{is}\ v & \mathrm{Indicator~of}\ u \cdot v = 1 \\ \mathrm{O} & \mathrm{Particular~Negative} & \mathrm{Some}\ u\ \mathrm{is}\ (v) & \mathrm{Indicator~of}\ u (v) = 1 \\ \end{array}\) |
The following Tables develop these ideas in more detail.
| \(u:\) \(v:\) |
1100 1010 |
\(f\!\) | \((\ell_{11})\) \(\text{No } u \) \(\text{is } v \) |
\((\ell_{10})\) \(\text{No } u \) \(\text{is }(v)\) |
\((\ell_{01})\) \(\text{No }(u)\) \(\text{is } v \) |
\((\ell_{00})\) \(\text{No }(u)\) \(\text{is }(v)\) |
\( \ell_{00} \) \(\text{Some }(u)\) \(\text{is }(v)\) |
\( \ell_{01} \) \(\text{Some }(u)\) \(\text{is } v \) |
\( \ell_{10} \) \(\text{Some } u \) \(\text{is }(v)\) |
\( \ell_{11} \) \(\text{Some } u \) \(\text{is } v \) |
| \(f_0\) | 0000 | \((~)\) | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| \(f_1\) | 0001 | \((u)(v)\!\) | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| \(f_2\) | 0010 | \((u) v\!\) | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| \(f_3\) | 0011 | \((u)\!\) | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| \(f_4\) | 0100 | \(u (v)\!\) | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| \(f_5\) | 0101 | \((v)\!\) | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| \(f_6\) | 0110 | \((u, v)\!\) | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| \(f_7\) | 0111 | \((u v)\!\) | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| \(f_8\) | 1000 | \(u v\!\) | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| \(f_9\) | 1001 | \(((u, v))\!\) | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| \(f_{10}\) | 1010 | \(v\!\) | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| \(f_{11}\) | 1011 | \((u (v))\!\) | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| \(f_{12}\) | 1100 | \(u\!\) | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| \(f_{13}\) | 1101 | \(((u) v)\!\) | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| \(f_{14}\) | 1110 | \(((u)(v))\!\) | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| \(f_{15}\) | 1111 | \(((~))\) | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| \(u:\) \(v:\) |
1100 1010 |
\(f\!\) | \((\ell_{11})\) \(\text{No } u \) \(\text{is } v \) |
\((\ell_{10})\) \(\text{No } u \) \(\text{is }(v)\) |
\((\ell_{01})\) \(\text{No }(u)\) \(\text{is } v \) |
\((\ell_{00})\) \(\text{No }(u)\) \(\text{is }(v)\) |
\( \ell_{00} \) \(\text{Some }(u)\) \(\text{is }(v)\) |
\( \ell_{01} \) \(\text{Some }(u)\) \(\text{is } v \) |
\( \ell_{10} \) \(\text{Some } u \) \(\text{is }(v)\) |
\( \ell_{11} \) \(\text{Some } u \) \(\text{is } v \) |
| \(f_0\) | 0000 | \((~)\) | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| \(f_1\) | 0001 | \((u)(v)\!\) | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| \(f_2\) | 0010 | \((u) v\!\) | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| \(f_4\) | 0100 | \(u (v)\!\) | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| \(f_8\) | 1000 | \(u v\!\) | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| \(f_3\) | 0011 | \((u)\!\) | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| \(f_{12}\) | 1100 | \(u\!\) | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| \(f_6\) | 0110 | \((u, v)\!\) | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| \(f_9\) | 1001 | \(((u, v))\!\) | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
| \(f_5\) | 0101 | \((v)\!\) | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| \(f_{10}\) | 1010 | \(v\!\) | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| \(f_7\) | 0111 | \((u v)\!\) | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| \(f_{11}\) | 1011 | \((u (v))\!\) | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| \(f_{13}\) | 1101 | \(((u) v)\!\) | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| \(f_{14}\) | 1110 | \(((u)(v))\!\) | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| \(f_{15}\) | 1111 | \(((~))\) | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| \(\text{Mnemonic}\) | \(\text{Category}\) | \(\text{Classical Form}\) | \(\text{Alternate Form}\) | \(\text{Symmetric Form}\) | \(\text{Operator}\) |
| \(\text{E}\!\) \(\text{Exclusive}\) |
\(\text{Universal}\) \(\text{Negative}\) |
\(\text{All}\ u\ \text{is}\ (v)\) | \(\text{No}\ u\ \text{is}\ v \) | \((\ell_{11})\) | |
| \(\text{A}\!\) \(\text{Absolute}\) |
\(\text{Universal}\) \(\text{Affirmative}\) |
\(\text{All}\ u\ \text{is}\ v \) | \(\text{No}\ u\ \text{is}\ (v)\) | \((\ell_{10})\) | |
| \(\text{All}\ v\ \text{is}\ u \) | \(\text{No}\ v\ \text{is}\ (u)\) | \(\text{No}\ (u)\ \text{is}\ v \) | \((\ell_{01})\) | ||
| \(\text{All}\ (v)\ \text{is}\ u \) | \(\text{No}\ (v)\ \text{is}\ (u)\) | \(\text{No}\ (u)\ \text{is}\ (v)\) | \((\ell_{00})\) | ||
| \(\text{Some}\ (u)\ \text{is}\ (v)\) | \(\text{Some}\ (u)\ \text{is}\ (v)\) | \(\ell_{00}\!\) | |||
| \(\text{Some}\ (u)\ \text{is}\ v\) | \(\text{Some}\ (u)\ \text{is}\ v\) | \(\ell_{01}\!\) | |||
| \(\text{O}\!\) \(\text{Obtrusive}\) |
\(\text{Particular}\) \(\text{Negative}\) |
\(\text{Some}\ u\ \text{is}\ (v)\) | \(\text{Some}\ u\ \text{is}\ (v)\) | \(\ell_{10}\!\) | |
| \(\text{I}\!\) \(\text{Indefinite}\) |
\(\text{Particular}\) \(\text{Affirmative}\) |
\(\text{Some}\ u\ \text{is}\ v\) | \(\text{Some}\ u\ \text{is}\ v\) | \(\ell_{11}\!\) |
Appendix : Generalized Umpire Operators
In order to get a handle on the space of higher order propositions and eventually to carry out a functional approach to quantification theory, it serves to construct some specialized tools. Specifically, I define a higher order operator \(\Upsilon,\!\) called the umpire operator, which takes up to three propositions as arguments and returns a single truth value as the result. Formally, this so-called multi-grade property of \(\Upsilon\!\) can be expressed as a union of function types, in the following manner:
| \(\Upsilon : \bigcup_{\ell = 1, 2, 3} ((\mathbb{B}^k \to \mathbb{B})^\ell \to \mathbb{B}).\) |
In contexts of application the intended sense can be discerned by the number of arguments that actually appear in the argument list. Often, the first and last arguments appear as indices, the one in the middle being treated as the main argument while the other two arguments serve to modify the sense of the operation in question. Thus, we have the following forms:
| \(\Upsilon_p^r q = \Upsilon (p, q, r)\!\) |
| \(\Upsilon_p^r : (\mathbb{B}^k \to \mathbb{B}) \to \mathbb{B}\) |
The intention of this operator is that we evaluate the proposition \(q\!\) on each model of the proposition \(p\!\) and combine the results according to the method indicated by the connective parameter \(r.\!\) In principle, the index \(r\!\) might specify any connective on as many as \(2^k\!\) arguments, but usually we have in mind a much simpler form of combination, most often either collective products or collective sums. By convention, each of the accessory indices \(p, r\!\) is assigned a default value that is understood to be in force when the corresponding argument place is left blank, specifically, the constant proposition \(1 : \mathbb{B}^k \to \mathbb{B}\) for the lower index \(p,\!\) and the continued conjunction or continued product operation \(\textstyle\prod\) for the upper index \(r.\!\) Taking the upper default value gives license to the following readings:
| \(\Upsilon_p (q) = \Upsilon (p, q) = \Upsilon (p, q, \textstyle\prod).\) |
| \(\Upsilon_p = \Upsilon (p, \underline{~~}, \textstyle\prod) : (\mathbb{B}^k \to \mathbb{B}) \to \mathbb{B}.\) |
This means that \(\Upsilon_p (q) = 1\!\) if and only if \(q\!\) holds for all models of \(p.\!\) In propositional terms, this is tantamount to the assertion that \(p \Rightarrow q,\) or that \(\underline{(p (q))} = \underline{1}.\)
Throwing in the lower default value permits the following abbreviations:
| \(\Upsilon q = \Upsilon (q) = \Upsilon_1 (q) = \Upsilon (1, q, \textstyle\prod).\) |
| \(\Upsilon = \Upsilon (1, \underline{~~}, \textstyle\prod)) : (\mathbb{B}^k\ \to \mathbb{B}) \to \mathbb{B}.\) |
This means that \(\Upsilon q = 1\!\) if and only if \(q\!\) holds for the whole universe of discourse in question, that is, if and only \(q\!\) is the constantly true proposition \(1 : \mathbb{B}^k \to \mathbb{B}.\) The ambiguities of this usage are not a problem so long as we distinguish the context of definition from the context of application and restrict all shorthand notations to the latter.
Document History
Inquiry and Analogy
| Author: | Jon Awbrey | November 1, 1995 |
| Course: | Engineering 690, Graduate Project | Cont'd from Winter 1995 |
| Supervisors: | F. Mili & M.A. Zohdy | Oakland University |
| Version: Draft 3.25 | Created: 01 Jan 1995 | Relayed: 01 Nov 1995 | Revised: 24 Dec 2001 | Revised: 12 Mar 2004
Functional Logic
Ontology List
- http://suo.ieee.org/ontology/msg05480.html
- http://suo.ieee.org/ontology/msg05481.html
- http://suo.ieee.org/ontology/msg05482.html
- http://suo.ieee.org/ontology/msg05483.html
- http://suo.ieee.org/ontology/msg05484.html
- http://suo.ieee.org/ontology/msg05485.html
Inquiry List
- http://stderr.org/pipermail/inquiry/2004-March/001256.html
- http://stderr.org/pipermail/inquiry/2004-March/001257.html
- http://stderr.org/pipermail/inquiry/2004-March/001258.html
- http://stderr.org/pipermail/inquiry/2004-March/001259.html
- http://stderr.org/pipermail/inquiry/2004-March/001260.html
- http://stderr.org/pipermail/inquiry/2004-March/001261.html
NKS Forum
- http://forum.wolframscience.com/showthread.php?threadid=254
- http://forum.wolframscience.com/showthread.php?threadid=598
- http://forum.wolframscience.com/showthread.php?postid=1957#post1957
- http://forum.wolframscience.com/showthread.php?postid=1960#post1960
- http://forum.wolframscience.com/showthread.php?postid=1961#post1961
- http://forum.wolframscience.com/showthread.php?postid=1962#post1962
- http://forum.wolframscience.com/showthread.php?postid=1964#post1964
- http://forum.wolframscience.com/showthread.php?postid=1966#post1966
- http://forum.wolframscience.com/showthread.php?postid=1968#post1968
- Adaptive Systems
- Artificial Intelligence
- Combinatorics
- Computer Science
- Cybernetics
- Differential Logic
- Discrete Systems
- Dynamical Systems
- Formal Languages
- Formal Sciences
- Formal Systems
- Functional Logic
- Graph Theory
- Group Theory
- Inquiry
- Knowledge Representation
- Linguistics
- Logic
- Logical Graphs
- Mathematics
- Mathematical Systems Theory
- Science
- Semiotics
- Philosophy
- Systems Science
- Visualization