Difference between revisions of "Directory:Jon Awbrey/Papers/Futures Of Logical Graphs"
Jon Awbrey (talk | contribs) (→Themes and variations: ← split off new section) |
Jon Awbrey (talk | contribs) (→Exemplary proofs: convert graphics + add Peirce's Law) |
||
| Line 783: | Line 783: | ||
|} | |} | ||
| − | ==Exemplary proofs== | + | ===Exemplary proofs=== |
| − | + | Based on the axioms given at the outest, and aided by the theorems recorded so far, it is possible to prove a multitude of much more complex theorems. A couple of all-time favorites are given next. | |
| − | + | ====Peirce's law==== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | : ''[[Peirce's law|Main article: Peirce's law]]'' | |
| − | | | + | |
| − | + | Peirce's law is commonly written in the following form: | |
| − | | | + | |
| − | | | + | {| align="center" cellpadding="10" |
| − | | | + | | <math>((p \Rightarrow q) \Rightarrow p) \Rightarrow p</math> |
| − | + | |} | |
| − | | | + | |
| − | | | + | The existential graph representation of Peirce's law is shown in Figure 31. |
| − | | | + | |
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:Logical_Graph_Figure_31.jpg|500px]] | |
| − | + | |} | |
| − | + | ||
| − | + | A graphical proof of Peirce's law is shown in Figure 32. | |
| − | + | ||
| − | | | + | {| align="center" cellpadding="10" |
| − | + | | [[Image:Logical_Graph_Figure_32.jpg|500px]] | |
| − | + | |} | |
| + | |||
| + | ====Praeclarum theorema==== | ||
| + | |||
| + | An illustrious example of a propositional theorem is the ''praeclarum theorema'', the ''admirable'', ''shining'', or ''splendid'' theorem of [[Leibniz]]. | ||
| + | |||
| + | <blockquote> | ||
| + | <p>If ''a'' is ''b'' and ''d'' is ''c'', then ''ad'' will be ''bc''.</p> | ||
| + | |||
| + | <p>This is a fine theorem, which is proved in this way:</p> | ||
| + | |||
| + | <p>''a'' is ''b'', therefore ''ad'' is ''bd'' (by what precedes),</p> | ||
| + | |||
| + | <p>''d'' is ''c'', therefore ''bd'' is ''bc'' (again by what precedes),</p> | ||
| + | |||
| + | <p>''ad'' is ''bd'', and ''bd'' is ''bc'', therefore ''ad'' is ''bc''. Q.E.D.</p> | ||
| + | |||
| + | <p>([[Leibniz]], ''Logical Papers'', p. 41).</p> | ||
| + | </blockquote> | ||
| + | |||
| + | Under the existential interpretation, the praeclarum theorema is represented by means of the following logical graph. | ||
| + | |||
| + | {| align="center" cellpadding="10" | ||
| + | | [[Image:Logical_Graph_Figure_33.jpg|500px]] | ||
| + | |} | ||
And here's a neat proof of that nice theorem. | And here's a neat proof of that nice theorem. | ||
| − | + | {| align="center" cellpadding="10" | |
| − | + | | [[Image:Logical_Graph_Figure_34.jpg|500px]] | |
| − | + | |} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Themes and variations== | ==Themes and variations== | ||
Revision as of 17:04, 29 July 2009
This article develops an extension of Charles Sanders Peirce's Logical Graphs.
Introduction
I think I am finally ready to speculate on the futures of logical graphs that will be able to rise to the challenge of embodying the fundamental logical insights of Peirce.
For the sake of those who may be unfamiliar with it, let us first divert ourselves with an exposition of a standard way that graphs of the order that Peirce considered, those embedded in a continuous manifold like a plane sheet of paper, without or without the paper bridges that Peirce used to augment his genus, can be represented as parse-strings in Asciiish and sculpted into pointer-structures in computer memory.
A blank sheet of paper can be represented as a blank space in a line of text, but that way of doing it tends to be confusing unless the logical expression under consideration is set off in a separate display.
For example, consider an equation of the following form:
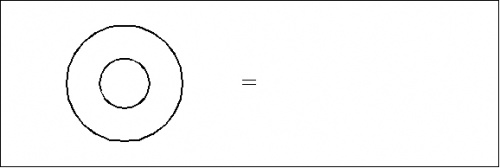
|
This can be written inline as “ \((~(~)~)~=\) ” or set off in a text display:
| \((~(~)~)\) | \(=\!\) |
When we turn to representing the corresponding expressions in computer memory, where they can be manipulated with utmost facility, we begin by transforming the planar graphs into their topological duals. The planar regions of the original graph correspond to nodes (or points) of the dual graph, and the boundaries between planar regions in the original graph correspond to edges (or lines) between the nodes of the dual graph.
For example, overlaying the corresponding dual graphs on the plane-embedded graphs shown above, we get the following composite picture:
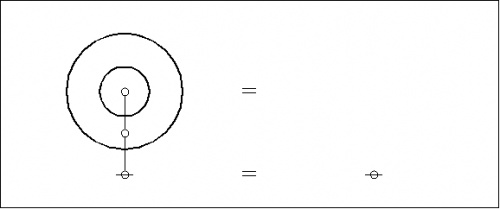
|
The outermost region of the plane-embedded graph is singled out for special consideration and the corresponding node of the dual graph is referred to as its root node. By way of graphical convention in the present text, the root node is indicated by means of a horizontal strike-through.
Extracting the dual graph from its composite matrix, we get this picture:

|
It is easy to see the relationship between the parenthetical expressions of Peirce's logical graphs, that somewhat clippedly picture the ordered containments of their formal contents, and the associated dual graphs, that constitute the species of rooted trees here to be described.
In the case of our last example, a moment's contemplation of the following picture will lead us to see that we can get the corresponding parenthesis string by starting at the root of the tree, climbing up the left side of the tree until we reach the top, then climbing back down the right side of the tree until we return to the root, all the while reading off the symbols, in this particular case either "(" or ")", that we happen to encounter in our travels.
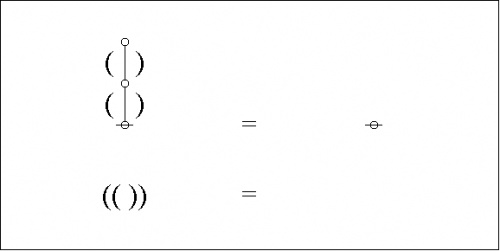
|
This ritual is called traversing the tree, and the string read off is often called the traversal string of the tree. The reverse ritual, that passes from the string to the tree, is called parsing the string, and the tree constructed is often called the parse graph of the string. I tend to be a bit loose in this language, often using parse string to mean the string that gets parsed into the associated graph.
This much preparation allows us to present the two most basic axioms of logical graphs, shown in graph and string forms below, along with handy names for referring to the different directions of applying the axioms.
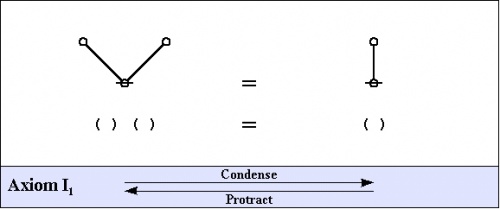
|
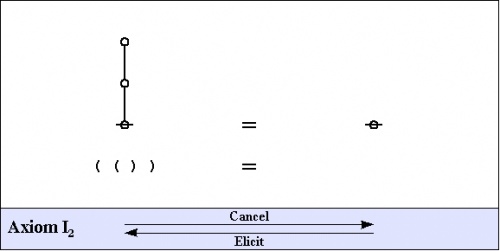
|
The parse graphs that we've been looking at so far are one step toward the pointer graphs that it takes to make trees live in computer memory, but they are still a couple of steps too abstract to properly suggest in much concrete detail the species of dynamic data structures that we need. I now proceed to flesh out the skeleton that I've drawn up to this point.
Nodes in a graph depict records in computer memory. A record is a collection of data that can be thought to reside at a specific address. For semioticians, an address can be recognized as a type of index, and is commonly spoken of, on analogy with demonstrative pronouns, as a pointer, even among computer programmers who are otherwise innocent of semiotics.
At the next level of concreteness, a pointer-record structure is represented as follows:
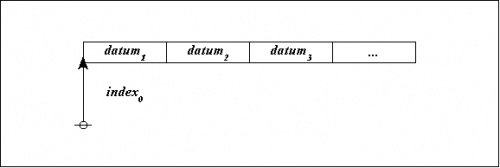
|
This portrays the pointer \(\mathit{index}_0\!\) as the address of a record that contains the following data:
| \(\mathit{datum}_1, \mathit{datum}_2, \mathit{datum}_3, \ldots,\!\) and so on. |
What makes it possible to represent graph-theoretical structures as data structures in computer memory is the fact that an address is just another datum, and so we may have a state of affairs like the following:
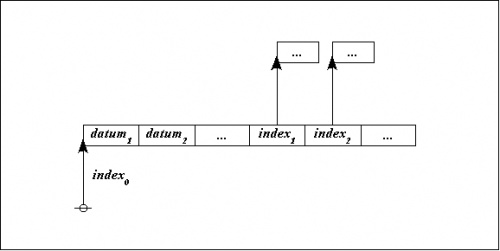
|
Back at the abstract level, it takes three nodes to represent the three data records, with a root node connected to two other nodes. The ordinary bits of data are then treated as labels on the nodes:

|
Notice that, with rooted trees like these, drawing the arrows is optional, since singling out a unique node as the root induces a unique orientation on all the edges of the tree, up being the same as away from the root.
We have already seen various forms of the axiom that is formulated in string form as " \(((~))~=\) ". For the sake of comparison, let's record the planar and dual forms of the axiom that is formulated in string form as "\((~)(~)~=~(~)\)".
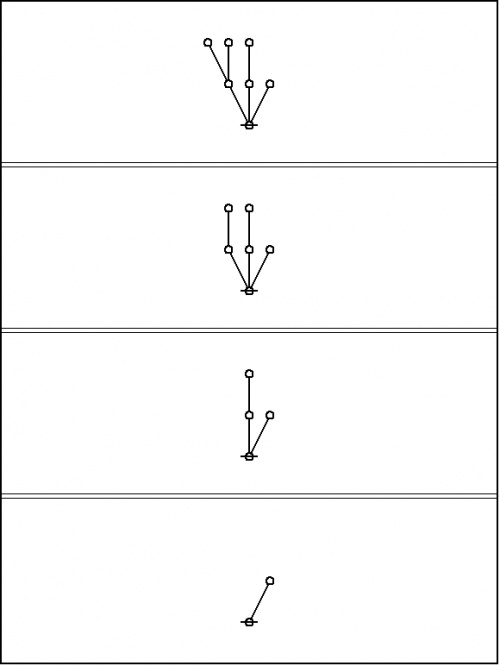
First the plane-embedded maps:
|
Next the planar maps and their dual trees superimposed:
|
Finally the dual trees by themselves:
|
And here are the parse trees with their traversal strings indicated:
|
Categories of structured individuals
We have at this point enough material to begin thinking about the forms of analogy, iconicity, metaphor, morphism, whatever you want to call it, that are pertinent to the use of logical graphs in their various logical interpretations, for instance, those that Peirce described as entitative and existential.
By way of providing a conceptual-technical framework for organizing that discussion, let me introduce the concept of a category of structured individuals (COSI). There may be some cause for some readers to rankle at the very idea of a structured individual, for taking the notion of an individual in its strictest etymology would render it absurd that an atom could have parts, but all we mean by individual in this context is an individual by dint of some conversational convention currently in play, not an individual on account of its intrinsic indivisibility. Incidentally, though, it will also be convenient to take in the case of a class or collection of individuals with no pertinent inner structure as a trivial case of a COSI.
For some reason — that I won't stop to examine right now — I tend to think category of structured individuals when the individuals in question have a whole lot of structure, but collection of structured items when the individuals have a minimal amount of internal structure. For example, any set is a COSI, so any relation in extension is a COSI, but a 1-adic relation is just a set of 1-tuples, that are in some lights indiscernible from their single components, and so its structured individuals have far less structure than the k-tuples of k-adic relations, when k exceeds one. This spectrum of differentiations among relational models will be useful to bear in mind when the time comes to say what distinguishes relational thinking proper from 1-adic and 2-adic thinking, that constitute its degenerate cases.
Still on our way to saying what brands of iconicity are worth buying, at least when it comes to graphical systems of logic, it will useful to introduce one more distinction that affects the types of mappings that can be formed between two COSI's.
One type of structure-preserving map is a system-wide iconic map (SWIM). The other is a type that we might call a pointwise-restricted iconic map, or a pointedly rigid iconic map (PRIM). I tried to make this nomenclature as self-explanatory as I could, but failing that I will explain it next time.
Because I plan this time around a somewhat leisurely excursion through the primordial wilds of logics that were so intrepidly explored by C.S. Peirce and again in recent times revisited by George Spencer Brown, let me just give a few extra pointers to those who wish to run on ahead of this torturous tortoise pace:
- Jon Awbrey, "Propositional Equation Reasoning Systems (PERS)", Eprint.
- Lou Kauffman, "Box Algebra, Boundary Mathematics, Logic, and Laws of Form", Eprint.
Two paces back I used the word "category" in a way that will turn out to be not too remote a cousin of its present day mathematical bearing, but also in way that's not unrelated to Peirce's theory of categories.
When I call to mind a category of structured individuals (COSI), I get a picture of a certain form, with blanks to be filled in as the thought of it develops, that can be sketched at first like so:
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` Category` ` ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `/`\` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` / ` \ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `/` ` `\` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` / ` ` ` \ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` `\` ` ` ` ` ` ` ` ` ` ` ` ` Individuals ` ` ` ` ` ` o ` `...` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `/`\` ` ` ` `/`\` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` / ` \ ` ` ` / ` \ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `/` ` `\` ` `/` ` `\` ` ` ` ` ` ` ` ` ` ` Structures` ` ` ` ` o->-o->-o ` o->-o->-o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
The various glyphs of this picturesque hierarchy serve to remind us that a COSI in general consists of many individuals, which in spite of their calling as such may have specific structures involving the ordering of their component parts. Of course, this generic picture may have degenerate realizations, as when we have a 1-adic relation, that may be viewed in most settings as nothing different than a set:
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` Category` ` ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `/`\` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` / ` \ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `/` ` `\` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` / ` ` ` \ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` `\` ` ` ` ` ` ` ` ` ` ` ` ` Individuals ` ` ` ` ` ` o ` `...` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` Structures` ` ` ` ` ` ` o ` `...` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
The practical use of Peirce's categories is simply to organize our thoughts about what sorts of formal models are demanded by a material situation, for instance, a domain of phenomena from atoms to biology to culture. To say that "k-ness" is involved in a phenomenon is simply to say that we need k-adic relations to model it adequately, and that the phenomenon itself appears to demand nothing less. Aside from this, Peirce's realization that k-ness for k = 1, 2, 3 affords us with a sufficient basis for all that we need to model is a formal fact that depends on a particular theorem in the logic of relatives. If it weren't for that, there would hardly be any reason to single out three.
In order to discuss the various forms of iconicity that might be involved in the application of Peirce's logical graphs and their kind to the object domain of logic itself, we will need to bring out two or three "categories of structured individuals" (COSI's), depending on how we count. These are called the "object domain", the "sign domain", and the "interpretant sign domain", which may be written O, S, I, respectively, or X, Y, Z, respectively, depending on the style that fits the current frame of discussion.
For the time being, I will be considering systems where the sign domain and the interpretant domain are the same sets of entities, although, of course, their roles in a given "sign relation", say, L ⊆ O × S × I or L ⊆ X × Y × Z, remain as distinct as ever. I will tend to use the term "semiotic domain" for the common set of elements that constitute the signs and the interpretant signs in any setting where the sign domain and the interpretant domain are equal as sets.
At the "alpha level", "primary arithmetic", or "zeroth order" of consideration that we have so far introduced, the sign domain is any one of the several "formal languages" that we have placed in one-to-one correspondence with each other, namely, the languages of non-intersecting plane closed curves, well-formed parenthesis strings, or rooted trees. The interpretant sign domain will for the present be taken to be any one of the same languages, and so I'll refer to any of them indifferently as the "semiotic domain".
Briefly if roughly put, icons are signs that denote their objects by virtue of sharing properties with them. To put it a bit more fully, icons are signs that receive their interpretant signs on account of having specific properties in common with their objects.
The family of related relationships that fall under the headings of analogy, icon, metaphor, model, simile, simulation, and so on forms an extremely important complex of ideas in mathematics, there being recognized under the generic idea of "structure-preserving mappings" and commonly formalized in the language of homomorphisms, morphisms, or "arrows", depending on the operative level of abstraction that's in play.
To consider how a system of logical graphs, taken together as a semiotic domain, might bear an iconic relationship to a system of logical objects that make up our object domain, we will next need to consider what our logical objects are.
A popular answer, if by popular one means that both Peirce and Frege agreed on it, is to say that our ultimate logical objects are without loss of generality most conveniently referred to as Truth and Falsity. If nothing else, it serves the end of beginning simply to go along with this thought for a while, and so we can start with an object domain that consists of just two objects or "values", to wit, O = B = {false, true}.
Given those two categories of structured individuals, namely, O = B = {false, true} and S = {logical graphs}, the next task is to consider the brands of morphisms from S to O that we might reasonably have in mind when we speak of the "arrows of interpretation".
With the aim of embedding our consideration of logical graphs, as seems most fitting, within Peirce's theory of triadic sign relations, we have declared the first layers of our object, sign, and interpretant domains. As we often do in formal studies, we've taken the sign and interpretant domains to be the same set, S = I, calling it the semiotic domain, or, as I see that I've done in some other notes, the syntactic domain.
Truth and Falsity, the objects that we've so far declared, are recognizable as abstract objects, and like so many other hypostatic abstractions that we use they have their use in moderating between a veritable profusion of more concrete objects and more concrete signs, in factoring complexity as some people say, despite the fact that some complexities are irreducible in fact.
That much of a stake in the ground will have to do as a philosophical tether for now, since we are about to play out the syntactic line just about as far as we can stretch it, and it can happen that some will forget this home port.
As agents of systems, whether that system is our own physiology or our own society, we move through what we commonly imagine to be a continuous manifold of states, but with distinctions being drawn in that space that are every bit as compelling to us, and often quite literally, as the difference between life and death. So the relation of discretion to continuity is not one of those issues that we can take lightly, or simply dissolve by choosing a side and ignoring the other, as we may imagine in abstraction. I'll try to get back to this point later, one in a long list of cautionary notes that experience tells me has to be attached to every tale of our pilgrimage, but for now we must get under way.
Returning to En and Ex, the two most popular interpretations of logical graphs, that happen to be dual to each other in a certain sense, let's see how they fly as "hermeneutic arrows" from the syntactical domain S to the objective domain O, at any rate, as their trajectories can be spied in the radar of what George Spencer Brown called the "primary arithmetic".
Taking En and Ex as arrows of the form En, Ex : S → O, at the level of arithmetic taking S = {rooted trees} and O = {Falsity, Truth}, let's factor each arrow across the domain of formal constants S0 = {O, |}, the domain that consists of a single rooted node plus a single rooted edge. As a strategic tactic, this allows each arrow to be broken into a purely syntactic part Ensyn, Exsyn : S → S0 and its purely semantic part Ensem, Exsem : S0 → O.
As things work out, the syntactic factors are formally the same, leaving our dualing interpretations to differ in their semantic components alone. Specifically, we have the following mappings:
- Ensem : @ ~> false, | ~> true
- Exsem : @ ~> true, | ~> false
On the other side of the ledger, because the syntactic factors, Ensyn and Exsyn, are indiscernible from each other, there is a syntactic contribution to the overall interpretation process that can be most readily investigated on purely formal grounds. That will be the task to face when next we meet on these lists.
Cast into the form of a 3-adic sign relation, the situation before us can now be given the following shape:
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` Y ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `Semiotic Domain` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o-------------------o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` Rooted Trees ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o-------------------o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` Syntactic ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` Reduction ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` v ` ` ` ` ` ` ` ` ` ` ` ` ` o-----------o ` ` En_sem` ` o-----------o ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` |<--------------| ` ` ` o ` | ` ` ` ` ` ` ` ` ` ` | ` F ` T ` | ` ` ` ` ` ` ` | ` O ` | ` | ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` |<--------------| ` ` ` @ ` | ` ` ` ` ` ` ` ` ` ` o-----------o ` ` Ex_sem` ` o-----------o ` ` ` ` ` ` ` ` ` ` ` ` ` X ` ` ` ` ` ` ` ` ` ` ` ` `Y_0` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` Canonical ` ` ` ` ` ` ` ` ` ` ` Object Domain ` ` ` ` ` ` ` `Sign Domain` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
The interpretation maps En, Ex : Y → X are factored into a shared syntactic part:
- Ensyn = Exsyn = Esyn : Y → Y0
and a couple of differential semantic parts:
- Ensem, Exsem : Y0 → X
The functional images of the syntactic reduction map Esyn : Y → Y0 are the two simplest signs or the most reduced pair of expressions, regarded as rooted trees taking the shapes @ and |, and these may be treated as the canonical representatives of their respective equivalence classes.
The more Peirce-systent among you, on contemplating that last picture, will 1st or 2nd or 3rd-naturally ask, "What happened to the irreducible 3-adicity of sign relations in this portrayal of logical graphs?"
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` Y ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `Semiotic Domain` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o-------------------o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` Rooted Trees ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o-------------------o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` Syntactic ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` Reduction ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` v ` ` ` ` ` ` ` ` ` ` ` ` ` o-----------o ` ` En_sem` ` o-----------o ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` |<--------------| ` ` ` o ` | ` ` ` ` ` ` ` ` ` ` | ` F ` T ` | ` ` ` ` ` ` ` | ` O ` | ` | ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` |<--------------| ` ` ` @ ` | ` ` ` ` ` ` ` ` ` ` o-----------o ` ` Ex_sem` ` o-----------o ` ` ` ` ` ` ` ` ` ` ` ` ` X ` ` ` ` ` ` ` ` ` ` ` ` `Y_0` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` Canonical ` ` ` ` ` ` ` ` ` ` ` Object Domain ` ` ` ` ` ` ` `Sign Domain` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
The answer is that the last bastion of 3-adic irreducibility presidios precisely in the duality of the dual interpretations Ensem and Exsem. To see this, consider the consequences of there being, contrary to all that we've assumed up to this point, some ultimately compelling reason to assert that the clean slate, the empty medium, the vacuum potential, whatever one wants to call it, is inherently more meaningful of either Falsity or Truth. This would issue in a conviction forthwith that the 3-adic sign relation involved in this case decomposes as a composition of a couple of functions, that is to say, reduces to a 2-adic relation.
The duality of interpretation for logical graphs tells us that the empty medium, the tabula rasa, what Peirce called the Sheet of Assertion (SA) is a genuine symbol, not to be found among the degenerate species of signs that make up icons and indices, nor, as the SA has no parts, can it number icons or indices among its parts. What goes for the medium must go for all of the signs that it mediates. Thus we have the kinds of signs that Peirce in one place called "pure symbols", naming a selection of signs for basic logical operators specifically among them.
Every word is a symbol. Every sentence is a symbol. Every book is a symbol. Every representamen depending upon conventions is a symbol. Just as a photograph is an index having an icon incorporated into it, that is, excited in the mind by its force, so a symbol may have an icon or an index incorporated into it, that is, the active law that it is may require its interpretation to involve the calling up of an image, or a composite photograph of many images of past experiences, as ordinary common nouns and verbs do; or it may require its interpretation to refer to the actual surrounding circumstances of the occasion of its embodiment, like such words as 'that', 'this', 'I', 'you', 'which', 'here', 'now', 'yonder', etc. Or it may be pure symbol, neither 'iconic' nor 'indicative', like the words 'and', 'or', 'of', etc. (C.S. Peirce, Collected Papers, CP 4.447).
Some will recall the many animadversions that we had on this topic, starting here:
- PS. Pure Symbols
- PS. Pure Symbols : Discussion
And some will find an ethical principle in this freedom of interpretation. The act of interpretation bears within it an inalienable degree of freedom. In consequence of this truth, as far as the activity of interpretation goes, freedom and responsibility are the very same thing. We cannot blame objects for what we say or what we think. We cannot blame symbols for what we do. We cannot escape our response ability. We cannot escape our freedom.
Though it may not seem too exciting, logically speaking, there are many good reasons for getting comfortable with the system of forms that is represented indifferently, topologically speaking, by rooted trees, well-formed strings of parentheses, or finite sets of non-intersecting simple closed curves in the plane. One reason is that it provides us with a respectable example of a sign domain to cut our semiotic teeth on, being non-trivial in the sense that it contains a countable infinity of signs. Another reason is that it allows us to study a simple form of computation that is recognizable as a species of semiotic process.
This space of forms, along with the two axioms that result in its being partitioned into just two equivalence classes, is what George Spencer Brown called the primary arithmetic.
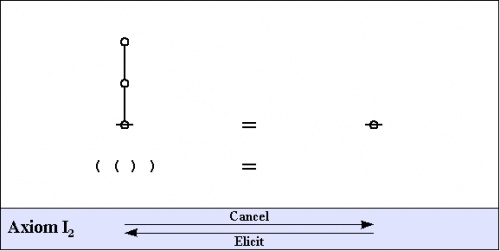
Here are the two arithmetic axioms:

|

|
Let \(S\!\) be the set of rooted trees and let \(S_0\!\) be the 2-element subset of \(S\!\) that consists of a rooted node and a rooted edge.
| \(S\!\) | \(=\!\) | \(\{ \text{rooted trees} \}\!\) |
| \(S_0\!\) | \(=\!\) | \(\{ \ominus, \vert \} = \{\) |
Simple intuition, or a simple inductive proof, assures us that any rooted tree can be reduced by way of the arithmetic initials either to a root node ![]() or else to a rooted edge
or else to a rooted edge ![]() .
.
For example, consider the reduction that proceeds as follows:
|
Regarded as a semiotic process, this amounts to a sequence of signs, every one after the first being the interpretant of its predecessor, ending in a sign that we may regard as the canonical sign for their common object, in the upshot, the result of the computation process. Simple as it is, this exhibits the main features of all computation, specifically, a semiotic process that proceeds from an obscure sign to a clear sign of the same object, in sum, a case of clarification.
Hard experience teaches that complex objects are best approached in a gradual, laminar, modular fashion, one step, one layer, one piece at a time, and it's just as much the way when the complexity of the object is irreducible, when the articulations of the representation will necessarily be joints that are cloven disjointedly from nature, some assembly required in the synthetic integrity of our intuitions.
That's my excuse, and I'm persistent about it, for spending so much time on the first half of zeroth order logic, that is, the primary arithmetic, that C.S. Peirce verged on intuiting at numerous points and times in his work on logical graphs, and that Spencer Brown named and brought to life.
Before it slips from mind, there is one other reason for lingering a bit longer in these forests primeval, and this is that our acquaintance with bare trees, those as yet unornamented with numerous and literal labels, will repay us at later stages of the game when we come to worry, as most folks do eventually, over such problems as the ontological status of variables.
It will be best to illustrate this theme in the setting of a concrete case, which we can do by revisiting the previous example of reductive evaluation:

|
The observation of several semioses of roughly this shape will most probably lead an observer with any observational facility whatever to notice that it doesn't really matter what sorts of branches happen to sprout from the side of the root aside from the lone edge that also grows there — the end will all be one.
Our observer might think to summarize the results of many such observations by introducing a label or variable to signify any shape of branch whatever, writing something like the following:
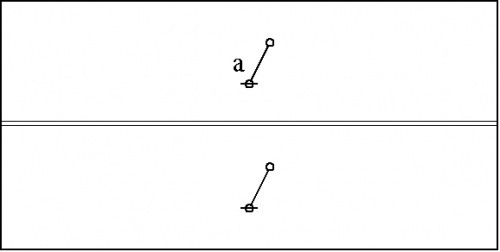
|
Observations like that, made about an arithmetic of any variety, germinated by their summarizations, are the root of all algebra.
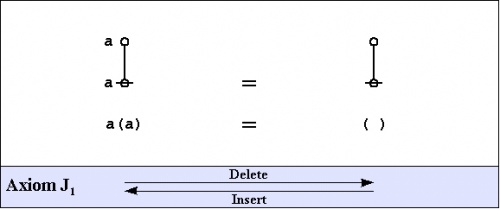
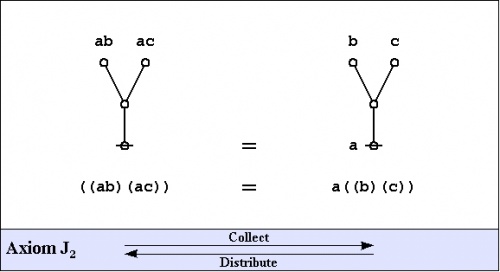
Speaking of algebra, and having seen one example of an algebraic law, we might as well introduce the axioms of the primary algebra, once again deriving their substance and their name from Charles S. Peirce and G. Spencer Brown, respectively.
|
|
The choice of axioms for any formal system is to some degree a matter of aesthetics, as it is commonly the case that many different selections of formal rules will serve as axioms to derive all the rest as theorems. As it happens, the example that we noticed first, as simple as it appears, proves to be provable as a theorem on the grounds of the foregoing axioms.
We might also notice at this point a subtle difference between the primary arithmetic and the primary algebra with respect to the grounds of justification that we have naturally if tacitly adopted for their respective sets of axioms.
The arithmetic axioms were introduced by fiat, in a quasi-apriori fashion, though of course it is only long prior experience with the practical uses of comparably developed generations of formal systems that would actually induce us to such a quasi-primal move. The algebraic axioms, in contrast, can be seen to derive their motive and their justice from the observation and summarization of patterns that are visible in the arithmetic spectrum.
Starting once again with the primary arithmetic, let us count the ways that this formal system might be iconic of our negative and positive logical objects, that which we'd avoid and that which we'd approach, or Falsity and Truth, respectively.
Before we go any further we need to observe that there is no fact of the matter as to whether a given sign is an icon of a given object, that is to say, in any way that fails to refer to the conduct of a given interpreter, which conduct is most conveniently and formally summed up in the fashion of an interpretant sign.
Thus, if you find youself in an argument with another interpreter who swears to the influence of some quality common to the object and the sign and that really does affect his or her conduct in regard to the two of them, then that argument is almost certainly bound to be utterly futile. I am sure we've all been there.
When I first became acquainted with the Entish and Extish hermenautics of logical graphs, back in the late great 1960's, I was struck in the spirit of those times by what I imagined to be their Zen and Zenoic sensibilities, the tao is silent wit of the Zen mind being the empty mind, that seems to go along with the Ex interpretation, and the way from the way that's marked is not the true way to the mark that's marked is not the remarkable mark and to the sign that's signed is not the significant sign of the En interpretation, reminding us that the sign is not the object, no matter how apt the image. And later, when my discovery of the cactus graph extension of logical graphs led to the leimons of neural pools, where En says that truth is an active condition, while Ex says that sooth is a quiescent mind, all these themes got reinforced more still.
We hold these truths to be self-iconic, but they come in complementary couples, in consort to the flip-side of the tao.
In light of the foregoing reflections on the forms of iconicity worth having, I will leave it to the reading tastes of the given hermenaut whether to read the uncut page as more iconic of falsity or truth. Once that choice is made, then it's perfectly natural for the chooser to think that the choice was the chosen one, and there is very little reason to become disillusioned about it.
But there are other orders of analogy, iconicity, metaphor, morphism, etc. that we need to attend to in the way that a system of signs can represent a system of objects. At the level of the primary arithmetic, this refers to the way that the distinction between falsity and truth, not the values alone, can be represented in the distinction between one sort of sign and another sort of sign.
A sort of signs is more formally known as an equivalence class (EC). There are in general many sorts of sorts of signs that we might wish to consider in this inquiry, but let's begin with the sort of signs all of whose members denote the same object as their referent, a sort of signs to be henceforth referred to as a referential equivalence class (REC).
- Cf: FOLG 5. http://stderr.org/pipermail/inquiry/2005-October/003113.html
- In: FOLG. http://stderr.org/pipermail/inquiry/2005-October/thread.html#3104
Toward the outset of this excursion, I mentioned the distinction between a pointwise-restricted iconic map or a pointedly rigid iconic map (PRIM) and a system-wide iconic map (SWIM). The time has come to make use of that mention.
We are once again concerned with categories of structured items (COSI's) and the categories of mappings between them, indeed, the two ideas are all but inseparable, there being many good reasons to consider the very notion of structure to be most clearly defined in terms of the brands of "arrows", maps, or morphisms between items that are admitted to the category in view.
At the level of the primary arithmetic (PAR), we have a set-up like this:
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
Categories` ` ` ` `!O!` ` ` ` ` ` ` ` ` ` ` ` `!S!` ` ` ` ` `
` ` ` ` ` ` ` ` ` `/`\` ` ` ` ` ` ` ` ` ` ` ` `/`\` ` ` ` ` `
` ` ` ` ` ` ` ` ` / ` \ ` ` ` ` ` ` ` ` ` ` ` / ` \ ` ` ` ` `
` ` ` ` ` ` ` ` `/` ` `\` ` ` ` ` ` ` ` ` ` `/` ` `\` ` ` ` `
` ` ` ` ` ` ` ` / ` ` ` \ ` ` ` ` ` ` ` ` ` / ` ` ` \ ` ` ` `
` ` ` ` ` ` ` `/` ` ` ` `\` ` Denotes ` ` `/` ` ` ` `\` ` ` `
Individuals `{F}` ` ` ` `{T}` <------ ` {...} ` ` ` {...} ` `
` ` ` ` ` ` ` | ` ` ` ` ` | ` ` ` ` ` ` `/|\` ` ` ` `/|\` ` `
` ` ` ` ` ` ` | ` ` ` ` ` | ` ` ` ` ` ` / | \ ` ` ` / | \ ` `
` ` ` ` ` ` ` | ` ` ` ` ` | ` ` ` ` ` `/` | `\` ` `/` | `\` `
Structures` ` F ` ` ` ` ` T ` ` ` ` ` o ` o ` o ` o ` o ` o `
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o `
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | `
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o o ` o ` ` ` ` o `
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | `\`/` ` ` ` ` | `
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o ` o ` o o ` o o `
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` | ` | `\`/` | `
` ` ` ` ` ` ` F ` ` ` ` ` T ` ` ` ` ` @ ` @ ` @ ` @ ` @ ` @ `
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
The object domain O is the boolean domain B = {Falsity, Truth}, the semiotic domain S is any of the spaces isomorphic to the set of rooted trees, matched-up parentheses, or unlabeled alpha graphs, and we treat a couple of denotation maps Den, Dex : S → O.
Either one of the denotation maps induces the same partition of S into REC's, a partition whose structure is suggested by the following two sets of strings:
- {
" ", "(( ))", "(( )( ))", ...},
- {
"( )", "( )( )", "((( )))", ...}.
These are of course the parenthesis strings that correspond to the rooted trees that are shown in the lower right corner of the Figure.
In thinking about mappings between categories of structured individuals, we can take each mapping in two parts. At the first level of analysis, there is the part that maps individuals to individuals. At the second level of analysis, there is the part that maps the structural parts of each individual to the structural parts of the individual that forms its counterpart under the first part of the mapping in question.
The general scheme of things is suggested by the following Figure, where the mapping f from COSI U to COSI V is analyzed in terms of a mapping g that takes individuals to individuals, ignoring their inner structures, and a set of mappings hj, where j ranges over the individuals of COSI U, and where hj specifies just how the parts of j map to the parts of g(j), its counterpart under g.
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` U ` ` ` ` ` ` ` f ` ` ` ` ` ` ` V ` ` ` ` ` ` ` ` ` ` ` ` ` ` @ ` ` --------------------> ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` `/`\` ` ` ` ` ` ` ` ` ` ` ` ` ` `/`\` ` ` ` ` ` ` ` ` ` ` ` ` / ` \ ` ` ` ` ` ` ` ` ` ` ` ` ` / ` \ ` ` ` ` ` ` ` ` ` ` ` `/` ` `\` ` ` ` ` ` ` ` ` ` ` ` `/` ` `\` ` ` ` ` ` ` ` ` ` ` / ` ` ` \ ` ` ` ` ` ` ` ` ` ` ` / ` ` ` \ ` ` ` ` ` ` ` ` ` `/` ` ` ` `\` ` ` ` ` g ` ` ` ` `/` ` ` ` `\` ` ` ` ` ` ` ` ` o ` `...` ` o ` ` --------> ` ` o ` `...` ` o ` ` ` ` ` ` ` `/`\` ` ` ` `/`\` ` ` ` ` ` ` ` `/`\` ` ` ` `/`\` ` ` ` ` ` ` / ` \ ` ` ` / ` \ ` ` ` ` ` ` ` / ` \ ` ` ` / ` \ ` ` ` ` ` `/` ` `\` ` `/` ` `\` ` ` ` ` ` `/` ` `\` ` `/` ` `\` ` ` ` ` o->-o->-o ` o->-o->-o ` ` ` ` ` o->-o->-o ` o->-o->-o ` ` ` ` `\` ` ` ` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` \ ` ` ` ` ` ` ` ` ` ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `\` ` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` \ ` ` ` ` ` ` ` ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `\` ` ` ` h_j ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o-------->----------o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
Next time we'll apply this general scheme to the En and Ex interpretations of logical graphs, and see how it helps us to sort out the varieties of iconic mapping that are involved in that setting.
Corresponding to the Entitative and Existential interpretations of the primary arithmetic, there are two distinct mappings from the sign domain S, containing the topological equivalents of bare and rooted trees, onto the object domain O, containing the two objects whose conventional, ordinary, or meta-language names are Falsity and Truth, respectively.
The next two Figures suggest how one might view the interpretation maps as mappings from a COSI S to a COSI O. Here I have placed names of categories at the bottom, indices of individuals at the next level, and extended upward from there whatever structures the individuals may have.
Here is the Figure for the Entitative interpretation:
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o ` ` ` o o ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` | `\`/` ` ` Structures` ` F ` ` ` ` ` T ` ` ` ` ` @ ` @ `...` @ ` @ `...` ` ` ` ` ` ` ` | ` ` ` ` ` | ` ` ` ` ` `\` | `/` ` `\` | `/` ` ` ` ` ` ` ` ` | ` ` ` ` ` | ` ` ` ` ` ` \ | / ` ` ` \ | / ` ` ` ` ` ` ` ` ` | ` ` ` ` ` | ` ` En` ` ` `\|/` ` ` ` `\|/` ` ` Individuals ` o ` ` ` ` ` o ` <-----` ` ` o ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` `\` ` ` ` `/` ` ` ` ` ` ` ` `\` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` \ ` ` ` / ` ` ` ` ` ` ` ` ` \ ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` `\`/` ` ` ` ` ` ` ` ` ` ` ` `\`/` ` ` ` ` ` Categories` ` ` ` `!O!` ` ` ` ` ` ` ` ` ` ` ` `!S!` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
Here is the Figure for the Existential interpretation:
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o o ` o ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | `\`/` ` ` ` ` | ` ` ` Structures` ` F ` ` ` ` ` T ` ` ` ` ` @ ` @ `...` @ ` @ `...` ` ` ` ` ` ` ` | ` ` ` ` ` | ` ` ` ` ` `\` | `/` ` `\` | `/` ` ` ` ` ` ` ` ` | ` ` ` ` ` | ` ` ` ` ` ` \ | / ` ` ` \ | / ` ` ` ` ` ` ` ` ` | ` ` ` ` ` | ` ` Ex` ` ` `\|/` ` ` ` `\|/` ` ` Individuals ` o ` ` ` ` ` o ` <-----` ` ` o ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` `\` ` ` ` `/` ` ` ` ` ` ` ` `\` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` \ ` ` ` / ` ` ` ` ` ` ` ` ` \ ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` `\`/` ` ` ` ` ` ` ` ` ` ` ` `\`/` ` ` ` ` ` Categories` ` ` ` `!O!` ` ` ` ` ` ` ` ` ` ` ` `!S!` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
Note that the structure of a tree begins at its root, marked by an "O". The objects in O have no further structure to speak of, so there is nothing much happening in the object domain O between the level of individuals and the level of structures. In the sign domain S, the individuals are the parts of the partition into referential equivalence classes, each part of which contains a countable infinity of syntactic structures, rooted trees, or whatever form one views their structures taking. The sense of the Figures is that the interpretation under consideration maps the individual on the left (right) side of S to the individual on the left (right) side of O.
An iconic mapping, that gets formalized in mathematical terms as a morphism, is said to be a structure-preserving map. This does not mean that all of the structure of the source domain is preserved in the map images of the target domain, but only some of the structure, that is, specific types of relation that are defined among the elements of the source and target, respectively.
For example, let's start with the archetype of all morphisms, namely, a linear function or a linear mapping f : X → Y.
To say that the function f is linear is to say that we have already got in mind a couple of relations on X and Y that have forms roughly analogous to "addition tables", so let's signify their operation by means of the symbols "#" for "addition in X" and "+" for "addition in Y".
More exactly, the use of "#" refers to a 3-adic relation LX ⊆ X × X × X that licenses the formula "a # b = c" just when <a, b, c> is in LX, and the use of "+" refers to a 3-adic relation LY ⊆ Y × Y × Y that licenses the formula "p + q = r" just when <p, q, r> is in LY.
In this setting, the mapping f : X → Y is said to be linear, and to preserve the structure of LX in the structure of LY, if and only if f(a # b) = f(a) + f(b), for all pairs a, b in X. In other words, f distributes over the additions # to +, just as if it were a form of multiplication, like m(a + b) = ma + mb.
Writing this more directly in terms of the 3-adic relations LX and LY instead of via their operation symbols, we would say that f : X → Y is linear with regard to LX and LY if and only if <a, b, c> being in the relation LX determines that its map image <f(a), f(b), f(c)> be in LY. To see this, observe that <a, b, c> being in LX implies that c = a # b, and <f(a), f(b), f(c)> being in LY implies that f(c) = f(a) + f(b), so we have that f(a # b) = f(c) = f(a) + f(b), and the two notions are one.
The idea of mappings that preserve 3-adic relations should ring a few bells here.
Once again into the breach between the interpretations En, Ex : S → O, drawing but a single Figure in the sand and relying on the reader to recall:
- En maps every tree on the left (right) of S to the left (right) of O.
- Ex maps every tree on the left (right) of S to the right (left) of O.
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o ` ` ` o o ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` | `\`/` ` ` Structures` ` F ` ` ` ` ` T ` ` ` ` ` @ ` @ `...` @ ` @ `...` ` ` ` ` ` ` ` | ` ` ` ` ` | ` ` ` ` ` `\` | `/` ` `\` | `/` ` ` ` ` ` ` ` ` | ` ` ` ` ` | ` ` ` ` ` ` \ | / ` ` ` \ | / ` ` ` ` ` ` ` ` ` | ` ` ` ` ` | ` ` En` ` ` `\|/` ` ` ` `\|/` ` ` Individuals ` o ` ` ` ` ` o ` <-----` ` ` o ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` `\` ` ` ` `/` ` ` Ex` ` ` ` `\` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` \ ` ` ` / ` ` ` ` ` ` ` ` ` \ ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` `\`/` ` ` ` ` ` ` ` ` ` ` ` `\`/` ` ` ` ` ` Categories` ` ` ` `!O!` ` ` ` ` ` ` ` ` ` ` ` `!S!` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
Now, those who wish to say that these logical signs are iconic of their logical objects must not only find some reason that logic itself singles out one interpretation over the other, but, even if they succeed in that, they must then make us believe that every sign for Truth is iconic of Truth, while every sign for Falsity is iconic of Falsity. Well, I confess that it strains my imagination, if not the over-abundant resources of theirs.
One of the questions that arises at this point, where we have a very small object domain O = {Falsity, Truth} and a very large sign domain S ≈ {rooted trees}, is the following:
- Why do we have so many ways of saying the same thing?
In other words, what possible utility is there in a language having so many signs to denote the same object? Why not just restrict the language to a canonical collection of signs, each of which denotes one and only one object, exclusively and uniquely?
Indeed, language reformers from time to time have proposed the design of languages that have just this property, but I think this is one of those places where natural evolution has luckily hit on a better plan than the sorts of intentional design that inexperienced designers typically craft.
The answer to the puzzle of semiotic multiplicity appears to have something to do with the use of language in interacting with a complex external world. The objective world throws its multiplicity of problems at us, and the first duty of language is to provide some expression of their structure, on the fly, as quickly as possible, in real time, as they come in, no matter how obscurely our quick and dirty expressions of the problematic situation might otherwise be.
Of course, very little of this can be apparent at the level of primary arithmetic, but I think it should become a little more obvious as we enter the primary algebra.
I will now give a reference version of the CSP-GSB axioms for the abstract calculus that is formally recognizable in several senses as giving form to propositional logic.
The first order of business is to give the exact forms of the axioms that I use, devolving from Peirce's "Logical Graphs" via Spencer-Brown's Laws of Form (LOF). In formal proofs, I will use a variation of the annotation scheme from LOF to mark each step of the proof according to which axiom, or initial, is being invoked to justify the corresponding step of syntactic transformation, whether it applies to graphs or to strings.
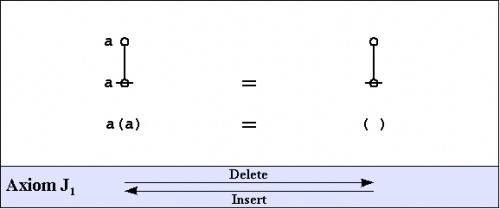
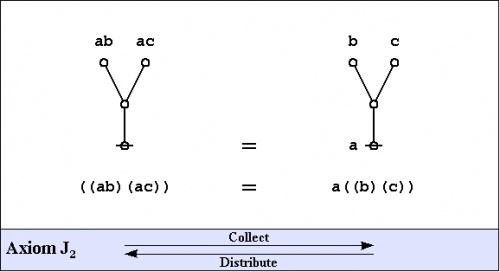
The axioms are just four in number, and they come in a couple of flavors: the arithmetic initials I1 and I2, and the algebraic initials J1 and J2.
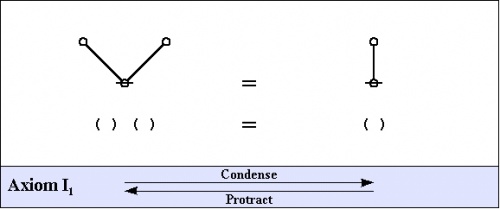
|
|
|
|
Notice that all of the axioms in this set have the form of equations. This means that all of the inference steps they allow are reversible. In the proof annotation scheme below, I will use a double bar "=====" to mark this fact, but I may at times leave it to the reader to pick which direction is the one required for applying the indicated axiom.
Frequently used theorems
The actual business of proof is a far more strategic affair than the simple cranking of inference rules might suggest. Part of the reason for this lies in the circumstance that the usual brands of inference rules combine the moving forward of a state of inquiry with the losing of information along the way that doesn't appear to be immediately relevant, at least, not as viewed in the local focus and the short run of the moment to moment proceedings of the proof in question. Over the long haul, this has the pernicious side-effect that one is forever strategically required to reconstruct much of the information that one had strategically thought to forget in earlier stages of the proof, if "before the proof started" can be counted as an earlier stage of the proof in view.
For this reason, among others, it is very instructive to study equational inference rules of the sort that our axioms have just provided. Although equational forms of reasoning are paramount in mathematics, they are less familiar to the student of conventional logic textbooks, who may find a few surprises here.
By way of gaining a minimal experience with how equational proofs look in the present forms of syntax, let us examine the proofs of a few essential theorems in the primary algebra.
C1. Double negation theorem
The first theorem goes under the names of Consequence 1 \((C_1)\!\), the double negation theorem (DNT), or Reflection.
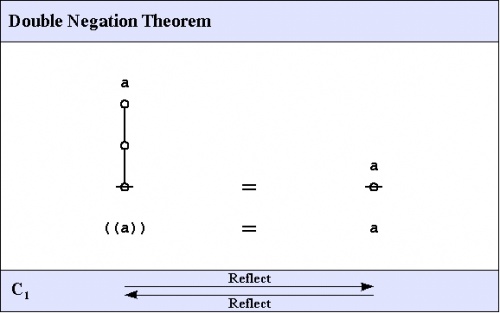
|
The proof that follows is adapted from the one that was given by George Spencer Brown in his book Laws of Form (LOF) and credited to two of his students, John Dawes and D.A. Utting.
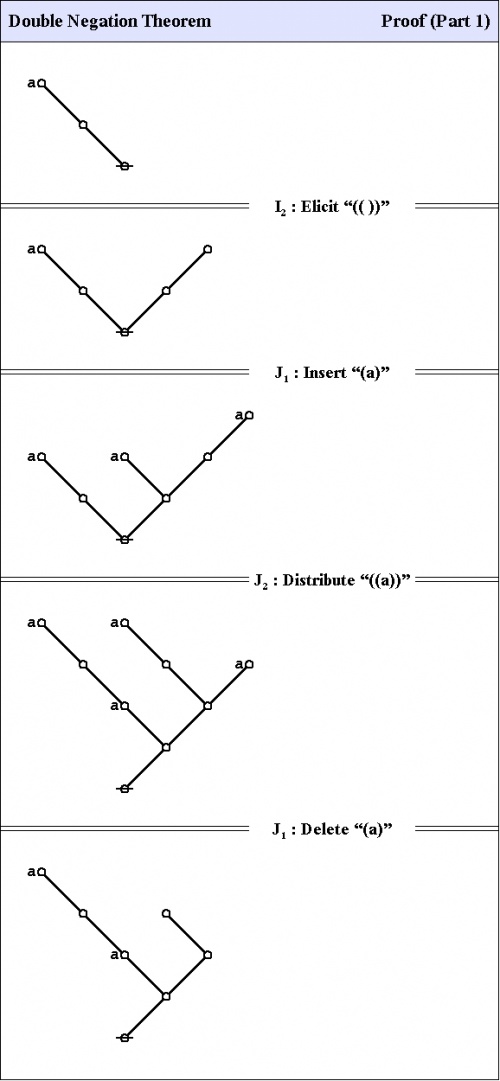
|
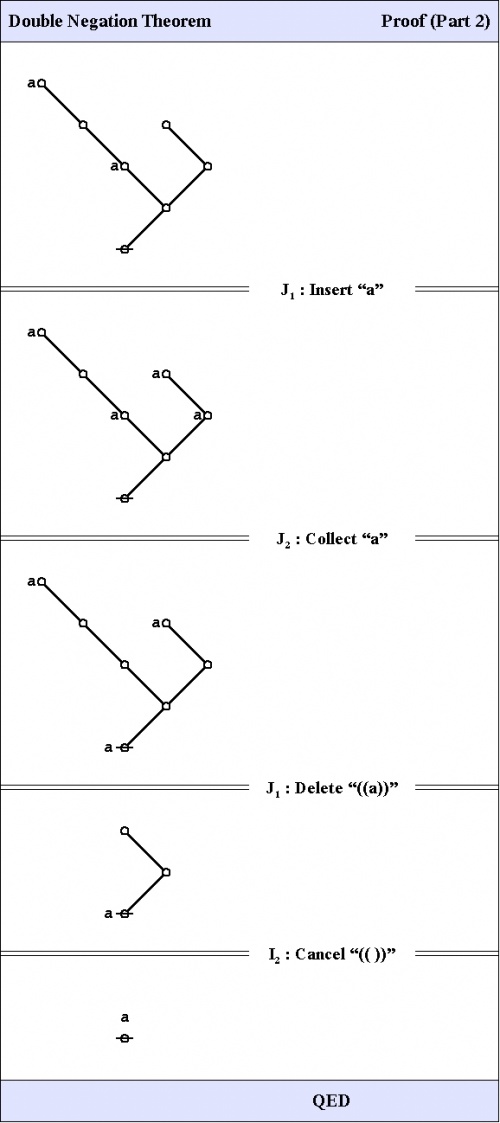
|
C2. Generation theorem
One theorem of frequent use goes under the nickname of the weed and seed theorem (WAST). The proof is just an exercise in mathematical induction, once a suitable basis is laid down, and it will be left as an exercise for the reader. What the WAST says is that a label can be freely distributed or freely erased anywhere in a subtree whose root is labeled with that label. The second in our list of frequently used theorems is in fact the base case of this weed and seed theorem. In LOF, it goes by the names of Consequence 2 \((C_2)\!\) or Generation.
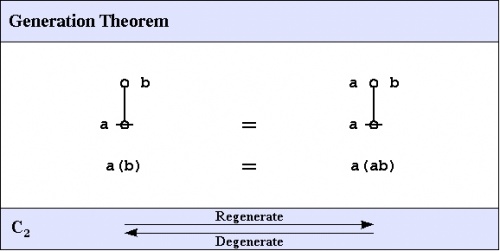
|
Here is a proof of the Generation Theorem.
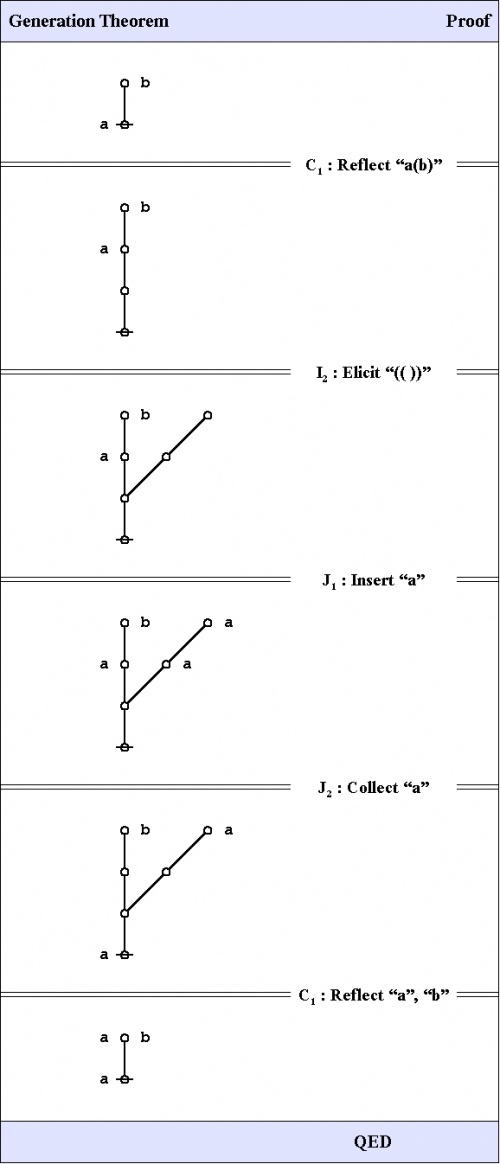
|
Now that we've seen a few — very simple but still non-trivial — examples of semiotic processes, namely, ones which fall under the headings of logical computation, evaluation, and proof, there are a number of questions that typically arise with respect to the relationship between sign relations and sign processes.
For concreteness, let's consider the example of logical evaluation that we looked at in Note 15.
o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` o o o ` ` ` ` ` ` o o ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` | | ` `\| | ` ` ` ` ` ` | | ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | ` ` o o o ` ` ` ` ` o o o ` ` ` ` ` ` o o ` ` ` ` ` ` o ` | | ` ` `\|/` ` ` ` ` ` `\|/` ` ` ` ` ` ` |/` ` ` ` ` ` ` | ` | | ` ` ` @ ` ` ` = ` ` ` @ ` ` ` = ` ` ` @ ` ` ` = ` ` ` @ ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | (()())(())()` = ` (())(())()` = ` ` (())()` ` = ` ` `( )` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o
What sorts of sign relation are implicated in this sign process? For simplicity, let's answer for the existential interpretation.
In Ex, all four of the listed signs are expressions of Falsity, and, viewed within the special type of semiotic procedure that is being considered here, each sign interprets its predecessor in the sequence. Thus we might begin by drawing up this Table:
o-------------------o-------------------o-------------------o | Object` ` ` ` ` ` | Sign` ` ` ` ` ` ` | Interpretant` ` ` | o-------------------o-------------------o-------------------o | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | Falsity ` ` ` ` ` | "(()())(())()"` ` | "(())(())()"` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | Falsity ` ` ` ` ` | "(())(())()"` ` ` | "(())()"` ` ` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | Falsity ` ` ` ` ` | "(())()"` ` ` ` ` | "()"` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | o-------------------o-------------------o-------------------o
That much of a sign relation is enough to cover the case before us, but of course it is only a small sample from the larger population of triples of the form <o, s, i> that is implied by the definition of the primary arithmetic.
Let's take another look at the semiotic sequence associated with a logical evaluation and the corresponding sample of a sign relation that we were looking at last time.
o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` o o o ` ` ` ` ` ` o o ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` | | ` `\| | ` ` ` ` ` ` | | ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | ` ` o o o ` ` ` ` ` o o o ` ` ` ` ` ` o o ` ` ` ` ` ` o ` | | ` ` `\|/` ` ` ` ` ` `\|/` ` ` ` ` ` ` |/` ` ` ` ` ` ` | ` | | ` ` ` @ ` ` ` = ` ` ` @ ` ` ` = ` ` ` @ ` ` ` = ` ` ` @ ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | (()())(())()` = ` (())(())()` = ` ` (())()` ` = ` ` `( )` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o o-------------------o-------------------o-------------------o | Object` ` ` ` ` ` | Sign` ` ` ` ` ` ` | Interpretant` ` ` | o-------------------o-------------------o-------------------o | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | Falsity ` ` ` ` ` | "(()())(())()"` ` | "(())(())()"` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | Falsity ` ` ` ` ` | "(())(())()"` ` ` | "(())()"` ` ` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | Falsity ` ` ` ` ` | "(())()"` ` ` ` ` | "()"` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | o-------------------o-------------------o-------------------o
The sign of equality "=", interpreted as logical equivalence "⇔", that marked our steps in the process of conducting the evaluation, is evidently intended to denote an equivalence relation, and this is a 2-adic relation that is reflexive, symmetric, and transitive. If we then pass to the reflexive, symmetric, transitive closure of the <s, i> pairs that occur in our initial sample, attaching the constant reference to Falsity in the object domain, we will sweep out a more complete selection of the sign relation that inheres in the definition of the primary logical arithmetic.
o-------------------o-------------------o-------------------o | Object` ` ` ` ` ` | Sign` ` ` ` ` ` ` | Interpretant` ` ` | o-------------------o-------------------o-------------------o | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | Falsity ` ` ` ` ` | "(()())(())()"` ` | "(()())(())()"` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | Falsity ` ` ` ` ` | "(()())(())()"` ` | "(())(())()"` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | Falsity ` ` ` ` ` | "(()())(())()"` ` | "(())()"` ` ` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | Falsity ` ` ` ` ` | "(()())(())()"` ` | "()"` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | o-------------------o-------------------o-------------------o | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | Falsity ` ` ` ` ` | "(())(())()"` ` ` | "(()())(())()"` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | Falsity ` ` ` ` ` | "(())(())()"` ` ` | "(())(())()"` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | Falsity ` ` ` ` ` | "(())(())()"` ` ` | "(())()"` ` ` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | Falsity ` ` ` ` ` | "(())(())()"` ` ` | "()"` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | o-------------------o-------------------o-------------------o | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | Falsity ` ` ` ` ` | "(())()"` ` ` ` ` | "(()())(())()"` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | Falsity ` ` ` ` ` | "(())()"` ` ` ` ` | "(())(())()"` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | Falsity ` ` ` ` ` | "(())()"` ` ` ` ` | "(())()"` ` ` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | Falsity ` ` ` ` ` | "(())()"` ` ` ` ` | "()"` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | o-------------------o-------------------o-------------------o | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | Falsity ` ` ` ` ` | "()"` ` ` ` ` ` ` | "(()())(())()"` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | Falsity ` ` ` ` ` | "()"` ` ` ` ` ` ` | "(())(())()"` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | Falsity ` ` ` ` ` | "()"` ` ` ` ` ` ` | "(())()"` ` ` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | Falsity ` ` ` ` ` | "()"` ` ` ` ` ` ` | "()"` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | o-------------------o-------------------o-------------------o
Earnest contemplation of the relationship between semiotic trajectories and the infrastructure of sign relations that is needed to support them may bring the seeker to a state of enlightenment about a motley crew of old knots in the semiotic web of maya, most pointedly the one that goes about raveling and reveiling the world in the name of infinite semiosis.
To see how the variety of misunderstandings about infinite semiosis got started, it may help to refresh our memories with regard to one of Peirce's last, best definitions of a sign relation:
A sign is something, A, which brings something, B, its interpretant sign determined or created by it, into the same sort of correspondence with something, C, its object, as that in which itself stands to C. (C.S. Peirce, NEM 4, pp. 20-21, cf. p. 54 (1902)).
Now it's true that Peirce's definition of a sign relation requires that every sign in a sign relation creates or determines an interpretant sign that serves as a sign in the very same sign relation, and which therefore creates or determines its own interpretant sign, and so on, 'ad infinitum'. But there is nothing that keeps this "infinite semiosis" from being bounded in the nutshell of a finite sign relation, because nothing says that all of the signs must be distinct, and nothing says that this formal determination has to be extended in a temporal sequence, though of course that may happen.
In sum, we may view the sign relation as a generative structure, as a matrix that funds the generation of many possible semioses.
Before we leave it for richer coasts — not to say we won't find ourselves returning eternally — let's note one other feature of our randomly chosen microcosm, one I suspect we'll see many echoes of in the macrocosm of our future wanderings.
o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` o o o ` ` ` ` ` ` o o ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` | | ` `\| | ` ` ` ` ` ` | | ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | ` ` o o o ` ` ` ` ` o o o ` ` ` ` ` ` o o ` ` ` ` ` ` o ` | | ` ` `\|/` ` ` ` ` ` `\|/` ` ` ` ` ` ` |/` ` ` ` ` ` ` | ` | | ` ` ` @ ` ` ` = ` ` ` @ ` ` ` = ` ` ` @ ` ` ` = ` ` ` @ ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | (()())(())()` = ` (())(())()` = ` ` (())()` ` = ` ` `( )` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o
One of the things that makes this sign sequence so special, amidst the generations of other sign sequences that can be generated from the sign relation of the primary arithmetic, is that it goes from a relatively obscure and verbose sign to an optimally clear and succinct sign for the same thing. For all its simplicity, then, it possesses a property that is characteristic of a semiotic process known as inquiry.
C3. Dominant form theorem
The third of the frequently used theorems of service to this survey is one that Spencer-Brown annotates as Consequence 3 \((C_3)\!\) or Integration. A better mnemonic might be dominance and recession theorem (DART), but perhaps the brevity of dominant form theorem (DFT) is sufficient reminder of its double-edged role in proofs.
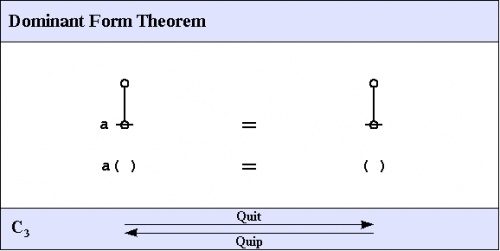
|
Here is a proof of the Dominant Form Theorem.
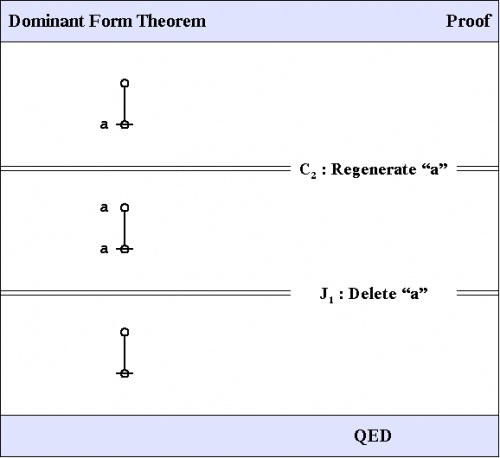
|
Exemplary proofs
Based on the axioms given at the outest, and aided by the theorems recorded so far, it is possible to prove a multitude of much more complex theorems. A couple of all-time favorites are given next.
Peirce's law
Peirce's law is commonly written in the following form:
| \(((p \Rightarrow q) \Rightarrow p) \Rightarrow p\) |
The existential graph representation of Peirce's law is shown in Figure 31.
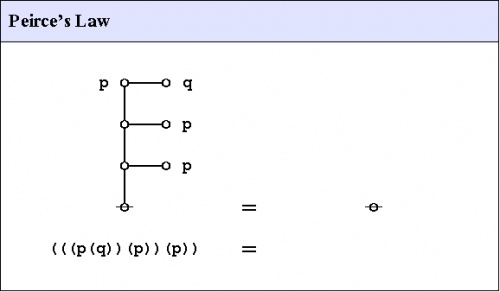
|
A graphical proof of Peirce's law is shown in Figure 32.
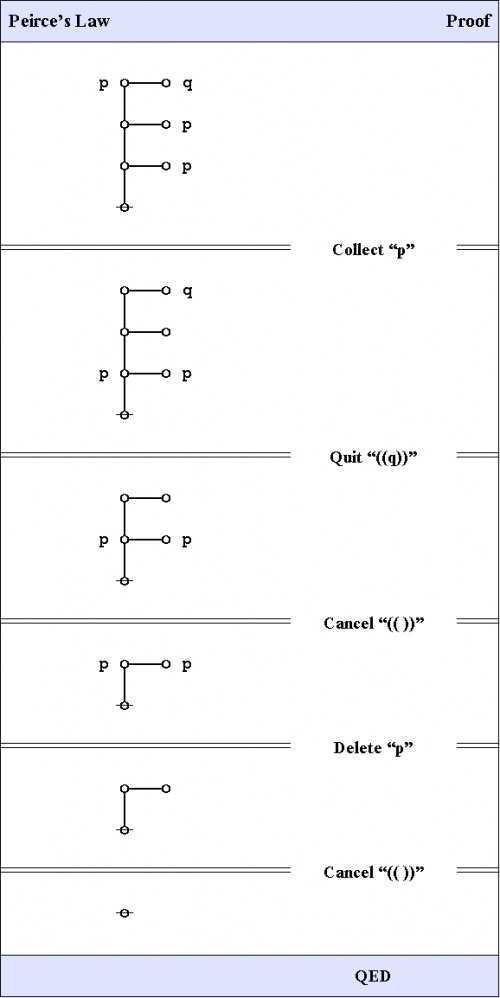
|
Praeclarum theorema
An illustrious example of a propositional theorem is the praeclarum theorema, the admirable, shining, or splendid theorem of Leibniz.
If a is b and d is c, then ad will be bc.
This is a fine theorem, which is proved in this way:
a is b, therefore ad is bd (by what precedes),
d is c, therefore bd is bc (again by what precedes),
ad is bd, and bd is bc, therefore ad is bc. Q.E.D.
(Leibniz, Logical Papers, p. 41).
Under the existential interpretation, the praeclarum theorema is represented by means of the following logical graph.
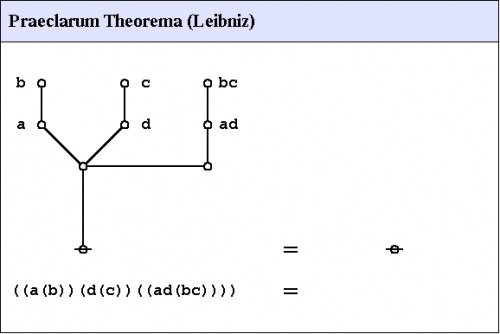
|
And here's a neat proof of that nice theorem.
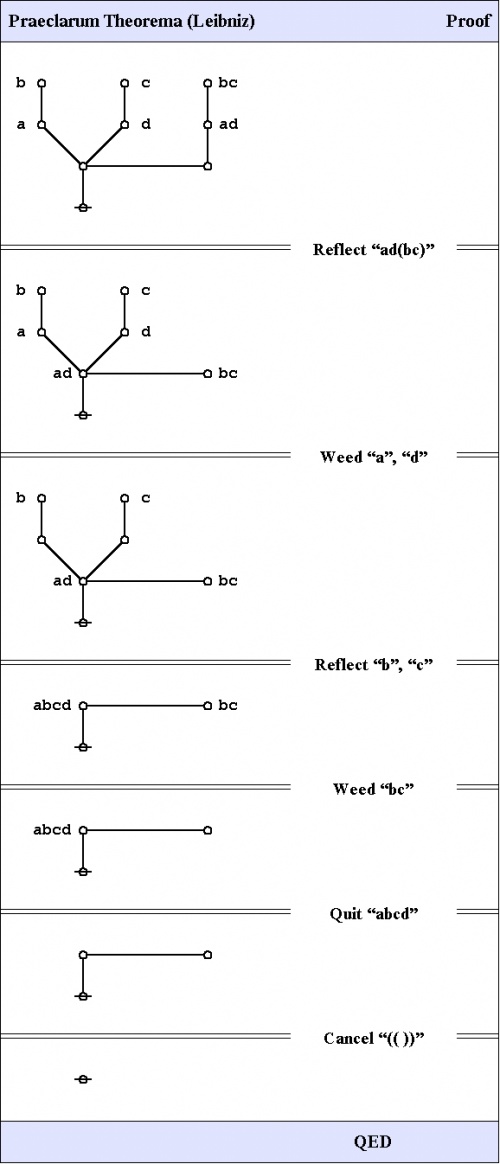
|
Themes and variations
The relation between the primary arithmetic and the primary algebra is founded on the idea that a variable name in the algebra indicates the contemplated absence or presence as an operand of any expression in the arithmetic, with the understanding that each appearance of the same variable name indicates the same state of contemplation with respect to the same expression of the arithmetic.
For example, consider the following expression:
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` a ` ` a ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o-----o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
We may regard this algebraic expression as a general expression for an infinite set of arithmetic expressions, starting like so:
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o ` ` o ` ` ` ` ` o ` o o ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` | ` ` ` ` ` `\`/` `\`/` ` ` ` ` ` ` o ` ` o o ` o o ` o o ` ` o o o o o o o o ` ` o ` ` ` ` ` ` ` | ` ` | `\`/` `\`/` | ` ` | `\|/` `\|/` | ` ` | ` ` o-----o ` o-----o ` o-----o ` o-----o ` o-----o ` o-----o ` ` | ` ` ` ` | ` ` ` ` | ` ` ` ` | ` ` ` ` | ` ` ` ` | ` ` ` ` ` | ` ` ` ` | ` ` ` ` | ` ` ` ` | ` ` ` ` | ` ` ` ` | ` ` ` ` ` @ ` ` ` ` @ ` ` ` ` @ ` ` ` ` @ ` ` ` ` @ ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
Now consider what this says about the following algebraic law:
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` a ` ` a ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o-----o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` @ ` ` ` ` = ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
It permits us to understand the algebraic law as saying, in effect, that every one of the arithmetic expressions of the contemplated pattern evaulates to the very same canonical expression as the upshot of that evaluation. This is, as far as I know, just about as close as we can come to a conceptually and ontologically minimal way of understanding the relation between an algebra and its corresponding arithmetic.
There was a wobbly construction in my last paragraph, so let me try to shore it up in this re-construction:
The suggested perspective on algebraic expressions allows us to understand the algebraic law as saying, in effect, that every one of the arithmetic expressions that fits the indicated algebraic pattern evaluates to the very same canonical expression for the end result of its evaluation. This is, as far as I can tell, just about as close as we can come to a conceptually and ontologically minimal way of understanding the relation between an algebra and its corresponding arithmetic.
Of course, it is not really necessary to consider every possible substitution of arithmetic expressions for the algebraic variables, since only the value of each arithmetic expression can make any difference to the end result. Nevertheless, taking an algebraic expression as a syntactic mechanism for singling out a particular subset of the primary arithmetic is a move that suggests very fruitful directions of generalization.
In particular, this point of view helps us to sidestep many of the mysteries that encumber particular mechanisms of substitution, which it takes all the rigors of combinator calculus and lambda calculus even to begin clearing up, and it also provides us with an alternative way of approaching the puzzles of so-called imaginary values.
But I will have to leave it with those hints for now, as there is still much to do at the elementary level.
In lieu of a field study requirement for my bachelor's degree program I spent a couple of years in several state and university libraries reading everything I could find by and about Peirce, poring most memorably through the 38 reels of microfilmed manuscripts that Michigan State had at the time, all in trying to track down some hint of a clue to some puzzling passages that I read in Peirce's "Simplest Mathematics", most acutely coming to a head with that bizzare line of type in CP 4.306, that the editors of CP, no doubt compromised by the typographer's resistance to cutting new symbols, transmogrified into an averse verse that's even more cryptic than the manuscript hieroglyphic.
The first key to the mystery is discovered in Peirce's use of operator variables, that he and his students Christine Ladd-Franklin and O.H. Mitchell explored in some depth. I will shortly discuss this theme as it affects logical graphs, but it may be useful to give a shorter and sweeter explanation of how the basic idea typically arises in common logical practice.
Think of De Morgan's rules:
- ~[A ∧ B] = ~A ∨ ~B
- ~[A ∨ B] = ~A ∧ ~B
We could capture the common form of these two rules in a single formula by letting "X" and "Y" be variable names that range over a pre-selected set of logical operators, and then by asking what X and Y would satisfy:
- ~[A X B] = ~A Y ~B
We already know two solutions to this operator equation, specifically, <X, Y> = <∧, ∨> and <X, Y> = <∨, ∧>. Wouldn't it be just like Peirce to ask if there are others? I will leave that as an exercise for the reader.
Now that it's come to logical operator variables (LOV's), I can find no grander way to elope than Peirce himself did:
I shall not further enlarge upon this matter at this point, although the conception mentioned opens a wide field; because it cannot be set in its proper light without overstepping the limits of dichotomic mathematics. (C.S. Peirce, Collected Papers, CP 4.306).
And that goes treble for me. The further exploration of operator laws and operator variables, touching as it does on the ground that was classically called second intentional logic, like the man said, "opens a wide field", one that we may have hopes of revisiting in a less whirlwind touristy way one of these days. For now I will tend to that corner of the field where this particular variety of logical graphs grows, communing with a few of the ways that operative variations and operative themes sprout therein.
To begin with a concrete case that's as easy as possible, let's examine this extremely simple algebraic expression:
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` a ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
In this context the variable name "a" appears as an operand name. In functional terms, "a" is called an argument name, but we are probably well advised to avoid the confusing connotations of the word "argument" here, as it also refers in logical discussions to a more or less specific pattern of reasoning. In syntactic terms, this same "a" would be classified as a terminal sign.
As we've already discussed, the algebraic variable name indicates the contemplated absence or presence of any arithmetic expression taking its place in the surrounding template, which expression is proxied well enough by its value, of which values we know but two. Thus, the given algebraic expression varies between these choices:
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` @ ` ` ` ` , ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
The above selection of arithmetic expressions is what it means to contemplate the absence or presence of the operand "a" in the algebraic expression "(a)". But what would it mean to contemplate the absence or presence of the operator "(_)" in the algebraic expression "(a)"?
We had been contemplating the penultimately simple algebraic expression "(a)" as a name for a set of arithmetic expressions, namely, (a) = {(), (())}, taking the equality sign in the appropriate sense.
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` `
` ` ` ` ` a ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` `
` ` ` ` ` o ` ` ` ` ` ` ` ` ` o ` ` ` ` o ` ` ` ` ` ` ` ` ` `
` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` | ` ` ` ` ` ` ` ` ` `
` ` ` ` ` @ ` ` ` ` = ` ` { ` @ ` `,` ` @ ` } ` ` ` ` ` ` ` `
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
Then we asked the corresponding question about the operator "(_)": The above selection of arithmetic expressions is what it means to contemplate the absence or presence of the operand "a" in the algebraic expression "(a)". But what would it mean to contemplate the absence or presence of the operator "(_)" in the algebraic expression "(a)"?
Clearly, a variation between the absence and the presence of the operator "(_)" in the algebraic expression "(a)" refers to a variation between the algebraic expressions "a" and "(a)", respectively, somewhat as pictured here:
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
` ` ` ` ` a ` ` ` ` ` ` ` ` ` ` ` ` ` ` a ` ` ` ` ` ` ` ` ` `
` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` `
` ` ` ` ` ? ` ` ` ` ` ` ` ` ` a ` ` ` ` | ` ` ` ` ` ` ` ` ` `
` ` ` ` ` @ ` ` ` ` = ` ` { ` @ ` `,` ` @ ` } ` ` ` ` ` ` ` `
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
But how shall we signify such variations in a coherent calculus?
In the days when I scribbled these things on the backs of computer punchcards, I think that the first thing I tried was drawing big loopy script characters, placing some inside the loops of others. Lower case alphas, betas, gammas, deltas, and so on worked the best, but here in Ascii I will ty to convey something approaching the same general impression by using p's and q's.
Here is how we might suggest an algebraic expression of the form "(q)" where the absence or presence of the operator "(_)" depends on the value of the algebraic expression "p", the operator "(_)" being absent whenever p is unmarked and present when whenever p is marked.
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
` ` ` ` ` o---o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
` ` ` ` ` | q | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
` ` ` ` ` o---o ` ` ` = ` ` ` { ` q ` , ` (q) ` } ` ` ` ` ` `
` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
It was obvious to me from the very outset that this sort of tactic would need some work to become a usable calculus, especially when it became time to feed those punchcards back into the computer.
One of the other tactics of syntax that I tried at this time — somewhere in the 70's ... when did we quit using punchcards? — by way of porting operator variables into logical graphs and the laws of form, was to hollow out a leg of Spencer-Brown's crosses, gnomons, markers, whatever you call them, like this:
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
` ` ` ` ` ----------o---o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
` ` ` ` ` ` ` ` ` ` | ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
` ` ` ` ` ` ` q ` ` | p | ` ` = ` ` { ` q ` , ` (q) ` } ` ` `
` ` ` ` ` ` ` ` ` ` | ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
The initial idea that I had in mind here was the same as before, that the operator over q is counted as absent when p evaluates to a space and counted as present when p evaluates to a cross.
However, much in the same way that operators with a shade of negativity to them tend to be more generative than the purely "positivistic" brand, it turned out to be slightly more useful to reverse this initial polarity of operation, letting the operator over q be counted as absent whenever p evaluates to a cross and be counted as present whenever p evaluates to a space.
So that is the convention that I shall adopt from here on.
A funny thing just happened. Let's see if we can tell where. We started with the algebraic expression "(a)", in which the operand "a" suggests the contemplated absence or presence of any arithmetic expression or its value, then we contemplated the absence of presence of the operator "(_)" in "(a)" to be indicated by a cross or a space, respectively, for the value of a newly introduced variable, "b", placed in a new slot of a newly extended operator form, as suggested by this picture:
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ----------o---o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` a ` ` | b | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
The funny thing that just happened — it's an acquired sense of humor — is that our contemplation of an operator variable just as quickly got converted into the contemplation of a newly introjected but otherwise quite ordinary operand variable, albeit within a newly-fanged formula. In its interpretation for logic, the new form of operation that forms here may be viewed as an extension of ordinary negation, specifically, a negation of the first variable that is "controlled" by the value of the second variable. Thus, we may regard this development as marking a form of "controlled reflection", or a form of "reflective control". By way of an inline syntax for this, I will employ the form "(a, b)".
Writing out a formal operation table yields the following summary:
o-------------------o-------------------o-------------------o | ` ` ` ` a ` ` ` ` | ` ` ` ` b ` ` ` ` | ` ` `(a , b)` ` ` | o-------------------o-------------------o-------------------o | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | ` ` ` blank ` ` ` | ` ` ` blank ` ` ` | ` ` ` cross ` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | ` ` ` blank ` ` ` | ` ` ` cross ` ` ` | ` ` ` blank ` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | ` ` ` cross ` ` ` | ` ` ` blank ` ` ` | ` ` ` blank ` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | ` ` ` cross ` ` ` | ` ` ` cross ` ` ` | ` ` ` cross ` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | o-------------------o-------------------o-------------------o
- En, for which blank = false and cross = true, calls this "equivalence".
- Ex, for which blank = true and cross = false, calls this "distinction".
The step of controlled reflection that we just took can be iterated just as far as we wish to take it, as suggested by the following set:
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ----------o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` a ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ----------o---o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` a ` ` | b | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ----------o---o---o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` | ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` a ` ` | b | c | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` | ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ----------o---o---o---o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` | ` | ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` a ` ` | b | c | d | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` | ` | ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
By way of inline syntax, I will transliterate these expressions as "(a)", "(a, b)", "(a, b, c)", "(a, b, c, d)", and so on, capturing the general style of expression in the form "(x1, x2, …, xk)". With this move we have passed beyond the graph-theoretical form of rooted trees to what graph theorists generally call rooted cacti.
I will discuss this cactus language and its logical interpretations next.
The following Table will suffice to suggest the syntactic correspondences among the "streamer-cross" forms that Peirce used in his essay on "Qualitative Logic" and Spencer Brown used in his book Laws of Form, as they become extended by successive steps of controlled reflection, the plaintext string syntax, and the rooted cactus graphs:
o-----------------------------o-----------------o-----------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` | ` ` ` ` ` | | ` ----------o ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` | ` ` a ` ` | | ` ` ` ` ` ` | ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` | ` ` o ` ` | | ` ` ` a ` ` | ` ` ` ` ` ` ` | ` (a) ` ` ` ` ` | ` ` | ` ` | | ` ` ` ` ` ` | ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` | ` ` @ ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` | ` ` ` ` ` | o-----------------------------o-----------------o-----------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` | ` ` ` ` ` | | ` ----------o---o ` ` ` ` ` | ` ` ` ` ` ` ` ` | ` a ` b ` | | ` ` ` ` ` ` | ` | ` ` ` ` ` | ` ` ` ` ` ` ` ` | ` o---o ` | | ` ` ` a ` ` | b | ` ` ` ` ` | ` (a , b)` ` ` | ` `\`/` ` | | ` ` ` ` ` ` | ` | ` ` ` ` ` | ` ` ` ` ` ` ` ` | ` ` @ ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` | ` ` ` ` ` | o-----------------------------o-----------------o-----------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` | ` ` ` ` ` | | ` ----------o---o---o ` ` ` | ` ` ` ` ` ` ` ` | ` a b c ` | | ` ` ` ` ` ` | ` | ` | ` ` ` | ` ` ` ` ` ` ` ` | ` o-o-o ` | | ` ` ` a ` ` | b | c | ` ` ` | ` (a , b , c) ` | ` `\`/` ` | | ` ` ` ` ` ` | ` | ` | ` ` ` | ` ` ` ` ` ` ` ` | ` ` @ ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` | ` ` ` ` ` | o-----------------------------o-----------------o-----------o | Reference: | | C.S. Peirce, "Qualitative Logic", MS 736, pp. 101-115 in: | Carolyn Eisele (ed.), 'The New Elements of Mathematics by | Charles S. Peirce, Volume 4, Mathematical Philosophy', | Mouton, The Hague, 1976. | | Cf. C.S. Peirce, "Qualitative Logic", MS 582 (Fall-Winter 1886), pp. 323-371 in: |'Writings of Charles S. Peirce: A Chronological Edition, Volume 5, 1884-1886', | Peirce Edition Project, Indiana University Press, Bloomington, IN, 1993. | | QUAL. Qualitative Logic | QUAL. http://stderr.org/pipermail/inquiry/2005-May/thread.html#2697 | QUAL. http://stderr.org/pipermail/inquiry/2005-June/thread.html#2776
Let us examine the formal operation table for the next in our series of reflective operations to see if we can elicit the general pattern.
o-------o-------o-------o-----------o | ` a ` | ` b ` | ` c ` | (a, b, c) | o-------o-------o-------o-----------o | ` ` ` | ` ` ` | ` ` ` | ` ` ` ` ` | | blank | blank | blank | ` cross ` | | ` ` ` | ` ` ` | ` ` ` | ` ` ` ` ` | | blank | blank | cross | ` blank ` | | ` ` ` | ` ` ` | ` ` ` | ` ` ` ` ` | | blank | cross | blank | ` blank ` | | ` ` ` | ` ` ` | ` ` ` | ` ` ` ` ` | | blank | cross | cross | ` cross ` | | ` ` ` | ` ` ` | ` ` ` | ` ` ` ` ` | | cross | blank | blank | ` blank ` | | ` ` ` | ` ` ` | ` ` ` | ` ` ` ` ` | | cross | blank | cross | ` cross ` | | ` ` ` | ` ` ` | ` ` ` | ` ` ` ` ` | | cross | cross | blank | ` cross ` | | ` ` ` | ` ` ` | ` ` ` | ` ` ` ` ` | | cross | cross | cross | ` cross ` | | ` ` ` | ` ` ` | ` ` ` | ` ` ` ` ` | o-------o-------o-------o-----------o
Or, thinking in terms of the graphic equivalents, writing "o" for a blank node and "|" for an edge:
o-------o-------o-------o-----------o | ` a ` | ` b ` | ` c ` | (a, b, c) | o-------o-------o-------o-----------o | ` ` ` | ` ` ` | ` ` ` | ` ` ` ` ` | | ` o ` | ` o ` | ` o ` | ` ` | ` ` | | ` ` ` | ` ` ` | ` ` ` | ` ` ` ` ` | | ` o ` | ` o ` | ` | ` | ` ` o ` ` | | ` ` ` | ` ` ` | ` ` ` | ` ` ` ` ` | | ` o ` | ` | ` | ` o ` | ` ` o ` ` | | ` ` ` | ` ` ` | ` ` ` | ` ` ` ` ` | | ` o ` | ` | ` | ` | ` | ` ` | ` ` | | ` ` ` | ` ` ` | ` ` ` | ` ` ` ` ` | | ` | ` | ` o ` | ` o ` | ` ` o ` ` | | ` ` ` | ` ` ` | ` ` ` | ` ` ` ` ` | | ` | ` | ` o ` | ` | ` | ` ` | ` ` | | ` ` ` | ` ` ` | ` ` ` | ` ` ` ` ` | | ` | ` | ` | ` | ` o ` | ` ` | ` ` | | ` ` ` | ` ` ` | ` ` ` | ` ` ` ` ` | | ` | ` | ` | ` | ` | ` | ` ` | ` ` | | ` ` ` | ` ` ` | ` ` ` | ` ` ` ` ` | o-------o-------o-------o-----------o
Evidently, the rule is that "(a, b, c)" denotes the value denoted by "o" if and only if exactly one of the variables has the value denoted by "|", otherwise it denotes the value denoted by "|". Examination of the whole sequence of reflective negations will show that this is the general rule.
- In the Entitative interpretation, where o = false and | = true, (x1, …, xk) interprets as "not just one of the xj is true".
- In the Existential interpretation, where o = true and | = false, (x1, …, xk) interprets as "just one of the xj is not true".
Partly through my reflections on Peirce's use of operator variables, I was led to the so-called reflective extension of logical graphs, or what I now refer to as the "cactus language", after its principal graph-theoretic data structure. It is generated by generalizing the negation operator "(_)" in a particular direction, treating "(_)" as the controlled, moderated, or reflective negation operator of order 1, and adding another such operator for each integer parameter greater than 1. In sum, these operators are symbolized by bracketed argument lists of the following types: "(_)", "(_, _)", "(_, _, _)", and so on, where the number of places is the order of the reflective negation operator in question.
The formal rule of evaluation for a "k-lobe" or "k-operator" is:
o-----------------------------------------------------------o | Evaluation Rule ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` x_1 `x_2` `...` x_k ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` `o----o-...-o----o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` \ ` ` ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` \ ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `@` ` ` ` ` ` ` = ` ` ` ` ` ` `@` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ( x_1, x_2, ..., x_k )` ` = ` ` ` ` ` <space> ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` IF AND ONLY IF` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `o` ` ` ` ` ` ` | | ` Just one of the x_1, x_2, ..., x_k` `=` `|` `=` `( )` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o
The interpretation of these operators, read as assertions about the values of their listed arguments, is as follows:
o-----------------------------------------------------------o | Interpretation Rule ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` x_1 `x_2` `...` x_k ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `o----o-...-o----o` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` ` ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | A "k-lobe operator" of the form "(x_1, ..., x_k)" ` ` ` ` | | enjoys two commonly employed interpretations for` ` ` ` ` | | propositional logic, in other words, two ways of` ` ` ` ` | | taking it as an assertion about, or a constraint` ` ` ` ` | | upon, the logical values of the listed arguments, ` ` ` ` | | the mentioned variables x_j, for j = 1 through k. ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | Entitative `Interpretation: ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` `"Not just one of the k arguments is true." ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | Existential Interpretation: ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` `"Just one of the k arguments is not true." ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o
Case analysis-synthesis theorem
The task at hand is to lay out what I think of as the pontoon bridge between the model-theoretic and the proof-theoretic shores, and thus between their diverging perspectives on logical procedure, even if I can construct it at a point but so close to their common source that it may not seem like it's worth the candle.
The substance of this principle was known to Boole a sesquicentury ago, tantamount to the Boolean Expansion that he uncovered while nameless. So the only novelty here will rest in a certain manner of presentation, in which I will prove the basic principle from the axioms given before. One name for this rule is the Case Analysis-Synthesis Theorem (CAST).
The preparatory materials that we need are these:
I am going to revert to my customarily sloppy workshop manners and refer to propositions and proposition expressions on rough analogy with functions and function expressions, which implies that a proposition will be regarded as the chief formal object of discussion, enjoying many proposition expressions, formulas, or sentences that express it, but worst of all I will probably just go ahead and use any and all of these terms as loosely as I see fit, taking a bit of extra care only when I see the need.
Let Q be a proposition with an unspecified, but context-fitting number of variables, say, none, or x, or x1, …, xk, as the case may be. (More precisely, I should've said "sentence Q".)
- Strings and graphs sans labels are called bare.
- A bare terminal node, "o", is known as a stone.
- A bare terminal edge, "|", is known as a stick.
Let the replacement expression of the form "Q[o/x]" denote the proposition that results from Q by replacing every token of the variable x with a blank, which is to say, erasing "x".
Let the replacement expression of the form "Q[|/x]" denote the proposition that results from Q by replacing every token of the variable x with a stick stemming from the site of "x".
In the case of a proposition Q, that is, an expression of it, not having a token of the designated variable "x", let it be stipulated that Q[o/x] = Q = Q[|/x].
I think that I am at long last ready to state the following:
o-----------------------------------------------------------o | Case Analysis-Synthesis Theorem (CAST)` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `x` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `o` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `x` `|` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` Q[o/x] o---o Q[|/x] ` ` | | ` ` ` ` ` ` `Q` ` ` ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` | | ` ` ` ` ` ` `@` ` ` ` ` ` ` = ` ` ` ` ` ` `@` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `Q` ` ` ` ` ` ` = ` ( Q[o/x] x , Q[|/x] (x) ) | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o
In order to think of tackling even the roughest sketch toward a proof of this theorem, we need to add a number of axioms and axiom schemata. Because I abandoned proof-theoretic purity somewhere in the middle of grinding this calculus into computational form, I never got around to finding the most elegant and minimal, or anything near a complete set of axioms for the cactus language, so what I list here are just the slimmest rudiments of the hodge-podge of rules of thumb that I have found over time to be necessary and useful in most working settings. Some of these special precepts are probably provable from genuine axioms, but I have yet to go looking for a more proper formulation.
o-----------------------------------------------------------o | Precept L_1.` Indifference` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` a ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` a ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` o---o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` @ ` ` ` ` = ` ` ` ` @ ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `(a, (a)) ` ` = ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` Split <---- | ----> Merge ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o
o-----------------------------------------------------------o | Precept L_2.` Equality. `The Following Are Equivalent:` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` b ` ` ` ` ` ` ` a ` b ` ` ` ` ` ` ` a ` ` ` ` ` | | ` ` ` ` ` o ` ` ` ` ` ` ` o---o ` ` ` ` ` ` ` o ` ` ` ` ` | | ` ` ` a ` | ` ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` | ` b ` ` ` | | ` ` ` o---o ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` o---o ` ` ` | | ` ` ` `\ /` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` `\ /` ` ` ` | | ` ` ` ` @ ` ` ` ` = ` ` ` ` @ ` ` ` ` = ` ` ` ` @ ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` `(a, (b)) ` ` = ` ` ((a , b)) ` ` = ` ` ((a), b)` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o
o-----------------------------------------------------------o | Precept L_3.` Dispersion` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | For k > 1, the following equation holds:` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` y_1 ` `y_2` `...` ` y_k ` ` x y_1 `x y_2` `...` x y_k ` | | ` `o------o-...-o------o` ` ` ` `o------o-...-o------o` ` | | ` ` \ ` ` ` ` ` ` ` ` / ` ` ` ` ` \ ` ` ` ` ` ` ` ` / ` ` | | ` ` `\` ` ` ` ` ` ` `/` ` ` ` ` ` `\` ` ` ` ` ` ` `/` ` ` | | ` ` ` \ ` ` ` ` ` ` / ` ` ` ` ` ` ` \ ` ` ` ` ` ` / ` ` ` | | ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` | | ` ` ` ` \ ` ` ` ` / ` ` ` ` ` ` ` ` ` \ ` ` ` ` / ` ` ` ` | | ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` | | ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` | | ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` | | ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` | | ` ` ` ` ` `x O` ` ` ` ` ` ` = ` ` ` ` ` ` `@` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` x (y_1, ..., y_k) ` ` ` = ` ` (x y_1, ..., x y_k) ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` Distill ` ` <---- | ----> ` ` Disperse` ` ` ` ` | o-----------------------------------------------------------o
To see why the Dispersion Rule holds, look at it this way: If x is true, then the presence of "x" makes no difference on either side of the equation, but if x is false, then both sides of the equation are false.
Here is a proof sketch for the Case Analysis-Synthesis Theorem (CAST):
o-----------------------------------------------------------o | Case Analysis-Synthesis Theorem.` Proof Sketch. ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `Q` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< L1. Split " " >=============o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `x` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `x` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `o---o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `Q O` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< L3. Disperse "Q" >==========o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `x` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `x` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `Q o---o Q` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< C1. Reflect "x" >===========o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `x` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `x` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `Q o---o Q[((x))/x] ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< C2. Weed "x", "(x)" >=======o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `x` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `x ` |` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` Q[o/x] o---o Q[|/x] ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< QES >=======================o
Nota Bene. QES = Quod Erat Sketchiendum.
Some of the jobs that the CAST can be usefully put to work on are proving propositional theorems and establishing equations between propositions. Once again, let us turn to the example of Leibniz's Praeclarum Theorema as a way of illustrating how. It will suffice to work within the Existential interpretation.
o-----------------------------------------------------------o | Praeclarum Theorema.` Proof by CAST.` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` b o ` o c ` ` o bc` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` | ` | ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` a o ` o d ` ` o ad` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `\ /` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` o---------o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< CAST "a" >==================o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `bc ` ` ` ` ` | | ` ` b o ` o c ` o bc` ` ` ` ` ` ` b o ` o c ` o o ` ` ` ` | | ` ` ` | ` | ` ` | ` ` ` ` ` ` ` ` ` | ` | ` ` |/` ` ` ` ` | | ` ` ` o ` o d ` o d ` ` ` ` ` ` `o--o ` o d ` o d ` ` ` ` | | ` ` ` `\ /` ` ` | ` ` ` ` ` ` ` ` ` `\ /` ` ` | ` ` ` ` ` | | ` ` ` ` o-------o ` ` ` ` ` ` ` ` ` ` o-------o ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | ` ` ` a o-----------------------------o---o a ` ` ` ` ` ` | | ` ` ` ` `\` ` ` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Domination >================o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` b o ` o c ` o bc` ` ` ` ` ` ` ` ` ` o c ` ` o ` ` ` ` | | ` ` ` | ` | ` ` | ` ` ` ` ` ` ` ` ` ` ` | ` ` `/` ` ` ` ` | | ` ` ` o ` o d ` o d ` ` ` ` ` ` `o--o ` o d ` o ` ` ` ` ` | | ` ` ` `\ /` ` ` | ` ` ` ` ` ` ` ` ` `\ /` ` ` | ` ` ` ` ` | | ` ` ` ` o-------o ` ` ` ` ` ` ` ` ` ` o-------o ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | ` ` ` a o-----------------------------o---o a ` ` ` ` ` ` | | ` ` ` ` `\` ` ` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Cancellation >==============o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` b o ` o c ` o bc` ` ` ` ` ` ` ` ` ` o c ` ` ` ` ` ` ` | | ` ` ` | ` | ` ` | ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` | | ` ` ` o ` o d ` o d ` ` ` ` ` ` ` ` ` ` o d ` ` ` ` ` ` ` | | ` ` ` `\ / ` ` `| ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` | | ` ` ` ` o-------o ` ` ` ` ` ` ` ` ` ` o-------o ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | ` ` ` a o-----------------------------o---o a ` ` ` ` ` ` | | ` ` ` ` `\` ` ` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Domination >================o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` b o ` o c ` o bc` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` | ` | ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` o ` o d ` o d ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `\ /` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` o-------o ` ` ` ` ` ` ` ` ` ` o-------o ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` | | ` ` ` a o-----------------------------o---o a ` ` ` ` ` ` | | ` ` ` ` `\` ` ` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Cancellation >==============o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` b o ` o c ` o bc` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` | ` | ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` o ` o d ` o d ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `\ /` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` o-------o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` a o-----------------------------o---o a ` ` ` ` ` ` | | ` ` ` ` `\` ` ` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< CAST "d" >==================o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` b ` c ` `bc ` ` ` ` ` ` ` | | ` ` b o ` o c ` o bc` ` ` ` ` ` o ` o o ` o o ` ` ` ` ` ` | | ` ` ` | ` | ` ` | ` ` ` ` ` ` ` | ` |/` ` |/` ` ` ` ` ` ` | | ` ` ` o ` o ` ` o ` ` ` ` ` ` ` o ` o ` ` o ` ` ` ` ` ` ` | | ` ` ` `\ /` ` ` | ` ` ` ` ` ` ` `\ /` ` ` | ` ` ` ` ` ` ` | | ` ` ` ` o-------o ` ` ` ` ` ` ` ` o-------o ` ` ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` d o-------------------------o---o d ` ` ` ` ` ` ` ` | | ` ` ` ` `\` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `a o---o---o a` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Domination >================o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` b ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` b o ` o c ` o bc` ` ` ` ` ` o ` ` o ` ` o ` ` ` ` ` ` | | ` ` ` | ` | ` ` | ` ` ` ` ` ` ` | ` `/` ` `/` ` ` ` ` ` ` | | ` ` ` o ` o ` ` o ` ` ` ` ` ` ` o ` o ` ` o ` ` ` ` ` ` ` | | ` ` ` `\ /` ` ` | ` ` ` ` ` ` ` `\ /` ` ` | ` ` ` ` ` ` ` | | ` ` ` ` o-------o ` ` ` ` ` ` ` ` o-------o ` ` ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` d o-------------------------o---o d ` ` ` ` ` ` ` ` | | ` ` ` ` `\` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `a o---o---o a` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Cancellation >==============o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` b ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` b o ` o c ` o bc` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` | ` | ` ` | ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` o ` o ` ` o ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `\ /` ` ` | ` ` ` ` ` ` ` `\` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` o-------o ` ` ` ` ` ` ` ` o-------o ` ` ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` d o-------------------------o---o d ` ` ` ` ` ` ` ` | | ` ` ` ` `\` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `a o---o---o a` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Domination >================o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` b o ` o c ` o bc` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` | ` | ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` o ` o ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `\ /` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` o-------o ` ` ` ` ` ` ` ` o-------o ` ` ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` d o-------------------------o---o d ` ` ` ` ` ` ` ` | | ` ` ` ` `\` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `a o---o---o a` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Cancellation >==============o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` b o ` o c ` o bc` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` | ` | ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` o ` o ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `\ /` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` o-------o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` d o-------------------------o---o d ` ` ` ` ` ` ` ` | | ` ` ` ` `\` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `a o---o---o a` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< CAST "b" >==================o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o ` ` ` ` o ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` | ` ` ` ` ` ` ` ` | | ` ` o ` o c ` o c ` ` ` ` ` ` o ` o c ` o c ` ` ` ` ` ` ` | | ` ` | ` | ` ` | ` ` ` ` ` ` ` | ` | ` ` | ` ` ` ` ` ` ` ` | | ` ` o ` o ` ` o ` ` ` ` ` ` ` o ` o ` ` o ` ` ` ` ` ` ` ` | | ` ` `\ /` ` ` | ` ` ` ` ` ` ` `\ /` ` ` | ` ` ` ` ` ` ` ` | | ` ` ` o-------o ` ` ` ` ` ` ` ` o-------o ` ` ` ` ` ` ` ` | | ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` b o-------------------------o---o b ` ` ` ` ` ` ` ` ` | | ` ` ` `\` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `d o---o---o d` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `a o---o---o a` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Cancellation >==============o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` | | ` ` ` ` o c ` o c ` ` ` ` ` ` ` ` o c ` o c ` ` ` ` ` ` ` | | ` ` ` ` | ` ` | ` ` ` ` ` ` ` ` ` | ` ` | ` ` ` ` ` ` ` ` | | ` ` ` ` o ` ` o ` ` ` ` ` ` ` o ` o ` ` o ` ` ` ` ` ` ` ` | | ` ` ` `/` ` ` | ` ` ` ` ` ` ` `\ /` ` ` | ` ` ` ` ` ` ` ` | | ` ` ` o-------o ` ` ` ` ` ` ` ` o-------o ` ` ` ` ` ` ` ` | | ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` b o-------------------------o---o b ` ` ` ` ` ` ` ` ` | | ` ` ` `\` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `d o---o---o d` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `a o---o---o a` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Domination >================o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` o c ` o c ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` | ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` o ` ` o ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `/` ` ` | ` ` ` ` ` ` ` `\` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` o-------o ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` b o-------------------------o---o b ` ` ` ` ` ` ` ` ` | | ` ` ` `\` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `d o---o---o d` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `a o---o---o a` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Cancellation >==============o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` o c ` o c ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` | ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` o ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `/` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` o-------o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` b o-------------------------o---o b ` ` ` ` ` ` ` ` ` | | ` ` ` `\` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `d o---o---o d` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `a o---o---o a` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< CAST "c" >==================o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o ` ` o ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` | ` ` ` ` ` ` ` ` ` | | ` ` ` o ` ` o ` ` ` ` ` ` ` ` ` o ` ` o ` ` ` ` ` ` ` ` ` | | ` ` ` | ` ` | ` ` ` ` ` ` ` ` ` | ` ` | ` ` ` ` ` ` ` ` ` | | ` ` ` o ` ` o ` ` ` ` ` ` ` ` ` o ` ` o ` ` ` ` ` ` ` ` ` | | ` ` `/` ` ` ` ` ` ` ` ` ` ` ` `/` ` ` | ` ` ` ` ` ` ` ` ` | | ` ` o-------o ` ` ` ` ` ` ` ` o-------o ` ` ` ` ` ` ` ` ` | | ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` c o-------------------------o---o c ` ` ` ` ` ` ` ` ` ` | | ` ` `\` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `\` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `b o---o---o b` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `d o---o---o d` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `a o---o---o a` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Cancellation >==============o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o ` ` o ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `/` ` ` | ` ` ` ` ` ` ` ` ` | | ` ` o-------o ` ` ` ` ` ` ` ` o-------o ` ` ` ` ` ` ` ` ` | | ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` | ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` c o-------------------------o---o c ` ` ` ` ` ` ` ` ` ` | | ` ` `\` ` ` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `\` ` ` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\` ` ` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `b o---o---o b` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `d o---o---o d` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `a o---o---o a` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Cancellation >==============o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `c o---o---o c` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `b o---o---o b` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `d o---o---o d` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `a o---o---o a` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< QED >=======================o
What we have harvested is the succulent equivalent of a disjunctive normal form (DNF) for the proposition with which we started. Remembering that a blank node is the graphical equivalent of a logical value true, we can read this brand of DNF in the following manner:
o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `c o---o---o c` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `b o---o---o b` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `d o---o---o d` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `a o---o---o a` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | Either not 'a' and thus 'true'` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` Or ` ` 'a' and thus ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `Either not 'd' and thus 'true' ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `Or ` ` 'd' and thus` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` Either not 'b' and thus 'true'` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` Or ` ` 'b' and thus ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `Either not 'c' and thus 'true' ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` `Or ` ` 'c' and thus true.` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o
This is tantamount to saying that the proposition being submitted for analysis is true in each case. Ergo we are justly entitled to title it Theorem.
Logic as sign transformation
We have been looking at various ways of transforming propositional expressions, expressed in the parallel formats of character strings and graphical structures, all the while preserving certain aspects of their "meaning" — and here I risk using that vaguest of all possible words, but only as a promissory note, hopefully to be cached out in a more meaningful species of currency as the discussion develops.
I cannot pretend to be acquainted with or to comprehend every form of intension that others might find of interest in a given form of expression, nor can I speak for every form of meaning that another might find in a given form of syntax. The best that I can hope to do is to specify what my object is in using these expressions, and to say what aspects of their syntax are meant to serve this object, lending these properties the interest I have in preserving them as I put the expressions through the paces of their transformations.
On behalf of this object I have been spinning in the form of this thread a developing example base of propositional expressions, in the data structures of graphs and strings, along with many examples of step-wise transformations on these expressions that preserve something of significant logical import, something that might be referred to as their logical equivalence class (LEC), and that we could as well call the constraint information or the denotative object of the expression in view.
To focus still more, let's return to that Splendid Theorem noted by Leibniz, and let's look more carefully at the two distinct ways of transforming its initial expression that were used to arrive at an equivalent expression, each of which, in its own way, made its tautologous character, or its theorematic nature, as evident as it could be.
Just to remind you, here is the Splendid Theorem again:
o-----------------------------------------------------------o | Praeclarum Theorema (PT)` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` b o ` o c ` ` o bc` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` | ` | ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` a o ` o d ` ` o ad` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `\ /` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` o---------o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` @ ` ` ` ` ` ` ` ` ` = ` ` ` ` ` ` ` ` ` @ ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | `((a(b))(d(c))((ad(bc)))) ` = ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o
The first way of transforming the expression that appears on the left hand side of the equation can be described as proof-theoretic in character. This appeared in Note 35.
The other way of transforming the expression that appears on the left hand side of the equation can be described as model-theoretic in character. This appeared in Note 50.
What we have here amounts to a couple of different styles of communicational conduct, or conductive communication, if you prefer, that is to say, two sequences of signs of the form e1, e2, …, en, each one beginning with a problematic expression and eventually ending with a clear expression of the appropriate logical equivalence class (LEC) to which each and every sign or expression in the sequence belongs.
Ordinarily, any orbit through a locus of signs can be taken to reflect an underlying sign-process, a case of semiosis. So what we have here are two very special cases of semiosis, and what we might just find it useful to contemplate is how to characterize them as two species of a very general class.
We are starting to delve into some fairly picayune details of a particular sign system, non-trivial enough in its own right but still rather simple compared to the types of our ultimate interest, and though I believe that this exercise will be worth the effort in prospect of understanding more complicated sign systems, I feel that I ought to say a few words about the larger reasons for going through this work.
My broader interest lies in the theory of inquiry as a special application or a special case of the theory of signs. Another name for the theory of inquiry is logic and another name for the theory of signs is semiotics. So I might as well have said that I am interested in logic as a special application or a special case of semiotics. But what sort of a special application? What sort of a special case? Well, I think of logic as formal semiotics — though, of course, I am not the first to have said such a thing — and by formal we say, in our etymological way, that logic is concerned with the form, indeed, with the animate beauty and the very life force of signs and sign actions. Yes, perhaps that is far too Latin a way of understanding logic, but it's all I've got.
Now, if you think about these things just a little more, I know that you will find them just a little suspicious, for what besides logic would I use to do this theory of signs that I would apply to this theory of inquiry that I'm also calling logic? But that is precisely one of the things signified by the word formal, for what I'd be required to use would have to be some brand of logic, that is, some sort of innate or inured skill at inquiry, but a style of logic that is casual, catch-as-catch-can, formative, incipient, inchoate, unformalized, a work in progress, partially built into our natural language and partially more primitive than our most artless language. In so far as I use it more than mention it, mention it more than describe it, and describe it more than fully formalize it, then to that extent it must be consigned to the realm of unformalized and unreflective logic, where some say "there be oracles", but I don't know.
Still, one of the aims of formalizing what acts of reasoning that we can is to draw them into an arena where we can examine them more carefully, perhaps to get better at their performance than we can unreflectively, and thus to live, to formalize again another day. Formalization is not the be-all end-all of human life, not by a long shot, but it has its uses on that behalf.
This looks like a good place to pause and take stock. The question arises: What's really going on here? There's all these signs, but what's the object?
One object worth the candle is simply to study a non-trivial example of a syntactic system, simple in design but not entirely a toy, just to see how similar systems tick.
More than that, we would like to understand how sign systems come to exist or come to be placed in relation to object systems, especially those types of object systems that give us compelling cause or independent reason to focus thought on.
What is the utility of setting up sets of strings and sets of graphs, and sorting them according to their semiotic equivalence class (SEC) based on this or that abstract notion of transformational equivalence?
Good questions.
I can only begin to tackle these questions in the present frame of work, and I can't hope to answer them in anything like a satisfactory fashion. Still, it will serve to guide the work if we keep them in mind as we go.
If you will excuse the bits of autobio-graphical anecdotage, it will help me to reconstruct the steps that I actually took in my thinking as I worked through these problems about logical graphs late in the last millennium.
By 1980 my logical graphs were becoming too large and complex to keep within the bounds of 2-dimensional manifolds of paper, and so I started to think once again, with extreme reluctance — given earlier traumatic experiences trying to use Fortran and a CDC 3600 mainframe to do my chem and physics lab work in an era when "turn-around time" was counted in days not microsecs — of representing logical graphs and logical transformations in the computer medium.
By a bit of serendipity that still amazes me, it happened that my earlier work on Peirce's use of operator variables, that led in its turn to my discovery of the cactus language, also turned out to provide workable solutions for several problems that arose in the process of trying to find efficient implementations for logical graphs and their logical transformations.
For a salient example, consider the existential graph for "p ⇔ q", to wit:
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o-----------------o ` ` ` o-----------------o ` ` ` ` ` ` ` ` | ` ` ` o-------o | ` ` ` | ` ` ` o-------o | ` ` ` ` ` ` ` ` | ` ` ` | ` ` ` | | ` ` ` | ` ` ` | ` ` ` | | ` ` ` ` ` ` ` ` | ` p ` | ` q ` | | ` ` ` | ` q ` | ` p ` | | ` ` ` ` ` ` ` ` | ` ` ` | ` ` ` | | ` ` ` | ` ` ` | ` ` ` | | ` ` ` ` ` ` ` ` | ` ` ` o-------o | ` ` ` | ` ` ` o-------o | ` ` ` ` ` ` ` ` o-----------------o ` ` ` o-----------------o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
This can be read as "not p without q and not q without p", or what's the same, "[p ⇒ q] and [q ⇒ p]", or "p ⇔ q".
Graphing the topological dual form, one obtains this rooted tree:
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` q o ` o p ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` p o ` o q ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `\`/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `(p (q))`(q (p))` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
Now it is not the sort of thing that I ever noticed until it came time to program a theorem prover for logical graphs at Peirce's alpha level, but expressions like these, that mention each variable twice simply in order to express a basic 2-variate operator, are extremely inefficient forms of representation, and their use is enough to bog down a routine logical modeler or an automatic theorem prover in a slough of despond.
However, the cactus graph expression for equivalence works much better:
` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` p o---o q ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `\`/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ((p , q)) ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `
The cactus language syntax also improves the reflective capacities of the logical calculus, in particular, it facilitates our ability to use the calculus to reflect on the process of proof, that is, the process of establishing equivalences between expressions.
Analyzing contingent truths
For all of the reasons mentioned above, and for the sake of a more compact illustration of the in and outs of a typical propositional equation reasoning system (PERS), let's now take up a much simpler example of a contingent proposition:
o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` q o ` o r ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` | ` | ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` p o ` o p ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `(p (q)) (p (r))` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o
For the sake of simplicity in discussing this example, I will revert to the existential interpretation (Ex) of logical graphs and their corresponding parse strings.
Under Ex the expression "(p (q))(p (r))" interprets as the vernacular expression "p ⇒ q ∧ p ⇒ r", so this is the reading that we'll want to keep in mind for the present.
Where brevity is required, and it occasionally is, we may invoke the propositional expression "(p (q))(p (r))" under the name "f" by making use of the following definition: "f = (p (q))(p (r))".
Since the expression "(p (q))(p (r))" involves just three variables, it may be worth the trouble to draw a venn diagram of the situation. There are in fact a couple of different ways to execute the picture.
Figure 1 indicates the points of the universe of discourse X for which the proposition f : X → B has the value 1 (= true). In this "paint by numbers" style of picture, one simply paints over the cells of a generic template for the universe X, going according to some previously adopted convention, for instance: Let the cells that get the value 0 under f remain untinted, and let the cells that get the value 1 under f be painted or shaded. In doing this, it may be good to remind ourselves that the value of the picture as a whole is not in the "paints", in other words, the 0, 1 in B, but in the pattern of regions that they indicate. NB. In this Ascii version, I use [```] for 0 and [^^^] for 1.
o-----------------------------------------------------------o | ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ | | ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ | | ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^o-------------o^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ | | ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ / ` ` ` ` ` ` ` \ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ | | ^ ^ ^ ^ ^ ^ ^ ^ ^ ^/` ` ` ` ` ` ` ` `\^ ^ ^ ^ ^ ^ ^ ^ ^ ^ | | ^ ^ ^ ^ ^ ^ ^ ^ ^ / ` ` ` ` ` ` ` ` ` \ ^ ^ ^ ^ ^ ^ ^ ^ ^ | | ^ ^ ^ ^ ^ ^ ^ ^ ^/` ` ` ` ` ` ` ` ` ` `\^ ^ ^ ^ ^ ^ ^ ^ ^ | | ^ ^ ^ ^ ^ ^ ^ ^ / ` ` ` ` ` ` ` ` ` ` ` \ ^ ^ ^ ^ ^ ^ ^ ^ | | ^ ^ ^ ^ ^ ^ ^ ^o` ` ` ` ` ` ` ` ` ` ` ` `o^ ^ ^ ^ ^ ^ ^ ^ | | ^ ^ ^ ^ ^ ^ ^ ^|` ` ` ` ` ` ` ` ` ` ` ` `|^ ^ ^ ^ ^ ^ ^ ^ | | ^ ^ ^ ^ ^ ^ ^ ^|` ` ` ` ` ` P ` ` ` ` ` `|^ ^ ^ ^ ^ ^ ^ ^ | | ^ ^ ^ ^ ^ ^ ^ ^|` ` ` ` ` ` ` ` ` ` ` ` `|^ ^ ^ ^ ^ ^ ^ ^ | | ^ ^ ^ ^ ^ ^ ^ ^|` ` ` ` ` ` ` ` ` ` ` ` `|^ ^ ^ ^ ^ ^ ^ ^ | | ^ ^ ^ ^ ^ ^ ^ ^|` ` ` ` ` ` ` ` ` ` ` ` `|^ ^ ^ ^ ^ ^ ^ ^ | | ^ ^ ^ ^ ^ ^ o--o----------o ` o----------o--o ^ ^ ^ ^ ^ ^ | | ^ ^ ^ ^ ^ ^/^ ^ \ ` ` ` ` `\`/` ` ` ` ` / ^ ^\^ ^ ^ ^ ^ ^ | | ^ ^ ^ ^ ^ / ^ ^ ^\` ` ` ` ` o ` ` ` ` `/^ ^ ^ \ ^ ^ ^ ^ ^ | | ^ ^ ^ ^ ^/^ ^ ^ ^ \ ` ` ` `/^\` ` ` ` / ^ ^ ^ ^\^ ^ ^ ^ ^ | | ^ ^ ^ ^ / ^ ^ ^ ^ ^\` ` ` / ^ \ ` ` `/^ ^ ^ ^ ^ \ ^ ^ ^ ^ | | ^ ^ ^ ^/^ ^ ^ ^ ^ ^ \ ` `/^ ^ ^\` ` / ^ ^ ^ ^ ^ ^\^ ^ ^ ^ | | ^ ^ ^ o ^ ^ ^ ^ ^ ^ ^o--o-------o--o^ ^ ^ ^ ^ ^ ^ o ^ ^ ^ | | ^ ^ ^ | ^ ^ ^ ^ ^ ^ ^ ^ | ^ ^ ^ | ^ ^ ^ ^ ^ ^ ^ ^ | ^ ^ ^ | | ^ ^ ^ | ^ ^ ^ ^ ^ ^ ^ ^ | ^ ^ ^ | ^ ^ ^ ^ ^ ^ ^ ^ | ^ ^ ^ | | ^ ^ ^ | ^ ^ ^ ^ ^ ^ ^ ^ | ^ ^ ^ | ^ ^ ^ ^ ^ ^ ^ ^ | ^ ^ ^ | | ^ ^ ^ | ^ ^ ^ Q ^ ^ ^ ^ | ^ ^ ^ | ^ ^ ^ ^ R ^ ^ ^ | ^ ^ ^ | | ^ ^ ^ | ^ ^ ^ ^ ^ ^ ^ ^ | ^ ^ ^ | ^ ^ ^ ^ ^ ^ ^ ^ | ^ ^ ^ | | ^ ^ ^ o ^ ^ ^ ^ ^ ^ ^ ^ o ^ ^ ^ o ^ ^ ^ ^ ^ ^ ^ ^ o ^ ^ ^ | | ^ ^ ^ ^\^ ^ ^ ^ ^ ^ ^ ^ ^\^ ^ ^/^ ^ ^ ^ ^ ^ ^ ^ ^/^ ^ ^ ^ | | ^ ^ ^ ^ \ ^ ^ ^ ^ ^ ^ ^ ^ \ ^ / ^ ^ ^ ^ ^ ^ ^ ^ / ^ ^ ^ ^ | | ^ ^ ^ ^ ^\^ ^ ^ ^ ^ ^ ^ ^ ^\^/^ ^ ^ ^ ^ ^ ^ ^ ^/^ ^ ^ ^ ^ | | ^ ^ ^ ^ ^ \ ^ ^ ^ ^ ^ ^ ^ ^ o ^ ^ ^ ^ ^ ^ ^ ^ / ^ ^ ^ ^ ^ | | ^ ^ ^ ^ ^ ^\^ ^ ^ ^ ^ ^ ^ ^/^\^ ^ ^ ^ ^ ^ ^ ^/^ ^ ^ ^ ^ ^ | | ^ ^ ^ ^ ^ ^ o-------------o ^ o-------------o ^ ^ ^ ^ ^ ^ | | ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ | | ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ ^ | o-----------------------------------------------------------o Figure 1. Venn Diagram for (p (q))(p (r))
There are a number of standard ways in mathematics and statistics for talking about "the subset W of the domain X that gets painted with the value z by the indicator function f : X → B". The subset W ⊆ X is called the "antecedent", the "fiber", the "inverse image", the "level set", or the "pre-image" in X of z under f, and is defined as W = f–1(z). Here, f–1 is called the "converse relation" or the "inverse relation" — it is not in general an inverse function — corresponding to the function f. Whenever possible in simple examples, I will use lower case letters for functions f : X → B, and I will try to employ capital letters for subsets of X, if possible, in such a way that F will be the fiber of 1 under f, in other words, F = f–1(1).
The easiest way to see the sense of the venn diagram is to notice that the expression "(p (q))", read as "p ⇒ q", can also be read as "not p without q". Its assertion effectively excludes any tincture of truth from the region of P that lies outside the rule of Q.
Likewise for the expression "(p (r))", read as "p ⇒ r", and also readable as "not p without r". Asserting it effectively excludes any tincture of truth from the region of P that lies outside the rule of R.
Figure 2 shows the other standard way of drawing a venn diagram for such a proposition. In this "punctured soap film" style of picture — others may elect to give it the more dignified title of a "logical quotient topology" or some such thing — one goes on from the previous picture to collapse the fiber of 0 under X down to the point of vanishing utterly from the realm of active contemplation, thereby arriving at a degenre of picture like so:
o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` o-------------o ` o-------------o ` ` ` ` ` ` | | ` ` ` ` ` `/` ` ` ` ` ` ` `\`/` ` ` ` ` ` ` `\` ` ` ` ` ` | | ` ` ` ` ` / ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` \ ` ` ` ` ` | | ` ` ` ` `/` ` ` ` ` ` ` ` `/`\` ` ` ` ` ` ` ` `\` ` ` ` ` | | ` ` ` ` / ` ` ` ` ` ` ` ` / P \ ` ` ` ` ` ` ` ` \ ` ` ` ` | | ` ` ` `/` ` ` ` ` ` ` ` `/` ` `\` ` ` ` ` ` ` ` `\` ` ` ` | | ` ` ` o ` ` ` ` ` ` ` ` o-------o ` ` ` ` ` ` ` ` o ` ` ` | | ` ` ` | ` ` ` ` ` ` ` ` | ` ` ` | ` ` ` ` ` ` ` ` | ` ` ` | | ` ` ` | ` ` ` ` ` ` ` ` | ` ` ` | ` ` ` ` ` ` ` ` | ` ` ` | | ` ` ` | ` ` ` ` Q ` ` ` | ` ` ` | ` ` ` R ` ` ` ` | ` ` ` | | ` ` ` | ` ` ` ` ` ` ` ` | ` ` ` | ` ` ` ` ` ` ` ` | ` ` ` | | ` ` ` | ` ` ` ` ` ` ` ` | ` ` ` | ` ` ` ` ` ` ` ` | ` ` ` | | ` ` ` o ` ` ` ` ` ` ` ` o ` ` ` o ` ` ` ` ` ` ` ` o ` ` ` | | ` ` ` `\` ` ` ` ` ` ` ` `\ ` ` /` ` ` ` ` ` ` ` `/` ` ` ` | | ` ` ` ` \ ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` / ` ` ` ` | | ` ` ` ` `\` ` ` ` ` ` ` ` `\`/` ` ` ` ` ` ` ` `/` ` ` ` ` | | ` ` ` ` ` \ ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` / ` ` ` ` ` | | ` ` ` ` ` `\` ` ` ` ` ` ` `/`\` ` ` ` ` ` ` `/` ` ` ` ` ` | | ` ` ` ` ` ` o-------------o ` o-------------o ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o Figure 2. Venn Diagram for (p (q r))
This diagram indicates that the region where p is true is wholly contained in the region where both q and r are true. Since only the regions that are painted true in the previous figure show up at all in this one, it is no longer necessary to distinguish the fiber of 1 under f by means of any stipple.
In sum, it is immediately obvious from the venn diagram that in drawing a representation of the propositional expression:
- (p (q))(p (r)),
in other words,
- [p ⇒ q] ∧ [p ⇒ r],
we are also looking at a picture of:
- (p (q r)),
in other words,
- p ⇒ [q ∧ r].
The variety of distributive law just observed can be expressed in the form of this propositional equation:
o-----------------------------------------------------------o | Equation E_1` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` q r ` ` ` ` ` ` | | ` ` ` ` `q o` `o r` ` ` ` ` ` ` ` ` ` ` ` `o` ` ` ` ` ` ` | | ` ` ` ` ` `|` `|` ` ` ` ` ` ` ` ` ` ` ` ` `|` ` ` ` ` ` ` | | ` ` ` ` `p o` `o p` ` ` ` ` ` ` ` ` ` ` `p o` ` ` ` ` ` ` | | ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` `|` ` ` ` ` ` ` | | ` ` ` ` ` ` `@` ` ` ` ` ` ` = ` ` ` ` ` ` `@` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` (p (q)) (p (r)) ` ` ` = ` ` ` ` `(p `(q r)) ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` [p=>q] & [p=>r] ` ` ` = ` ` ` ` `[p=>[q&r]] ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o
There are three distinct ways that I can think of right off as to how we might go about formally proving or systematically checking the proposed equivalence, the evidence of whose truth we already have before us clearly enough, and in a visually intuitive form, from the venn diagrams that we examined above.
While we go through each of these ways let us keep one eye out for the character and the conduct of each type of proceeding as a semiotic process, that is, as an orbit, in this case discrete, through a locus of signs, in this case propositional expressions, and as it happens in this case, a sequence of transformations that perseveres in the denotative objective of each expression, that is, in the abstract proposition that it expresses, while it preserves the informed constraint on the universe of discourse that gives us one viable candidate for the informational content of each expression in the interpretive chain of sign metamorphoses.
A sign relation L is a subset of a cartesian product O × S × I, where O, S, I are sets known as the object domain, the sign domain, and the interpretant sign domain, respectively. One writes L ⊆ O × S × I, where the symbol "⊆" denotes the subset relation contained as a subset of. Accordingly, a sign relation L consists of ordered 3-tuples of the form <o, s, i>, where o, s, i are elements of the domains O, S, I, respectively.
The semiotic domain or the syntactic domain of a sign relation L ⊆ O × S × I is just the set-theoretic union S ∪ I of its sign domain S and its interpretant domain I.
It is not uncommon, especially in formal examples, for the sign domain and the interpretant domain to be equal as sets, in short, to have S = I.
Elsewhere I have discussed examples of sign relations that consist of a finite set of triples of the form <o, s, i>, where o, s, i are the the object, the sign, and the interpretant sign, respectively, of what is called the sign triple or the elementary sign relation <o, s, i>.
We will be taking a bit of a jump up from the finite case now, since most of the examples of sign relations that we treat in logic will have S and I be infinite sets, and usually !O! will be infinite, too, in the long run, at least, although we will frequently work up to the infinite object domains by way of gradual stages and various series of finite approximations.
With that preamble behind us, let us turn to consider the case of semiosis, or sign transformation process, that is generated by our first proof of the propositional equation E1.
o-----------------------------------------------------------o | Equation E_1. `Proof 1. ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `q o` `o r` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `|` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `p o` `o p` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` (p (q)) (p (r)) ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Double Negation >===========o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `q o` `o r` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `|` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `p o` `o p` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` `(( (p (q)) (p (r)) ))` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Collection >================o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `q o` `o r` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `|` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `o` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `p o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` `(p ( ((q)) ((r)) ))` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Double Negation >===========o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` q r ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `p o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `(p (q r))` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< QED >=======================o
For some reason I always think of this as the way that our DNA would prove it.
We are in the process of examining various proofs of the propositional equation "(p (q))(p (r)) = (p (q r))", and viewing them in the light of their character as semiotic processes, in essence, as sign-theoretic transformations.
Here is a reminder of the propositional equation in question, formulating what is tantamount to a form of distributive law:
o-----------------------------------------------------------o | Equation E_1` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` q r ` ` ` ` ` ` | | ` ` ` ` `q o` `o r` ` ` ` ` ` ` ` ` ` ` ` `o` ` ` ` ` ` ` | | ` ` ` ` ` `|` `|` ` ` ` ` ` ` ` ` ` ` ` ` `|` ` ` ` ` ` ` | | ` ` ` ` `p o` `o p` ` ` ` ` ` ` ` ` ` ` `p o` ` ` ` ` ` ` | | ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` `|` ` ` ` ` ` ` | | ` ` ` ` ` ` `@` ` ` ` ` ` ` = ` ` ` ` ` ` `@` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` (p (q)) (p (r)) ` ` ` = ` ` ` ` `(p `(q r)) ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` [p=>q] & [p=>r] ` ` ` = ` ` ` ` `[p=>[q&r]] ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o
The second way of establishing the truth of this equation is one that I see, rather loosely, as model-theoretic, for no better reason than the sense of its ending with a pattern of expression, a variant of the disjunctive normal form (DNF), that is commonly recognized to be the form that one extracts from a truth table by pulling out the rows of the table that evaluate to true and constructing the disjunctive expression that sums up the senses of the corresponding interpretations.
In order to apply this model-theoretic method to an equation between a couple of contingent expressions, one must transform each expression into its associated DNF and then compare those to see if they are equal. In the current setting, these DNF's may indeed end up as identical expressions, but it is possible, also, for them to turn out slightly off-kilter from each other, and so the ultimate comparison may not be absolutely immediate. The explanation of this is that, for the sake of computational efficiency, it is useful to tailor the DNF that gets developed as the output of a DNF algorithm to the particular form of the propositional expression that is given as input.
o-----------------------------------------------------------o | Equation E_1. `Proof 2, 1st Half. ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` q o ` o r ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` | ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` p o ` o p ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< CAST "p" >==================o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` q ` r ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` q o ` o r ` o o ` o o ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` | ` | ` ` `\| ` |/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` o ` o ` ` ` o ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\ /` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` p o-----------o---o p ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` \ ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\`/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Domination >================o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` q o ` o r ` o ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` | ` | ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` o ` o ` ` ` o ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\ /` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` p o-----------o---o p ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` \ ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\`/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Cancellation >==============o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` q o ` o r ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` | ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` o ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` p o-----------o---o p ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` \ ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\`/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< CAST "q" >==================o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` o ` o r ` ` o ` o r ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` | ` | ` ` ` | ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` o ` o ` ` ` o ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `\ /` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` q o-----------o---o q ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` \ ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\`/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` p o-------o---o p ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Cancellation >==============o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` o r ` ` ` ` o r ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` | ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` o ` ` ` o ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `/` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` q o-----------o---o q ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` \ ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\`/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` p o-------o---o p ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Domination >================o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` o r ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` o ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `/` ` ` ` `\` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` q o-----------o---o q ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` \ ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\`/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` p o-------o---o p ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< CAST "r" >==================o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` o ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` | ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` o ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` `/` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` r o-----------o---o r ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` `\` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` \ ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` \ ` / ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\`/` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` q o-------o---o q ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` p o-------o---o p ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Cancellation >==============o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` r o-------o---o r ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` \ ` / ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\ /` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` q o-------o---o q ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` p o-------o---o p ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< DNF >=======================o
What we have harvested is the succulent equivalent of a disjunctive normal form (DNF) for the proposition with which we started. Remembering that a blank node is the graphical equivalent of a logical value true, we can read this brand of DNF in the following manner:
o-----------------------------------------------------------o | DNF of "(p (q))(p (r))" ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` r o-------o---o r ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` \ ` / ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\ /` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` q o-------o---o q ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` p o-------o---o p ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | Either not 'p' and thus 'true'` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` Or ` ` 'p' and thus ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `Either not 'q' and thus 'false'` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `Or ` ` 'q' and thus` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` Either not 'r' and thus 'false' ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` Or ` ` 'r' and thus 'true'. ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o
We are still in the middle of contemplating a particular example of a propositional equation, namely, "(p (q))(p (r)) = (p (q r))", and we are still considering the second of three formal methods that I intend to illustrate in the process of thrice-over establishing it.
o-----------------------------------------------------------o | Equation E_1` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` q r ` ` ` ` ` ` | | ` ` ` ` `q o` `o r` ` ` ` ` ` ` ` ` ` ` ` `o` ` ` ` ` ` ` | | ` ` ` ` ` `|` `|` ` ` ` ` ` ` ` ` ` ` ` ` `|` ` ` ` ` ` ` | | ` ` ` ` `p o` `o p` ` ` ` ` ` ` ` ` ` ` `p o` ` ` ` ` ` ` | | ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` `|` ` ` ` ` ` ` | | ` ` ` ` ` ` `@` ` ` ` ` ` ` = ` ` ` ` ` ` `@` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` (p (q)) (p (r)) ` ` ` = ` ` ` ` `(p `(q r)) ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` [p=>q] & [p=>r] ` ` ` = ` ` ` ` `[p=>[q&r]] ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o
I know that it must seem tedious, but I probably ought to go ahead and carry out the second half of this analogically model-theoretic strategy, just so that we will have the security of this concrete and shared experience on which to fall back at every later point in what may quickly become a rather abstruse discussion. Here then is the rest of the necessary chain of equations:
o-----------------------------------------------------------o | Equation E_1. `Proof 2, 2nd Half. ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `q r` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` p o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< CAST "p" >==================o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `q r` ` ` q r ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` o ` ` o o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` | ` ` `\| ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` o ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` | ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` p o-------o---o p ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Domination >================o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `q r` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` o ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` | ` ` `\` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` o ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` | ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` p o-------o---o p ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Cancellation >==============o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `q r` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` p o-------o---o p ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< CAST "q" >==================o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` o r ` ` o r ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` | ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` o ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` | ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` q o-------o---o q ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` p o-------o---o p ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Domination >================o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` o r ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` | ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` o ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` | ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` q o-------o---o q ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` p o-------o---o p ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Cancellation >==============o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` o r ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` o ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` | ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` q o-------o---o q ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` p o-------o---o p ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< CAST "r" >==================o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` o ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` | ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` o ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` | ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` r o-------o---o r ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` \ ` / ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\ /` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` q o-------o---o q ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` p o-------o---o p ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< Cancellation >==============o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` r o-------o---o r ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` \ ` / ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\ /` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` q o-------o---o q ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` p o-------o---o p ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o=============================< DNF >=======================o
This is not only a logically equivalent DNF, but exactly the same DNF expression that we obtained before, so we have established the given equation "(p (q))(p (r)) = (p (q r))".
Incidentally, one may wish to note that this DNF expression quickly folds into the following form:
o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` pqr o-------o---o p ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` (p q r, (p))` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o
This can be read to say "either p q r, or not p", which gives us yet another expression equivalent to the sentences "(p (q))(p (r))" and "(p (q r))".
Still another way of writing the same thing would be like so:
o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` p o-------o pqr ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ((p , p q r)) ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o
In other words, "p is equivalent to p and q and r".
Let's pause to refresh ourselves with a few morsels of lemmas bread. One lemma that I can see just far enough ahead to see our imminent need of is the principle that I canonize as the Emptiness Rule. It says that a bare lobe expression like "(… , …)", with any number of places for arguments but nothing but blanks as filler, is logically tantamount to the proto-typical expression of its type, namely, the constant expression "()" that ExG interprets as denoting the logical value false. To depict the rule in graphical form, we have this continuing sequence of equations:
o-----------------------------------------------------------o | Emptiness Rule` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` o ` ` ` ` o---o ` ` ` o-o-o ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` | ` ` ` ` `\ /` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` @ ` ` = ` ` @ ` ` = ` ` @ ` ` = ` `...` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` `( )` ` = ` ( , ) ` = `( , , )` = ` `...` ` ` ` ` ` | o-----------------------------------------------------------o
Yet another rule that we'll need is the following:
o-----------------------------------------------------------o | Indistinctness Rule ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` a ` a ` ` ` a a a ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` o ` ` ` ` o---o ` ` ` o-o-o ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` | ` ` ` ` `\ /` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` @ ` ` = ` ` @ ` ` = ` ` @ ` ` = ` `...` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` `( )` ` = ` (a,a) ` = `(a,a,a)` = ` `...` ` ` ` ` ` | o-----------------------------------------------------------o
This one is easy enough to derive from rules that are already known, but I call it the Indistinctness Rule just on behalf of ready reference and easy employment.
Finally, let me introduce a rule-of-thumb that is a bit more suited to routine computation, and that will serve to replace the indistinctness rule in many of the cases where we actually have to call on it. This is actually just a special case of the evaluation rule listed above:
o-----------------------------------------------------------o | Evaluation Rule ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` | `x_2` `... x_k` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` o---o-...-o---o ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` \ ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` x_2 ... x_k ` ` ` ` | | ` ` ` ` ` ` `@` ` ` ` ` ` ` = ` ` ` ` ` ` `@` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ((), x_2, ..., x_k) ` ` = ` ` ` ` x_2 ... x_k ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` `Setup` ` ` <---- | ----> ` ` `Spike` ` ` ` ` ` | o-----------------------------------------------------------o
To continue with the beating of this still kicking horse that is known as the propositional equation "(p (q))(p (r)) = (p (q r))", let's now take up the third way that I mentioned for examining propositional equations, but I believe that you will be relieved to know that it is literally a third way only at the very outset, almost immediately breaking up according to whether one proceeds by way of the more routine model-theoretic path or else by way of the more strategic proof-theoretic path. I think that I'll take the low road today.
Let's convert the equation between propositions:
- (p (q))(p (r)) = (p (q r)),
into the corresponding equational proposition:
- (( (p (q))(p (r)) , (p (q r)) )).
If you're like me, you'd rather see it in pictures:
o-----------------------------------------------------------o | Equation E_1, Written as an Equation in Cactus Language ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `q o` `o r` `q o r` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `|` `|` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `p o` `o p` `p o` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `o---------o` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` \ ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` `\` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` \ ` / ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` `\ /` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` o ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` @ ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` `(( `(p (q))` (p (r)) ` , ` (p` (q r))` ))` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` [[p=>q] & [p=>r]] `<=>` [p=>[q&r]]` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o
We may now interrogate the alleged equation for the third time, working by way of the case analysis-synthesis theorem (CAST).
o-----------------------------------------------------------o | Equation E_1. `Proof 3. ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o-----------------------------------------------------------o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` q o ` o r ` q o r ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` | ` | ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` p o ` o p ` p o ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\ /` ` ` ` | ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` o---------o ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `\ ` ` ` /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \` ` `/ ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `\ ` /` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o==================================< CAST "p" >=============o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `q` `r` ` q r ` `q` `r` ` qr` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `o` `o` ` `o` ` `o o o o` `o o` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `|` `|` ` `|` ` `|/ `|/ ` `|/ ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `o` `o` ` `o` ` `o` `o` ` `o` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` \ / ` ` `|` ` ` \ / ` ` `|` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `o-------o` ` ` `o-------o` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` ` / ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` `/` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` \ / ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `o` ` ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `p o---------------o---o p` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` ` ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o==================================< Domination >===========o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `q` `r` ` q r ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `o` `o` ` `o` ` ` `o` `o` ` `o` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `|` `|` ` `|` ` ` / ` / ` ` / ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `o` `o` ` `o` ` `o` `o` ` `o` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` \ / ` ` `|` ` ` \ / ` ` `|` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `o-------o` ` ` `o-------o` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` ` / ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` `/` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` \ / ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `o` ` ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `p o---------------o---o p` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` ` ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o==================================< Cancellation >=========o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `q` `r` ` q r ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `o` `o` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `|` `|` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `o` `o` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` \ / ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `o-------o` ` ` `o-------o` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` ` / ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` `/` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` \ / ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `o` ` ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `p o---------------o---o p` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` ` ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o==================================< Emptiness >============o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `q` `r` ` q r ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `o` `o` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `|` `|` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `o` `o` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` \ / ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `o-------o` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` ` / ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` `/` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` \ / ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `o` ` ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `p o---------------o---o p` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` ` ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o==================================< Cancellation >=========o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `q` `r` ` q r ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `o` `o` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `|` `|` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `o` `o` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` \ / ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `o-------o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `p o---------------o---o p` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` ` ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o==================================< CAST "q" >=============o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `o` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `r` ` `r` ` `|` `r` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` `o` `o` ` `o` ` `o` `o` ` `o r` ` ` ` ` ` ` ` ` ` ` ` | | ` ` `|` `|` ` `|` ` `|` `|` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` `o` `o` ` `o` ` `o` `o` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` \ / ` ` `|` ` ` \ / ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `o-------o` ` ` `o-------o` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` \ ` ` / ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\` `/` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` \ / ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `o` ` ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `q o---------------o---o q` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` ` ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` \ ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `p o-------o---o p` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o==================================< Domination >===========o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `o` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `r` ` `r` ` `|` `r` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` `o` `o` ` `o` ` `o` `o` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` `|` `|` ` `|` ` `|` `|` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` `o` `o` ` `o` ` `o` `o` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` \ / ` ` `|` ` ` \ / ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `o-------o` ` ` `o-------o` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` \ ` ` / ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\` `/` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` \ / ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `o` ` ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `q o---------------o---o q` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` ` ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` \ ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `p o-------o---o p` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o==================================< Cancellation >=========o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `r` ` `r` ` ` ` `r` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `o` ` `o` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `|` ` `|` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `o` ` `o` ` `o` `o` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` / ` ` `|` ` ` \ / ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `o-------o` ` ` `o-------o` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` \ ` ` / ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\` `/` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` \ / ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `o` ` ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `q o---------------o---o q` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` ` ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` \ ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `p o-------o---o p` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o==================================< Domination >===========o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `r` ` `r` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `o` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `|` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `o` ` `o` ` `o` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` / ` ` `|` ` ` \ ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `o-------o` ` ` `o-------o` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` \ ` ` / ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\` `/` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` \ / ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `o` ` ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `q o---------------o---o q` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` ` ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` \ ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `p o-------o---o p` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o==================================< Spike >================o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `r` ` `r` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `o` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `|` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `o` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` / ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `o-------o` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` \ ` ` / ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\` `/` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` \ / ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `o` ` ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `q o---------------o---o q` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` ` ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` \ ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `p o-------o---o p` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o==================================< Cancellation >=========o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `r` ` `r` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `o` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `|` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `o` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` / ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `o-------o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `q o---------------o---o q` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` ` ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` \ ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `p o-------o---o p` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o==================================< CAST "r" >=============o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `o` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `|` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` `o` ` `o` ` ` ` `o` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` `|` ` `|` ` ` ` `|` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` `o` ` `o` ` ` ` `o` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` / ` ` `|` ` ` ` / ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` `o-------o` ` ` `o-------o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` \ ` ` / ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` `\` `/` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` \ / ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `o` ` ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` `r o---------------o---o r` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` \ ` ` ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` \ ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `q o-------o---o q` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `p o-------o---o p` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o==================================< Cancellation >=========o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `o` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` / ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` `o-------o` ` ` `o-------o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` \ ` ` / ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` `\` `/` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` \ / ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `o` ` ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` `r o---------------o---o r` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` \ ` ` ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` \ ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `q o-------o---o q` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `p o-------o---o p` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o==================================< Emptiness & Spike >====o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `o` ` ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `o` ` ` ` ` ` ` `o` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` `|` ` ` ` ` ` ` `|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` `r o---------------o---o r` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` \ ` ` ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `\` ` ` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` \ ` ` ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` `\` ` ` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `q o-------o---o q` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `p o-------o---o p` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o==================================< Cancellation >=========o | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` `r o-------o---o r` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` `q o-------o---o q` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` `p o-------o---o p` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` \ ` ` / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` `\` `/` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` \ / ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` `@` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | | ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` | o==================================< QED >==================o
And that, of course, is the DNF of a theorem.
Proof as semiosis
We have been looking at several different ways of proving one particular example of a propositional equation, and along the way we have been exemplifying the species of sign transforming process that is commonly known as a proof, more specifically, an equational proof of the propositional equation in question.
Let us now draw out these semiotic features of the business of proof and place them in relief.
Our syntactic domain !S! contains an infinite number of signs or expressions, any of which we may choose to view in either a string form or a graphic form, glossing over for now the many details of their particular correspondence.
Here are some of the expressions that we find salient enough to single out and confer an epithetic nickname on:
- e0 = "()"
- e1 = " "
- e2 = "(p (q))(p (r))"
- e3 = "(p (q r))"
- e4 = "(p q r, (p))"
- e5 = "(( (p (q))(p (r)) , (p (q r)) ))"
Under ExG we have the following interpretations:
- e0 expresses the logical constant "false"
- e1 expresses the logical constant "true"
- e2 says "not p without q, and not p without r"
- e3 says "not p without q and r"
- e4 says "p and q and r, or else not p"
- e5 says that e_2 and e_3 say the same thing
We took up the Equation E1 that reads as follows:
- (p (q))(p (r)) = (p (q r)).
Each of our proofs is a finite sequence of signs, and thus, for a finite integer n, takes the form:
- s1, s2, s3, …, sn.
Proof 1 proceeded by the straightforward approach, starting with e2 as s1 and ending with e3 as sn. That is, it commenced from the sign "(p (q))(p (r))" and ended up at the sign "(p (q r))" by legal moves.
Proof 2 lit on by burning the candle at both ends, changing e2 into a normal form that reduced to e4, changing e3 into a normal form that reduced to e_4, in this way tethering e2 and e3 to a common point. We got that (p (q))(p (r)) is equal to (p q r, (p)), then we got that (p (q r)) is equal to (p q r, (p)), so we got that (p (q))(p (r)) is equal to (p (q r)).
Proof 3 took the path of reflection, expressing the meta-equation between e2 and e3 via the object equation e5, then taking e5 as s1 and exchanging it by dint of value preserving steps for e1 as sn. Thus we went from "(( (p (q))(p (r)) , (p (q r)) ))" to the blank expression that Ex recognizes as true.
I need to say something about the concept of reflection that I've been using according to my informal intuitions about it at numerous points in this discussion. This is, of course, distinct from the use of the word "reflection" to license an application of the double negation theorem.
Generally speaking, I think of reflection in connection with any sort of system that has any sort of order relation defined on it, and I think of the system in question as manifesting "reflection" in proportion to the extent that statements about that order can be found to be reflected in elements of that order. Accordingly, it must be possible to interpret certain elements of the ordered system as making statements about the order in which they reside.
More on that later, as many delightful distractions take their precedence in the order of the day.
Still speaking generally, the hermeneutic hedge about reflection that runs, "it must be possible to interpret certain elements of the ordered system as making statements about the order in which they reside", should serve to remind us of the hidden catch that the forms of interpretation that manifest reflection of an order on itself may not be obvious at first sight, but will in general have to be sought out by abductive reason, "by hook or by crook".
But speaking more specifically about orders of systems so simple as alpha graphs, propositional calculus, zeroth order logic, and their ilk, we find at least some modes of reflection that strike the mind's eye right off as being manifestly natural and obvious.
For instance, propositions over a finitary universe of discourse, of the order that we see illustrated in euler-venn diagrams, are ordered by the relation of implication, making "⇒" analogous to the generic order relation "less than or equal to", notated "<".
But those statements about the implicational order relation that take the form "p ⇒ q" are themselves statements that have their place within that very same implicational order relation. Hence, propositional logic has a moderate degree of reflective capacity.
Viewing relations of distinction and equivalence as special cases of order relations, a measure of reflection with respect to these types of relation is a way of turning some of the statements that we might make about difference or equality of elements in a given ordered system into elements residing within that very same order.
Ordinary propositional calculus, in whatever brand of syntax is adequate to its tasks, will enjoy this type of reflection, since statements about equivalence or inequivalence, taking the shapes "p ⇔ q" or "p <≠> q", respectively, will themselves be statements that fall within the purview of its propositional order.
In the light of this reflection on distinction and equivalence, however, we have already observed that some styles of syntactic calculi are more direct, efficient, flexible, and succinct than others in the expression of logical differences and equations, and it's a curious fact that both Peirce's alpha graphs and Spencer-Brown's primary algebra, in which the roles of distinctions and equational inferences are so paramount, don't afford us better expressions of logical difference and logical equality.
This is yet another one of those deficiencies that the cactus language, which arose after all from the application of reflective operations to forms of expression, namely, the use of operator variables to discover additional layers of lawfulness in formal expressions, seems unusually well suited to supply.
References
- Peirce, C.S. (1902), [Application to the Carnegie Institution] (L 75), pp. 13–73 in The New Elements of Mathematics by Charles S. Peirce, Volume 4, Mathematical Philosophy, Carolyn Eisele (ed.), Mouton, The Hague, 1976. Eprint.
- Peirce, C.S. (c. 1903), "Logical Tracts, No. 2", in Collected Papers, CP 4.418–509. Eprint.
See also
Related essays and projects
- Information = Comprehension × Extension
- Inquiry Driven Systems
- Introduction to Inquiry Driven Systems
- Peirce’s Logic Of Information
- Propositional Equation Reasoning Systems
- Semiotic Theory Of Information
Related concepts and topics
Template:Col-breakTemplate:Col-breakTemplate:Col-endDocument history
Futures Of Logical Graphs (2005)
- http://stderr.org/pipermail/inquiry/2005-October/thread.html#3104
- http://stderr.org/pipermail/inquiry/2005-November/thread.html#3165
- http://stderr.org/pipermail/inquiry/2005-October/003104.html
- http://stderr.org/pipermail/inquiry/2005-October/003105.html
- http://stderr.org/pipermail/inquiry/2005-October/003106.html
- http://stderr.org/pipermail/inquiry/2005-October/003107.html
- http://stderr.org/pipermail/inquiry/2005-October/003113.html
- http://stderr.org/pipermail/inquiry/2005-October/003114.html
- http://stderr.org/pipermail/inquiry/2005-October/003115.html
- http://stderr.org/pipermail/inquiry/2005-October/003118.html
- http://stderr.org/pipermail/inquiry/2005-October/003119.html
- http://stderr.org/pipermail/inquiry/2005-October/003120.html
- http://stderr.org/pipermail/inquiry/2005-October/003121.html
- http://stderr.org/pipermail/inquiry/2005-October/003131.html
- http://stderr.org/pipermail/inquiry/2005-October/003132.html
- http://stderr.org/pipermail/inquiry/2005-October/003133.html
- http://stderr.org/pipermail/inquiry/2005-October/003134.html
- http://stderr.org/pipermail/inquiry/2005-October/003141.html
- http://stderr.org/pipermail/inquiry/2005-October/003144.html
- http://stderr.org/pipermail/inquiry/2005-October/003149.html
- http://stderr.org/pipermail/inquiry/2005-October/003153.html
- http://stderr.org/pipermail/inquiry/2005-October/003157.html
- http://stderr.org/pipermail/inquiry/2005-October/003160.html
- http://stderr.org/pipermail/inquiry/2005-November/003165.html
- http://stderr.org/pipermail/inquiry/2005-November/003170.html
- http://stderr.org/pipermail/inquiry/2005-November/003171.html
- http://stderr.org/pipermail/inquiry/2005-November/003181.html
- http://stderr.org/pipermail/inquiry/2005-November/003197.html
- http://stderr.org/pipermail/inquiry/2005-November/003199.html
- http://stderr.org/pipermail/inquiry/2005-November/003200.html
- http://stderr.org/pipermail/inquiry/2005-November/003203.html
- http://stderr.org/pipermail/inquiry/2005-November/003204.html
- http://stderr.org/pipermail/inquiry/2005-November/003205.html
- http://stderr.org/pipermail/inquiry/2005-November/003206.html
- http://stderr.org/pipermail/inquiry/2005-November/003210.html
- http://stderr.org/pipermail/inquiry/2005-November/003212.html
- http://stderr.org/pipermail/inquiry/2005-November/003214.html
- http://stderr.org/pipermail/inquiry/2005-November/003217.html
- http://stderr.org/pipermail/inquiry/2005-November/003220.html
- http://stderr.org/pipermail/inquiry/2005-November/003221.html
- http://stderr.org/pipermail/inquiry/2005-November/003224.html
- http://stderr.org/pipermail/inquiry/2005-November/003226.html
- http://stderr.org/pipermail/inquiry/2005-November/003227.html
- http://stderr.org/pipermail/inquiry/2005-November/003228.html
- http://stderr.org/pipermail/inquiry/2005-November/003229.html
- http://stderr.org/pipermail/inquiry/2005-November/003230.html
- http://stderr.org/pipermail/inquiry/2005-November/003231.html
- http://stderr.org/pipermail/inquiry/2005-November/003233.html
- http://stderr.org/pipermail/inquiry/2005-November/003235.html
- http://stderr.org/pipermail/inquiry/2005-November/003236.html
- http://stderr.org/pipermail/inquiry/2005-November/003237.html
- http://stderr.org/pipermail/inquiry/2005-November/003238.html
- http://stderr.org/pipermail/inquiry/2005-November/003240.html
- http://stderr.org/pipermail/inquiry/2005-November/003241.html
- http://stderr.org/pipermail/inquiry/2005-November/003242.html
- http://stderr.org/pipermail/inquiry/2005-November/003244.html
- http://stderr.org/pipermail/inquiry/2005-November/003245.html
- http://stderr.org/pipermail/inquiry/2005-November/003246.html
- http://stderr.org/pipermail/inquiry/2005-November/003247.html
- http://stderr.org/pipermail/inquiry/2005-November/003248.html
- http://stderr.org/pipermail/inquiry/2005-November/003249.html
- http://stderr.org/pipermail/inquiry/2005-November/003250.html
- http://stderr.org/pipermail/inquiry/2005-November/003251.html
- http://stderr.org/pipermail/inquiry/2005-November/003256.html
- http://stderr.org/pipermail/inquiry/2005-November/003257.html
- http://stderr.org/pipermail/inquiry/2005-November/003258.html
Futures Of Logical Graphs : Discussion (2005)
- http://stderr.org/pipermail/inquiry/2005-October/thread.html#3135
- http://stderr.org/pipermail/inquiry/2005-November/thread.html#3167
- http://stderr.org/pipermail/inquiry/2005-October/003135.html
- http://stderr.org/pipermail/inquiry/2005-October/003136.html
- http://stderr.org/pipermail/inquiry/2005-October/003137.html
- http://stderr.org/pipermail/inquiry/2005-October/003138.html
- http://stderr.org/pipermail/inquiry/2005-October/003139.html
- http://stderr.org/pipermail/inquiry/2005-October/003140.html
- http://stderr.org/pipermail/inquiry/2005-October/003143.html
- http://stderr.org/pipermail/inquiry/2005-October/003145.html
- http://stderr.org/pipermail/inquiry/2005-October/003148.html
- http://stderr.org/pipermail/inquiry/2005-October/003154.html
- http://stderr.org/pipermail/inquiry/2005-October/003155.html
- http://stderr.org/pipermail/inquiry/2005-October/003159.html
- http://stderr.org/pipermail/inquiry/2005-October/003161.html
- http://stderr.org/pipermail/inquiry/2005-October/003162.html
- http://stderr.org/pipermail/inquiry/2005-October/003163.html
- http://stderr.org/pipermail/inquiry/2005-October/003164.html
- http://stderr.org/pipermail/inquiry/2005-November/003167.html
- http://stderr.org/pipermail/inquiry/2005-November/003169.html
- http://stderr.org/pipermail/inquiry/2005-November/003173.html
- http://stderr.org/pipermail/inquiry/2005-November/003174.html
- http://stderr.org/pipermail/inquiry/2005-November/003175.html
- http://stderr.org/pipermail/inquiry/2005-November/003176.html
- http://stderr.org/pipermail/inquiry/2005-November/003177.html
- http://stderr.org/pipermail/inquiry/2005-November/003178.html
- http://stderr.org/pipermail/inquiry/2005-November/003179.html
- http://stderr.org/pipermail/inquiry/2005-November/003180.html
- http://stderr.org/pipermail/inquiry/2005-November/003182.html
- http://stderr.org/pipermail/inquiry/2005-November/003184.html
- http://stderr.org/pipermail/inquiry/2005-November/003185.html
- http://stderr.org/pipermail/inquiry/2005-November/003188.html
- http://stderr.org/pipermail/inquiry/2005-November/003194.html
- http://stderr.org/pipermail/inquiry/2005-November/003195.html
- http://stderr.org/pipermail/inquiry/2005-November/003196.html
- http://stderr.org/pipermail/inquiry/2005-November/003202.html
- http://stderr.org/pipermail/inquiry/2005-November/003209.html
- http://stderr.org/pipermail/inquiry/2005-November/003211.html
- http://stderr.org/pipermail/inquiry/2005-November/003213.html
- http://stderr.org/pipermail/inquiry/2005-November/003215.html
- http://stderr.org/pipermail/inquiry/2005-November/003216.html
- http://stderr.org/pipermail/inquiry/2005-November/003218.html
- http://stderr.org/pipermail/inquiry/2005-November/003219.html
<sharethis />