Difference between revisions of "Directory:Jon Awbrey/Papers/Cactus Language"
Jon Awbrey (talk | contribs) (→Note 8: markup) |
Jon Awbrey (talk | contribs) (→Note 8: ASCII → JPEG) |
||
| Line 5,850: | Line 5,850: | ||
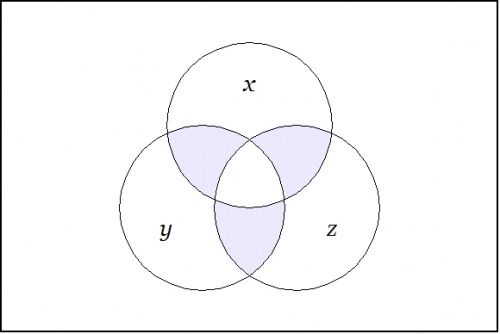
For example, consider the proposition <math>f\!</math> of concrete type <math>f : X \times Y \times Z \to \mathbb{B}</math> and abstract type <math>f : \mathbb{B}^3 \to \mathbb{B}</math> that is written <math>\texttt{(} x, y, z \texttt{)}</math> in cactus syntax. Taken as an assertion in what Peirce called the ''existential interpretation'', <math>\texttt{(} x, y, z \texttt{)}</math> says that just one of <math>x, y, z\!</math> is false. It is useful to consider this assertion in relation to the conjunction <math>xyz\!</math> of the features that are engaged as its arguments. A venn diagram of <math>\texttt{(} x, y, z \texttt{)}</math> looks like this: | For example, consider the proposition <math>f\!</math> of concrete type <math>f : X \times Y \times Z \to \mathbb{B}</math> and abstract type <math>f : \mathbb{B}^3 \to \mathbb{B}</math> that is written <math>\texttt{(} x, y, z \texttt{)}</math> in cactus syntax. Taken as an assertion in what Peirce called the ''existential interpretation'', <math>\texttt{(} x, y, z \texttt{)}</math> says that just one of <math>x, y, z\!</math> is false. It is useful to consider this assertion in relation to the conjunction <math>xyz\!</math> of the features that are engaged as its arguments. A venn diagram of <math>\texttt{(} x, y, z \texttt{)}</math> looks like this: | ||
| − | {| align="center" cellpadding=" | + | {| align="center" cellpadding="10" |
| − | + | | [[Image:Minimal Negation Operator (x,y,z).jpg|500px]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
Revision as of 20:02, 1 June 2009
The Cactus Patch
|
Thus, what looks to us like a sphere of scientific knowledge more accurately should be represented as the inside of a highly irregular and spiky object, like a pincushion or porcupine, with very sharp extensions in certain directions, and virtually no knowledge in immediately adjacent areas. If our intellectual gaze could shift slightly, it would alter each quill's direction, and suddenly our entire reality would change. |
| — Herbert J. Bernstein, "Idols of Modern Science", [HJB, 38] |
In this and the four subsections that follow, I describe a calculus for representing propositions as sentences, in other words, as syntactically defined sequences of signs, and for manipulating these sentences chiefly in the light of their semantically defined contents, in other words, with respect to their logical values as propositions. In their computational representation, the expressions of this calculus parse into a class of tree-like data structures called painted cacti. This is a family of graph-theoretic data structures that can be observed to have especially nice properties, turning out to be not only useful from a computational standpoint but also quite interesting from a theoretical point of view. The rest of this subsection serves to motivate the development of this calculus and treats a number of general issues that surround the topic.
In order to facilitate the use of propositions as indicator functions it helps to acquire a flexible notation for referring to propositions in that light, for interpreting sentences in a corresponding role, and for negotiating the requirements of mutual sense between the two domains. If none of the formalisms that are readily available or in common use are able to meet all of the design requirements that come to mind, then it is necessary to contemplate the design of a new language that is especially tailored to the purpose. In the present application, there is a pressing need to devise a general calculus for composing propositions, computing their values on particular arguments, and inverting their indications to arrive at the sets of things in the universe that are indicated by them.
For computational purposes, it is convenient to have a middle ground or an intermediate language for negotiating between the koine of sentences regarded as strings of literal characters and the realm of propositions regarded as objects of logical value, even if this renders it necessary to introduce an artificial medium of exchange between these two domains. If one envisions these computations to be carried out in any organized fashion, and ultimately or partially by means of the familiar sorts of machines, then the strings that express these logical propositions are likely to find themselves parsed into tree-like data structures at some stage of the game. With regard to their abstract structures as graphs, there are several species of graph-theoretic data structures that can be used to accomplish this job in a reasonably effective and efficient way.
Over the course of this project, I plan to use two species of graphs:
- Painted And Rooted Cacti (PARCAI).
- Painted And Rooted Conifers (PARCOI).
For now, it is enough to discuss the former class of data structures, leaving the consideration of the latter class to a part of the project where their distinctive features are key to developments at that stage. Accordingly, within the context of the current patch of discussion, or until it becomes necessary to attach further notice to the conceivable varieties of parse graphs, the acronym "PARC" is sufficient to indicate the pertinent genus of abstract graphs that are under consideration.
By way of making these tasks feasible to carry out on a regular basis, a prospective language designer is required not only to supply a fluent medium for the expression of propositions, but further to accompany the assertions of their sentences with a canonical mechanism for teasing out the fibers of their indicator functions. Accordingly, with regard to a body of conceivable propositions, one needs to furnish a standard array of techniques for following the threads of their indications from their objective universe to their values for the mind and back again, that is, for tracing the clues that sentences provide from the universe of their objects to the signs of their values, and, in turn, from signs to objects. Ultimately, one seeks to render propositions so functional as indicators of sets and so essential for examining the equality of sets that they can constitute a veritable criterion for the practical conceivability of sets. Tackling this task requires me to introduce a number of new definitions and a collection of additional notational devices, to which I now turn.
Depending on whether a formal language is called by the type of sign that makes it up or whether it is named after the type of object that its signs are intended to denote, one may refer to this cactus language as a sentential calculus or as a propositional calculus, respectively.
When the syntactic definition of the language is well enough understood, then the language can begin to acquire a semantic function. In natural circumstances, the syntax and the semantics are likely to be engaged in a process of co-evolution, whether in ontogeny or in phylogeny, that is, the two developments probably form parallel sides of a single bootstrap. But this is not always the easiest way, at least, at first, to formally comprehend the nature of their action or the power of their interaction.
According to the customary mode of formal reconstruction, the language is first presented in terms of its syntax, in other words, as a formal language of strings called sentences, amounting to a particular subset of the possible strings that can be formed on a finite alphabet of signs. A syntactic definition of the cactus language, one that proceeds along purely formal lines, is carried out in the next Subsection. After that, the development of the language's more concrete aspects can be seen as a matter of defining two functions:
- The first is a function that takes each sentence of the language into a computational data structure, to be exact, a tree-like parse graph called a painted cactus.
- The second is a function that takes each sentence of the language, or its interpolated parse graph, into a logical proposition, in effect, ending up with an indicator function as the object denoted by the sentence.
The discussion of syntax brings up a number of associated issues that have to be clarified before going on. These are questions of style, that is, the sort of description, grammar, or theory that one finds available or chooses as preferable for a given language. These issues are discussed in the Subsection after next (Subsection 1.3.10.10).
There is an aspect of syntax that is so schematic in its basic character that it can be conveyed by computational data structures, so algorithmic in its uses that it can be automated by routine mechanisms, and so fixed in its nature that its practical exploitation can be served by the usual devices of computation. Because it involves the transformation of signs, it can be recognized as an aspect of semiotics. Since it can be carried out in abstraction from meaning, it is not up to the level of semantics, much less a complete pragmatics, though it does incline to the pragmatic aspects of computation that are auxiliary to and incidental to the human use of language. Therefore, I refer to this aspect of formal language use as the algorithmics or the mechanics of language processing. A mechanical conversion of the cactus language into its associated data structures is discussed in Subsection 1.3.10.11.
In the usual way of proceeding on formal grounds, meaning is added by giving each grammatical sentence, or each syntactically distinguished string, an interpretation as a logically meaningful sentence, in effect, equipping or providing each abstractly well-formed sentence with a logical proposition for it to denote. A semantic interpretation of the cactus language is carried out in Subsection 1.3.10.12.
The Cactus Language : Syntax
|
Picture two different configurations of such an irregular shape, superimposed on each other in space, like a double exposure photograph. Of the two images, the only part which coincides is the body. The two different sets of quills stick out into very different regions of space. The objective reality we see from within the first position, seemingly so full and spherical, actually agrees with the shifted reality only in the body of common knowledge. In every direction in which we look at all deeply, the realm of discovered scientific truth could be quite different. Yet in each of those two different situations, we would have thought the world complete, firmly known, and rather round in its penetration of the space of possible knowledge. |
| — Herbert J. Bernstein, "Idols of Modern Science", [HJB, 38] |
In this Subsection, I describe the syntax of a family of formal languages that I intend to use as a sentential calculus, and thus to interpret for the purpose of reasoning about propositions and their logical relations. In order to carry out the discussion, I need a way of referring to signs as if they were objects like any others, in other words, as the sorts of things that are subject to being named, indicated, described, discussed, and renamed if necessary, that can be placed, arranged, and rearranged within a suitable medium of expression, or else manipulated in the mind, that can be articulated and decomposed into their elementary signs, and that can be strung together in sequences to form complex signs. Signs that have signs as their objects are called higher order signs, and this is a topic that demands an apt formalization, but in due time. The present discussion requires a quicker way to get into this subject, even if it takes informal means that cannot be made absolutely precise.
As a temporary notation, let the relationship between a particular sign \(s\!\) and a particular object \(o\!\), namely, the fact that \(s\!\) denotes \(o\!\) or the fact that \(o\!\) is denoted by \(s\!\), be symbolized in one of the following two ways:
|
\(\begin{array}{lccc} 1. & s & \rightarrow & o \\ \\ 2. & o & \leftarrow & s \\ \end{array}\) |
Now consider the following paradigm:
|
\(\begin{array}{llccc} 1. & \operatorname{If} & ^{\backprime\backprime}\operatorname{A}^{\prime\prime} & \rightarrow & \operatorname{Ann}, \\ & \operatorname{that~is}, & ^{\backprime\backprime}\operatorname{A}^{\prime\prime} & \operatorname{denotes} & \operatorname{Ann}, \\ & \operatorname{then} & \operatorname{A} & = & \operatorname{Ann} \\ & \operatorname{and} & \operatorname{Ann} & = & \operatorname{A}. \\ & \operatorname{Thus} & ^{\backprime\backprime}\operatorname{Ann}^{\prime\prime} & \rightarrow & \operatorname{A}, \\ & \operatorname{that~is}, & ^{\backprime\backprime}\operatorname{Ann}^{\prime\prime} & \operatorname{denotes} & \operatorname{A}. \\ \end{array}\) |
|
\(\begin{array}{llccc} 2. & \operatorname{If} & \operatorname{Bob} & \leftarrow & ^{\backprime\backprime}\operatorname{B}^{\prime\prime}, \\ & \operatorname{that~is}, & \operatorname{Bob} & \operatorname{is~denoted~by} & ^{\backprime\backprime}\operatorname{B}^{\prime\prime}, \\ & \operatorname{then} & \operatorname{Bob} & = & \operatorname{B} \\ & \operatorname{and} & \operatorname{B} & = & \operatorname{Bob}. \\ & \operatorname{Thus} & \operatorname{B} & \leftarrow & ^{\backprime\backprime}\operatorname{Bob}^{\prime\prime}, \\ & \operatorname{that~is}, & \operatorname{B} & \operatorname{is~denoted~by} & ^{\backprime\backprime}\operatorname{Bob}^{\prime\prime}. \\ \end{array}\) |
When I say that the sign "blank" denotes the sign " ", it means that the string of characters inside the first pair of quotation marks can be used as another name for the string of characters inside the second pair of quotes. In other words, "blank" is a higher order sign whose object is " ", and the string of five characters inside the first pair of quotation marks is a sign at a higher level of signification than the string of one character inside the second pair of quotation marks. This relationship can be abbreviated in either one of the following ways:
|
\(\begin{array}{lll} ^{\backprime\backprime}\operatorname{~}^{\prime\prime} & \leftarrow & ^{\backprime\backprime}\operatorname{blank}^{\prime\prime} \\ \\ ^{\backprime\backprime}\operatorname{blank}^{\prime\prime} & \rightarrow & ^{\backprime\backprime}\operatorname{~}^{\prime\prime} \\ \end{array}\) |
Using the raised dot "\(\cdot\)" as a sign to mark the articulation of a quoted string into a sequence of possibly shorter quoted strings, and thus to mark the concatenation of a sequence of quoted strings into a possibly larger quoted string, one can write:
|
\(\begin{array}{lllll} ^{\backprime\backprime}\operatorname{~}^{\prime\prime} & \leftarrow & ^{\backprime\backprime}\operatorname{blank}^{\prime\prime} & = & ^{\backprime\backprime}\operatorname{b}^{\prime\prime} \, \cdot \, ^{\backprime\backprime}\operatorname{l}^{\prime\prime} \, \cdot \, ^{\backprime\backprime}\operatorname{a}^{\prime\prime} \, \cdot \, ^{\backprime\backprime}\operatorname{n}^{\prime\prime} \, \cdot \, ^{\backprime\backprime}\operatorname{k}^{\prime\prime} \\ \end{array}\) |
This usage allows us to refer to the blank as a type of character, and also to refer any blank we choose as a token of this type, referring to either of them in a marked way, but without the use of quotation marks, as I just did. Now, since a blank is just what the name "blank" names, it is possible to represent the denotation of the sign " " by the name "blank" in the form of an identity between the named objects, thus:
|
\(\begin{array}{lll} ^{\backprime\backprime}\operatorname{~}^{\prime\prime} & = & \operatorname{blank} \\ \end{array}\) |
With these kinds of identity in mind, it is possible to extend the use of the "\(\cdot\)" sign to mark the articulation of either named or quoted strings into both named and quoted strings. For example:
|
\(\begin{array}{lclcl} ^{\backprime\backprime}\operatorname{~~}^{\prime\prime} & = & ^{\backprime\backprime}\operatorname{~}^{\prime\prime} \, \cdot \, ^{\backprime\backprime}\operatorname{~}^{\prime\prime} & = & \operatorname{blank} \, \cdot \, \operatorname{blank} \\ \\ ^{\backprime\backprime}\operatorname{~blank}^{\prime\prime} & = & ^{\backprime\backprime}\operatorname{~}^{\prime\prime} \, \cdot \, ^{\backprime\backprime}\operatorname{blank}^{\prime\prime} & = & \operatorname{blank} \, \cdot \, ^{\backprime\backprime}\operatorname{blank}^{\prime\prime} \\ \\ ^{\backprime\backprime}\operatorname{blank~}^{\prime\prime} & = & ^{\backprime\backprime}\operatorname{blank}^{\prime\prime} \, \cdot \, ^{\backprime\backprime}\operatorname{~}^{\prime\prime} & = & ^{\backprime\backprime}\operatorname{blank}^{\prime\prime} \, \cdot \, \operatorname{blank} \end{array}\) |
A few definitions from formal language theory are required at this point.
An alphabet is a finite set of signs, typically, \(\mathfrak{A} = \{ \mathfrak{a}_1, \ldots, \mathfrak{a}_n \}.\)
A string over an alphabet \(\mathfrak{A}\) is a finite sequence of signs from \(\mathfrak{A}.\)
The length of a string is just its length as a sequence of signs.
The empty string is the unique sequence of length 0. It is sometimes denoted by an empty pair of quotation marks, \(^{\backprime\backprime\prime\prime},\) but more often by the Greek symbols epsilon or lambda.
A sequence of length \(k > 0\!\) is typically presented in the concatenated forms:
|
\(s_1 s_2 \ldots s_{k-1} s_k\!\) |
or
|
\(s_1 \cdot s_2 \cdot \ldots \cdot s_{k-1} \cdot s_k\) |
with \(s_j \in \mathfrak{A}\) for all \(j = 1 \ldots k.\)
Two alternative notations are often useful:
| \(\varepsilon\) | = | \(^{\backprime\backprime\prime\prime}\) | = | the empty string. |
| \(\underline\varepsilon\) | = | \(\{ \varepsilon \}\) | = | the language consisting of a single empty string. |
The kleene star \(\mathfrak{A}^*\) of alphabet \(\mathfrak{A}\) is the set of all strings over \(\mathfrak{A}.\) In particular, \(\mathfrak{A}^*\) includes among its elements the empty string \(\varepsilon.\)
The kleene plus \(\mathfrak{A}^+\) of an alphabet \(\mathfrak{A}\) is the set of all positive length strings over \(\mathfrak{A},\) in other words, everything in \(\mathfrak{A}^*\) but the empty string.
A formal language \(\mathfrak{L}\) over an alphabet \(\mathfrak{A}\) is a subset of \(\mathfrak{A}^*.\) In brief, \(\mathfrak{L} \subseteq \mathfrak{A}^*.\) If \(s\!\) is a string over \(\mathfrak{A}\) and if \(s\!\) is an element of \(\mathfrak{L},\) then it is customary to call \(s\!\) a sentence of \(\mathfrak{L}.\) Thus, a formal language \(\mathfrak{L}\) is defined by specifying its elements, which amounts to saying what it means to be a sentence of \(\mathfrak{L}.\)
One last device turns out to be useful in this connection. If \(s\!\) is a string that ends with a sign \(t,\!\) then \(s \cdot t^{-1}\) is the string that results by deleting from \(s\!\) the terminal \(t.\!\)
In this context, I make the following distinction:
- To delete an appearance of a sign is to replace it with an appearance of the empty string "".
- To erase an appearance of a sign is to replace it with an appearance of the blank symbol " ".
A token is a particular appearance of a sign.
The informal mechanisms that have been illustrated in the immediately preceding discussion are enough to equip the rest of this discussion with a moderately exact description of the so-called cactus language that I intend to use in both my conceptual and my computational representations of the minimal formal logical system that is variously known to sundry communities of interpretation as propositional logic, sentential calculus, or more inclusively, zeroth order logic (ZOL).
The painted cactus language \(\mathfrak{C}\) is actually a parameterized family of languages, consisting of one language \(\mathfrak{C}(\mathfrak{P})\) for each set \(\mathfrak{P}\) of paints.
The alphabet \(\mathfrak{A} = \mathfrak{M} \cup \mathfrak{P}\) is the disjoint union of two sets of symbols:
-
\(\mathfrak{M}\) is the alphabet of measures, the set of punctuation marks, or the collection of syntactic constants that is common to all of the languages \(\mathfrak{C}(\mathfrak{P}).\) This set of signs is given as follows:
\(\begin{array}{lccccccccccc} \mathfrak{M} & = & \{ & \mathfrak{m}_1 & , & \mathfrak{m}_2 & , & \mathfrak{m}_3 & , & \mathfrak{m}_4 & \} \\ & = & \{ & ^{\backprime\backprime} \, \operatorname{~} \, ^{\prime\prime} & , & ^{\backprime\backprime} \, \operatorname{(} \, ^{\prime\prime} & , & ^{\backprime\backprime} \, \operatorname{,} \, ^{\prime\prime} & , & ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime} & \} \\ & = & \{ & \operatorname{blank} & , & \operatorname{links} & , & \operatorname{comma} & , & \operatorname{right} & \} \\ \end{array}\)
-
\(\mathfrak{P}\) is the palette, the alphabet of paints, or the collection of syntactic variables that is peculiar to the language \(\mathfrak{C}(\mathfrak{P}).\) This set of signs is given as follows:
\(\mathfrak{P} = \{ \mathfrak{p}_j : j \in J \}.\)
The easiest way to define the language \(\mathfrak{C}(\mathfrak{P})\) is to indicate the general sorts of operations that suffice to construct the greater share of its sentences from the specified few of its sentences that require a special election. In accord with this manner of proceeding, I introduce a family of operations on strings of \(\mathfrak{A}^*\) that are called syntactic connectives. If the strings on which they operate are exclusively sentences of \(\mathfrak{C}(\mathfrak{P}),\) then these operations are tantamount to sentential connectives, and if the syntactic sentences, considered as abstract strings of meaningless signs, are given a semantics in which they denote propositions, considered as indicator functions over some universe, then these operations amount to propositional connectives.
Rather than presenting the most concise description of these languages right from the beginning, it serves comprehension to develop a picture of their forms in gradual stages, starting from the most natural ways of viewing their elements, if somewhat at a distance, and working through the most easily grasped impressions of their structures, if not always the sharpest acquaintances with their details.
The first step is to define two sets of basic operations on strings of \(\mathfrak{A}^*.\)
-
The concatenation of one string \(s_1\!\) is just the string \(s_1.\!\)
The concatenation of two strings \(s_1, s_2\!\) is the string \(s_1 \cdot s_2.\!\)
The concatenation of the \(k\!\) strings \((s_j)_{j = 1}^k\) is the string of the form \(s_1 \cdot \ldots \cdot s_k.\!\)
-
The surcatenation of one string \(s_1\!\) is the string \(^{\backprime\backprime} \, \operatorname{(} \, ^{\prime\prime} \, \cdot \, s_1 \, \cdot \, ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime}.\)
The surcatenation of two strings \(s_1, s_2\!\) is \(^{\backprime\backprime} \, \operatorname{(} \, ^{\prime\prime} \, \cdot \, s_1 \, \cdot \, ^{\backprime\backprime} \, \operatorname{,} \, ^{\prime\prime} \, \cdot \, s_2 \, \cdot \, ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime}.\)
The surcatenation of the \(k\!\) strings \((s_j)_{j = 1}^k\) is the string of the form \(^{\backprime\backprime} \, \operatorname{(} \, ^{\prime\prime} \, \cdot \, s_1 \, \cdot \, ^{\backprime\backprime} \, \operatorname{,} \, ^{\prime\prime} \, \cdot \, \ldots \, \cdot \, ^{\backprime\backprime} \, \operatorname{,} \, ^{\prime\prime} \, \cdot \, s_k \, \cdot \, ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime}.\)
These definitions can be made a little more succinct by defining the following sorts of generic operators on strings:
- The concatenation \(\operatorname{Conc}_{j=1}^k\) of the sequence of \(k\!\) strings \((s_j)_{j=1}^k\) is defined recursively as follows:
- \(\operatorname{Conc}_{j=1}^1 s_j \ = \ s_1.\)
-
For \(\ell > 1,\!\)
\(\operatorname{Conc}_{j=1}^\ell s_j \ = \ \operatorname{Conc}_{j=1}^{\ell - 1} s_j \, \cdot \, s_\ell.\)
- The surcatenation \(\operatorname{Surc}_{j=1}^k\) of the sequence of \(k\!\) strings \((s_j)_{j=1}^k\) is defined recursively as follows:
- \(\operatorname{Surc}_{j=1}^1 s_j \ = \ ^{\backprime\backprime} \, \operatorname{(} \, ^{\prime\prime} \, \cdot \, s_1 \, \cdot \, ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime}.\)
-
For \(\ell > 1,\!\)
\(\operatorname{Surc}_{j=1}^\ell s_j \ = \ \operatorname{Surc}_{j=1}^{\ell - 1} s_j \, \cdot \, ( \, ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime} \, )^{-1} \, \cdot \, ^{\backprime\backprime} \, \operatorname{,} \, ^{\prime\prime} \, \cdot \, s_\ell \, \cdot \, ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime}.\)
The definitions of these syntactic operations can now be organized in a slightly better fashion by making a few additional conventions and auxiliary definitions.
-
The conception of the \(k\!\)-place concatenation operation can be extended to include its natural prequel:
\(\operatorname{Conc}^0 \ = \ ^{\backprime\backprime\prime\prime}\) = the empty string.
Next, the construction of the \(k\!\)-place concatenation can be broken into stages by means of the following conceptions:
-
The precatenation \(\operatorname{Prec} (s_1, s_2)\) of the two strings \(s_1, s_2\!\) is the string that is defined as follows:
\(\operatorname{Prec} (s_1, s_2) \ = \ s_1 \cdot s_2.\)
-
The concatenation of the sequence of \(k\!\) strings \(s_1, \ldots, s_k\!\) can now be defined as an iterated precatenation over the sequence of \(k+1\!\) strings that begins with the string \(s_0 = \operatorname{Conc}^0 \, = \, ^{\backprime\backprime\prime\prime}\) and then continues on through the other \(k\!\) strings:
-
\(\operatorname{Conc}_{j=0}^0 s_j \ = \ \operatorname{Conc}^0 \ = \ ^{\backprime\backprime\prime\prime}.\)
-
For \(\ell > 0,\!\)
\(\operatorname{Conc}_{j=1}^\ell s_j \ = \ \operatorname{Prec}(\operatorname{Conc}_{j=0}^{\ell - 1} s_j, s_\ell).\)
-
The conception of the \(k\!\)-place surcatenation operation can be extended to include its natural "prequel":
\(\operatorname{Surc}^0 \ = \ ^{\backprime\backprime} \, \operatorname{()} \, ^{\prime\prime}.\)
Finally, the construction of the \(k\!\)-place surcatenation can be broken into stages by means of the following conceptions:
-
A subclause in \(\mathfrak{A}^*\) is a string that ends with a \(^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime}.\)
-
The subcatenation \(\operatorname{Subc} (s_1, s_2)\) of a subclause \(s_1\!\) by a string \(s_2\!\) is the string that is defined as follows:
\(\operatorname{Subc} (s_1, s_2) \ = \ s_1 \, \cdot \, ( \, ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime} \, )^{-1} \, \cdot \, ^{\backprime\backprime} \, \operatorname{,} \, ^{\prime\prime} \, \cdot \, s_2 \, \cdot \, ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime}.\)
-
The surcatenation of the \(k\!\) strings \(s_1, \ldots, s_k\!\) can now be defined as an iterated subcatenation over the sequence of \(k+1\!\) strings that starts with the string \(s_0 \ = \ \operatorname{Surc}^0 \ = \ ^{\backprime\backprime} \, \operatorname{()} \, ^{\prime\prime}\) and then continues on through the other \(k\!\) strings:
-
\(\operatorname{Surc}_{j=0}^0 s_j \ = \ \operatorname{Surc}^0 \ = \ ^{\backprime\backprime} \, \operatorname{()} \, ^{\prime\prime}.\)
-
For \(\ell > 0,\!\)
\(\operatorname{Surc}_{j=1}^\ell s_j \ = \ \operatorname{Subc}(\operatorname{Surc}_{j=0}^{\ell - 1} s_j, s_\ell).\)
-
Notice that the expressions \(\operatorname{Conc}_{j=0}^0 s_j\) and \(\operatorname{Surc}_{j=0}^0 s_j\) are defined in such a way that the respective operators \(\operatorname{Conc}^0\) and \(\operatorname{Surc}^0\) simply ignore, in the manner of constants, whatever sequences of strings \(s_j\!\) may be listed as their ostensible arguments.
Having defined the basic operations of concatenation and surcatenation on arbitrary strings, in effect, giving them operational meaning for the all-inclusive language \(\mathfrak{L} = \mathfrak{A}^*,\) it is time to adjoin the notion of a more discriminating grammaticality, in other words, a more properly restrictive concept of a sentence.
If \(\mathfrak{L}\) is an arbitrary formal language over an alphabet of the sort that we are talking about, that is, an alphabet of the form \(\mathfrak{A} = \mathfrak{M} \cup \mathfrak{P},\) then there are a number of basic structural relations that can be defined on the strings of \(\mathfrak{L}.\)
| 1. | \(s\!\) is the concatenation of \(s_1\!\) and \(s_2\!\) in \(\mathfrak{L}\) if and only if |
| \(s_1\!\) is a sentence of \(\mathfrak{L},\) \(s_2\!\) is a sentence of \(\mathfrak{L},\) and | |
| \(s = s_1 \cdot s_2.\) | |
| 2. | \(s\!\) is the concatenation of the \(k\!\) strings \(s_1, \ldots, s_k\!\) in \(\mathfrak{L},\) |
| if and only if \(s_j\!\) is a sentence of \(\mathfrak{L},\) for all \(j = 1 \ldots k,\) and | |
| \(s = \operatorname{Conc}_{j=1}^k s_j = s_1 \cdot \ldots \cdot s_k.\) | |
| 3. | \(s\!\) is the discatenation of \(s_1\!\) by \(t\!\) if and only if |
| \(s_1\!\) is a sentence of \(\mathfrak{L},\) \(t\!\) is an element of \(\mathfrak{A},\) and | |
| \(s_1 = s \cdot t.\) | |
| When this is the case, one more commonly writes: | |
| \(s = s_1 \cdot t^{-1}.\) | |
| 4. | \(s\!\) is a subclause of \(\mathfrak{L}\) if and only if |
| \(s\!\) is a sentence of \(\mathfrak{L}\) and \(s\!\) ends with a \(^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime}.\) | |
| 5. | \(s\!\) is the subcatenation of \(s_1\!\) by \(s_2\!\) if and only if |
| \(s_1\!\) is a subclause of \(\mathfrak{L},\) \(s_2\!\) is a sentence of \(\mathfrak{L},\) and | |
| \(s = s_1 \, \cdot \, ( \, ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime} \, )^{-1} \, \cdot \, ^{\backprime\backprime} \, \operatorname{,} \, ^{\prime\prime} \, \cdot \, s_2 \, \cdot \, ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime}.\) | |
| 6. | \(s\!\) is the surcatenation of the \(k\!\) strings \(s_1, \ldots, s_k\!\) in \(\mathfrak{L},\) |
| if and only if \(s_j\!\) is a sentence of \(\mathfrak{L},\) for all \(j = 1 \ldots k,\!\) and | |
| \(s \ = \ \operatorname{Surc}_{j=1}^k s_j \ = \ ^{\backprime\backprime} \, \operatorname{(} \, ^{\prime\prime} \, \cdot \, s_1 \, \cdot \, ^{\backprime\backprime} \, \operatorname{,} \, ^{\prime\prime} \, \cdot \, \ldots \, \cdot \, ^{\backprime\backprime} \, \operatorname{,} \, ^{\prime\prime} \, \cdot \, s_k \, \cdot \, ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime}.\) |
The converses of these decomposition relations are tantamount to the corresponding forms of composition operations, making it possible for these complementary forms of analysis and synthesis to articulate the structures of strings and sentences in two directions.
The painted cactus language with paints in the set \(\mathfrak{P} = \{ p_j : j \in J \}\) is the formal language \(\mathfrak{L} = \mathfrak{C} (\mathfrak{P}) \subseteq \mathfrak{A}^* = (\mathfrak{M} \cup \mathfrak{P})^*\) that is defined as follows:
| PC 1. | The blank symbol \(m_1\!\) is a sentence. |
| PC 2. | The paint \(p_j\!\) is a sentence, for each \(j\!\) in \(J.\!\) |
| PC 3. | \(\operatorname{Conc}^0\) and \(\operatorname{Surc}^0\) are sentences. |
| PC 4. | For each positive integer \(k,\!\) |
| if \(s_1, \ldots, s_k\!\) are sentences, | |
| then \(\operatorname{Conc}_{j=1}^k s_j\) is a sentence, | |
| and \(\operatorname{Surc}_{j=1}^k s_j\) is a sentence. |
As usual, saying that \(s\!\) is a sentence is just a conventional way of stating that the string \(s\!\) belongs to the relevant formal language \(\mathfrak{L}.\) An individual sentence of \(\mathfrak{C} (\mathfrak{P}),\) for any palette \(\mathfrak{P},\) is referred to as a painted and rooted cactus expression (PARCE) on the palette \(\mathfrak{P},\) or a cactus expression, for short. Anticipating the forms that the parse graphs of these PARCE's will take, to be described in the next Subsection, the language \(\mathfrak{L} = \mathfrak{C} (\mathfrak{P})\) is also described as the set \(\operatorname{PARCE} (\mathfrak{P})\) of PARCE's on the palette \(\mathfrak{P},\) more generically, as the PARCE's that constitute the language \(\operatorname{PARCE}.\)
A bare PARCE, a bit loosely referred to as a bare cactus expression, is a PARCE on the empty palette \(\mathfrak{P} = \varnothing.\) A bare PARCE is a sentence in the bare cactus language, \(\mathfrak{C}^0 = \mathfrak{C} (\varnothing) = \operatorname{PARCE}^0 = \operatorname{PARCE} (\varnothing).\) This set of strings, regarded as a formal language in its own right, is a sublanguage of every cactus language \(\mathfrak{C} (\mathfrak{P}).\) A bare cactus expression is commonly encountered in practice when one has occasion to start with an arbitrary PARCE and then finds a reason to delete or to erase all of its paints.
Only one thing remains to cast this description of the cactus language into a form that is commonly found acceptable. As presently formulated, the principle PC 4 appears to be attempting to define an infinite number of new concepts all in a single step, at least, it appears to invoke the indefinitely long sequences of operators, \(\operatorname{Conc}^k\) and \(\operatorname{Surc}^k,\) for all \(k > 0.\!\) As a general rule, one prefers to have an effectively finite description of conceptual objects, and this means restricting the description to a finite number of schematic principles, each of which involves a finite number of schematic effects, that is, a finite number of schemata that explicitly relate conditions to results.
A start in this direction, taking steps toward an effective description of the cactus language, a finitary conception of its membership conditions, and a bounded characterization of a typical sentence in the language, can be made by recasting the present description of these expressions into the pattern of what is called, more or less roughly, a formal grammar.
A notation in the style of \(S :> T\!\) is now introduced, to be read among many others in this manifold of ways:
| \(S\ \operatorname{covers}\ T\) |
| \(S\ \operatorname{governs}\ T\) |
| \(S\ \operatorname{rules}\ T\) |
| \(S\ \operatorname{subsumes}\ T\) |
| \(S\ \operatorname{types~over}\ T\) |
The form \(S :> T\!\) is here recruited for polymorphic employment in at least the following types of roles:
- To signify that an individually named or quoted string \(T\!\) is being typed as a sentence \(S\!\) of the language of interest \(\mathfrak{L}.\)
- To express the fact or to make the assertion that each member of a specified set of strings \(T \subseteq \mathfrak{A}^*\) also belongs to the syntactic category \(S,\!\) the one that qualifies a string as being a sentence in the relevant formal language \(\mathfrak{L}.\)
- To specify the intension or to signify the intention that every string that fits the conditions of the abstract type \(T\!\) must also fall under the grammatical heading of a sentence, as indicated by the type \(S,\!\) all within the target language \(\mathfrak{L}.\)
In these types of situation the letter \(^{\backprime\backprime} S \, ^{\prime\prime}\) that signifies the type of a sentence in the language of interest, is called the initial symbol or the sentence symbol of a candidate formal grammar for the language, while any number of letters like \(^{\backprime\backprime} T \, ^{\prime\prime}\) signifying other types of strings that are necessary to a reasonable account or a rational reconstruction of the sentences that belong to the language, are collectively referred to as intermediate symbols.
Combining the singleton set \(\{ ^{\backprime\backprime} S \, ^{\prime\prime} \}\) whose sole member is the initial symbol with the set \(\mathfrak{Q}\) that assembles together all of the intermediate symbols results in the set \(\{ ^{\backprime\backprime} S \, ^{\prime\prime} \} \cup \mathfrak{Q}\) of non-terminal symbols. Completing the package, the alphabet \(\mathfrak{A}\) of the language is also known as the set of terminal symbols. In this discussion, I will adopt the convention that \(\mathfrak{Q}\) is the set of intermediate symbols, but I will often use \(q\!\) as a typical variable that ranges over all of the non-terminal symbols, \(q \in \{ ^{\backprime\backprime} S \, ^{\prime\prime} \} \cup \mathfrak{Q}.\) Finally, it is convenient to refer to all of the symbols in \(\{ ^{\backprime\backprime} S \, ^{\prime\prime} \} \cup \mathfrak{Q} \cup \mathfrak{A}\) as the augmented alphabet of the prospective grammar for the language, and accordingly to describe the strings in \(( \{ ^{\backprime\backprime} S \, ^{\prime\prime} \} \cup \mathfrak{Q} \cup \mathfrak{A} )^*\) as the augmented strings, in effect, expressing the forms that are superimposed on a language by one of its conceivable grammars. In certain settings it becomes desirable to separate the augmented strings that contain the symbol \(^{\backprime\backprime} S \, ^{\prime\prime}\) from all other sorts of augmented strings. In these situations the strings in the disjoint union \(\{ ^{\backprime\backprime} S \, ^{\prime\prime} \} \cup (\mathfrak{Q} \cup \mathfrak{A} )^*\) are known as the sentential forms of the associated grammar.
In forming a grammar for a language statements of the form \(W :> W',\!\) where \(W\!\) and \(W'\!\) are augmented strings or sentential forms of specified types that depend on the style of the grammar that is being sought, are variously known as characterizations, covering rules, productions, rewrite rules, subsumptions, transformations, or typing rules. These are collected together into a set \(\mathfrak{K}\) that serves to complete the definition of the formal grammar in question.
Correlative with the use of this notation, an expression of the form \(T <: S,\!\) read to say that \(T\!\) is covered by \(S,\!\) can be interpreted to say that \(T\!\) is of the type \(S.\!\) Depending on the context, this can be taken in either one of two ways:
- Treating \(T\!\) as a string variable, it means that the individual string \(T\!\) is typed as \(S.\!\)
- Treating \(T\!\) as a type name, it means that any instance of the type \(T\!\) also falls under the type \(S.\!\)
In accordance with these interpretations, an expression of the form \(t <: T\!\) can be read in all of the ways that one typically reads an expression of the form \(t : T.\!\)
There are several abuses of notation that commonly tolerated in the use of covering relations. The worst offense is that of allowing symbols to stand equivocally either for individual strings or else for their types. There is a measure of consistency to this practice, considering the fact that perfectly individual entities are rarely if ever grasped by means of signs and finite expressions, which entails that every appearance of an apparent token is only a type of more particular tokens, and meaning in the end that there is never any recourse but to the sort of discerning interpretation that can decide just how each sign is intended. In view of all this, I continue to permit expressions like \(t <: T\!\) and \(T <: S,\!\) where any of the symbols \(t, T, S\!\) can be taken to signify either the tokens or the subtypes of their covering types.
Note. For some time to come in the discussion that follows, although I will continue to focus on the cactus language as my principal object example, my more general purpose will be to develop the subject matter of the formal languages and grammars. I will do this by taking up a particular method of stepwise refinement and using it to extract a rigorous formal grammar for the cactus language, starting with little more than a rough description of the target language and applying a systematic analysis to develop a sequence of increasingly more effective and more exact approximations to the desired grammar.
Employing the notion of a covering relation it becomes possible to redescribe the cactus language \(\mathfrak{L} = \mathfrak{C} (\mathfrak{P})\) in the following ways.
Grammar 1
Grammar 1 is something of a misnomer. It is nowhere near exemplifying any kind of a standard form and it is only intended as a starting point for the initiation of more respectable grammars. Such as it is, it uses the terminal alphabet \(\mathfrak{A} = \mathfrak{M} \cup \mathfrak{P}\) that comes with the territory of the cactus language \(\mathfrak{C} (\mathfrak{P}),\) it specifies \(\mathfrak{Q} = \varnothing,\) in other words, it employs no intermediate symbols, and it embodies the covering set \(\mathfrak{K}\) as listed in the following display.
|
\(\mathfrak{C} (\mathfrak{P}) : \text{Grammar 1}\!\) |
\(\mathfrak{Q} = \varnothing\) |
|
\(\begin{array}{rcll} 1. & S & :> & m_1 \ = \ ^{\backprime\backprime} \operatorname{~} ^{\prime\prime} \\ 2. & S & :> & p_j, \, \text{for each} \, j \in J \\ 3. & S & :> & \operatorname{Conc}^0 \ = \ ^{\backprime\backprime\prime\prime} \\ 4. & S & :> & \operatorname{Surc}^0 \ = \ ^{\backprime\backprime} \, \operatorname{()} \, ^{\prime\prime} \\ 5. & S & :> & S^* \\ 6. & S & :> & ^{\backprime\backprime} \, \operatorname{(} \, ^{\prime\prime} \, \cdot \, S \, \cdot \, ( \, ^{\backprime\backprime} \operatorname{,} ^{\prime\prime} \, \cdot \, S \, )^* \, \cdot \, ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime} \\ \end{array}\) | |
In this formulation, the last two lines specify that:
- The concept of a sentence in \(\mathfrak{L}\) covers any concatenation of sentences in \(\mathfrak{L},\) in effect, any number of freely chosen sentences that are available to be concatenated one after another.
- The concept of a sentence in \(\mathfrak{L}\) covers any surcatenation of sentences in \(\mathfrak{L},\) in effect, any string that opens with a \(^{\backprime\backprime} \, \operatorname{(} \, ^{\prime\prime},\) continues with a sentence, possibly empty, follows with a finite number of phrases of the form \(^{\backprime\backprime} \operatorname{,} ^{\prime\prime} \, \cdot \, S,\) and closes with a \(^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime}.\)
This appears to be just about the most concise description of the cactus language \(\mathfrak{C} (\mathfrak{P})\) that one can imagine, but there are a couple of problems that are commonly felt to afflict this style of presentation and to make it less than completely acceptable. Briefly stated, these problems turn on the following properties of the presentation:
- The invocation of the kleene star operation is not reduced to a manifestly finitary form.
- The type \(S\!\) that indicates a sentence is allowed to cover not only itself but also the empty string.
I will discuss these issues at first in general, and especially in regard to how the two features interact with one another, and then I return to address in further detail the questions that they engender on their individual bases.
In the process of developing a grammar for a language, it is possible to notice a number of organizational, pragmatic, and stylistic questions, whose moment to moment answers appear to decide the ongoing direction of the grammar that develops and the impact of whose considerations work in tandem to determine, or at least to influence, the sort of grammar that turns out. The issues that I can see arising at this point I can give the following prospective names, putting off the discussion of their natures and the treatment of their details to the points in the development of the present example where they evolve their full import.
- The degree of intermediate organization in a grammar.
- The distinction between empty and significant strings, and thus the distinction between empty and significant types of strings.
- The principle of intermediate significance. This is a constraint on the grammar that arises from considering the interaction of the first two issues.
In responding to these issues, it is advisable at first to proceed in a stepwise fashion, all the better to accommodate the chances of pursuing a series of parallel developments in the grammar, to allow for the possibility of reversing many steps in its development, indeed, to take into account the near certain necessity of having to revisit, to revise, and to reverse many decisions about how to proceed toward an optimal description or a satisfactory grammar for the language. Doing all this means exploring the effects of various alterations and innovations as independently from each other as possible.
The degree of intermediate organization in a grammar is measured by how many intermediate symbols it has and by how they interact with each other by means of its productions. With respect to this issue, Grammar 1 has no intermediate symbols at all, \(\mathfrak{Q} = \varnothing,\) and therefore remains at an ostensibly trivial degree of intermediate organization. Some additions to the list of intermediate symbols are practically obligatory in order to arrive at any reasonable grammar at all, other inclusions appear to have a more optional character, though obviously useful from the standpoints of clarity and ease of comprehension.
One of the troubles that is perceived to affect Grammar 1 is that it wastes so much of the available potential for efficient description in recounting over and over again the simple fact that the empty string is present in the language. This arises in part from the statement that \(S :> S^*,\!\) which implies that:
|
\(\begin{array}{lcccccccccccc} S & :> & S^* & = & \underline\varepsilon & \cup & S & \cup & S \cdot S & \cup & S \cdot S \cdot S & \cup & \ldots \\ \end{array}\) |
There is nothing wrong with the more expansive pan of the covered equation, since it follows straightforwardly from the definition of the kleene star operation, but the covering statement to the effect that \(S :> S^*\!\) is not a very productive piece of information, in the sense of telling very much about the language that falls under the type of a sentence \(S.\!\) In particular, since it implies that \(S :> \underline\varepsilon,\) and since \(\underline\varepsilon \cdot \mathfrak{L} \, = \, \mathfrak{L} \cdot \underline\varepsilon \, = \, \mathfrak{L},\) for any formal language \(\mathfrak{L},\) the empty string \(\varepsilon\) is counted over and over in every term of the union, and every non-empty sentence under \(S\!\) appears again and again in every term of the union that follows the initial appearance of \(S.\!\) As a result, this style of characterization has to be classified as true but not very informative. If at all possible, one prefers to partition the language of interest into a disjoint union of subsets, thereby accounting for each sentence under its proper term, and one whose place under the sum serves as a useful parameter of its character or its complexity. In general, this form of description is not always possible to achieve, but it is usually worth the trouble to actualize it whenever it is.
Suppose that one tries to deal with this problem by eliminating each use of the kleene star operation, by reducing it to a purely finitary set of steps, or by finding an alternative way to cover the sublanguage that it is used to generate. This amounts, in effect, to recognizing a type, a complex process that involves the following steps:
- Noticing a category of strings that is generated by iteration or recursion.
- Acknowledging the fact that it needs to be covered by a non-terminal symbol.
- Making a note of it by instituting an explicitly-named grammatical category.
In sum, one introduces a non-terminal symbol for each type of sentence and each part of speech or sentential component that is generated by means of iteration or recursion under the ruling constraints of the grammar. In order to do this one needs to analyze the iteration of each grammatical operation in a way that is analogous to a mathematically inductive definition, but further in a way that is not forced explicitly to recognize a distinct and separate type of expression merely to account for and to recount every increment in the parameter of iteration.
Returning to the case of the cactus language, the process of recognizing an iterative type or a recursive type can be illustrated in the following way. The operative phrases in the simplest sort of recursive definition are its initial part and its generic part. For the cactus language \(\mathfrak{C} (\mathfrak{P}),\) one has the following definitions of concatenation as iterated precatenation and of surcatenation as iterated subcatenation, respectively:
|
\(\begin{array}{llll} 1. & \operatorname{Conc}_{j=1}^0 & = & ^{\backprime\backprime\prime\prime} \\ \\ & \operatorname{Conc}_{j=1}^k S_j & = & \operatorname{Prec} (\operatorname{Conc}_{j=1}^{k-1} S_j, S_k) \\ \\ 2. & \operatorname{Surc}_{j=1}^0 & = & ^{\backprime\backprime} \, \operatorname{()} \, ^{\prime\prime} \\ \\ & \operatorname{Surc}_{j=1}^k S_j & = & \operatorname{Subc} (\operatorname{Surc}_{j=1}^{k-1} S_j, S_k) \\ \\ \end{array}\) |
In order to transform these recursive definitions into grammar rules, one introduces a new pair of intermediate symbols, \(\operatorname{Conc}\) and \(\operatorname{Surc},\) corresponding to the operations that share the same names but ignoring the inflexions of their individual parameters \(j\!\) and \(k.\!\) Recognizing the type of a sentence by means of the initial symbol \(S\!\) and interpreting \(\operatorname{Conc}\) and \(\operatorname{Surc}\) as names for the types of strings that are generated by concatenation and by surcatenation, respectively, one arrives at the following transformation of the ruling operator definitions into the form of covering grammar rules:
|
\(\begin{array}{llll} 1. & \operatorname{Conc} & :> & ^{\backprime\backprime\prime\prime} \\ \\ & \operatorname{Conc} & :> & \operatorname{Conc} \cdot S \\ \\ 2. & \operatorname{Surc} & :> & ^{\backprime\backprime} \, \operatorname{()} \, ^{\prime\prime} \\ \\ & \operatorname{Surc} & :> & ^{\backprime\backprime} \, \operatorname{(} \, ^{\prime\prime} \, \cdot \, S \, \cdot \, ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime} \\ \\ & \operatorname{Surc} & :> & \operatorname{Surc} \, \cdot \, ( \, ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime} \, )^{-1} \, \cdot \, ^{\backprime\backprime} \operatorname{,} ^{\prime\prime} \, \cdot \, S \, \cdot \, ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime} \end{array}\) |
As given, this particular fragment of the intended grammar contains a couple of features that are desirable to amend.
- Given the covering \(S :> \operatorname{Conc},\) the covering rule \(\operatorname{Conc} :> \operatorname{Conc} \cdot S\) says no more than the covering rule \(\operatorname{Conc} :> S \cdot S.\) Consequently, all of the information contained in these two covering rules is already covered by the statement that \(S :> S \cdot S.\)
- A grammar rule that invokes a notion of decatenation, deletion, erasure, or any other sort of retrograde production, is frequently considered to be lacking in elegance, and a there is a style of critique for grammars that holds it preferable to avoid these types of operations if it is at all possible to do so. Accordingly, contingent on the prescriptions of the informal rule in question, and pursuing the stylistic dictates that are writ in the realm of its aesthetic regime, it becomes necessary for us to backtrack a little bit, to temporarily withdraw the suggestion of employing these elliptical types of operations, but without, of course, eliding the record of doing so.
Grammar 2
One way to analyze the surcatenation of any number of sentences is to introduce an auxiliary type of string, not in general a sentence, but a proper component of any sentence that is formed by surcatenation. Doing this brings one to the following definition:
A tract is a concatenation of a finite sequence of sentences, with a literal comma \(^{\backprime\backprime} \operatorname{,} ^{\prime\prime}\) interpolated between each pair of adjacent sentences. Thus, a typical tract \(T\!\) takes the form:
|
\(\begin{array}{lllllllllll} T & = & S_1 & \cdot & ^{\backprime\backprime} \operatorname{,} ^{\prime\prime} & \cdot & \ldots & \cdot & ^{\backprime\backprime} \operatorname{,} ^{\prime\prime} & \cdot & S_k \\ \end{array}\) |
A tract must be distinguished from the abstract sequence of sentences, \(S_1, \ldots, S_k,\!\) where the commas that appear to come to mind, as if being called up to separate the successive sentences of the sequence, remain as partially abstract conceptions, or as signs that retain a disengaged status on the borderline between the text and the mind. In effect, the types of commas that appear to follow in the abstract sequence continue to exist as conceptual abstractions and fail to be cognized in a wholly explicit fashion, whether as concrete tokens in the object language, or as marks in the strings of signs that are able to engage one's parsing attention.
Returning to the case of the painted cactus language \(\mathfrak{L} = \mathfrak{C} (\mathfrak{P}),\) it is possible to put the currently assembled pieces of a grammar together in the light of the presently adopted canons of style, to arrive a more refined analysis of the fact that the concept of a sentence covers any concatenation of sentences and any surcatenation of sentences, and so to obtain the following form of a grammar:
|
\(\mathfrak{C} (\mathfrak{P}) : \text{Grammar 2}\!\) |
\(\mathfrak{Q} = \{ \, ^{\backprime\backprime} T \, ^{\prime\prime} \, \}\) |
|
\(\begin{array}{rcll} 1. & S & :> & \varepsilon \\ 2. & S & :> & m_1 \\ 3. & S & :> & p_j, \, \text{for each} \, j \in J \\ 4. & S & :> & S \, \cdot \, S \\ 5. & S & :> & ^{\backprime\backprime} \, \operatorname{(} \, ^{\prime\prime} \, \cdot \, T \, \cdot \, ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime} \\ 6. & T & :> & S \\ 7. & T & :> & T \, \cdot \, ^{\backprime\backprime} \operatorname{,} ^{\prime\prime} \, \cdot \, S \\ \end{array}\) | |
In this rendition, a string of type \(T\!\) is not in general a sentence itself but a proper part of speech, that is, a strictly lesser component of a sentence in any suitable ordering of sentences and their components. In order to see how the grammatical category \(T\!\) gets off the ground, that is, to detect its minimal strings and to discover how its ensuing generations get started from these, it is useful to observe that the covering rule \(T :> S\!\) means that \(T\!\) inherits all of the initial conditions of \(S,\!\) namely, \(T \, :> \, \varepsilon, m_1, p_j.\) In accord with these simple beginnings it comes to parse that the rule \(T \, :> \, T \, \cdot \, ^{\backprime\backprime} \operatorname{,} ^{\prime\prime} \, \cdot \, S,\) with the substitutions \(T = \varepsilon\) and \(S = \varepsilon\) on the covered side of the rule, bears the germinal implication that \(T \, :> \, ^{\backprime\backprime} \operatorname{,} ^{\prime\prime}.\)
Grammar 2 achieves a portion of its success through a higher degree of intermediate organization. Roughly speaking, the level of organization can be seen as reflected in the cardinality of the intermediate alphabet \(\mathfrak{Q} = \{ \, ^{\backprime\backprime} T \, ^{\prime\prime} \, \}\) but it is clearly not explained by this simple circumstance alone, since it is taken for granted that the intermediate symbols serve a purpose, a purpose that is easily recognizable but that may not be so easy to pin down and to specify exactly. Nevertheless, it is worth the trouble of exploring this aspect of organization and this direction of development a little further.
Grammar 3
Although it is not strictly necessary to do so, it is possible to organize the materials of our developing grammar in a slightly better fashion by recognizing two recurrent types of strings that appear in the typical cactus expression. In doing this, one arrives at the following two definitions:
A rune is a string of blanks and paints concatenated together. Thus, a typical rune \(R\!\) is a string over \(\{ m_1 \} \cup \mathfrak{P},\) possibly the empty string:
| \(R\ \in\ ( \{ m_1 \} \cup \mathfrak{P} )^*\) |
When there is no possibility of confusion, the letter \(^{\backprime\backprime} R \, ^{\prime\prime}\) can be used either as a string variable that ranges over the set of runes or else as a type name for the class of runes. The latter reading amounts to the enlistment of a fresh intermediate symbol, \(^{\backprime\backprime} R \, ^{\prime\prime} \in \mathfrak{Q},\) as a part of a new grammar for \(\mathfrak{C} (\mathfrak{P}).\) In effect, \(^{\backprime\backprime} R \, ^{\prime\prime}\) affords a grammatical recognition for any rune that forms a part of a sentence in \(\mathfrak{C} (\mathfrak{P}).\) In situations where these variant usages are likely to be confused, the types of strings can be indicated by means of expressions like \(r <: R\!\) and \(W <: R.\!\)
A foil is a string of the form \(^{\backprime\backprime} \, \operatorname{(} \, ^{\prime\prime} \, \cdot \, T \, \cdot \, ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime},\) where \(T\!\) is a tract. Thus, a typical foil \(F\!\) has the form:
|
\(\begin{array}{lllllllllllllll} F & = & ^{\backprime\backprime} \, \operatorname{(} \, ^{\prime\prime} & \cdot & S_1 & \cdot & ^{\backprime\backprime} \operatorname{,} ^{\prime\prime} & \cdot & \ldots & \cdot & ^{\backprime\backprime} \operatorname{,} ^{\prime\prime} & \cdot & S_k & \cdot & ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime} \\ \end{array}\) |
This is just the surcatenation of the sentences \(S_1, \ldots, S_k.\!\) Given the possibility that this sequence of sentences is empty, and thus that the tract \(T\!\) is the empty string, the minimum foil \(F\!\) is the expression \(^{\backprime\backprime} \, \operatorname{()} \, ^{\prime\prime}.\) Explicitly marking each foil \(F\!\) that is embodied in a cactus expression is tantamount to recognizing another intermediate symbol, \(^{\backprime\backprime} F \, ^{\prime\prime} \in \mathfrak{Q},\) further articulating the structures of sentences and expanding the grammar for the language \(\mathfrak{C} (\mathfrak{P}).\) All of the same remarks about the versatile uses of the intermediate symbols, as string variables and as type names, apply again to the letter \(^{\backprime\backprime} F \, ^{\prime\prime}.\)
|
\(\mathfrak{C} (\mathfrak{P}) : \text{Grammar 3}\!\) |
\(\mathfrak{Q} = \{ \, ^{\backprime\backprime} F \, ^{\prime\prime}, \, ^{\backprime\backprime} R \, ^{\prime\prime}, \, ^{\backprime\backprime} T \, ^{\prime\prime} \, \}\) |
|
\(\begin{array}{rcll} 1. & S & :> & R \\ 2. & S & :> & F \\ 3. & S & :> & S \, \cdot \, S \\ 4. & R & :> & \varepsilon \\ 5. & R & :> & m_1 \\ 6. & R & :> & p_j, \, \text{for each} \, j \in J \\ 7. & R & :> & R \, \cdot \, R \\ 8. & F & :> & ^{\backprime\backprime} \, \operatorname{(} \, ^{\prime\prime} \, \cdot \, T \, \cdot \, ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime} \\ 9. & T & :> & S \\ 10. & T & :> & T \, \cdot \, ^{\backprime\backprime} \operatorname{,} ^{\prime\prime} \, \cdot \, S \\ \end{array}\) | |
In Grammar 3, the first three Rules say that a sentence (a string of type \(S\!\)), is a rune (a string of type \(R\!\)), a foil (a string of type \(F\!\)), or an arbitrary concatenation of strings of these two types. Rules 4 through 7 specify that a rune \(R\!\) is an empty string \(\varepsilon,\) a blank symbol \(m_1,\!\) a paint \(p_j,\!\) or any concatenation of strings of these three types. Rule 8 characterizes a foil \(F\!\) as a string of the form \(^{\backprime\backprime} \, \operatorname{(} \, ^{\prime\prime} \, \cdot \, T \, \cdot \, ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime},\) where \(T\!\) is a tract. The last two Rules say that a tract \(T\!\) is either a sentence \(S\!\) or else the concatenation of a tract, a comma, and a sentence, in that order.
At this point in the succession of grammars for \(\mathfrak{C} (\mathfrak{P}),\) the explicit uses of indefinite iterations, like the kleene star operator, are now completely reduced to finite forms of concatenation, but the problems that some styles of analysis have with allowing non-terminal symbols to cover both themselves and the empty string are still present.
Any degree of reflection on this difficulty raises the general question: What is a practical strategy for accounting for the empty string in the organization of any formal language that counts it among its sentences? One answer that presents itself is this: If the empty string belongs to a formal language, it suffices to count it once at the beginning of the formal account that enumerates its sentences and then to move on to more interesting materials.
Returning to the case of the cactus language \(\mathfrak{C} (\mathfrak{P}),\) in other words, the formal language \(\operatorname{PARCE}\) of painted and rooted cactus expressions, it serves the purpose of efficient accounting to partition the language into the following couple of sublanguages:
-
The emptily painted and rooted cactus expressions make up the language \(\operatorname{EPARCE}\) that consists of a single empty string as its only sentence. In short:
\(\operatorname{EPARCE} \ = \ \underline\varepsilon \ = \ \{ \varepsilon \}\)
-
The significantly painted and rooted cactus expressions make up the language \(\operatorname{SPARCE}\) that consists of everything else, namely, all of the non-empty strings in the language \(\operatorname{PARCE}.\) In sum:
\(\operatorname{SPARCE} \ = \ \operatorname{PARCE} \setminus \varepsilon\)
As a result of marking the distinction between empty and significant sentences, that is, by categorizing each of these three classes of strings as an entity unto itself and by conceptualizing the whole of its membership as falling under a distinctive symbol, one obtains an equation of sets that connects the three languages being marked:
| \(\operatorname{SPARCE} \ = \ \operatorname{PARCE} \ - \ \operatorname{EPARCE}\) |
In sum, one has the disjoint union:
| \(\operatorname{PARCE} \ = \ \operatorname{EPARCE} \ \cup \ \operatorname{SPARCE}\) |
For brevity in the present case, and to serve as a generic device in any similar array of situations, let \(S\!\) be the type of an arbitrary sentence, possibly empty, and let \(S'\!\) be the type of a specifically non-empty sentence. In addition, let \(\underline\varepsilon\) be the type of the empty sentence, in effect, the language \(\underline\varepsilon = \{ \varepsilon \}\) that contains a single empty string, and let a plus sign \(^{\backprime\backprime} + ^{\prime\prime}\) signify a disjoint union of types. In the most general type of situation, where the type \(S\!\) is permitted to include the empty string, one notes the following relation among types:
| \(S \ = \ \underline\varepsilon \ + \ S'\) |
With the distinction between empty and significant expressions in mind, I return to the grasp of the cactus language \(\mathfrak{L} = \mathfrak{C} (\mathfrak{P}) = \operatorname{PARCE} (\mathfrak{P})\) that is afforded by Grammar 2, and, taking that as a point of departure, explore other avenues of possible improvement in the comprehension of these expressions. In order to observe the effects of this alteration as clearly as possible, in isolation from any other potential factors, it is useful to strip away the higher levels intermediate organization that are present in Grammar 3, and start again with a single intermediate symbol, as used in Grammar 2. One way of carrying out this strategy leads on to a grammar of the variety that will be articulated next.
Grammar 4
If one imposes the distinction between empty and significant types on each non-terminal symbol in Grammar 2, then the non-terminal symbols \(^{\backprime\backprime} S \, ^{\prime\prime}\) and \(^{\backprime\backprime} T \, ^{\prime\prime}\) give rise to the expanded set of non-terminal symbols \(^{\backprime\backprime} S \, ^{\prime\prime}, \, ^{\backprime\backprime} S' \, ^{\prime\prime}, \, ^{\backprime\backprime} T \, ^{\prime\prime}, \, ^{\backprime\backprime} T' \, ^{\prime\prime},\) leaving the last three of these to form the new intermediate alphabet. Grammar 4 has the intermediate alphabet \(\mathfrak{Q} \, = \, \{ \, ^{\backprime\backprime} S' \, ^{\prime\prime}, \, ^{\backprime\backprime} T \, ^{\prime\prime}, \, ^{\backprime\backprime} T' \, ^{\prime\prime} \, \},\) with the set \(\mathfrak{K}\) of covering rules as listed in the next display.
|
\(\mathfrak{C} (\mathfrak{P}) : \text{Grammar 4}\!\) |
\(\mathfrak{Q} = \{ \, ^{\backprime\backprime} S' \, ^{\prime\prime}, \, ^{\backprime\backprime} T \, ^{\prime\prime}, \, ^{\backprime\backprime} T' \, ^{\prime\prime} \, \}\) |
|
\(\begin{array}{rcll} 1. & S & :> & \varepsilon \\ 2. & S & :> & S' \\ 3. & S' & :> & m_1 \\ 4. & S' & :> & p_j, \, \text{for each} \, j \in J \\ 5. & S' & :> & ^{\backprime\backprime} \, \operatorname{(} \, ^{\prime\prime} \, \cdot \, T \, \cdot \, ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime} \\ 6. & S' & :> & S' \, \cdot \, S' \\ 7. & T & :> & \varepsilon \\ 8. & T & :> & T' \\ 9. & T' & :> & T \, \cdot \, ^{\backprime\backprime} \operatorname{,} ^{\prime\prime} \, \cdot \, S \\ \end{array}\) | |
In this version of a grammar for \(\mathfrak{L} = \mathfrak{C} (\mathfrak{P}),\) the intermediate type \(T\!\) is partitioned as \(T = \underline\varepsilon + T',\) thereby parsing the intermediate symbol \(T\!\) in parallel fashion with the division of its overlying type as \(S = \underline\varepsilon + S'.\) This is an option that I will choose to close off for now, but leave it open to consider at a later point. Thus, it suffices to give a brief discussion of what it involves, in the process of moving on to its chief alternative.
There does not appear to be anything radically wrong with trying this approach to types. It is reasonable and consistent in its underlying principle, and it provides a rational and a homogeneous strategy toward all parts of speech, but it does require an extra amount of conceptual overhead, in that every non-trivial type has to be split into two parts and comprehended in two stages. Consequently, in view of the largely practical difficulties of making the requisite distinctions for every intermediate symbol, it is a common convention, whenever possible, to restrict intermediate types to covering exclusively non-empty strings.
For the sake of future reference, it is convenient to refer to this restriction on intermediate symbols as the intermediate significance constraint. It can be stated in a compact form as a condition on the relations between non-terminal symbols \(q \in \{ \, ^{\backprime\backprime} S \, ^{\prime\prime} \, \} \cup \mathfrak{Q}\) and sentential forms \(W \in \{ \, ^{\backprime\backprime} S \, ^{\prime\prime} \, \} \cup (\mathfrak{Q} \cup \mathfrak{A})^*.\)
|
\(\text{Condition On Intermediate Significance}\!\) |
|
\(\begin{array}{lccc} \text{If} & q & :> & W \\ \text{and} & W & = & \varepsilon \\ \text{then} & q & = & ^{\backprime\backprime} S \, ^{\prime\prime} \\ \end{array}\) |
If this is beginning to sound like a monotone condition, then it is not absurd to sharpen the resemblance and render the likeness more acute. This is done by declaring a couple of ordering relations, denoting them under variant interpretations by the same sign, \(^{\backprime\backprime}\!< \, ^{\prime\prime}.\)
- The ordering \(^{\backprime\backprime}\!< \, ^{\prime\prime}\) on the set of non-terminal symbols, \(q \in \{ \, ^{\backprime\backprime} S \, ^{\prime\prime} \, \} \cup \mathfrak{Q},\) ordains the initial symbol \(^{\backprime\backprime} S \, ^{\prime\prime}\) to be strictly prior to every intermediate symbol. This is tantamount to the axiom that \(^{\backprime\backprime} S \, ^{\prime\prime} < q,\) for all \(q \in \mathfrak{Q}.\)
- The ordering \(^{\backprime\backprime}\!< \, ^{\prime\prime}\) on the collection of sentential forms, \(W \in \{ \, ^{\backprime\backprime} S \, ^{\prime\prime} \, \} \cup (\mathfrak{Q} \cup \mathfrak{A})^*,\) ordains the empty string to be strictly minor to every other sentential form. This is stipulated in the axiom that \(\varepsilon < W,\) for every non-empty sentential form \(W.\!\)
Given these two orderings, the constraint in question on intermediate significance can be stated as follows:
|
\(\text{Condition On Intermediate Significance}\!\) |
|
\(\begin{array}{lccc} \text{If} & q & :> & W \\ \text{and} & q & > & ^{\backprime\backprime} S \, ^{\prime\prime} \\ \text{then} & W & > & \varepsilon \\ \end{array}\) |
Achieving a grammar that respects this convention typically requires a more detailed account of the initial setting of a type, both with regard to the type of context that incites its appearance and also with respect to the minimal strings that arise under the type in question. In order to find covering productions that satisfy the intermediate significance condition, one must be prepared to consider a wider variety of calling contexts or inciting situations that can be noted to surround each recognized type, and also to enumerate a larger number of the smallest cases that can be observed to fall under each significant type.
Grammar 5
With the foregoing array of considerations in mind, one is gradually led to a grammar for \(\mathfrak{L} = \mathfrak{C} (\mathfrak{P})\) in which all of the covering productions have either one of the following two forms:
|
\(\begin{array}{ccll} S & :> & \varepsilon & \\ q & :> & W, & \text{with} \ q \in \{ \, ^{\backprime\backprime} S \, ^{\prime\prime} \, \} \cup \mathfrak{Q} \ \text{and} \ W \in (\mathfrak{Q} \cup \mathfrak{A})^+ \\ \end{array}\) |
A grammar that fits into this mold is called a context-free grammar. The first type of rewrite rule is referred to as a special production, while the second type of rewrite rule is called an ordinary production. An ordinary derivation is one that employs only ordinary productions. In ordinary productions, those that have the form \(q :> W,\!\) the replacement string \(W\!\) is never the empty string, and so the lengths of the augmented strings or the sentential forms that follow one another in an ordinary derivation, on account of using the ordinary types of rewrite rules, never decrease at any stage of the process, up to and including the terminal string that is finally generated by the grammar. This type of feature is known as the non-contracting property of productions, derivations, and grammars. A grammar is said to have the property if all of its covering productions, with the possible exception of \(S :> \varepsilon,\) are non-contracting. In particular, context-free grammars are special cases of non-contracting grammars. The presence of the non-contracting property within a formal grammar makes the length of the augmented string available as a parameter that can figure into mathematical inductions and motivate recursive proofs, and this handle on the generative process makes it possible to establish the kinds of results about the generated language that are not easy to achieve in more general cases, nor by any other means even in these brands of special cases.
Grammar 5 is a context-free grammar for the painted cactus language that uses \(\mathfrak{Q} = \{ \, ^{\backprime\backprime} S' \, ^{\prime\prime}, \, ^{\backprime\backprime} T \, ^{\prime\prime} \, \},\) with \(\mathfrak{K}\) as listed in the next display.
|
\(\mathfrak{C} (\mathfrak{P}) : \text{Grammar 5}\!\) |
\(\mathfrak{Q} = \{ \, ^{\backprime\backprime} S' \, ^{\prime\prime}, \, ^{\backprime\backprime} T \, ^{\prime\prime} \, \}\) |
|
\(\begin{array}{rcll} 1. & S & :> & \varepsilon \\ 2. & S & :> & S' \\ 3. & S' & :> & m_1 \\ 4. & S' & :> & p_j, \, \text{for each} \, j \in J \\ 5. & S' & :> & S' \, \cdot \, S' \\ 6. & S' & :> & ^{\backprime\backprime} \, \operatorname{()} \, ^{\prime\prime} \\ 7. & S' & :> & ^{\backprime\backprime} \, \operatorname{(} \, ^{\prime\prime} \, \cdot \, T \, \cdot \, ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime} \\ 8. & T & :> & ^{\backprime\backprime} \, \operatorname{,} \, ^{\prime\prime} \\ 9. & T & :> & S' \\ 10. & T & :> & T \, \cdot \, ^{\backprime\backprime} \, \operatorname{,} \, ^{\prime\prime} \\ 11. & T & :> & T \, \cdot \, ^{\backprime\backprime} \, \operatorname{,} \, ^{\prime\prime} \, \cdot \, S' \\ \end{array}\) | |
Finally, it is worth trying to bring together the advantages of these diverse styles of grammar, to whatever extent that they are compatible. To do this, a prospective grammar must be capable of maintaining a high level of intermediate organization, like that arrived at in Grammar 2, while respecting the principle of intermediate significance, and thus accumulating all the benefits of the context-free format in Grammar 5. A plausible synthesis of most of these features is given in Grammar 6.
Grammar 6
Grammar 6 has the intermediate alphabet \(\mathfrak{Q} = \{ \, ^{\backprime\backprime} S' \, ^{\prime\prime}, \, ^{\backprime\backprime} F \, ^{\prime\prime}, \, ^{\backprime\backprime} R \, ^{\prime\prime}, \, ^{\backprime\backprime} T \, ^{\prime\prime} \, \},\) with the production set \(\mathfrak{K}\) as listed in the next display.
|
\(\mathfrak{C} (\mathfrak{P}) : \text{Grammar 6}\!\) |
\(\mathfrak{Q} = \{ \, ^{\backprime\backprime} S' \, ^{\prime\prime}, \, ^{\backprime\backprime} F \, ^{\prime\prime}, \, ^{\backprime\backprime} R \, ^{\prime\prime}, \, ^{\backprime\backprime} T \, ^{\prime\prime} \, \}\) |
|
\(\begin{array}{rcll} 1. & S & :> & \varepsilon \\ 2. & S & :> & S' \\ 3. & S' & :> & R \\ 4. & S' & :> & F \\ 5. & S' & :> & S' \, \cdot \, S' \\ 6. & R & :> & m_1 \\ 7. & R & :> & p_j, \, \text{for each} \, j \in J \\ 8. & R & :> & R \, \cdot \, R \\ 9. & F & :> & ^{\backprime\backprime} \, \operatorname{()} \, ^{\prime\prime} \\ 10. & F & :> & ^{\backprime\backprime} \, \operatorname{(} \, ^{\prime\prime} \, \cdot \, T \, \cdot \, ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime} \\ 11. & T & :> & ^{\backprime\backprime} \, \operatorname{,} \, ^{\prime\prime} \\ 12. & T & :> & S' \\ 13. & T & :> & T \, \cdot \, ^{\backprime\backprime} \, \operatorname{,} \, ^{\prime\prime} \\ 14. & T & :> & T \, \cdot \, ^{\backprime\backprime} \, \operatorname{,} \, ^{\prime\prime} \, \cdot \, S' \\ \end{array}\) | |
The preceding development provides a typical example of how an initially effective and conceptually succinct description of a formal language, but one that is terse to the point of allowing its prospective interpreter to waste exorbitant amounts of energy in trying to unravel its implications, can be converted into a form that is more efficient from the operational point of view, even if slightly more ungainly in regard to its elegance.
The basic idea behind all of this machinery remains the same: Besides the select body of formulas that are introduced as boundary conditions, it merely institutes the following general rule:
| \(\operatorname{If}\) | the strings \(S_1, \ldots, S_k\!\) are sentences, |
| \(\operatorname{Then}\) | their concatenation in the form |
| \(\operatorname{Conc}_{j=1}^k S_j \ = \ S_1 \, \cdot \, \ldots \, \cdot \, S_k\) | |
| is a sentence, | |
| \(\operatorname{And}\) | their surcatenation in the form |
| \(\operatorname{Surc}_{j=1}^k S_j \ = \ ^{\backprime\backprime} \, \operatorname{(} \, ^{\prime\prime} \, \cdot \, S_1 \, \cdot \, ^{\backprime\backprime} \, \operatorname{,} \, ^{\prime\prime} \, \cdot \, \ldots \, \cdot \, ^{\backprime\backprime} \, \operatorname{,} \, ^{\prime\prime} \, \cdot \, S_k \, \cdot \, ^{\backprime\backprime} \, \operatorname{)} \, ^{\prime\prime}\) | |
| is a sentence. |
Generalities About Formal Grammars
It is fitting to wrap up the foregoing developments by summarizing the notion of a formal grammar that appeared to evolve in the present case. For the sake of future reference and the chance of a wider application, it is also useful to try to extract the scheme of a formalization that potentially holds for any formal language. The following presentation of the notion of a formal grammar is adapted, with minor modifications, from the treatment in (DDQ, 60–61).
A formal grammar \(\mathfrak{G}\) is given by a four-tuple \(\mathfrak{G} = ( \, ^{\backprime\backprime} S \, ^{\prime\prime}, \, \mathfrak{Q}, \, \mathfrak{A}, \, \mathfrak{K} \, )\) that takes the following form of description:
- \(^{\backprime\backprime} S \, ^{\prime\prime}\) is the initial, special, start, or sentence symbol. Since the letter \(^{\backprime\backprime} S \, ^{\prime\prime}\) serves this function only in a special setting, its employment in this role need not create any confusion with its other typical uses as a string variable or as a sentence variable.
- \(\mathfrak{Q} = \{ q_1, \ldots, q_m \}\) is a finite set of intermediate symbols, all distinct from \(^{\backprime\backprime} S \, ^{\prime\prime}.\)
- \(\mathfrak{A} = \{ a_1, \dots, a_n \}\) is a finite set of terminal symbols, also known as the alphabet of \(\mathfrak{G},\) all distinct from \(^{\backprime\backprime} S \, ^{\prime\prime}\) and disjoint from \(\mathfrak{Q}.\) Depending on the particular conception of the language \(\mathfrak{L}\) that is covered, generated, governed, or ruled by the grammar \(\mathfrak{G},\) that is, whether \(\mathfrak{L}\) is conceived to be a set of words, sentences, paragraphs, or more extended structures of discourse, it is usual to describe \(\mathfrak{A}\) as the alphabet, lexicon, vocabulary, liturgy, or phrase book of both the grammar \(\mathfrak{G}\) and the language \(\mathfrak{L}\) that it regulates.
- \(\mathfrak{K}\) is a finite set of characterizations. Depending on how they come into play, these are variously described as covering rules, formations, productions, rewrite rules, subsumptions, transformations, or typing rules.
To describe the elements of \(\mathfrak{K}\) it helps to define some additional terms:
- The symbols in \(\{ \, ^{\backprime\backprime} S \, ^{\prime\prime} \, \} \cup \mathfrak{Q} \cup \mathfrak{A}\) form the augmented alphabet of \(\mathfrak{G}.\)
- The symbols in \(\{ \, ^{\backprime\backprime} S \, ^{\prime\prime} \, \} \cup \mathfrak{Q}\) are the non-terminal symbols of \(\mathfrak{G}.\)
- The symbols in \(\mathfrak{Q} \cup \mathfrak{A}\) are the non-initial symbols of \(\mathfrak{G}.\)
- The strings in \(( \{ \, ^{\backprime\backprime} S \, ^{\prime\prime} \, \} \cup \mathfrak{Q} \cup \mathfrak{A} )^*\) are the augmented strings for \(\mathfrak{G}.\)
- The strings in \(\{ \, ^{\backprime\backprime} S \, ^{\prime\prime} \, \} \cup (\mathfrak{Q} \cup \mathfrak{A})^*\) are the sentential forms for \(\mathfrak{G}.\)
Each characterization in \(\mathfrak{K}\) is an ordered pair of strings \((S_1, S_2)\!\) that takes the following form:
| \(S_1 \ = \ Q_1 \cdot q \cdot Q_2,\) |
| \(S_2 \ = \ Q_1 \cdot W \cdot Q_2.\) |
In this scheme, \(S_1\!\) and \(S_2\!\) are members of the augmented strings for \(\mathfrak{G},\) more precisely, \(S_1\!\) is a non-empty string and a sentential form over \(\mathfrak{G},\) while \(S_2\!\) is a possibly empty string and also a sentential form over \(\mathfrak{G}.\)
Here also, \(q\!\) is a non-terminal symbol, that is, \(q \in \{ \, ^{\backprime\backprime} S \, ^{\prime\prime} \, \} \cup \mathfrak{Q},\) while \(Q_1, Q_2,\!\) and \(W\!\) are possibly empty strings of non-initial symbols, a fact that can be expressed in the form, \(Q_1, Q_2, W \in (\mathfrak{Q} \cup \mathfrak{A})^*.\)
In practice, the couplets in \(\mathfrak{K}\) are used to derive, to generate, or to produce sentences of the corresponding language \(\mathfrak{L} = \mathfrak{L} (\mathfrak{G}).\) The language \(\mathfrak{L}\) is then said to be governed, licensed, or regulated by the grammar \(\mathfrak{G},\) a circumstance that is expressed in the form \(\mathfrak{L} = \langle \mathfrak{G} \rangle.\) In order to facilitate this active employment of the grammar, it is conventional to write the abstract characterization \((S_1, S_2)\!\) and the specific characterization \((Q_1 \cdot q \cdot Q_2, \ Q_1 \cdot W \cdot Q_2)\) in the following forms, respectively:
|
\(\begin{array}{lll} S_1 & :> & S_2 \\ Q_1 \cdot q \cdot Q_2 & :> & Q_1 \cdot W \cdot Q_2 \\ \end{array}\) |
In this usage, the characterization \(S_1 :> S_2\!\) is tantamount to a grammatical license to transform a string of the form \(Q_1 \cdot q \cdot Q_2\) into a string of the form \(Q1 \cdot W \cdot Q2,\) in effect, replacing the non-terminal symbol \(q\!\) with the non-initial string \(W\!\) in any selected, preserved, and closely adjoining context of the form \(Q1 \cdot \underline{~~~} \cdot Q2.\) In this application the notation \(S_1 :> S_2\!\) can be read to say that \(S_1\!\) produces \(S_2\!\) or that \(S_1\!\) transforms into \(S_2.\!\)
An immediate derivation in \(\mathfrak{G}\) is an ordered pair \((W, W')\!\) of sentential forms in \(\mathfrak{G}\) such that:
|
\(\begin{array}{llll} W = Q_1 \cdot X \cdot Q_2, & W' = Q_1 \cdot Y \cdot Q_2, & \text{and} & (X, Y) \in \mathfrak{K}. \end{array}\) |
As noted above, it is usual to express the condition \((X, Y) \in \mathfrak{K}\) by writing \(X :> Y \, \text{in} \, \mathfrak{G}.\)
The immediate derivation relation is indicated by saying that \(W\!\) immediately derives \(W',\!\) by saying that \(W'\!\) is immediately derived from \(W\!\) in \(\mathfrak{G},\) and also by writing:
| \(W ::> W'.\!\) |
A derivation in \(\mathfrak{G}\) is a finite sequence \((W_1, \ldots, W_k)\!\) of sentential forms over \(\mathfrak{G}\) such that each adjacent pair \((W_j, W_{j+1})\!\) of sentential forms in the sequence is an immediate derivation in \(\mathfrak{G},\) in other words, such that:
| \(W_j ::> W_{j+1},\ \text{for all}\ j = 1\ \text{to}\ k - 1.\) |
If there exists a derivation \((W_1, \ldots, W_k)\!\) in \(\mathfrak{G},\) one says that \(W_1\!\) derives \(W_k\!\) in \(\mathfrak{G}\) or that \(W_k\!\) is derivable from \(W_1\!\) in \(\mathfrak{G},\) and one typically summarizes the derivation by writing:
| \(W_1 :\!*\!:> W_k.\!\) |
The language \(\mathfrak{L} = \mathfrak{L} (\mathfrak{G}) = \langle \mathfrak{G} \rangle\) that is generated by the formal grammar \(\mathfrak{G} = ( \, ^{\backprime\backprime} S \, ^{\prime\prime}, \, \mathfrak{Q}, \, \mathfrak{A}, \, \mathfrak{K} \, )\) is the set of strings over the terminal alphabet \(\mathfrak{A}\) that are derivable from the initial symbol \(^{\backprime\backprime} S \, ^{\prime\prime}\) by way of the intermediate symbols in \(\mathfrak{Q}\) according to the characterizations in \(\mathfrak{K}.\) In sum:
| \(\mathfrak{L} (\mathfrak{G}) \ = \ \langle \mathfrak{G} \rangle \ = \ \{ \, W \in \mathfrak{A}^* \, : \, ^{\backprime\backprime} S \, ^{\prime\prime} \, :\!*\!:> \, W \, \}.\) |
Finally, a string \(W\!\) is called a word, a sentence, or so on, of the language generated by \(\mathfrak{G}\) if and only if \(W\!\) is in \(\mathfrak{L} (\mathfrak{G}).\)
The Cactus Language : Stylistics
|
As a result, we can hardly conceive of how many possibilities there are for what we call objective reality. Our sharp quills of knowledge are so narrow and so concentrated in particular directions that with science there are myriads of totally different real worlds, each one accessible from the next simply by slight alterations — shifts of gaze — of every particular discipline and subspecialty. |
| — Herbert J. Bernstein, "Idols of Modern Science", [HJB, 38] |
This Subsection highlights an issue of style that arises in describing a formal language. In broad terms, I use the word style to refer to a loosely specified class of formal systems, typically ones that have a set of distinctive features in common. For instance, a style of proof system usually dictates one or more rules of inference that are acknowledged as conforming to that style. In the present context, the word style is a natural choice to characterize the varieties of formal grammars, or any other sorts of formal systems that can be contemplated for deriving the sentences of a formal language.
In looking at what seems like an incidental issue, the discussion arrives at a critical point. The question is: What decides the issue of style? Taking a given language as the object of discussion, what factors enter into and determine the choice of a style for its presentation, that is, a particular way of arranging and selecting the materials that come to be involved in a description, a grammar, or a theory of the language? To what degree is the determination accidental, empirical, pragmatic, rhetorical, or stylistic, and to what extent is the choice essential, logical, and necessary? For that matter, what determines the order of signs in a word, a sentence, a text, or a discussion? All of the corresponding parallel questions about the character of this choice can be posed with regard to the constituent part as well as with regard to the main constitution of the formal language.
In order to answer this sort of question, at any level of articulation, one has to inquire into the type of distinction that it invokes, between arrangements and orders that are essential, logical, and necessary and orders and arrangements that are accidental, rhetorical, and stylistic. As a rough guide to its comprehension, a logical order, if it resides in the subject at all, can be approached by considering all of the ways of saying the same things, in all of the languages that are capable of saying roughly the same things about that subject. Of course, the all that appears in this rule of thumb has to be interpreted as a fittingly qualified sort of universal. For all practical purposes, it simply means all of the ways that a person can think of and all of the languages that a person can conceive of, with all things being relative to the particular moment of investigation. For all of these reasons, the rule must stand as little more than a rough idea of how to approach its object.
If it is demonstrated that a given formal language can be presented in any one of several styles of formal grammar, then the choice of a format is accidental, optional, and stylistic to the very extent that it is free. But if it can be shown that a particular language cannot be successfully presented in a particular style of grammar, then the issue of style is no longer free and rhetorical, but becomes to that very degree essential, necessary, and obligatory, in other words, a question of the objective logical order that can be found to reside in the object language.
As a rough illustration of the difference between logical and rhetorical orders, consider the kinds of order that are expressed and exhibited in the following conjunction of implications:
| \(X \Rightarrow Y\ \operatorname{and}\ Y \Rightarrow Z.\) |
Here, there is a happy conformity between the logical content and the rhetorical form, indeed, to such a degree that one hardly notices the difference between them. The rhetorical form is given by the order of sentences in the two implications and the order of implications in the conjunction. The logical content is given by the order of propositions in the extended implicational sequence:
| \(X\ \le\ Y\ \le\ Z.\) |
To see the difference between form and content, or manner and matter, it is enough to observe a few of the ways that the expression can be varied without changing its meaning, for example:
| \(Z \Leftarrow Y\ \operatorname{and}\ Y \Leftarrow X.\) |
Any style of declarative programming, also called logic programming, depends on a capacity, as embodied in a programming language or other formal system, to describe the relation between problems and solutions in logical terms. A recurring problem in building this capacity is in bridging the gap between ostensibly non-logical orders and the logical orders that are used to describe and to represent them. For instance, to mention just a couple of the most pressing cases, and the ones that are currently proving to be the most resistant to a complete analysis, one has the orders of dynamic evolution and rhetorical transition that manifest themselves in the process of inquiry and in the communication of its results.
This patch of the ongoing discussion is concerned with describing a particular variety of formal languages, whose typical representative is the painted cactus language \(\mathfrak{L} = \mathfrak{C} (\mathfrak{P}).\) It is the intention of this work to interpret this language for propositional logic, and thus to use it as a sentential calculus, an order of reasoning that forms an active ingredient and a significant component of all logical reasoning. To describe this language, the standard devices of formal grammars and formal language theory are more than adequate, but this only raises the next question: What sorts of devices are exactly adequate, and fit the task to a "T"? The ultimate desire is to turn the tables on the order of description, and so begins a process of eversion that evolves to the point of asking: To what extent can the language capture the essential features and laws of its own grammar and describe the active principles of its own generation? In other words: How well can the language be described by using the language itself to do so?
In order to speak to these questions, I have to express what a grammar says about a language in terms of what a language can say on its own. In effect, it is necessary to analyze the kinds of meaningful statements that grammars are capable of making about languages in general and to relate them to the kinds of meaningful statements that the syntactic sentences of the cactus language might be interpreted as making about the very same topics. So far in the present discussion, the sentences of the cactus language do not make any meaningful statements at all, much less any meaningful statements about languages and their constitutions. As of yet, these sentences subsist in the form of purely abstract, formal, and uninterpreted combinatorial constructions.
Before the capacity of a language to describe itself can be evaluated, the missing link to meaning has to be supplied for each of its strings. This calls for a dimension of semantics and a notion of interpretation, topics that are taken up for the case of the cactus language \(\mathfrak{C} (\mathfrak{P})\) in Subsection 1.3.10.12. Once a plausible semantics is prescribed for this language it will be possible to return to these questions and to address them in a meaningful way.
The prominent issue at this point is the distinct placements of formal languages and formal grammars with respect to the question of meaning. The sentences of a formal language are merely the abstract strings of abstract signs that happen to belong to a certain set. They do not by themselves make any meaningful statements at all, not without mounting a separate effort of interpretation, but the rules of a formal grammar make meaningful statements about a formal language, to the extent that they say what strings belong to it and what strings do not. Thus, the formal grammar, a formalism that appears to be even more skeletal than the formal language, still has bits and pieces of meaning attached to it. In a sense, the question of meaning is factored into two parts, structure and value, leaving the aspect of value reduced in complexity and subtlety to the simple question of belonging. Whether this single bit of meaningful value is enough to encompass all of the dimensions of meaning that we require, and whether it can be compounded to cover the complexity that actually exists in the realm of meaning — these are questions for an extended future inquiry.
Perhaps I ought to comment on the differences between the present and the standard definition of a formal grammar, since I am attempting to strike a compromise with several alternative conventions of usage, and thus to leave certain options open for future exploration. All of the changes are minor, in the sense that they are not intended to alter the classes of languages that are able to be generated, but only to clear up various ambiguities and sundry obscurities that affect their conception.
Primarily, the conventional scope of non-terminal symbols was expanded to encompass the sentence symbol, mainly on account of all the contexts where the initial and the intermediate symbols are naturally invoked in the same breath. By way of compensating for the usual exclusion of the sentence symbol from the non-terminal class, an equivalent distinction was introduced in the fashion of a distinction between the initial and the intermediate symbols, and this serves its purpose in all of those contexts where the two kind of symbols need to be treated separately.
At the present point, I remain a bit worried about the motivations and the justifications for introducing this distinction, under any name, in the first place. It is purportedly designed to guarantee that the process of derivation at least gets started in a definite direction, while the real questions have to do with how it all ends. The excuses of efficiency and expediency that I offered as plausible and sufficient reasons for distinguishing between empty and significant sentences are likely to be ephemeral, if not entirely illusory, since intermediate symbols are still permitted to characterize or to cover themselves, not to mention being allowed to cover the empty string, and so the very types of traps that one exerts oneself to avoid at the outset are always there to afflict the process at all of the intervening times.
If one reflects on the form of grammar that is being prescribed here, it looks as if one sought, rather futilely, to avoid the problems of recursion by proscribing the main program from calling itself, while allowing any subprogram to do so. But any trouble that is avoidable in the part is also avoidable in the main, while any trouble that is inevitable in the part is also inevitable in the main. Consequently, I am reserving the right to change my mind at a later stage, perhaps to permit the initial symbol to characterize, to cover, to regenerate, or to produce itself, if that turns out to be the best way in the end.
Before I leave this Subsection, I need to say a few things about the manner in which the abstract theory of formal languages and the pragmatic theory of sign relations interact with each other.
Formal language theory can seem like an awfully picky subject at times, treating every symbol as a thing in itself the way it does, sorting out the nominal types of symbols as objects in themselves, and singling out the passing tokens of symbols as distinct entities in their own rights. It has to continue doing this, if not for any better reason than to aid in clarifying the kinds of languages that people are accustomed to use, to assist in writing computer programs that are capable of parsing real sentences, and to serve in designing programming languages that people would like to become accustomed to use. As a matter of fact, the only time that formal language theory becomes too picky, or a bit too myopic in its focus, is when it leads one to think that one is dealing with the thing itself and not just with the sign of it, in other words, when the people who use the tools of formal language theory forget that they are dealing with the mere signs of more interesting objects and not with the objects of ultimate interest in and of themselves.
As a result, there a number of deleterious effects that can arise from the extreme pickiness of formal language theory, arising, as is often the case, when formal theorists forget the practical context of theorization. It frequently happens that the exacting task of defining the membership of a formal language leads one to think that this object and this object alone is the justifiable end of the whole exercise. The distractions of this mediate objective render one liable to forget that one's penultimate interest lies always with various kinds of equivalence classes of signs, not entirely or exclusively with their more meticulous representatives.
When this happens, one typically goes on working oblivious to the fact that many details about what transpires in the meantime do not matter at all in the end, and one is likely to remain in blissful ignorance of the circumstance that many special details of language membership are bound, destined, and pre-determined to be glossed over with some measure of indifference, especially when it comes down to the final constitution of those equivalence classes of signs that are able to answer for the genuine objects of the whole enterprise of language. When any form of theory, against its initial and its best intentions, leads to this kind of absence of mind that is no longer beneficial in all of its main effects, the situation calls for an antidotal form of theory, one that can restore the presence of mind that all forms of theory are meant to augment.
The pragmatic theory of sign relations is called for in settings where everything that can be named has many other names, that is to say, in the usual case. Of course, one would like to replace this superfluous multiplicity of signs with an organized system of canonical signs, one for each object that needs to be denoted, but reducing the redundancy too far, beyond what is necessary to eliminate the factor of "noise" in the language, that is, to clear up its effectively useless distractions, can destroy the very utility of a typical language, which is intended to provide a ready means to express a present situation, clear or not, and to describe an ongoing condition of experience in just the way that it seems to present itself. Within this fleshed out framework of language, moreover, the process of transforming the manifestations of a sign from its ordinary appearance to its canonical aspect is the whole problem of computation in a nutshell.
It is a well-known truth, but an often forgotten fact, that nobody computes with numbers, but solely with numerals in respect of numbers, and numerals themselves are symbols. Among other things, this renders all discussion of numeric versus symbolic computation a bit beside the point, since it is only a question of what kinds of symbols are best for one's immediate application or for one's selection of ongoing objectives. The numerals that everybody knows best are just the canonical symbols, the standard signs or the normal terms for numbers, and the process of computation is a matter of getting from the arbitrarily obscure signs that the data of a situation are capable of throwing one's way to the indications of its character that are clear enough to motivate action.
Having broached the distinction between propositions and sentences, one can see its similarity to the distinction between numbers and numerals. What are the implications of the foregoing considerations for reasoning about propositions and for the realm of reckonings in sentential logic? If the purpose of a sentence is just to denote a proposition, then the proposition is just the object of whatever sign is taken for a sentence. This means that the computational manifestation of a piece of reasoning about propositions amounts to a process that takes place entirely within a language of sentences, a procedure that can rationalize its account by referring to the denominations of these sentences among propositions.
The application of these considerations in the immediate setting is this: Do not worry too much about what roles the empty string \(\varepsilon \, = \, ^{\backprime\backprime\prime\prime}\) and the blank symbol \(m_1 \, = \, ^{\backprime\backprime} \operatorname{~} ^{\prime\prime}\) are supposed to play in a given species of formal languages. As it happens, it is far less important to wonder whether these types of formal tokens actually constitute genuine sentences than it is to decide what equivalence classes it makes sense to form over all of the sentences in the resulting language, and only then to bother about what equivalence classes these limiting cases of sentences are most conveniently taken to represent.
These concerns about boundary conditions betray a more general issue. Already by this point in discussion the limits of the purely syntactic approach to a language are beginning to be visible. It is not that one cannot go a whole lot further by this road in the analysis of a particular language and in the study of languages in general, but when it comes to the questions of understanding the purpose of a language, of extending its usage in a chosen direction, or of designing a language for a particular set of uses, what matters above all else are the pragmatic equivalence classes of signs that are demanded by the application and intended by the designer, and not so much the peculiar characters of the signs that represent these classes of practical meaning.
Any description of a language is bound to have alternative descriptions. More precisely, a circumscribed description of a formal language, as any effectively finite description is bound to be, is certain to suggest the equally likely existence and the possible utility of other descriptions. A single formal grammar describes but a single formal language, but any formal language is described by many different formal grammars, not all of which afford the same grasp of its structure, provide an equivalent comprehension of its character, or yield an interchangeable view of its aspects. Consequently, even with respect to the same formal language, different formal grammars are typically better for different purposes.
With the distinctions that evolve among the different styles of grammar, and with the preferences that different observers display toward them, there naturally comes the question: What is the root of this evolution?
One dimension of variation in the styles of formal grammars can be seen by treating the union of languages, and especially the disjoint union of languages, as a sum, by treating the concatenation of languages as a product, and then by distinguishing the styles of analysis that favor sums of products from those that favor products of sums as their canonical forms of description. If one examines the relation between languages and grammars carefully enough to see the presence and the influence of these different styles, and when one comes to appreciate the ways that different styles of grammars can be used with different degrees of success for different purposes, then one begins to see the possibility that alternative styles of description can be based on altogether different linguistic and logical operations.
It possible to trace this divergence of styles to an even more primitive division, one that distinguishes the additive or the parallel styles from the multiplicative or the serial styles. The issue is somewhat confused by the fact that an additive analysis is typically expressed in the form of a series, in other words, a disjoint union of sets or a linear sum of their independent effects. But it is easy enough to sort this out if one observes the more telling connection between parallel and independent. Another way to keep the right associations straight is to employ the term sequential in preference to the more misleading term serial. Whatever one calls this broad division of styles, the scope and sweep of their dimensions of variation can be delineated in the following way:
- The additive or parallel styles favor sums of products \((\textstyle\sum\prod)\) as canonical forms of expression, pulling sums, unions, co-products, and logical disjunctions to the outermost layers of analysis and synthesis, while pushing products, intersections, concatenations, and logical conjunctions to the innermost levels of articulation and generation. In propositional logic, this style leads to the disjunctive normal form (DNF).
- The multiplicative or serial styles favor products of sums \((\textstyle\prod\sum)\) as canonical forms of expression, pulling products, intersections, concatenations, and logical conjunctions to the outermost layers of analysis and synthesis, while pushing sums, unions, co-products, and logical disjunctions to the innermost levels of articulation and generation. In propositional logic, this style leads to the conjunctive normal form (CNF).
There is a curious sort of diagnostic clue that often serves to reveal the dominance of one mode or the other within an individual thinker's cognitive style. Examined on the question of what constitutes the natural numbers, an additive thinker tends to start the sequence at 0, while a multiplicative thinker tends to regard it as beginning at 1.
In any style of description, grammar, or theory of a language, it is usually possible to tease out the influence of these contrasting traits, namely, the additive attitude versus the mutiplicative tendency that go to make up the particular style in question, and even to determine the dominant inclination or point of view that establishes its perspective on the target domain.
In each style of formal grammar, the multiplicative aspect is present in the sequential concatenation of signs, both in the augmented strings and in the terminal strings. In settings where the non-terminal symbols classify types of strings, the concatenation of the non-terminal symbols signifies the cartesian product over the corresponding sets of strings.
In the context-free style of formal grammar, the additive aspect is easy enough to spot. It is signaled by the parallel covering of many augmented strings or sentential forms by the same non-terminal symbol. Expressed in active terms, this calls for the independent rewriting of that non-terminal symbol by a number of different successors, as in the following scheme:
|
\(\begin{matrix} q & :> & W_1 \\ \\ \cdots & \cdots & \cdots \\ \\ q & :> & W_k \\ \end{matrix}\) |
It is useful to examine the relationship between the grammatical covering or production relation \((:>\!)\) and the logical relation of implication \((\Rightarrow),\) with one eye to what they have in common and one eye to how they differ. The production \(q :> W\!\) says that the appearance of the symbol \(q\!\) in a sentential form implies the possibility of exchanging it for \(W.\!\) Although this sounds like a possible implication, to the extent that \(q\!\) implies a possible \(W\!\) or that \(q\!\) possibly implies \(W,\!\) the qualifiers possible and possibly are the critical elements in these statements, and they are crucial to the meaning of what is actually being implied. In effect, these qualifications reverse the direction of implication, yielding \(^{\backprime\backprime} \, q \Leftarrow W \, ^{\prime\prime}\) as the best analogue for the sense of the production.
One way to sum this up is to say that non-terminal symbols have the significance of hypotheses. The terminal strings form the empirical matter of a language, while the non-terminal symbols mark the patterns or the types of substrings that can be noticed in the profusion of data. If one observes a portion of a terminal string that falls into the pattern of the sentential form \(W,\!\) then it is an admissible hypothesis, according to the theory of the language that is constituted by the formal grammar, that this piece not only fits the type \(q\!\) but even comes to be generated under the auspices of the non-terminal symbol \(^{\backprime\backprime} q ^{\prime\prime}.\)
A moment's reflection on the issue of style, giving due consideration to the received array of stylistic choices, ought to inspire at least the question: "Are these the only choices there are?" In the present setting, there are abundant indications that other options, more differentiated varieties of description and more integrated ways of approaching individual languages, are likely to be conceivable, feasible, and even more ultimately viable. If a suitably generic style, one that incorporates the full scope of logical combinations and operations, is broadly available, then it would no longer be necessary, or even apt, to argue in universal terms about which style is best, but more useful to investigate how we might adapt the local styles to the local requirements. The medium of a generic style would yield a viable compromise between additive and multiplicative canons, and render the choice between parallel and serial a false alternative, at least, when expressed in the globally exclusive terms that are currently most commonly adopted to pose it.
One set of indications comes from the study of machines, languages, and computation, especially the theories of their structures and relations. The forms of composition and decomposition that are generally known as parallel and serial are merely the extreme special cases, in variant directions of specialization, of a more generic form, usually called the cascade form of combination. This is a well-known fact in the theories that deal with automata and their associated formal languages, but its implications do not seem to be widely appreciated outside these fields. In particular, it dispells the need to choose one extreme or the other, since most of the natural cases are likely to exist somewhere in between.
Another set of indications appears in algebra and category theory, where forms of composition and decomposition related to the cascade combination, namely, the semi-direct product and its special case, the wreath product, are encountered at higher levels of generality than the cartesian products of sets or the direct products of spaces.
In these domains of operation, one finds it necessary to consider also the co-product of sets and spaces, a construction that artificially creates a disjoint union of sets, that is, a union of spaces that are being treated as independent. It does this, in effect, by indexing, coloring, or preparing the otherwise possibly overlapping domains that are being combined. What renders this a chimera or a hybrid form of combination is the fact that this indexing is tantamount to a cartesian product of a singleton set, namely, the conventional index, color, or affix in question, with the individual domain that is entering as a factor, a term, or a participant in the final result.
One of the insights that arises out of Peirce's logical work is that the set operations of complementation, intersection, and union, along with the logical operations of negation, conjunction, and disjunction that operate in isomorphic tandem with them, are not as fundamental as they first appear. This is because all of them can be constructed from or derived from a smaller set of operations, in fact, taking the logical side of things, from either one of two sole sufficient operators, called amphecks by Peirce, strokes by those who re-discovered them later, and known in computer science as the NAND and the NNOR operators. For this reason, that is, by virtue of their precedence in the orders of construction and derivation, these operations have to be regarded as the simplest and the most primitive in principle, even if they are scarcely recognized as lying among the more familiar elements of logic.
I am throwing together a wide variety of different operations into each of the bins labeled additive and multiplicative, but it is easy to observe a natural organization and even some relations approaching isomorphisms among and between the members of each class.
The relation between logical disjunction and set-theoretic union and the relation between logical conjunction and set-theoretic intersection ought to be clear enough for the purposes of the immediately present context. In any case, all of these relations are scheduled to receive a thorough examination in a subsequent discussion (Subsection 1.3.10.13). But the relation of a set-theoretic union to a category-theoretic co-product and the relation of a set-theoretic intersection to a syntactic concatenation deserve a closer look at this point.
The effect of a co-product as a disjointed union, in other words, that creates an object tantamount to a disjoint union of sets in the resulting co-product even if some of these sets intersect non-trivially and even if some of them are identical in reality, can be achieved in several ways. The most usual conception is that of making a separate copy, for each part of the intended co-product, of the set that is intended to go there. Often one thinks of the set that is assigned to a particular part of the co-product as being distinguished by a particular color, in other words, by the attachment of a distinct index, label, or tag, being a marker that is inherited by and passed on to every element of the set in that part. A concrete image of this construction can be achieved by imagining that each set and each element of each set is placed in an ordered pair with the sign of its color, index, label, or tag. One describes this as the injection of each set into the corresponding part of the co-product.
For example, given the sets \(P\!\) and \(Q,\!\) overlapping or not, one can define the indexed or marked sets \(P_{[1]}\!\) and \(Q_{[2]},\!\) amounting to the copy of \(P\!\) into the first part of the co-product and the copy of \(Q\!\) into the second part of the co-product, in the following manner:
|
\(\begin{array}{lllll} P_{[1]} & = & (P, 1) & = & \{ (x, 1) : x \in P \}, \\ Q_{[2]} & = & (Q, 2) & = & \{ (x, 2) : x \in Q \}. \\ \end{array}\) |
Using the coproduct operator (\(\textstyle\coprod\)) for this construction, the sum, the coproduct, or the disjointed union of \(P\!\) and \(Q\!\) in that order can be represented as the ordinary union of \(P_{[1]}\!\) and \(Q_{[2]}.\!\)
|
\(\begin{array}{lll} P \coprod Q & = & P_{[1]} \cup Q_{[2]}. \\ \end{array}\) |
The concatenation \(\mathfrak{L}_1 \cdot \mathfrak{L}_2\) of the formal languages \(\mathfrak{L}_1\) and \(\mathfrak{L}_2\) is just the cartesian product of sets \(\mathfrak{L}_1 \times \mathfrak{L}_2\) without the extra \(\times\)'s, but the relation of cartesian products to set-theoretic intersections and thus to logical conjunctions is far from being clear. One way of seeing a type of relation is to focus on the information that is needed to specify each construction, and thus to reflect on the signs that are used to carry this information. As a first approach to the topic of information, according to a strategy that seeks to be as elementary and as informal as possible, I introduce the following set of ideas, intended to be taken in a very provisional way.
A stricture is a specification of a certain set in a certain place, relative to a number of other sets, yet to be specified. It is assumed that one knows enough to tell if two strictures are equivalent as pieces of information, but any more determinate indications, like names for the places that are mentioned in the stricture, or bounds on the number of places that are involved, are regarded as being extraneous impositions, outside the proper concern of the definition, no matter how convenient they are found to be for a particular discussion. As a schematic form of illustration, a stricture can be pictured in the following shape:
\(^{\backprime\backprime}\) \(\ldots \times X \times Q \times X \times \ldots\) \(^{\prime\prime}\)
A strait is the object that is specified by a stricture, in effect, a certain set in a certain place of an otherwise yet to be specified relation. Somewhat sketchily, the strait that corresponds to the stricture just given can be pictured in the following shape:
\(\ldots \times X \times Q \times X \times \ldots\)
In this picture \(Q\!\) is a certain set and \(X\!\) is the universe of discourse that is relevant to a given discussion. Since a stricture does not, by itself, contain a sufficient amount of information to specify the number of sets that it intends to set in place, or even to specify the absolute location of the set that its does set in place, it appears to place an unspecified number of unspecified sets in a vague and uncertain strait. Taken out of its interpretive context, the residual information that a stricture can convey makes all of the following potentially equivalent as strictures:
|
\(\begin{array}{ccccccc} ^{\backprime\backprime} Q ^{\prime\prime} & , & ^{\backprime\backprime} X \times Q \times X ^{\prime\prime} & , & ^{\backprime\backprime} X \times X \times Q \times X \times X ^{\prime\prime} & , & \ldots \\ \end{array}\) |
With respect to what these strictures specify, this leaves all of the following equivalent as straits:
|
\(\begin{array}{ccccccc} Q & = & X \times Q \times X & = & X \times X \times Q \times X \times X & = & \ldots \\ \end{array}\) |
Within the framework of a particular discussion, it is customary to set a bound on the number of places and to limit the variety of sets that are regarded as being under active consideration, and it is also convenient to index the places of the indicated relations, and of their encompassing cartesian products, in some fixed way. But the whole idea of a stricture is to specify a strait that is capable of extending through and beyond any fixed frame of discussion. In other words, a stricture is conceived to constrain a strait at a certain point, and then to leave it literally embedded, if tacitly expressed, in a yet to be fully specified relation, one that involves an unspecified number of unspecified domains.
A quantity of information is a measure of constraint. In this respect, a set of comparable strictures is ordered on account of the information that each one conveys, and a system of comparable straits is ordered in accord with the amount of information that it takes to pin each one of them down. Strictures that are more constraining and straits that are more constrained are placed at higher levels of information than those that are less so, and entities that involve more information are said to have a greater complexity in comparison with those entities that involve less information, that are said to have a greater simplicity.
In order to create a concrete example, let me now institute a frame of discussion where the number of places in a relation is bounded at two, and where the variety of sets under active consideration is limited to the typical subsets \(P\!\) and \(Q\!\) of a universe \(X.\!\) Under these conditions, one can use the following sorts of expression as schematic strictures:
|
\(\begin{matrix} ^{\backprime\backprime} X ^{\prime\prime} & ^{\backprime\backprime} P ^{\prime\prime} & ^{\backprime\backprime} Q ^{\prime\prime} \\ \\ ^{\backprime\backprime} X \times X ^{\prime\prime} & ^{\backprime\backprime} X \times P ^{\prime\prime} & ^{\backprime\backprime} X \times Q ^{\prime\prime} \\ \\ ^{\backprime\backprime} P \times X ^{\prime\prime} & ^{\backprime\backprime} P \times P ^{\prime\prime} & ^{\backprime\backprime} P \times Q ^{\prime\prime} \\ \\ ^{\backprime\backprime} Q \times X ^{\prime\prime} & ^{\backprime\backprime} Q \times P ^{\prime\prime} & ^{\backprime\backprime} Q \times Q ^{\prime\prime} \\ \end{matrix}\) |
These strictures and their corresponding straits are stratified according to their amounts of information, or their levels of constraint, as follows:
|
\(\begin{array}{lcccc} \text{High:} & ^{\backprime\backprime} P \times P ^{\prime\prime} & ^{\backprime\backprime} P \times Q ^{\prime\prime} & ^{\backprime\backprime} Q \times P ^{\prime\prime} & ^{\backprime\backprime} Q \times Q ^{\prime\prime} \\ \\ \text{Med:} & ^{\backprime\backprime} P ^{\prime\prime} & ^{\backprime\backprime} X \times P ^{\prime\prime} & ^{\backprime\backprime} P \times X ^{\prime\prime} \\ \\ \text{Med:} & ^{\backprime\backprime} Q ^{\prime\prime} & ^{\backprime\backprime} X \times Q ^{\prime\prime} & ^{\backprime\backprime} Q \times X ^{\prime\prime} \\ \\ \text{Low:} & ^{\backprime\backprime} X ^{\prime\prime} & ^{\backprime\backprime} X \times X ^{\prime\prime} \\ \end{array}\) |
Within this framework, the more complex strait \(P \times Q\) can be expressed in terms of the simpler straits, \(P \times X\) and \(X \times Q.\) More specifically, it lends itself to being analyzed as their intersection, in the following way:
|
\(\begin{array}{lllll} P \times Q & = & P \times X & \cap & X \times Q. \\ \end{array}\) |
From here it is easy to see the relation of concatenation, by virtue of these types of intersection, to the logical conjunction of propositions. The cartesian product \(P \times Q\) is described by a conjunction of propositions, namely, \(P_{[1]} \land Q_{[2]},\) subject to the following interpretation:
- \(P_{[1]}\!\) asserts that there is an element from the set \(P\!\) in the first place of the product.
- \(Q_{[2]}\!\) asserts that there is an element from the set \(Q\!\) in the second place of the product.
The integration of these two pieces of information can be taken in that measure to specify a yet to be fully determined relation.
In a corresponding fashion at the level of the elements, the ordered pair \((p, q)\!\) is described by a conjunction of propositions, namely, \(p_{[1]} \land q_{[2]},\) subject to the following interpretation:
- \(p_{[1]}\!\) says that \(p\!\) is in the first place of the product element under construction.
- \(q_{[2]}\!\) says that \(q\!\) is in the second place of the product element under construction.
Notice that, in construing the cartesian product of the sets \(P\!\) and \(Q\!\) or the concatenation of the languages \(\mathfrak{L}_1\) and \(\mathfrak{L}_2\) in this way, one shifts the level of the active construction from the tupling of the elements in \(P\!\) and \(Q\!\) or the concatenation of the strings that are internal to the languages \(\mathfrak{L}_1\) and \(\mathfrak{L}_2\) to the concatenation of the external signs that it takes to indicate these sets or these languages, in other words, passing to a conjunction of indexed propositions, \(P_{[1]}\!\) and \(Q_{[2]},\!\) or to a conjunction of assertions, \((\mathfrak{L}_1)_{[1]}\) and \((\mathfrak{L}_2)_{[2]},\) that marks the sets or the languages in question for insertion in the indicated places of a product set or a product language, respectively. In effect, the subscripting by the indices \(^{\backprime\backprime} [1] ^{\prime\prime}\) and \(^{\backprime\backprime} [2] ^{\prime\prime}\) can be recognized as a special case of concatenation, albeit through the posting of editorial remarks from an external mark-up language.
In order to systematize the relations that strictures and straits placed at higher levels of complexity, constraint, information, and organization have with those that are placed at the associated lower levels, I introduce the following pair of definitions:
The \(j^\text{th}\!\) excerpt of a stricture of the form \(^{\backprime\backprime} \, S_1 \times \ldots \times S_k \, ^{\prime\prime},\) regarded within a frame of discussion where the number of places is limited to \(k,\!\) is the stricture of the form \(^{\backprime\backprime} \, X \times \ldots \times S_j \times \ldots \times X \, ^{\prime\prime}.\) In the proper context, this can be written more succinctly as the stricture \(^{\backprime\backprime} \, (S_j)_{[j]} \, ^{\prime\prime},\) an assertion that places the \(j^\text{th}\!\) set in the \(j^\text{th}\!\) place of the product.
The \(j^\text{th}\!\) extract of a strait of the form \(S_1 \times \ldots \times S_k,\!\) constrained to a frame of discussion where the number of places is restricted to \(k,\!\) is the strait of the form \(X \times \ldots \times S_j \times \ldots \times X.\) In the appropriate context, this can be denoted more succinctly by the stricture \(^{\backprime\backprime} \, (S_j)_{[j]} \, ^{\prime\prime},\) an assertion that places the \(j^\text{th}\!\) set in the \(j^\text{th}\!\) place of the product.
In these terms, a stricture of the form \(^{\backprime\backprime} \, S_1 \times \ldots \times S_k \, ^{\prime\prime}\) can be expressed in terms of simpler strictures, to wit, as a conjunction of its \(k\!\) excerpts:
|
\(\begin{array}{lll} ^{\backprime\backprime} \, S_1 \times \ldots \times S_k \, ^{\prime\prime} & = & ^{\backprime\backprime} \, (S_1)_{[1]} \, ^{\prime\prime} \, \land \, \ldots \, \land \, ^{\backprime\backprime} \, (S_k)_{[k]} \, ^{\prime\prime}. \end{array}\) |
In a similar vein, a strait of the form \(S_1 \times \ldots \times S_k\!\) can be expressed in terms of simpler straits, namely, as an intersection of its \(k\!\) extracts:
|
\(\begin{array}{lll} S_1 \times \ldots \times S_k & = & (S_1)_{[1]} \, \cap \, \ldots \, \cap \, (S_k)_{[k]}. \end{array}\) |
There is a measure of ambiguity that remains in this formulation, but it is the best that I can do in the present informal context.
The Cactus Language : Mechanics
|
We are only now beginning to see how this works. Clearly one of the mechanisms for picking a reality is the sociohistorical sense of what is important — which research program, with all its particularity of knowledge, seems most fundamental, most productive, most penetrating. The very judgments which make us push narrowly forward simultaneously make us forget how little we know. And when we look back at history, where the lesson is plain to find, we often fail to imagine ourselves in a parallel situation. We ascribe the differences in world view to error, rather than to unexamined but consistent and internally justified choice. |
| — Herbert J. Bernstein, "Idols of Modern Science", [HJB, 38] |
In this Subsection, I discuss the mechanics of parsing the cactus language into the corresponding class of computational data structures. This provides each sentence of the language with a translation into a computational form that articulates its syntactic structure and prepares it for automated modes of processing and evaluation. For this purpose, it is necessary to describe the target data structures at a fairly high level of abstraction only, ignoring the details of address pointers and record structures and leaving the more operational aspects of implementation to the imagination of prospective programmers. In this way, I can put off to another stage of elaboration and refinement the description of the program that constructs these pointers and operates on these graph-theoretic data structures.
The structure of a painted cactus, insofar as it presents itself to the visual imagination, can be described as follows. The overall structure, as given by its underlying graph, falls within the species of graph that is commonly known as a rooted cactus, and the only novel feature that it adds to this is that each of its nodes can be painted with a finite sequence of paints, chosen from a palette that is given by the parametric set \(\{ \, ^{\backprime\backprime} \operatorname{~} ^{\prime\prime} \, \} \cup \mathfrak{P} = \{ m_1 \} \cup \{ p_1, \ldots, p_k \}.\)
It is conceivable, from a purely graph-theoretical point of view, to have a class of cacti that are painted but not rooted, and so it is frequently necessary, for the sake of precision, to more exactly pinpoint the target species of graphical structure as a painted and rooted cactus (PARC).
A painted cactus, as a rooted graph, has a distinguished node that is called its root. By starting from the root and working recursively, the rest of its structure can be described in the following fashion.
Each node of a PARC consists of a graphical point or vertex plus a finite sequence of attachments, described in relative terms as the attachments at or to that node. An empty sequence of attachments defines the empty node. Otherwise, each attachment is one of three kinds: a blank, a paint, or a type of PARC that is called a lobe.
Each lobe of a PARC consists of a directed graphical cycle plus a finite sequence of accoutrements, described in relative terms as the accoutrements of or on that lobe. Recalling the circumstance that every lobe that comes under consideration comes already attached to a particular node, exactly one vertex of the corresponding cycle is the vertex that comes from that very node. The remaining vertices of the cycle have their definitions filled out according to the accoutrements of the lobe in question. An empty sequence of accoutrements is taken to be tantamount to a sequence that contains a single empty node as its unique accoutrement, and either one of these ways of approaching it can be regarded as defining a graphical structure that is called a needle or a terminal edge. Otherwise, each accoutrement of a lobe is itself an arbitrary PARC.
Although this definition of a lobe in terms of its intrinsic structural components is logically sufficient, it is also useful to characterize the structure of a lobe in comparative terms, that is, to view the structure that typifies a lobe in relation to the structures of other PARC's and to mark the inclusion of this special type within the general run of PARC's. This approach to the question of types results in a form of description that appears to be a bit more analytic, at least, in mnemonic or prima facie terms, if not ultimately more revealing. Working in this vein, a lobe can be characterized as a special type of PARC that is called an unpainted root plant (UR-plant).
An UR-plant is a PARC of a simpler sort, at least, with respect to the recursive ordering of structures that is being followed here. As a type, it is defined by the presence of two properties, that of being planted and that of having an unpainted root. These are defined as follows:
- A PARC is planted if its list of attachments has just one PARC.
- A PARC is UR if its list of attachments has no blanks or paints.
In short, an UR-planted PARC has a single PARC as its only attachment, and since this attachment is prevented from being a blank or a paint, the single attachment at its root has to be another sort of structure, that which we call a lobe.
To express the description of a PARC in terms of its nodes, each node can be specified in the fashion of a functional expression, letting a citation of the generic function name "\(\operatorname{Node}\)" be followed by a list of arguments that enumerates the attachments of the node in question, and letting a citation of the generic function name "\(\operatorname{Lobe}\)" be followed by a list of arguments that details the accoutrements of the lobe in question. Thus, one can write expressions of the following forms:
| \(1.\!\) | \(\operatorname{Node}^0\) | \(=\!\) | \(\operatorname{Node}()\) |
| \(=\!\) | a node with no attachments. | ||
| \(\operatorname{Node}_{j=1}^k C_j\) | \(=\!\) | \(\operatorname{Node} (C_1, \ldots, C_k)\) | |
| \(=\!\) | a node with the attachments \(C_1, \ldots, C_k.\) | ||
| \(2.\!\) | \(\operatorname{Lobe}^0\) | \(=\!\) | \(\operatorname{Lobe}()\) |
| \(=\!\) | a lobe with no accoutrements. | ||
| \(\operatorname{Lobe}_{j=1}^k C_j\) | \(=\!\) | \(\operatorname{Lobe} (C_1, \ldots, C_k)\) | |
| \(=\!\) | a lobe with the accoutrements \(C_1, \ldots, C_k.\) |
Working from a structural description of the cactus language, or any suitable formal grammar for \(\mathfrak{C} (\mathfrak{P}),\) it is possible to give a recursive definition of the function called \(\operatorname{Parse}\) that maps each sentence in \(\operatorname{PARCE} (\mathfrak{P})\) to the corresponding graph in \(\operatorname{PARC} (\mathfrak{P}).\) One way to do this proceeds as follows:
- The parse of the concatenation \(\operatorname{Conc}_{j=1}^k\) of the \(k\!\) sentences \((s_j)_{j=1}^k\) is defined recursively as follows:
- \(\operatorname{Parse} (\operatorname{Conc}^0) ~=~ \operatorname{Node}^0.\)
-
For \(k > 0,\!\)
\(\operatorname{Parse} (\operatorname{Conc}_{j=1}^k s_j) ~=~ \operatorname{Node}_{j=1}^k \operatorname{Parse} (s_j).\)
- The parse of the surcatenation \(\operatorname{Surc}_{j=1}^k\) of the \(k\!\) sentences \((s_j)_{j=1}^k\) is defined recursively as follows:
- \(\operatorname{Parse} (\operatorname{Surc}^0) ~=~ \operatorname{Lobe}^0.\)
-
For \(k > 0,\!\)
\(\operatorname{Parse} (\operatorname{Surc}_{j=1}^k s_j) ~=~ \operatorname{Lobe}_{j=1}^k \operatorname{Parse} (s_j).\)
For ease of reference, Table 13 summarizes the mechanics of these parsing rules.
| ||||||
| ||||||
|
A substructure of a PARC is defined recursively as follows. Starting at the root node of the cactus \(C,\!\) any attachment is a substructure of \(C.\!\) If a substructure is a blank or a paint, then it constitutes a minimal substructure, meaning that no further substructures of \(C\!\) arise from it. If a substructure is a lobe, then each one of its accoutrements is also a substructure of \(C,\!\) and has to be examined for further substructures.
The concept of substructure can be used to define varieties of deletion and erasure operations that respect the structure of the abstract graph. For the purposes of this depiction, a blank symbol \(^{\backprime\backprime} ~ ^{\prime\prime}\) is treated as a primer, in other words, as a clear paint or a neutral tint. In effect, one is letting \(m_1 = p_0.\!\) In this frame of discussion, it is useful to make the following distinction:
- To delete a substructure is to replace it with an empty node, in effect, to reduce the whole structure to a trivial point.
- To erase a substructure is to replace it with a blank symbol, in effect, to paint it out of the picture or to overwrite it.
A bare PARC, loosely referred to as a bare cactus, is a PARC on the empty palette \(\mathfrak{P} = \varnothing.\) In other veins, a bare cactus can be described in several different ways, depending on how the form arises in practice.
- Leaning on the definition of a bare PARCE, a bare PARC can be described as the kind of a parse graph that results from parsing a bare cactus expression, in other words, as the kind of a graph that issues from the requirements of processing a sentence of the bare cactus language \(\mathfrak{C}^0 = \operatorname{PARCE}^0.\)
- To express it more in its own terms, a bare PARC can be defined by tracing the recursive definition of a generic PARC, but then by detaching an independent form of description from the source of that analogy. The method is sufficiently sketched as follows:
- A bare PARC is a PARC whose attachments are limited to blanks and bare lobes.
- A bare lobe is a lobe whose accoutrements are limited to bare PARC's.
- In practice, a bare cactus is usually encountered in the process of analyzing or handling an arbitrary PARC, the circumstances of which frequently call for deleting or erasing all of its paints. In particular, this generally makes it easier to observe the various properties of its underlying graphical structure.
The Cactus Language : Semantics
|
Alas, and yet what are you, my written and painted thoughts! It is not long ago that you were still so many-coloured, young and malicious, so full of thorns and hidden spices you made me sneeze and laugh — and now? You have already taken off your novelty and some of you, I fear, are on the point of becoming truths: they already look so immortal, so pathetically righteous, so boring! |
| — Nietzsche, Beyond Good and Evil, [Nie-2, ¶ 296] |
In this Subsection, I describe a particular semantics for the painted cactus language, telling what meanings I aim to attach to its bare syntactic forms. This supplies an interpretation for this parametric family of formal languages, but it is good to remember that it forms just one of many such interpretations that are conceivable and even viable. In deed, the distinction between the object domain and the sign domain can be observed in the fact that many languages can be deployed to depict the same set of objects and that any language worth its salt is bound to to give rise to many different forms of interpretive saliency.
In formal settings, it is common to speak of interpretation as if it created a direct connection between the signs of a formal language and the objects of the intended domain, in other words, as if it determined the denotative component of a sign relation. But a closer attention to what goes on reveals that the process of interpretation is more indirect, that what it does is to provide each sign of a prospectively meaningful source language with a translation into an already established target language, where already established means that its relationship to pragmatic objects is taken for granted at the moment in question.
With this in mind, it is clear that interpretation is an affair of signs that at best respects the objects of all of the signs that enter into it, and so it is the connotative aspect of semiotics that is at stake here. There is nothing wrong with my saying that I interpret a sentence of a formal language as a sign that refers to a function or to a proposition, so long as you understand that this reference is likely to be achieved by way of more familiar and perhaps less formal signs that you already take to denote those objects.
On entering a context where a logical interpretation is intended for the sentences of a formal language there are a few conventions that make it easier to make the translation from abstract syntactic forms to their intended semantic senses. Although these conventions are expressed in unnecessarily colorful terms, from a purely abstract point of view, they do provide a useful array of connotations that help to negotiate what is otherwise a difficult transition. This terminology is introduced as the need for it arises in the process of interpreting the cactus language.
The task of this Subsection is to specify a semantic function for the sentences of the cactus language \(\mathfrak{L} = \mathfrak{C}(\mathfrak{P}),\) in other words, to define a mapping that "interprets" each sentence of \(\mathfrak{C}(\mathfrak{P})\) as a sentence that says something, as a sentence that bears a meaning, in short, as a sentence that denotes a proposition, and thus as a sign of an indicator function. When the syntactic sentences of a formal language are given a referent significance in logical terms, for example, as denoting propositions or indicator functions, then each form of syntactic combination takes on a corresponding form of logical significance.
By way of providing a logical interpretation for the cactus language, I introduce a family of operators on indicator functions that are called propositional connectives, and I distinguish these from the associated family of syntactic combinations that are called sentential connectives, where the relationship between these two realms of connection is exactly that between objects and their signs. A propositional connective, as an entity of a well-defined functional and operational type, can be treated in every way as a logical or a mathematical object, and thus as the type of object that can be denoted by the corresponding form of syntactic entity, namely, the sentential connective that is appropriate to the case in question.
There are two basic types of connectives, called the blank connectives and the bound connectives, respectively, with one connective of each type for each natural number \(k = 0, 1, 2, 3, \ldots.\)
-
The blank connective of \(k\!\) places is signified by the concatenation of the \(k\!\) sentences that fill those places.
For the special case of \(k = 0,\!\) the blank connective is taken to be an empty string or a blank symbol — it does not matter which, since both are assigned the same denotation among propositions.
For the generic case of \(k > 0,\!\) the blank connective takes the form \(s_1 \cdot \ldots \cdot s_k.\) In the type of data that is called a text, the use of the center dot \((\cdot)\) is generally supplanted by whatever number of spaces and line breaks serve to improve the readability of the resulting text.
-
The bound connective of \(k\!\) places is signified by the surcatenation of the \(k\!\) sentences that fill those places.
For the special case of \(k = 0,\!\) the bound connective is taken to be an empty closure — an expression enjoying one of the forms \(\underline{(} \underline{)}, \, \underline{(} ~ \underline{)}, \, \underline{(} ~~ \underline{)}, \, \ldots\) with any number of blank symbols between the parentheses — all of which are assigned the same logical denotation among propositions.
For the generic case of \(k > 0,\!\) the bound connective takes the form \(\underline{(} s_1, \ldots, s_k \underline{)}.\)
At this point, there are actually two different dialects, scripts, or modes of presentation for the cactus language that need to be interpreted, in other words, that need to have a semantic function defined on their domains.
- There is the literal formal language of strings in \(\operatorname{PARCE} (\mathfrak{P}),\) the painted and rooted cactus expressions that constitute the language \(\mathfrak{L} = \mathfrak{C} (\mathfrak{P}) \subseteq \mathfrak{A}^* = (\mathfrak{M} \cup \mathfrak{P})^*.\)
- There is the figurative formal language of graphs in \(\operatorname{PARC} (\mathfrak{P}),\) the painted and rooted cacti themselves, a parametric family of graphs or a species of computational data structures that is graphically analogous to the language of literal strings.
Of course, these two modalities of formal language, like written and spoken natural languages, are meant to have compatible interpretations, and so it is usually sufficient to give just the meanings of either one. All that remains is to provide a codomain or a target space for the intended semantic function, in other words, to supply a suitable range of logical meanings for the memberships of these languages to map into. Out of the many interpretations that are formally possible to arrange, one way of doing this proceeds by making the following definitions:
-
The conjunction \(\operatorname{Conj}_j^J q_j\) of a set of propositions, \(\{ q_j : j \in J \},\) is a proposition that is true if and only if every one of the \(q_j\!\) is true.
\(\operatorname{Conj}_j^J q_j\) is true \(\Leftrightarrow\) \(q_j\!\) is true for every \(j \in J.\)
-
The surjunction \(\operatorname{Surj}_j^J q_j\) of a set of propositions, \(\{ q_j : j \in J \},\) is a proposition that is true if and only if exactly one of the \(q_j\!\) is untrue.
\(\operatorname{Surj}_j^J q_j\) is true \(\Leftrightarrow\) \(q_j\!\) is untrue for unique \(j \in J.\)
If the number of propositions that are being joined together is finite, then the conjunction and the surjunction can be represented by means of sentential connectives, incorporating the sentences that represent these propositions into finite strings of symbols.
If \(J\!\) is finite, for instance, if \(J\!\) consists of the integers in the interval \(j = 1 ~\text{to}~ k,\) and if each proposition \(q_j\!\) is represented by a sentence \(s_j,\!\) then the following strategies of expression are open:
-
The conjunction \(\operatorname{Conj}_j^J q_j\) can be represented by a sentence that is constructed by concatenating the \(s_j\!\) in the following fashion:
\(\operatorname{Conj}_j^J q_j ~\leftrightsquigarrow~ s_1 s_2 \ldots s_k.\)
-
The surjunction \(\operatorname{Surj}_j^J q_j\) can be represented by a sentence that is constructed by surcatenating the \(s_j\!\) in the following fashion:
\(\operatorname{Surj}_j^J q_j ~\leftrightsquigarrow~ \underline{(} s_1, s_2, \ldots, s_k \underline{)}.\)
If one opts for a mode of interpretation that moves more directly from the parse graph of a sentence to the potential logical meaning of both the PARC and the PARCE, then the following specifications are in order:
A cactus rooted at a particular node is taken to represent what that node denotes, its logical denotation or its logical interpretation.
- The logical denotation of a node is the logical conjunction of that node's arguments, which are defined as the logical denotations of that node's attachments. The logical denotation of either a blank symbol or an empty node is the boolean value \(\underline{1} = \operatorname{true}.\) The logical denotation of the paint \(\mathfrak{p}_j\!\) is the proposition \(p_j,\!\) a proposition that is regarded as primitive, at least, with respect to the level of analysis that is represented in the current instance of \(\mathfrak{C} (\mathfrak{P}).\)
- The logical denotation of a lobe is the logical surjunction of that lobe's arguments, which are defined as the logical denotations of that lobe's accoutrements. As a corollary, the logical denotation of the parse graph of \(\underline{(} \underline{)},\) otherwise called a needle, is the boolean value \(\underline{0} = \operatorname{false}.\)
If one takes the point of view that PARCs and PARCEs amount to a pair of intertranslatable languages for the same domain of objects, then denotation brackets of the form \(\downharpoonleft \ldots \downharpoonright\) can be used to indicate the logical denotation \(\downharpoonleft C_j \downharpoonright\) of a cactus \(C_j\!\) or the logical denotation \(\downharpoonleft s_j \downharpoonright\) of a sentence \(s_j.\!\)
Tables 14 and 15 summarize the relations that serve to connect the formal language of sentences with the logical language of propositions. Between these two realms of expression there is a family of graphical data structures that arise in parsing the sentences and that serve to facilitate the performance of computations on the indicator functions. The graphical language supplies an intermediate form of representation between the formal sentences and the indicator functions, and the form of mediation that it provides is very useful in rendering the possible connections between the other two languages conceivable in fact, not to mention in carrying out the necessary translations on a practical basis. These Tables include this intermediate domain in their Central Columns. Between their First and Middle Columns they illustrate the mechanics of parsing the abstract sentences of the cactus language into the graphical data structures of the corresponding species. Between their Middle and Final Columns they summarize the semantics of interpreting the graphical forms of representation for the purposes of reasoning with propositions.
| ||||||||||
| ||||||||||
| ||||||||||
|
| ||||||||||
| ||||||||||
| ||||||||||
|
Aside from their common topic, the two Tables present slightly different ways of conceptualizing the operations that go to establish their maps. Table 14 records the functional associations that connect each domain with the next, taking the triplings of a sentence \(s_j,\!\) a cactus \(C_j,\!\) and a proposition \(q_j\!\) as basic data, and fixing the rest by recursion on these. Table 15 records these associations in the form of equations, treating sentences and graphs as alternative kinds of signs, and generalizing the denotation bracket operator to indicate the proposition that either denotes. It should be clear at this point that either scheme of translation puts the sentences, the graphs, and the propositions that it associates with each other roughly in the roles of the signs, the interpretants, and the objects, respectively, whose triples define an appropriate sign relation. Indeed, the "roughly" can be made "exactly" as soon as the domains of a suitable sign relation are specified precisely.
A good way to illustrate the action of the conjunction and surjunction operators is to demonstrate how they can be used to construct the boolean functions on any finite number of variables. Let us begin by doing this for the first three cases, \(k = 0, 1, 2.\!\)
A boolean function \(F^{(0)}\!\) on \(0\!\) variables is just an element of the boolean domain \(\underline\mathbb{B} = \{ \underline{0}, \underline{1} \}.\) Table 16 shows several different ways of referring to these elements, just for the sake of consistency using the same format that will be used in subsequent Tables, no matter how degenerate it tends to appear in the initial case.
| \(F\!\) | \(F\!\) | \(F()\!\) | \(F\!\) |
| \(\underline{0}\) | \(F_0^{(0)}\!\) | \(\underline{0}\) | \((~)\) |
| \(\underline{1}\) | \(F_1^{(0)}\!\) | \(\underline{1}\) | \(((~))\) |
Column 1 lists each boolean element or boolean function under its ordinary constant name or under a succinct nickname, respectively.
Column 2 lists each boolean function in a style of function name \(F_j^{(k)}\!\) that is constructed as follows: The superscript \((k)\!\) gives the dimension of the functional domain, that is, the number of its functional variables, and the subscript \(j\!\) is a binary string that recapitulates the functional values, using the obvious translation of boolean values into binary values.
Column 3 lists the functional values for each boolean function, or possibly a boolean element appearing in the guise of a function, for each combination of its domain values.
Column 4 shows the usual expressions of these elements in the cactus language, conforming to the practice of omitting the underlines in display formats. Here I illustrate also the convention of using the expression \(^{\backprime\backprime} ((~)) ^{\prime\prime}\) as a visible stand-in for the expression of the logical value \(\operatorname{true},\) a value that is minimally represented by a blank expression that tends to elude our giving it much notice in the context of more demonstrative texts.
Table 17 presents the boolean functions on one variable, \(F^{(1)} : \underline\mathbb{B} \to \underline\mathbb{B},\) of which there are precisely four.
| \(F\!\) | \(F\!\) | \(F(x)\!\) | \(F\!\) | |
| \(F(\underline{1})\) | \(F(\underline{0})\) | |||
| \(F_0^{(1)}\!\) | \(F_{00}^{(1)}\!\) | \(\underline{0}\) | \(\underline{0}\) | \((~)\) |
| \(F_1^{(1)}\!\) | \(F_{01}^{(1)}\!\) | \(\underline{0}\) | \(\underline{1}\) | \((x)\!\) |
| \(F_2^{(1)}\!\) | \(F_{10}^{(1)}\!\) | \(\underline{1}\) | \(\underline{0}\) | \(x\!\) |
| \(F_3^{(1)}\!\) | \(F_{11}^{(1)}\!\) | \(\underline{1}\) | \(\underline{1}\) | \(((~))\) |
Here, Column 1 codes the contents of Column 2 in a more concise form, compressing the lists of boolean values, recorded as bits in the subscript string, into their decimal equivalents. Naturally, the boolean constants reprise themselves in this new setting as constant functions on one variable. Thus, one has the synonymous expressions for constant functions that are expressed in the next two chains of equations:
|
\(\begin{matrix} F_0^{(1)} & = & F_{00}^{(1)} & = & \underline{0} ~:~ \underline\mathbb{B} \to \underline\mathbb{B} \\ \\ F_3^{(1)} & = & F_{11}^{(1)} & = & \underline{1} ~:~ \underline\mathbb{B} \to \underline\mathbb{B} \end{matrix}\) |
As for the rest, the other two functions are easily recognized as corresponding to the one-place logical connectives, or the monadic operators on \(\underline\mathbb{B}.\) Thus, the function \(F_1^{(1)} = F_{01}^{(1)}\) is recognizable as the negation operation, and the function \(F_2^{(1)} = F_{10}^{(1)}\) is obviously the identity operation.
Table 18 presents the boolean functions on two variables, \(F^{(2)} : \underline\mathbb{B}^2 \to \underline\mathbb{B},\) of which there are precisely sixteen.
| \(F\!\) | \(F\!\) | \(F(x, y)\!\) | \(F\!\) | |||
| \(F(\underline{1}, \underline{1})\) | \(F(\underline{1}, \underline{0})\) | \(F(\underline{0}, \underline{1})\) | \(F(\underline{0}, \underline{0})\) | |||
| \(F_{0}^{(2)}\!\) | \(F_{0000}^{(2)}\!\) | \(\underline{0}\) | \(\underline{0}\) | \(\underline{0}\) | \(\underline{0}\) | \((~)\) |
| \(F_{1}^{(2)}\!\) | \(F_{0001}^{(2)}\!\) | \(\underline{0}\) | \(\underline{0}\) | \(\underline{0}\) | \(\underline{1}\) | \((x)(y)\!\) |
| \(F_{2}^{(2)}\!\) | \(F_{0010}^{(2)}\!\) | \(\underline{0}\) | \(\underline{0}\) | \(\underline{1}\) | \(\underline{0}\) | \((x) y\!\) |
| \(F_{3}^{(2)}\!\) | \(F_{0011}^{(2)}\!\) | \(\underline{0}\) | \(\underline{0}\) | \(\underline{1}\) | \(\underline{1}\) | \((x)\!\) |
| \(F_{4}^{(2)}\!\) | \(F_{0100}^{(2)}\!\) | \(\underline{0}\) | \(\underline{1}\) | \(\underline{0}\) | \(\underline{0}\) | \(x (y)\!\) |
| \(F_{5}^{(2)}\!\) | \(F_{0101}^{(2)}\!\) | \(\underline{0}\) | \(\underline{1}\) | \(\underline{0}\) | \(\underline{1}\) | \((y)\!\) |
| \(F_{6}^{(2)}\!\) | \(F_{0110}^{(2)}\!\) | \(\underline{0}\) | \(\underline{1}\) | \(\underline{1}\) | \(\underline{0}\) | \((x, y)\!\) |
| \(F_{7}^{(2)}\!\) | \(F_{0111}^{(2)}\!\) | \(\underline{0}\) | \(\underline{1}\) | \(\underline{1}\) | \(\underline{1}\) | \((x y)\!\) |
| \(F_{8}^{(2)}\!\) | \(F_{1000}^{(2)}\!\) | \(\underline{1}\) | \(\underline{0}\) | \(\underline{0}\) | \(\underline{0}\) | \(x y\!\) |
| \(F_{9}^{(2)}\!\) | \(F_{1001}^{(2)}\!\) | \(\underline{1}\) | \(\underline{0}\) | \(\underline{0}\) | \(\underline{1}\) | \(((x, y))\!\) |
| \(F_{10}^{(2)}\!\) | \(F_{1010}^{(2)}\!\) | \(\underline{1}\) | \(\underline{0}\) | \(\underline{1}\) | \(\underline{0}\) | \(y\!\) |
| \(F_{11}^{(2)}\!\) | \(F_{1011}^{(2)}\!\) | \(\underline{1}\) | \(\underline{0}\) | \(\underline{1}\) | \(\underline{1}\) | \((x (y))\!\) |
| \(F_{12}^{(2)}\!\) | \(F_{1100}^{(2)}\!\) | \(\underline{1}\) | \(\underline{1}\) | \(\underline{0}\) | \(\underline{0}\) | \(x\!\) |
| \(F_{13}^{(2)}\!\) | \(F_{1101}^{(2)}\!\) | \(\underline{1}\) | \(\underline{1}\) | \(\underline{0}\) | \(\underline{1}\) | \(((x)y)\!\) |
| \(F_{14}^{(2)}\!\) | \(F_{1110}^{(2)}\!\) | \(\underline{1}\) | \(\underline{1}\) | \(\underline{1}\) | \(\underline{0}\) | \(((x)(y))\!\) |
| \(F_{15}^{(2)}\!\) | \(F_{1111}^{(2)}\!\) | \(\underline{1}\) | \(\underline{1}\) | \(\underline{1}\) | \(\underline{1}\) | \(((~))\) |
As before, all of the boolean functions of fewer variables are subsumed in this Table, though under a set of alternative names and possibly different interpretations. Just to acknowledge a few of the more notable pseudonyms:
- The constant function \(\underline{0} ~:~ \underline\mathbb{B}^2 \to \underline\mathbb{B}\) appears under the name \(F_{0}^{(2)}.\)
- The constant function \(\underline{1} ~:~ \underline\mathbb{B}^2 \to \underline\mathbb{B}\) appears under the name \(F_{15}^{(2)}.\)
- The negation and identity of the first variable are \(F_{3}^{(2)}\) and \(F_{12}^{(2)},\) respectively.
- The negation and identity of the second variable are \(F_{5}^{(2)}\) and \(F_{10}^{(2)},\) respectively.
- The logical conjunction is given by the function \(F_{8}^{(2)} (x, y) = x \cdot y.\)
- The logical disjunction is given by the function \(F_{14}^{(2)} (x, y) = \underline{((} ~x~ \underline{)(} ~y~ \underline{))}.\)
Functions expressing the conditionals, implications, or if-then statements are given in the following ways:
\[[x \Rightarrow y] = F_{11}^{(2)} (x, y) = \underline{(} ~x~ \underline{(} ~y~ \underline{))} = [\operatorname{not}~ x ~\operatorname{without}~ y].\]
\[[x \Leftarrow y] = F_{13}^{(2)} (x, y) = \underline{((} ~x~ \underline{)} ~y~ \underline{)} = [\operatorname{not}~ y ~\operatorname{without}~ x].\]
The function that corresponds to the biconditional, the equivalence, or the if and only statement is exhibited in the following fashion:
\[[x \Leftrightarrow y] = [x = y] = F_{9}^{(2)} (x, y) = \underline{((} ~x~,~y~ \underline{))}.\]
Finally, there is a boolean function that is logically associated with the exclusive disjunction, inequivalence, or not equals statement, algebraically associated with the binary sum operation, and geometrically associated with the symmetric difference of sets. This function is given by:
\[[x \neq y] = [x + y] = F_{6}^{(2)} (x, y) = \underline{(} ~x~,~y~ \underline{)}.\]
Let me now address one last question that may have occurred to some. What has happened, in this suggested scheme of functional reasoning, to the distinction that is quite pointedly made by careful logicians between (1) the connectives called conditionals and symbolized by the signs \((\rightarrow)\) and \((\leftarrow),\) and (2) the assertions called implications and symbolized by the signs \((\Rightarrow)\) and \((\Leftarrow)\), and, in a related question: What has happened to the distinction that is equally insistently made between (3) the connective called the biconditional and signified by the sign \((\leftrightarrow)\) and (4) the assertion that is called an equivalence and signified by the sign \((\Leftrightarrow)\)? My answer is this: For my part, I am deliberately avoiding making these distinctions at the level of syntax, preferring to treat them instead as distinctions in the use of boolean functions, turning on whether the function is mentioned directly and used to compute values on arguments, or whether its inverse is being invoked to indicate the fibers of truth or untruth under the propositional function in question.
Stretching Exercises
The arrays of boolean connections described above, namely, the boolean functions \(F^{(k)} : \underline\mathbb{B}^k \to \underline\mathbb{B},\) for \(k\!\) in \(\{ 0, 1, 2 \},\!\) supply enough material to demonstrate the use of the stretch operation in a variety of concrete cases.
For example, suppose that \(F\!\) is a connection of the form \(F : \underline\mathbb{B}^2 \to \underline\mathbb{B},\) that is, any one of the sixteen possibilities in Table 18, while \(p\!\) and \(q\!\) are propositions of the form \(p, q : X \to \underline\mathbb{B},\) that is, propositions about things in the universe \(X,\!\) or else the indicators of sets contained in \(X.\!\)
Then one has the imagination \(\underline{f} = (f_1, f_2) = (p, q) : (X \to \underline\mathbb{B})^2,\) and the stretch of the connection \(F\!\) to \(\underline{f}\) on \(X\!\) amounts to a proposition \(F^\$ (p, q) : X \to \underline\mathbb{B}\) that may be read as the stretch of \(F\!\) to \(p\!\) and \(q.\!\) If one is concerned with many different propositions about things in \(X,\!\) or if one is abstractly indifferent to the particular choices for \(p\!\) and \(q,\!\) then one may detach the operator \(F^\$ : (X \to \underline\mathbb{B}))^2 \to (X \to \underline\mathbb{B})),\) called the stretch of \(F\!\) over \(X,\!\) and consider it in isolation from any concrete application.
When the cactus notation is used to represent boolean functions, a single \(\$\) sign at the end of the expression is enough to remind the reader that the connections are meant to be stretched to several propositions on a universe \(X.\!\)
For example, take the connection \(F : \underline\mathbb{B}^2 \to \underline\mathbb{B}\) such that:
\[F(x, y) ~=~ F_{6}^{(2)} (x, y) ~=~ \underline{(}~x~,~y~\underline{)}\]
The connection in question is a boolean function on the variables \(x, y\!\) that returns a value of \(\underline{1}\) just when just one of the pair \(x, y\!\) is not equal to \(\underline{1},\) or what amounts to the same thing, just when just one of the pair \(x, y\!\) is equal to \(\underline{1}.\) There is clearly an isomorphism between this connection, viewed as an operation on the boolean domain \(\underline\mathbb{B} = \{ \underline{0}, \underline{1} \},\) and the dyadic operation on binary values \(x, y \in \mathbb{B} = \operatorname{GF}(2)\) that is otherwise known as \(x + y\!.\)
The same connection \(F : \underline\mathbb{B}^2 \to \underline\mathbb{B}\) can also be read as a proposition about things in the universe \(X = \underline\mathbb{B}^2.\) If \(s\!\) is a sentence that denotes the proposition \(F,\!\) then the corresponding assertion says exactly what one states in uttering the sentence \(^{\backprime\backprime} \, x ~\operatorname{is~not~equal~to}~ y \, ^{\prime\prime}.\) In such a case, one has \(\downharpoonleft s \downharpoonright \, = F,\) and all of the following expressions are ordinarily taken as equivalent descriptions of the same set: