Difference between revisions of "User:Jon Awbrey/ATLAS"
Jon Awbrey (talk | contribs) (→Table 58. Cast of Characters: Expansive Subtypes of Objects and Operators: copy model table) |
Jon Awbrey (talk | contribs) (add image stub) |
||
| (69 intermediate revisions by the same user not shown) | |||
| Line 1,141: | Line 1,141: | ||
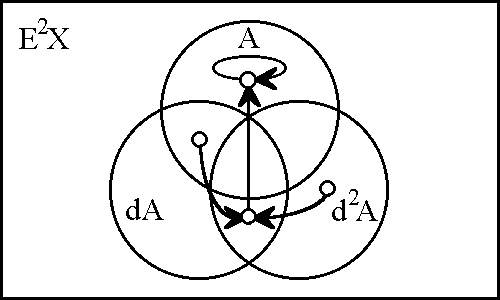
Figure 12. The Anchor | Figure 12. The Anchor | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 12 -- The Anchor.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 12. The Anchor'''</font></center></p> | ||
===Figure 13. The Tiller=== | ===Figure 13. The Tiller=== | ||
| Line 1,174: | Line 1,178: | ||
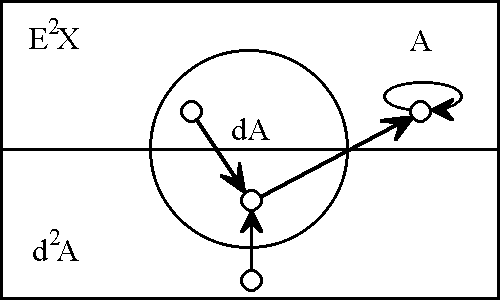
Figure 13. The Tiller | Figure 13. The Tiller | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 13 -- The Tiller.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 13. The Tiller'''</font></center></p> | ||
===Table 14. Differential Propositions=== | ===Table 14. Differential Propositions=== | ||
| Line 1,667: | Line 1,675: | ||
|} | |} | ||
</font><br> | </font><br> | ||
| + | |||
| + | ===Figure 16. A Couple of Fourth Gear Orbits=== | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 16 -- A Couple of Fourth Gear Orbits.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 16. A Couple of Fourth Gear Orbits'''</font></center></p> | ||
===Figure 16-a. A Couple of Fourth Gear Orbits: 1=== | ===Figure 16-a. A Couple of Fourth Gear Orbits: 1=== | ||
| Line 2,064: | Line 2,078: | ||
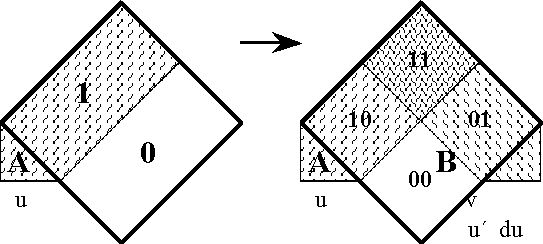
Figure 18-a. Extension from 1 to 2 Dimensions: Areal | Figure 18-a. Extension from 1 to 2 Dimensions: Areal | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 18-a -- Extension from 1 to 2 Dimensions.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 18-a. Extension from 1 to 2 Dimensions: Areal'''</font></center></p> | ||
===Figure 18-b. Extension from 1 to 2 Dimensions: Bundle=== | ===Figure 18-b. Extension from 1 to 2 Dimensions: Bundle=== | ||
| Line 2,093: | Line 2,111: | ||
Figure 18-b. Extension from 1 to 2 Dimensions: Bundle | Figure 18-b. Extension from 1 to 2 Dimensions: Bundle | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 18-b -- Extension from 1 to 2 Dimensions.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 18-b. Extension from 1 to 2 Dimensions: Bundle'''</font></center></p> | ||
===Figure 18-c. Extension from 1 to 2 Dimensions: Compact=== | ===Figure 18-c. Extension from 1 to 2 Dimensions: Compact=== | ||
| Line 2,124: | Line 2,146: | ||
Figure 18-c. Extension from 1 to 2 Dimensions: Compact | Figure 18-c. Extension from 1 to 2 Dimensions: Compact | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 18-c -- Extension from 1 to 2 Dimensions.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 18-c. Extension from 1 to 2 Dimensions: Compact'''</font></center></p> | ||
===Figure 18-d. Extension from 1 to 2 Dimensions: Digraph=== | ===Figure 18-d. Extension from 1 to 2 Dimensions: Digraph=== | ||
| Line 2,143: | Line 2,169: | ||
Figure 18-d. Extension from 1 to 2 Dimensions: Digraph | Figure 18-d. Extension from 1 to 2 Dimensions: Digraph | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 18-d -- Extension from 1 to 2 Dimensions.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 18-d. Extension from 1 to 2 Dimensions: Digraph'''</font></center></p> | ||
===Figure 19-a. Extension from 2 to 4 Dimensions: Areal=== | ===Figure 19-a. Extension from 2 to 4 Dimensions: Areal=== | ||
| Line 2,186: | Line 2,216: | ||
Figure 19-a. Extension from 2 to 4 Dimensions: Areal | Figure 19-a. Extension from 2 to 4 Dimensions: Areal | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 19-a -- Extension from 2 to 4 Dimensions.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 19-a. Extension from 2 to 4 Dimensions: Areal'''</font></center></p> | ||
===Figure 19-b. Extension from 2 to 4 Dimensions: Bundle=== | ===Figure 19-b. Extension from 2 to 4 Dimensions: Bundle=== | ||
| Line 2,247: | Line 2,281: | ||
Figure 19-b. Extension from 2 to 4 Dimensions: Bundle | Figure 19-b. Extension from 2 to 4 Dimensions: Bundle | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 19-b -- Extension from 2 to 4 Dimensions.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 19-b. Extension from 2 to 4 Dimensions: Bundle'''</font></center></p> | ||
===Figure 19-c. Extension from 2 to 4 Dimensions: Compact=== | ===Figure 19-c. Extension from 2 to 4 Dimensions: Compact=== | ||
| Line 2,287: | Line 2,325: | ||
Figure 19-c. Extension from 2 to 4 Dimensions: Compact | Figure 19-c. Extension from 2 to 4 Dimensions: Compact | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 19-c -- Extension from 2 to 4 Dimensions.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 19-c. Extension from 2 to 4 Dimensions: Compact'''</font></center></p> | ||
===Figure 19-d. Extension from 2 to 4 Dimensions: Digraph=== | ===Figure 19-d. Extension from 2 to 4 Dimensions: Digraph=== | ||
| Line 2,330: | Line 2,372: | ||
Figure 19-d. Extension from 2 to 4 Dimensions: Digraph | Figure 19-d. Extension from 2 to 4 Dimensions: Digraph | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 19-d -- Extension from 2 to 4 Dimensions.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 19-d. Extension from 2 to 4 Dimensions: Digraph'''</font></center></p> | ||
===Figure 20-i. Thematization of Conjunction (Stage 1)=== | ===Figure 20-i. Thematization of Conjunction (Stage 1)=== | ||
| Line 2,360: | Line 2,406: | ||
Figure 20-i. Thematization of Conjunction (Stage 1) | Figure 20-i. Thematization of Conjunction (Stage 1) | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 20-i -- Thematization of Conjunction (Stage 1).gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 20-i. Thematization of Conjunction (Stage 1)'''</font></center></p> | ||
===Figure 20-ii. Thematization of Conjunction (Stage 2)=== | ===Figure 20-ii. Thematization of Conjunction (Stage 2)=== | ||
| Line 2,407: | Line 2,457: | ||
Figure 20-ii. Thematization of Conjunction (Stage 2) | Figure 20-ii. Thematization of Conjunction (Stage 2) | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 20-ii -- Thematization of Conjunction (Stage 2).gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 20-ii. Thematization of Conjunction (Stage 2)'''</font></center></p> | ||
===Figure 20-iii. Thematization of Conjunction (Stage 3)=== | ===Figure 20-iii. Thematization of Conjunction (Stage 3)=== | ||
| Line 2,450: | Line 2,504: | ||
Figure 20-iii. Thematization of Conjunction (Stage 3) | Figure 20-iii. Thematization of Conjunction (Stage 3) | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 20-iii -- Thematization of Conjunction (Stage 3).gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 20-iii. Thematization of Conjunction (Stage 3)'''</font></center></p> | ||
===Figure 21. Thematization of Disjunction and Equality=== | ===Figure 21. Thematization of Disjunction and Equality=== | ||
| Line 2,516: | Line 2,574: | ||
Figure 21. Thematization of Disjunction and Equality | Figure 21. Thematization of Disjunction and Equality | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 21 -- Thematization of Disjunction and Equality.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 21. Thematization of Disjunction and Equality'''</font></center></p> | ||
===Table 22. Disjunction ''f'' and Equality ''g''=== | ===Table 22. Disjunction ''f'' and Equality ''g''=== | ||
| Line 3,673: | Line 3,735: | ||
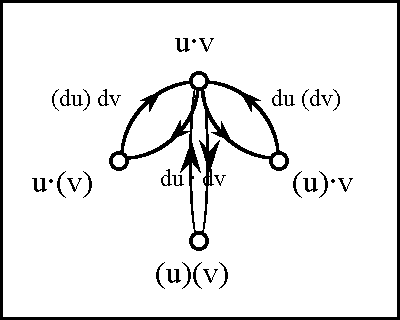
Figure 30. Generic Frame of a Logical Transformation | Figure 30. Generic Frame of a Logical Transformation | ||
</pre> | </pre> | ||
| + | |||
| + | '''Note.''' The following image was corrupted in transit between software platforms. | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 30 -- Generic Frame of a Logical Transformation.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 30. Generic Frame of a Logical Transformation'''</font></center></p> | ||
===Formula Display 3=== | ===Formula Display 3=== | ||
| Line 3,729: | Line 3,797: | ||
Figure 31. Operator Diagram (1) | Figure 31. Operator Diagram (1) | ||
</pre> | </pre> | ||
| + | |||
| + | '''Note.''' The following image was corrupted in transit between software platforms. | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 31 -- Operator Diagram (1).gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 31. Operator Diagram (1)'''</font></center></p> | ||
===Figure 32. Operator Diagram (2)=== | ===Figure 32. Operator Diagram (2)=== | ||
| Line 3,754: | Line 3,828: | ||
Figure 32. Operator Diagram (2) | Figure 32. Operator Diagram (2) | ||
</pre> | </pre> | ||
| + | |||
| + | '''Note.''' The following image was corrupted in transit between software platforms. | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 32 -- Operator Diagram (2).gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 32. Operator Diagram (2)'''</font></center></p> | ||
===Figure 33-i. Analytic Diagram (1)=== | ===Figure 33-i. Analytic Diagram (1)=== | ||
| Line 3,774: | Line 3,854: | ||
Figure 33-i. Analytic Diagram (1) | Figure 33-i. Analytic Diagram (1) | ||
</pre> | </pre> | ||
| + | |||
| + | '''Note.''' The following image was corrupted in transit between software platforms. | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 33-i -- Analytic Diagram (1).gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 33-i. Analytic Diagram (1)'''</font></center></p> | ||
===Figure 33-ii. Analytic Diagram (2)=== | ===Figure 33-ii. Analytic Diagram (2)=== | ||
| Line 3,794: | Line 3,880: | ||
Figure 33-ii. Analytic Diagram (2) | Figure 33-ii. Analytic Diagram (2) | ||
</pre> | </pre> | ||
| + | |||
| + | '''Note.''' The following image was corrupted in transit between software platforms. | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 33-ii -- Analytic Diagram (2).gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 33-ii. Analytic Diagram (2)'''</font></center></p> | ||
===Formula Display 4=== | ===Formula Display 4=== | ||
| Line 4,012: | Line 4,104: | ||
Figure 34. Tangent Functor Diagram | Figure 34. Tangent Functor Diagram | ||
</pre> | </pre> | ||
| + | |||
| + | '''Note.''' The following image was corrupted in transit between software platforms. | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 34 -- Tangent Functor Diagram.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 34. Tangent Functor Diagram'''</font></center></p> | ||
===Figure 35. Conjunction as Transformation=== | ===Figure 35. Conjunction as Transformation=== | ||
| Line 4,067: | Line 4,165: | ||
Figure 35. Conjunction as Transformation | Figure 35. Conjunction as Transformation | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 35 -- A Conjunction Viewed as a Transformation.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 35. Conjunction as Transformation'''</font></center></p> | ||
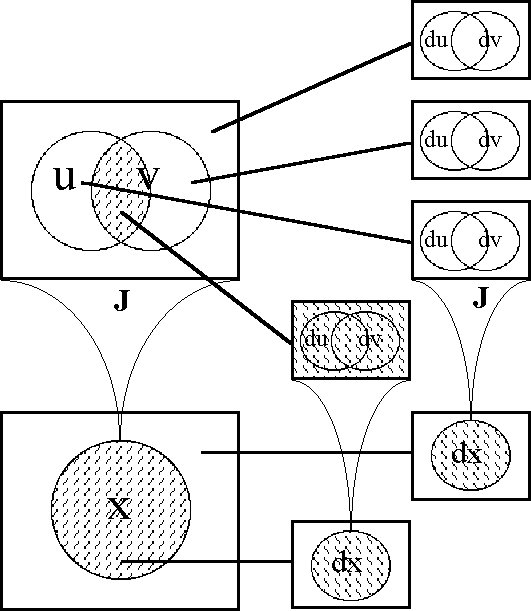
===Table 36. Computation of !e!J=== | ===Table 36. Computation of !e!J=== | ||
| Line 4,140: | Line 4,242: | ||
</font><br> | </font><br> | ||
| − | ===Figure 37-a. Tacit Extension of J (Areal)=== | + | ===Figure 37-a. Tacit Extension of ''J'' (Areal)=== |
<pre> | <pre> | ||
| Line 4,183: | Line 4,285: | ||
</pre> | </pre> | ||
| − | ===Figure 37-b. Tacit Extension of J (Bundle)=== | + | <br> |
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 37-a -- Tacit Extension of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 37-a. Tacit Extension of ''J'' (Areal)'''</font></center></p> | ||
| + | |||
| + | ===Figure 37-b. Tacit Extension of ''J'' (Bundle)=== | ||
<pre> | <pre> | ||
| Line 4,252: | Line 4,358: | ||
</pre> | </pre> | ||
| − | ===Figure 37-c. Tacit Extension of J (Compact)=== | + | <br> |
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 37-b -- Tacit Extension of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 37-b. Tacit Extension of ''J'' (Bundle)'''</font></center></p> | ||
| + | |||
| + | ===Figure 37-c. Tacit Extension of ''J'' (Compact)=== | ||
<pre> | <pre> | ||
| Line 4,292: | Line 4,402: | ||
</pre> | </pre> | ||
| − | ===Figure 37-d. Tacit Extension of J (Digraph)=== | + | <br> |
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 37-c -- Tacit Extension of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 37-c. Tacit Extension of ''J'' (Compact)'''</font></center></p> | ||
| + | |||
| + | ===Figure 37-d. Tacit Extension of ''J'' (Digraph)=== | ||
<pre> | <pre> | ||
| Line 4,333: | Line 4,447: | ||
Figure 37-d. Tacit Extension of J (Digraph) | Figure 37-d. Tacit Extension of J (Digraph) | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 37-d -- Tacit Extension of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 37-d. Tacit Extension of ''J'' (Digraph)'''</font></center></p> | ||
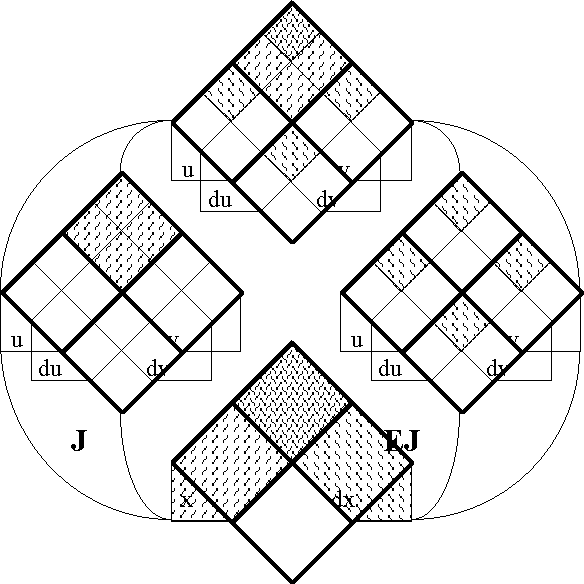
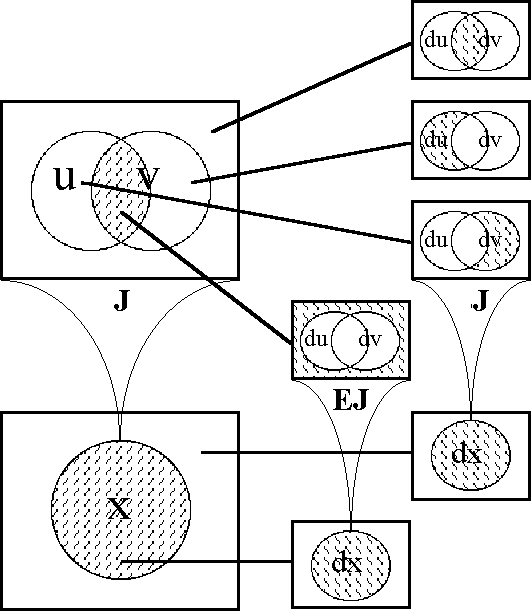
===Table 38. Computation of EJ (Method 1)=== | ===Table 38. Computation of EJ (Method 1)=== | ||
| Line 4,504: | Line 4,622: | ||
</font><br> | </font><br> | ||
| − | ===Figure 40-a. Enlargement of J (Areal)=== | + | ===Figure 40-a. Enlargement of ''J'' (Areal)=== |
<pre> | <pre> | ||
| Line 4,547: | Line 4,665: | ||
</pre> | </pre> | ||
| − | ===Figure 40-b. Enlargement of J (Bundle)=== | + | <br> |
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 40-a -- Enlargement of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 40-a. Enlargement of ''J'' (Areal)'''</font></center></p> | ||
| + | |||
| + | ===Figure 40-b. Enlargement of ''J'' (Bundle)=== | ||
<pre> | <pre> | ||
| Line 4,616: | Line 4,738: | ||
</pre> | </pre> | ||
| − | ===Figure 40-c. Enlargement of J (Compact)=== | + | <br> |
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 40-b -- Enlargement of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 40-b. Enlargement of ''J'' (Bundle)'''</font></center></p> | ||
| + | |||
| + | ===Figure 40-c. Enlargement of ''J'' (Compact)=== | ||
<pre> | <pre> | ||
| Line 4,656: | Line 4,782: | ||
</pre> | </pre> | ||
| − | ===Figure 40-d. Enlargement of J (Digraph)=== | + | <br> |
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 40-c -- Enlargement of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 40-c. Enlargement of ''J'' (Compact)'''</font></center></p> | ||
| + | |||
| + | ===Figure 40-d. Enlargement of ''J'' (Digraph)=== | ||
<pre> | <pre> | ||
| Line 4,697: | Line 4,827: | ||
Figure 40-d. Enlargement of J (Digraph) | Figure 40-d. Enlargement of J (Digraph) | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 40-d -- Enlargement of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 40-d. Enlargement of ''J'' (Digraph)'''</font></center></p> | ||
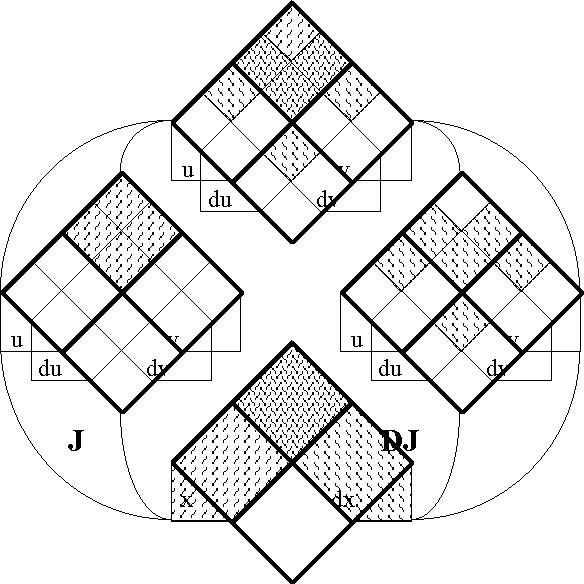
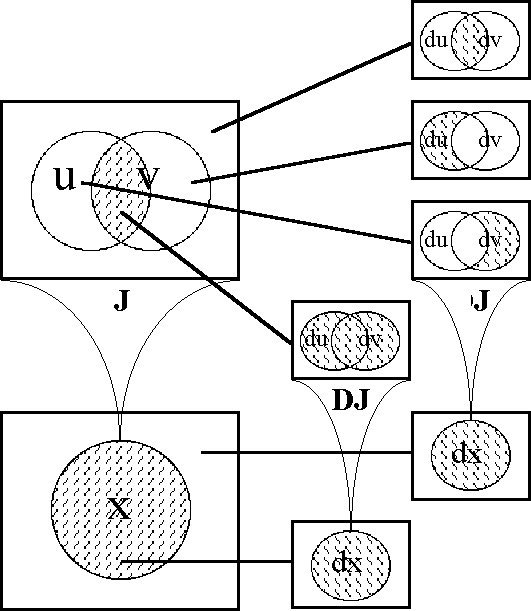
===Table 41. Computation of DJ (Method 1)=== | ===Table 41. Computation of DJ (Method 1)=== | ||
| Line 4,964: | Line 5,098: | ||
</font><br> | </font><br> | ||
| − | ===Figure 44-a. Difference Map of J (Areal)=== | + | ===Figure 44-a. Difference Map of ''J'' (Areal)=== |
<pre> | <pre> | ||
| Line 5,007: | Line 5,141: | ||
</pre> | </pre> | ||
| − | ===Figure 44-b. Difference Map of J (Bundle)=== | + | <br> |
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 44-a -- Difference Map of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 44-a. Difference Map of ''J'' (Areal)'''</font></center></p> | ||
| + | |||
| + | ===Figure 44-b. Difference Map of ''J'' (Bundle)=== | ||
<pre> | <pre> | ||
| Line 5,076: | Line 5,214: | ||
</pre> | </pre> | ||
| − | ===Figure 44-c. Difference Map of J (Compact)=== | + | <br> |
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 44-b -- Difference Map of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 44-b. Difference Map of ''J'' (Bundle)'''</font></center></p> | ||
| + | |||
| + | ===Figure 44-c. Difference Map of ''J'' (Compact)=== | ||
<pre> | <pre> | ||
| Line 5,117: | Line 5,259: | ||
</pre> | </pre> | ||
| − | ===Figure 44-d. Difference Map of J (Digraph)=== | + | <br> |
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 44-c -- Difference Map of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 44-c. Difference Map of ''J'' (Compact)'''</font></center></p> | ||
| + | |||
| + | ===Figure 44-d. Difference Map of ''J'' (Digraph)=== | ||
<pre> | <pre> | ||
| Line 5,155: | Line 5,301: | ||
Figure 44-d. Difference Map of J (Digraph) | Figure 44-d. Difference Map of J (Digraph) | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 44-d -- Difference Map of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 44-d. Difference Map of ''J'' (Digraph)'''</font></center></p> | ||
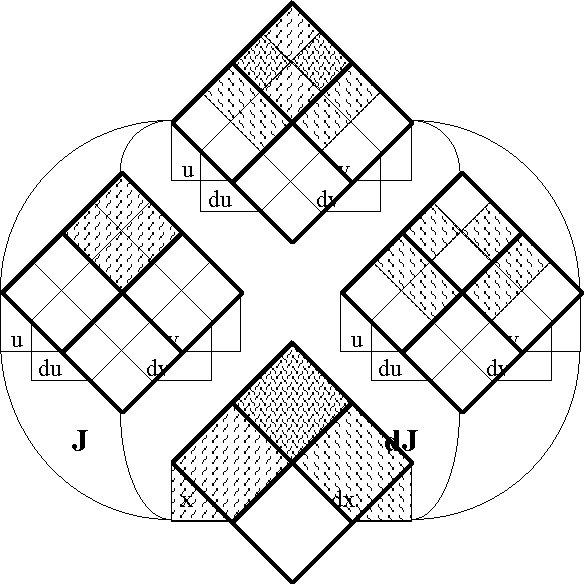
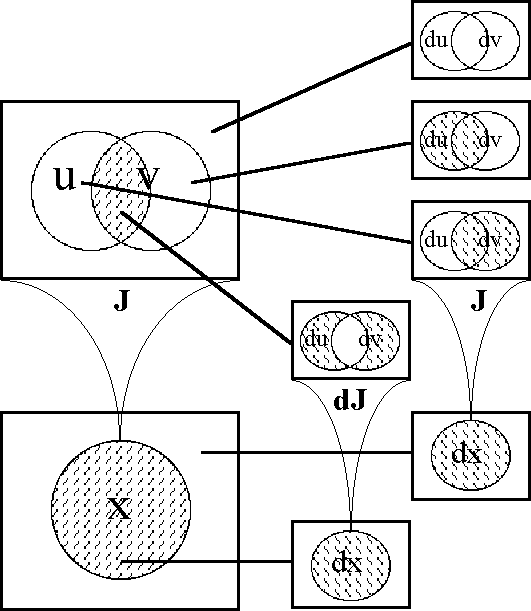
===Table 45. Computation of dJ=== | ===Table 45. Computation of dJ=== | ||
| Line 5,193: | Line 5,343: | ||
</font><br> | </font><br> | ||
| − | ===Figure 46-a. Differential of J (Areal)=== | + | ===Figure 46-a. Differential of ''J'' (Areal)=== |
<pre> | <pre> | ||
| Line 5,236: | Line 5,386: | ||
</pre> | </pre> | ||
| − | ===Figure 46-b. Differential of J (Bundle)=== | + | <br> |
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 46-a -- Differential of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 46-a. Differential of ''J'' (Areal)'''</font></center></p> | ||
| + | |||
| + | ===Figure 46-b. Differential of ''J'' (Bundle)=== | ||
<pre> | <pre> | ||
| Line 5,305: | Line 5,459: | ||
</pre> | </pre> | ||
| − | ===Figure 46-c. Differential of J (Compact)=== | + | <br> |
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 46-b -- Differential of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 46-b. Differential of ''J'' (Bundle)'''</font></center></p> | ||
| + | |||
| + | ===Figure 46-c. Differential of ''J'' (Compact)=== | ||
<pre> | <pre> | ||
| Line 5,342: | Line 5,500: | ||
</pre> | </pre> | ||
| − | ===Figure 46-d. Differential of J (Digraph)=== | + | <br> |
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 46-c -- Differential of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 46-c. Differential of ''J'' (Compact)'''</font></center></p> | ||
| + | |||
| + | ===Figure 46-d. Differential of ''J'' (Digraph)=== | ||
<pre> | <pre> | ||
| Line 5,378: | Line 5,540: | ||
Figure 46-d. Differential of J (Digraph) | Figure 46-d. Differential of J (Digraph) | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 46-d -- Differential of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 46-d. Differential of ''J'' (Digraph)'''</font></center></p> | ||
===Table 47. Computation of rJ=== | ===Table 47. Computation of rJ=== | ||
| Line 5,439: | Line 5,605: | ||
</font><br> | </font><br> | ||
| − | ===Figure 48-a. Remainder of J (Areal)=== | + | ===Figure 48-a. Remainder of ''J'' (Areal)=== |
<pre> | <pre> | ||
| Line 5,482: | Line 5,648: | ||
</pre> | </pre> | ||
| − | ===Figure 48-b. Remainder of J (Bundle)=== | + | <br> |
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 48-a -- Remainder of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 48-a. Remainder of ''J'' (Areal)'''</font></center></p> | ||
| + | |||
| + | ===Figure 48-b. Remainder of ''J'' (Bundle)=== | ||
<pre> | <pre> | ||
| Line 5,551: | Line 5,721: | ||
</pre> | </pre> | ||
| − | ===Figure 48-c. Remainder of J (Compact)=== | + | <br> |
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 48-b -- Remainder of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 48-b. Remainder of ''J'' (Bundle)'''</font></center></p> | ||
| + | |||
| + | ===Figure 48-c. Remainder of ''J'' (Compact)=== | ||
<pre> | <pre> | ||
| Line 5,591: | Line 5,765: | ||
</pre> | </pre> | ||
| − | ===Figure 48-d. Remainder of J (Digraph)=== | + | <br> |
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 48-c -- Remainder of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 48-c. Remainder of ''J'' (Compact)'''</font></center></p> | ||
| + | |||
| + | ===Figure 48-d. Remainder of ''J'' (Digraph)=== | ||
<pre> | <pre> | ||
| Line 5,627: | Line 5,805: | ||
Figure 48-d. Remainder of J (Digraph) | Figure 48-d. Remainder of J (Digraph) | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 48-d -- Remainder of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 48-d. Remainder of ''J'' (Digraph)'''</font></center></p> | ||
===Table 49. Computation Summary for J=== | ===Table 49. Computation Summary for J=== | ||
| Line 6,228: | Line 6,410: | ||
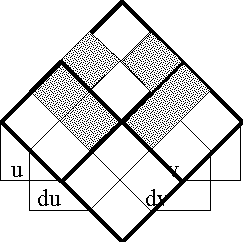
Figure 52. Decomposition of the Enlarged Conjunction EJ = (J, DJ) | Figure 52. Decomposition of the Enlarged Conjunction EJ = (J, DJ) | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 52 -- Decomposition of EJ.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 52. Decomposition of E''J'''''</font></center></p> | ||
===Figure 53. Decomposition of the Differed Conjunction DJ = (dJ, ddJ)=== | ===Figure 53. Decomposition of the Differed Conjunction DJ = (dJ, ddJ)=== | ||
| Line 6,279: | Line 6,465: | ||
Figure 53. Decomposition of the Differed Conjunction DJ = (dJ, ddJ) | Figure 53. Decomposition of the Differed Conjunction DJ = (dJ, ddJ) | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 53 -- Decomposition of DJ.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 53. Decomposition of D''J'''''</font></center></p> | ||
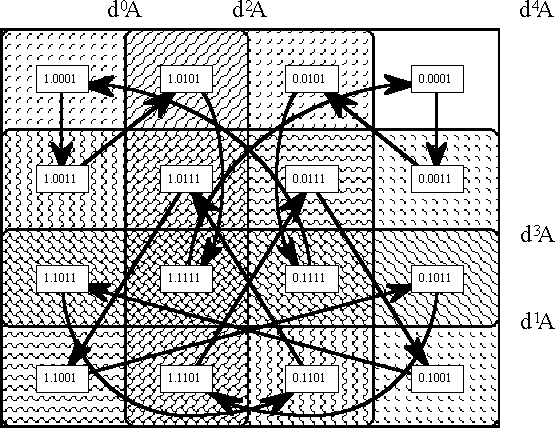
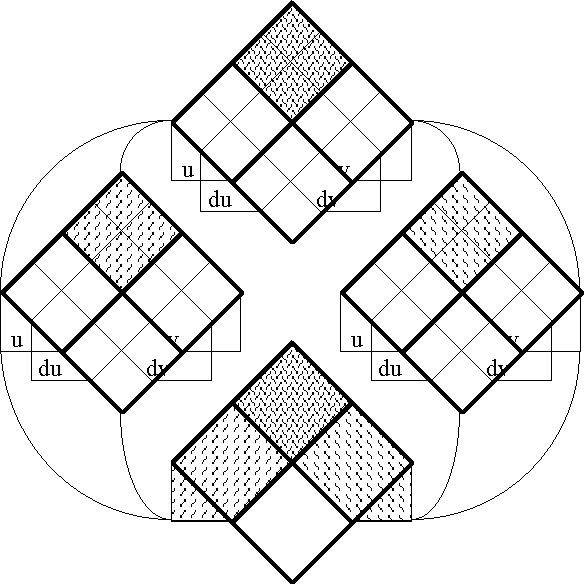
===Table 54. Cast of Characters: Expansive Subtypes of Objects and Operators=== | ===Table 54. Cast of Characters: Expansive Subtypes of Objects and Operators=== | ||
| Line 6,981: | Line 7,171: | ||
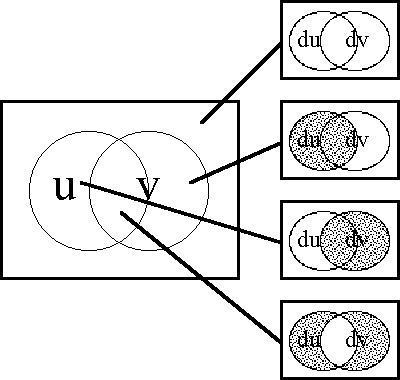
Figure 56-a1. Radius Map of the Conjunction J = uv | Figure 56-a1. Radius Map of the Conjunction J = uv | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 56-a1 -- Radius Map of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 56-a1. Radius Map of the Conjunction ''J'' = ''uv'''''</font></center></p> | ||
===Figure 56-a2. Secant Map of the Conjunction J = uv=== | ===Figure 56-a2. Secant Map of the Conjunction J = uv=== | ||
| Line 7,049: | Line 7,243: | ||
Figure 56-a2. Secant Map of the Conjunction J = uv | Figure 56-a2. Secant Map of the Conjunction J = uv | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 56-a2 -- Secant Map of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 56-a2. Secant Map of the Conjunction ''J'' = ''uv'''''</font></center></p> | ||
===Figure 56-a3. Chord Map of the Conjunction J = uv=== | ===Figure 56-a3. Chord Map of the Conjunction J = uv=== | ||
| Line 7,117: | Line 7,315: | ||
Figure 56-a3. Chord Map of the Conjunction J = uv | Figure 56-a3. Chord Map of the Conjunction J = uv | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 56-a3 -- Chord Map of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 56-a3. Chord Map of the Conjunction ''J'' = ''uv'''''</font></center></p> | ||
===Figure 56-a4. Tangent Map of the Conjunction J = uv=== | ===Figure 56-a4. Tangent Map of the Conjunction J = uv=== | ||
| Line 7,185: | Line 7,387: | ||
Figure 56-a4. Tangent Map of the Conjunction J = uv | Figure 56-a4. Tangent Map of the Conjunction J = uv | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 56-a4 -- Tangent Map of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 56-a4. Tangent Map of the Conjunction ''J'' = ''uv'''''</font></center></p> | ||
===Figure 56-b1. Radius Map of the Conjunction J = uv=== | ===Figure 56-b1. Radius Map of the Conjunction J = uv=== | ||
| Line 7,285: | Line 7,491: | ||
Figure 56-b1. Radius Map of the Conjunction J = uv | Figure 56-b1. Radius Map of the Conjunction J = uv | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 56-b1 -- Radius Map of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 56-b1. Radius Map of the Conjunction ''J'' = ''uv'''''</font></center></p> | ||
===Figure 56-b2. Secant Map of the Conjunction J = uv=== | ===Figure 56-b2. Secant Map of the Conjunction J = uv=== | ||
| Line 7,385: | Line 7,595: | ||
Figure 56-b2. Secant Map of the Conjunction J = uv | Figure 56-b2. Secant Map of the Conjunction J = uv | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 56-b2 -- Secant Map of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 56-b2. Secant Map of the Conjunction ''J'' = ''uv'''''</font></center></p> | ||
===Figure 56-b3. Chord Map of the Conjunction J = uv=== | ===Figure 56-b3. Chord Map of the Conjunction J = uv=== | ||
| Line 7,485: | Line 7,699: | ||
Figure 56-b3. Chord Map of the Conjunction J = uv | Figure 56-b3. Chord Map of the Conjunction J = uv | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 56-b3 -- Chord Map of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 56-b3. Chord Map of the Conjunction ''J'' = ''uv'''''</font></center></p> | ||
===Figure 56-b4. Tangent Map of the Conjunction J = uv=== | ===Figure 56-b4. Tangent Map of the Conjunction J = uv=== | ||
| Line 7,585: | Line 7,803: | ||
Figure 56-b4. Tangent Map of the Conjunction J = uv | Figure 56-b4. Tangent Map of the Conjunction J = uv | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 56-b4 -- Tangent Map of J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 56-b4. Tangent Map of the Conjunction ''J'' = ''uv'''''</font></center></p> | ||
===Figure 57-1. Radius Operator Diagram for the Conjunction J = uv=== | ===Figure 57-1. Radius Operator Diagram for the Conjunction J = uv=== | ||
| Line 7,655: | Line 7,877: | ||
Figure 57-1. Radius Operator Diagram for the Conjunction J = uv | Figure 57-1. Radius Operator Diagram for the Conjunction J = uv | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 57-1 -- Radius Operator Diagram for J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 57-1. Radius Operator Diagram for the Conjunction ''J'' = ''uv'''''</font></center></p> | ||
===Figure 57-2. Secant Operator Diagram for the Conjunction J = uv=== | ===Figure 57-2. Secant Operator Diagram for the Conjunction J = uv=== | ||
| Line 7,725: | Line 7,951: | ||
Figure 57-2. Secant Operator Diagram for the Conjunction J = uv | Figure 57-2. Secant Operator Diagram for the Conjunction J = uv | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 57-2 -- Secant Operator Diagram for J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 57-2. Secant Operator Diagram for the Conjunction ''J'' = ''uv'''''</font></center></p> | ||
===Figure 57-3. Chord Operator Diagram for the Conjunction J = uv=== | ===Figure 57-3. Chord Operator Diagram for the Conjunction J = uv=== | ||
| Line 7,795: | Line 8,025: | ||
Figure 57-3. Chord Operator Diagram for the Conjunction J = uv | Figure 57-3. Chord Operator Diagram for the Conjunction J = uv | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 57-3 -- Chord Operator Diagram for J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 57-3. Chord Operator Diagram for the Conjunction ''J'' = ''uv'''''</font></center></p> | ||
===Figure 57-4. Tangent Functor Diagram for the Conjunction J = uv=== | ===Figure 57-4. Tangent Functor Diagram for the Conjunction J = uv=== | ||
| Line 7,865: | Line 8,099: | ||
Figure 57-4. Tangent Functor Diagram for the Conjunction J = uv | Figure 57-4. Tangent Functor Diagram for the Conjunction J = uv | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 57-4 -- Tangent Functor Diagram for J.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 57-4. Tangent Functor Diagram for the Conjunction ''J'' = ''uv'''''</font></center></p> | ||
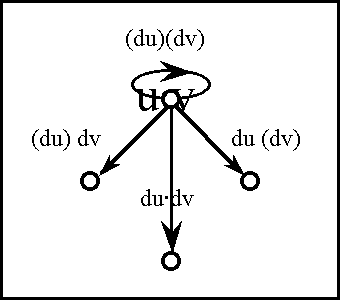
===Formula Display 11=== | ===Formula Display 11=== | ||
| Line 8,025: | Line 8,263: | ||
{| align="center" border="1" cellpadding="8" cellspacing="0" style="background:lightcyan; text-align:left; width:96%" | {| align="center" border="1" cellpadding="8" cellspacing="0" style="background:lightcyan; text-align:left; width:96%" | ||
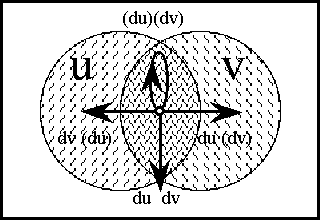
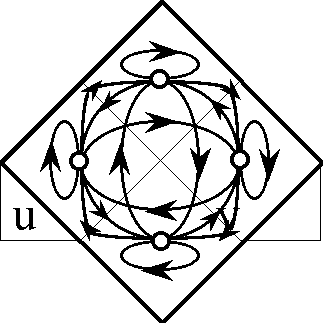
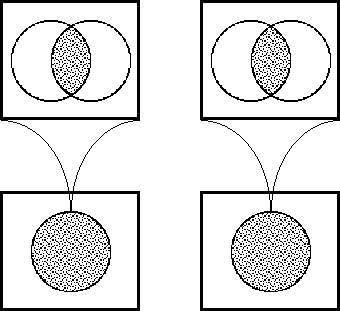
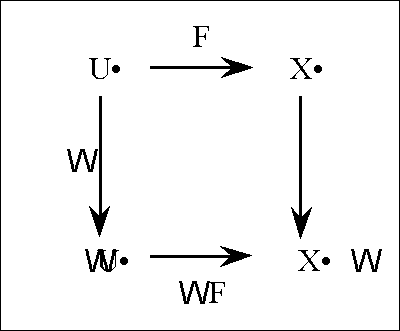
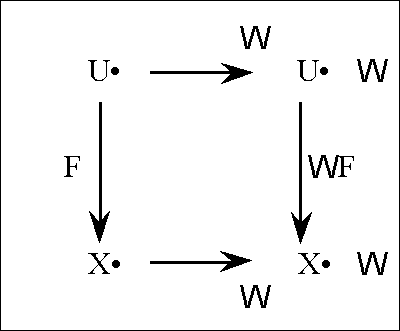
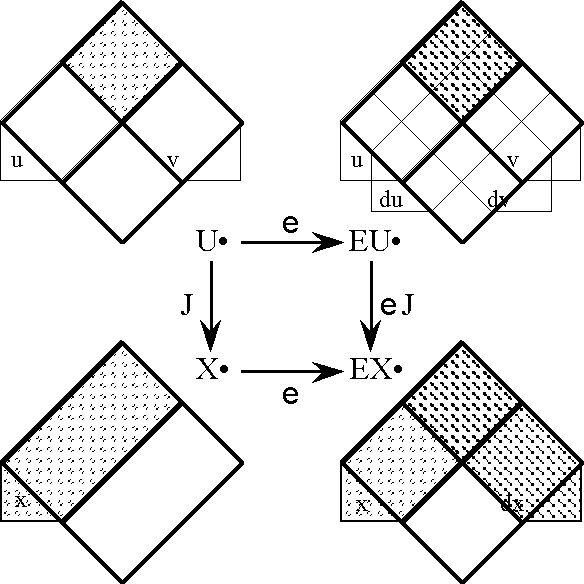
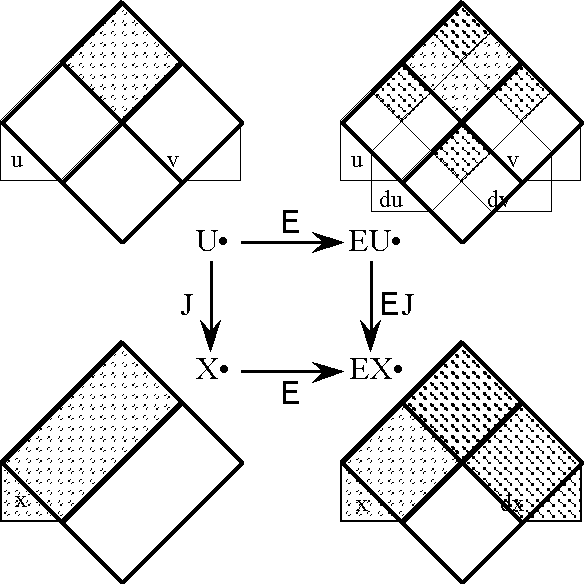
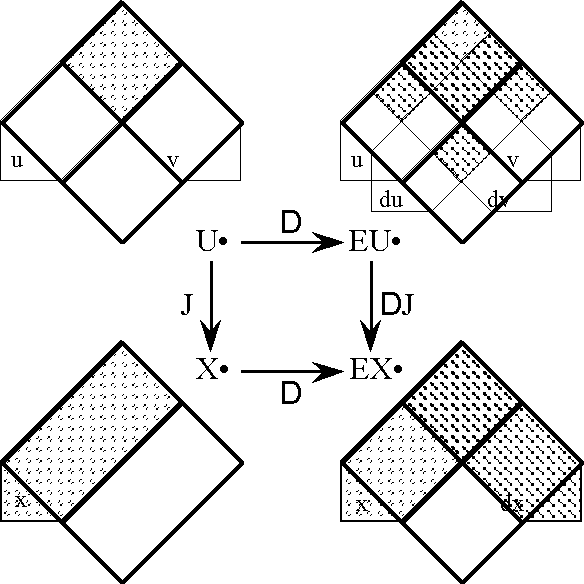
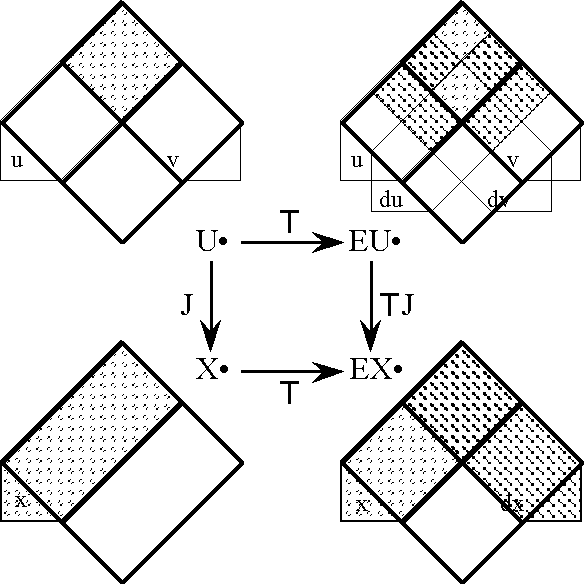
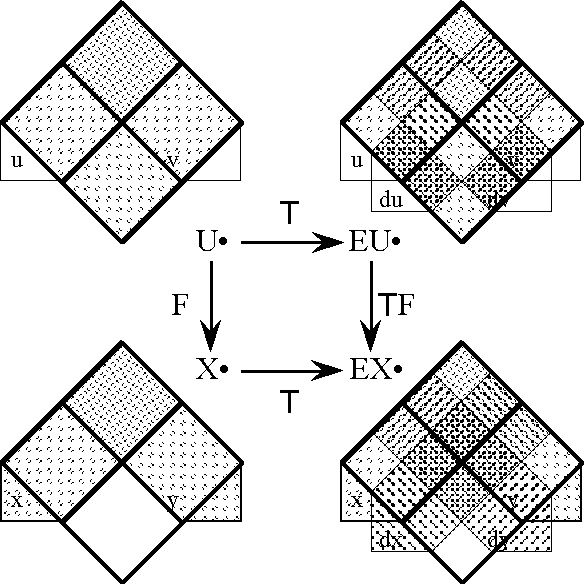
| − | |+ '''Table | + | |+ '''Table 58. Cast of Characters: Expansive Subtypes of Objects and Operators''' |
|- style="background:paleturquoise" | |- style="background:paleturquoise" | ||
! Item | ! Item | ||
| Line 8,032: | Line 8,270: | ||
! Type | ! Type | ||
|- | |- | ||
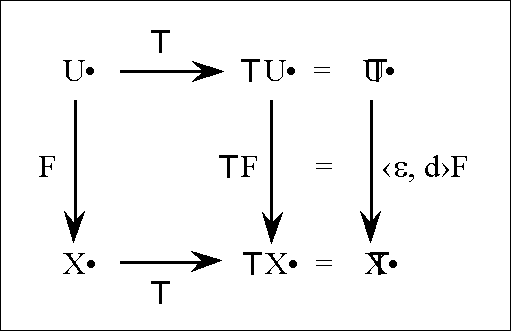
| − | | ''U''<sup> •</sup> | + | | valign="top" | ''U''<sup> •</sup> |
| − | | = [''u'', ''v''] | + | | valign="top" | <font face="courier new">= </font>[''u'', ''v''] |
| − | | Source Universe | + | | valign="top" | Source Universe |
| − | | ['''B'''<sup> | + | | valign="top" | ['''B'''<sup>''n''</sup>] |
| + | |- | ||
| + | | valign="top" | ''X''<sup> •</sup> | ||
| + | | valign="top" | | ||
| + | {| align="left" border="0" cellpadding="0" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | ||
| + | | <font face="courier new">= </font>[''x'', ''y''] | ||
| + | |- | ||
| + | | <font face="courier new">= </font>[''f'', ''g''] | ||
| + | |} | ||
| + | | valign="top" | Target Universe | ||
| + | | valign="top" | ['''B'''<sup>''k''</sup>] | ||
| + | |- | ||
| + | | valign="top" | E''U''<sup> •</sup> | ||
| + | | valign="top" | <font face="courier new">= </font>[''u'', ''v'', d''u'', d''v''] | ||
| + | | valign="top" | Extended Source Universe | ||
| + | | valign="top" | ['''B'''<sup>''n''</sup> × '''D'''<sup>''n''</sup>] | ||
| + | |- | ||
| + | | valign="top" | E''X''<sup> •</sup> | ||
| + | | valign="top" | | ||
| + | {| align="left" border="0" cellpadding="0" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | ||
| + | | <font face="courier new">= </font>[''x'', ''y'', d''x'', d''y''] | ||
| + | |- | ||
| + | | <font face="courier new">= </font>[''f'', ''g'', d''f'', d''g''] | ||
| + | |} | ||
| + | | valign="top" | Extended Target Universe | ||
| + | | valign="top" | ['''B'''<sup>''k''</sup> × '''D'''<sup>''k''</sup>] | ||
| + | |- | ||
| + | | ''F'' | ||
| + | | ''F'' = ‹''f'', ''g''› : ''U''<sup> •</sup> → ''X''<sup> •</sup> | ||
| + | | Transformation, or Mapping | ||
| + | | ['''B'''<sup>''n''</sup>] → ['''B'''<sup>''k''</sup>] | ||
| + | |- | ||
| + | | valign="top" | | ||
| + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | ||
| + | | | ||
|- | |- | ||
| − | | '' | + | | ''f'' |
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | | + | | ''g'' |
| − | | | + | |} |
| − | + | | valign="top" | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| + | | ''f'', ''g'' : ''U'' → '''B''' | ||
|- | |- | ||
| − | | | + | | ''f'' : ''U'' → [''x''] ⊆ ''X''<sup> •</sup> |
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | '' | + | | ''g'' : ''U'' → [''y''] ⊆ ''X''<sup> •</sup> |
| − | + | |} | |
| + | | valign="top" | | ||
| + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | ||
| Proposition | | Proposition | ||
| − | | | + | |} |
| + | | valign="top" | | ||
| + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100" | ||
| + | | '''B'''<sup>''n''</sup> → '''B''' | ||
| + | |- | ||
| + | | ∈ ('''B'''<sup>''n''</sup>, '''B'''<sup>''n''</sup> → '''B''') | ||
|- | |- | ||
| − | | '' | + | | = ('''B'''<sup>''n''</sup> +→ '''B''') = ['''B'''<sup>''n''</sup>] |
| − | + | |} | |
| − | |||
| − | |||
|- | |- | ||
| valign="top" | | | valign="top" | | ||
| Line 8,092: | Line 8,364: | ||
| | | | ||
|- | |- | ||
| − | | ['''B'''<sup> | + | | ['''B'''<sup>''n''</sup>] → ['''B'''<sup>''n''</sup> × '''D'''<sup>''n''</sup>] , |
|- | |- | ||
| − | | ['''B'''<sup> | + | | ['''B'''<sup>''k''</sup>] → ['''B'''<sup>''k''</sup> × '''D'''<sup>''k''</sup>] , |
|- | |- | ||
| − | | (['''B'''<sup> | + | | (['''B'''<sup>''n''</sup>] → ['''B'''<sup>''k''</sup>]) |
|- | |- | ||
| → | | → | ||
|- | |- | ||
| − | | (['''B'''<sup> | + | | (['''B'''<sup>''n''</sup> × '''D'''<sup>''n''</sup>] → ['''B'''<sup>''k''</sup> × '''D'''<sup>''k''</sup>]) |
|- | |- | ||
| | | | ||
| Line 8,163: | Line 8,435: | ||
| | | | ||
|- | |- | ||
| − | | ['''B'''<sup> | + | | ['''B'''<sup>''n''</sup>] → ['''B'''<sup>''n''</sup> × '''D'''<sup>''n''</sup>] , |
|- | |- | ||
| − | | ['''B'''<sup> | + | | ['''B'''<sup>''k''</sup>] → ['''B'''<sup>''k''</sup> × '''D'''<sup>''k''</sup>] , |
|- | |- | ||
| − | | (['''B'''<sup> | + | | (['''B'''<sup>''n''</sup>] → ['''B'''<sup>''k''</sup>]) |
|- | |- | ||
| → | | → | ||
|- | |- | ||
| − | | (['''B'''<sup> | + | | (['''B'''<sup>''n''</sup> × '''D'''<sup>''n''</sup>] → ['''B'''<sup>''k''</sup> × '''D'''<sup>''k''</sup>]) |
|- | |- | ||
| | | | ||
| Line 8,294: | Line 8,566: | ||
</pre> | </pre> | ||
| − | + | {| align="center" border="1" cellpadding="4" cellspacing="0" style="background:lightcyan; text-align:left; width:96%" | |
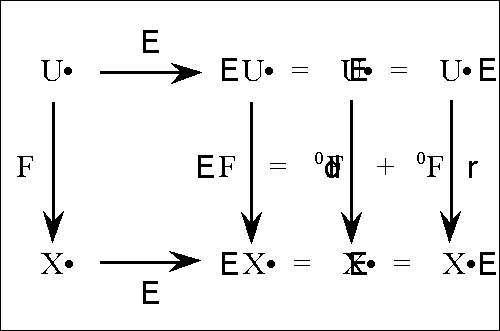
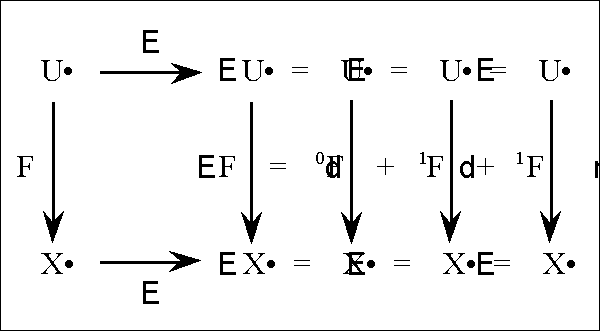
| − | + | |+ '''Table 59. Synopsis of Terminology: Restrictive and Alternative Subtypes''' | |
| − | + | |- style="background:paleturquoise" | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | {| align="center" border="1" cellpadding=" | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | = | ||
| − | |||
| | | | ||
| + | | align="center" | '''Operator<br>or<br>Operand''' | ||
| + | | align="center" | '''Proposition<br>or<br>Component''' | ||
| + | | align="center" | '''Transformation<br>or<br>Mapping''' | ||
| + | |- | ||
| + | | Operand | ||
| + | | valign="top" | | ||
| + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | ||
| + | | ''F'' = ‹''F''<sub>1</sub>, ''F''<sub>2</sub>› | ||
| + | |- | ||
| + | | ''F'' = ‹''f'', ''g''› : ''U'' → ''X'' | ||
| + | |} | ||
| + | | valign="top" | | ||
| + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | ||
| + | | ''F''<sub>''i''</sub> : 〈''u'', ''v''〉 → '''B''' | ||
|- | |- | ||
| − | + | | ''F''<sub>''i''</sub> : '''B'''<sup>''n''</sup> → '''B''' | |
| − | | '' | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| + | | valign="top" | | ||
| + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100" | ||
| + | | ''F'' : [''u'', ''v''] → [''x'', ''y''] | ||
| + | |- | ||
| + | | ''F'' : '''B'''<sup>''n''</sup> → '''B'''<sup>''k''</sup> | ||
|} | |} | ||
| − | + | |- | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | {| align=" | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" |
| − | | | + | | Tacit |
| − | + | |- | |
| − | + | | Extension | |
| − | | | + | |} |
| − | | | + | | |
| + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | ||
| + | | <math>\epsilon</math> : | ||
| + | |- | ||
| + | | ''U''<sup> •</sup> → E''U''<sup> •</sup> , ''X''<sup> •</sup> → E''X''<sup> •</sup> , | ||
| + | |- | ||
| + | | (''U''<sup> •</sup> → ''X''<sup> •</sup>) → (E''U''<sup> •</sup> → ''X''<sup> •</sup>) | ||
|} | |} | ||
| + | | | ||
| + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | ||
| + | | <math>\epsilon</math>''F''<sub>''i''</sub> : | ||
| + | |- | ||
| + | | 〈''u'', ''v'', d''u'', d''v''〉 → '''B''' | ||
| + | |- | ||
| + | | '''B'''<sup>''n''</sup> × '''D'''<sup>''n''</sup> → '''B''' | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| | | | ||
| − | {| align=" | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" |
| − | | | + | | <math>\epsilon</math>''F'' : |
| − | + | |- | |
| − | + | | [''u'', ''v'', d''u'', d''v''] → [''x'', ''y''] | |
| − | + | |- | |
| − | | | + | | ['''B'''<sup>''n''</sup> × '''D'''<sup>''n''</sup>] → ['''B'''<sup>''k''</sup>] |
| − | | | ||
| − | |||
|} | |} | ||
| + | |- | ||
| + | | | ||
| + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | ||
| + | | Trope | ||
| + | |- | ||
| + | | Extension | ||
|} | |} | ||
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | === | + | | <math>\eta</math> : |
| − | + | |- | |
| − | < | + | | ''U''<sup> •</sup> → E''U''<sup> •</sup> , ''X''<sup> •</sup> → E''X''<sup> •</sup> , |
| − | + | |- | |
| − | + | | (''U''<sup> •</sup> → ''X''<sup> •</sup>) → (E''U''<sup> •</sup> → d''X''<sup> •</sup>) | |
| − | | | + | |} |
| − | + | | | |
| − | | | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" |
| − | | | + | | <math>\eta</math>''F''<sub>''i''</sub> : |
| − | | | + | |- |
| − | | | + | | 〈''u'', ''v'', d''u'', d''v''〉 → '''D''' |
| − | | | + | |- |
| − | + | | '''B'''<sup>''n''</sup> × '''D'''<sup>''n''</sup> → '''D''' | |
| − | | | + | |} |
| − | | | + | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | <math>\eta</math>''F'' : | |
| − | | | + | |- |
| − | + | | [''u'', ''v'', d''u'', d''v''] → [d''x'', d''y''] | |
| − | </ | + | |- |
| − | + | | ['''B'''<sup>''n''</sup> × '''D'''<sup>''n''</sup>] → ['''D'''<sup>''k''</sup>] | |
| − | === | + | |} |
| − | + | |- | |
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | Enlargement | |
| − | + | |- | |
| − | + | | Operator | |
| − | + | |} | |
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | E : | |
| − | + | |- | |
| − | + | | ''U''<sup> •</sup> → E''U''<sup> •</sup> , ''X''<sup> •</sup> → E''X''<sup> •</sup> , | |
| − | + | |- | |
| − | + | | (''U''<sup> •</sup> → ''X''<sup> •</sup>) → (E''U''<sup> •</sup> → d''X''<sup> •</sup>) | |
| − | + | |} | |
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | E''F''<sub>''i''</sub> : | |
| − | + | |- | |
| − | + | | 〈''u'', ''v'', d''u'', d''v''〉 → '''D''' | |
| − | + | |- | |
| − | + | | '''B'''<sup>''n''</sup> × '''D'''<sup>''n''</sup> → '''D''' | |
| − | + | |} | |
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | E''F'' : | |
| − | + | |- | |
| − | + | | [''u'', ''v'', d''u'', d''v''] → [d''x'', d''y''] | |
| − | + | |- | |
| − | + | | ['''B'''<sup>''n''</sup> × '''D'''<sup>''n''</sup>] → ['''D'''<sup>''k''</sup>] | |
| − | + | |} | |
| − | + | |- | |
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | Difference | |
| − | + | |- | |
| − | | | + | | Operator |
| − | | | + | |} |
| − | | | + | | |
| − | | | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" |
| − | | | + | | D : |
| − | | | + | |- |
| − | | | + | | ''U''<sup> •</sup> → E''U''<sup> •</sup> , ''X''<sup> •</sup> → E''X''<sup> •</sup> , |
| − | | | + | |- |
| − | | | + | | (''U''<sup> •</sup> → ''X''<sup> •</sup>) → (E''U''<sup> •</sup> → d''X''<sup> •</sup>) |
| − | + | |} | |
| − | | | + | | |
| − | | | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" |
| − | | | + | | D''F''<sub>''i''</sub> : |
| − | + | |- | |
| − | + | | 〈''u'', ''v'', d''u'', d''v''〉 → '''D''' | |
| − | + | |- | |
| − | + | | '''B'''<sup>''n''</sup> × '''D'''<sup>''n''</sup> → '''D''' | |
| − | + | |} | |
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | D''F'' : | |
| − | + | |- | |
| − | + | | [''u'', ''v'', d''u'', d''v''] → [d''x'', d''y''] | |
| − | + | |- | |
| − | + | | ['''B'''<sup>''n''</sup> × '''D'''<sup>''n''</sup>] → ['''D'''<sup>''k''</sup>] | |
| − | + | |} | |
| − | + | |- | |
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | Differential | |
| − | + | |- | |
| − | + | | Operator | |
| − | + | |} | |
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | d : | |
| − | + | |- | |
| − | + | | ''U''<sup> •</sup> → E''U''<sup> •</sup> , ''X''<sup> •</sup> → E''X''<sup> •</sup> , | |
| − | + | |- | |
| − | + | | (''U''<sup> •</sup> → ''X''<sup> •</sup>) → (E''U''<sup> •</sup> → d''X''<sup> •</sup>) | |
| − | + | |} | |
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | d''F''<sub>''i''</sub> : | |
| − | + | |- | |
| − | + | | 〈''u'', ''v'', d''u'', d''v''〉 → '''D''' | |
| − | < | + | |- |
| − | + | | '''B'''<sup>''n''</sup> × '''D'''<sup>''n''</sup> → '''D''' | |
| − | + | |} | |
| − | + | | | |
| − | < | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" |
| − | + | | d''F'' : | |
| − | | | + | |- |
| − | + | | [''u'', ''v'', d''u'', d''v''] → [d''x'', d''y''] | |
| − | | | + | |- |
| − | | | + | | ['''B'''<sup>''n''</sup> × '''D'''<sup>''n''</sup>] → ['''D'''<sup>''k''</sup>] |
| − | | | + | |} |
| − | | | + | |- |
| − | | | + | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | | | + | | Remainder |
| − | | | + | |- |
| − | + | | Operator | |
| − | | | + | |} |
| − | | | + | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | r : | |
| − | + | |- | |
| − | + | | ''U''<sup> •</sup> → E''U''<sup> •</sup> , ''X''<sup> •</sup> → E''X''<sup> •</sup> , | |
| − | + | |- | |
| − | + | | (''U''<sup> •</sup> → ''X''<sup> •</sup>) → (E''U''<sup> •</sup> → d''X''<sup> •</sup>) | |
| − | + | |} | |
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | r''F''<sub>''i''</sub> : | |
| − | + | |- | |
| − | + | | 〈''u'', ''v'', d''u'', d''v''〉 → '''D''' | |
| − | | | + | |- |
| − | | | + | | '''B'''<sup>''n''</sup> × '''D'''<sup>''n''</sup> → '''D''' |
| − | + | |} | |
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | r''F'' : | |
| − | + | |- | |
| − | + | | [''u'', ''v'', d''u'', d''v''] → [d''x'', d''y''] | |
| − | + | |- | |
| − | + | | ['''B'''<sup>''n''</sup> × '''D'''<sup>''n''</sup>] → ['''D'''<sup>''k''</sup>] | |
| − | + | |} | |
| − | + | |- | |
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | Radius | |
| − | + | |- | |
| − | + | | Operator | |
| − | + | |} | |
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | <font face=georgia>'''e'''</font> = ‹<math>\epsilon</math>, <math>\eta</math>› : | |
| − | + | |- | |
| − | + | | ''U''<sup> •</sup> → E''U''<sup> •</sup> , ''X''<sup> •</sup> → E''X''<sup> •</sup> , | |
| − | + | |- | |
| − | + | | (''U''<sup> •</sup> → ''X''<sup> •</sup>) → (E''U''<sup> •</sup> → E''X''<sup> •</sup>) | |
| − | + | |} | |
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | | |
| − | + | |- | |
| − | + | | | |
| − | + | |- | |
| − | + | | | |
| − | + | |} | |
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | <font face=georgia>'''e'''</font>''F'' : | |
| − | + | |- | |
| − | + | | [''u'', ''v'', d''u'', d''v''] → [''x'', ''y'', d''x'', d''y''] | |
| − | + | |- | |
| − | + | | ['''B'''<sup>''n''</sup> × '''D'''<sup>''n''</sup>] → ['''B'''<sup>''k''</sup> × '''D'''<sup>''k''</sup>] | |
| − | + | |} | |
| − | + | |- | |
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | Secant | |
| − | + | |- | |
| − | + | | Operator | |
| − | + | |} | |
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | <font face=georgia>'''E'''</font> = ‹<math>\epsilon</math>, E› : | |
| − | + | |- | |
| − | + | | ''U''<sup> •</sup> → E''U''<sup> •</sup> , ''X''<sup> •</sup> → E''X''<sup> •</sup> , | |
| − | + | |- | |
| − | + | | (''U''<sup> •</sup> → ''X''<sup> •</sup>) → (E''U''<sup> •</sup> → E''X''<sup> •</sup>) | |
| − | + | |} | |
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | | |
| − | + | |- | |
| − | + | | | |
| − | + | |- | |
| − | + | | | |
| − | + | |} | |
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | <font face=georgia>'''E'''</font>''F'' : | |
| − | + | |- | |
| − | + | | [''u'', ''v'', d''u'', d''v''] → [''x'', ''y'', d''x'', d''y''] | |
| − | + | |- | |
| − | + | | ['''B'''<sup>''n''</sup> × '''D'''<sup>''n''</sup>] → ['''B'''<sup>''k''</sup> × '''D'''<sup>''k''</sup>] | |
| − | + | |} | |
| − | + | |- | |
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | Chord | |
| − | + | |- | |
| − | + | | Operator | |
| − | + | |} | |
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | <font face=georgia>'''D'''</font> = ‹<math>\epsilon</math>, D› : | |
| − | + | |- | |
| − | + | | ''U''<sup> •</sup> → E''U''<sup> •</sup> , ''X''<sup> •</sup> → E''X''<sup> •</sup> , | |
| − | + | |- | |
| − | + | | (''U''<sup> •</sup> → ''X''<sup> •</sup>) → (E''U''<sup> •</sup> → E''X''<sup> •</sup>) | |
| − | + | |} | |
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| − | + | | | |
| − | + | |- | |
| − | + | | | |
| − | + | |- | |
| − | + | | | |
| − | + | |} | |
| − | + | | | |
| − | + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | |
| + | | <font face=georgia>'''D'''</font>''F'' : | ||
| + | |- | ||
| + | | [''u'', ''v'', d''u'', d''v''] → [''x'', ''y'', d''x'', d''y''] | ||
| + | |- | ||
| + | | ['''B'''<sup>''n''</sup> × '''D'''<sup>''n''</sup>] → ['''B'''<sup>''k''</sup> × '''D'''<sup>''k''</sup>] | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | ||
| + | | Tangent | ||
| + | |- | ||
| + | | Functor | ||
| + | |} | ||
| + | | | ||
| + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | ||
| + | | <font face=georgia>'''T'''</font> = ‹<math>\epsilon</math>, d› : | ||
| + | |- | ||
| + | | ''U''<sup> •</sup> → E''U''<sup> •</sup> , ''X''<sup> •</sup> → E''X''<sup> •</sup> , | ||
| + | |- | ||
| + | | (''U''<sup> •</sup> → ''X''<sup> •</sup>) → (E''U''<sup> •</sup> → E''X''<sup> •</sup>) | ||
| + | |} | ||
| + | | | ||
| + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | ||
| + | | d''F''<sub>''i''</sub> : | ||
| + | |- | ||
| + | | 〈''u'', ''v'', d''u'', d''v''〉 → '''D''' | ||
| + | |- | ||
| + | | '''B'''<sup>''n''</sup> × '''D'''<sup>''n''</sup> → '''D''' | ||
| + | |} | ||
| + | | | ||
| + | {| align="left" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; text-align:left; width:100%" | ||
| + | | <font face=georgia>'''T'''</font>''F'' : | ||
| + | |- | ||
| + | | [''u'', ''v'', d''u'', d''v''] → [''x'', ''y'', d''x'', d''y''] | ||
| + | |- | ||
| + | | ['''B'''<sup>''n''</sup> × '''D'''<sup>''n''</sup>] → ['''B'''<sup>''k''</sup> × '''D'''<sup>''k''</sup>] | ||
| + | |} | ||
| + | |}<br> | ||
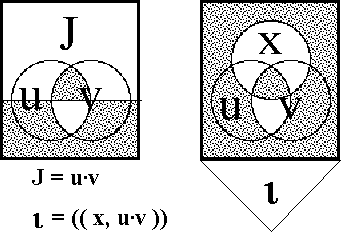
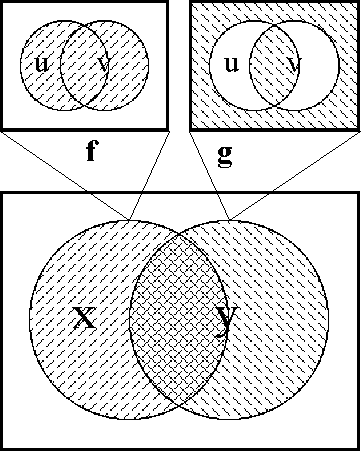
| − | === | + | ===Formula Display 12=== |
<pre> | <pre> | ||
| − | + | o-----------------------------------------------------------o | |
| − | o----- | + | | | |
| − | | u v | | + | | x = f(u, v) = ((u)(v)) | |
| − | + | | | | |
| − | + | | y = g(u, v) = ((u, v)) | | |
| − | | | + | | | |
| − | + | o-----------------------------------------------------------o | |
| − | | 0 | + | </pre> |
| − | | | + | |
| − | | | + | <br><font face="courier new"> |
| − | | | + | {| align="center" border="1" cellpadding="8" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:96%" |
| − | + | | | |
| − | + | {| align="center" border="0" cellpadding="8" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | |
| − | + | | | |
| − | + | | ''x'' | |
| − | + | | = | |
| − | </ | + | | ''f''‹''u'', ''v''› |
| + | | = | ||
| + | | ((''u'')(''v'')) | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | | ''y'' | ||
| + | | = | ||
| + | | ''g''‹''u'', ''v''› | ||
| + | | = | ||
| + | | ((''u'', ''v'')) | ||
| + | | | ||
| + | |} | ||
| + | |} | ||
| + | </font><br> | ||
| − | === | + | ===Formula Display 13=== |
<pre> | <pre> | ||
| − | + | o-----------------------------------------------------------o | |
| − | + | | | | |
| − | + | | <x, y> = F<u, v> = <((u)(v)), ((u, v))> | | |
| − | + | | | | |
| − | | | + | o-----------------------------------------------------------o |
| − | | | + | </pre> |
| − | + | ||
| − | + | <br><font face="courier new"> | |
| − | + | {| align="center" border="1" cellpadding="8" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:96%" | |
| − | + | | | |
| − | + | {| align="center" border="0" cellpadding="8" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | |
| − | + | | ‹''x'', ''y''› | |
| − | + | | = | |
| − | + | | ''F''‹''u'', ''v''› | |
| − | + | | = | |
| − | + | | ‹((''u'')(''v'')), ((''u'', ''v''))› | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | o---------- | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | </pre> | ||
| − | |||
| − | <br><font face="courier new"> | ||
| − | {| align="center" border="1" cellpadding=" | ||
| − | | | ||
| − | {| align=" | ||
| − | | | ||
| − | |||
| − | | | ||
|} | |} | ||
|} | |} | ||
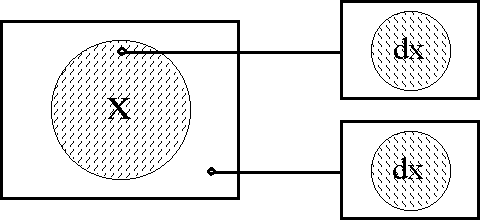
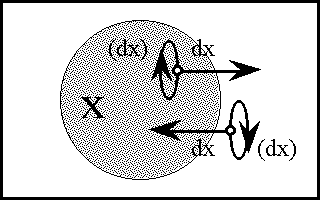
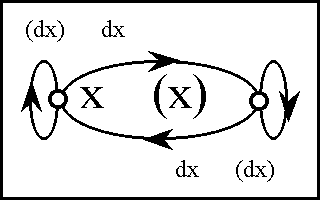
</font><br> | </font><br> | ||
| − | + | <br><font face="courier new"> | |
| − | + | {| align="center" border="1" cellpadding="8" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:96%" | |
| − | + | | | |
| − | + | {| align="center" border="0" cellpadding="8" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | |
| − | + | | | |
| − | + | | ‹''x'', ''y''› | |
| − | + | | = | |
| − | + | | ''F''‹''u'', ''v''› | |
| − | + | | = | |
| − | + | | ‹((''u'')(''v'')), ((''u'', ''v''))› | |
| − | + | | | |
| − | |||
| − | <br><font face="courier new"> | ||
| − | {| align="center" border="1" cellpadding=" | ||
| − | | | ||
| − | {| align=" | ||
| − | | | ||
| − | |||
| − | | | ||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
|} | |} | ||
</font><br> | </font><br> | ||
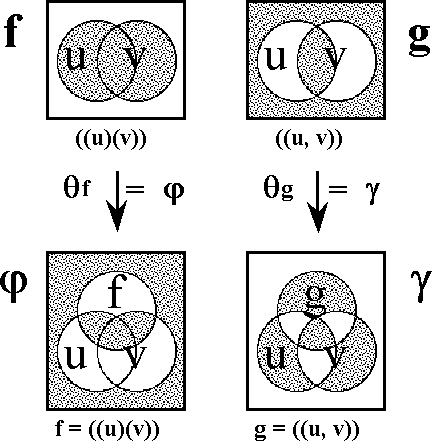
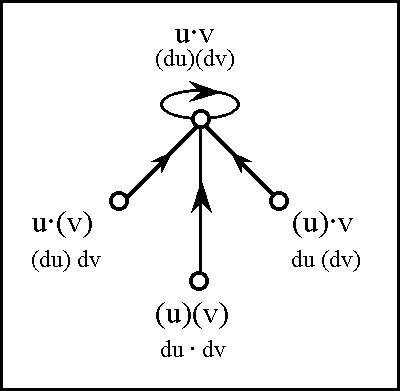
| − | === | + | ===Table 60. Propositional Transformation=== |
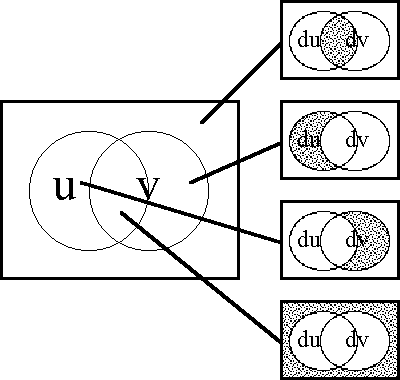
<pre> | <pre> | ||
| − | o-------------------------------------------------o | + | Table 60. Propositional Transformation |
| − | | | + | o-------------o-------------o-------------o-------------o |
| − | | | + | | u | v | f | g | |
| − | + | o-------------o-------------o-------------o-------------o | |
| − | + | | | | | | | |
| − | + | | 0 | 0 | 0 | 1 | | |
| − | o-------------------------------------------------o | + | | | | | | |
| + | | 0 | 1 | 1 | 0 | | ||
| + | | | | | | | ||
| + | | 1 | 0 | 1 | 0 | | ||
| + | | | | | | | ||
| + | | 1 | 1 | 1 | 1 | | ||
| + | | | | | | | ||
| + | o-------------o-------------o-------------o-------------o | ||
| + | | | | ((u)(v)) | ((u, v)) | | ||
| + | o-------------o-------------o-------------o-------------o | ||
</pre> | </pre> | ||
| − | + | <font face="courier new"> | |
| − | {| align="center" border="1" cellpadding=" | + | {| align="center" border="1" cellpadding="4" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:96%" |
| − | | | + | |+ '''Table 60. Propositional Transformation''' |
| − | {| align=" | + | |- style="background:paleturquoise" |
| − | | width=" | + | | width="25%" | ''u'' |
| − | | width="4%" | + | | width="25%" | ''v'' |
| − | | | + | | width="25%" | ''f'' |
| + | | width="25%" | ''g'' | ||
| + | |- | ||
| + | | width="25%" | | ||
| + | {| align="center" border="0" cellpadding="4" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 | ||
| + | |- | ||
| + | | 0 | ||
| + | |- | ||
| + | | 1 | ||
| + | |- | ||
| + | | 1 | ||
| + | |} | ||
| + | | width="25%" | | ||
| + | {| align="center" border="0" cellpadding="4" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 | ||
| + | |- | ||
| + | | 1 | ||
| + | |- | ||
| + | | 0 | ||
| + | |- | ||
| + | | 1 | ||
| + | |} | ||
| + | | width="25%" | | ||
| + | {| align="center" border="0" cellpadding="4" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 | ||
| + | |- | ||
| + | | 1 | ||
| + | |- | ||
| + | | 1 | ||
| + | |- | ||
| + | | 1 | ||
| + | |} | ||
| + | | width="25%" | | ||
| + | {| align="center" border="0" cellpadding="4" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 1 | ||
| + | |- | ||
| + | | 0 | ||
| + | |- | ||
| + | | 0 | ||
|- | |- | ||
| − | | | + | | 1 |
| − | |||
| − | |||
|} | |} | ||
| + | |- | ||
| + | | width="25%" | | ||
| + | | width="25%" | | ||
| + | | width="25%" | ((''u'')(''v'')) | ||
| + | | width="25%" | ((''u'', ''v'')) | ||
|} | |} | ||
</font><br> | </font><br> | ||
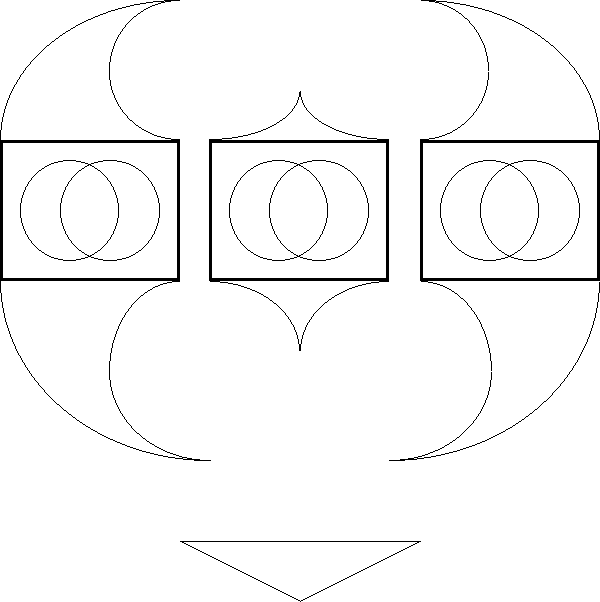
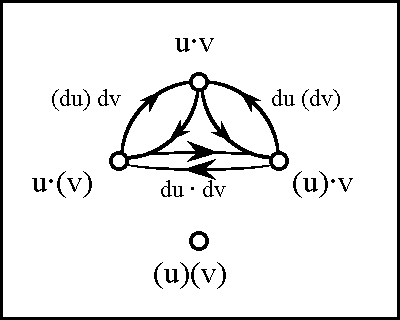
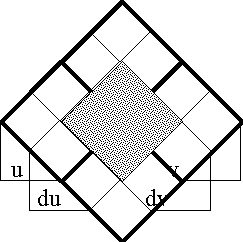
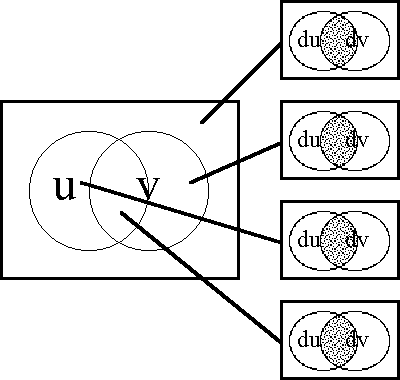
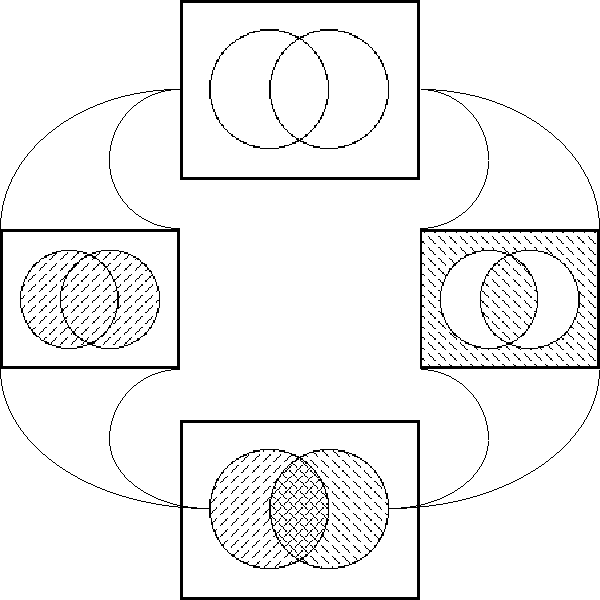
| − | === | + | ===Figure 61. Propositional Transformation=== |
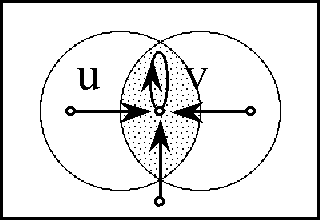
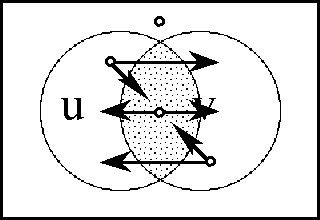
<pre> | <pre> | ||
| − | o-------------------------------------------------o | + | o-----------------------------------------------------o |
| − | | | + | | U | |
| − | | | + | | | |
| − | | | + | | o-----------o o-----------o | |
| − | | | + | | / \ / \ | |
| − | | | + | | / o \ | |
| − | o-------------------------------------------------o | + | | / / \ \ | |
| − | + | | / / \ \ | | |
| − | + | | o o o o | | |
| − | + | | | | | | | | |
| − | + | | | u | | v | | | |
| − | | | + | | | | | | | |
| − | + | | o o o o | | |
| − | | | + | | \ \ / / | |
| − | | | + | | \ \ / / | |
| − | | | + | | \ o / | |
| − | | | + | | \ / \ / | |
| − | | | + | | o-----------o o-----------o | |
| − | | | + | | | |
| − | | | + | | | |
| − | | | + | o-----------------------------------------------------o |
| − | | | + | / \ / \ |
| − | | | + | / \ / \ |
| − | | | + | / \ / \ |
| − | | | + | / \ / \ |
| − | | | + | / \ / \ |
| − | + | / \ / \ | |
| − | + | / \ / \ | |
| − | + | / \ / \ | |
| − | + | / \ / \ | |
| − | + | / \ / \ | |
| − | + | / \ / \ | |
| − | o--------------------------------------------------------------------------------o | + | / \ / \ |
| − | | | + | o-------------------------o o-------------------------o |
| − | | | + | | U | |\U \\\\\\\\\\\\\\\\\\\\\\| |
| − | | | + | | o---o o---o | |\\\\\\o---o\\\o---o\\\\\\| |
| − | | | + | | //////\ //////\ | |\\\\\/ \\/ \\\\\\| |
| − | | | + | | ////////o///////\ | |\\\\/ o \\\\\| |
| − | | | + | | //////////\///////\ | |\\\/ /\\ \\\\| |
| − | | | + | | o///////o///o///////o | |\\o o\\\o o\\| |
| − | | | + | | |// u //|///|// v //| | |\\| u |\\\| v |\\| |
| − | | | + | | o///////o///o///////o | |\\o o\\\o o\\| |
| − | | | + | | \///////\////////// | |\\\\ \\/ /\\\| |
| − | | | + | | \///////o//////// | |\\\\\ o /\\\\| |
| − | o---------------------- | + | | \////// \////// | |\\\\\\ /\\ /\\\\\| |
| + | | o---o o---o | |\\\\\\o---o\\\o---o\\\\\\| | ||
| + | | | |\\\\\\\\\\\\\\\\\\\\\\\\\| | ||
| + | o-------------------------o o-------------------------o | ||
| + | \ | | / | ||
| + | \ | | / | ||
| + | \ | | / | ||
| + | \ f | | g / | ||
| + | \ | | / | ||
| + | \ | | / | ||
| + | \ | | / | ||
| + | \ | | / | ||
| + | \ | | / | ||
| + | \ | | / | ||
| + | o-------\----|---------------------------|----/-------o | ||
| + | | X \ | | / | | ||
| + | | \| |/ | | ||
| + | | o-----------o o-----------o | | ||
| + | | //////////////\ /\\\\\\\\\\\\\\ | | ||
| + | | ////////////////o\\\\\\\\\\\\\\\\ | | ||
| + | | /////////////////X\\\\\\\\\\\\\\\\\ | | ||
| + | | /////////////////XXX\\\\\\\\\\\\\\\\\ | | ||
| + | | o///////////////oXXXXXo\\\\\\\\\\\\\\\o | | ||
| + | | |///////////////|XXXXX|\\\\\\\\\\\\\\\| | | ||
| + | | |////// x //////|XXXXX|\\\\\\ y \\\\\\| | | ||
| + | | |///////////////|XXXXX|\\\\\\\\\\\\\\\| | | ||
| + | | o///////////////oXXXXXo\\\\\\\\\\\\\\\o | | ||
| + | | \///////////////\XXX/\\\\\\\\\\\\\\\/ | | ||
| + | | \///////////////\X/\\\\\\\\\\\\\\\/ | | ||
| + | | \///////////////o\\\\\\\\\\\\\\\/ | | ||
| + | | \////////////// \\\\\\\\\\\\\\/ | | ||
| + | | o-----------o o-----------o | | ||
| + | | | | ||
| + | | | | ||
| + | o-----------------------------------------------------o | ||
| + | Figure 61. Propositional Transformation | ||
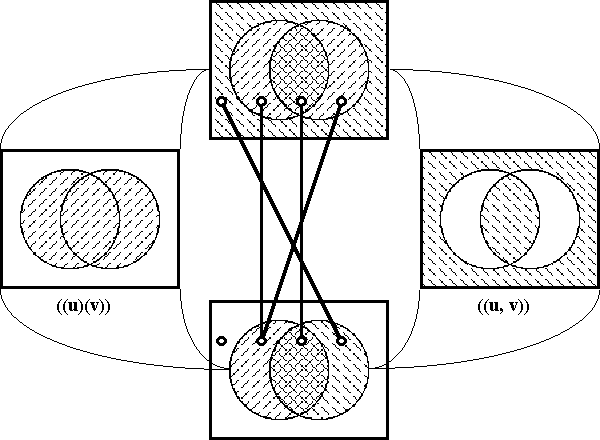
</pre> | </pre> | ||
| − | < | + | <br> |
| − | + | <p>[[Image:Diff Log Dyn Sys -- Figure 61 -- Propositional Transformation.gif|center]]</p> | |
| − | + | <p><center><font size="+1">'''Figure 61. Propositional Transformation'''</font></center></p> | |
| − | | | + | |
| − | + | ===Figure 62. Propositional Transformation (Short Form)=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
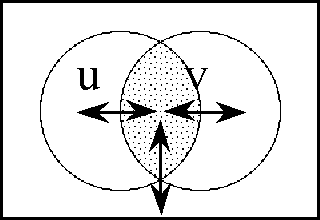
| − | === | ||
<pre> | <pre> | ||
| − | + | o-------------------------o o-------------------------o | |
| − | o--------------------------------------------------------------------------------o | + | | U | |\U \\\\\\\\\\\\\\\\\\\\\\| |
| − | | | + | | o---o o---o | |\\\\\\o---o\\\o---o\\\\\\| |
| − | | | + | | //////\ //////\ | |\\\\\/ \\/ \\\\\\| |
| − | | | + | | ////////o///////\ | |\\\\/ o \\\\\| |
| − | | | + | | //////////\///////\ | |\\\/ /\\ \\\\| |
| − | | | + | | o///////o///o///////o | |\\o o\\\o o\\| |
| − | | | + | | |// u //|///|// v //| | |\\| u |\\\| v |\\| |
| − | | | + | | o///////o///o///////o | |\\o o\\\o o\\| |
| − | | | + | | \///////\////////// | |\\\\ \\/ /\\\| |
| − | | | + | | \///////o//////// | |\\\\\ o /\\\\| |
| − | | | + | | \////// \////// | |\\\\\\ /\\ /\\\\\| |
| − | | | + | | o---o o---o | |\\\\\\o---o\\\o---o\\\\\\| |
| − | o---------------------- | + | | | |\\\\\\\\\\\\\\\\\\\\\\\\\| |
| + | o-------------------------o o-------------------------o | ||
| + | \ / \ / | ||
| + | \ / \ / | ||
| + | \ / \ / | ||
| + | \ f / \ g / | ||
| + | \ / \ / | ||
| + | \ / \ / | ||
| + | \ / \ / | ||
| + | \ / \ / | ||
| + | \ / \ / | ||
| + | o---------\-----/---------------------\-----/---------o | ||
| + | | X \ / \ / | | ||
| + | | \ / \ / | | ||
| + | | o-----------o o-----------o | | ||
| + | | //////////////\ /\\\\\\\\\\\\\\ | | ||
| + | | ////////////////o\\\\\\\\\\\\\\\\ | | ||
| + | | /////////////////X\\\\\\\\\\\\\\\\\ | | ||
| + | | /////////////////XXX\\\\\\\\\\\\\\\\\ | | ||
| + | | o///////////////oXXXXXo\\\\\\\\\\\\\\\o | | ||
| + | | |///////////////|XXXXX|\\\\\\\\\\\\\\\| | | ||
| + | | |////// x //////|XXXXX|\\\\\\ y \\\\\\| | | ||
| + | | |///////////////|XXXXX|\\\\\\\\\\\\\\\| | | ||
| + | | o///////////////oXXXXXo\\\\\\\\\\\\\\\o | | ||
| + | | \///////////////\XXX/\\\\\\\\\\\\\\\/ | | ||
| + | | \///////////////\X/\\\\\\\\\\\\\\\/ | | ||
| + | | \///////////////o\\\\\\\\\\\\\\\/ | | ||
| + | | \////////////// \\\\\\\\\\\\\\/ | | ||
| + | | o-----------o o-----------o | | ||
| + | | | | ||
| + | | | | ||
| + | o-----------------------------------------------------o | ||
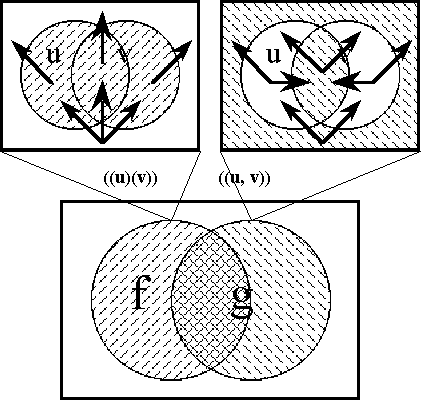
| + | Figure 62. Propositional Transformation (Short Form) | ||
</pre> | </pre> | ||
| − | <font | + | <br> |
| − | + | <p>[[Image:Diff Log Dyn Sys -- Figure 62 -- Propositional Transformation (Short Form).gif|center]]</p> | |
| − | | | + | <p><center><font size="+1">'''Figure 62. Propositional Transformation (Short Form)'''</font></center></p> |
| − | | | + | |
| − | + | ===Figure 63. Transformation of Positions=== | |
| − | | | + | |
| − | | | + | <pre> |
| − | | | + | o-----------------------------------------------------o |
| − | | | + | |`U` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `| |
| − | | | + | |` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `| |
| − | | | + | |` ` ` ` ` ` o-----------o ` o-----------o ` ` ` ` ` `| |
| − | | | + | |` ` ` ` ` `/' ' ' ' ' ' '\`/' ' ' ' ' ' '\` ` ` ` ` `| |
| − | | | + | |` ` ` ` ` / ' ' ' ' ' ' ' o ' ' ' ' ' ' ' \ ` ` ` ` `| |
| − | | | + | |` ` ` ` `/' ' ' ' ' ' ' '/^\' ' ' ' ' ' ' '\` ` ` ` `| |
| − | | | + | |` ` ` ` / ' ' ' ' ' ' ' /^^^\ ' ' ' ' ' ' ' \ ` ` ` `| |
| − | | | + | |` ` ` `o' ' ' ' ' ' ' 'o^^^^^o' ' ' ' ' ' ' 'o` ` ` `| |
| − | + | |` ` ` `|' ' ' ' ' ' ' '|^^^^^|' ' ' ' ' ' ' '|` ` ` `| | |
| − | + | |` ` ` `|' ' ' ' u ' ' '|^^^^^|' ' ' v ' ' ' '|` ` ` `| | |
| − | + | |` ` ` `|' ' ' ' ' ' ' '|^^^^^|' ' ' ' ' ' ' '|` ` ` `| | |
| − | + | |` `@` `o' ' ' ' @ ' ' 'o^^@^^o' ' ' @ ' ' ' 'o` ` ` `| | |
| − | + | |` ` \ ` \ ' ' ' | ' ' ' \^|^/ ' ' ' | ' ' ' / ` ` ` `| | |
| − | | | + | |` ` `\` `\' ' ' | ' ' ' '\|/' ' ' ' | ' ' '/` ` ` ` `| |
| − | |- | + | |` ` ` \ ` \ ' ' | ' ' ' ' | ' ' ' ' | ' ' / ` ` ` ` `| |
| − | | | + | |` ` ` `\` `\' ' | ' ' ' '/|\' ' ' ' | ' '/` ` ` ` ` `| |
| − | | | + | |` ` ` ` \ ` o---|-------o | o-------|---o ` ` ` ` ` `| |
| − | | | + | |` ` ` ` `\` ` ` | ` ` ` ` | ` ` ` ` | ` ` ` ` ` ` ` `| |
| − | | | + | |` ` ` ` ` \ ` ` | ` ` ` ` | ` ` ` ` | ` ` ` ` ` ` ` `| |
| − | | | + | o-----------\----|---------|---------|----------------o |
| − | | | + | " " \ | | | " " |
| − | | | + | " " \ | | | " " |
| − | + | " " \ | | | " " | |
| − | | | + | " " \| | | " " |
| − | | | + | o-------------------------o \ | | o-------------------------o |
| − | + | | U | |\ | | |`U```````````````````````| | |
| − | + | | o---o o---o | | \ | | |``````o---o```o---o``````| | |
| − | + | | /'''''\ /'''''\ | | \ | | |`````/ \`/ \`````| | |
| − | </ | + | | /'''''''o'''''''\ | | \ | | |````/ o \````| |
| − | + | | /'''''''/'\'''''''\ | | \ | | |```/ /`\ \```| | |
| − | ===Table | + | | o'''''''o'''o'''''''o | | \ | | |``o o```o o``| |
| + | | |'''u'''|'''|'''v'''| | | \ | | |``| u |```| v |``| | ||
| + | | o'''''''o'''o'''''''o | | \ | | |``o o```o o``| | ||
| + | | \'''''''\'/'''''''/ | | \| | |```\ \`/ /```| | ||
| + | | \'''''''o'''''''/ | | \ | |````\ o /````| | ||
| + | | \'''''/ \'''''/ | | |\ | |`````\ /`\ /`````| | ||
| + | | o---o o---o | | | \ | |``````o---o```o---o``````| | ||
| + | | | | | \ * |`````````````````````````| | ||
| + | o-------------------------o | | \ / o-------------------------o | ||
| + | \ | | | \ / | / | ||
| + | \ ((u)(v)) | | | \/ | ((u, v)) / | ||
| + | \ | | | /\ | / | ||
| + | \ | | | / \ | / | ||
| + | \ | | | / \ | / | ||
| + | \ | | | / * | / | ||
| + | \ | | | / | | / | ||
| + | \ | | |/ | | / | ||
| + | \ | | / | | / | ||
| + | \ | | /| | | / | ||
| + | o-------\----|---|-------/-|---------|---|----/-------o | ||
| + | | X \ | | / | | | / | | ||
| + | | \| | / | | |/ | | ||
| + | | o---|----/--o | o-------|---o | | ||
| + | | /' ' | ' / ' '\|/` ` ` ` | ` `\ | | ||
| + | | / ' ' | '/' ' ' | ` ` ` ` | ` ` \ | | ||
| + | | /' ' ' | / ' ' '/|\` ` ` ` | ` ` `\ | | ||
| + | | / ' ' ' |/' ' ' /^|^\ ` ` ` | ` ` ` \ | | ||
| + | | @ o' ' ' ' @ ' ' 'o^^@^^o` ` ` @ ` ` ` `o | | ||
| + | | |' ' ' ' ' ' ' '|^^^^^|` ` ` ` ` ` ` `| | | ||
| + | | |' ' ' ' f ' ' '|^^^^^|` ` ` g ` ` ` `| | | ||
| + | | |' ' ' ' ' ' ' '|^^^^^|` ` ` ` ` ` ` `| | | ||
| + | | o' ' ' ' ' ' ' 'o^^^^^o` ` ` ` ` ` ` `o | | ||
| + | | \ ' ' ' ' ' ' ' \^^^/ ` ` ` ` ` ` ` / | | ||
| + | | \' ' ' ' ' ' ' '\^/` ` ` ` ` ` ` `/ | | ||
| + | | \ ' ' ' ' ' ' ' o ` ` ` ` ` ` ` / | | ||
| + | | \' ' ' ' ' ' '/ \` ` ` ` ` ` `/ | | ||
| + | | o-----------o o-----------o | | ||
| + | | | | ||
| + | | | | ||
| + | o-----------------------------------------------------o | ||
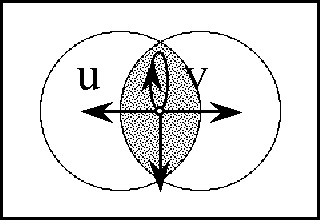
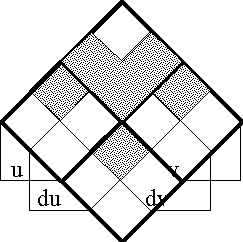
| + | Figure 63. Transformation of Positions | ||
| + | </pre> | ||
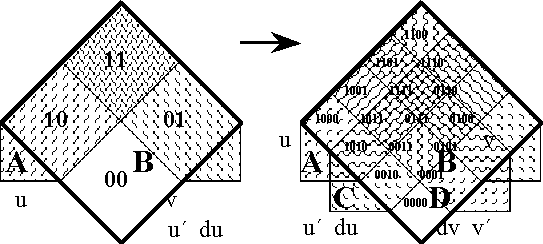
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 63 -- Transformation of Positions.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 63. Transformation of Positions'''</font></center></p> | ||
| + | |||
| + | ===Table 64. Transformation of Positions=== | ||
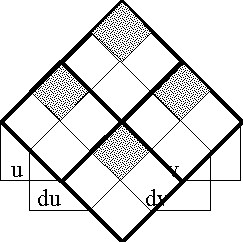
<pre> | <pre> | ||
| − | Table | + | Table 64. Transformation of Positions |
| − | o-------- | + | o-----o----------o----------o-------o-------o--------o--------o-------------o |
| − | | | + | | u v | x | y | x y | x(y) | (x)y | (x)(y) | X% = [x, y] | |
| − | o | + | o-----o----------o----------o-------o-------o--------o--------o-------------o |
| − | + | | | | | | | | | ^ | | |
| − | + | | 0 0 | 0 | 1 | 0 | 0 | 1 | 0 | | | | |
| − | + | | | | | | | | | | | |
| − | + | | 0 1 | 1 | 0 | 0 | 1 | 0 | 0 | F | | |
| − | + | | | | | | | | | = | | |
| − | + | | 1 0 | 1 | 0 | 0 | 1 | 0 | 0 | <f , g> | | |
| − | + | | | | | | | | | | | |
| − | + | | 1 1 | 1 | 1 | 1 | 0 | 0 | 0 | ^ | | |
| − | + | | | | | | | | | | | | |
| − | + | o-----o----------o----------o-------o-------o--------o--------o-------------o | |
| − | | | + | | | ((u)(v)) | ((u, v)) | u v | (u,v) | (u)(v) | 0 | U% = [u, v] | |
| − | + | o-----o----------o----------o-------o-------o--------o--------o-------------o | |
| − | | | ||
| − | | | ||
| − | |||
| − | | | ||
| − | | | ||
| − | |||
| − | | | ||
| − | |||
| − | | | ||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | | | ||
| − | | | ||
| − | |||
| − | o-------- | ||
| − | | | ||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | o-------- | ||
</pre> | </pre> | ||
| − | ===Table | + | {| align="center" border="1" cellpadding="8" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:96%" |
| − | + | |+ '''Table 64. Transformation of Positions''' | |
| − | + | |- style="background:paleturquoise" | |
| − | + | | ''u'' ''v'' | |
| − | + | | ''x'' | |
| − | | | + | | ''y'' |
| − | + | | ''x'' ''y'' | |
| − | | | + | | ''x'' (''y'') |
| − | | 0 0 | 0 | + | | (''x'') ''y'' |
| − | | | + | | (''x'')(''y'') |
| − | | 0 | + | | ''X''<sup> •</sup> = [''x'', ''y'' ] |
| − | | | + | |- |
| − | | | + | | width="12%" | |
| − | | | + | {| align="center" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" |
| − | | | + | | 0 0 |
| − | | | + | |- |
| − | + | | 0 1 | |
| − | + | |- | |
| − | + | | 1 0 | |
| − | + | |- | |
| − | + | | 1 1 | |
| − | + | |} | |
| − | + | | width="12%" | | |
| − | | | + | {| align="center" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" |
| − | + | | 0 | |
| − | | | + | |- |
| − | | | + | | 1 |
| − | + | |- | |
| − | + | | 1 | |
| − | + | |- | |
| − | + | | 1 | |
| − | + | |} | |
| − | + | | width="12%" | | |
| − | | | + | {| align="center" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" |
| − | + | | 1 | |
| − | | | + | |- |
| − | | | + | | 0 |
| − | | | + | |- |
| − | | | + | | 0 |
| − | | | + | |- |
| − | | | + | | 1 |
| − | | | + | |} |
| − | | | + | | width="12%" | |
| − | | | + | {| align="center" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" |
| − | | | + | | 0 |
| − | | | + | |- |
| − | | | + | | 0 |
| − | | | + | |- |
| − | + | | 0 | |
| − | + | |- | |
| − | + | | 1 | |
| − | + | |} | |
| − | + | | width="12%" | | |
| − | + | {| align="center" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | |
| − | + | | 0 | |
| − | + | |- | |
| − | + | | 1 | |
| − | + | |- | |
| − | <pre> | + | | 1 |
| − | o-----------------------------------o o-----------------------------------o | + | |- |
| − | | U | |`U`````````````````````````````````| | + | | 0 |
| − | | | |```````````````````````````````````| | + | |} |
| − | | ^ | |```````````````````````````````````| | + | | width="12%" | |
| − | | | | |```````````````````````````````````| | + | {| align="center" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" |
| − | | o-------o | o-------o | |```````o-------o```o-------o```````| | + | | 1 |
| − | | ^ /`````````\|/`````````\ ^ | | ^ ```/ ^ \`/ ^ \``` ^ | | + | |- |
| − | | \ /```````````|```````````\ / | |``\``/ \ o / \``/``| | + | | 0 |
| − | | \/`````u`````/|\`````v`````\/ | |```\/ u \/`\/ v \/```| | + | |- |
| − | | /\``````````/`|`\``````````/\ | |```/\ /\`/\ /\```| | + | | 0 |
| − | | o``\````````o``@``o````````/``o | |``o \ o``@``o / o``| | + | |- |
| − | | |```\```````|`````|```````/```| | |``| \ |`````| / |``| | + | | 0 |
| − | | |````@``````|`````|``````@````| | |``| @-------->`<--------@ |``| | + | |} |
| + | | width="12%" | | ||
| + | {| align="center" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 | ||
| + | |- | ||
| + | | 0 | ||
| + | |- | ||
| + | | 0 | ||
| + | |- | ||
| + | | 0 | ||
| + | |} | ||
| + | | width="12%" | | ||
| + | {| align="center" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | ↑ | ||
| + | |- | ||
| + | | ''F'' | ||
| + | |- | ||
| + | | ‹''f'', ''g'' › | ||
| + | |- | ||
| + | | ↑ | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | | ((''u'')(''v'')) | ||
| + | | ((''u'', ''v'')) | ||
| + | | ''u'' ''v'' | ||
| + | | (''u'', ''v'') | ||
| + | | (''u'')(''v'') | ||
| + | | ( ) | ||
| + | | ''U''<sup> •</sup> = [''u'', ''v'' ] | ||
| + | |} | ||
| + | <br> | ||
| + | |||
| + | ===Table 65. Induced Transformation on Propositions=== | ||
| + | |||
| + | <pre> | ||
| + | Table 65. Induced Transformation on Propositions | ||
| + | o------------o---------------------------------o------------o | ||
| + | | X% | <--- F = <f , g> <--- | U% | | ||
| + | o------------o----------o-----------o----------o------------o | ||
| + | | | u = | 1 1 0 0 | = u | | | ||
| + | | | v = | 1 0 1 0 | = v | | | ||
| + | | f_i <x, y> o----------o-----------o----------o f_j <u, v> | | ||
| + | | | x = | 1 1 1 0 | = f<u,v> | | | ||
| + | | | y = | 1 0 0 1 | = g<u,v> | | | ||
| + | o------------o----------o-----------o----------o------------o | ||
| + | | | | | | | | ||
| + | | f_0 | () | 0 0 0 0 | () | f_0 | | ||
| + | | | | | | | | ||
| + | | f_1 | (x)(y) | 0 0 0 1 | () | f_0 | | ||
| + | | | | | | | | ||
| + | | f_2 | (x) y | 0 0 1 0 | (u)(v) | f_1 | | ||
| + | | | | | | | | ||
| + | | f_3 | (x) | 0 0 1 1 | (u)(v) | f_1 | | ||
| + | | | | | | | | ||
| + | | f_4 | x (y) | 0 1 0 0 | (u, v) | f_6 | | ||
| + | | | | | | | | ||
| + | | f_5 | (y) | 0 1 0 1 | (u, v) | f_6 | | ||
| + | | | | | | | | ||
| + | | f_6 | (x, y) | 0 1 1 0 | (u v) | f_7 | | ||
| + | | | | | | | | ||
| + | | f_7 | (x y) | 0 1 1 1 | (u v) | f_7 | | ||
| + | | | | | | | | ||
| + | o------------o----------o-----------o----------o------------o | ||
| + | | | | | | | | ||
| + | | f_8 | x y | 1 0 0 0 | u v | f_8 | | ||
| + | | | | | | | | ||
| + | | f_9 | ((x, y)) | 1 0 0 1 | u v | f_8 | | ||
| + | | | | | | | | ||
| + | | f_10 | y | 1 0 1 0 | ((u, v)) | f_9 | | ||
| + | | | | | | | | ||
| + | | f_11 | (x (y)) | 1 0 1 1 | ((u, v)) | f_9 | | ||
| + | | | | | | | | ||
| + | | f_12 | x | 1 1 0 0 | ((u)(v)) | f_14 | | ||
| + | | | | | | | | ||
| + | | f_13 | ((x) y) | 1 1 0 1 | ((u)(v)) | f_14 | | ||
| + | | | | | | | | ||
| + | | f_14 | ((x)(y)) | 1 1 1 0 | (()) | f_15 | | ||
| + | | | | | | | | ||
| + | | f_15 | (()) | 1 1 1 1 | (()) | f_15 | | ||
| + | | | | | | | | ||
| + | o------------o----------o-----------o----------o------------o | ||
| + | </pre> | ||
| + | |||
| + | <br><font face="courier new"> | ||
| + | {| align="center" border="1" cellpadding="4" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:96%" | ||
| + | |+ Table 65. Induced Transformation on Propositions | ||
| + | |- style="background:paleturquoise" | ||
| + | | ''X''<sup> •</sup> | ||
| + | | colspan="3" | | ||
| + | {| align="center" border="0" cellpadding="4" cellspacing="0" style="background:paleturquoise; font-weight:bold; text-align:center; width:80%" | ||
| + | | ← | ||
| + | | ''F'' = ‹''f'' , ''g''› | ||
| + | | ← | ||
| + | |} | ||
| + | | ''U''<sup> •</sup> | ||
| + | |- style="background:paleturquoise" | ||
| + | | rowspan="2" | ''f''<sub>''i''</sub>‹''x'', ''y''› | ||
| + | | | ||
| + | {| align="right" style="background:paleturquoise; text-align:right" | ||
| + | | ''u'' = | ||
| + | |- | ||
| + | | ''v'' = | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" style="background:paleturquoise; text-align:center" | ||
| + | | 1 1 0 0 | ||
| + | |- | ||
| + | | 1 0 1 0 | ||
| + | |} | ||
| + | | | ||
| + | {| align="left" style="background:paleturquoise; text-align:left" | ||
| + | | = ''u'' | ||
| + | |- | ||
| + | | = ''v'' | ||
| + | |} | ||
| + | | rowspan="2" | ''f''<sub>''j''</sub>‹''u'', ''v''› | ||
| + | |- style="background:paleturquoise" | ||
| + | | | ||
| + | {| align="right" style="background:paleturquoise; text-align:right" | ||
| + | | ''x'' = | ||
| + | |- | ||
| + | | ''y'' = | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" style="background:paleturquoise; text-align:center" | ||
| + | | 1 1 1 0 | ||
| + | |- | ||
| + | | 1 0 0 1 | ||
| + | |} | ||
| + | | | ||
| + | {| align="left" style="background:paleturquoise; text-align:left" | ||
| + | | = ''f''‹''u'', ''v''› | ||
| + | |- | ||
| + | | = ''g''‹''u'', ''v''› | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {| cellpadding="2" style="background:lightcyan" | ||
| + | | ''f''<sub>0</sub> | ||
| + | |- | ||
| + | | ''f''<sub>1</sub> | ||
| + | |- | ||
| + | | ''f''<sub>2</sub> | ||
| + | |- | ||
| + | | ''f''<sub>3</sub> | ||
| + | |- | ||
| + | | ''f''<sub>4</sub> | ||
| + | |- | ||
| + | | ''f''<sub>5</sub> | ||
| + | |- | ||
| + | | ''f''<sub>6</sub> | ||
| + | |- | ||
| + | | ''f''<sub>7</sub> | ||
| + | |} | ||
| + | | | ||
| + | {| cellpadding="2" style="background:lightcyan" | ||
| + | | () | ||
| + | |- | ||
| + | | (''x'')(''y'') | ||
| + | |- | ||
| + | | (''x'') ''y'' | ||
| + | |- | ||
| + | | (''x'') | ||
| + | |- | ||
| + | | ''x'' (''y'') | ||
| + | |- | ||
| + | | (''y'') | ||
| + | |- | ||
| + | | (''x'', ''y'') | ||
| + | |- | ||
| + | | (''x'' ''y'') | ||
| + | |} | ||
| + | | | ||
| + | {| cellpadding="2" style="background:lightcyan" | ||
| + | | 0 0 0 0 | ||
| + | |- | ||
| + | | 0 0 0 1 | ||
| + | |- | ||
| + | | 0 0 1 0 | ||
| + | |- | ||
| + | | 0 0 1 1 | ||
| + | |- | ||
| + | | 0 1 0 0 | ||
| + | |- | ||
| + | | 0 1 0 1 | ||
| + | |- | ||
| + | | 0 1 1 0 | ||
| + | |- | ||
| + | | 0 1 1 1 | ||
| + | |} | ||
| + | | | ||
| + | {| cellpadding="2" style="background:lightcyan" | ||
| + | | () | ||
| + | |- | ||
| + | | () | ||
| + | |- | ||
| + | | (''u'')(''v'') | ||
| + | |- | ||
| + | | (''u'')(''v'') | ||
| + | |- | ||
| + | | (''u'', ''v'') | ||
| + | |- | ||
| + | | (''u'', ''v'') | ||
| + | |- | ||
| + | | (''u'' ''v'') | ||
| + | |- | ||
| + | | (''u'' ''v'') | ||
| + | |} | ||
| + | | | ||
| + | {| cellpadding="2" style="background:lightcyan" | ||
| + | | ''f''<sub>0</sub> | ||
| + | |- | ||
| + | | ''f''<sub>0</sub> | ||
| + | |- | ||
| + | | ''f''<sub>1</sub> | ||
| + | |- | ||
| + | | ''f''<sub>1</sub> | ||
| + | |- | ||
| + | | ''f''<sub>6</sub> | ||
| + | |- | ||
| + | | ''f''<sub>6</sub> | ||
| + | |- | ||
| + | | ''f''<sub>7</sub> | ||
| + | |- | ||
| + | | ''f''<sub>7</sub> | ||
| + | |} | ||
| + | |- | ||
| + | | | ||
| + | {| cellpadding="2" style="background:lightcyan" | ||
| + | | ''f''<sub>8</sub> | ||
| + | |- | ||
| + | | ''f''<sub>9</sub> | ||
| + | |- | ||
| + | | ''f''<sub>10</sub> | ||
| + | |- | ||
| + | | ''f''<sub>11</sub> | ||
| + | |- | ||
| + | | ''f''<sub>12</sub> | ||
| + | |- | ||
| + | | ''f''<sub>13</sub> | ||
| + | |- | ||
| + | | ''f''<sub>14</sub> | ||
| + | |- | ||
| + | | ''f''<sub>15</sub> | ||
| + | |} | ||
| + | | | ||
| + | {| cellpadding="2" style="background:lightcyan" | ||
| + | | ''x'' ''y'' | ||
| + | |- | ||
| + | | ((''x'', ''y'')) | ||
| + | |- | ||
| + | | ''y'' | ||
| + | |- | ||
| + | | (''x'' (''y'')) | ||
| + | |- | ||
| + | | ''x'' | ||
| + | |- | ||
| + | | ((''x'') ''y'') | ||
| + | |- | ||
| + | | ((''x'')(''y'')) | ||
| + | |- | ||
| + | | (()) | ||
| + | |} | ||
| + | | | ||
| + | {| cellpadding="2" style="background:lightcyan" | ||
| + | | 1 0 0 0 | ||
| + | |- | ||
| + | | 1 0 0 1 | ||
| + | |- | ||
| + | | 1 0 1 0 | ||
| + | |- | ||
| + | | 1 0 1 1 | ||
| + | |- | ||
| + | | 1 1 0 0 | ||
| + | |- | ||
| + | | 1 1 0 1 | ||
| + | |- | ||
| + | | 1 1 1 0 | ||
| + | |- | ||
| + | | 1 1 1 1 | ||
| + | |} | ||
| + | | | ||
| + | {| cellpadding="2" style="background:lightcyan" | ||
| + | | ''u'' ''v'' | ||
| + | |- | ||
| + | | ''u'' ''v'' | ||
| + | |- | ||
| + | | ((''u'', ''v'')) | ||
| + | |- | ||
| + | | ((''u'', ''v'')) | ||
| + | |- | ||
| + | | ((''u'')(''v'')) | ||
| + | |- | ||
| + | | ((''u'')(''v'')) | ||
| + | |- | ||
| + | | (()) | ||
| + | |- | ||
| + | | (()) | ||
| + | |} | ||
| + | | | ||
| + | {| cellpadding="2" style="background:lightcyan" | ||
| + | | ''f''<sub>8</sub> | ||
| + | |- | ||
| + | | ''f''<sub>8</sub> | ||
| + | |- | ||
| + | | ''f''<sub>9</sub> | ||
| + | |- | ||
| + | | ''f''<sub>9</sub> | ||
| + | |- | ||
| + | | ''f''<sub>14</sub> | ||
| + | |- | ||
| + | | ''f''<sub>14</sub> | ||
| + | |- | ||
| + | | ''f''<sub>15</sub> | ||
| + | |- | ||
| + | | ''f''<sub>15</sub> | ||
| + | |} | ||
| + | |} | ||
| + | </font><br> | ||
| + | |||
| + | ===Formula Display 14=== | ||
| + | |||
| + | <pre> | ||
| + | o-------------------------------------------------o | ||
| + | | | | ||
| + | | EG_i = G_i <u + du, v + dv> | | ||
| + | | | | ||
| + | o-------------------------------------------------o | ||
| + | </pre> | ||
| + | |||
| + | <br><font face="courier new"> | ||
| + | {| align="center" border="1" cellpadding="12" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:left; width:96%" | ||
| + | | | ||
| + | {| align="left" border="0" cellpadding="12" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:left; width:100%" | ||
| + | | width="8%" | E''G''<sub>''i''</sub> | ||
| + | | width="4%" | = | ||
| + | | width="88%" | ''G''<sub>''i''</sub>‹''u'' + d''u'', ''v'' + d''v''› | ||
| + | |} | ||
| + | |} | ||
| + | </font><br> | ||
| + | |||
| + | ===Formula Display 15=== | ||
| + | |||
| + | <pre> | ||
| + | o-------------------------------------------------o | ||
| + | | | | ||
| + | | DG_i = G_i <u, v> + EG_i <u, v, du, dv> | | ||
| + | | | | ||
| + | | = G_i <u, v> + G_i <u + du, v + dv> | | ||
| + | | | | ||
| + | o-------------------------------------------------o | ||
| + | </pre> | ||
| + | |||
| + | <br><font face="courier new"> | ||
| + | {| align="center" border="1" cellpadding="12" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:left; width:96%" | ||
| + | | | ||
| + | {| align="left" border="0" cellpadding="12" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:left; width:100%" | ||
| + | | width="8%" | D''G''<sub>''i''</sub> | ||
| + | | width="4%" | = | ||
| + | | width="20%" | ''G''<sub>''i''</sub>‹''u'', ''v''› | ||
| + | | width="4%" | + | ||
| + | | width="64%" | E''G''<sub>''i''</sub>‹''u'', ''v'', d''u'', d''v''› | ||
| + | |- | ||
| + | | width="8%" | | ||
| + | | width="4%" | = | ||
| + | | width="20%" | ''G''<sub>''i''</sub>‹''u'', ''v''› | ||
| + | | width="4%" | + | ||
| + | | width="64%" | ''G''<sub>''i''</sub>‹''u'' + d''u'', ''v'' + d''v''› | ||
| + | |} | ||
| + | |} | ||
| + | </font><br> | ||
| + | |||
| + | ===Formula Display 16=== | ||
| + | |||
| + | <pre> | ||
| + | o-------------------------------------------------o | ||
| + | | | | ||
| + | | Ef = ((u + du)(v + dv)) | | ||
| + | | | | ||
| + | | Eg = ((u + du, v + dv)) | | ||
| + | | | | ||
| + | o-------------------------------------------------o | ||
| + | </pre> | ||
| + | |||
| + | <br><font face="courier new"> | ||
| + | {| align="center" border="1" cellpadding="12" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:left; width:96%" | ||
| + | | | ||
| + | {| align="left" border="0" cellpadding="12" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:left; width:100%" | ||
| + | | width="8%" | E''f'' | ||
| + | | width="4%" | = | ||
| + | | width="88%" | ((''u'' + d''u'')(''v'' + d''v'')) | ||
| + | |- | ||
| + | | width="8%" | E''g'' | ||
| + | | width="4%" | = | ||
| + | | width="88%" | ((''u'' + d''u'', ''v'' + d''v'')) | ||
| + | |} | ||
| + | |} | ||
| + | </font><br> | ||
| + | |||
| + | ===Formula Display 17=== | ||
| + | |||
| + | <pre> | ||
| + | o-------------------------------------------------o | ||
| + | | | | ||
| + | | Df = ((u)(v)) + ((u + du)(v + dv)) | | ||
| + | | | | ||
| + | | Dg = ((u, v)) + ((u + du, v + dv)) | | ||
| + | | | | ||
| + | o-------------------------------------------------o | ||
| + | </pre> | ||
| + | |||
| + | <br><font face="courier new"> | ||
| + | {| align="center" border="1" cellpadding="12" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:left; width:96%" | ||
| + | | | ||
| + | {| align="left" border="0" cellpadding="12" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:left; width:100%" | ||
| + | | width="8%" | D''f'' | ||
| + | | width="4%" | = | ||
| + | | width="20%" | ((''u'')(''v'')) | ||
| + | | width="4%" | + | ||
| + | | width="64%" | ((''u'' + d''u'')(''v'' + d''v'')) | ||
| + | |- | ||
| + | | width="8%" | D''g'' | ||
| + | | width="4%" | = | ||
| + | | width="20%" | ((''u'', ''v'')) | ||
| + | | width="4%" | + | ||
| + | | width="64%" | ((''u'' + d''u'', ''v'' + d''v'')) | ||
| + | |} | ||
| + | |} | ||
| + | </font><br> | ||
| + | |||
| + | ===Table 66-i. Computation Summary for f‹u, v› = ((u)(v))=== | ||
| + | |||
| + | <pre> | ||
| + | Table 66-i. Computation Summary for f<u, v> = ((u)(v)) | ||
| + | o--------------------------------------------------------------------------------o | ||
| + | | | | ||
| + | | !e!f = uv. 1 + u(v). 1 + (u)v. 1 + (u)(v). 0 | | ||
| + | | | | ||
| + | | Ef = uv. (du dv) + u(v). (du (dv)) + (u)v.((du) dv) + (u)(v).((du)(dv)) | | ||
| + | | | | ||
| + | | Df = uv. du dv + u(v). du (dv) + (u)v. (du) dv + (u)(v).((du)(dv)) | | ||
| + | | | | ||
| + | | df = uv. 0 + u(v). du + (u)v. dv + (u)(v). (du, dv) | | ||
| + | | | | ||
| + | | rf = uv. du dv + u(v). du dv + (u)v. du dv + (u)(v). du dv | | ||
| + | | | | ||
| + | o--------------------------------------------------------------------------------o | ||
| + | </pre> | ||
| + | |||
| + | <font face="courier new"> | ||
| + | {| align="center" border="1" cellpadding="8" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:96%" | ||
| + | |+ Table 66-i. Computation Summary for ''f''‹''u'', ''v''› = ((''u'')(''v'')) | ||
| + | | | ||
| + | {| align="left" border="0" cellpadding="1" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | <math>\epsilon</math>''f'' | ||
| + | | = || ''uv'' || <math>\cdot</math> || 1 | ||
| + | | + || ''u''(''v'') || <math>\cdot</math> || 1 | ||
| + | | + || (''u'')''v'' || <math>\cdot</math> || 1 | ||
| + | | + || (''u'')(''v'') || <math>\cdot</math> || 0 | ||
| + | |- | ||
| + | | E''f'' | ||
| + | | = || ''uv'' || <math>\cdot</math> || (d''u'' d''v'') | ||
| + | | + || ''u''(''v'') || <math>\cdot</math> || (d''u (d''v'')) | ||
| + | | + || (''u'')''v'' || <math>\cdot</math> || ((d''u'') d''v'') | ||
| + | | + || (''u'')(''v'') || <math>\cdot</math> || ((d''u'')(d''v'')) | ||
| + | |- | ||
| + | | D''f'' | ||
| + | | = || ''uv'' || <math>\cdot</math> || d''u'' d''v'' | ||
| + | | + || ''u''(''v'') || <math>\cdot</math> || d''u'' (d''v'') | ||
| + | | + || (''u'')''v'' || <math>\cdot</math> || (d''u'') d''v'' | ||
| + | | + || (''u'')(''v'') || <math>\cdot</math> || ((d''u'')(d''v'')) | ||
| + | |- | ||
| + | | d''f'' | ||
| + | | = || ''uv'' || <math>\cdot</math> || 0 | ||
| + | | + || ''u''(''v'') || <math>\cdot</math> || d''u'' | ||
| + | | + || (''u'')''v'' || <math>\cdot</math> || d''v'' | ||
| + | | + || (''u'')(''v'') || <math>\cdot</math> || (d''u'', d''v'') | ||
| + | |- | ||
| + | | r''f'' | ||
| + | | = || ''uv'' || <math>\cdot</math> || d''u'' d''v'' | ||
| + | | + || ''u''(''v'') || <math>\cdot</math> || d''u'' d''v'' | ||
| + | | + || (''u'')''v'' || <math>\cdot</math> || d''u'' d''v'' | ||
| + | | + || (''u'')(''v'') || <math>\cdot</math> || d''u'' d''v'' | ||
| + | |} | ||
| + | |} | ||
| + | </font><br> | ||
| + | |||
| + | ===Table 66-ii. Computation Summary for g‹u, v› = ((u, v))=== | ||
| + | |||
| + | <pre> | ||
| + | Table 66-ii. Computation Summary for g<u, v> = ((u, v)) | ||
| + | o--------------------------------------------------------------------------------o | ||
| + | | | | ||
| + | | !e!g = uv. 1 + u(v). 0 + (u)v. 0 + (u)(v). 1 | | ||
| + | | | | ||
| + | | Eg = uv.((du, dv)) + u(v). (du, dv) + (u)v. (du, dv) + (u)(v).((du, dv)) | | ||
| + | | | | ||
| + | | Dg = uv. (du, dv) + u(v). (du, dv) + (u)v. (du, dv) + (u)(v). (du, dv) | | ||
| + | | | | ||
| + | | dg = uv. (du, dv) + u(v). (du, dv) + (u)v. (du, dv) + (u)(v). (du, dv) | | ||
| + | | | | ||
| + | | rg = uv. 0 + u(v). 0 + (u)v. 0 + (u)(v). 0 | | ||
| + | | | | ||
| + | o--------------------------------------------------------------------------------o | ||
| + | </pre> | ||
| + | |||
| + | <font face="courier new"> | ||
| + | {| align="center" border="1" cellpadding="8" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:96%" | ||
| + | |+ Table 66-ii. Computation Summary for g‹''u'', ''v''› = ((''u'', ''v'')) | ||
| + | | | ||
| + | {| align="left" border="0" cellpadding="1" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | <math>\epsilon</math>''g'' | ||
| + | | = || ''uv'' || <math>\cdot</math> || 1 | ||
| + | | + || ''u''(''v'') || <math>\cdot</math> || 0 | ||
| + | | + || (''u'')''v'' || <math>\cdot</math> || 0 | ||
| + | | + || (''u'')(''v'') || <math>\cdot</math> || 1 | ||
| + | |- | ||
| + | | E''g'' | ||
| + | | = || ''uv'' || <math>\cdot</math> || ((d''u'', d''v'')) | ||
| + | | + || ''u''(''v'') || <math>\cdot</math> || (d''u'', d''v'') | ||
| + | | + || (''u'')''v'' || <math>\cdot</math> || (d''u'', d''v'') | ||
| + | | + || (''u'')(''v'') || <math>\cdot</math> || ((d''u'', d''v'')) | ||
| + | |- | ||
| + | | D''g'' | ||
| + | | = || ''uv'' || <math>\cdot</math> || (d''u'', d''v'') | ||
| + | | + || ''u''(''v'') || <math>\cdot</math> || (d''u'', d''v'') | ||
| + | | + || (''u'')''v'' || <math>\cdot</math> || (d''u'', d''v'') | ||
| + | | + || (''u'')(''v'') || <math>\cdot</math> || (d''u'', d''v'') | ||
| + | |- | ||
| + | | d''g'' | ||
| + | | = || ''uv'' || <math>\cdot</math> || (d''u'', d''v'') | ||
| + | | + || ''u''(''v'') || <math>\cdot</math> || (d''u'', d''v'') | ||
| + | | + || (''u'')''v'' || <math>\cdot</math> || (d''u'', d''v'') | ||
| + | | + || (''u'')(''v'') || <math>\cdot</math> || (d''u'', d''v'') | ||
| + | |- | ||
| + | | r''g'' | ||
| + | | = || ''uv'' || <math>\cdot</math> || 0 | ||
| + | | + || ''u''(''v'') || <math>\cdot</math> || 0 | ||
| + | | + || (''u'')''v'' || <math>\cdot</math> || 0 | ||
| + | | + || (''u'')(''v'') || <math>\cdot</math> || 0 | ||
| + | |} | ||
| + | |} | ||
| + | </font><br> | ||
| + | |||
| + | ===Table 67. Computation of an Analytic Series in Terms of Coordinates=== | ||
| + | |||
| + | <pre> | ||
| + | Table 67. Computation of an Analytic Series in Terms of Coordinates | ||
| + | o--------o-------o-------o--------o-------o-------o-------o-------o | ||
| + | | u v | du dv | u' v' | f g | Ef Eg | Df Dg | df dg | rf rg | | ||
| + | o--------o-------o-------o--------o-------o-------o-------o-------o | ||
| + | | | | | | | | | | | ||
| + | | 0 0 | 0 0 | 0 0 | 0 1 | 0 1 | 0 0 | 0 0 | 0 0 | | ||
| + | | | | | | | | | | | ||
| + | | | 0 1 | 0 1 | | 1 0 | 1 1 | 1 1 | 0 0 | | ||
| + | | | | | | | | | | | ||
| + | | | 1 0 | 1 0 | | 1 0 | 1 1 | 1 1 | 0 0 | | ||
| + | | | | | | | | | | | ||
| + | | | 1 1 | 1 1 | | 1 1 | 1 0 | 0 0 | 1 0 | | ||
| + | | | | | | | | | | | ||
| + | o--------o-------o-------o--------o-------o-------o-------o-------o | ||
| + | | | | | | | | | | | ||
| + | | 0 1 | 0 0 | 0 1 | 1 0 | 1 0 | 0 0 | 0 0 | 0 0 | | ||
| + | | | | | | | | | | | ||
| + | | | 0 1 | 0 0 | | 0 1 | 1 1 | 1 1 | 0 0 | | ||
| + | | | | | | | | | | | ||
| + | | | 1 0 | 1 1 | | 1 1 | 0 1 | 0 1 | 0 0 | | ||
| + | | | | | | | | | | | ||
| + | | | 1 1 | 1 0 | | 1 0 | 0 0 | 1 0 | 1 0 | | ||
| + | | | | | | | | | | | ||
| + | o--------o-------o-------o--------o-------o-------o-------o-------o | ||
| + | | | | | | | | | | | ||
| + | | 1 0 | 0 0 | 1 0 | 1 0 | 1 0 | 0 0 | 0 0 | 0 0 | | ||
| + | | | | | | | | | | | ||
| + | | | 0 1 | 1 1 | | 1 1 | 0 1 | 0 1 | 0 0 | | ||
| + | | | | | | | | | | | ||
| + | | | 1 0 | 0 0 | | 0 1 | 1 1 | 1 1 | 0 0 | | ||
| + | | | | | | | | | | | ||
| + | | | 1 1 | 0 1 | | 1 0 | 0 0 | 1 0 | 1 0 | | ||
| + | | | | | | | | | | | ||
| + | o--------o-------o-------o--------o-------o-------o-------o-------o | ||
| + | | | | | | | | | | | ||
| + | | 1 1 | 0 0 | 1 1 | 1 1 | 1 1 | 0 0 | 0 0 | 0 0 | | ||
| + | | | | | | | | | | | ||
| + | | | 0 1 | 1 0 | | 1 0 | 0 1 | 0 1 | 0 0 | | ||
| + | | | | | | | | | | | ||
| + | | | 1 0 | 0 1 | | 1 0 | 0 1 | 0 1 | 0 0 | | ||
| + | | | | | | | | | | | ||
| + | | | 1 1 | 0 0 | | 0 1 | 1 0 | 0 0 | 1 0 | | ||
| + | | | | | | | | | | | ||
| + | o--------o-------o-------o--------o-------o-------o-------o-------o | ||
| + | </pre> | ||
| + | |||
| + | {| align="center" border="1" cellpadding="0" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:96%" | ||
| + | |+ Table 67. Computation of an Analytic Series in Terms of Coordinates | ||
| + | | | ||
| + | {| align="center" border="1" cellpadding="0" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:paleturquoise; font-weight:bold; text-align:center; width:100%" | ||
| + | | ''u'' | ||
| + | | ''v'' | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:paleturquoise; font-weight:bold; text-align:center; width:100%" | ||
| + | | d''u'' | ||
| + | | d''v'' | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:paleturquoise; font-weight:bold; text-align:center; width:100%" | ||
| + | | ''u''<font face="courier new">’</font> | ||
| + | | ''v''<font face="courier new">’</font> | ||
| + | |} | ||
| + | |- | ||
| + | | valign="top" | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 || 0 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 0 || 1 | ||
| + | |- | ||
| + | | 1 || 0 | ||
| + | |- | ||
| + | | 1 || 1 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 0 || 1 | ||
| + | |- | ||
| + | | 1 || 0 | ||
| + | |- | ||
| + | | 1 || 1 | ||
| + | |} | ||
| + | |- | ||
| + | | valign="top" | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 || 1 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 0 || 1 | ||
| + | |- | ||
| + | | 1 || 0 | ||
| + | |- | ||
| + | | 1 || 1 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 || 1 | ||
| + | |- | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 1 || 1 | ||
| + | |- | ||
| + | | 1 || 0 | ||
| + | |} | ||
| + | |- | ||
| + | | valign="top" | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 1 || 0 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 0 || 1 | ||
| + | |- | ||
| + | | 1 || 0 | ||
| + | |- | ||
| + | | 1 || 1 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 1 || 0 | ||
| + | |- | ||
| + | | 1 || 1 | ||
| + | |- | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 0 || 1 | ||
| + | |} | ||
| + | |- | ||
| + | | valign="top" | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 1 || 1 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 1 || 1 | ||
| + | |- | ||
| + | | 1 || 0 | ||
| + | |- | ||
| + | | 0 || 1 | ||
| + | |- | ||
| + | | 0 || 0 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 0 || 1 | ||
| + | |- | ||
| + | | 1 || 0 | ||
| + | |- | ||
| + | | 1 || 1 | ||
| + | |} | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="1" cellpadding="0" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:paleturquoise; font-weight:bold; text-align:center; width:100%" | ||
| + | | <math>\epsilon</math>''f'' | ||
| + | | <math>\epsilon</math>''g'' | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:paleturquoise; font-weight:bold; text-align:center; width:100%" | ||
| + | | E''f'' | ||
| + | | E''g'' | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:paleturquoise; font-weight:bold; text-align:center; width:100%" | ||
| + | | D''f'' | ||
| + | | D''g'' | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:paleturquoise; font-weight:bold; text-align:center; width:100%" | ||
| + | | d''f'' | ||
| + | | d''g'' | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:paleturquoise; font-weight:bold; text-align:center; width:100%" | ||
| + | | d<sup>2</sup>''f'' | ||
| + | | d<sup>2</sup>''g'' | ||
| + | |} | ||
| + | |- | ||
| + | | valign="top" | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 || 1 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 || 1 | ||
| + | |- | ||
| + | | 1 || 0 | ||
| + | |- | ||
| + | | 1 || 0 | ||
| + | |- | ||
| + | | 1 || 1 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 1 || 1 | ||
| + | |- | ||
| + | | 1 || 1 | ||
| + | |- | ||
| + | | 1 || 0 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 1 || 1 | ||
| + | |- | ||
| + | | 1 || 1 | ||
| + | |- | ||
| + | | 0 || 0 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 1 || 0 | ||
| + | |} | ||
| + | |- | ||
| + | | valign="top" | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 1 || 0 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 1 || 0 | ||
| + | |- | ||
| + | | 0 || 1 | ||
| + | |- | ||
| + | | 1 || 1 | ||
| + | |- | ||
| + | | 1 || 0 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 1 || 1 | ||
| + | |- | ||
| + | | 0 || 1 | ||
| + | |- | ||
| + | | 0 || 0 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 1 || 1 | ||
| + | |- | ||
| + | | 0 || 1 | ||
| + | |- | ||
| + | | 1 || 0 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 1 || 0 | ||
| + | |} | ||
| + | |- | ||
| + | | valign="top" | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 1 || 0 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 1 || 0 | ||
| + | |- | ||
| + | | 1 || 1 | ||
| + | |- | ||
| + | | 0 || 1 | ||
| + | |- | ||
| + | | 1 || 0 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 0 || 1 | ||
| + | |- | ||
| + | | 1 || 1 | ||
| + | |- | ||
| + | | 0 || 0 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 0 || 1 | ||
| + | |- | ||
| + | | 1 || 1 | ||
| + | |- | ||
| + | | 1 || 0 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 1 || 0 | ||
| + | |} | ||
| + | |- | ||
| + | | valign="top" | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 1 || 1 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 1 || 1 | ||
| + | |- | ||
| + | | 1 || 0 | ||
| + | |- | ||
| + | | 1 || 0 | ||
| + | |- | ||
| + | | 0 || 1 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 0 || 1 | ||
| + | |- | ||
| + | | 0 || 1 | ||
| + | |- | ||
| + | | 1 || 0 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 0 || 1 | ||
| + | |- | ||
| + | | 0 || 1 | ||
| + | |- | ||
| + | | 0 || 0 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="6" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 0 || 0 | ||
| + | |- | ||
| + | | 1 || 0 | ||
| + | |} | ||
| + | |} | ||
| + | |} | ||
| + | <br> | ||
| + | |||
| + | ===Table 68. Computation of an Analytic Series in Symbolic Terms=== | ||
| + | |||
| + | <pre> | ||
| + | Table 68. Computation of an Analytic Series in Symbolic Terms | ||
| + | o-----o-----o------------o----------o----------o----------o----------o----------o | ||
| + | | u v | f g | Df | Dg | df | dg | rf | rg | | ||
| + | o-----o-----o------------o----------o----------o----------o----------o----------o | ||
| + | | | | | | | | | | | ||
| + | | 0 0 | 0 1 | ((du)(dv)) | (du, dv) | (du, dv) | (du, dv) | du dv | () | | ||
| + | | | | | | | | | | | ||
| + | | 0 1 | 1 0 | (du) dv | (du, dv) | dv | (du, dv) | du dv | () | | ||
| + | | | | | | | | | | | ||
| + | | 1 0 | 1 0 | du (dv) | (du, dv) | du | (du, dv) | du dv | () | | ||
| + | | | | | | | | | | | ||
| + | | 1 1 | 1 1 | du dv | (du, dv) | () | (du, dv) | du dv | () | | ||
| + | | | | | | | | | | | ||
| + | o-----o-----o------------o----------o----------o----------o----------o----------o | ||
| + | </pre> | ||
| + | |||
| + | {| align="center" border="1" cellpadding="8" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:96%" | ||
| + | |+ '''Table 68. Computation of an Analytic Series in Symbolic Terms''' | ||
| + | |- style="background:paleturquoise" | ||
| + | | ''u'' ''v'' | ||
| + | | ''f'' ''g'' | ||
| + | | D''f'' | ||
| + | | D''g'' | ||
| + | | d''f'' | ||
| + | | d''g'' | ||
| + | | d<sup>2</sup>''f'' | ||
| + | | d<sup>2</sup>''g'' | ||
| + | |- | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 0 | ||
| + | |- | ||
| + | | 0 1 | ||
| + | |- | ||
| + | | 1 0 | ||
| + | |- | ||
| + | | 1 1 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | 0 1 | ||
| + | |- | ||
| + | | 1 0 | ||
| + | |- | ||
| + | | 1 0 | ||
| + | |- | ||
| + | | 1 1 | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | ((d''u'')(d''v'')) | ||
| + | |- | ||
| + | | (d''u'') d''v'' | ||
| + | |- | ||
| + | | d''u'' (d''v'') | ||
| + | |- | ||
| + | | d''u'' d''v'' | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | (d''u'', d''v'') | ||
| + | |- | ||
| + | | (d''u'', d''v'') | ||
| + | |- | ||
| + | | (d''u'', d''v'') | ||
| + | |- | ||
| + | | (d''u'', d''v'') | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | (d''u'', d''v'') | ||
| + | |- | ||
| + | | d''v'' | ||
| + | |- | ||
| + | | d''u'' | ||
| + | |- | ||
| + | | ( ) | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | (d''u'', d''v'') | ||
| + | |- | ||
| + | | (d''u'', d''v'') | ||
| + | |- | ||
| + | | (d''u'', d''v'') | ||
| + | |- | ||
| + | | (d''u'', d''v'') | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | d''u'' d''v'' | ||
| + | |- | ||
| + | | d''u'' d''v'' | ||
| + | |- | ||
| + | | d''u'' d''v'' | ||
| + | |- | ||
| + | | d''u'' d''v'' | ||
| + | |} | ||
| + | | | ||
| + | {| align="center" border="0" cellpadding="2" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | ( ) | ||
| + | |- | ||
| + | | ( ) | ||
| + | |- | ||
| + | | ( ) | ||
| + | |- | ||
| + | | ( ) | ||
| + | |} | ||
| + | |} | ||
| + | <br> | ||
| + | |||
| + | ===Formula Display 18=== | ||
| + | |||
| + | <pre> | ||
| + | o-------------------------------------------------------------------------o | ||
| + | | | | ||
| + | | Df = uv. du dv + u(v). du (dv) + (u)v.(du) dv + (u)(v).((du)(dv)) | | ||
| + | | | | ||
| + | | Dg = uv.(du, dv) + u(v).(du, dv) + (u)v.(du, dv) + (u)(v). (du, dv) | | ||
| + | | | | ||
| + | o-------------------------------------------------------------------------o | ||
| + | </pre> | ||
| + | |||
| + | <br><font face="courier new"> | ||
| + | {| align="center" border="1" cellpadding="8" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:96%" | ||
| + | | | ||
| + | {| align="left" border="0" cellpadding="1" cellspacing="0" style="background:lightcyan; font-weight:bold; text-align:center; width:100%" | ||
| + | | | ||
| + | |- | ||
| + | | D''f'' | ||
| + | | = || ''uv'' || <math>\cdot</math> || d''u'' d''v'' | ||
| + | | + || ''u''(''v'') || <math>\cdot</math> || d''u'' (d''v'') | ||
| + | | + || (''u'')''v'' || <math>\cdot</math> || (d''u'') d''v'' | ||
| + | | + || (''u'')(''v'') || <math>\cdot</math> || ((d''u'')(d''v'')) | ||
| + | |- | ||
| + | | | ||
| + | |- | ||
| + | | D''g'' | ||
| + | | = || ''uv'' || <math>\cdot</math> || (d''u'', d''v'') | ||
| + | | + || ''u''(''v'') || <math>\cdot</math> || (d''u'', d''v'') | ||
| + | | + || (''u'')''v'' || <math>\cdot</math> || (d''u'', d''v'') | ||
| + | | + || (''u'')(''v'') || <math>\cdot</math> || (d''u'', d''v'') | ||
| + | |- | ||
| + | | | ||
| + | |} | ||
| + | |} | ||
| + | </font><br> | ||
| + | |||
| + | ===Figure 69. Difference Map of F = ‹f, g› = ‹((u)(v)), ((u, v))›=== | ||
| + | |||
| + | <pre> | ||
| + | o-----------------------------------o o-----------------------------------o | ||
| + | | U | |`U`````````````````````````````````| | ||
| + | | | |```````````````````````````````````| | ||
| + | | ^ | |```````````````````````````````````| | ||
| + | | | | |```````````````````````````````````| | ||
| + | | o-------o | o-------o | |```````o-------o```o-------o```````| | ||
| + | | ^ /`````````\|/`````````\ ^ | | ^ ```/ ^ \`/ ^ \``` ^ | | ||
| + | | \ /```````````|```````````\ / | |``\``/ \ o / \``/``| | ||
| + | | \/`````u`````/|\`````v`````\/ | |```\/ u \/`\/ v \/```| | ||
| + | | /\``````````/`|`\``````````/\ | |```/\ /\`/\ /\```| | ||
| + | | o``\````````o``@``o````````/``o | |``o \ o``@``o / o``| | ||
| + | | |```\```````|`````|```````/```| | |``| \ |`````| / |``| | ||
| + | | |````@``````|`````|``````@````| | |``| @-------->`<--------@ |``| | ||
| |```````````|`````|```````````| | |``| |`````| |``| | | |```````````|`````|```````````| | |``| |`````| |``| | ||
| o```````````o` ^ `o```````````o | |``o o`````o o``| | | o```````````o` ^ `o```````````o | |``o o`````o o``| | ||
| Line 9,068: | Line 10,515: | ||
Figure 69. Difference Map of F = <f, g> = <((u)(v)), ((u, v))> | Figure 69. Difference Map of F = <f, g> = <((u)(v)), ((u, v))> | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 69 -- Difference Map (Short Form).gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 69. Difference Map of F = ‹f, g› = ‹((u)(v)), ((u, v))›'''</font></center></p> | ||
===Formula Display 19=== | ===Formula Display 19=== | ||
| Line 9,106: | Line 10,557: | ||
</font><br> | </font><br> | ||
| − | ===Figure 70-a. Tangent Functor Diagram for F‹u, v› = ‹((u)(v)), ((u, v))›=== | + | ===Figure 70-a. Tangent Functor Diagram for F‹u, v› = ‹((u)(v)), ((u, v))›=== |
<pre> | <pre> | ||
| Line 9,191: | Line 10,642: | ||
Figure 70-a. Tangent Functor Diagram for F‹u, v› = <((u)(v)), ((u, v))> | Figure 70-a. Tangent Functor Diagram for F‹u, v› = <((u)(v)), ((u, v))> | ||
</pre> | </pre> | ||
| + | |||
| + | <br> | ||
| + | <p>[[Image:Diff Log Dyn Sys -- Figure 70-a -- Tangent Functor Diagram.gif|center]]</p> | ||
| + | <p><center><font size="+1">'''Figure 70-a. Tangent Functor Diagram for F‹u, v› = ‹((u)(v)), ((u, v))›'''</font></center></p> | ||
===Figure 70-b. Tangent Functor Ferris Wheel for F‹u, v› = ‹((u)(v)), ((u, v))›=== | ===Figure 70-b. Tangent Functor Ferris Wheel for F‹u, v› = ‹((u)(v)), ((u, v))›=== | ||
| − | |||
| − | |||
<pre> | <pre> | ||
| Line 9,374: | Line 10,827: | ||
Figure 70-b. Tangent Functor Ferris Wheel for F<u, v> = <((u)(v)), ((u, v))> | Figure 70-b. Tangent Functor Ferris Wheel for F<u, v> = <((u)(v)), ((u, v))> | ||
</pre> | </pre> | ||
| + | |||
| + | [[Image:Tangent_Functor_Ferris_Wheel.gif|frame|<font size="3">'''Figure 70-b. Tangent Functor Ferris Wheel for F‹u, v› = ‹((u)(v)), ((u, v))›'''</font>]] | ||
Latest revision as of 15:00, 25 August 2007
Differential Logic and Dynamic Systems
Table 1. Syntax & Semantics of a Calculus for Propositional Logic
Table 1. Syntax & Semantics of a Calculus for Propositional Logic o-------------------o-------------------o-------------------o | Expression | Interpretation | Other Notations | o-------------------o-------------------o-------------------o | " " | True. | 1 | o-------------------o-------------------o-------------------o | () | False. | 0 | o-------------------o-------------------o-------------------o | A | A. | A | o-------------------o-------------------o-------------------o | (A) | Not A. | A' | | | | ~A | o-------------------o-------------------o-------------------o | A B C | A and B and C. | A & B & C | o-------------------o-------------------o-------------------o | ((A)(B)(C)) | A or B or C. | A v B v C | o-------------------o-------------------o-------------------o | (A (B)) | A implies B. | A => B | | | If A then B. | | o-------------------o-------------------o-------------------o | (A, B) | A not equal to B. | A =/= B | | | A exclusive-or B. | A + B | o-------------------o-------------------o-------------------o | ((A, B)) | A is equal to B. | A = B | | | A if & only if B. | A <=> B | o-------------------o-------------------o-------------------o | (A, B, C) | Just one of | A'B C v | | | A, B, C | A B'C v | | | is false. | A B C' | o-------------------o-------------------o-------------------o | ((A),(B),(C)) | Just one of | A B'C' v | | | A, B, C | A'B C' v | | | is true. | A'B'C | | | | | | | Partition all | | | | into A, B, C. | | o-------------------o-------------------o-------------------o | ((A, B), C) | Oddly many of | A + B + C | | (A, (B, C)) | A, B, C | | | | are true. | A B C v | | | | A B'C' v | | | | A'B C' v | | | | A'B'C | o-------------------o-------------------o-------------------o | (Q, (A),(B),(C)) | Partition Q | Q'A'B'C' v | | | into A, B, C. | Q A B'C' v | | | | Q A'B C' v | | | Genus Q comprises | Q A'B'C | | | species A, B, C. | | o-------------------o-------------------o-------------------o
| Expression | Interpretation | Other Notations |
|---|---|---|
| " " | True. | 1 |
| ( ) | False. | 0 |
| A | A. | A |
| (A) | Not A. | A’ ~A ¬A |
| A B C | A and B and C. | A ∧ B ∧ C |
| ((A)(B)(C)) | A or B or C. | A ∨ B ∨ C |
| (A (B)) | A implies B. If A then B. |
A ⇒ B |
| (A, B) | A not equal to B. A exclusive-or B. |
A ≠ B A + B |
| ((A, B)) | A is equal to B. A if & only if B. |
A = B A ⇔ B |
| (A, B, C) | Just one of A, B, C is false. |
A’B C ∨ |
| ((A),(B),(C)) | Just one of A, B, C is true. Partition all |
A B’C’ ∨ |
| ((A, B), C) (A, (B, C)) |
Oddly many of A, B, C are true. |
A + B + C |
| (Q, (A),(B),(C)) | Partition Q into A, B, C. Genus Q comprises |
Q’A’B’C’ ∨ |
Table 2. Fundamental Notations for Propositional Calculus
Table 2. Fundamental Notations for Propositional Calculus
o---------o-------------------o-------------------o-------------------o
| Symbol | Notation | Description | Type |
o---------o-------------------o-------------------o-------------------o
| !A! | {a_1, ..., a_n} | Alphabet | [n] = #n# |
o---------o-------------------o-------------------o-------------------o
| A_i | {(a_i), a_i} | Dimension i | B |
o---------o-------------------o-------------------o-------------------o
| A | <|!A!|> | Set of cells, | B^n |
| | <|a_i, ..., a_n|> | coordinate tuples,| |
| | {<a_i, ..., a_n>} | interpretations, | |
| | A_1 x ... x A_n | points, or vectors| |
| | Prod_i A_i | in the universe | |
o---------o-------------------o-------------------o-------------------o
| A* | (hom : A -> B) | Linear functions | (B^n)* = B^n |
o---------o-------------------o-------------------o-------------------o
| A^ | (A -> B) | Boolean functions | B^n -> B |
o---------o-------------------o-------------------o-------------------o
| A% | [!A!] | Universe of Disc. | (B^n, (B^n -> B)) |
| | (A, A^) | based on features | (B^n +-> B) |
| | (A +-> B) | {a_1, ..., a_n} | [B^n] |
| | (A, (A -> B)) | | |
| | [a_1, ..., a_n] | | |
o---------o-------------------o-------------------o-------------------o
| Symbol | Notation | Description | Type |
|---|---|---|---|
| A | {a1, …, an} | Alphabet | [n] = n |
| Ai | {(ai), ai} | Dimension i | B |
| A |
〈A〉 |
Set of cells, |
Bn |
| A* | (hom : A → B) | Linear functions | (Bn)* = Bn |
| A^ | (A → B) | Boolean functions | Bn → B |
| A• |
[A] |
Universe of discourse |
(Bn, (Bn → B)) |
Table 3. Analogy of Real and Boolean Types
Table 3. Analogy of Real and Boolean Types o-------------------------o-------------------------o-------------------------o | Real Domain R | <-> | Boolean Domain B | o-------------------------o-------------------------o-------------------------o | R^n | Basic Space | B^n | o-------------------------o-------------------------o-------------------------o | R^n -> R | Function Space | B^n -> B | o-------------------------o-------------------------o-------------------------o | (R^n -> R) -> R | Tangent Vector | (B^n -> B) -> B | o-------------------------o-------------------------o-------------------------o | R^n -> ((R^n -> R) -> R)| Vector Field | B^n -> ((B^n -> B) -> B)| o-------------------------o-------------------------o-------------------------o | (R^n x (R^n -> R)) -> R | ditto | (B^n x (B^n -> B)) -> B | o-------------------------o-------------------------o-------------------------o | ((R^n -> R) x R^n) -> R | ditto | ((B^n -> B) x B^n) -> B | o-------------------------o-------------------------o-------------------------o | (R^n -> R) -> (R^n -> R)| Derivation | (B^n -> B) -> (B^n -> B)| o-------------------------o-------------------------o-------------------------o | R^n -> R^m | Basic Transformation | B^n -> B^m | o-------------------------o-------------------------o-------------------------o | (R^n -> R) -> (R^m -> R)| Function Transformation | (B^n -> B) -> (B^m -> B)| o-------------------------o-------------------------o-------------------------o | ... | ... | ... | o-------------------------o-------------------------o-------------------------o
| Real Domain R | ←→ | Boolean Domain B |
|---|---|---|
| Rn | Basic Space | Bn |
| Rn → R | Function Space | Bn → B |
| (Rn→R) → R | Tangent Vector | (Bn→B) → B |
| Rn → ((Rn→R)→R) | Vector Field | Bn → ((Bn→B)→B) |
| (Rn × (Rn→ R)) → R | ditto | (Bn × (Bn→ B)) → B |
| ((Rn→R) × Rn) → R | ditto | ((Bn→B) × Bn) → B |
| (Rn→R) → (Rn→R) | Derivation | (Bn→B) → (Bn→B) |
| Rn → Rm | Basic Transformation | Bn → Bm |
| (Rn→R) → (Rm→R) | Function Transformation | (Bn→B) → (Bm→B) |
| ... | ... | ... |
Table 4. An Equivalence Based on the Propositions as Types Analogy
Table 4. An Equivalence Based on the Propositions as Types Analogy o-------------------------o------------------------o--------------------------o | Pattern | Construction | Instance | o-------------------------o------------------------o--------------------------o | X -> (Y -> Z) | Vector Field | K^n -> ((K^n -> K) -> K) | o-------------------------o------------------------o--------------------------o | (X x Y) -> Z | | (K^n x (K^n -> K)) -> K | o-------------------------o------------------------o--------------------------o | (Y x X) -> Z | | ((K^n -> K) x K^n) -> K | o-------------------------o------------------------o--------------------------o | Y -> (X -> Z) | Derivation | (K^n -> K) -> (K^n -> K) | o-------------------------o------------------------o--------------------------o
| Pattern | Construction | Instance |
|---|---|---|
| X → (Y → Z) | Vector Field | Kn → ((Kn → K) → K) |
| (X × Y) → Z | (Kn × (Kn → K)) → K | |
| (Y × X) → Z | ((Kn → K) × Kn) → K | |
| Y → (X → Z) | Derivation | (Kn → K) → (Kn → K) |
Table 5. A Bridge Over Troubled Waters
Table 5. A Bridge Over Troubled Waters
o-------------------------o-------------------------o-------------------------o
| Linear Space | Liminal Space | Logical Space |
o-------------------------o-------------------------o-------------------------o
| | | |
| !X! | !`X`! | !A! |
| | | |
| {x_1, ..., x_n} | {`x`_1, ..., `x`_n} | {a_1, ..., a_n} |
| | | |
| cardinality n | cardinality n | cardinality n |
o-------------------------o-------------------------o-------------------------o
| | | |
| X_i | `X`_i | A_i |
| | | |
| <|x_i|> | {(`x`_i), `x`_i} | {(a_i), a_i} |
| | | |
| isomorphic to K | isomorphic to B | isomorphic to B |
o-------------------------o-------------------------o-------------------------o
| | | |
| X | `X` | A |
| | | |
| <|!X!|> | <|!`X`!|> | <|!A!|> |
| | | |
| <|x_1, ..., x_n|> | <|`x`_1, ..., `x`_n|> | <|a_1, ..., a_n|> |
| | | |
| {<x_1, ..., x_n>} | {<`x`_1, ..., `x`_n>} | {<a_1, ..., a_n>} |
| | | |
| X_1 x ... x X_n | `X`_1 x ... x `X`_n | A_1 x ... x A_n |
| | | |
| Prod_i X_i | Prod_i `X`_i | Prod_i A_i |
| | | |
| isomorphic to K^n | isomorphic to B^n | isomorphic to B^n |
o-------------------------o-------------------------o-------------------------o
| | | |
| X* | `X`* | A* |
| | | |
| (hom : X -> K) | (hom : `X` -> B) | (hom : A -> B) |
| | | |
| isomorphic to K^n | isomorphic to B^n | isomorphic to B^n |
o-------------------------o-------------------------o-------------------------o
| | | |
| X^ | `X`^ | A^ |
| | | |
| (X -> K) | (`X` -> B) | (A -> B) |
| | | |
| isomorphic to (K^n -> K)| isomorphic to (B^n -> B)| isomorphic to (B^n -> B)|
o-------------------------o-------------------------o-------------------------o
| | | |
| X% | `X`% | A% |
| | | |
| [!X!] | [!`X`!] | [!A!] |
| | | |
| [x_1, ..., x_n] | [`x`_1, ..., `x`_n] | [a_1, ..., a_n] |
| | | |
| (X, X^) | (`X`, `X`^) | (A, A^) |
| | | |
| (X +-> K) | (`X` +-> B) | (A +-> B) |
| | | |
| (X, (X -> K)) | (`X`, (`X` -> B)) | (A, (A -> B)) |
| | | |
| isomorphic to: | isomorphic to: | isomorphic to: |
| | | |
| (K^n, (K^n -> K)) | (B^n, (B^n -> B)) | (B^n, (B^n -> K)) |
| | | |
| (K^n +-> K) | (B^n +-> B) | (B^n +-> B) |
| | | |
| [K^n] | [B^n] | [B^n] |
o-------------------------o-------------------------o-------------------------o
| Linear Space | Liminal Space | Logical Space |
|---|---|---|
|
X |
X |
A |
|
Xi |
Xi |
Ai |
|
X |
X |
A |
|
X* |
X* |
A* |
|
X^ |
X^ |
A^ |
|
X• |
X• |
A• |
Table 6. Propositional Forms on One Variable
Table 6. Propositional Forms on One Variable o---------o---------o---------o----------o------------------o----------o | L_1 | L_2 | L_3 | L_4 | L_5 | L_6 | | | | | | | | | Decimal | Binary | Vector | Cactus | English | Ordinary | o---------o---------o---------o----------o------------------o----------o | | x : 1 0 | | | | o---------o---------o---------o----------o------------------o----------o | | | | | | | | f_0 | f_00 | 0 0 | ( ) | false | 0 | | | | | | | | | f_1 | f_01 | 0 1 | (x) | not x | ~x | | | | | | | | | f_2 | f_10 | 1 0 | x | x | x | | | | | | | | | f_3 | f_11 | 1 1 | (( )) | true | 1 | | | | | | | | o---------o---------o---------o----------o------------------o----------o
| L1 Decimal |
L2 Binary |
L3 Vector |
L4 Cactus |
L5 English |
L6 Ordinary |
|---|---|---|---|---|---|
| x : | 1 0 | ||||
| f0 | f00 | 0 0 | ( ) | false | 0 |
| f1 | f01 | 0 1 | (x) | not x | ~x |
| f2 | f10 | 1 0 | x | x | x |
| f3 | f11 | 1 1 | (( )) | true | 1 |
Table 7. Propositional Forms on Two Variables
Table 7. Propositional Forms on Two Variables o---------o---------o---------o----------o------------------o----------o | L_1 | L_2 | L_3 | L_4 | L_5 | L_6 | | | | | | | | | Decimal | Binary | Vector | Cactus | English | Ordinary | o---------o---------o---------o----------o------------------o----------o | | x : 1 1 0 0 | | | | | | y : 1 0 1 0 | | | | o---------o---------o---------o----------o------------------o----------o | | | | | | | | f_0 | f_0000 | 0 0 0 0 | () | false | 0 | | | | | | | | | f_1 | f_0001 | 0 0 0 1 | (x)(y) | neither x nor y | ~x & ~y | | | | | | | | | f_2 | f_0010 | 0 0 1 0 | (x) y | y and not x | ~x & y | | | | | | | | | f_3 | f_0011 | 0 0 1 1 | (x) | not x | ~x | | | | | | | | | f_4 | f_0100 | 0 1 0 0 | x (y) | x and not y | x & ~y | | | | | | | | | f_5 | f_0101 | 0 1 0 1 | (y) | not y | ~y | | | | | | | | | f_6 | f_0110 | 0 1 1 0 | (x, y) | x not equal to y | x + y | | | | | | | | | f_7 | f_0111 | 0 1 1 1 | (x y) | not both x and y | ~x v ~y | | | | | | | | | f_8 | f_1000 | 1 0 0 0 | x y | x and y | x & y | | | | | | | | | f_9 | f_1001 | 1 0 0 1 | ((x, y)) | x equal to y | x = y | | | | | | | | | f_10 | f_1010 | 1 0 1 0 | y | y | y | | | | | | | | | f_11 | f_1011 | 1 0 1 1 | (x (y)) | not x without y | x => y | | | | | | | | | f_12 | f_1100 | 1 1 0 0 | x | x | x | | | | | | | | | f_13 | f_1101 | 1 1 0 1 | ((x) y) | not y without x | x <= y | | | | | | | | | f_14 | f_1110 | 1 1 1 0 | ((x)(y)) | x or y | x v y | | | | | | | | | f_15 | f_1111 | 1 1 1 1 | (()) | true | 1 | | | | | | | | o---------o---------o---------o----------o------------------o----------o
| L1 Decimal |
L2 Binary |
L3 Vector |
L4 Cactus |
L5 English |
L6 Ordinary |
|---|---|---|---|---|---|
| x : | 1 1 0 0 | ||||
| y : | 1 0 1 0 | ||||
| f0 | f0000 | 0 0 0 0 | ( ) | false | 0 |
| f1 | f0001 | 0 0 0 1 | (x)(y) | neither x nor y | ¬x ∧ ¬y |
| f2 | f0010 | 0 0 1 0 | (x) y | y and not x | ¬x ∧ y |
| f3 | f0011 | 0 0 1 1 | (x) | not x | ¬x |
| f4 | f0100 | 0 1 0 0 | x (y) | x and not y | x ∧ ¬y |
| f5 | f0101 | 0 1 0 1 | (y) | not y | ¬y |
| f6 | f0110 | 0 1 1 0 | (x, y) | x not equal to y | x ≠ y |
| f7 | f0111 | 0 1 1 1 | (x y) | not both x and y | ¬x ∨ ¬y |
| f8 | f1000 | 1 0 0 0 | x y | x and y | x ∧ y |
| f9 | f1001 | 1 0 0 1 | ((x, y)) | x equal to y | x = y |
| f10 | f1010 | 1 0 1 0 | y | y | y |
| f11 | f1011 | 1 0 1 1 | (x (y)) | not x without y | x → y |
| f12 | f1100 | 1 1 0 0 | x | x | x |
| f13 | f1101 | 1 1 0 1 | ((x) y) | not y without x | x ← y |
| f14 | f1110 | 1 1 1 0 | ((x)(y)) | x or y | x ∨ y |
| f15 | f1111 | 1 1 1 1 | (( )) | true | 1 |
Table 8. Notation for the Differential Extension of Propositional Calculus
Table 8. Notation for the Differential Extension of Propositional Calculus
o---------o-------------------o-------------------o-------------------o
| Symbol | Notation | Description | Type |
o---------o-------------------o-------------------o-------------------o
| d!A! | {da_1, ..., da_n} | Alphabet of | [n] = #n# |
| | | differential | |
| | | features | |
o---------o-------------------o-------------------o-------------------o
| dA_i | {(da_i), da_i} | Differential | D |
| | | dimension i | |
o---------o-------------------o-------------------o-------------------o
| dA | <|d!A!|> | Tangent space | D^n |
| | <|da_i,...,da_n|> | at a point: | |
| | {<da_i,...,da_n>} | Set of changes, | |
| | dA_1 x ... x dA_n | motions, steps, | |
| | Prod_i dA_i | tangent vectors | |
| | | at a point | |
o---------o-------------------o-------------------o-------------------o
| dA* | (hom : dA -> B) | Linear functions | (D^n)* ~=~ D^n |
| | | on dA | |
o---------o-------------------o-------------------o-------------------o
| dA^ | (dA -> B) | Boolean functions | D^n -> B |
| | | on dA | |
o---------o-------------------o-------------------o-------------------o
| dA% | [d!A!] | Tangent universe | (D^n, (D^n -> B)) |
| | (dA, dA^) | at a point of A%, | (D^n +-> B) |
| | (dA +-> B) | based on the | [D^n] |
| | (dA, (dA -> B)) | tangent features | |
| | [da_1, ..., da_n] | {da_1, ..., da_n} | |
o---------o-------------------o-------------------o-------------------o
| Symbol | Notation | Description | Type |
|---|---|---|---|
| dA | {da1, …, dan} |
Alphabet of |
[n] = n |
| dAi | {(dai), dai} |
Differential |
D |
| dA |
〈dA〉 |
Tangent space |
Dn |
| dA* | (hom : dA → B) |
Linear functions |
(Dn)* = Dn |
| dA^ | (dA → B) |
Boolean functions |
Dn → B |
| dA• |
[dA] |
Tangent universe |
(Dn, (Dn → B)) |
Table 9. Higher Order Differential Features
Table 9. Higher Order Differential Features
o----------------------------------------o----------------------------------------o
| | |
| !A! = d^0.!A! = {a_1, ..., a_n} | E^0.!A! = d^0.!A! |
| | |
| d!A! = d^1.!A! = {da_1, ..., da_n} | E^1.!A! = d^0.!A! |_| d^1.!A! |
| | |
| d^k.!A! = {d^k.a_1,...,d^k.a_n}| E^k.!A! = d^0.!A! |_| ... |_| d^k.!A! |
| | |
| d*!A! = {d^0.!A!, ..., d^k.!A!, ...} | E^oo.!A! = |_| d*!A! |
| | |
o----------------------------------------o----------------------------------------o
|
A = d0A = {a1, …, an} |
E0A = d0A |
|
|
Table 10. A Realm of Intentional Features
Table 10. A Realm of Intentional Features
o---------------------------------------o----------------------------------------o
| | |
| p^0.!A! = !A! = {a_1, ..., a_n} | Q^0.!A! = !A! |
| | |
| p^1.!A! = !A!' = {a_1', ..., a_n'} | Q^1.!A! = !A! |_| !A!' |
| | |
| p^2.!A! = !A!" = {a_1", ..., a_n"} | Q^2.!A! = !A! |_| !A!' |_| !A!" |
| | |
| ... ... ... | ... ... |
| | |
| p^k.!A! = {p^k.a_1, ..., p^k.a_n} | Q^k.!A! = !A! |_| ... |_| p^k.!A! |
| | |
o---------------------------------------o----------------------------------------o
|
|
Formula Display 1
o-------------------------------------------------o | | | From (A) & (dA) infer (A) next. | | | | From (A) & dA infer A next. | | | | From A & (dA) infer A next. | | | | From A & dA infer (A) next. | | | o-------------------------------------------------o
|
Table 11. A Pair of Commodious Trajectories
Table 11. A Pair of Commodious Trajectories o---------o-------------------o-------------------o | Time | Trajectory 1 | Trajectory 2 | o---------o-------------------o-------------------o | | | | | 0 | A dA (d^2.A) | (A) (dA) d^2.A | | | | | | 1 | (A) dA d^2.A | (A) dA d^2.A | | | | | | 2 | A (dA) (d^2.A) | A (dA) (d^2.A) | | | | | | 3 | A (dA) (d^2.A) | A (dA) (d^2.A) | | | | | | 4 | " " " | " " " | | | | | o---------o-------------------o-------------------o
| Time | Trajectory 1 | Trajectory 2 | |||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
Figure 12. The Anchor
o-------------------------------------------------o | E^2.X | | | | o-------------o | | / \ | | / A \ | | / \ | | / ->- \ | | o / \ o | | | \ / | | | | -o- | | | | ^ | | | o---o---------o | o---------o---o | | / \ \|/ / \ | | / \ o | / \ | | / \ | /|\ / \ | | / \ | / | \ / \ | | o o-|-o--|--o---o o | | | | | | | | | | | ---->o<----o | | | | | | | | | o dA o o d^2.A o | | \ \ / / | | \ \ / / | | \ o / | | \ / \ / | | o-------------o o-------------o | | | | | o-------------------------------------------------o Figure 12. The Anchor
Figure 13. The Tiller
o-------------------------------------------------o | | | ->- | | / \ | | \ / | | o-------------o -o- | | / \ ^ | | / dA \/ A | | / /\ | | / / \ | | o o / o | | | \ / | | | | \ / | | o------------|-------\-------/-------|------------o | | \ / | | | | \ / | | | o v / o | | \ o / | | \ ^ / | | \ | / d^2.A | | \ | / | | o------|------o | | | | | | | | o | | | o-------------------------------------------------o Figure 13. The Tiller
Table 14. Differential Propositions
Table 14. Differential Propositions o-------o--------o---------o-----------o-------------------o----------o | | A : 1 1 0 0 | | | | | | dA : 1 0 1 0 | | | | o-------o--------o---------o-----------o-------------------o----------o | | | | | | | | f_0 | g_0 | 0 0 0 0 | () | False | 0 | | | | | | | | o-------o--------o---------o-----------o-------------------o----------o | | | | | | | | | g_1 | 0 0 0 1 | (A)(dA) | Neither A nor dA | ~A & ~dA | | | | | | | | | | g_2 | 0 0 1 0 | (A) dA | Not A but dA | ~A & dA | | | | | | | | | | g_4 | 0 1 0 0 | A (dA) | A but not dA | A & ~dA | | | | | | | | | | g_8 | 1 0 0 0 | A dA | A and dA | A & dA | | | | | | | | o-------o--------o---------o-----------o-------------------o----------o | | | | | | | | f_1 | g_3 | 0 0 1 1 | (A) | Not A | ~A | | | | | | | | | f_2 | g_12 | 1 1 0 0 | A | A | A | | | | | | | | o-------o--------o---------o-----------o-------------------o----------o | | | | | | | | | g_6 | 0 1 1 0 | (A, dA) | A not equal to dA | A + dA | | | | | | | | | | g_9 | 1 0 0 1 | ((A, dA)) | A equal to dA | A = dA | | | | | | | | o-------o--------o---------o-----------o-------------------o----------o | | | | | | | | | g_5 | 0 1 0 1 | (dA) | Not dA | ~dA | | | | | | | | | | g_10 | 1 0 1 0 | dA | dA | dA | | | | | | | | o-------o--------o---------o-----------o-------------------o----------o | | | | | | | | | g_7 | 0 1 1 1 | (A dA) | Not both A and dA | ~A v ~dA | | | | | | | | | | g_11 | 1 0 1 1 | (A (dA)) | Not A without dA | A => dA | | | | | | | | | | g_13 | 1 1 0 1 | ((A) dA) | Not dA without A | A <= dA | | | | | | | | | | g_14 | 1 1 1 0 | ((A)(dA)) | A or dA | A v dA | | | | | | | | o-------o--------o---------o-----------o-------------------o----------o | | | | | | | | f_3 | g_15 | 1 1 1 1 | (()) | True | 1 | | | | | | | | o-------o--------o---------o-----------o-------------------o----------o
| A : | 1 1 0 0 | ||||
| dA : | 1 0 1 0 | ||||
| f0 | g0 | 0 0 0 0 | ( ) | False | 0 |
| g1 | 0 0 0 1 | (A)(dA) | Neither A nor dA | ¬A ∧ ¬dA | |
| g2 | 0 0 1 0 | (A) dA | Not A but dA | ¬A ∧ dA | |
| g4 | 0 1 0 0 | A (dA) | A but not dA | A ∧ ¬dA | |
| g8 | 1 0 0 0 | A dA | A and dA | A ∧ dA | |
| f1 | g3 | 0 0 1 1 | (A) | Not A | ¬A |
| f2 | g12 | 1 1 0 0 | A | A | A |
| g6 | 0 1 1 0 | (A, dA) | A not equal to dA | A ≠ dA | |
| g9 | 1 0 0 1 | ((A, dA)) | A equal to dA | A = dA | |
| g5 | 0 1 0 1 | (dA) | Not dA | ¬dA | |
| g10 | 1 0 1 0 | dA | dA | dA | |
| g7 | 0 1 1 1 | (A dA) | Not both A and dA | ¬A ∨ ¬dA | |
| g11 | 1 0 1 1 | (A (dA)) | Not A without dA | A → dA | |
| g13 | 1 1 0 1 | ((A) dA) | Not dA without A | A ← dA | |
| g14 | 1 1 1 0 | ((A)(dA)) | A or dA | A ∨ dA | |
| f3 | g15 | 1 1 1 1 | (( )) | True | 1 |
| A : | 1 1 0 0 | ||||||||||
| dA : | 1 0 1 0 | ||||||||||
| f0 | g0 | 0 0 0 0 | ( ) | False | 0 | ||||||
|
|
|
|
|
| ||||||
|
|
|
|
|
| ||||||
|
|
|
|
|
| ||||||
|
|
|
|
|
| ||||||
|
|
|
|
|
| ||||||
| f3 | g15 | 1 1 1 1 | (( )) | True | 1 |
Table 15. Tacit Extension of [A] to [A, dA]
Table 15. Tacit Extension of [A] to [A, dA] o---------------------------------------------------------------------o | | | 0 = 0 . ((dA), dA) = 0 | | | | (A) = (A) . ((dA), dA) = (A)(dA) + (A) dA | | | | A = A . ((dA), dA) = A (dA) + A dA | | | | 1 = 1 . ((dA), dA) = 1 | | | o---------------------------------------------------------------------o
|
Figure 16. A Couple of Fourth Gear Orbits
Figure 16-a. A Couple of Fourth Gear Orbits: 1
o-------------------------------------------------o | | | o | | / \ | | / \ | | / \ | | / \ | | o o | | / \ / \ | | / \ / \ | | / \ / \ | | / \ / \ | | o o o | | / \ / \ / \ | | / \ / \ / \ | | / \ / \ / \ | | / \ / \ / \ | | o 5 o 7 o o | | / \ ^| / \ ^| / \ / \ | | / \/ | / \/ | / \ / \ | | / /\ | / /\ | / \ / \ | | / / \|/ / \|/ \ / \ | | o 4<---|----/----|----3 o o | | |\ /|\ / /|\ ^ / \ /| | | | \ / | \/ / | \/ / \ / | | | | \ / | /\ / | /\ / \ / | | | | \ / v/ \ / |/ \ / \ / | | | | o 6 o | o o | | | | |\ / \ /| / \ /| | | | | | \ / \/ | / \ / | | | | | | \ / /\ | / \ / | | | | | d^0.A \ / / \|/ \ / d^1.A | | | o----+----o 2<---|----1 o----+----o | | | \ /|\ ^ / | | | | \ / | \/ / | | | | \ / | /\ / | | | | d^2.A \ / v/ \ / d^3.A | | | o---------o 0 o---------o | | \ / | | \ / | | \ / | | \ / | | o | | | o-------------------------------------------------o Figure 16-a. A Couple of Fourth Gear Orbits: 1
Figure 16-b. A Couple of Fourth Gear Orbits: 2
o-------------------------------------------------o | | | o | | / \ | | / \ | | / \ | | / \ | | o 0 o | | / \ / \ | | / \ / \ | | / \ / \ | | / \ / \ | | o 5 o 2 o | | / \ / \ / \ | | / \ / \ / \ | | / \ / \ / \ | | / \ / \ / \ | | o o o 6 o | | / \ / \ / \ / \ | | / \ / \ / \ / \ | | / \ / \ / \ / \ | | / \ / \ / \ / \ | | o o 7 o o 4 o | | |\ / \ / \ / \ /| | | | \ / \ / \ / \ / | | | | \ / \ / \ / \ / | | | | \ / \ / \ / \ / | | | | o o 3 o 1 o | | | | |\ / \ / \ /| | | | | | \ / \ / \ / | | | | | | \ / \ / \ / | | | | | d^0.A \ / \ / \ / d^1.A | | | o----+----o o o----+----o | | | \ / \ / | | | | \ / \ / | | | | \ / \ / | | | | d^2.A \ / \ / d^3.A | | | o---------o o---------o | | \ / | | \ / | | \ / | | \ / | | o | | | o-------------------------------------------------o Figure 16-b. A Couple of Fourth Gear Orbits: 2
Formula Display 2
o-------------------------------------------------------------------------------o | | | r(q) = Sum_k d_k . 2^(-k) = Sum_k d^k.A(q) . 2^(-k) | | | | = | | | | s(q)/t = (Sum_k d_k . 2^(m-k)) / 2^m = (Sum_k d^k.A(q) . 2^(m-k)) / 2^m | | | o-------------------------------------------------------------------------------o
|
|
Table 17-a. A Couple of Orbits in Fourth Gear: Orbit 1
Table 17-a. A Couple of Orbits in Fourth Gear: Orbit 1 o---------o---------o---------o---------o---------o---------o---------o | Time | State | A | dA | | | | | p_i | q_j | d^0.A | d^1.A | d^2.A | d^3.A | d^4.A | o---------o---------o---------o---------o---------o---------o---------o | | | | | p_0 | q_01 | 0. 0 0 0 1 | | | | | | p_1 | q_03 | 0. 0 0 1 1 | | | | | | p_2 | q_05 | 0. 0 1 0 1 | | | | | | p_3 | q_15 | 0. 1 1 1 1 | | | | | | p_4 | q_17 | 1. 0 0 0 1 | | | | | | p_5 | q_19 | 1. 0 0 1 1 | | | | | | p_6 | q_21 | 1. 0 1 0 1 | | | | | | p_7 | q_31 | 1. 1 1 1 1 | | | | | o---------o---------o---------o---------o---------o---------o---------o
| Time | State | A | dA | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| pi | qj | d0A | d1A | d2A | d3A | d4A | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table 17-b. A Couple of Orbits in Fourth Gear: Orbit 2
Table 17-b. A Couple of Orbits in Fourth Gear: Orbit 2 o---------o---------o---------o---------o---------o---------o---------o | Time | State | A | dA | | | | | p_i | q_j | d^0.A | d^1.A | d^2.A | d^3.A | d^4.A | o---------o---------o---------o---------o---------o---------o---------o | | | | | p_0 | q_25 | 1. 1 0 0 1 | | | | | | p_1 | q_11 | 0. 1 0 1 1 | | | | | | p_2 | q_29 | 1. 1 1 0 1 | | | | | | p_3 | q_07 | 0. 0 1 1 1 | | | | | | p_4 | q_09 | 0. 1 0 0 1 | | | | | | p_5 | q_27 | 1. 1 0 1 1 | | | | | | p_6 | q_13 | 0. 1 1 0 1 | | | | | | p_7 | q_23 | 1. 0 1 1 1 | | | | | o---------o---------o---------o---------o---------o---------o---------o
| Time | State | A | dA | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| pi | qj | d0A | d1A | d2A | d3A | d4A | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Figure 18-a. Extension from 1 to 2 Dimensions: Areal
o-----------------------------------------------------------o | | | o o | | / \ / \ | | / \ / \ | | / \ / \ | | / \ / \ | | / o o 1 1 o | | / / \ / \ / \ | | / / \ / \ / \ | | / 1 / \ / \ / \ | | / / \ !e! / \ / \ | | o / o ----> o 1 0 o 0 1 o | | |\ / / |\ / \ /| | | | \ / 0 / | \ / \ / | | | | \ / / | \ / \ / | | | |x_1\ / / |x_1\ / \ /x_2| | | o----o / o----o 0 0 o----o | | \ / \ / | | \ / \ / | | \ / \ / | | \ / \ / | | o o | | | o-----------------------------------------------------------o Figure 18-a. Extension from 1 to 2 Dimensions: Areal
Figure 18-b. Extension from 1 to 2 Dimensions: Bundle
o-----------------------------o o-------------------o | | | | | | | o-------o | | o---------o | | / \ | | / \ | | o o | | / o------------------------| | dx | | | / \ | | o o | | / \ | | \ / | | o o | | o-------o | | | | | | | | | | | o-------------------o | | x | | | | | | o-------------------o | | | | | | | o o | | o-------o | | \ / | | / \ | | \ / | | o o | | \ / o------------| | dx | | | \ / | | o o | | o---------o | | \ / | | | | o-------o | | | | | o-----------------------------o o-------------------o Figure 18-b. Extension from 1 to 2 Dimensions: Bundle
Figure 18-c. Extension from 1 to 2 Dimensions: Compact
o-----------------------------------------------------------o | | | | | o-----------------o | | / o \ | | / (dx) / \ \ dx | | / v o--------------------->o | | / \ / \ | | / o \ | | o o | | | | | | | | | | | x | (x) | | | | | | | | | | o o | | \ / o | | \ / / \ | | \ o<---------------------o v | | \ / dx \ / (dx) | | \ / o | | o-----------------o | | | | | o-----------------------------------------------------------o Figure 18-c. Extension from 1 to 2 Dimensions: Compact
Figure 18-d. Extension from 1 to 2 Dimensions: Digraph
o-----------------------------------------------------------o | | | | | dx | | .--. .---------->----------. .--. | | | \ / \ / | | | (dx) ^ @ x (x) @ v (dx) | | | / \ / \ | | | *--* *----------<----------* *--* | | dx | | | | | o-----------------------------------------------------------o Figure 18-d. Extension from 1 to 2 Dimensions: Digraph
Figure 19-a. Extension from 2 to 4 Dimensions: Areal
o-------------------------------------------------------------------------------o | | | o o | | / \ / \ | | / \ / \ | | / \ / \ | | / \ o 1100 o | | / \ / \ / \ | | / \ / \ / \ | | / \ !e! / \ / \ | | o 1 1 o ----> o 1101 o 1110 o | | / \ / \ / \ / \ / \ | | / \ / \ / \ / \ / \ | | / \ / \ / \ / \ / \ | | / \ / \ o 1001 o 1111 o 0110 o | | / \ / \ / \ / \ / \ / \ | | / \ / \ / \ / \ / \ / \ | | / \ / \ / \ / \ / \ / \ | | o 1 0 o 0 1 o o 1000 o 1011 o 0111 o 0100 o | | |\ / \ /| |\ / \ / \ / \ /| | | | \ / \ / | | \ / \ / \ / \ / | | | | \ / \ / | | \ / \ / \ / \ / | | | | \ / \ / | | o 1010 o 0011 o 0101 o | | | | \ / \ / | | |\ / \ / \ /| | | | | \ / \ / | | | \ / \ / \ / | | | | | x_1 \ / \ / x_2 | |x_1| \ / \ / \ / |x_2| | | o-------o 0 0 o-------o o---+---o 0010 o 0001 o---+---o | | \ / | \ / \ / | | | \ / | \ / \ / | | | \ / | x_3 \ / \ / x_4 | | | \ / o-------o 0000 o-------o | | \ / \ / | | \ / \ / | | \ / \ / | | o o | | | o-------------------------------------------------------------------------------o Figure 19-a. Extension from 2 to 4 Dimensions: Areal
Figure 19-b. Extension from 2 to 4 Dimensions: Bundle
o-----------------------------o
| o-----o o-----o |
| / \ / \ |
| / o \ |
| / / \ \ |
| o o o o |
@ | du | | dv | |
/| o o o o |
/ | \ \ / / |
/ | \ o / |
/ | \ / \ / |
/ | o-----o o-----o |
/ o-----------------------------o
/
o-----------------------------------------/---o o-----------------------------o
| / | | o-----o o-----o |
| @ | | / \ / \ |
| o---------o o---------o | | / o \ |
| / \ / \ | | / / \ \ |
| / o \ | | o o o o |
| / / \ @-------\-----------@ | du | | dv | |
| / / @ \ \ | | o o o o |
| / / \ \ \ | | \ \ / / |
| / / \ \ \ | | \ o / |
| o o \ o o | | \ / \ / |
| | | \| | | | o-----o o-----o |
| | | | | | o-----------------------------o
| | u | |\ v | |
| | | | \ | | o-----------------------------o
| | | | \ | | | o-----o o-----o |
| o o o \ o | | / \ / \ |
| \ \ / \ / | | / o \ |
| \ \ / \ / | | / / \ \ |
| \ \ / \ / | | o o o o |
| \ @-----\-/-----------\-------------@ | du | | dv | |
| \ o / | | o o o o |
| \ / \ / \ | | \ \ / / |
| o---------o o---------o \ | | \ o / |
| \ | | \ / \ / |
| \ | | o-----o o-----o |
o-----------------------------------------\---o o-----------------------------o
\
\ o-----------------------------o
\ | o-----o o-----o |
\ | / \ / \ |
\ | / o \ |
\ | / / \ \ |
\| o o o o |
@ | du | | dv | |
| o o o o |
| \ \ / / |
| \ o / |
| \ / \ / |
| o-----o o-----o |
o-----------------------------o
Figure 19-b. Extension from 2 to 4 Dimensions: Bundle
Figure 19-c. Extension from 2 to 4 Dimensions: Compact
o---------------------------------------------------------------------o | | | | | o-------------------o o-------------------o | | / \ / \ | | / o \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | o o (du).(dv) o o | | | | -->-- | | | | | | \ / | | | | | dv .(du) | \ / | du .(dv) | | | | u <---------------@---------------> v | | | | | | | | | | | | | | | | | | | | | | | | o o | o o | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \|/ / | | \ | / | | \ /|\ / | | o-------------------o | o-------------------o | | | | | du . dv | | | | | V | | | o---------------------------------------------------------------------o Figure 19-c. Extension from 2 to 4 Dimensions: Compact
Figure 19-d. Extension from 2 to 4 Dimensions: Digraph
o-----------------------------------------------------------o | | | .->-. | | | | | | * * | | \ / | | .-->--@--<--. | | / / \ \ | | / / \ \ | | / . . \ | | / | | \ | | / | | \ | | / | | \ | | . | | . | | | | | | | | v | | v | | .--. | .---------->----------. | .--. | | | \|/ | | \|/ | | | ^ @ ^ v @ v | | | /|\ | | /|\ | | | *--* | *----------<----------* | *--* | | ^ | | ^ | | | | | | | | * | | * | | \ | | / | | \ | | / | | \ | | / | | \ . . / | | \ \ / / | | \ \ / / | | *-->--@--<--* | | / \ | | . . | | | | | | *-<-* | | | o-----------------------------------------------------------o Figure 19-d. Extension from 2 to 4 Dimensions: Digraph
Figure 20-i. Thematization of Conjunction (Stage 1)
o-------------------------------o o-------------------------------o
| | | |
| o-----o o-----o | | o-----o o-----o |
| / \ / \ | | / \ / \ |
| / o \ | | / o \ |
| / /`\ \ | | / /`\ \ |
| o o```o o | | o o```o o |
| | u |```| v | | | | u |```| v | |
| o o```o o | | o o```o o |
| \ \`/ / | | \ \`/ / |
| \ o / | | \ o / |
| \ / \ / | | \ / \ / |
| o-----o o-----o | | o-----o o-----o |
| | | |
o-------------------------------o o-------------------------------o
\ /
\ /
\ /
u v \ J /
\ /
\ /
\ /
\ /
o
Figure 20-i. Thematization of Conjunction (Stage 1)
Figure 20-ii. Thematization of Conjunction (Stage 2)
o-------------------------------o o-------------------------------o
| | | |
| o-----o o-----o | | o-----o o-----o |
| / \ / \ | | / \ / \ |
| / o \ | | / o \ |
| / /`\ \ | | / /`\ \ |
| o o```o o | | o o```o o |
| | u |```| v | | | | u |```| v | |
| o o```o o | | o o```o o |
| \ \`/ / | | \ \`/ / |
| \ o / | | \ o / |
| \ / \ / | | \ / \ / |
| o-----o o-----o | | o-----o o-----o |
| | | |
o-------------------------------o o-------------------------------o
\ / \ /
\ / \ /
\ / \ J /
\ / \ /
\ / \ /
o----------\---------/----------o o----------\---------/----------o
| \ / | | \ / |
| \ / | | \ / |
| o-----@-----o | | o-----@-----o |
| /`````````````\ | | /`````````````\ |
| /```````````````\ | | /```````````````\ |
| /`````````````````\ | | /`````````````````\ |
| o```````````````````o | | o```````````````````o |
| |```````````````````| | | |```````````````````| |
| |```````` J ````````| | | |```````` x ````````| |
| |```````````````````| | | |```````````````````| |
| o```````````````````o | | o```````````````````o |
| \`````````````````/ | | \`````````````````/ |
| \```````````````/ | | \```````````````/ |
| \`````````````/ | | \`````````````/ |
| o-----------o | | o-----------o |
| | | |
| | | |
o-------------------------------o o-------------------------------o
J = u v x = J<u, v>
Figure 20-ii. Thematization of Conjunction (Stage 2)
Figure 20-iii. Thematization of Conjunction (Stage 3)
o-------------------------------o o-------------------------------o
| | |```````````````````````````````|
| | |````````````o-----o````````````|
| | |```````````/ \```````````|
| | |``````````/ \``````````|
| | |`````````/ \`````````|
| | |````````/ \````````|
| J | |```````o x o```````|
| | |```````| |```````|
| | |```````| |```````|
| | |```````| |```````|
| o-----o o-----o | |```````o-----o o-----o```````|
| / \ / \ | |``````/`\ \ / /`\``````|
| / o \ | |`````/```\ o /```\`````|
| / /`\ \ | |````/`````\ /`\ /`````\````|
| / /```\ \ | |```/```````\ /```\ /```````\```|
| o o`````o o | |``o`````````o-----o`````````o``|
| | u |`````| v | | |``|`````````| |`````````|``|
o--o---------o-----o---------o--o |``|``` u ```| |``` v ```|``|
|``|`````````| |`````````|``| |``|`````````| |`````````|``|
|``o`````````o o`````````o``| |``o`````````o o`````````o``|
|```\`````````\ /`````````/```| |```\`````````\ /`````````/```|
|````\`````````\ /`````````/````| |````\`````````\ /`````````/````|
|`````\`````````o`````````/`````| |`````\`````````o`````````/`````|
|``````\```````/`\```````/``````| |``````\```````/`\```````/``````|
|```````o-----o```o-----o```````| |```````o-----o```o-----o```````|
|```````````````````````````````| |```````````````````````````````|
o-------------------------------o o-------------------------------o
\ /
\ /
J = u v \ /
\ !j! /
\ /
!j! = (( x , u v )) \ /
\ /
\ /
@
Figure 20-iii. Thematization of Conjunction (Stage 3)
Figure 21. Thematization of Disjunction and Equality
f g
o-------------------------------o o-------------------------------o
| | |```````````````````````````````|
| o-----o o-----o | |```````o-----o```o-----o```````|
| /```````\ /```````\ | |``````/ \`/ \``````|
| /`````````o`````````\ | |`````/ o \`````|
| /`````````/`\`````````\ | |````/ /`\ \````|
| /`````````/```\`````````\ | |```/ /```\ \```|
| o`````````o`````o```````` o | |``o o`````o o``|
| |`````````|`````|`````````| | |``| |`````| |``|
| |``` u ```|`````|``` v ```| | |``| u |`````| v |``|
| |`````````|`````|`````````| | |``| |`````| |``|
| o`````````o`````o`````````o | |``o o`````o o``|
| \`````````\```/`````````/ | |```\ \```/ /```|
| \`````````\`/`````````/ | |````\ \`/ /````|
| \`````````o`````````/ | |`````\ o /`````|
| \```````/ \```````/ | |``````\ /`\ /``````|
| o-----o o-----o | |```````o-----o```o-----o```````|
| | |```````````````````````````````|
o-------------------------------o o-------------------------------o
((u)(v)) ((u , v))
| |
| |
theta theta
| |
| |
v v
!f! !g!
o-------------------------------o o-------------------------------o
|```````````````````````````````| | |
|````````````o-----o````````````| | o-----o |
|```````````/ \```````````| | /```````\ |
|``````````/ \``````````| | /`````````\ |
|`````````/ \`````````| | /```````````\ |
|````````/ \````````| | /`````````````\ |
|```````o f o```````| | o`````` g ``````o |
|```````| |```````| | |```````````````| |
|```````| |```````| | |```````````````| |
|```````| |```````| | |```````````````| |
|```````o-----o o-----o```````| | o-----o```o-----o |
|``````/ \`````\ /`````/ \``````| | /`\ \`/ /`\ |
|`````/ \`````o`````/ \`````| | /```\ o /```\ |
|````/ \```/`\```/ \````| | /`````\ /`\ /`````\ |
|```/ \`/```\`/ \```| | /```````\ /```\ /```````\ |
|``o o-----o o``| | o`````````o-----o`````````o |
|``| | | |``| | |`````````| |`````````| |
|``| u | | v |``| | |``` u ```| |``` v ```| |
|``| | | |``| | |`````````| |`````````| |
|``o o o o``| | o`````````o o`````````o |
|```\ \ / /```| | \`````````\ /`````````/ |
|````\ \ / /````| | \`````````\ /`````````/ |
|`````\ o /`````| | \`````````o`````````/ |
|``````\ /`\ /``````| | \```````/ \```````/ |
|```````o-----o```o-----o```````| | o-----o o-----o |
|```````````````````````````````| | |
o-------------------------------o o-------------------------------o
((f , ((u)(v)) )) ((g , ((u , v)) ))
Figure 21. Thematization of Disjunction and Equality
Table 22. Disjunction f and Equality g
Table 22. Disjunction f and Equality g o-------------------o-------------------o | u v | f g | o-------------------o-------------------o | | | | 0 0 | 0 1 | | | | | 0 1 | 1 0 | | | | | 1 0 | 1 0 | | | | | 1 1 | 1 1 | | | | o-------------------o-------------------o
|
| ||||||||||||||||
|
|
Tables 23-i and 23-ii. Thematics of Disjunction and Equality (1)
Tables 23-i and 23-ii. Thematics of Disjunction and Equality (1) o-----------------o-----------o o-----------------o-----------o | u v f | x !f! | | u v g | y !g! | o-----------------o-----------o o-----------------o-----------o | | | | | | | 0 0 --> | 0 1 | | 0 0 --> | 1 1 | | | | | | | | 0 1 --> | 1 1 | | 0 1 --> | 0 1 | | | | | | | | 1 0 --> | 1 1 | | 1 0 --> | 0 1 | | | | | | | | 1 1 --> | 1 1 | | 1 1 --> | 1 1 | | | | | | | o-----------------o-----------o o-----------------o-----------o | | | | | | | 0 0 | 1 0 | | 0 0 | 0 0 | | | | | | | | 0 1 | 0 0 | | 0 1 | 1 0 | | | | | | | | 1 0 | 0 0 | | 1 0 | 1 0 | | | | | | | | 1 1 | 0 0 | | 1 1 | 0 0 | | | | | | | o-----------------o-----------o o-----------------o-----------o
|
|
Tables 24-i and 24-ii. Thematics of Disjunction and Equality (2)
Tables 24-i and 24-ii. Thematics of Disjunction and Equality (2) o-----------------------o-----o o-----------------------o-----o | u v f x | !f! | | u v g y | !g! | o-----------------------o-----o o-----------------------o-----o | | | | | | | 0 0 --> 0 | 1 | | 0 0 0 | 0 | | | | | | | | 0 0 1 | 0 | | 0 0 --> 1 | 1 | | | | | | | | 0 1 0 | 0 | | 0 1 --> 0 | 1 | | | | | | | | 0 1 --> 1 | 1 | | 0 1 1 | 0 | | | | | | | o-----------------------o-----o o-----------------------o-----o | | | | | | | 1 0 0 | 0 | | 1 0 --> 0 | 1 | | | | | | | | 1 0 --> 1 | 1 | | 1 0 1 | 0 | | | | | | | | 1 1 0 | 0 | | 1 1 0 | 0 | | | | | | | | 1 1 --> 1 | 1 | | 1 1 --> 1 | 1 | | | | | | | o-----------------------o-----o o-----------------------o-----o
|
|
Tables 25-i and 25-ii. Thematics of Disjunction and Equality (3)
Tables 25-i and 25-ii. Thematics of Disjunction and Equality (3) o-----------------------o-----o o-----------------------o-----o | u v f x | !f! | | u v g y | !g! | o-----------------------o-----o o-----------------------o-----o | | | | | | | 0 0 --> 0 | 1 | | 0 0 0 | 0 | | | | | | | | 0 1 0 | 0 | | 0 1 --> 0 | 1 | | | | | | | | 1 0 0 | 0 | | 1 0 --> 0 | 1 | | | | | | | | 1 1 0 | 0 | | 1 1 0 | 0 | | | | | | | o-----------------------o-----o o-----------------------o-----o | | | | | | | 0 0 1 | 0 | | 0 0 --> 1 | 1 | | | | | | | | 0 1 --> 1 | 1 | | 0 1 1 | 0 | | | | | | | | 1 0 --> 1 | 1 | | 1 0 1 | 0 | | | | | | | | 1 1 --> 1 | 1 | | 1 1 --> 1 | 1 | | | | | | | o-----------------------o-----o o-----------------------o-----o
|
|
Tables 26-i and 26-ii. Tacit Extension and Thematization
Tables 26-i and 26-ii. Tacit Extension and Thematization o-----------------o-----------o o-----------------o-----------o | u v x | !e!f !f! | | u v y | !e!g !g! | o-----------------o-----------o o-----------------o-----------o | | | | | | | 0 0 0 | 0 1 | | 0 0 0 | 1 0 | | | | | | | | 0 0 1 | 0 0 | | 0 0 1 | 1 1 | | | | | | | | 0 1 0 | 1 0 | | 0 1 0 | 0 1 | | | | | | | | 0 1 1 | 1 1 | | 0 1 1 | 0 0 | | | | | | | o-----------------o-----------o o-----------------o-----------o | | | | | | | 1 0 0 | 1 0 | | 1 0 0 | 0 1 | | | | | | | | 1 0 1 | 1 1 | | 1 0 1 | 0 0 | | | | | | | | 1 1 0 | 1 0 | | 1 1 0 | 1 0 | | | | | | | | 1 1 1 | 1 1 | | 1 1 1 | 1 1 | | | | | | | o-----------------o-----------o o-----------------o-----------o
|
|
Table 27. Thematization of Bivariate Propositions
Table 27. Thematization of Bivariate Propositions o---------o---------o----------o--------------------o--------------------o | u : 1 1 0 0 | f | theta (f) | theta (f) | | v : 1 0 1 0 | | | | o---------o---------o----------o--------------------o--------------------o | | | | | | | f_0 | 0 0 0 0 | () | (( f , () )) | f + 1 | | | | | | | | f_1 | 0 0 0 1 | (u)(v) | (( f , (u)(v) )) | f + u + v + uv | | | | | | | | f_2 | 0 0 1 0 | (u) v | (( f , (u) v )) | f + v + uv + 1 | | | | | | | | f_3 | 0 0 1 1 | (u) | (( f , (u) )) | f + u | | | | | | | | f_4 | 0 1 0 0 | u (v) | (( f , u (v) )) | f + u + uv + 1 | | | | | | | | f_5 | 0 1 0 1 | (v) | (( f , (v) )) | f + v | | | | | | | | f_6 | 0 1 1 0 | (u, v) | (( f , (u, v) )) | f + u + v + 1 | | | | | | | | f_7 | 0 1 1 1 | (u v) | (( f , (u v) )) | f + uv | | | | | | | o---------o---------o----------o--------------------o--------------------o | | | | | | | f_8 | 1 0 0 0 | u v | (( f , u v )) | f + uv + 1 | | | | | | | | f_9 | 1 0 0 1 | ((u, v)) | (( f , ((u, v)) )) | f + u + v | | | | | | | | f_10 | 1 0 1 0 | v | (( f , v )) | f + v + 1 | | | | | | | | f_11 | 1 0 1 1 | (u (v)) | (( f , (u (v)) )) | f + u + uv | | | | | | | | f_12 | 1 1 0 0 | u | (( f , u )) | f + u + 1 | | | | | | | | f_13 | 1 1 0 1 | ((u) v) | (( f , ((u) v) )) | f + v + uv | | | | | | | | f_14 | 1 1 1 0 | ((u)(v)) | (( f , ((u)(v)) )) | f + u + v + uv + 1 | | | | | | | | f_15 | 1 1 1 1 | (()) | (( f , (()) )) | f | | | | | | | o---------o---------o----------o--------------------o--------------------o
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
Table 28. Propositions on Two Variables
Table 28. Propositions on Two Variables o-------o-----o----------------------------------------------------------------o | u v | | f f f f f f f f f f f f f f f f | | | | 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 | o-------o-----o----------------------------------------------------------------o | | | | | 0 0 | | 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 | | | | | | 0 1 | | 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 | | | | | | 1 0 | | 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 | | | | | | 1 1 | | 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 | | | | | o-------o-----o----------------------------------------------------------------o
| u v | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 | |
| 0 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | |
| 0 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | |
| 1 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 1 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
|
|
Table 29. Thematic Extensions of Bivariate Propositions
Table 29. Thematic Extensions of Bivariate Propositions o-------o-----o----------------------------------------------------------------o | u v | f^¢ |!f! !f! !f! !f! !f! !f! !f! !f! !f! !f! !f! !f! !f! !f! !f! !f! | | | | 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 | o-------o-----o----------------------------------------------------------------o | | | | | 0 0 | 0 | 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 | | | | | | 0 0 | 1 | 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 | | | | | | 0 1 | 0 | 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0 0 | | | | | | 0 1 | 1 | 0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 | | | | | | 1 0 | 0 | 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 | | | | | | 1 0 | 1 | 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 | | | | | | 1 1 | 0 | 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 | | | | | | 1 1 | 1 | 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 | | | | | o-------o-----o----------------------------------------------------------------o
|
Figure 30. Generic Frame of a Logical Transformation
o-------------------------------------------------------o
| U |
| |
| o-----------o o-----------o |
| / \ / \ |
| / o \ |
| / / \ \ |
| / / \ \ |
| o o o o |
| | | | | |
| | u | | v | |
| | | | | |
| o o o o |
| \ \ / / |
| \ \ / / |
| \ o / |
| \ / \ / |
| o-----------o o-----------o |
| |
| |
o---------------------------o---------------------------o
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
/ \ / \ / \
o-------------------------o o-------------------------o o-------------------------o
| U | | U | | U |
| o---o o---o | | o---o o---o | | o---o o---o |
| / \ / \ | | / \ / \ | | / \ / \ |
| / o \ | | / o \ | | / o \ |
| / / \ \ | | / / \ \ | | / / \ \ |
| o o o o | | o o o o | | o o o o |
| | u | | v | | | | u | | v | | | | u | | v | |
| o o o o | | o o o o | | o o o o |
| \ \ / / | | \ \ / / | | \ \ / / |
| \ o / | | \ o / | | \ o / |
| \ / \ / | | \ / \ / | | \ / \ / |
| o---o o---o | | o---o o---o | | o---o o---o |
| | | | | |
o-------------------------o o-------------------------o o-------------------------o
\ | \ / | /
\ | \ / | /
\ | \ / | /
\ | \ / | /
\ g | \ f / | h /
\ | \ / | /
\ | \ / | /
\ | \ / | /
\ | \ / | /
\ o----------|-----------\-----/-----------|----------o /
\ | X | \ / | | /
\ | | \ / | | /
\ | | o-----o-----o | | /
\| | / \ | |/
\ | / \ | /
|\ | / \ | /|
| \ | / \ | / |
| \ | / \ | / |
| \ | o x o | / |
| \ | | | | / |
| \ | | | | / |
| \ | | | | / |
| \ | | | | / |
| \ | | | | / |
| \| | | |/ |
| o--o--------o o--------o--o |
| / \ \ / / \ |
| / \ \ / / \ |
| / \ o / \ |
| / \ / \ / \ |
| / \ / \ / \ |
| o o--o-----o--o o |
| | | | | |
| | | | | |
| | | | | |
| | y | | z | |
| | | | | |
| | | | | |
| o o o o |
| \ \ / / |
| \ \ / / |
| \ o / |
| \ / \ / |
| \ / \ / |
| o-----------o o-----------o |
| |
| |
o---------------------------------------------------o
\ /
\ /
\ /
\ /
\ /
\ p , q /
\ /
\ /
\ /
\ /
\ /
\ /
\ /
o
Figure 30. Generic Frame of a Logical Transformation
Note. The following image was corrupted in transit between software platforms.
Formula Display 3
o-------------------------------------------------o | | | x = f<u, v> | | | | y = g<u, v> | | | | z = h<u, v> | | | o-------------------------------------------------o
|
Figure 31. Operator Diagram (1)
o---------------------------------------o | | | | | U% F X% | | o------------------>o | | | | | | | | | | | | | | | | | | !W! | | !W! | | | | | | | | | | | | | | v v | | o------------------>o | | !W!U% !W!F !W!X% | | | | | o---------------------------------------o Figure 31. Operator Diagram (1)
Note. The following image was corrupted in transit between software platforms.
Figure 32. Operator Diagram (2)
o---------------------------------------o | | | | | U% !W! !W!U% | | o------------------>o | | | | | | | | | | | | | | | | | | F | | !W!F | | | | | | | | | | | | | | v v | | o------------------>o | | X% !W! !W!X% | | | | | o---------------------------------------o Figure 32. Operator Diagram (2)
Note. The following image was corrupted in transit between software platforms.
Figure 33-i. Analytic Diagram (1)
U% $E$ $E$U% $E$U% $E$U% o------------------>o============o============o | | | | | | | | | | | | | | | | F | | $E$F = | $d$^0.F + | $r$^0.F | | | | | | | | | | | | v v v v o------------------>o============o============o X% $E$ $E$X% $E$X% $E$X% Figure 33-i. Analytic Diagram (1)
Note. The following image was corrupted in transit between software platforms.
Figure 33-ii. Analytic Diagram (2)
U% $E$ $E$U% $E$U% $E$U% $E$U% o------------------>o============o============o============o | | | | | | | | | | | | | | | | | | | | F | | $E$F = | $d$^0.F + | $d$^1.F + | $r$^1.F | | | | | | | | | | | | | | | v v v v v o------------------>o============o============o============o X% $E$ $E$X% $E$X% $E$X% $E$X% Figure 33-ii. Analytic Diagram (2)
Note. The following image was corrupted in transit between software platforms.
Formula Display 4
o--------------------------------------------------------------------------------------o | | | x_1 = !e!F_1 <u_1, ..., u_n, du_1, ..., du_n> = F_1 <u_1, ..., u_n> | | | | ... | | | | x_k = !e!F_k <u_1, ..., u_n, du_1, ..., du_n> = F_k <u_1, ..., u_n> | | | | | | dx_1 = EF_1 <u_1, ..., u_n, du_1, ..., du_n> = F_1 <u_1 + du_1, ..., u_n + du_n> | | | | ... | | | | dx_k = EF_k <u_1, ..., u_n, du_1, ..., du_n> = F_k <u_1 + du_1, ..., u_n + du_n> | | | o--------------------------------------------------------------------------------------o
| |||||||||||
|
Formula Display 5
o--------------------------------------------------------------------------------o | | | x_1 = !e!F_1 <u_1, ..., u_n, du_1, ..., du_n> = F_1 <u_1, ..., u_n> | | | | ... | | | | x_k = !e!F_k <u_1, ..., u_n, du_1, ..., du_n> = F_k <u_1, ..., u_n> | | | | | | dx_1 = !e!F_1 <u_1, ..., u_n, du_1, ..., du_n> = F_1 <u_1, ..., u_n> | | | | ... | | | | dx_k = !e!F_k <u_1, ..., u_n, du_1, ..., du_n> = F_k <u_1, ..., u_n> | | | o--------------------------------------------------------------------------------o
| |||||||||||
|
Formula Display 6
o--------------------------------------------------------------------------------o | | | dx_1 = !e!F_1 <u_1, ..., u_n, du_1, ..., du_n> = F_1 <u_1, ..., u_n> | | | | ... | | | | dx_k = !e!F_k <u_1, ..., u_n, du_1, ..., du_n> = F_k <u_1, ..., u_n> | | | o--------------------------------------------------------------------------------o
|
Formula Display 7
o-------------------------------------------------o | | | $D$ = $E$ - $e$ | | | | = $r$^0 | | | | = $d$^1 + $r$^1 | | | | = $d$^1 + ... + $d$^m + $r$^m | | | | = Sum_(i = 1 ... m) $d$^i + $r$^m | | | o-------------------------------------------------o
|
Figure 34. Tangent Functor Diagram
U% $T$ $T$U% $T$U% o------------------>o============o | | | | | | | | | | | | F | | $T$F = | <!e!, d> F | | | | | | | | | v v v o------------------>o============o X% $T$ $T$X% $T$X% Figure 34. Tangent Functor Diagram
Note. The following image was corrupted in transit between software platforms.
Figure 35. Conjunction as Transformation
o---------------------------------------o
| |
| |
| o---------o o---------o |
| / \ / \ |
| / o \ |
| / /`\ \ |
| / /```\ \ |
| o o`````o o |
| | |`````| | |
| | u |`````| v | |
| | |`````| | |
| o o`````o o |
| \ \```/ / |
| \ \`/ / |
| \ o / |
| \ / \ / |
| o---------o o---------o |
| |
| |
o---------------------------------------o
\ /
\ /
\ /
\ J /
\ /
\ /
\ /
o--------------\---------/--------------o
| \ / |
| \ / |
| o------@------o |
| /```````````````\ |
| /`````````````````\ |
| /```````````````````\ |
| /`````````````````````\ |
| o```````````````````````o |
| |```````````````````````| |
| |`````````` x ``````````| |
| |```````````````````````| |
| o```````````````````````o |
| \`````````````````````/ |
| \```````````````````/ |
| \`````````````````/ |
| \```````````````/ |
| o-------------o |
| |
| |
o---------------------------------------o
Figure 35. Conjunction as Transformation
Table 36. Computation of !e!J
Table 36. Computation of !e!J o---------------------------------------------------------------------o | | | !e!J = J<u, v> | | | | = u v | | | | = u v (du)(dv) + u v (du) dv + u v du (dv) + u v du dv | | | o---------------------------------------------------------------------o | | | !e!J = u v (du)(dv) + | | u v (du) dv + | | u v du (dv) + | | u v du dv | | | o---------------------------------------------------------------------o
| ||||||||||||||||||||
|
Figure 37-a. Tacit Extension of J (Areal)
o---------------------------------------o | | | o | | /%\ | | /%%%\ | | /%%%%%\ | | o%%%%%%%o | | /%\%%%%%/%\ | | /%%%\%%%/%%%\ | | /%%%%%\%/%%%%%\ | | o%%%%%%%o%%%%%%%o | | / \%%%%%/%\%%%%%/ \ | | / \%%%/%%%\%%%/ \ | | / \%/%%%%%\%/ \ | | o o%%%%%%%o o | | / \ / \%%%%%/ \ / \ | | / \ / \%%%/ \ / \ | | / \ / \%/ \ / \ | | o o o o o | | |\ / \ / \ / \ /| | | | \ / \ / \ / \ / | | | | \ / \ / \ / \ / | | | | o o o o | | | | |\ / \ / \ /| | | | | | \ / \ / \ / | | | | | u | \ / \ / \ / | v | | | o---+---o o o---+---o | | | \ / \ / | | | | \ / \ / | | | | du \ / \ / dv | | | o-------o o-------o | | \ / | | \ / | | \ / | | o | | | o---------------------------------------o Figure 37-a. Tacit Extension of J (Areal)
Figure 37-b. Tacit Extension of J (Bundle)
o-----------------------------o
| |
| o-----o o-----o |
| / \ / \ |
| / o \ |
| / / \ \ |
| o o o o |
@ | du | | dv | |
/| o o o o |
/ | \ \ / / |
/ | \ o / |
/ | \ / \ / |
/ | o-----o o-----o |
/ | |
/ o-----------------------------o
/
o----------------------------------------/----o o-----------------------------o
| / | | |
| @ | | o-----o o-----o |
| | | / \ / \ |
| o---------o o---------o | | / o \ |
| / \ / \ | | / / \ \ |
| / o \ | | o o o o |
| / /`\ @------\-----------@ | du | | dv | |
| / /```\ \ | | o o o o |
| / /`````\ \ | | \ \ / / |
| / /```````\ \ | | \ o / |
| o o`````````o o | | \ / \ / |
| | |````@````| | | | o-----o o-----o |
| | |`````\```| | | | |
| | |``````\``| | | o-----------------------------o
| | u |```````\`| v | |
| | |````````\| | | o-----------------------------o
| | |`````````| | | | |
| | |`````````|\ | | | o-----o o-----o |
| o o`````````o \ o | | / \ / \ |
| \ \```````/ \ / | | / o \ |
| \ \`````/ \ / | | / / \ \ |
| \ \```/ \ / | | o o o o |
| \ @------\-/---------\---------------@ | du | | dv | |
| \ o \ / | | o o o o |
| \ / \ / | | \ \ / / |
| o---------o o---------o \ | | \ o / |
| \ | | \ / \ / |
| \ | | o-----o o-----o |
| \ | | |
o----------------------------------------\----o o-----------------------------o
\
\ o-----------------------------o
\ |`````````````````````````````|
\ |````` o-----o```o-----o``````|
\ |`````/```````\`/```````\`````|
\ |````/`````````o`````````\````|
\ |```/`````````/`\`````````\```|
\|``o`````````o```o`````````o``|
@``|```du````|```|````dv```|``|
|``o`````````o```o`````````o``|
|```\`````````\`/`````````/```|
|````\`````````o`````````/````|
|`````\```````/`\```````/`````|
|``````o-----o```o-----o``````|
|`````````````````````````````|
o-----------------------------o
Figure 37-b. Tacit Extension of J (Bundle)
Figure 37-c. Tacit Extension of J (Compact)
o---------------------------------------------------------------------o | | | | | o-------------------o o-------------------o | | / \ / \ | | / o \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | o o (du).(dv) o o | | | | -->-- | | | | | | \ / | | | | | dv .(du) | \ / | du .(dv) | | | | u <---------------@---------------> v | | | | | | | | | | | | | | | | | | | | | | | | o o | o o | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \|/ / | | \ | / | | \ /|\ / | | o-------------------o | o-------------------o | | | | | du . dv | | | | | V | | | o---------------------------------------------------------------------o Figure 37-c. Tacit Extension of J (Compact)
Figure 37-d. Tacit Extension of J (Digraph)
o-----------------------------------------------------------o | | | (du).(dv) | | --->--- | | \ / | | \ / | | \ / | | u @ v | | /|\ | | / | \ | | / | \ | | / | \ | | / | \ | | (du) dv / | \ du (dv) | | / | \ | | / | \ | | / | \ | | / | \ | | v | v | | @ | @ | | u (v) | (u) v | | | | | | | | | | | | | | du . dv | | | | | | | | | | | | | | v | | @ | | | | (u).(v) | | | o-----------------------------------------------------------o Figure 37-d. Tacit Extension of J (Digraph)
Table 38. Computation of EJ (Method 1)
Table 38. Computation of EJ (Method 1) o-------------------------------------------------------------------------------o | | | EJ = J<u + du, v + dv> | | | | = (u, du)(v, dv) | | | | = u v J<1 + du, 1 + dv> + | | | | u (v) J<1 + du, 0 + dv> + | | | | (u) v J<0 + du, 1 + dv> + | | | | (u)(v) J<0 + du, 0 + dv> | | | | = u v J<(du), (dv)> + | | | | u (v) J<(du), dv > + | | | | (u) v J< du , (dv)> + | | | | (u)(v) J< du , dv > | | | o-------------------------------------------------------------------------------o | | | EJ = u v (du)(dv) | | + u (v)(du) dv | | + (u) v du (dv) | | + (u)(v) du dv | | | o-------------------------------------------------------------------------------o
| |||||||||||||||||||||||||||||||||||||||||||
|
Table 39. Computation of EJ (Method 2)
Table 39. Computation of EJ (Method 2) o-------------------------------------------------------------------------------o | | | EJ = <u + du> <v + dv> | | | | = u v + u dv + v du + du dv | | | | EJ = u v (du)(dv) + u (v)(du) dv + (u) v du (dv) + (u)(v) du dv | | | o-------------------------------------------------------------------------------o
| |||||||||||||||||
Figure 40-a. Enlargement of J (Areal)
o---------------------------------------o | | | o | | /%\ | | /%%%\ | | /%%%%%\ | | o%%%%%%%o | | / \%%%%%/ \ | | / \%%%/ \ | | / \%/ \ | | o o o | | /%\ / \ /%\ | | /%%%\ / \ /%%%\ | | /%%%%%\ / \ /%%%%%\ | | o%%%%%%%o o%%%%%%%o | | / \%%%%%/ \ / \%%%%%/ \ | | / \%%%/ \ / \%%%/ \ | | / \%/ \ / \%/ \ | | o o o o o | | |\ / \ /%\ / \ /| | | | \ / \ /%%%\ / \ / | | | | \ / \ /%%%%%\ / \ / | | | | o o%%%%%%%o o | | | | |\ / \%%%%%/ \ /| | | | | | \ / \%%%/ \ / | | | | | u | \ / \%/ \ / | v | | | o---+---o o o---+---o | | | \ / \ / | | | | \ / \ / | | | | du \ / \ / dv | | | o-------o o-------o | | \ / | | \ / | | \ / | | o | | | o---------------------------------------o Figure 40-a. Enlargement of J (Areal)
Figure 40-b. Enlargement of J (Bundle)
o-----------------------------o
| |
| o-----o o-----o |
| / \ / \ |
| / o \ |
| / /%\ \ |
| o o%%%o o |
@ | du |%%%| dv | |
/| o o%%%o o |
/ | \ \%/ / |
/ | \ o / |
/ | \ / \ / |
/ | o-----o o-----o |
/ | |
/ o-----------------------------o
/
o----------------------------------------/----o o-----------------------------o
| / | | |
| @ | | o-----o o-----o |
| | | /%%%%%%%\ / \ |
| o---------o o---------o | | /%%%%%%%%%o \ |
| / \ / \ | | /%%%%%%%%%/ \ \ |
| / o \ | | o%%%%%%%%%o o o |
| / /`\ @------\-----------@ |%% du %%%| | dv | |
| / /```\ \ | | o%%%%%%%%%o o o |
| / /`````\ \ | | \%%%%%%%%%\ / / |
| / /```````\ \ | | \%%%%%%%%%o / |
| o o`````````o o | | \%%%%%%%/ \ / |
| | |````@````| | | | o-----o o-----o |
| | |`````\```| | | | |
| | |``````\``| | | o-----------------------------o
| | u |```````\`| v | |
| | |````````\| | | o-----------------------------o
| | |`````````| | | | |
| | |`````````|\ | | | o-----o o-----o |
| o o`````````o \ o | | / \ /%%%%%%%\ |
| \ \```````/ \ / | | / o%%%%%%%%%\ |
| \ \`````/ \ / | | / / \%%%%%%%%%\ |
| \ \```/ \ / | | o o o%%%%%%%%%o |
| \ @------\-/---------\---------------@ | du | |%%% dv %%| |
| \ o \ / | | o o o%%%%%%%%%o |
| \ / \ / | | \ \ /%%%%%%%%%/ |
| o---------o o---------o \ | | \ o%%%%%%%%%/ |
| \ | | \ / \%%%%%%%/ |
| \ | | o-----o o-----o |
| \ | | |
o----------------------------------------\----o o-----------------------------o
\
\ o-----------------------------o
\ |%%%%%%%%%%%%%%%%%%%%%%%%%%%%%|
\ |%%%%%%o-----o%%%o-----o%%%%%%|
\ |%%%%%/ \%/ \%%%%%|
\ |%%%%/ o \%%%%|
\ |%%%/ / \ \%%%|
\|%%o o o o%%|
@%%| du | | dv |%%|
|%%o o o o%%|
|%%%\ \ / /%%%|
|%%%%\ o /%%%%|
|%%%%%\ /%\ /%%%%%|
|%%%%%%o-----o%%%o-----o%%%%%%|
|%%%%%%%%%%%%%%%%%%%%%%%%%%%%%|
o-----------------------------o
Figure 40-b. Enlargement of J (Bundle)
Figure 40-c. Enlargement of J (Compact)
o---------------------------------------------------------------------o | | | | | o-------------------o o-------------------o | | / \ / \ | | / o \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | o o (du).(dv) o o | | | | -->-- | | | | | | \ / | | | | | dv .(du) | \ / | du .(dv) | | | | u o---------------->@<----------------o v | | | | | ^ | | | | | | | | | | | | | | | | | | o o | o o | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \|/ / | | \ | / | | \ /|\ / | | o-------------------o | o-------------------o | | | | | du . dv | | | | | o | | | o---------------------------------------------------------------------o Figure 40-c. Enlargement of J (Compact)
Figure 40-d. Enlargement of J (Digraph)
o-----------------------------------------------------------o | | | (du).(dv) | | --->--- | | \ / | | \ / | | \ / | | u @ v | | ^^^ | | / | \ | | / | \ | | / | \ | | / | \ | | (du) dv / | \ du (dv) | | / | \ | | / | \ | | / | \ | | / | \ | | / | \ | | @ | @ | | u (v) | (u) v | | | | | | | | | | | | | | du . dv | | | | | | | | | | | | | | | | | @ | | | | (u).(v) | | | o-----------------------------------------------------------o Figure 40-d. Enlargement of J (Digraph)
Table 41. Computation of DJ (Method 1)
Table 41. Computation of DJ (Method 1) o-------------------------------------------------------------------------------o | | | DJ = EJ + !e!J | | | | = J<u + du, v + dv> + J<u, v> | | | | = (u, du)(v, dv) + u v | | | o-------------------------------------------------------------------------------o | | | DJ = 0 | | | | + u v (du) dv + u (v)(du) dv | | | | + u v du (dv) + (u) v du (dv) | | | | + u v du dv + (u)(v) du dv | | | o-------------------------------------------------------------------------------o | | | DJ = u v ((du)(dv)) + u (v)(du) dv + (u) v du (dv) + (u)(v) du dv | | | o-------------------------------------------------------------------------------o
| ||||||||||||||||||||||||
| ||||||||||||||||||||||||
|
Table 42. Computation of DJ (Method 2)
Table 42. Computation of DJ (Method 2) o-------------------------------------------------------------------------------o | | | DJ = !e!J + EJ | | | | = J<u, v> + J<u + du, v + dv> | | | | = u v + (u, du)(v, dv) | | | | = 0 + u dv + v du + du dv | | | | = 0 + u (du) dv + v du (dv) + ((u, v)) du dv | | | o-------------------------------------------------------------------------------o
| |||||||||||||||||||||||||||||||||||||||||||||
Table 43. Computation of DJ (Method 3)
Table 43. Computation of DJ (Method 3) o-------------------------------------------------------------------------------o | | | DJ = !e!J + EJ | | | o-------------------------------------------------------------------------------o | | | !e!J = u v (du)(dv) + u v (du) dv + u v du (dv) + u v du dv | | | | EJ = u v (du)(dv) + u (v)(du) dv + (u) v du (dv) + (u)(v) du dv | | | o-------------------------------------------------------------------------------o | | | DJ = 0 . (du)(dv) + u . (du) dv + v . du (dv) + ((u, v)) du dv | | | o-------------------------------------------------------------------------------o
| ||||||||||
| ||||||||||
|
Formula Display 8
o-------------------------------------------------------------------------------o
| |
| !e!J = {Dispositions from J to J } + {Dispositions from J to (J)} |
| |
| EJ = {Dispositions from J to J } + {Dispositions from (J) to J } |
| |
| DJ = (!e!J, EJ) |
| |
| DJ = {Dispositions from J to (J)} + {Dispositions from (J) to J } |
| |
o-------------------------------------------------------------------------------o
|
Figure 44-a. Difference Map of J (Areal)
o---------------------------------------o | | | o | | / \ | | / \ | | / \ | | o o | | /%\ /%\ | | /%%%\ /%%%\ | | /%%%%%\ /%%%%%\ | | o%%%%%%%o%%%%%%%o | | /%\%%%%%/%\%%%%%/%\ | | /%%%\%%%/%%%\%%%/%%%\ | | /%%%%%\%/%%%%%\%/%%%%%\ | | o%%%%%%%o%%%%%%%o%%%%%%%o | | / \%%%%%/ \%%%%%/ \%%%%%/ \ | | / \%%%/ \%%%/ \%%%/ \ | | / \%/ \%/ \%/ \ | | o o o o o | | |\ / \ /%\ / \ /| | | | \ / \ /%%%\ / \ / | | | | \ / \ /%%%%%\ / \ / | | | | o o%%%%%%%o o | | | | |\ / \%%%%%/ \ /| | | | | | \ / \%%%/ \ / | | | | | u | \ / \%/ \ / | v | | | o---+---o o o---+---o | | | \ / \ / | | | | \ / \ / | | | | du \ / \ / dv | | | o-------o o-------o | | \ / | | \ / | | \ / | | o | | | o---------------------------------------o Figure 44-a. Difference Map of J (Areal)
Figure 44-b. Difference Map of J (Bundle)
o-----------------------------o
| |
| o-----o o-----o |
| / \ / \ |
| / o \ |
| / /%\ \ |
| o o%%%o o |
@ | du |%%%| dv | |
/| o o%%%o o |
/ | \ \%/ / |
/ | \ o / |
/ | \ / \ / |
/ | o-----o o-----o |
/ | |
/ o-----------------------------o
/
o----------------------------------------/----o o-----------------------------o
| / | | |
| @ | | o-----o o-----o |
| | | /%%%%%%%\ / \ |
| o---------o o---------o | | /%%%%%%%%%o \ |
| / \ / \ | | /%%%%%%%%%/ \ \ |
| / o \ | | o%%%%%%%%%o o o |
| / /`\ @------\-----------@ |%% du %%%| | dv | |
| / /```\ \ | | o%%%%%%%%%o o o |
| / /`````\ \ | | \%%%%%%%%%\ / / |
| / /```````\ \ | | \%%%%%%%%%o / |
| o o`````````o o | | \%%%%%%%/ \ / |
| | |````@````| | | | o-----o o-----o |
| | |`````\```| | | | |
| | |``````\``| | | o-----------------------------o
| | u |```````\`| v | |
| | |````````\| | | o-----------------------------o
| | |`````````| | | | |
| | |`````````|\ | | | o-----o o-----o |
| o o`````````o \ o | | / \ /%%%%%%%\ |
| \ \```````/ \ / | | / o%%%%%%%%%\ |
| \ \`````/ \ / | | / / \%%%%%%%%%\ |
| \ \```/ \ / | | o o o%%%%%%%%%o |
| \ @------\-/---------\---------------@ | du | |%%% dv %%| |
| \ o \ / | | o o o%%%%%%%%%o |
| \ / \ / | | \ \ /%%%%%%%%%/ |
| o---------o o---------o \ | | \ o%%%%%%%%%/ |
| \ | | \ / \%%%%%%%/ |
| \ | | o-----o o-----o |
| \ | | |
o----------------------------------------\----o o-----------------------------o
\
\ o-----------------------------o
\ | |
\ | o-----o o-----o |
\ | /%%%%%%%\ /%%%%%%%\ |
\ | /%%%%%%%%%o%%%%%%%%%\ |
\ | /%%%%%%%%%/%\%%%%%%%%%\ |
\| o%%%%%%%%%o%%%o%%%%%%%%%o |
@ |%% du %%%|%%%|%%% dv %%| |
| o%%%%%%%%%o%%%o%%%%%%%%%o |
| \%%%%%%%%%\%/%%%%%%%%%/ |
| \%%%%%%%%%o%%%%%%%%%/ |
| \%%%%%%%/ \%%%%%%%/ |
| o-----o o-----o |
| |
o-----------------------------o
Figure 44-b. Difference Map of J (Bundle)
Figure 44-c. Difference Map of J (Compact)
o---------------------------------------------------------------------o | | | | | o-------------------o o-------------------o | | / \ / \ | | / o \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | o o o o | | | | | | | | | | | | | | | dv .(du) | | du .(dv) | | | | u @<--------------->@<--------------->@ v | | | | | ^ | | | | | | | | | | | | | | | | | | o o | o o | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \|/ / | | \ | / | | \ /|\ / | | o-------------------o | o-------------------o | | | | | du . dv | | | | | v | | @ | | | o---------------------------------------------------------------------o Figure 44-c. Difference Map of J (Compact)
Figure 44-d. Difference Map of J (Digraph)
o-----------------------------------------------------------o | | | u v | | | | @ | | ^^^ | | / | \ | | / | \ | | / | \ | | / | \ | | (du) dv / | \ du (dv) | | / | \ | | / | \ | | / | \ | | / | \ | | v | v | | @ | @ | | u (v) | (u) v | | | | | | | | | | | | | | du | dv | | | | | | | | | | | | | | v | | @ | | | | (u) (v) | | | o-----------------------------------------------------------o Figure 44-d. Difference Map of J (Digraph)
Table 45. Computation of dJ
Table 45. Computation of dJ o-------------------------------------------------------------------------------o | | | DJ = u v ((du)(dv)) + u (v)(du) dv + (u) v du (dv) + (u)(v) du dv | | | | => | | | | dJ = u v (du, dv) + u (v) dv + (u) v du + (u)(v) . 0 | | | o-------------------------------------------------------------------------------o
|
Figure 46-a. Differential of J (Areal)
o---------------------------------------o | | | o | | / \ | | / \ | | / \ | | o o | | /%\ /%\ | | /%%%\ /%%%\ | | /%%%%%\ /%%%%%\ | | o%%%%%%%o%%%%%%%o | | /%\%%%%%/ \%%%%%/%\ | | /%%%\%%%/ \%%%/%%%\ | | /%%%%%\%/ \%/%%%%%\ | | o%%%%%%%o o%%%%%%%o | | / \%%%%%/%\ /%\%%%%%/ \ | | / \%%%/%%%\ /%%%\%%%/ \ | | / \%/%%%%%\ /%%%%%\%/ \ | | o o%%%%%%%o%%%%%%%o o | | |\ / \%%%%%/ \%%%%%/ \ /| | | | \ / \%%%/ \%%%/ \ / | | | | \ / \%/ \%/ \ / | | | | o o o o | | | | |\ / \ / \ /| | | | | | \ / \ / \ / | | | | | u | \ / \ / \ / | v | | | o---+---o o o---+---o | | | \ / \ / | | | | \ / \ / | | | | du \ / \ / dv | | | o-------o o-------o | | \ / | | \ / | | \ / | | o | | | o---------------------------------------o Figure 46-a. Differential of J (Areal)
Figure 46-b. Differential of J (Bundle)
o-----------------------------o
| |
| o-----o o-----o |
| / \ / \ |
| / o \ |
| / / \ \ |
| o o o o |
@ | du | | dv | |
/| o o o o |
/ | \ \ / / |
/ | \ o / |
/ | \ / \ / |
/ | o-----o o-----o |
/ | |
/ o-----------------------------o
/
o----------------------------------------/----o o-----------------------------o
| / | | |
| @ | | o-----o o-----o |
| | | /%%%%%%%\ / \ |
| o---------o o---------o | | /%%%%%%%%%o \ |
| / \ / \ | | /%%%%%%%%%/%\ \ |
| / o \ | | o%%%%%%%%%o%%%o o |
| / /`\ @------\-----------@ |%% du %%%|%%%| dv | |
| / /```\ \ | | o%%%%%%%%%o%%%o o |
| / /`````\ \ | | \%%%%%%%%%\%/ / |
| / /```````\ \ | | \%%%%%%%%%o / |
| o o`````````o o | | \%%%%%%%/ \ / |
| | |````@````| | | | o-----o o-----o |
| | |`````\```| | | | |
| | |``````\``| | | o-----------------------------o
| | u |```````\`| v | |
| | |````````\| | | o-----------------------------o
| | |`````````| | | | |
| | |`````````|\ | | | o-----o o-----o |
| o o`````````o \ o | | / \ /%%%%%%%\ |
| \ \```````/ \ / | | / o%%%%%%%%%\ |
| \ \`````/ \ / | | / /%\%%%%%%%%%\ |
| \ \```/ \ / | | o o%%%o%%%%%%%%%o |
| \ @------\-/---------\---------------@ | du |%%%|%%% dv %%| |
| \ o \ / | | o o%%%o%%%%%%%%%o |
| \ / \ / | | \ \%/%%%%%%%%%/ |
| o---------o o---------o \ | | \ o%%%%%%%%%/ |
| \ | | \ / \%%%%%%%/ |
| \ | | o-----o o-----o |
| \ | | |
o----------------------------------------\----o o-----------------------------o
\
\ o-----------------------------o
\ | |
\ | o-----o o-----o |
\ | /%%%%%%%\ /%%%%%%%\ |
\ | /%%%%%%%%%o%%%%%%%%%\ |
\ | /%%%%%%%%%/ \%%%%%%%%%\ |
\| o%%%%%%%%%o o%%%%%%%%%o |
@ |%% du %%%| |%%% dv %%| |
| o%%%%%%%%%o o%%%%%%%%%o |
| \%%%%%%%%%\ /%%%%%%%%%/ |
| \%%%%%%%%%o%%%%%%%%%/ |
| \%%%%%%%/ \%%%%%%%/ |
| o-----o o-----o |
| |
o-----------------------------o
Figure 46-b. Differential of J (Bundle)
Figure 46-c. Differential of J (Compact)
o---------------------------------------------------------------------o | | | | | o-------------------o o-------------------o | | / \ / \ | | / o \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / @ \ \ | | / / ^ ^ \ \ | | o o / \ o o | | | | / \ | | | | | | / \ | | | | | |/ \| | | | | u (du)/ dv du \(dv) v | | | | /| |\ | | | | / | | \ | | | | / | | \ | | | o / o o \ o | | \ / \ / \ / | | \ v \ du dv / v / | | \ @<----------------------->@ / | | \ \ / / | | \ \ / / | | \ o / | | \ / \ / | | o-------------------o o-------------------o | | | | | o---------------------------------------------------------------------o Figure 46-c. Differential of J (Compact)
Figure 46-d. Differential of J (Digraph)
o-----------------------------------------------------------o | | | u v | | @ | | ^ ^ | | / \ | | / \ | | / \ | | / \ | | (du) dv / \ du (dv) | | / \ | | / \ | | / \ | | / \ | | v v | | u (v) @<--------------------->@ (u) v | | du dv | | | | | | | | | | | | | | | | | | | | | | @ | | (u) (v) | | | o-----------------------------------------------------------o Figure 46-d. Differential of J (Digraph)
Table 47. Computation of rJ
Table 47. Computation of rJ o-------------------------------------------------------------------------------o | | | rJ = DJ + dJ | | | o-------------------------------------------------------------------------------o | | | DJ = u v ((du)(dv)) + u (v)(du) dv + (u) v du (dv) + (u)(v) du dv | | | | dJ = u v (du, dv) + u (v) dv + (u) v du + (u)(v) . 0 | | | o-------------------------------------------------------------------------------o | | | rJ = u v du dv + u (v) du dv + (u) v du dv + (u)(v) du dv | | | o-------------------------------------------------------------------------------o
| ||||||||||
| ||||||||||
|
Figure 48-a. Remainder of J (Areal)
o---------------------------------------o | | | o | | / \ | | / \ | | / \ | | o o | | / \ / \ | | / \ / \ | | / \ / \ | | o o o | | / \ /%\ / \ | | / \ /%%%\ / \ | | / \ /%%%%%\ / \ | | o o%%%%%%%o o | | / \ /%\%%%%%/%\ / \ | | / \ /%%%\%%%/%%%\ / \ | | / \ /%%%%%\%/%%%%%\ / \ | | o o%%%%%%%o%%%%%%%o o | | |\ / \%%%%%/%\%%%%%/ \ /| | | | \ / \%%%/%%%\%%%/ \ / | | | | \ / \%/%%%%%\%/ \ / | | | | o o%%%%%%%o o | | | | |\ / \%%%%%/ \ /| | | | | | \ / \%%%/ \ / | | | | | u | \ / \%/ \ / | v | | | o---+---o o o---+---o | | | \ / \ / | | | | \ / \ / | | | | du \ / \ / dv | | | o-------o o-------o | | \ / | | \ / | | \ / | | o | | | o---------------------------------------o Figure 48-a. Remainder of J (Areal)
Figure 48-b. Remainder of J (Bundle)
o-----------------------------o
| |
| o-----o o-----o |
| / \ / \ |
| / o \ |
| / /%\ \ |
| o o%%%o o |
@ | du |%%%| dv | |
/| o o%%%o o |
/ | \ \%/ / |
/ | \ o / |
/ | \ / \ / |
/ | o-----o o-----o |
/ | |
/ o-----------------------------o
/
o----------------------------------------/----o o-----------------------------o
| / | | |
| @ | | o-----o o-----o |
| | | / \ / \ |
| o---------o o---------o | | / o \ |
| / \ / \ | | / /%\ \ |
| / o \ | | o o%%%o o |
| / /`\ @------\-----------@ | du |%%%| dv | |
| / /```\ \ | | o o%%%o o |
| / /`````\ \ | | \ \%/ / |
| / /```````\ \ | | \ o / |
| o o`````````o o | | \ / \ / |
| | |````@````| | | | o-----o o-----o |
| | |`````\```| | | | |
| | |``````\``| | | o-----------------------------o
| | u |```````\`| v | |
| | |````````\| | | o-----------------------------o
| | |`````````| | | | |
| | |`````````|\ | | | o-----o o-----o |
| o o`````````o \ o | | / \ / \ |
| \ \```````/ \ / | | / o \ |
| \ \`````/ \ / | | / /%\ \ |
| \ \```/ \ / | | o o%%%o o |
| \ @------\-/---------\---------------@ | du |%%%| dv | |
| \ o \ / | | o o%%%o o |
| \ / \ / | | \ \%/ / |
| o---------o o---------o \ | | \ o / |
| \ | | \ / \ / |
| \ | | o-----o o-----o |
| \ | | |
o----------------------------------------\----o o-----------------------------o
\
\ o-----------------------------o
\ | |
\ | o-----o o-----o |
\ | / \ / \ |
\ | / o \ |
\ | / /%\ \ |
\| o o%%%o o |
@ | du |%%%| dv | |
| o o%%%o o |
| \ \%/ / |
| \ o / |
| \ / \ / |
| o-----o o-----o |
| |
o-----------------------------o
Figure 48-b. Remainder of J (Bundle)
Figure 48-c. Remainder of J (Compact)
o---------------------------------------------------------------------o | | | | | o-------------------o o-------------------o | | / \ / \ | | / o \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | / / \ \ | | o o o o | | | | | | | | | | | | | | | | du dv | | | | | u @<------------------------->@ v | | | | | | | | | | | | | | | | | | | | | o o @ o o | | \ \ ^ / / | | \ \ | / / | | \ \ | / / | | \ \ | / / | | \ \|/ / | | \ du | dv / | | \ /|\ / | | o-------------------o | o-------------------o | | | | | | | | v | | @ | | | o---------------------------------------------------------------------o Figure 48-c. Remainder of J (Compact)
Figure 48-d. Remainder of J (Digraph)
o-----------------------------------------------------------o | | | u v | | @ | | ^ | | | | | | | | | | | | | | | | | | | | | | | | | | | | | du | dv | | u (v) @<----------|---------->@ (u) v | | du | dv | | | | | | | | | | | | | | | | | | | | | | | | | | | | | v | | @ | | (u) (v) | | | o-----------------------------------------------------------o Figure 48-d. Remainder of J (Digraph)
Table 49. Computation Summary for J
Table 49. Computation Summary for J o-------------------------------------------------------------------------------o | | | !e!J = uv . 1 + u(v) . 0 + (u)v . 0 + (u)(v) . 0 | | | | EJ = uv . (du)(dv) + u(v) . (du)dv + (u)v . du(dv) + (u)(v) . du dv | | | | DJ = uv . ((du)(dv)) + u(v) . (du)dv + (u)v . du(dv) + (u)(v) . du dv | | | | dJ = uv . (du, dv) + u(v) . dv + (u)v . du + (u)(v) . 0 | | | | rJ = uv . du dv + u(v) . du dv + (u)v . du dv + (u)(v) . du dv | | | o-------------------------------------------------------------------------------o
|
Table 50. Computation of an Analytic Series in Terms of Coordinates
Table 50. Computation of an Analytic Series in Terms of Coordinates o-----------o-------------o-------------oo-------------o---------o-------------o | u v | du dv | u' v' || !e!J EJ | DJ | dJ d^2.J | o-----------o-------------o-------------oo-------------o---------o-------------o | | | || | | | | 0 0 | 0 0 | 0 0 || 0 0 | 0 | 0 0 | | | | || | | | | | 0 1 | 0 1 || 0 | 0 | 0 0 | | | | || | | | | | 1 0 | 1 0 || 0 | 0 | 0 0 | | | | || | | | | | 1 1 | 1 1 || 1 | 1 | 0 1 | | | | || | | | o-----------o-------------o-------------oo-------------o---------o-------------o | | | || | | | | 0 1 | 0 0 | 0 1 || 0 0 | 0 | 0 0 | | | | || | | | | | 0 1 | 0 0 || 0 | 0 | 0 0 | | | | || | | | | | 1 0 | 1 1 || 1 | 1 | 1 0 | | | | || | | | | | 1 1 | 1 0 || 0 | 0 | 1 1 | | | | || | | | o-----------o-------------o-------------oo-------------o---------o-------------o | | | || | | | | 1 0 | 0 0 | 1 0 || 0 0 | 0 | 0 0 | | | | || | | | | | 0 1 | 1 1 || 1 | 1 | 1 0 | | | | || | | | | | 1 0 | 0 0 || 0 | 0 | 0 0 | | | | || | | | | | 1 1 | 0 1 || 0 | 0 | 1 1 | | | | || | | | o-----------o-------------o-------------oo-------------o---------o-------------o | | | || | | | | 1 1 | 0 0 | 1 1 || 1 1 | 0 | 0 0 | | | | || | | | | | 0 1 | 1 0 || 0 | 1 | 1 0 | | | | || | | | | | 1 0 | 0 1 || 0 | 1 | 1 0 | | | | || | | | | | 1 1 | 0 0 || 0 | 1 | 0 1 | | | | || | | | o-----------o-------------o-------------oo-------------o---------o-------------o
|
|
Formula Display 9
o-------------------------------------------------o | | | u' = u + du = (u, du) | | | | v' = v + du = (v, dv) | | | o-------------------------------------------------o
|
Formula Display 10
o--------------------------------------------------------------o | | | EJ<u, v, du, dv> = J<u + du, v + dv> = J<u', v'> | | | o--------------------------------------------------------------o
|
Table 51. Computation of an Analytic Series in Symbolic Terms
Table 51. Computation of an Analytic Series in Symbolic Terms o-----------o---------o------------o------------o------------o-----------o | u v | J | EJ | DJ | dJ | d^2.J | o-----------o---------o------------o------------o------------o-----------o | | | | | | | | 0 0 | 0 | du dv | du dv | () | du dv | | | | | | | | | 0 1 | 0 | du (dv) | du (dv) | du | du dv | | | | | | | | | 1 0 | 0 | (du) dv | (du) dv | dv | du dv | | | | | | | | | 1 1 | 1 | (du)(dv) | ((du)(dv)) | (du, dv) | du dv | | | | | | | | o-----------o---------o------------o------------o------------o-----------o
|
|
|
|
|
| ||||||||||||||||||||||||||||
|
|
|
|
|
|
Figure 52. Decomposition of the Enlarged Conjunction EJ = (J, DJ)
o o o
/%\ /%\ / \
/%%%\ /%%%\ / \
o%%%%%o o%%%%%o o o
/ \%%%/ \ /%\%%%/%\ /%\ /%\
/ \%/ \ /%%%\%/%%%\ /%%%\ /%%%\
o o o o%%%%%o%%%%%o o%%%%%o%%%%%o
/%\ / \ /%\ / \%%%/%\%%%/ \ /%\%%%/%\%%%/%\
/%%%\ / \ /%%%\ / \%/%%%\%/ \ /%%%\%/%%%\%/%%%\
o%%%%%o o%%%%%o o o%%%%%o o o%%%%%o%%%%%o%%%%%o
/ \%%%/ \ / \%%%/ \ / \ / \%%%/ \ / \ / \%%%/ \%%%/ \%%%/ \
/ \%/ \ / \%/ \ / \ / \%/ \ / \ / \%/ \%/ \%/ \
o o o o o o o o o o o o o o o
|\ / \ /%\ / \ /| |\ / \ / \ / \ /| |\ / \ /%\ / \ /|
| \ / \ /%%%\ / \ / | | \ / \ / \ / \ / | | \ / \ /%%%\ / \ / |
| o o%%%%%o o | | o o o o | | o o%%%%%o o |
| |\ / \%%%/ \ /| | | |\ / \ / \ /| | | |\ / \%%%/ \ /| |
|u | \ / \%/ \ / | v| |u | \ / \ / \ / | v| |u | \ / \%/ \ / | v|
o--+--o o o--+--o o--+--o o o--+--o o--+--o o o--+--o
| \ / \ / | | \ / \ / | | \ / \ / |
| du \ / \ / dv | | du \ / \ / dv | | du \ / \ / dv |
o-----o o-----o o-----o o-----o o-----o o-----o
\ / \ / \ /
\ / \ / \ /
o o o
EJ = J + DJ
o-----------------------o o-----------------------o o-----------------------o
| | | | | |
| o--o o--o | | o--o o--o | | o--o o--o |
| / \ / \ | | / \ / \ | | / \ / \ |
| / o \ | | / o \ | | / o \ |
| / u / \ v \ | | / u / \ v \ | | / u / \ v \ |
| o /->-\ o | | o /->-\ o | | o / \ o |
| | o \ / o | | | | o \ / o | | | | o o | |
| | @--|->@<-|--@ | | | | @<-|--@--|->@ | | | | @<-|->@<-|->@ | |
| | o ^ o | | | | o | o | | | | o ^ o | |
| o \ | / o | | o \ | / o | | o \ | / o |
| \ \|/ / | | \ \|/ / | | \ \|/ / |
| \ | / | | \ | / | | \ | / |
| \ /|\ / | | \ /|\ / | | \ /|\ / |
| o--o | o--o | | o--o v o--o | | o--o v o--o |
| @ | | @ | | @ |
o-----------------------o o-----------------------o o-----------------------o
Figure 52. Decomposition of the Enlarged Conjunction EJ = (J, DJ)
Figure 53. Decomposition of the Differed Conjunction DJ = (dJ, ddJ)
o o o
/ \ / \ / \
/ \ / \ / \
o o o o o o
/%\ /%\ /%\ /%\ / \ / \
/%%%\ /%%%\ /%%%\%/%%%\ / \ / \
o%%%%%o%%%%%o o%%%%%o%%%%%o o o o
/%\%%%/%\%%%/%\ /%\%%%/ \%%%/%\ / \ /%\ / \
/%%%\%/%%%\%/%%%\ /%%%\%/ \%/%%%\ / \ /%%%\ / \
o%%%%%o%%%%%o%%%%%o o%%%%%o o%%%%%o o o%%%%%o o
/ \%%%/ \%%%/ \%%%/ \ / \%%%/%\ /%\%%%/ \ / \ /%\%%%/%\ / \
/ \%/ \%/ \%/ \ / \%/%%%\ /%%%\%/ \ / \ /%%%\%/%%%\ / \
o o o o o o o%%%%%o%%%%%o o o o%%%%%o%%%%%o o
|\ / \ /%\ / \ /| |\ / \%%%/ \%%%/ \ /| |\ / \%%%/%\%%%/ \ /|
| \ / \ /%%%\ / \ / | | \ / \%/ \%/ \ / | | \ / \%/%%%\%/ \ / |
| o o%%%%%o o | | o o o o | | o o%%%%%o o |
| |\ / \%%%/ \ /| | | |\ / \ / \ /| | | |\ / \%%%/ \ /| |
|u | \ / \%/ \ / | v| |u | \ / \ / \ / | v| |u | \ / \%/ \ / | v|
o--+--o o o--+--o o--+--o o o--+--o o--+--o o o--+--o
| \ / \ / | | \ / \ / | | \ / \ / |
| du \ / \ / dv | | du \ / \ / dv | | du \ / \ / dv |
o-----o o-----o o-----o o-----o o-----o o-----o
\ / \ / \ /
\ / \ / \ /
o o o
DJ = dJ + ddJ
o-----------------------o o-----------------------o o-----------------------o
| | | | | |
| o--o o--o | | o--o o--o | | o--o o--o |
| / \ / \ | | / \ / \ | | / \ / \ |
| / o \ | | / o \ | | / o \ |
| / u / \ v \ | | / u / \ v \ | | / u / \ v \ |
| o / \ o | | o / \ o | | o / \ o |
| | o o | | | | o o | | | | o o | |
| | @<-|->@<-|->@ | | | | @<-|->@<-|->@ | | | | @<-|-----|->@ | |
| | o ^ o | | | | ^ o o ^ | | | | o @ o | |
| o \ | / o | | o \ \ / / o | | o \ ^ / o |
| \ \|/ / | | \ --\-/-- / | | \ \|/ / |
| \ | / | | \ o / | | \ | / |
| \ /|\ / | | \ / \ / | | \ /|\ / |
| o--o v o--o | | o--o o--o | | o--o v o--o |
| @ | | @ | | @ |
o-----------------------o o-----------------------o o-----------------------o
Figure 53. Decomposition of the Differed Conjunction DJ = (dJ, ddJ)
Table 54. Cast of Characters: Expansive Subtypes of Objects and Operators
Table 54. Cast of Characters: Expansive Subtypes of Objects and Operators o------o-------------------------o------------------o----------------------------o | Item | Notation | Description | Type | o------o-------------------------o------------------o----------------------------o | | | | | | U% | = [u, v] | Source Universe | [B^2] | | | | | | o------o-------------------------o------------------o----------------------------o | | | | | | X% | = [x] | Target Universe | [B^1] | | | | | | o------o-------------------------o------------------o----------------------------o | | | | | | EU% | = [u, v, du, dv] | Extended | [B^2 x D^2] | | | | Source Universe | | | | | | | o------o-------------------------o------------------o----------------------------o | | | | | | EX% | = [x, dx] | Extended | [B^1 x D^1] | | | | Target Universe | | | | | | | o------o-------------------------o------------------o----------------------------o | | | | | | J | J : U -> B | Proposition | (B^2 -> B) c [B^2] | | | | | | o------o-------------------------o------------------o----------------------------o | | | | | | J | J : U% -> X% | Transformation, | [B^2] -> [B^1] | | | | or Mapping | | | | | | | o------o-------------------------o------------------o----------------------------o | | | | | | W | W : | Operator | | | | U% -> EU%, | | [B^2] -> [B^2 x D^2], | | | X% -> EX%, | | [B^1] -> [B^1 x D^1], | | | (U%->X%)->(EU%->EX%), | | ([B^2] -> [B^1]) | | | for each W among: | | -> | | | e!, !h!, E, D, d | | ([B^2 x D^2]->[B^1 x D^1]) | | | | | | o------o-------------------------o------------------o----------------------------o | | | | | !e! | | Tacit Extension Operator !e! | | !h! | | Trope Extension Operator !h! | | E | | Enlargement Operator E | | D | | Difference Operator D | | d | | Differential Operator d | | | | | o------o-------------------------o------------------o----------------------------o | | | | | | $W$ | $W$ : | Operator | | | | U% -> $T$U% = EU%, | | [B^2] -> [B^2 x D^2], | | | X% -> $T$X% = EX%, | | [B^1] -> [B^1 x D^1], | | | (U%->X%)->($T$U%->$T$X%)| | ([B^2] -> [B^1]) | | | for each $W$ among: | | -> | | | $e$, $E$, $D$, $T$ | | ([B^2 x D^2]->[B^1 x D^1]) | | | | | | o------o-------------------------o------------------o----------------------------o | | | | | $e$ | | Radius Operator $e$ = <!e!, !h!> | | $E$ | | Secant Operator $E$ = <!e!, E > | | $D$ | | Chord Operator $D$ = <!e!, D > | | $T$ | | Tangent Functor $T$ = <!e!, d > | | | | | o------o-------------------------o-----------------------------------------------o
| Item | Notation | Description | Type | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| U • | = [u, v] | Source Universe | [B2] | ||||||||||||||||||
| X • | = [x] | Target Universe | [B1] | ||||||||||||||||||
| EU • | = [u, v, du, dv] | Extended Source Universe | [B2 × D2] | ||||||||||||||||||
| EX • | = [x, dx] | Extended Target Universe | [B1 × D1] | ||||||||||||||||||
| J | J : U → B | Proposition | (B2 → B) ∈ [B2] | ||||||||||||||||||
| J | J : U • → X • | Transformation, or Mapping | [B2] → [B1] | ||||||||||||||||||
|
|
|
| ||||||||||||||||||
|
| ||||||||||||||||||||
|
|
|
| ||||||||||||||||||
|
| ||||||||||||||||||||
Table 55. Synopsis of Terminology: Restrictive and Alternative Subtypes
Table 55. Synopsis of Terminology: Restrictive and Alternative Subtypes o--------------o----------------------o--------------------o----------------------o | | Operator | Proposition | Map | o--------------o----------------------o--------------------o----------------------o | | | | | | Tacit | !e! : | !e!J : | !e!J : | | Extension | U%->EU%, X%->EX%, | <|u,v,du,dv|> -> B | [u,v,du,dv]->[x] | | | (U%->X%)->(EU%->X%) | B^2 x D^2 -> B | [B^2 x D^2]->[B^1] | | | | | | o--------------o----------------------o--------------------o----------------------o | | | | | | Trope | !h! : | !h!J : | !h!J : | | Extension | U%->EU%, X%->EX%, | <|u,v,du,dv|> -> D | [u,v,du,dv]->[dx] | | | (U%->X%)->(EU%->dX%) | B^2 x D^2 -> D | [B^2 x D^2]->[D^1] | | | | | | o--------------o----------------------o--------------------o----------------------o | | | | | | Enlargement | E : | EJ : | EJ : | | Operator | U%->EU%, X%->EX%, | <|u,v,du,dv|> -> D | [u,v,du,dv]->[dx] | | | (U%->X%)->(EU%->dX%) | B^2 x D^2 -> D | [B^2 x D^2]->[D^1] | | | | | | o--------------o----------------------o--------------------o----------------------o | | | | | | Difference | D : | DJ : | DJ : | | Operator | U%->EU%, X%->EX%, | <|u,v,du,dv|> -> D | [u,v,du,dv]->[dx] | | | (U%->X%)->(EU%->dX%) | B^2 x D^2 -> D | [B^2 x D^2]->[D^1] | | | | | | o--------------o----------------------o--------------------o----------------------o | | | | | | Differential | d : | dJ : | dJ : | | Operator | U%->EU%, X%->EX%, | <|u,v,du,dv|> -> D | [u,v,du,dv]->[dx] | | | (U%->X%)->(EU%->dX%) | B^2 x D^2 -> D | [B^2 x D^2]->[D^1] | | | | | | o--------------o----------------------o--------------------o----------------------o | | | | | | Remainder | r : | rJ : | rJ : | | Operator | U%->EU%, X%->EX%, | <|u,v,du,dv|> -> D | [u,v,du,dv]->[dx] | | | (U%->X%)->(EU%->dX%) | B^2 x D^2 -> D | [B^2 x D^2]->[D^1] | | | | | | o--------------o----------------------o--------------------o----------------------o | | | | | | Radius | $e$ = <!e!, !h!> : | | $e$J : | | Operator | U%->EU%, X%->EX%, | | [u,v,du,dv]->[x, dx] | | | (U%->X%)->(EU%->EX%) | | [B^2 x D^2]->[B x D] | | | | | | o--------------o----------------------o--------------------o----------------------o | | | | | | Secant | $E$ = <!e!, E> : | | $E$J : | | Operator | U%->EU%, X%->EX%, | | [u,v,du,dv]->[x, dx] | | | (U%->X%)->(EU%->EX%) | | [B^2 x D^2]->[B x D] | | | | | | o--------------o----------------------o--------------------o----------------------o | | | | | | Chord | $D$ = <!e!, D> : | | $D$J : | | Operator | U%->EU%, X%->EX%, | | [u,v,du,dv]->[x, dx] | | | (U%->X%)->(EU%->EX%) | | [B^2 x D^2]->[B x D] | | | | | | o--------------o----------------------o--------------------o----------------------o | | | | | | Tangent | $T$ = <!e!, d> : | dJ : | $T$J : | | Functor | U%->EU%, X%->EX%, | <|u,v,du,dv|> -> D | [u,v,du,dv]->[x, dx] | | | (U%->X%)->(EU%->EX%) | B^2 x D^2 -> D | [B^2 x D^2]->[B x D] | | | | | | o--------------o----------------------o--------------------o----------------------o
| Operator | Proposition | Map | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
| |||||||||||
|
|
|
| |||||||||||
|
|
|
| |||||||||||
|
|
|
| |||||||||||
|
|
|
| |||||||||||
|
|
|
| |||||||||||
|
|
|
| |||||||||||
|
|
|
| |||||||||||
|
|
|
| |||||||||||
|
|
|
|
Figure 56-a1. Radius Map of the Conjunction J = uv
o
/X\
/XXX\
oXXXXXo
/X\XXX/X\
/XXX\X/XXX\
oXXXXXoXXXXXo
/ \XXX/X\XXX/ \
/ \X/XXX\X/ \
o oXXXXXo o
/ \ / \XXX/ \ / \
/ \ / \X/ \ / \
o o o o o
=|\ / \ / \ / \ /|=
= | \ / \ / \ / \ / | =
= | o o o o | =
= | |\ / \ / \ /| | =
= |u | \ / \ / \ / | v| =
o o--+--o o o--+--o o
//\ | \ / \ / | /\\
////\ | du \ / \ / dv | /\\\\
o/////o o-----o o-----o o\\\\\o
//\/////\ \ / /\\\\\/\\
////\/////\ \ / /\\\\\/\\\\
o/////o/////o o o\\\\\o\\\\\o
/ \/////\//// \ = = / \\\\/\\\\\/ \
/ \/////\// \ = = / \\/\\\\\/ \
o o/////o o = = o o\\\\\o o
/ \ / \//// \ / \ = = / \ / \\\\/ \ / \
/ \ / \// \ / \ = = / \ / \\/ \ / \
o o o o o o o o o o
|\ / \ / \ / \ /| |\ / \ / \ / \ /|
| \ / \ / \ / \ / | | \ / \ / \ / \ / |
| o o o o | | o o o o |
| |\ / \ / \ /| | | |\ / \ / \ /| |
|u | \ / \ / \ / | v| |u | \ / \ / \ / | v|
o--+--o o o--+--o o o--+--o o o--+--o
. | \ / \ / | /X\ | \ / \ / | .
.| du \ / \ / dv | /XXX\ | du \ / \ / dv |.
o-----o o-----o /XXXXX\ o-----o o-----o
. \ / /XXXXXXX\ \ / .
. \ / /XXXXXXXXX\ \ / .
. o oXXXXXXXXXXXo o .
. //\XXXXXXXXX/\\ .
. ////\XXXXXXX/\\\\ .
!e!J //////\XXXXX/\\\\\\ !h!J
. ////////\XXX/\\\\\\\\ .
. //////////\X/\\\\\\\\\\ .
. o///////////o\\\\\\\\\\\o .
. |\////////// \\\\\\\\\\/| .
. | \//////// \\\\\\\\/ | .
. | \////// \\\\\\/ | .
. | \//// \\\\/ | .
.| x \// \\/ dx |.
o-----o o-----o
\ /
\ /
x = uv \ / dx = uv
\ /
\ /
o
Figure 56-a1. Radius Map of the Conjunction J = uv
Figure 56-a2. Secant Map of the Conjunction J = uv
o
/X\
/XXX\
oXXXXXo
//\XXX//\
////\X////\
o/////o/////o
/\\/////\////\\
/\\\\/////\//\\\\
o\\\\\o/////o\\\\\o
/ \\\\/ \//// \\\\/ \
/ \\/ \// \\/ \
o o o o o
=|\ / \ /\\ / \ /|=
= | \ / \ /\\\\ / \ / | =
= | o o\\\\\o o | =
= | |\ / \\\\/ \ /| | =
= |u | \ / \\/ \ / | v| =
o o--+--o o o--+--o o
//\ | \ / \ / | /\\
////\ | du \ / \ / dv | /\\\\
o/////o o-----o o-----o o\\\\\o
//\/////\ \ / / \\\\/ \
////\/////\ \ / / \\/ \
o/////o/////o o o o o
/ \/////\//// \ = = /\\ / \ /\\
/ \/////\// \ = = /\\\\ / \ /\\\\
o o/////o o = = o\\\\\o o\\\\\o
/ \ / \//// \ / \ = = / \\\\/ \ / \\\\/ \
/ \ / \// \ / \ = = / \\/ \ / \\/ \
o o o o o o o o o o
|\ / \ / \ / \ /| |\ / \ /\\ / \ /|
| \ / \ / \ / \ / | | \ / \ /\\\\ / \ / |
| o o o o | | o o\\\\\o o |
| |\ / \ / \ /| | | |\ / \\\\/ \ /| |
|u | \ / \ / \ / | v| |u | \ / \\/ \ / | v|
o--+--o o o--+--o o o--+--o o o--+--o
. | \ / \ / | /X\ | \ / \ / | .
.| du \ / \ / dv | /XXX\ | du \ / \ / dv |.
o-----o o-----o /XXXXX\ o-----o o-----o
. \ / /XXXXXXX\ \ / .
. \ / /XXXXXXXXX\ \ / .
. o oXXXXXXXXXXXo o .
. //\XXXXXXXXX/\\ .
. ////\XXXXXXX/\\\\ .
!e!J //////\XXXXX/\\\\\\ EJ
. ////////\XXX/\\\\\\\\ .
. //////////\X/\\\\\\\\\\ .
. o///////////o\\\\\\\\\\\o .
. |\////////// \\\\\\\\\\/| .
. | \//////// \\\\\\\\/ | .
. | \////// \\\\\\/ | .
. | \//// \\\\/ | .
.| x \// \\/ dx |.
o-----o o-----o
\ /
\ / dx = (u, du)(v, dv)
x = uv \ /
\ / dx = uv + u dv + v du + du dv
\ /
o
Figure 56-a2. Secant Map of the Conjunction J = uv
Figure 56-a3. Chord Map of the Conjunction J = uv
o
//\
////\
o/////o
/X\////X\
/XXX\//XXX\
oXXXXXoXXXXXo
/\\XXX/X\XXX/\\
/\\\\X/XXX\X/\\\\
o\\\\\oXXXXXo\\\\\o
/ \\\\/ \XXX/ \\\\/ \
/ \\/ \X/ \\/ \
o o o o o
=|\ / \ /\\ / \ /|=
= | \ / \ /\\\\ / \ / | =
= | o o\\\\\o o | =
= | |\ / \\\\/ \ /| | =
= |u | \ / \\/ \ / | v| =
o o--+--o o o--+--o o
//\ | \ / \ / | / \
////\ | du \ / \ / dv | / \
o/////o o-----o o-----o o o
//\/////\ \ / /\\ /\\
////\/////\ \ / /\\\\ /\\\\
o/////o/////o o o\\\\\o\\\\\o
/ \/////\//// \ = = /\\\\\/\\\\\/\\
/ \/////\// \ = = /\\\\\/\\\\\/\\\\
o o/////o o = = o\\\\\o\\\\\o\\\\\o
/ \ / \//// \ / \ = = / \\\\/ \\\\/ \\\\/ \
/ \ / \// \ / \ = = / \\/ \\/ \\/ \
o o o o o o o o o o
|\ / \ / \ / \ /| |\ / \ /\\ / \ /|
| \ / \ / \ / \ / | | \ / \ /\\\\ / \ / |
| o o o o | | o o\\\\\o o |
| |\ / \ / \ /| | | |\ / \\\\/ \ /| |
|u | \ / \ / \ / | v| |u | \ / \\/ \ / | v|
o--+--o o o--+--o o o--+--o o o--+--o
. | \ / \ / | /X\ | \ / \ / | .
.| du \ / \ / dv | /XXX\ | du \ / \ / dv |.
o-----o o-----o /XXXXX\ o-----o o-----o
. \ / /XXXXXXX\ \ / .
. \ / /XXXXXXXXX\ \ / .
. o oXXXXXXXXXXXo o .
. //\XXXXXXXXX/\\ .
. ////\XXXXXXX/\\\\ .
!e!J //////\XXXXX/\\\\\\ DJ
. ////////\XXX/\\\\\\\\ .
. //////////\X/\\\\\\\\\\ .
. o///////////o\\\\\\\\\\\o .
. |\////////// \\\\\\\\\\/| .
. | \//////// \\\\\\\\/ | .
. | \////// \\\\\\/ | .
. | \//// \\\\/ | .
.| x \// \\/ dx |.
o-----o o-----o
\ /
\ / dx = (u, du)(v, dv) - uv
x = uv \ /
\ / dx = u dv + v du + du dv
\ /
o
Figure 56-a3. Chord Map of the Conjunction J = uv
Figure 56-a4. Tangent Map of the Conjunction J = uv
o
//\
////\
o/////o
/X\////X\
/XXX\//XXX\
oXXXXXoXXXXXo
/\\XXX//\XXX/\\
/\\\\X////\X/\\\\
o\\\\\o/////o\\\\\o
/ \\\\/\\////\\\\\/ \
/ \\/\\\\//\\\\\/ \
o o\\\\\o\\\\\o o
=|\ / \\\\/ \\\\/ \ /|=
= | \ / \\/ \\/ \ / | =
= | o o o o | =
= | |\ / \ / \ /| | =
= |u | \ / \ / \ / | v| =
o o--+--o o o--+--o o
//\ | \ / \ / | / \
////\ | du \ / \ / dv | / \
o/////o o-----o o-----o o o
//\/////\ \ / /\\ /\\
////\/////\ \ / /\\\\ /\\\\
o/////o/////o o o\\\\\o\\\\\o
/ \/////\//// \ = = /\\\\\/ \\\\/\\
/ \/////\// \ = = /\\\\\/ \\/\\\\
o o/////o o = = o\\\\\o o\\\\\o
/ \ / \//// \ / \ = = / \\\\/\\ /\\\\\/ \
/ \ / \// \ / \ = = / \\/\\\\ /\\\\\/ \
o o o o o o o\\\\\o\\\\\o o
|\ / \ / \ / \ /| |\ / \\\\/ \\\\/ \ /|
| \ / \ / \ / \ / | | \ / \\/ \\/ \ / |
| o o o o | | o o o o |
| |\ / \ / \ /| | | |\ / \ / \ /| |
|u | \ / \ / \ / | v| |u | \ / \ / \ / | v|
o--+--o o o--+--o o o--+--o o o--+--o
. | \ / \ / | /X\ | \ / \ / | .
.| du \ / \ / dv | /XXX\ | du \ / \ / dv |.
o-----o o-----o /XXXXX\ o-----o o-----o
. \ / /XXXXXXX\ \ / .
. \ / /XXXXXXXXX\ \ / .
. o oXXXXXXXXXXXo o .
. //\XXXXXXXXX/\\ .
. ////\XXXXXXX/\\\\ .
!e!J //////\XXXXX/\\\\\\ dJ
. ////////\XXX/\\\\\\\\ .
. //////////\X/\\\\\\\\\\ .
. o///////////o\\\\\\\\\\\o .
. |\////////// \\\\\\\\\\/| .
. | \//////// \\\\\\\\/ | .
. | \////// \\\\\\/ | .
. | \//// \\\\/ | .
.| x \// \\/ dx |.
o-----o o-----o
\ /
\ /
x = uv \ / dx = u dv + v du
\ /
\ /
o
Figure 56-a4. Tangent Map of the Conjunction J = uv
Figure 56-b1. Radius Map of the Conjunction J = uv
o-----------------------o
| |
| |
| |
| o--o o--o |
| / \ / \ |
| / o \ |
| / du / \ dv \ |
| o / \ o |
| | o o | |
| | | | | |
| | o o | |
| o \ / o |
| \ \ / / |
| \ o / |
| \ / \ / |
| o--o o--o |
| |
| |
| |
o-----------------------@
\
o-----------------------o \
| | \
| | \
| | \
| o--o o--o | \
| / \ / \ | \
| / o \ | \
| / du / \ dv \ | \
| o / \ o | \
| | o o | @ \
| | | | | |\ \
| | o o | | \ \
| o \ / o | \ \
| \ \ / / | \ \
| \ o / | \ \
| \ / \ / | \ \
| o--o o--o | \ \
| | \ \
| | \ \
| | \ \
o-----------------------o \ \
\ \
o-----------------------@ o--------\----------\---o o-----------------------o
| |\ | \ \ | |```````````````````````|
| | \ | \ @ | |```````````````````````|
| | \| \ | |```````````````````````|
| o--o o--o | \ o--o \o--o | |``````o--o```o--o``````|
| / \ / \ | |\ / \ /\ \ | |`````/````\`/````\`````|
| / o \ | | \ / o @ \ | |````/``````o``````\````|
| / du / \ dv \ | | \/ du /`\ dv \ | |```/``du``/`\``dv``\```|
| o / \ o | | o\ /```\ o | |``o``````/```\``````o``|
| | o o | | | | \ o`````o | | |``|`````o`````o`````|``|
| | | | | | | | @ |``@--|-----|------@``|`````|`````|`````|``|
| | o o | | | | o`````o | | |``|`````o`````o`````|``|
| o \ / o | | o \```/ o | |``o``````\```/``````o``|
| \ \ / / | | \ \`/ / | |```\``````\`/``````/```|
| \ o / | | \ o / | |````\``````o``````/````|
| \ / \ / | | \ / \ / | |`````\````/`\````/`````|
| o--o o--o | | o--o o--o | |``````o--o```o--o``````|
| | | | |```````````````````````|
| | | | |```````````````````````|
| | | | |```````````````````````|
o-----------------------o o-----------------------o o-----------------------o
\ / \ / \ /
\ !h!J / \ J / \ !h!J /
\ / \ / \ /
\ / o----------\---------/----------o \ /
\ / | \ / | \ /
\ / | \ / | \ /
\ / | o-----o-----o | \ /
\ / | /`````````````\ | \ /
\ / | /```````````````\ | \ /
o------\---/------o | /`````````````````\ | o------\---/------o
| \ / | | /```````````````````\ | | \ / |
| o--o--o | | /`````````````````````\ | | o--o--o |
| /```````\ | | o```````````````````````o | | /```````\ |
| /`````````\ | | |```````````````````````| | | /`````````\ |
| o```````````o | | |```````````````````````| | | o```````````o |
| |````dx`````| @----@ |```````````x`````@-----|------@ |``` dx ````| |
| o```````````o | | |```````````````````````| | | o```````````o |
| \`````````/ | | |```````````````````````| | | \`````````/ |
| \```````/ | | o```````````````````````o | | \```````/ |
| o-----o | | \`````````````````````/ | | o-----o |
| | | \```````````````````/ | | |
o-----------------o | \`````````````````/ | o-----------------o
| \```````````````/ |
| \`````````````/ |
| o-----------o |
| |
| |
o-------------------------------o
Figure 56-b1. Radius Map of the Conjunction J = uv
Figure 56-b2. Secant Map of the Conjunction J = uv
o-----------------------o
| |
| |
| |
| o--o o--o |
| / \ / \ |
| / o \ |
| / du /`\ dv \ |
| o /```\ o |
| | o`````o | |
| | |`````| | |
| | o`````o | |
| o \```/ o |
| \ \`/ / |
| \ o / |
| \ / \ / |
| o--o o--o |
| |
| |
| |
o-----------------------@
\
o-----------------------o \
| | \
| | \
| | \
| o--o o--o | \
| /````\ / \ | \
| /``````o \ | \
| /``du``/ \ dv \ | \
| o``````/ \ o | \
| |`````o o | @ \
| |`````| | | |\ \
| |`````o o | | \ \
| o``````\ / o | \ \
| \``````\ / / | \ \
| \``````o / | \ \
| \````/ \ / | \ \
| o--o o--o | \ \
| | \ \
| | \ \
| | \ \
o-----------------------o \ \
\ \
o-----------------------@ o--------\----------\---o o-----------------------o
| |\ | \ \ | |```````````````````````|
| | \ | \ @ | |```````````````````````|
| | \| \ | |```````````````````````|
| o--o o--o | \ o--o \o--o | |``````o--o```o--o``````|
| / \ /````\ | |\ / \ /\ \ | |`````/ \`/ \`````|
| / o``````\ | | \ / o @ \ | |````/ o \````|
| / du / \``dv``\ | | \/ du /`\ dv \ | |```/ du / \ dv \```|
| o / \``````o | | o\ /```\ o | |``o / \ o``|
| | o o`````| | | | \ o`````o | | |``| o o |``|
| | | |`````| | | | @ |``@--|-----|------@``| | | |``|
| | o o`````| | | | o`````o | | |``| o o |``|
| o \ /``````o | | o \```/ o | |``o \ / o``|
| \ \ /``````/ | | \ \`/ / | |```\ \ / /```|
| \ o``````/ | | \ o / | |````\ o /````|
| \ / \````/ | | \ / \ / | |`````\ /`\ /`````|
| o--o o--o | | o--o o--o | |``````o--o```o--o``````|
| | | | |```````````````````````|
| | | | |```````````````````````|
| | | | |```````````````````````|
o-----------------------o o-----------------------o o-----------------------o
\ / \ / \ /
\ EJ / \ J / \ EJ /
\ / \ / \ /
\ / o----------\---------/----------o \ /
\ / | \ / | \ /
\ / | \ / | \ /
\ / | o-----o-----o | \ /
\ / | /`````````````\ | \ /
\ / | /```````````````\ | \ /
o------\---/------o | /`````````````````\ | o------\---/------o
| \ / | | /```````````````````\ | | \ / |
| o--o--o | | /`````````````````````\ | | o--o--o |
| /```````\ | | o```````````````````````o | | /```````\ |
| /`````````\ | | |```````````````````````| | | /`````````\ |
| o```````````o | | |```````````````````````| | | o```````````o |
| |````dx`````| @----@ |```````````x`````@-----|------@ |``` dx ````| |
| o```````````o | | |```````````````````````| | | o```````````o |
| \`````````/ | | |```````````````````````| | | \`````````/ |
| \```````/ | | o```````````````````````o | | \```````/ |
| o-----o | | \`````````````````````/ | | o-----o |
| | | \```````````````````/ | | |
o-----------------o | \`````````````````/ | o-----------------o
| \```````````````/ |
| \`````````````/ |
| o-----------o |
| |
| |
o-------------------------------o
Figure 56-b2. Secant Map of the Conjunction J = uv
Figure 56-b3. Chord Map of the Conjunction J = uv
o-----------------------o
| |
| |
| |
| o--o o--o |
| / \ / \ |
| / o \ |
| / du /`\ dv \ |
| o /```\ o |
| | o`````o | |
| | |`````| | |
| | o`````o | |
| o \```/ o |
| \ \`/ / |
| \ o / |
| \ / \ / |
| o--o o--o |
| |
| |
| |
o-----------------------@
\
o-----------------------o \
| | \
| | \
| | \
| o--o o--o | \
| /````\ / \ | \
| /``````o \ | \
| /``du``/ \ dv \ | \
| o``````/ \ o | \
| |`````o o | @ \
| |`````| | | |\ \
| |`````o o | | \ \
| o``````\ / o | \ \
| \``````\ / / | \ \
| \``````o / | \ \
| \````/ \ / | \ \
| o--o o--o | \ \
| | \ \
| | \ \
| | \ \
o-----------------------o \ \
\ \
o-----------------------@ o--------\----------\---o o-----------------------o
| |\ | \ \ | | |
| | \ | \ @ | | |
| | \| \ | | |
| o--o o--o | \ o--o \o--o | | o--o o--o |
| / \ /````\ | |\ / \ /\ \ | | /````\ /````\ |
| / o``````\ | | \ / o @ \ | | /``````o``````\ |
| / du / \``dv``\ | | \/ du /`\ dv \ | | /``du``/`\``dv``\ |
| o / \``````o | | o\ /```\ o | | o``````/```\``````o |
| | o o`````| | | | \ o`````o | | | |`````o`````o`````| |
| | | |`````| | | | @ |``@--|-----|------@ |`````|`````|`````| |
| | o o`````| | | | o`````o | | | |`````o`````o`````| |
| o \ /``````o | | o \```/ o | | o``````\```/``````o |
| \ \ /``````/ | | \ \`/ / | | \``````\`/``````/ |
| \ o``````/ | | \ o / | | \``````o``````/ |
| \ / \````/ | | \ / \ / | | \````/ \````/ |
| o--o o--o | | o--o o--o | | o--o o--o |
| | | | | |
| | | | | |
| | | | | |
o-----------------------o o-----------------------o o-----------------------o
\ / \ / \ /
\ DJ / \ J / \ DJ /
\ / \ / \ /
\ / o----------\---------/----------o \ /
\ / | \ / | \ /
\ / | \ / | \ /
\ / | o-----o-----o | \ /
\ / | /`````````````\ | \ /
\ / | /```````````````\ | \ /
o------\---/------o | /`````````````````\ | o------\---/------o
| \ / | | /```````````````````\ | | \ / |
| o--o--o | | /`````````````````````\ | | o--o--o |
| /```````\ | | o```````````````````````o | | /```````\ |
| /`````````\ | | |```````````````````````| | | /`````````\ |
| o```````````o | | |```````````````````````| | | o```````````o |
| |````dx`````| @----@ |```````````x`````@-----|------@ |``` dx ````| |
| o```````````o | | |```````````````````````| | | o```````````o |
| \`````````/ | | |```````````````````````| | | \`````````/ |
| \```````/ | | o```````````````````````o | | \```````/ |
| o-----o | | \`````````````````````/ | | o-----o |
| | | \```````````````````/ | | |
o-----------------o | \`````````````````/ | o-----------------o
| \```````````````/ |
| \`````````````/ |
| o-----------o |
| |
| |
o-------------------------------o
Figure 56-b3. Chord Map of the Conjunction J = uv
Figure 56-b4. Tangent Map of the Conjunction J = uv
o-----------------------o
| |
| |
| |
| o--o o--o |
| / \ / \ |
| / o \ |
| / du / \ dv \ |
| o / \ o |
| | o o | |
| | | | | |
| | o o | |
| o \ / o |
| \ \ / / |
| \ o / |
| \ / \ / |
| o--o o--o |
| |
| |
| |
o-----------------------@
\
o-----------------------o \
| | \
| | \
| | \
| o--o o--o | \
| /````\ / \ | \
| /``````o \ | \
| /``du``/`\ dv \ | \
| o``````/```\ o | \
| |`````o`````o | @ \
| |`````|`````| | |\ \
| |`````o`````o | | \ \
| o``````\```/ o | \ \
| \``````\`/ / | \ \
| \``````o / | \ \
| \````/ \ / | \ \
| o--o o--o | \ \
| | \ \
| | \ \
| | \ \
o-----------------------o \ \
\ \
o-----------------------@ o--------\----------\---o o-----------------------o
| |\ | \ \ | | |
| | \ | \ @ | | |
| | \| \ | | |
| o--o o--o | \ o--o \o--o | | o--o o--o |
| / \ /````\ | |\ / \ /\ \ | | /````\ /````\ |
| / o``````\ | | \ / o @ \ | | /``````o``````\ |
| / du /`\``dv``\ | | \/ du /`\ dv \ | | /``du``/ \``dv``\ |
| o /```\``````o | | o\ /```\ o | | o``````/ \``````o |
| | o`````o`````| | | | \ o`````o | | | |`````o o`````| |
| | |`````|`````| | | | @ |``@--|-----|------@ |`````| |`````| |
| | o`````o`````| | | | o`````o | | | |`````o o`````| |
| o \```/``````o | | o \```/ o | | o``````\ /``````o |
| \ \`/``````/ | | \ \`/ / | | \``````\ /``````/ |
| \ o``````/ | | \ o / | | \``````o``````/ |
| \ / \````/ | | \ / \ / | | \````/ \````/ |
| o--o o--o | | o--o o--o | | o--o o--o |
| | | | | |
| | | | | |
| | | | | |
o-----------------------o o-----------------------o o-----------------------o
\ / \ / \ /
\ dJ / \ J / \ dJ /
\ / \ / \ /
\ / o----------\---------/----------o \ /
\ / | \ / | \ /
\ / | \ / | \ /
\ / | o-----o-----o | \ /
\ / | /`````````````\ | \ /
\ / | /```````````````\ | \ /
o------\---/------o | /`````````````````\ | o------\---/------o
| \ / | | /```````````````````\ | | \ / |
| o--o--o | | /`````````````````````\ | | o--o--o |
| /```````\ | | o```````````````````````o | | /```````\ |
| /`````````\ | | |```````````````````````| | | /`````````\ |
| o```````````o | | |```````````````````````| | | o```````````o |
| |````dx`````| @----@ |```````````x`````@-----|------@ |``` dx ````| |
| o```````````o | | |```````````````````````| | | o```````````o |
| \`````````/ | | |```````````````````````| | | \`````````/ |
| \```````/ | | o```````````````````````o | | \```````/ |
| o-----o | | \`````````````````````/ | | o-----o |
| | | \```````````````````/ | | |
o-----------------o | \`````````````````/ | o-----------------o
| \```````````````/ |
| \`````````````/ |
| o-----------o |
| |
| |
o-------------------------------o
Figure 56-b4. Tangent Map of the Conjunction J = uv
Figure 57-1. Radius Operator Diagram for the Conjunction J = uv
o o
//\ /X\
////\ /XXX\
//////\ oXXXXXo
////////\ /X\XXX/X\
//////////\ /XXX\X/XXX\
o///////////o oXXXXXoXXXXXo
/ \////////// \ / \XXX/X\XXX/ \
/ \//////// \ / \X/XXX\X/ \
/ \////// \ o oXXXXXo o
/ \//// \ / \ / \XXX/ \ / \
/ \// \ / \ / \X/ \ / \
o o o o o o o o
|\ / \ /| |\ / \ / \ / \ /|
| \ / \ / | | \ / \ / \ / \ / |
| \ / \ / | | o o o o |
| \ / \ / | | |\ / \ / \ /| |
| u \ / \ / v | |u | \ / \ / \ / | v|
o-----o o-----o o--+--o o o--+--o
\ / | \ / \ / |
\ / | du \ / \ / dv |
\ / o-----o o-----o
\ / \ /
\ / \ /
o o
U% $e$ $E$U%
o------------------>o
| |
| |
| |
| |
J | | $e$J
| |
| |
| |
v v
o------------------>o
X% $e$ $E$X%
o o
//\ /X\
////\ /XXX\
//////\ /XXXXX\
////////\ /XXXXXXX\
//////////\ /XXXXXXXXX\
////////////o oXXXXXXXXXXXo
///////////// \ //\XXXXXXXXX/\\
///////////// \ ////\XXXXXXX/\\\\
///////////// \ //////\XXXXX/\\\\\\
///////////// \ ////////\XXX/\\\\\\\\
///////////// \ //////////\X/\\\\\\\\\\
o//////////// o o///////////o\\\\\\\\\\\o
|\////////// / |\////////// \\\\\\\\\\/|
| \//////// / | \//////// \\\\\\\\/ |
| \////// / | \////// \\\\\\/ |
| \//// / | \//// \\\\/ |
| x \// / | x \// \\/ dx |
o-----o / o-----o o-----o
\ / \ /
\ / \ /
\ / \ /
\ / \ /
\ / \ /
o o
Figure 57-1. Radius Operator Diagram for the Conjunction J = uv
Figure 57-2. Secant Operator Diagram for the Conjunction J = uv
o o
//\ /X\
////\ /XXX\
//////\ oXXXXXo
////////\ //\XXX//\
//////////\ ////\X////\
o///////////o o/////o/////o
/ \////////// \ /\\/////\////\\
/ \//////// \ /\\\\/////\//\\\\
/ \////// \ o\\\\\o/////o\\\\\o
/ \//// \ / \\\\/ \//// \\\\/ \
/ \// \ / \\/ \// \\/ \
o o o o o o o o
|\ / \ /| |\ / \ /\\ / \ /|
| \ / \ / | | \ / \ /\\\\ / \ / |
| \ / \ / | | o o\\\\\o o |
| \ / \ / | | |\ / \\\\/ \ /| |
| u \ / \ / v | |u | \ / \\/ \ / | v|
o-----o o-----o o--+--o o o--+--o
\ / | \ / \ / |
\ / | du \ / \ / dv |
\ / o-----o o-----o
\ / \ /
\ / \ /
o o
U% $E$ $E$U%
o------------------>o
| |
| |
| |
| |
J | | $E$J
| |
| |
| |
v v
o------------------>o
X% $E$ $E$X%
o o
//\ /X\
////\ /XXX\
//////\ /XXXXX\
////////\ /XXXXXXX\
//////////\ /XXXXXXXXX\
////////////o oXXXXXXXXXXXo
///////////// \ //\XXXXXXXXX/\\
///////////// \ ////\XXXXXXX/\\\\
///////////// \ //////\XXXXX/\\\\\\
///////////// \ ////////\XXX/\\\\\\\\
///////////// \ //////////\X/\\\\\\\\\\
o//////////// o o///////////o\\\\\\\\\\\o
|\////////// / |\////////// \\\\\\\\\\/|
| \//////// / | \//////// \\\\\\\\/ |
| \////// / | \////// \\\\\\/ |
| \//// / | \//// \\\\/ |
| x \// / | x \// \\/ dx |
o-----o / o-----o o-----o
\ / \ /
\ / \ /
\ / \ /
\ / \ /
\ / \ /
o o
Figure 57-2. Secant Operator Diagram for the Conjunction J = uv
Figure 57-3. Chord Operator Diagram for the Conjunction J = uv
o o
//\ //\
////\ ////\
//////\ o/////o
////////\ /X\////X\
//////////\ /XXX\//XXX\
o///////////o oXXXXXoXXXXXo
/ \////////// \ /\\XXX/X\XXX/\\
/ \//////// \ /\\\\X/XXX\X/\\\\
/ \////// \ o\\\\\oXXXXXo\\\\\o
/ \//// \ / \\\\/ \XXX/ \\\\/ \
/ \// \ / \\/ \X/ \\/ \
o o o o o o o o
|\ / \ /| |\ / \ /\\ / \ /|
| \ / \ / | | \ / \ /\\\\ / \ / |
| \ / \ / | | o o\\\\\o o |
| \ / \ / | | |\ / \\\\/ \ /| |
| u \ / \ / v | |u | \ / \\/ \ / | v|
o-----o o-----o o--+--o o o--+--o
\ / | \ / \ / |
\ / | du \ / \ / dv |
\ / o-----o o-----o
\ / \ /
\ / \ /
o o
U% $D$ $E$U%
o------------------>o
| |
| |
| |
| |
J | | $D$J
| |
| |
| |
v v
o------------------>o
X% $D$ $E$X%
o o
//\ /X\
////\ /XXX\
//////\ /XXXXX\
////////\ /XXXXXXX\
//////////\ /XXXXXXXXX\
////////////o oXXXXXXXXXXXo
///////////// \ //\XXXXXXXXX/\\
///////////// \ ////\XXXXXXX/\\\\
///////////// \ //////\XXXXX/\\\\\\
///////////// \ ////////\XXX/\\\\\\\\
///////////// \ //////////\X/\\\\\\\\\\
o//////////// o o///////////o\\\\\\\\\\\o
|\////////// / |\////////// \\\\\\\\\\/|
| \//////// / | \//////// \\\\\\\\/ |
| \////// / | \////// \\\\\\/ |
| \//// / | \//// \\\\/ |
| x \// / | x \// \\/ dx |
o-----o / o-----o o-----o
\ / \ /
\ / \ /
\ / \ /
\ / \ /
\ / \ /
o o
Figure 57-3. Chord Operator Diagram for the Conjunction J = uv
Figure 57-4. Tangent Functor Diagram for the Conjunction J = uv
o o
//\ //\
////\ ////\
//////\ o/////o
////////\ /X\////X\
//////////\ /XXX\//XXX\
o///////////o oXXXXXoXXXXXo
/ \////////// \ /\\XXX//\XXX/\\
/ \//////// \ /\\\\X////\X/\\\\
/ \////// \ o\\\\\o/////o\\\\\o
/ \//// \ / \\\\/\\////\\\\\/ \
/ \// \ / \\/\\\\//\\\\\/ \
o o o o o\\\\\o\\\\\o o
|\ / \ /| |\ / \\\\/ \\\\/ \ /|
| \ / \ / | | \ / \\/ \\/ \ / |
| \ / \ / | | o o o o |
| \ / \ / | | |\ / \ / \ /| |
| u \ / \ / v | |u | \ / \ / \ / | v|
o-----o o-----o o--+--o o o--+--o
\ / | \ / \ / |
\ / | du \ / \ / dv |
\ / o-----o o-----o
\ / \ /
\ / \ /
o o
U% $T$ $E$U%
o------------------>o
| |
| |
| |
| |
J | | $T$J
| |
| |
| |
v v
o------------------>o
X% $T$ $E$X%
o o
//\ /X\
////\ /XXX\
//////\ /XXXXX\
////////\ /XXXXXXX\
//////////\ /XXXXXXXXX\
////////////o oXXXXXXXXXXXo
///////////// \ //\XXXXXXXXX/\\
///////////// \ ////\XXXXXXX/\\\\
///////////// \ //////\XXXXX/\\\\\\
///////////// \ ////////\XXX/\\\\\\\\
///////////// \ //////////\X/\\\\\\\\\\
o//////////// o o///////////o\\\\\\\\\\\o
|\////////// / |\////////// \\\\\\\\\\/|
| \//////// / | \//////// \\\\\\\\/ |
| \////// / | \////// \\\\\\/ |
| \//// / | \//// \\\\/ |
| x \// / | x \// \\/ dx |
o-----o / o-----o o-----o
\ / \ /
\ / \ /
\ / \ /
\ / \ /
\ / \ /
o o
Figure 57-4. Tangent Functor Diagram for the Conjunction J = uv
Formula Display 11
o-----------------------------------------------------------o | | | F = <f, g> = <F_1, F_2> : [u, v] -> [x, y] | | | | where f = F_1 : [u, v] -> [x] | | | | and g = F_2 : [u, v] -> [y] | | | o-----------------------------------------------------------o
| |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
Table 58. Cast of Characters: Expansive Subtypes of Objects and Operators
Table 58. Cast of Characters: Expansive Subtypes of Objects and Operators o------o-------------------------o------------------o----------------------------o | Item | Notation | Description | Type | o------o-------------------------o------------------o----------------------------o | | | | | | U% | = [u, v] | Source Universe | [B^n] | | | | | | o------o-------------------------o------------------o----------------------------o | | | | | | X% | = [x, y] | Target Universe | [B^k] | | | = [f, g] | | | | | | | | o------o-------------------------o------------------o----------------------------o | | | | | | EU% | = [u, v, du, dv] | Extended | [B^n x D^n] | | | | Source Universe | | | | | | | o------o-------------------------o------------------o----------------------------o | | | | | | EX% | = [x, y, dx, dy] | Extended | [B^k x D^k] | | | = [f, g, df, dg] | Target Universe | | | | | | | o------o-------------------------o------------------o----------------------------o | | | | | | F | F = <f, g> : U% -> X% | Transformation, | [B^n] -> [B^k] | | | | or Mapping | | | | | | | o------o-------------------------o------------------o----------------------------o | | | | | | | f, g : U -> B | Proposition, | B^n -> B | | | | special case | | | f | f : U -> [x] c X% | of a mapping, | c (B^n, B^n -> B) | | | | or component | | | g | g : U -> [y] c X% | of a mapping. | = (B^n +-> B) = [B^n] | | | | | | o------o-------------------------o------------------o----------------------------o | | | | | | W | W : | Operator | | | | U% -> EU%, | | [B^n] -> [B^n x D^n], | | | X% -> EX%, | | [B^k] -> [B^k x D^k], | | | (U%->X%)->(EU%->EX%), | | ([B^n] -> [B^k]) | | | for each W among: | | -> | | | !e!, !h!, E, D, d | | ([B^n x D^n]->[B^k x D^k]) | | | | | | o------o-------------------------o------------------o----------------------------o | | | | | !e! | | Tacit Extension Operator !e! | | !h! | | Trope Extension Operator !h! | | E | | Enlargement Operator E | | D | | Difference Operator D | | d | | Differential Operator d | | | | | o------o-------------------------o------------------o----------------------------o | | | | | | $W$ | $W$ : | Operator | | | | U% -> $T$U% = EU%, | | [B^n] -> [B^n x D^n], | | | X% -> $T$X% = EX%, | | [B^k] -> [B^k x D^k], | | | (U%->X%)->($T$U%->$T$X%)| | ([B^n] -> [B^k]) | | | for each $W$ among: | | -> | | | $e$, $E$, $D$, $T$ | | ([B^n x D^n]->[B^k x D^k]) | | | | | | o------o-------------------------o------------------o----------------------------o | | | | | $e$ | | Radius Operator $e$ = <!e!, !h!> | | $E$ | | Secant Operator $E$ = <!e!, E > | | $D$ | | Chord Operator $D$ = <!e!, D > | | $T$ | | Tangent Functor $T$ = <!e!, d > | | | | | o------o-------------------------o-----------------------------------------------o
| Item | Notation | Description | Type | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| U • | = [u, v] | Source Universe | [Bn] | ||||||||||||||||||
| X • |
|
Target Universe | [Bk] | ||||||||||||||||||
| EU • | = [u, v, du, dv] | Extended Source Universe | [Bn × Dn] | ||||||||||||||||||
| EX • |
|
Extended Target Universe | [Bk × Dk] | ||||||||||||||||||
| F | F = ‹f, g› : U • → X • | Transformation, or Mapping | [Bn] → [Bk] | ||||||||||||||||||
|
|
|
| ||||||||||||||||||
|
|
|
| ||||||||||||||||||
|
| ||||||||||||||||||||
|
|
|
| ||||||||||||||||||
|
| ||||||||||||||||||||
Table 59. Synopsis of Terminology: Restrictive and Alternative Subtypes
Table 59. Synopsis of Terminology: Restrictive and Alternative Subtypes o--------------o----------------------o--------------------o----------------------o | | Operator | Proposition | Transformation | | | or | or | or | | | Operand | Component | Mapping | o--------------o----------------------o--------------------o----------------------o | | | | | | Operand | F = <F_1, F_2> | F_i : <|u,v|> -> B | F : [u, v] -> [x, y] | | | | | | | | F = <f, g> : U -> X | F_i : B^n -> B | F : B^n -> B^k | | | | | | o--------------o----------------------o--------------------o----------------------o | | | | | | Tacit | !e! : | !e!F_i : | !e!F : | | Extension | U%->EU%, X%->EX%, | <|u,v,du,dv|> -> B | [u,v,du,dv]->[x, y] | | | (U%->X%)->(EU%->X%) | B^n x D^n -> B | [B^n x D^n]->[B^k] | | | | | | o--------------o----------------------o--------------------o----------------------o | | | | | | Trope | !h! : | !h!F_i : | !h!F : | | Extension | U%->EU%, X%->EX%, | <|u,v,du,dv|> -> D | [u,v,du,dv]->[dx,dy] | | | (U%->X%)->(EU%->dX%) | B^n x D^n -> D | [B^n x D^n]->[D^k] | | | | | | o--------------o----------------------o--------------------o----------------------o | | | | | | Enlargement | E : | EF_i : | EF : | | Operator | U%->EU%, X%->EX%, | <|u,v,du,dv|> -> D | [u,v,du,dv]->[dx,dy] | | | (U%->X%)->(EU%->dX%) | B^n x D^n -> D | [B^n x D^n]->[D^k] | | | | | | o--------------o----------------------o--------------------o----------------------o | | | | | | Difference | D : | DF_i : | DF : | | Operator | U%->EU%, X%->EX%, | <|u,v,du,dv|> -> D | [u,v,du,dv]->[dx,dy] | | | (U%->X%)->(EU%->dX%) | B^n x D^n -> D | [B^n x D^n]->[D^k] | | | | | | o--------------o----------------------o--------------------o----------------------o | | | | | | Differential | d : | dF_i : | dF : | | Operator | U%->EU%, X%->EX%, | <|u,v,du,dv|> -> D | [u,v,du,dv]->[dx,dy] | | | (U%->X%)->(EU%->dX%) | B^n x D^n -> D | [B^n x D^n]->[D^k] | | | | | | o--------------o----------------------o--------------------o----------------------o | | | | | | Remainder | r : | rF_i : | rF : | | Operator | U%->EU%, X%->EX%, | <|u,v,du,dv|> -> D | [u,v,du,dv]->[dx,dy] | | | (U%->X%)->(EU%->dX%) | B^n x D^n -> D | [B^n x D^n]->[D^k] | | | | | | o--------------o----------------------o--------------------o----------------------o | | | | | | Radius | $e$ = <!e!, !h!> : | | $e$F : | | Operator | | | | | | U%->EU%, X%->EX%, | | [u, v, du, dv] -> | | | (U%->X%)->(EU%->EX%) | | [x, y, dx, dy], | | | | | | | | | | [B^n x D^n] -> | | | | | [B^k x D^k] | | | | | | o--------------o----------------------o--------------------o----------------------o | | | | | | Secant | $E$ = <!e!, E> : | | $E$F : | | Operator | | | | | | U%->EU%, X%->EX%, | | [u, v, du, dv] -> | | | (U%->X%)->(EU%->EX%) | | [x, y, dx, dy], | | | | | | | | | | [B^n x D^n] -> | | | | | [B^k x D^k] | | | | | | o--------------o----------------------o--------------------o----------------------o | | | | | | Chord | $D$ = <!e!, D> : | | $D$F : | | Operator | | | | | | U%->EU%, X%->EX%, | | [u, v, du, dv] -> | | | (U%->X%)->(EU%->EX%) | | [x, y, dx, dy], | | | | | | | | | | [B^n x D^n] -> | | | | | [B^k x D^k] | | | | | | o--------------o----------------------o--------------------o----------------------o | | | | | | Tangent | $T$ = <!e!, d> : | dF_i : | $T$F : | | Functor | | | | | | U%->EU%, X%->EX%, | <|u,v,du,dv|> -> D | [u, v, du, dv] -> | | | (U%->X%)->(EU%->EX%) | | [x, y, dx, dy], | | | | | | | | | B^n x D^n -> D | [B^n x D^n] -> | | | | | [B^k x D^k] | | | | | | o--------------o----------------------o--------------------o----------------------o
| Operator or Operand |
Proposition or Component |
Transformation or Mapping | ||||||||||||
| Operand |
|
|
| |||||||||||
|
|
|
| |||||||||||
|
|
|
| |||||||||||
|
|
|
| |||||||||||
|
|
|
| |||||||||||
|
|
|
| |||||||||||
|
|
|
| |||||||||||
|
|
|
| |||||||||||
|
|
|
| |||||||||||
|
|
|
| |||||||||||
|
|
|
|
Formula Display 12
o-----------------------------------------------------------o | | | x = f(u, v) = ((u)(v)) | | | | y = g(u, v) = ((u, v)) | | | o-----------------------------------------------------------o
|
Formula Display 13
o-----------------------------------------------------------o | | | <x, y> = F<u, v> = <((u)(v)), ((u, v))> | | | o-----------------------------------------------------------o
|
|
Table 60. Propositional Transformation
Table 60. Propositional Transformation o-------------o-------------o-------------o-------------o | u | v | f | g | o-------------o-------------o-------------o-------------o | | | | | | 0 | 0 | 0 | 1 | | | | | | | 0 | 1 | 1 | 0 | | | | | | | 1 | 0 | 1 | 0 | | | | | | | 1 | 1 | 1 | 1 | | | | | | o-------------o-------------o-------------o-------------o | | | ((u)(v)) | ((u, v)) | o-------------o-------------o-------------o-------------o
| u | v | f | g | ||||||||||||||||
|
|
|
| ||||||||||||||||
| ((u)(v)) | ((u, v)) |
Figure 61. Propositional Transformation
o-----------------------------------------------------o
| U |
| |
| o-----------o o-----------o |
| / \ / \ |
| / o \ |
| / / \ \ |
| / / \ \ |
| o o o o |
| | | | | |
| | u | | v | |
| | | | | |
| o o o o |
| \ \ / / |
| \ \ / / |
| \ o / |
| \ / \ / |
| o-----------o o-----------o |
| |
| |
o-----------------------------------------------------o
/ \ / \
/ \ / \
/ \ / \
/ \ / \
/ \ / \
/ \ / \
/ \ / \
/ \ / \
/ \ / \
/ \ / \
/ \ / \
/ \ / \
o-------------------------o o-------------------------o
| U | |\U \\\\\\\\\\\\\\\\\\\\\\|
| o---o o---o | |\\\\\\o---o\\\o---o\\\\\\|
| //////\ //////\ | |\\\\\/ \\/ \\\\\\|
| ////////o///////\ | |\\\\/ o \\\\\|
| //////////\///////\ | |\\\/ /\\ \\\\|
| o///////o///o///////o | |\\o o\\\o o\\|
| |// u //|///|// v //| | |\\| u |\\\| v |\\|
| o///////o///o///////o | |\\o o\\\o o\\|
| \///////\////////// | |\\\\ \\/ /\\\|
| \///////o//////// | |\\\\\ o /\\\\|
| \////// \////// | |\\\\\\ /\\ /\\\\\|
| o---o o---o | |\\\\\\o---o\\\o---o\\\\\\|
| | |\\\\\\\\\\\\\\\\\\\\\\\\\|
o-------------------------o o-------------------------o
\ | | /
\ | | /
\ | | /
\ f | | g /
\ | | /
\ | | /
\ | | /
\ | | /
\ | | /
\ | | /
o-------\----|---------------------------|----/-------o
| X \ | | / |
| \| |/ |
| o-----------o o-----------o |
| //////////////\ /\\\\\\\\\\\\\\ |
| ////////////////o\\\\\\\\\\\\\\\\ |
| /////////////////X\\\\\\\\\\\\\\\\\ |
| /////////////////XXX\\\\\\\\\\\\\\\\\ |
| o///////////////oXXXXXo\\\\\\\\\\\\\\\o |
| |///////////////|XXXXX|\\\\\\\\\\\\\\\| |
| |////// x //////|XXXXX|\\\\\\ y \\\\\\| |
| |///////////////|XXXXX|\\\\\\\\\\\\\\\| |
| o///////////////oXXXXXo\\\\\\\\\\\\\\\o |
| \///////////////\XXX/\\\\\\\\\\\\\\\/ |
| \///////////////\X/\\\\\\\\\\\\\\\/ |
| \///////////////o\\\\\\\\\\\\\\\/ |
| \////////////// \\\\\\\\\\\\\\/ |
| o-----------o o-----------o |
| |
| |
o-----------------------------------------------------o
Figure 61. Propositional Transformation
Figure 62. Propositional Transformation (Short Form)
o-------------------------o o-------------------------o
| U | |\U \\\\\\\\\\\\\\\\\\\\\\|
| o---o o---o | |\\\\\\o---o\\\o---o\\\\\\|
| //////\ //////\ | |\\\\\/ \\/ \\\\\\|
| ////////o///////\ | |\\\\/ o \\\\\|
| //////////\///////\ | |\\\/ /\\ \\\\|
| o///////o///o///////o | |\\o o\\\o o\\|
| |// u //|///|// v //| | |\\| u |\\\| v |\\|
| o///////o///o///////o | |\\o o\\\o o\\|
| \///////\////////// | |\\\\ \\/ /\\\|
| \///////o//////// | |\\\\\ o /\\\\|
| \////// \////// | |\\\\\\ /\\ /\\\\\|
| o---o o---o | |\\\\\\o---o\\\o---o\\\\\\|
| | |\\\\\\\\\\\\\\\\\\\\\\\\\|
o-------------------------o o-------------------------o
\ / \ /
\ / \ /
\ / \ /
\ f / \ g /
\ / \ /
\ / \ /
\ / \ /
\ / \ /
\ / \ /
o---------\-----/---------------------\-----/---------o
| X \ / \ / |
| \ / \ / |
| o-----------o o-----------o |
| //////////////\ /\\\\\\\\\\\\\\ |
| ////////////////o\\\\\\\\\\\\\\\\ |
| /////////////////X\\\\\\\\\\\\\\\\\ |
| /////////////////XXX\\\\\\\\\\\\\\\\\ |
| o///////////////oXXXXXo\\\\\\\\\\\\\\\o |
| |///////////////|XXXXX|\\\\\\\\\\\\\\\| |
| |////// x //////|XXXXX|\\\\\\ y \\\\\\| |
| |///////////////|XXXXX|\\\\\\\\\\\\\\\| |
| o///////////////oXXXXXo\\\\\\\\\\\\\\\o |
| \///////////////\XXX/\\\\\\\\\\\\\\\/ |
| \///////////////\X/\\\\\\\\\\\\\\\/ |
| \///////////////o\\\\\\\\\\\\\\\/ |
| \////////////// \\\\\\\\\\\\\\/ |
| o-----------o o-----------o |
| |
| |
o-----------------------------------------------------o
Figure 62. Propositional Transformation (Short Form)
Figure 63. Transformation of Positions
o-----------------------------------------------------o
|`U` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `|
|` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` ` `|
|` ` ` ` ` ` o-----------o ` o-----------o ` ` ` ` ` `|
|` ` ` ` ` `/' ' ' ' ' ' '\`/' ' ' ' ' ' '\` ` ` ` ` `|
|` ` ` ` ` / ' ' ' ' ' ' ' o ' ' ' ' ' ' ' \ ` ` ` ` `|
|` ` ` ` `/' ' ' ' ' ' ' '/^\' ' ' ' ' ' ' '\` ` ` ` `|
|` ` ` ` / ' ' ' ' ' ' ' /^^^\ ' ' ' ' ' ' ' \ ` ` ` `|
|` ` ` `o' ' ' ' ' ' ' 'o^^^^^o' ' ' ' ' ' ' 'o` ` ` `|
|` ` ` `|' ' ' ' ' ' ' '|^^^^^|' ' ' ' ' ' ' '|` ` ` `|
|` ` ` `|' ' ' ' u ' ' '|^^^^^|' ' ' v ' ' ' '|` ` ` `|
|` ` ` `|' ' ' ' ' ' ' '|^^^^^|' ' ' ' ' ' ' '|` ` ` `|
|` `@` `o' ' ' ' @ ' ' 'o^^@^^o' ' ' @ ' ' ' 'o` ` ` `|
|` ` \ ` \ ' ' ' | ' ' ' \^|^/ ' ' ' | ' ' ' / ` ` ` `|
|` ` `\` `\' ' ' | ' ' ' '\|/' ' ' ' | ' ' '/` ` ` ` `|
|` ` ` \ ` \ ' ' | ' ' ' ' | ' ' ' ' | ' ' / ` ` ` ` `|
|` ` ` `\` `\' ' | ' ' ' '/|\' ' ' ' | ' '/` ` ` ` ` `|
|` ` ` ` \ ` o---|-------o | o-------|---o ` ` ` ` ` `|
|` ` ` ` `\` ` ` | ` ` ` ` | ` ` ` ` | ` ` ` ` ` ` ` `|
|` ` ` ` ` \ ` ` | ` ` ` ` | ` ` ` ` | ` ` ` ` ` ` ` `|
o-----------\----|---------|---------|----------------o
" " \ | | | " "
" " \ | | | " "
" " \ | | | " "
" " \| | | " "
o-------------------------o \ | | o-------------------------o
| U | |\ | | |`U```````````````````````|
| o---o o---o | | \ | | |``````o---o```o---o``````|
| /'''''\ /'''''\ | | \ | | |`````/ \`/ \`````|
| /'''''''o'''''''\ | | \ | | |````/ o \````|
| /'''''''/'\'''''''\ | | \ | | |```/ /`\ \```|
| o'''''''o'''o'''''''o | | \ | | |``o o```o o``|
| |'''u'''|'''|'''v'''| | | \ | | |``| u |```| v |``|
| o'''''''o'''o'''''''o | | \ | | |``o o```o o``|
| \'''''''\'/'''''''/ | | \| | |```\ \`/ /```|
| \'''''''o'''''''/ | | \ | |````\ o /````|
| \'''''/ \'''''/ | | |\ | |`````\ /`\ /`````|
| o---o o---o | | | \ | |``````o---o```o---o``````|
| | | | \ * |`````````````````````````|
o-------------------------o | | \ / o-------------------------o
\ | | | \ / | /
\ ((u)(v)) | | | \/ | ((u, v)) /
\ | | | /\ | /
\ | | | / \ | /
\ | | | / \ | /
\ | | | / * | /
\ | | | / | | /
\ | | |/ | | /
\ | | / | | /
\ | | /| | | /
o-------\----|---|-------/-|---------|---|----/-------o
| X \ | | / | | | / |
| \| | / | | |/ |
| o---|----/--o | o-------|---o |
| /' ' | ' / ' '\|/` ` ` ` | ` `\ |
| / ' ' | '/' ' ' | ` ` ` ` | ` ` \ |
| /' ' ' | / ' ' '/|\` ` ` ` | ` ` `\ |
| / ' ' ' |/' ' ' /^|^\ ` ` ` | ` ` ` \ |
| @ o' ' ' ' @ ' ' 'o^^@^^o` ` ` @ ` ` ` `o |
| |' ' ' ' ' ' ' '|^^^^^|` ` ` ` ` ` ` `| |
| |' ' ' ' f ' ' '|^^^^^|` ` ` g ` ` ` `| |
| |' ' ' ' ' ' ' '|^^^^^|` ` ` ` ` ` ` `| |
| o' ' ' ' ' ' ' 'o^^^^^o` ` ` ` ` ` ` `o |
| \ ' ' ' ' ' ' ' \^^^/ ` ` ` ` ` ` ` / |
| \' ' ' ' ' ' ' '\^/` ` ` ` ` ` ` `/ |
| \ ' ' ' ' ' ' ' o ` ` ` ` ` ` ` / |
| \' ' ' ' ' ' '/ \` ` ` ` ` ` `/ |
| o-----------o o-----------o |
| |
| |
o-----------------------------------------------------o
Figure 63. Transformation of Positions
Table 64. Transformation of Positions
Table 64. Transformation of Positions o-----o----------o----------o-------o-------o--------o--------o-------------o | u v | x | y | x y | x(y) | (x)y | (x)(y) | X% = [x, y] | o-----o----------o----------o-------o-------o--------o--------o-------------o | | | | | | | | ^ | | 0 0 | 0 | 1 | 0 | 0 | 1 | 0 | | | | | | | | | | | | | 0 1 | 1 | 0 | 0 | 1 | 0 | 0 | F | | | | | | | | | = | | 1 0 | 1 | 0 | 0 | 1 | 0 | 0 | <f , g> | | | | | | | | | | | 1 1 | 1 | 1 | 1 | 0 | 0 | 0 | ^ | | | | | | | | | | | o-----o----------o----------o-------o-------o--------o--------o-------------o | | ((u)(v)) | ((u, v)) | u v | (u,v) | (u)(v) | 0 | U% = [u, v] | o-----o----------o----------o-------o-------o--------o--------o-------------o
| u v | x | y | x y | x (y) | (x) y | (x)(y) | X • = [x, y ] | ||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||
| ((u)(v)) | ((u, v)) | u v | (u, v) | (u)(v) | ( ) | U • = [u, v ] |
Table 65. Induced Transformation on Propositions
Table 65. Induced Transformation on Propositions o------------o---------------------------------o------------o | X% | <--- F = <f , g> <--- | U% | o------------o----------o-----------o----------o------------o | | u = | 1 1 0 0 | = u | | | | v = | 1 0 1 0 | = v | | | f_i <x, y> o----------o-----------o----------o f_j <u, v> | | | x = | 1 1 1 0 | = f<u,v> | | | | y = | 1 0 0 1 | = g<u,v> | | o------------o----------o-----------o----------o------------o | | | | | | | f_0 | () | 0 0 0 0 | () | f_0 | | | | | | | | f_1 | (x)(y) | 0 0 0 1 | () | f_0 | | | | | | | | f_2 | (x) y | 0 0 1 0 | (u)(v) | f_1 | | | | | | | | f_3 | (x) | 0 0 1 1 | (u)(v) | f_1 | | | | | | | | f_4 | x (y) | 0 1 0 0 | (u, v) | f_6 | | | | | | | | f_5 | (y) | 0 1 0 1 | (u, v) | f_6 | | | | | | | | f_6 | (x, y) | 0 1 1 0 | (u v) | f_7 | | | | | | | | f_7 | (x y) | 0 1 1 1 | (u v) | f_7 | | | | | | | o------------o----------o-----------o----------o------------o | | | | | | | f_8 | x y | 1 0 0 0 | u v | f_8 | | | | | | | | f_9 | ((x, y)) | 1 0 0 1 | u v | f_8 | | | | | | | | f_10 | y | 1 0 1 0 | ((u, v)) | f_9 | | | | | | | | f_11 | (x (y)) | 1 0 1 1 | ((u, v)) | f_9 | | | | | | | | f_12 | x | 1 1 0 0 | ((u)(v)) | f_14 | | | | | | | | f_13 | ((x) y) | 1 1 0 1 | ((u)(v)) | f_14 | | | | | | | | f_14 | ((x)(y)) | 1 1 1 0 | (()) | f_15 | | | | | | | | f_15 | (()) | 1 1 1 1 | (()) | f_15 | | | | | | | o------------o----------o-----------o----------o------------o
| X • |
|
U • | ||||||||||||||||||||||||||||||||||||||||||
| fi‹x, y› |
|
|
|
fj‹u, v› | ||||||||||||||||||||||||||||||||||||||||
|
|
| ||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||
Formula Display 14
o-------------------------------------------------o | | | EG_i = G_i <u + du, v + dv> | | | o-------------------------------------------------o
|
Formula Display 15
o-------------------------------------------------o | | | DG_i = G_i <u, v> + EG_i <u, v, du, dv> | | | | = G_i <u, v> + G_i <u + du, v + dv> | | | o-------------------------------------------------o
|
Formula Display 16
o-------------------------------------------------o | | | Ef = ((u + du)(v + dv)) | | | | Eg = ((u + du, v + dv)) | | | o-------------------------------------------------o
|
Formula Display 17
o-------------------------------------------------o | | | Df = ((u)(v)) + ((u + du)(v + dv)) | | | | Dg = ((u, v)) + ((u + du, v + dv)) | | | o-------------------------------------------------o
|
Table 66-i. Computation Summary for f‹u, v› = ((u)(v))
Table 66-i. Computation Summary for f<u, v> = ((u)(v)) o--------------------------------------------------------------------------------o | | | !e!f = uv. 1 + u(v). 1 + (u)v. 1 + (u)(v). 0 | | | | Ef = uv. (du dv) + u(v). (du (dv)) + (u)v.((du) dv) + (u)(v).((du)(dv)) | | | | Df = uv. du dv + u(v). du (dv) + (u)v. (du) dv + (u)(v).((du)(dv)) | | | | df = uv. 0 + u(v). du + (u)v. dv + (u)(v). (du, dv) | | | | rf = uv. du dv + u(v). du dv + (u)v. du dv + (u)(v). du dv | | | o--------------------------------------------------------------------------------o
|
Table 66-ii. Computation Summary for g‹u, v› = ((u, v))
Table 66-ii. Computation Summary for g<u, v> = ((u, v)) o--------------------------------------------------------------------------------o | | | !e!g = uv. 1 + u(v). 0 + (u)v. 0 + (u)(v). 1 | | | | Eg = uv.((du, dv)) + u(v). (du, dv) + (u)v. (du, dv) + (u)(v).((du, dv)) | | | | Dg = uv. (du, dv) + u(v). (du, dv) + (u)v. (du, dv) + (u)(v). (du, dv) | | | | dg = uv. (du, dv) + u(v). (du, dv) + (u)v. (du, dv) + (u)(v). (du, dv) | | | | rg = uv. 0 + u(v). 0 + (u)v. 0 + (u)(v). 0 | | | o--------------------------------------------------------------------------------o
|
Table 67. Computation of an Analytic Series in Terms of Coordinates
Table 67. Computation of an Analytic Series in Terms of Coordinates o--------o-------o-------o--------o-------o-------o-------o-------o | u v | du dv | u' v' | f g | Ef Eg | Df Dg | df dg | rf rg | o--------o-------o-------o--------o-------o-------o-------o-------o | | | | | | | | | | 0 0 | 0 0 | 0 0 | 0 1 | 0 1 | 0 0 | 0 0 | 0 0 | | | | | | | | | | | | 0 1 | 0 1 | | 1 0 | 1 1 | 1 1 | 0 0 | | | | | | | | | | | | 1 0 | 1 0 | | 1 0 | 1 1 | 1 1 | 0 0 | | | | | | | | | | | | 1 1 | 1 1 | | 1 1 | 1 0 | 0 0 | 1 0 | | | | | | | | | | o--------o-------o-------o--------o-------o-------o-------o-------o | | | | | | | | | | 0 1 | 0 0 | 0 1 | 1 0 | 1 0 | 0 0 | 0 0 | 0 0 | | | | | | | | | | | | 0 1 | 0 0 | | 0 1 | 1 1 | 1 1 | 0 0 | | | | | | | | | | | | 1 0 | 1 1 | | 1 1 | 0 1 | 0 1 | 0 0 | | | | | | | | | | | | 1 1 | 1 0 | | 1 0 | 0 0 | 1 0 | 1 0 | | | | | | | | | | o--------o-------o-------o--------o-------o-------o-------o-------o | | | | | | | | | | 1 0 | 0 0 | 1 0 | 1 0 | 1 0 | 0 0 | 0 0 | 0 0 | | | | | | | | | | | | 0 1 | 1 1 | | 1 1 | 0 1 | 0 1 | 0 0 | | | | | | | | | | | | 1 0 | 0 0 | | 0 1 | 1 1 | 1 1 | 0 0 | | | | | | | | | | | | 1 1 | 0 1 | | 1 0 | 0 0 | 1 0 | 1 0 | | | | | | | | | | o--------o-------o-------o--------o-------o-------o-------o-------o | | | | | | | | | | 1 1 | 0 0 | 1 1 | 1 1 | 1 1 | 0 0 | 0 0 | 0 0 | | | | | | | | | | | | 0 1 | 1 0 | | 1 0 | 0 1 | 0 1 | 0 0 | | | | | | | | | | | | 1 0 | 0 1 | | 1 0 | 0 1 | 0 1 | 0 0 | | | | | | | | | | | | 1 1 | 0 0 | | 0 1 | 1 0 | 0 0 | 1 0 | | | | | | | | | | o--------o-------o-------o--------o-------o-------o-------o-------o
|
|
Table 68. Computation of an Analytic Series in Symbolic Terms
Table 68. Computation of an Analytic Series in Symbolic Terms o-----o-----o------------o----------o----------o----------o----------o----------o | u v | f g | Df | Dg | df | dg | rf | rg | o-----o-----o------------o----------o----------o----------o----------o----------o | | | | | | | | | | 0 0 | 0 1 | ((du)(dv)) | (du, dv) | (du, dv) | (du, dv) | du dv | () | | | | | | | | | | | 0 1 | 1 0 | (du) dv | (du, dv) | dv | (du, dv) | du dv | () | | | | | | | | | | | 1 0 | 1 0 | du (dv) | (du, dv) | du | (du, dv) | du dv | () | | | | | | | | | | | 1 1 | 1 1 | du dv | (du, dv) | () | (du, dv) | du dv | () | | | | | | | | | | o-----o-----o------------o----------o----------o----------o----------o----------o
| u v | f g | Df | Dg | df | dg | d2f | d2g | ||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Formula Display 18
o-------------------------------------------------------------------------o | | | Df = uv. du dv + u(v). du (dv) + (u)v.(du) dv + (u)(v).((du)(dv)) | | | | Dg = uv.(du, dv) + u(v).(du, dv) + (u)v.(du, dv) + (u)(v). (du, dv) | | | o-------------------------------------------------------------------------o
|
Figure 69. Difference Map of F = ‹f, g› = ‹((u)(v)), ((u, v))›
o-----------------------------------o o-----------------------------------o
| U | |`U`````````````````````````````````|
| | |```````````````````````````````````|
| ^ | |```````````````````````````````````|
| | | |```````````````````````````````````|
| o-------o | o-------o | |```````o-------o```o-------o```````|
| ^ /`````````\|/`````````\ ^ | | ^ ```/ ^ \`/ ^ \``` ^ |
| \ /```````````|```````````\ / | |``\``/ \ o / \``/``|
| \/`````u`````/|\`````v`````\/ | |```\/ u \/`\/ v \/```|
| /\``````````/`|`\``````````/\ | |```/\ /\`/\ /\```|
| o``\````````o``@``o````````/``o | |``o \ o``@``o / o``|
| |```\```````|`````|```````/```| | |``| \ |`````| / |``|
| |````@``````|`````|``````@````| | |``| @-------->`<--------@ |``|
| |```````````|`````|```````````| | |``| |`````| |``|
| o```````````o` ^ `o```````````o | |``o o`````o o``|
| \```````````\`|`/```````````/ | |```\ \```/ /```|
| \```` ^ ````\|/```` ^ ````/ | |````\ ^ \`/ ^ /````|
| \`````\`````|`````/`````/ | |`````\ \ o / /`````|
| \`````\```/|\```/`````/ | |``````\ \ /`\ / /``````|
| o-----\-o | o-/-----o | |```````o-----\-o```o-/-----o```````|
| \ | / | |``````````````\`````/``````````````|
| \ | / | |```````````````\```/```````````````|
| \|/ | |````````````````\`/````````````````|
| @ | |`````````````````@`````````````````|
o-----------------------------------o o-----------------------------------o
\ / \ /
\ / \ /
\ ((u)(v)) / \ ((u, v)) /
\ / \ /
\ / \ /
o----------\-------------/-----------------------\-------------/----------o
| X \ / \ / |
| \ / \ / |
| \ / \ / |
| o----------------o o----------------o |
| / \ / \ |
| / o \ |
| / / \ \ |
| / / \ \ |
| / / \ \ |
| / / \ \ |
| / / \ \ |
| o o o o |
| | | | | |
| | | | | |
| | f | | g | |
| | | | | |
| | | | | |
| o o o o |
| \ \ / / |
| \ \ / / |
| \ \ / / |
| \ \ / / |
| \ \ / / |
| \ o / |
| \ / \ / |
| o----------------o o----------------o |
| |
| |
| |
o-------------------------------------------------------------------------o
Figure 69. Difference Map of F = <f, g> = <((u)(v)), ((u, v))>
Formula Display 19
o-------------------------------------------------------------------------------o | | | df = uv. 0 + u(v). du + (u)v. dv + (u)(v).(du, dv) | | | | dg = uv.(du, dv) + u(v).(du, dv) + (u)v.(du, dv) + (u)(v).(du, dv) | | | o-------------------------------------------------------------------------------o
|
Figure 70-a. Tangent Functor Diagram for F‹u, v› = ‹((u)(v)), ((u, v))›
o o
/ \ / \
/ \ / \
/ \ / O \
/ \ o /@\ o
/ \ / \ / \
/ \ / \ / \
/ O \ / O \ / O \
o /@\ o o /@\ o /@\ o
/ \ / \ / \ \ / \ \ / \
/ \ / \ / \ / \ / \
/ \ / \ / O \ / O \ / O \
/ \ / \ o /@ o /@\ o /@ o
/ \ / \ / \ \ / \ / \ \ / \
/ \ / \ / \ / \ / \ / \
/ O \ / O \ / O \ / O \ / O \ / O \
o /@ o /@ o o /@ o /@ o /@ o /@ o
|\ / \ /| |\ / \ / / \ / / \ /|
| \ / \ / | | \ / \ / \ / \ / |
| \ / \ / | | \ / O \ / O \ / O \ / |
| \ / \ / | | o /@ o @\ o /@ o |
| \ / \ / | | |\ / \ / \ / \ / \ /| |
| \ / \ / | | | \ / \ / \ / | |
| u \ / O \ / v | | u | \ / O \ / O \ / | v |
o-------o @\ o-------o o---+---o @\ o @\ o---+---o
\ / | \ / \ / \ / \ / |
\ / | \ / \ / |
\ / | du \ / O \ / dv |
\ / o-------o @\ o-------o
\ / \ /
\ / \ /
\ / \ /
o o
U% $T$ $E$U%
o------------------>o
| |
| |
| |
| |
F | | $T$F
| |
| |
| |
v v
o------------------>o
X% $T$ $E$X%
o o
/ \ / \
/ \ / \
/ \ / O \
/ \ o /@\ o
/ \ / \ / \
/ \ / \ / \
/ O \ / O \ / O \
o /@\ o o /@\ o /@\ o
/ \ / \ / \ \ / \ / / \
/ \ / \ / \ / \ / \
/ \ / \ / O \ / O \ / O \
/ \ / \ o /@ o /@\ o @\ o
/ \ / \ / \ \ / \ / \ / \ / / \
/ \ / \ / \ / \ / \ / \
/ O \ / O \ / O \ / O \ / O \ / O \
o /@ o @\ o o /@ o /@ o @\ o @\ o
|\ / \ /| |\ / \ / \ / \ / \ / \ /|
| \ / \ / | | \ / \ / \ / \ / |
| \ / \ / | | \ / O \ / O \ / O \ / |
| \ / \ / | | o /@ o @ o @\ o |
| \ / \ / | | |\ / / \ / \ / \ \ /| |
| \ / \ / | | | \ / \ / \ / | |
| x \ / O \ / y | | x | \ / O \ / O \ / | y |
o-------o @ o-------o o---+---o @ o @ o---+---o
\ / | \ / / \ \ / |
\ / | \ / \ / |
\ / | dx \ / O \ / dy |
\ / o-------o @ o-------o
\ / \ /
\ / \ /
\ / \ /
o o
Figure 70-a. Tangent Functor Diagram for F‹u, v› = <((u)(v)), ((u, v))>
Figure 70-b. Tangent Functor Ferris Wheel for F‹u, v› = ‹((u)(v)), ((u, v))›
o-----------------------o o-----------------------o o-----------------------o
| dU | | dU | | dU |
| o--o o--o | | o--o o--o | | o--o o--o |
| /////\ /////\ | | /XXXX\ /XXXX\ | | /\\\\\ /\\\\\ |
| ///////o//////\ | | /XXXXXXoXXXXXX\ | | /\\\\\\o\\\\\\\ |
| //////// \//////\ | | /XXXXXX/ \XXXXXX\ | | /\\\\\\/ \\\\\\\\ |
| o/////// \//////o | | oXXXXXX/ \XXXXXXo | | o\\\\\\/ \\\\\\\o |
| |/////o o/////| | | |XXXXXo oXXXXX| | | |\\\\\o o\\\\\| |
| |/du//| |//dv/| | | |XXXXX| |XXXXX| | | |\du\\| |\\dv\| |
| |/////o o/////| | | |XXXXXo oXXXXX| | | |\\\\\o o\\\\\| |
| o//////\ ///////o | | oXXXXXX\ /XXXXXXo | | o\\\\\\\ /\\\\\\o |
| \//////\ //////// | | \XXXXXX\ /XXXXXX/ | | \\\\\\\\ /\\\\\\/ |
| \//////o/////// | | \XXXXXXoXXXXXX/ | | \\\\\\\o\\\\\\/ |
| \///// \///// | | \XXXX/ \XXXX/ | | \\\\\/ \\\\\/ |
| o--o o--o | | o--o o--o | | o--o o--o |
| | | | | |
o-----------------------o o-----------------------o o-----------------------o
= du' @ (u)(v) o-----------------------o dv' @ (u)(v) =
= | dU' | =
= | o--o o--o | =
= | /////\ /\\\\\ | =
= | ///////o\\\\\\\ | =
= | ////////X\\\\\\\\ | =
= | o///////XXX\\\\\\\o | =
= | |/////oXXXXXo\\\\\| | =
= = = = = = = = = = =|/du'/|XXXXX|\dv'\|= = = = = = = = = = =
| |/////oXXXXXo\\\\\| |
| o//////\XXX/\\\\\\o |
| \//////\X/\\\\\\/ |
| \//////o\\\\\\/ |
| \///// \\\\\/ |
| o--o o--o |
| |
o-----------------------o
o-----------------------o o-----------------------o o-----------------------o
| dU | | dU | | dU |
| o--o o--o | | o--o o--o | | o--o o--o |
| / \ /////\ | | /\\\\\ /XXXX\ | | /\\\\\ /\\\\\ |
| / o//////\ | | /\\\\\\oXXXXXX\ | | /\\\\\\o\\\\\\\ |
| / //\//////\ | | /\\\\\\//\XXXXXX\ | | /\\\\\\/ \\\\\\\\ |
| o ////\//////o | | o\\\\\\////\XXXXXXo | | o\\\\\\/ \\\\\\\o |
| | o/////o/////| | | |\\\\\o/////oXXXXX| | | |\\\\\o o\\\\\| |
| | du |/////|//dv/| | | |\\\\\|/////|XXXXX| | | |\du\\| |\\dv\| |
| | o/////o/////| | | |\\\\\o/////oXXXXX| | | |\\\\\o o\\\\\| |
| o \//////////o | | o\\\\\\\////XXXXXXo | | o\\\\\\\ /\\\\\\o |
| \ \///////// | | \\\\\\\\//XXXXXX/ | | \\\\\\\\ /\\\\\\/ |
| \ o/////// | | \\\\\\\oXXXXXX/ | | \\\\\\\o\\\\\\/ |
| \ / \///// | | \\\\\/ \XXXX/ | | \\\\\/ \\\\\/ |
| o--o o--o | | o--o o--o | | o--o o--o |
| | | | | |
o-----------------------o o-----------------------o o-----------------------o
= du' @ (u) v o-----------------------o dv' @ (u) v =
= | dU' | =
= | o--o o--o | =
= | /////\ /\\\\\ | =
= | ///////o\\\\\\\ | =
= | ////////X\\\\\\\\ | =
= | o///////XXX\\\\\\\o | =
= | |/////oXXXXXo\\\\\| | =
= = = = = = = = = = =|/du'/|XXXXX|\dv'\|= = = = = = = = = = =
| |/////oXXXXXo\\\\\| |
| o//////\XXX/\\\\\\o |
| \//////\X/\\\\\\/ |
| \//////o\\\\\\/ |
| \///// \\\\\/ |
| o--o o--o |
| |
o-----------------------o
o-----------------------o o-----------------------o o-----------------------o
| dU | | dU | | dU |
| o--o o--o | | o--o o--o | | o--o o--o |
| /////\ / \ | | /XXXX\ /\\\\\ | | /\\\\\ /\\\\\ |
| ///////o \ | | /XXXXXXo\\\\\\\ | | /\\\\\\o\\\\\\\ |
| /////////\ \ | | /XXXXXX//\\\\\\\\ | | /\\\\\\/ \\\\\\\\ |
| o//////////\ o | | oXXXXXX////\\\\\\\o | | o\\\\\\/ \\\\\\\o |
| |/////o/////o | | | |XXXXXo/////o\\\\\| | | |\\\\\o o\\\\\| |
| |/du//|/////| dv | | | |XXXXX|/////|\\\\\| | | |\du\\| |\\dv\| |
| |/////o/////o | | | |XXXXXo/////o\\\\\| | | |\\\\\o o\\\\\| |
| o//////\//// o | | oXXXXXX\////\\\\\\o | | o\\\\\\\ /\\\\\\o |
| \//////\// / | | \XXXXXX\//\\\\\\/ | | \\\\\\\\ /\\\\\\/ |
| \//////o / | | \XXXXXXo\\\\\\/ | | \\\\\\\o\\\\\\/ |
| \///// \ / | | \XXXX/ \\\\\/ | | \\\\\/ \\\\\/ |
| o--o o--o | | o--o o--o | | o--o o--o |
| | | | | |
o-----------------------o o-----------------------o o-----------------------o
= du' @ u (v) o-----------------------o dv' @ u (v) =
= | dU' | =
= | o--o o--o | =
= | /////\ /\\\\\ | =
= | ///////o\\\\\\\ | =
= | ////////X\\\\\\\\ | =
= | o///////XXX\\\\\\\o | =
= | |/////oXXXXXo\\\\\| | =
= = = = = = = = = = =|/du'/|XXXXX|\dv'\|= = = = = = = = = = =
| |/////oXXXXXo\\\\\| |
| o//////\XXX/\\\\\\o |
| \//////\X/\\\\\\/ |
| \//////o\\\\\\/ |
| \///// \\\\\/ |
| o--o o--o |
| |
o-----------------------o
o-----------------------o o-----------------------o o-----------------------o
| dU | | dU | | dU |
| o--o o--o | | o--o o--o | | o--o o--o |
| / \ / \ | | /\\\\\ /\\\\\ | | /\\\\\ /\\\\\ |
| / o \ | | /\\\\\\o\\\\\\\ | | /\\\\\\o\\\\\\\ |
| / / \ \ | | /\\\\\\/ \\\\\\\\ | | /\\\\\\/ \\\\\\\\ |
| o / \ o | | o\\\\\\/ \\\\\\\o | | o\\\\\\/ \\\\\\\o |
| | o o | | | |\\\\\o o\\\\\| | | |\\\\\o o\\\\\| |
| | du | | dv | | | |\\\\\| |\\\\\| | | |\du\\| |\\dv\| |
| | o o | | | |\\\\\o o\\\\\| | | |\\\\\o o\\\\\| |
| o \ / o | | o\\\\\\\ /\\\\\\o | | o\\\\\\\ /\\\\\\o |
| \ \ / / | | \\\\\\\\ /\\\\\\/ | | \\\\\\\\ /\\\\\\/ |
| \ o / | | \\\\\\\o\\\\\\/ | | \\\\\\\o\\\\\\/ |
| \ / \ / | | \\\\\/ \\\\\/ | | \\\\\/ \\\\\/ |
| o--o o--o | | o--o o--o | | o--o o--o |
| | | | | |
o-----------------------o o-----------------------o o-----------------------o
= du' @ u v o-----------------------o dv' @ u v =
= | dU' | =
= | o--o o--o | =
= | /////\ /\\\\\ | =
= | ///////o\\\\\\\ | =
= | ////////X\\\\\\\\ | =
= | o///////XXX\\\\\\\o | =
= | |/////oXXXXXo\\\\\| | =
= = = = = = = = = = =|/du'/|XXXXX|\dv'\|= = = = = = = = = = =
| |/////oXXXXXo\\\\\| |
| o//////\XXX/\\\\\\o |
| \//////\X/\\\\\\/ |
| \//////o\\\\\\/ |
| \///// \\\\\/ |
| o--o o--o |
| |
o-----------------------o
o-----------------------o o-----------------------o o-----------------------o
| U | |\U\\\\\\\\\\\\\\\\\\\\\| |\U\\\\\\\\\\\\\\\\\\\\\|
| o--o o--o | |\\\\\\o--o\\\o--o\\\\\\| |\\\\\\o--o\\\o--o\\\\\\|
| /////\ /////\ | |\\\\\/////\\/////\\\\\\| |\\\\\/ \\/ \\\\\\|
| ///////o//////\ | |\\\\///////o//////\\\\\| |\\\\/ o \\\\\|
| /////////\//////\ | |\\\////////X\//////\\\\| |\\\/ /\\ \\\\|
| o//////////\//////o | |\\o///////XXX\//////o\\| |\\o /\\\\ o\\|
| |/////o/////o/////| | |\\|/////oXXXXXo/////|\\| |\\| o\\\\\o |\\|
| |//u//|/////|//v//| | |\\|//u//|XXXXX|//v//|\\| |\\| u |\\\\\| v |\\|
| |/////o/////o/////| | |\\|/////oXXXXXo/////|\\| |\\| o\\\\\o |\\|
| o//////\//////////o | |\\o//////\XXX///////o\\| |\\o \\\\/ o\\|
| \//////\///////// | |\\\\//////\X////////\\\| |\\\\ \\/ /\\\|
| \//////o/////// | |\\\\\//////o///////\\\\| |\\\\\ o /\\\\|
| \///// \///// | |\\\\\\/////\\/////\\\\\| |\\\\\\ /\\ /\\\\\|
| o--o o--o | |\\\\\\o--o\\\o--o\\\\\\| |\\\\\\o--o\\\o--o\\\\\\|
| | |\\\\\\\\\\\\\\\\\\\\\\\| |\\\\\\\\\\\\\\\\\\\\\\\|
o-----------------------o o-----------------------o o-----------------------o
= u' o-----------------------o v' =
= | U' | =
= | o--o o--o | =
= | /////\ /\\\\\ | =
= | ///////o\\\\\\\ | =
= | ////////X\\\\\\\\ | =
= | o///////XXX\\\\\\\o | =
= | |/////oXXXXXo\\\\\| | =
= = = = = = = = = = =|/u'//|XXXXX|\\v'\|= = = = = = = = = = =
| |/////oXXXXXo\\\\\| |
| o//////\XXX/\\\\\\o |
| \//////\X/\\\\\\/ |
| \//////o\\\\\\/ |
| \///// \\\\\/ |
| o--o o--o |
| |
o-----------------------o
Figure 70-b. Tangent Functor Ferris Wheel for F<u, v> = <((u)(v)), ((u, v))>