Difference between revisions of "Minimal negation operator"
Jon Awbrey (talk | contribs) (spacing) |
Jon Awbrey (talk | contribs) (expand discussion of properties) |
||
| Line 46: | Line 46: | ||
If we think of the point <math>x = (x_1, \ldots, x_k) \in \mathbb{B}^k</math> as indicated by the boolean product <math>x_1 \cdot \ldots \cdot x_k</math> or the logical conjunction <math>x_1 \land \ldots \land x_k,</math> then the minimal negation <math>\texttt{(} x_1, \ldots, x_k \texttt{)}</math> indicates the set of points in <math>\mathbb{B}^k</math> that differ from <math>x\!</math> in exactly one coordinate. This makes <math>\texttt{(} x_1, \ldots, x_k \texttt{)}</math> a discrete functional analogue of a ''point omitted neighborhood'' in analysis, more exactly, a ''point omitted distance one neighborhood''. In this light, the minimal negation operator can be recognized as a differential construction, an observation that opens a very wide field. It also serves to explain a variety of other names for the same concept, for example, ''logical boundary operator'', ''limen operator'', ''threshold operator'', or ''least action operator'', to name but a few. | If we think of the point <math>x = (x_1, \ldots, x_k) \in \mathbb{B}^k</math> as indicated by the boolean product <math>x_1 \cdot \ldots \cdot x_k</math> or the logical conjunction <math>x_1 \land \ldots \land x_k,</math> then the minimal negation <math>\texttt{(} x_1, \ldots, x_k \texttt{)}</math> indicates the set of points in <math>\mathbb{B}^k</math> that differ from <math>x\!</math> in exactly one coordinate. This makes <math>\texttt{(} x_1, \ldots, x_k \texttt{)}</math> a discrete functional analogue of a ''point omitted neighborhood'' in analysis, more exactly, a ''point omitted distance one neighborhood''. In this light, the minimal negation operator can be recognized as a differential construction, an observation that opens a very wide field. It also serves to explain a variety of other names for the same concept, for example, ''logical boundary operator'', ''limen operator'', ''threshold operator'', or ''least action operator'', to name but a few. | ||
| − | + | In what follows, the boolean domain <math>\mathbb{B} = \{ 0, 1 \}</math> is interpreted so that <math>0 = \operatorname{false}</math> and <math>1 = \operatorname{true}.</math> In this context, the plus sign <math>(+)\!</math> and the summation symbol <math>(\textstyle\sum)</math> both refer to addition modulo 2. This has the following consequences: | |
| + | |||
| + | {| align="center" cellpadding="4" width="90%" | ||
| + | | valign="top" | <big>•</big> | ||
| + | | The operation <math>x + y\!</math> is a function equivalent to the exclusive disjunction of <math>x\!</math> and <math>y,\!</math> while its fiber of 1 is the relation of inequality between <math>x\!</math> and <math>y.\!</math> | ||
| + | |- | ||
| + | | valign="top" | <big>•</big> | ||
| + | | The operation <math>\textstyle\sum_{j=1}^k x_j</math> maps the bit sequence <math>(x_1, \ldots, x_k)\!</math> to its ''parity''. | ||
| + | |} | ||
| + | |||
| + | The following properties of the minimal negation operators <math>\nu_k : \mathbb{B}^k \to \mathbb{B}</math> may be noted: | ||
| + | |||
| + | {| align="center" cellpadding="4" width="90%" | ||
| + | | valign="top" | <big>•</big> | ||
| + | | The function <math>\texttt{(x, y)}</math> is the same as that associated with the operation <math>x + y\!</math> and the relation <math>x \ne y.</math></p> | ||
| + | |- | ||
| + | | valign="top" | <big>•</big> | ||
| + | | In contrast, <math>\texttt{(x, y, z)}</math> is not identical to <math>x + y + z.\!</math> | ||
| + | |- | ||
| + | | valign="top" | <big>•</big> | ||
| + | | More generally, the function <math>\nu_k (x_1, \dots, x_k)</math> for <math>k > 2\!</math> is not identical to the boolean sum <math>\textstyle\sum_{j=1}^k x_j.</math></p> | ||
| + | |- | ||
| + | | valign="top" | <big>•</big> | ||
| + | | The inclusive disjunctions indicated for the <math>\nu_k\!</math> of more than one argument may be replaced with exclusive disjunctions without affecting the meaning, since the terms disjoined are already disjoint.</p> | ||
| + | |} | ||
==Truth tables== | ==Truth tables== | ||
Revision as of 19:29, 24 August 2009
The minimal negation operator \(\nu\!\) is a multigrade operator \((\nu_k)_{k \in \mathbb{N}}\) where each \(\nu_k\!\) is a \(k\!\)-ary boolean function defined in such a way that \(\nu_k (x_1, \ldots , x_k) = 1\) in just those cases where exactly one of the arguments \(x_j\!\) is \(0.\!\)
In contexts where the initial letter \(\nu\!\) is understood, the minimal negation operators can be indicated by argument lists in parentheses. In the following text a distinctive typeface will be used for logical expressions based on minimal negation operators, for example, \(\texttt{(x, y, z)}\) = \(\nu (x, y, z).\!\)
The first four members of this family of operators are shown below, with paraphrases in a couple of other notations, where tildes and primes, respectively, indicate logical negation.
|
\(\begin{matrix} \texttt{()} & = & \nu_0 & = & 0 & = & \operatorname{false} \'"`UNIQ-MathJax1-QINU`"' * The point \((0, 0, \ldots , 0, 0)\) with all 0's as coordinates is the point where the conjunction of all negated variables evaluates to \(1,\!\) namely, the point where:
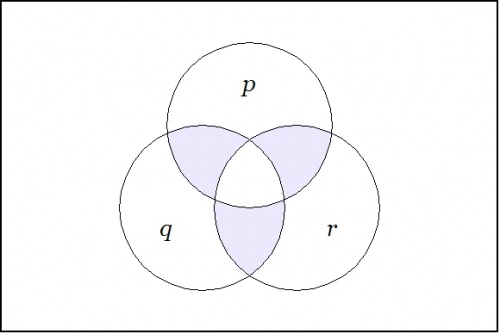
To pass from these limiting examples to the general case, observe that a singular proposition \(s : \mathbb{B}^k \to \mathbb{B}\) can be given canonical expression as a conjunction of literals, \(s = e_1 e_2 \ldots e_{k-1} e_k\). Then the proposition \(\nu (e_1, e_2, \ldots, e_{k-1}, e_k)\) is \(1\!\) on the points adjacent to the point where \(s\!\) is \(1,\!\) and 0 everywhere else on the cube. For example, consider the case where \(k = 3.\!\) Then the minimal negation operation \(\nu (p, q, r)\!\) — written more simply as \(\texttt{(p, q, r)}\) — has the following venn diagram:
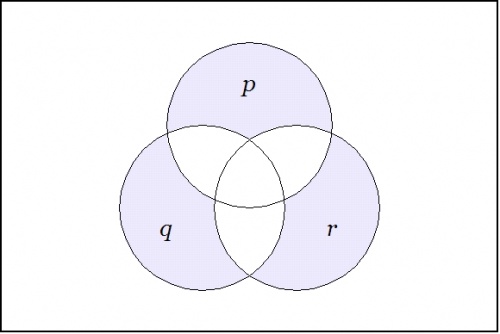
For a contrasting example, the boolean function expressed by the form \(\texttt{((p),(q),(r))}\) has the following venn diagram:
Glossary of basic terms
See alsoTemplate:Col-break
External links
|