Difference between revisions of "Minimal negation operator"
Jon Awbrey (talk | contribs) (add exposition) |
Jon Awbrey (talk | contribs) (expand a bit) |
||
| Line 9: | Line 9: | ||
<math>\begin{matrix} | <math>\begin{matrix} | ||
\texttt{()} | \texttt{()} | ||
| + | & = & \nu_0 | ||
& = & 0 | & = & 0 | ||
& = & \operatorname{false} | & = & \operatorname{false} | ||
\\[6pt] | \\[6pt] | ||
\texttt{(x)} | \texttt{(x)} | ||
| + | & = & \nu_1 (x) | ||
& = & \tilde{x} | & = & \tilde{x} | ||
& = & x^\prime | & = & x^\prime | ||
\\[6pt] | \\[6pt] | ||
\texttt{(x, y)} | \texttt{(x, y)} | ||
| + | & = & \nu (x, y) | ||
& = & \tilde{x}y \lor x\tilde{y} | & = & \tilde{x}y \lor x\tilde{y} | ||
& = & x^\prime y \lor x y^\prime | & = & x^\prime y \lor x y^\prime | ||
\\[6pt] | \\[6pt] | ||
\texttt{(x, y, z)} | \texttt{(x, y, z)} | ||
| + | & = & \nu (x, y, z) | ||
& = & \tilde{x}yz \lor x\tilde{y}z \lor xy\tilde{z} | & = & \tilde{x}yz \lor x\tilde{y}z \lor xy\tilde{z} | ||
& = & x^\prime y z \lor x y^\prime z \lor x y z^\prime | & = & x^\prime y z \lor x y^\prime z \lor x y z^\prime | ||
| Line 26: | Line 30: | ||
|} | |} | ||
| − | + | To express the general case of <math>\nu_k\!</math> in terms of familiar operations, it helps to make a preliminary definition. | |
| − | '''Definition.''' Let the function <math>\lnot_j : \mathbb{B}^k \to \mathbb{B},</math> | + | '''Definition.''' Let the function <math>\lnot_j : \mathbb{B}^k \to \mathbb{B},</math> where <math>j\!</math> is an integer in the interval <math>[1, k],\!</math> be defined by the following equation: |
{| align="center" cellpadding="8" width="90%" | {| align="center" cellpadding="8" width="90%" | ||
Revision as of 11:14, 24 August 2009
The minimal negation operator \(\nu\!\) is a multigrade operator \((\nu_k)_{k \in \mathbb{N}}\) where each \(\nu_k\!\) is a \(k\!\)-ary boolean function defined in such a way that \(\nu_k (x_1, \ldots , x_k) = 1\) if and only if exactly one of the arguments \(x_j\!\) is \(0.\!\)
In contexts where the initial letter \(\nu\!\) is understood, the minimal negation operators may be indicated by argument lists in parentheses. In the following text, a distinctive typeface will be used for logical expressions based on minimal negation operators, for example, \(\texttt{(x, y, z)}\) = \(\nu (x, y, z).\!\)
The first four members of this family of operators are shown below, with paraphrases in a couple of other notations, where tildes and primes, respectively, indicate logical negation
|
\(\begin{matrix} \texttt{()} & = & \nu_0 & = & 0 & = & \operatorname{false} \'"`UNIQ-MathJax1-QINU`"' * The point \((0, 0, \ldots , 0, 0)\) with all 0's as coordinates is the point where the conjunction of all negated variables evaluates to \(1,\!\) namely, the point where:
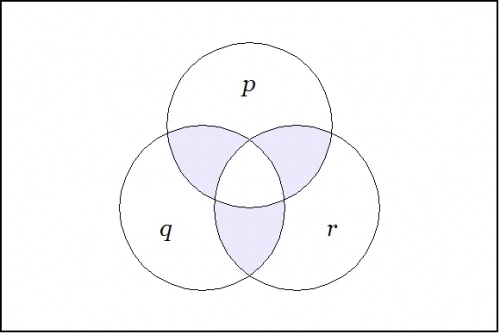
To pass from these limiting examples to the general case, observe that a singular proposition \(s : \mathbb{B}^k \to \mathbb{B}\) can be given canonical expression as a conjunction of literals, \(s = e_1 e_2 \ldots e_{k-1} e_k\). Then the proposition \(\nu (e_1, e_2, \ldots, e_{k-1}, e_k)\) is \(1\!\) on the points adjacent to the point where \(s\!\) is \(1,\!\) and 0 everywhere else on the cube. For example, consider the case where \(k = 3.\!\) Then the minimal negation operation \(\nu (p, q, r)\!\) — written more simply as \(\texttt{(p, q, r)}\) — has the following venn diagram:
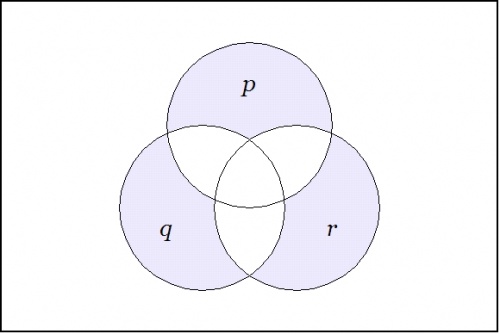
For a contrasting example, the boolean function expressed by the form \(\texttt{((p),(q),(r))}\) has the following venn diagram:
Glossary of basic terms
See alsoTemplate:Col-break
External links
|