Difference between revisions of "Directory:Jon Awbrey/Papers/Differential Propositional Calculus"
Jon Awbrey (talk | contribs) (→Casual introduction: table background) |
Jon Awbrey (talk | contribs) (→Formal development: table colors) |
||
| Line 280: | Line 280: | ||
A set of logical features, <math>\mathcal{A} = \{ a_1, \ldots, a_n \},</math> affords a basis for generating an <math>n\!</math>-dimensional universe of discourse, written <math>A^\circ = [ \mathcal{A} ] = [ a_1, \ldots, a_n ].</math> It is useful to consider a universe of discourse as a categorical object that incorporates both the set of points <math>A = \langle a_1, \ldots, a_n \rangle</math> and the set of propositions <math>A^\uparrow = \{ f : A \to \mathbb{B} \}</math> that are implicit with the ordinary picture of a venn diagram on <math>n\!</math> features. Accordingly, the universe of discourse <math>A^\circ</math> may be regarded as an ordered pair <math>(A, A^\uparrow)</math> having the type <math>(\mathbb{B}^n, (\mathbb{B}^n \to \mathbb{B})),</math> and this last type designation may be abbreviated as <math>\mathbb{B}^n\ +\!\to \mathbb{B},</math> or even more succinctly as <math>[ \mathbb{B}^n ].</math> For convenience, the data type of a finite set on <math>n\!</math> elements may be indicated by either one of the equivalent notations, <math>[n]\!</math> or <math>\mathbf{n}.</math> | A set of logical features, <math>\mathcal{A} = \{ a_1, \ldots, a_n \},</math> affords a basis for generating an <math>n\!</math>-dimensional universe of discourse, written <math>A^\circ = [ \mathcal{A} ] = [ a_1, \ldots, a_n ].</math> It is useful to consider a universe of discourse as a categorical object that incorporates both the set of points <math>A = \langle a_1, \ldots, a_n \rangle</math> and the set of propositions <math>A^\uparrow = \{ f : A \to \mathbb{B} \}</math> that are implicit with the ordinary picture of a venn diagram on <math>n\!</math> features. Accordingly, the universe of discourse <math>A^\circ</math> may be regarded as an ordered pair <math>(A, A^\uparrow)</math> having the type <math>(\mathbb{B}^n, (\mathbb{B}^n \to \mathbb{B})),</math> and this last type designation may be abbreviated as <math>\mathbb{B}^n\ +\!\to \mathbb{B},</math> or even more succinctly as <math>[ \mathbb{B}^n ].</math> For convenience, the data type of a finite set on <math>n\!</math> elements may be indicated by either one of the equivalent notations, <math>[n]\!</math> or <math>\mathbf{n}.</math> | ||
| − | Table 5 summarizes the notations that are needed to describe ordinary propositional calculi in a systematic fashion. | + | Table 5 summarizes the notations that are needed to describe ordinary propositional calculi in a systematic fashion. |
| − | {| align="center" border="1" cellpadding="8" cellspacing="0" style="text-align:left; width: | + | <br> |
| + | |||
| + | {| align="center" border="1" cellpadding="8" cellspacing="0" style="background:#f8f8ff; text-align:left; width:90%" | ||
|+ '''Table 5. Propositional Calculus : Basic Notation''' | |+ '''Table 5. Propositional Calculus : Basic Notation''' | ||
| − | |- style="background: | + | |- style="background:#e6e6ff" |
! Symbol | ! Symbol | ||
! Notation | ! Notation | ||
| Line 306: | Line 308: | ||
|- | |- | ||
| <math>A\!</math> | | <math>A\!</math> | ||
| − | | <math>\langle \mathcal{A} \rangle</math><br> | + | | |
| + | <math>\langle \mathcal{A} \rangle</math><br> | ||
<math>\langle a_1, \ldots, a_n \rangle</math><br> | <math>\langle a_1, \ldots, a_n \rangle</math><br> | ||
<math>\{ (a_1, \ldots, a_n) \}\!</math> | <math>\{ (a_1, \ldots, a_n) \}\!</math> | ||
<math>A_1 \times \ldots \times A_n</math><br> | <math>A_1 \times \ldots \times A_n</math><br> | ||
<math>\textstyle \prod_i A_i\!</math> | <math>\textstyle \prod_i A_i\!</math> | ||
| − | | Set of cells,<br> | + | | |
| + | Set of cells,<br> | ||
coordinate tuples,<br> | coordinate tuples,<br> | ||
points, or vectors<br> | points, or vectors<br> | ||
| Line 329: | Line 333: | ||
|- | |- | ||
| <math>A^\circ</math> | | <math>A^\circ</math> | ||
| − | | <math>[ \mathcal{A} ]</math><br> | + | | |
| + | <math>[ \mathcal{A} ]</math><br> | ||
<math>(A, A^\uparrow)</math><br> | <math>(A, A^\uparrow)</math><br> | ||
<math>(A\ +\!\to \mathbb{B})</math><br> | <math>(A\ +\!\to \mathbb{B})</math><br> | ||
<math>(A, (A \to \mathbb{B}))</math><br> | <math>(A, (A \to \mathbb{B}))</math><br> | ||
<math>[ a_1, \ldots, a_n ]</math> | <math>[ a_1, \ldots, a_n ]</math> | ||
| − | | Universe of discourse<br> | + | | |
| + | Universe of discourse<br> | ||
based on the features<br> | based on the features<br> | ||
<math>\{ a_1, \ldots, a_n \}</math> | <math>\{ a_1, \ldots, a_n \}</math> | ||
| − | | <math>(\mathbb{B}^n, (\mathbb{B}^n \to \mathbb{B}))</math><br> | + | | |
| + | <math>(\mathbb{B}^n, (\mathbb{B}^n \to \mathbb{B}))</math><br> | ||
<math>(\mathbb{B}^n\ +\!\to \mathbb{B})</math><br> | <math>(\mathbb{B}^n\ +\!\to \mathbb{B})</math><br> | ||
<math>[\mathbb{B}^n]</math> | <math>[\mathbb{B}^n]</math> | ||
|} | |} | ||
| + | |||
<br> | <br> | ||
| Line 375: | Line 383: | ||
A proposition in a differential extension of a universe of discourse is called a ''differential proposition'' and forms the analogue of a system of differential equations in ordinary calculus. With these constructions, the first order extended universe <math>\operatorname{E}A^\circ</math> and the first order differential proposition <math>f : \operatorname{E}A \to \mathbb{B},</math> we have arrived, in concept at least, at the foothills of [[differential logic]]. | A proposition in a differential extension of a universe of discourse is called a ''differential proposition'' and forms the analogue of a system of differential equations in ordinary calculus. With these constructions, the first order extended universe <math>\operatorname{E}A^\circ</math> and the first order differential proposition <math>f : \operatorname{E}A \to \mathbb{B},</math> we have arrived, in concept at least, at the foothills of [[differential logic]]. | ||
| − | Table 6 summarizes the notations that are needed to describe the first order differential extensions of propositional calculi in a systematic manner. | + | Table 6 summarizes the notations that are needed to describe the first order differential extensions of propositional calculi in a systematic manner. |
| + | |||
| + | <br> | ||
| − | {| align="center" border="1" cellpadding="8" cellspacing="0" style="text-align:left; width: | + | {| align="center" border="1" cellpadding="8" cellspacing="0" style="background:#f8f8ff; text-align:left; width:90%" |
|+ '''Table 6. Differential Extension : Basic Notation''' | |+ '''Table 6. Differential Extension : Basic Notation''' | ||
| − | |- style="background: | + | |- style="background:#e6e6ff" |
! Symbol | ! Symbol | ||
! Notation | ! Notation | ||
| Line 387: | Line 397: | ||
| <math>\operatorname{d}\mathfrak{A}</math> | | <math>\operatorname{d}\mathfrak{A}</math> | ||
| <math>\lbrace\!</math> “<math>\operatorname{d}a_1</math>” <math>, \ldots,\!</math> “<math>\operatorname{d}a_n</math>” <math>\rbrace\!</math> | | <math>\lbrace\!</math> “<math>\operatorname{d}a_1</math>” <math>, \ldots,\!</math> “<math>\operatorname{d}a_n</math>” <math>\rbrace\!</math> | ||
| − | | Alphabet of<br> | + | | |
| + | Alphabet of<br> | ||
differential<br> | differential<br> | ||
symbols | symbols | ||
| Line 394: | Line 405: | ||
| <math>\operatorname{d}\mathcal{A}</math> | | <math>\operatorname{d}\mathcal{A}</math> | ||
| <math>\{ \operatorname{d}a_1, \ldots, \operatorname{d}a_n \}</math> | | <math>\{ \operatorname{d}a_1, \ldots, \operatorname{d}a_n \}</math> | ||
| − | | Basis of<br> | + | | |
| + | Basis of<br> | ||
differential<br> | differential<br> | ||
features | features | ||
| Line 401: | Line 413: | ||
| <math>\operatorname{d}A_i</math> | | <math>\operatorname{d}A_i</math> | ||
| <math>\{ \overline{\operatorname{d}a_i}, \operatorname{d}a_i \}</math> | | <math>\{ \overline{\operatorname{d}a_i}, \operatorname{d}a_i \}</math> | ||
| − | | Differential<br> | + | | |
| + | Differential<br> | ||
dimension <math>i\!</math> | dimension <math>i\!</math> | ||
| <math>\mathbb{D}</math> | | <math>\mathbb{D}</math> | ||
|- | |- | ||
| <math>\operatorname{d}A</math> | | <math>\operatorname{d}A</math> | ||
| − | | <math>\langle \operatorname{d}\mathcal{A} \rangle</math><br> | + | | |
| + | <math>\langle \operatorname{d}\mathcal{A} \rangle</math><br> | ||
<math>\langle \operatorname{d}a_1, \ldots, \operatorname{d}a_n \rangle</math><br> | <math>\langle \operatorname{d}a_1, \ldots, \operatorname{d}a_n \rangle</math><br> | ||
<math>\{ (\operatorname{d}a_1, \ldots, \operatorname{d}a_n) \}</math><br> | <math>\{ (\operatorname{d}a_1, \ldots, \operatorname{d}a_n) \}</math><br> | ||
<math>\operatorname{d}A_1 \times \ldots \times \operatorname{d}A_n</math><br> | <math>\operatorname{d}A_1 \times \ldots \times \operatorname{d}A_n</math><br> | ||
<math>\textstyle \prod_i \operatorname{d}A_i</math> | <math>\textstyle \prod_i \operatorname{d}A_i</math> | ||
| − | | Tangent space<br> | + | | |
| + | Tangent space<br> | ||
at a point:<br> | at a point:<br> | ||
Set of changes,<br> | Set of changes,<br> | ||
| Line 421: | Line 436: | ||
| <math>\operatorname{d}A^*</math> | | <math>\operatorname{d}A^*</math> | ||
| <math>(\operatorname{hom} : \operatorname{d}A \to \mathbb{B})</math> | | <math>(\operatorname{hom} : \operatorname{d}A \to \mathbb{B})</math> | ||
| − | | Linear functions<br> | + | | |
| + | Linear functions<br> | ||
on <math>\operatorname{d}A</math> | on <math>\operatorname{d}A</math> | ||
| <math>(\mathbb{D}^n)^* \cong \mathbb{D}^n</math> | | <math>(\mathbb{D}^n)^* \cong \mathbb{D}^n</math> | ||
| Line 427: | Line 443: | ||
| <math>\operatorname{d}A^\uparrow</math> | | <math>\operatorname{d}A^\uparrow</math> | ||
| <math>(\operatorname{d}A \to \mathbb{B})</math> | | <math>(\operatorname{d}A \to \mathbb{B})</math> | ||
| − | | Boolean functions<br> | + | | |
| + | Boolean functions<br> | ||
on <math>\operatorname{d}A</math> | on <math>\operatorname{d}A</math> | ||
| <math>\mathbb{D}^n \to \mathbb{B}</math> | | <math>\mathbb{D}^n \to \mathbb{B}</math> | ||
|- | |- | ||
| <math>\operatorname{d}A^\circ</math> | | <math>\operatorname{d}A^\circ</math> | ||
| − | | <math>[\operatorname{d}\mathcal{A}]</math><br> | + | | |
| + | <math>[\operatorname{d}\mathcal{A}]</math><br> | ||
<math>(\operatorname{d}A, \operatorname{d}A^\uparrow)</math><br> | <math>(\operatorname{d}A, \operatorname{d}A^\uparrow)</math><br> | ||
<math>(\operatorname{d}A\ +\!\to \mathbb{B})</math><br> | <math>(\operatorname{d}A\ +\!\to \mathbb{B})</math><br> | ||
<math>(\operatorname{d}A, (\operatorname{d}A \to \mathbb{B}))</math><br> | <math>(\operatorname{d}A, (\operatorname{d}A \to \mathbb{B}))</math><br> | ||
<math>[\operatorname{d}a_1, \ldots, \operatorname{d}a_n]</math> | <math>[\operatorname{d}a_1, \ldots, \operatorname{d}a_n]</math> | ||
| − | | Tangent universe<br> | + | | |
| + | Tangent universe<br> | ||
at a point of <math>A^\circ,</math><br> | at a point of <math>A^\circ,</math><br> | ||
based on the<br> | based on the<br> | ||
tangent features<br> | tangent features<br> | ||
<math>\{ \operatorname{d}a_1, \ldots, \operatorname{d}a_n \}</math> | <math>\{ \operatorname{d}a_1, \ldots, \operatorname{d}a_n \}</math> | ||
| − | | <math>(\mathbb{D}^n, (\mathbb{D}^n \to \mathbb{B}))</math><br> | + | | |
| + | <math>(\mathbb{D}^n, (\mathbb{D}^n \to \mathbb{B}))</math><br> | ||
<math>(\mathbb{D}^n\ +\!\to \mathbb{B})</math><br> | <math>(\mathbb{D}^n\ +\!\to \mathbb{B})</math><br> | ||
<math>[\mathbb{D}^n]</math> | <math>[\mathbb{D}^n]</math> | ||
|} | |} | ||
| + | |||
<br> | <br> | ||
Revision as of 19:40, 26 May 2009
A differential propositional calculus is a propositional calculus extended by a set of terms for describing aspects of change and difference, for example, processes that take place in a universe of discourse or transformations that map a source universe into a target universe.
Work In Progress
Casual introduction
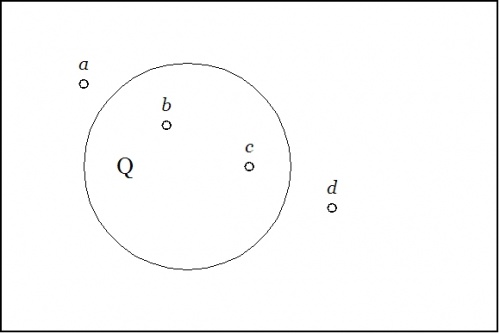
Consider the situation represented by the venn diagram in Figure 1.
|
Figure 1. Local Habitations, And Names |
The area of the rectangle represents a universe of discourse, \(X.\!\) This might be a population of individuals having various additional properties or it might be a collection of locations that various individuals occupy. The area of the "circle" represents the individuals that have the property \(q\!\) or the locations that fall within the corresponding region \(Q.\!\) Four individuals, \(a, b, c, d,\!\) are singled out by name. It happens that \(b\!\) and \(c\!\) currently reside in region \(Q\!\) while \(a\!\) and \(d\!\) do not.
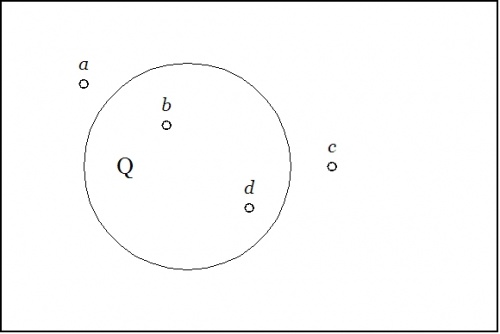
Now consider the situation represented by the venn diagram in Figure 2.
|
Figure 2. Same Names, Different Habitations |
Figure 2 differs from Figure 1 solely in the circumstance that the object \(c\!\) is outside the region \(Q\!\) while the object \(d\!\) is inside the region \(Q.\!\) So far, there is nothing that says that our encountering these Figures in this order is other than purely accidental, but if we interpret the present sequence of frames as a "moving picture" representation of their natural order in a temporal process, then it would be natural to say that \(a\!\) and \(b\!\) have remained as they were with regard to quality \(q\!\) while \(c\!\) and \(d\!\) have changed their standings in that respect. In particular, \(c\!\) has moved from the region where \(q\!\) is \(true\!\) to the region where \(q\!\) is \(false\!\) while \(d\!\) has moved from the region where \(q\!\) is \(false\!\) to the region where \(q\!\) is \(true.\!\)
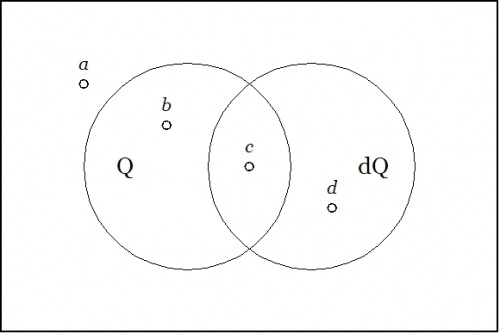
Figure 1′ reprises the situation shown in Figure 1, but this time interpolates a new quality that is specifically tailored to account for the relation between Figure 1 and Figure 2.
|
Figure 1′. Back, To The Future |
This new quality, \(\operatorname{d}q,\!\) is an example of a differential quality, since its absence or presence qualifies the absence or presence of change occurring in another quality. As with any other quality, it is represented in the venn diagram by means of a "circle" that distinguishes two halves of the universe of discourse, in this case, the portions of \(X\!\) outside and inside the region \(\operatorname{d}Q.\!\)
Figure 1 represents a universe of discourse, \(X,\!\) together with a basis of discussion, \(\{ q \},\!\) for expressing propositions about the contents of that universe. Once the quality \(q\!\) is given a name, say, the symbol "\(q\!\)", we have the basis for a formal language that is specifically cut out for discussing \(X\!\) in terms of \(q,\!\) and this formal language is more formally known as the propositional calculus with alphabet \(\{\!\)"\(q\!\)"\(\}.\!\)
In the context marked by \(X\!\) and \(\{ q \}\!\) there are but four different pieces of information that can be expressed in the corresponding propositional calculus, namely, the propositions\[false,\!\] \(\lnot q,\!\) \(q,\!\) \(true.\!\) Referring to the sample of points in Figure 1, \(false\!\) holds of no points, \(\lnot q\!\) holds of \(a\!\) and \(d,\!\) \(q\!\) holds of \(b\!\) and \(c,\!\) and \(true\!\) holds of all points in the sample.
Figure 1′ preserves the same universe of discourse and extends the basis of discussion to a set of two qualities, \(\{ q, \operatorname{d}q \}.\!\) In parallel fashion, the initial propositional calculus is extended by means of the enlarged alphabet, \(\{\!\)"\(q\!\)"\(,\!\) "\(\operatorname{d}q\!\)"\(\}.\!\) Any propositional calculus over two basic propositions allows for the expression of 16 propositions all together. Just by way of salient examples in the present setting, we can pick out the most informative propositions that apply to each of our sample points. Using overlines to express logical negation, these are given as follows:
\(\overline{q}\ \overline{\operatorname{d}q}\) describes \(a\!\)
\(\overline{q}\ \operatorname{d}q\) describes \(d\!\)
\(q\ \overline{\operatorname{d}q}\) describes \(b\!\)
\(q\ \operatorname{d}q\) describes \(c\!\)
Table 3 exhibits the rules of inference that give the differential quality \(\operatorname{d}q\!\) its meaning in practice.
|
Cactus calculus
Table 4 outlines a syntax for propositional calculus based on two types of logical connectives, both of variable \(k\!\)-ary scope.
- A bracketed list of propositional expressions in the form \((e_1, e_2, \ldots, e_{k-1}, e_k)\) indicates that exactly one of the propositions \(e_1, e_2, \ldots, e_{k-1}, e_k\) is false.
- A concatenation of propositional expressions in the form \(e_1~e_2~\ldots~e_{k-1}~e_k\) indicates that all of the propositions \(e_1, e_2, \ldots, e_{k-1}, e_k\) are true, in other words, that their logical conjunction is true.
| Expression | Interpretation | Other Notations |
|---|---|---|
| \(~\) | \(\operatorname{True}\) | \(1\!\) |
| \((~)\) | \(\operatorname{False}\) | \(0\!\) |
| \(x\!\) | \(x\!\) | \(x\!\) |
| \((x)\!\) | \(\operatorname{Not}\ x\) |
\(\begin{matrix} x' \\ \tilde{x} \\ \lnot x \\ \end{matrix}\) |
| \(x\ y\ z\) | \(x\ \operatorname{and}\ y\ \operatorname{and}\ z\) | \(x \land y \land z\) |
| \(((x)(y)(z))\!\) | \(x\ \operatorname{or}\ y\ \operatorname{or}\ z\) | \(x \lor y \lor z\) |
| \((x\ (y))\!\) |
\(\begin{matrix} x\ \operatorname{implies}\ y \\ \operatorname{If}\ x\ \operatorname{then}\ y \\ \end{matrix}\) |
\(x \Rightarrow y\!\) |
| \((x, y)\!\) |
\(\begin{matrix} x\ \operatorname{not~equal~to}\ y \\ x\ \operatorname{exclusive~or}\ y \\ \end{matrix}\) |
\(\begin{matrix} x \neq y \\ x + y \\ \end{matrix}\) |
| \(((x, y))\!\) |
\(\begin{matrix} x\ \operatorname{is~equal~to}\ y \\ x\ \operatorname{if~and~only~if}\ y \\ \end{matrix}\) |
\(\begin{matrix} x = y \\ x \Leftrightarrow y \\ \end{matrix}\) |
| \((x, y, z)\!\) |
\(\begin{matrix} \operatorname{Just~one~of} \\ x, y, z \\ \operatorname{is~false}. \\ \end{matrix}\) |
\(\begin{matrix} x'y~z~ & \lor \\ x~y'z~ & \lor \\ x~y~z' & \\ \end{matrix}\) |
| \(((x),(y),(z))\!\) |
\(\begin{matrix} \operatorname{Just~one~of} \\ x, y, z \\ \operatorname{is~true}. \\ & \\ \operatorname{Partition~all} \\ \operatorname{into}\ x, y, z. \\ \end{matrix}\) |
\(\begin{matrix} x~y'z' & \lor \\ x'y~z' & \lor \\ x'y'z~ & \\ \end{matrix}\) |
|
\(\begin{matrix} ((x, y), z) \\ & \\ (x, (y, z)) \\ \end{matrix}\) |
\(\begin{matrix} \operatorname{Oddly~many~of} \\ x, y, z \\ \operatorname{are~true}. \\ \end{matrix}\) |
\(x + y + z\!\)
\(\begin{matrix} x~y~z~ & \lor \\ x~y'z' & \lor \\ x'y~z' & \lor \\ x'y'z~ & \\ \end{matrix}\) |
| \((w, (x),(y),(z))\!\) |
\(\begin{matrix} \operatorname{Partition}\ w \\ \operatorname{into}\ x, y, z. \\ & \\ \operatorname{Genus}\ w\ \operatorname{comprises} \\ \operatorname{species}\ x, y, z. \\ \end{matrix}\) |
\(\begin{matrix} w'x'y'z' & \lor \\ w~x~y'z' & \lor \\ w~x'y~z' & \lor \\ w~x'y'z~ & \\ \end{matrix}\) |
All other propositional connectives can be obtained through combinations of these two forms. Strictly speaking, the concatenation form is dispensable in light of the bracket form, but it is convenient to maintain it as an abbreviation for more complicated bracket expressions. The briefest expression for logical truth is the empty word, abstractly denoted \(\varepsilon\!\) or \(\lambda\!\) in formal languages, where it forms the identity element for concatenation. It can be given visible expression in this context by means of the logically equivalent expression "\(((~))\)", or, especially if operating in an algebraic context, by a simple "\(1\!\)". Also when working in an algebraic mode, the plus sign "\(+\!\) may be used for exclusive disjunction. For example, we have the following paraphrases of algebraic expressions by bracket expressions:
\(\begin{matrix} x + y & = & (x, y) \end{matrix}\)
\(\begin{matrix} x + y + z & = & ((x, y), z) & = & (x, (y, z)) \end{matrix}\)
It is important to note that the last expressions are not equivalent to the triple bracket \((x, y, z).\!\)
For more information about this syntax for propositional calculus, see the entries on minimal negation operators, zeroth order logic, and Table A1 in Appendix 1.
Formal development
The preceding discussion outlined the ideas leading to the differential extension of propositional logic. The next task is to lay out the concepts and terminology that are needed to describe various orders of differential propositional calculi.
Elementary notions
Logical description of a universe of discourse begins with a set of logical signs. For the sake of simplicity in a first approach, assume that these logical signs are collected in the form of a finite alphabet, \(\mathfrak{A} = \lbrace\!\) “\(a_1\!\)” \(, \ldots,\!\) “\(a_n\!\)” \(\rbrace.\!\) Each of these signs is interpreted as denoting a logical feature, for instance, a property that objects in the universe of discourse may have or a proposition about objects in the universe of discourse. Corresponding to the alphabet \(\mathfrak{A}\) there is then a set of logical features, \(\mathcal{A} = \{ a_1, \ldots, a_n \}.\)
A set of logical features, \(\mathcal{A} = \{ a_1, \ldots, a_n \},\) affords a basis for generating an \(n\!\)-dimensional universe of discourse, written \(A^\circ = [ \mathcal{A} ] = [ a_1, \ldots, a_n ].\) It is useful to consider a universe of discourse as a categorical object that incorporates both the set of points \(A = \langle a_1, \ldots, a_n \rangle\) and the set of propositions \(A^\uparrow = \{ f : A \to \mathbb{B} \}\) that are implicit with the ordinary picture of a venn diagram on \(n\!\) features. Accordingly, the universe of discourse \(A^\circ\) may be regarded as an ordered pair \((A, A^\uparrow)\) having the type \((\mathbb{B}^n, (\mathbb{B}^n \to \mathbb{B})),\) and this last type designation may be abbreviated as \(\mathbb{B}^n\ +\!\to \mathbb{B},\) or even more succinctly as \([ \mathbb{B}^n ].\) For convenience, the data type of a finite set on \(n\!\) elements may be indicated by either one of the equivalent notations, \([n]\!\) or \(\mathbf{n}.\)
Table 5 summarizes the notations that are needed to describe ordinary propositional calculi in a systematic fashion.
| Symbol | Notation | Description | Type |
|---|---|---|---|
| \(\mathfrak{A}\) | \(\lbrace\!\) “\(a_1\!\)” \(, \ldots,\!\) “\(a_n\!\)” \(\rbrace\!\) | Alphabet | \([n] = \mathbf{n}\) |
| \(\mathcal{A}\) | \(\{ a_1, \ldots, a_n \}\) | Basis | \([n] = \mathbf{n}\) |
| \(A_i\!\) | \(\{ \overline{a_i}, a_i \}\!\) | Dimension \(i\!\) | \(\mathbb{B}\) |
| \(A\!\) |
\(\langle \mathcal{A} \rangle\) |
Set of cells, |
\(\mathbb{B}^n\) |
| \(A^*\!\) | \((\operatorname{hom} : A \to \mathbb{B})\) | Linear functions | \((\mathbb{B}^n)^* \cong \mathbb{B}^n\) |
| \(A^\uparrow\) | \((A \to \mathbb{B})\) | Boolean functions | \(\mathbb{B}^n \to \mathbb{B}\) |
| \(A^\circ\) |
\([ \mathcal{A} ]\) |
Universe of discourse |
\((\mathbb{B}^n, (\mathbb{B}^n \to \mathbb{B}))\) |
Special classes of propositions
A basic proposition, coordinate proposition, or simple proposition in the universe of discourse \([a_1, \ldots, a_n]\) is one of the propositions in the set \(\{ a_1, \ldots, a_n \}.\)
Among the \(2^{2^n}\) propositions in \([a_1, \ldots, a_n]\) are several families of \(2^n\!\) propositions each that take on special forms with respect to the basis \(\{ a_1, \ldots, a_n \}.\) Three of these families are especially prominent in the present context, the linear, the positive, and the singular propositions. Each family is naturally parameterized by the coordinate \(n\!\)-tuples in \(\mathbb{B}^n\) and falls into \(n + 1\!\) ranks, with a binomial coefficient \(\tbinom{n}{k}\) giving the number of propositions that have rank or weight \(k.\!\)
The linear propositions, \(\{ \ell : \mathbb{B}^n \to \mathbb{B} \} = (\mathbb{B}^n \xrightarrow{\ell} \mathbb{B}),\) may be written as sums:
\(\sum_{i=1}^n e_i = e_1 + \ldots + e_n\) where \(e_i = a_i\!\) or \(e_i = 0\!\) for \(i = 1\!\) to \(n.\!\)
The positive propositions, \(\{ p : \mathbb{B}^n \to \mathbb{B} \} = (\mathbb{B}^n \xrightarrow{p} \mathbb{B}),\) may be written as products:
\(\prod_{i=1}^n e_i = e_1 \cdot \ldots \cdot e_n\) where \(e_i = a_i\!\) or \(e_i = 1\!\) for \(i = 1\!\) to \(n.\!\)
The singular propositions, \(\{ \mathbf{x} : \mathbb{B}^n \to \mathbb{B} \} = (\mathbb{B}^n \xrightarrow{s} \mathbb{B}),\) may be written as products:
\(\prod_{i=1}^n e_i = e_1 \cdot \ldots \cdot e_n\) where \(e_i = a_i\!\) or \(e_i = (a_i)\!\) for \(i = 1\!\) to \(n.\!\)
In each case the rank \(k\!\) ranges from \(0\!\) to \(n\!\) and counts the number of positive appearances of the coordinate propositions \(a_1, \ldots, a_n\!\) in the resulting expression. For example, for \(n = 3,\!\) the linear proposition of rank \(0\!\) is \(0,\!\) the positive proposition of rank \(0\!\) is \(1,\!\) and the singular proposition of rank \(0\!\) is \((a_1)(a_2)(a_3).\!\)
The basic propositions \(a_i : \mathbb{B}^n \to \mathbb{B}\) are both linear and positive. So these two kinds of propositions, the linear and the positive, may be viewed as two different ways of generalizing the class of basic propositions.
Finally, it is important to note that all of the above distinctions are relative to the choice of a particular logical basis \(\mathcal{A} = \{ a_1, \ldots, a_n \}.\) For example, a singular proposition with respect to the basis \(\mathcal{A}\) will not remain singular if \(\mathcal{A}\) is extended by a number of new and independent features. Even if one keeps to the original set of pairwise options \(\{ a_i \} \cup \{ (a_i) \}\) to pick out a new basis, the sets of linear propositions and positive propositions are both determined by the choice of basic propositions, and this whole determination is tantamount to the purely conventional choice of a cell as origin.
Differential extensions
An initial universe of discourse, \(A^\circ,\) supplies the groundwork for any number of further extensions, beginning with the first order differential extension, \(\operatorname{E}A^\circ.\) The construction of \(\operatorname{E}A^\circ\) can be described in the following stages:
The initial alphabet, \(\mathfrak{A} = \lbrace\!\) “\(a_1\!\)” \(, \ldots,\!\) “\(a_n\!\)” \(\rbrace,\!\) is extended by a first order differential alphabet, \(\operatorname{d}\mathfrak{A} = \lbrace\!\) “\(\operatorname{d}a_1\!\)” \(, \ldots,\!\) “\(\operatorname{d}a_n\!\)” \(\rbrace,\!\) resulting in a first order extended alphabet, \(\operatorname{E}\mathfrak{A},\) defined as follows:
\(\operatorname{E}\mathfrak{A} = \mathfrak{A}\ \cup\ \operatorname{d}\mathfrak{A} = \lbrace\!\) “\(a_1\!\)” \(, \ldots,\!\) “\(a_n\!\)”\(,\!\) “\(\operatorname{d}a_1\!\)” \(, \ldots,\!\) “\(\operatorname{d}a_n\!\)” \(\rbrace.\!\)
The initial basis, \(\mathcal{A} = \{ a_1, \ldots, a_n \},\) is extended by a first order differential basis, \(\operatorname{d}\mathcal{A} = \{ \operatorname{d}a_1, \ldots, \operatorname{d}a_n \},\) resulting in a first order extended basis, \(\operatorname{E}\mathcal{A},\) defined as follows:
\(\operatorname{E}\mathcal{A} = \mathcal{A}\ \cup\ \operatorname{d}\mathcal{A} = \{ a_1, \ldots, a_n, \operatorname{d}a_1, \ldots, \operatorname{d}a_n \}.\)
The initial space, \(A = \langle a_1, \ldots, a_n \rangle,\) is extended by a first order differential space or tangent space, \(\operatorname{d}A = \langle \operatorname{d}a_1, \ldots, \operatorname{d}a_n \rangle,\) at each point of \(A,\!\) resulting in a first order extended space or tangent bundle space, \(\operatorname{E}A,\) defined as follows:
\(\operatorname{E}A = A \times \operatorname{d}A = \langle \operatorname{E}\mathcal{A} \rangle = \langle \mathcal{A} \cup \operatorname{d}\mathcal{A} \rangle = \langle a_1, \ldots, a_n, \operatorname{d}a_1, \ldots, \operatorname{d}a_n \rangle.\)
Finally, the initial universe, \(A^\circ = [ a_1, \ldots, a_n ],\) is extended by a first order differential universe or tangent universe, \(\operatorname{d}A^\circ = [ \operatorname{d}a_1, \ldots, \operatorname{d}a_n ],\) at each point of \(A^\circ,\) resulting in a first order extended universe or tangent bundle universe, \(\operatorname{E}A^\circ,\) defined as follows:
\(\operatorname{E}A^\circ = [ \operatorname{E}\mathcal{A} ] = [ \mathcal{A}\ \cup\ \operatorname{d}\mathcal{A} ] = [ a_1, \ldots, a_n, \operatorname{d}a_1, \ldots, \operatorname{d}a_n ].\)
This gives \(\operatorname{E}A^\circ\) the type:
\([ \mathbb{B}^n \times \mathbb{D}^n ] = (\mathbb{B}^n \times \mathbb{D}^n\ +\!\to \mathbb{B}) = (\mathbb{B}^n \times \mathbb{D}^n, \mathbb{B}^n \times \mathbb{D}^n \to \mathbb{B}).\)
A proposition in a differential extension of a universe of discourse is called a differential proposition and forms the analogue of a system of differential equations in ordinary calculus. With these constructions, the first order extended universe \(\operatorname{E}A^\circ\) and the first order differential proposition \(f : \operatorname{E}A \to \mathbb{B},\) we have arrived, in concept at least, at the foothills of differential logic.
Table 6 summarizes the notations that are needed to describe the first order differential extensions of propositional calculi in a systematic manner.
| Symbol | Notation | Description | Type |
|---|---|---|---|
| \(\operatorname{d}\mathfrak{A}\) | \(\lbrace\!\) “\(\operatorname{d}a_1\)” \(, \ldots,\!\) “\(\operatorname{d}a_n\)” \(\rbrace\!\) |
Alphabet of |
\([n] = \mathbf{n}\) |
| \(\operatorname{d}\mathcal{A}\) | \(\{ \operatorname{d}a_1, \ldots, \operatorname{d}a_n \}\) |
Basis of |
\([n] = \mathbf{n}\) |
| \(\operatorname{d}A_i\) | \(\{ \overline{\operatorname{d}a_i}, \operatorname{d}a_i \}\) |
Differential |
\(\mathbb{D}\) |
| \(\operatorname{d}A\) |
\(\langle \operatorname{d}\mathcal{A} \rangle\) |
Tangent space |
\(\mathbb{D}^n\) |
| \(\operatorname{d}A^*\) | \((\operatorname{hom} : \operatorname{d}A \to \mathbb{B})\) |
Linear functions |
\((\mathbb{D}^n)^* \cong \mathbb{D}^n\) |
| \(\operatorname{d}A^\uparrow\) | \((\operatorname{d}A \to \mathbb{B})\) |
Boolean functions |
\(\mathbb{D}^n \to \mathbb{B}\) |
| \(\operatorname{d}A^\circ\) |
\([\operatorname{d}\mathcal{A}]\) |
Tangent universe |
\((\mathbb{D}^n, (\mathbb{D}^n \to \mathbb{B}))\) |
…
Expository examples
…
Consider the logical proposition represented by the following venn diagram:
o-----------------------------------------------------------o | X . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . .o-------------o. . . . . . . . . . . | | . . . . . . . . . . / . . . . . . . \ . . . . . . . . . . | | . . . . . . . . . ./. . . . . . . . .\. . . . . . . . . . | | . . . . . . . . . / . . . . . . . . . \ . . . . . . . . . | | . . . . . . . . ./. . . . . . . . . . .\. . . . . . . . . | | . . . . . . . . / . . . . . . . . . . . \ . . . . . . . . | | . . . . . . . .o. . . . . . . . . . . . .o. . . . . . . . | | . . . . . . . .|. . . . . . U . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . o--o----------o . o----------o--o . . . . . . | | . . . . . ./. . \%%%%%%%%%%\./%%%%%%%%%%/ . .\. . . . . . | | . . . . . / . . .\%%%%%%%%%%o%%%%%%%%%%/. . . \ . . . . . | | . . . . ./. . . . \%%%%%%%%/%\%%%%%%%%/ . . . .\. . . . . | | . . . . / . . . . .\%%%%%%/%%%\%%%%%%/. . . . . \ . . . . | | . . . ./. . . . . . \%%%%/%%%%%\%%%%/ . . . . . .\. . . . | | . . . o . . . . . . .o--o-------o--o. . . . . . . o . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . | . . . .V. . . . |%%%%%%%| . . . .W. . . . | . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . o . . . . . . . . o%%%%%%%o . . . . . . . . o . . . | | . . . .\. . . . . . . . .\%%%%%/. . . . . . . . ./. . . . | | . . . . \ . . . . . . . . \%%%/ . . . . . . . . / . . . . | | . . . . .\. . . . . . . . .\%/. . . . . . . . ./. . . . . | | . . . . . \ . . . . . . . . o . . . . . . . . / . . . . . | | . . . . . .\. . . . . . . ./.\. . . . . . . ./. . . . . . | | . . . . . . o-------------o . o-------------o . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | o-----------------------------------------------------------o
Figure 1. Proposition \(q : X \to \mathbb{B}\)
The following language is useful in describing the facts represented by the venn diagram.
- The universe of discourse is a set, \(X,\!\) represented by the area inside the large rectangle.
- The boolean domain is a set of two elements, \(\mathbb{B} = \{ 0, 1 \},\) represented by the two distinct shadings of the regions inside the rectangle.
- According to the conventions observed in this context, the algebraic value 0 is interpreted as the logical value \(\operatorname{false}\) and represented by the lighter shading, while the algebraic value 1 is interpreted as the logical value \(\operatorname{true}\) and represented by the darker shading.
- The universe of discourse \(X\!\) is the domain of three functions \(u, v, w : X \to \mathbb{B}\) called basic, coordinate, or simple propositions.
- As with any proposition, \(p : X \to \mathbb{B},\) a simple proposition partitions \(X\!\) into two fibers, the fiber of 0 under \(p,\!\) defined as \(p^{-1}(0) \subseteq X,\) and the fiber of 1 under \(p,\!\) defined as \(p^{-1}(1) \subseteq X.\)
- Each coordinate proposition is represented by a "circle", or a simple closed curve, that divides the rectangular region into the region exterior to the circle, representing the fiber of 0 under \(p,\!\) and the region interior to the circle, representing the fiber of 1 under \(p.\!\)
- The fibers of 1 under the propositions \(u, v, w\!\) are the respective subsets \(U, V, W \subseteq X.\)
…
Material To Be Collated
Differential Logic : First Approach
Linear Topics : The Differential Theory of Qualitative Equations
The most fundamental concept in cybernetics is that of "difference", either that two things are recognisably different or that one thing has changed with time.
— William Ross Ashby, Cybernetics
This chapter is titled "Linear Topics" because that is the heading under which the derivatives and the differentials of any functions usually come up in mathematics, namely, in relation to the problem of computing "locally linear approximations" to the more arbitrary, unrestricted brands of functions that one finds in a given setting.
To denote lists of propositions and to detail their components, we use notations like:
\[\mathbf{a} = (a, b, c),\ \mathbf{p} = (p, q, r),\ \mathbf{x} = (x, y, z),\!\]
or, in more complicated situations:
\[x = (x_1, x_2, x_3),\ y = (y_1, y_2, y_3),\ z = (z_1, z_2, z_3).\!\]
In a universe where some region is ruled by a proposition, it is natural to ask whether we can change the value of that proposition by changing the features of our current state.
Given a venn diagram with a shaded region and starting from any cell in that universe, what sequences of feature changes, what traverses of cell walls, will take us from shaded to unshaded areas, or the reverse?
In order to discuss questions of this type, it is useful to define several "operators" on functions. An operator is nothing more than a function between sets that happen to have functions as members.
A typical operator \(\operatorname{F}\) takes us from thinking about a given function \(f\!\) to thinking about another function \(g\!\). To express the fact that \(g\!\) can be obtained by applying the operator \(\operatorname{F}\) to \(f\!\), we write \(g = \operatorname{F}f.\)
The first operator, \(\operatorname{E}\), associates with a function \(f : X \to Y\) another function \(\operatorname{E}f\), where \(\operatorname{E}f : X \times X \to Y\) is defined by the following equation:
\[\operatorname{E}f(x, y) = f(x + y).\]
\(\operatorname{E}\) is called a "shift operator" because it takes us from contemplating the value of \(f\!\) at a place \(x\!\) to considering the value of \(f\!\) at a shift of \(y\!\) away. Thus, \(\operatorname{E}\) tells us the absolute effect on \(f\!\) that is obtained by changing its argument from \(x\!\) by an amount that is equal to \(y\!\).
Historical Note. The "shift operator" \(\operatorname{E}\) was originally called the "enlargement operator", hence the initial "E" of the usual notation.
The next operator, \(\operatorname{D}\), associates with a function \(f : X \to Y\) another function \(\operatorname{D}f\), where \(\operatorname{D}f : X \times X \to Y\) is defined by the following equation:
\[\operatorname{D}f(x, y) = \operatorname{E}f(x, y) - f(x),\]
or, equivalently,
\[\operatorname{D}f(x, y) = f(x + y) - f(x).\]
\(\operatorname{D}\) is called a "difference operator" because it tells us about the relative change in the value of \(f\!\) along the shift from \(x\!\) to \(x + y.\!\)
In practice, one of the variables, \(x\!\) or \(y\!\), is often considered to be "less variable" than the other one, being fixed in the context of a concrete discussion. Thus, we might find any one of the following idioms:
\[\operatorname{D}f : X \times X \to Y,\]
\[\operatorname{D}f(c, x) = f(c + x) - f(c).\]
Here, \(c\!\) is held constant and \(\operatorname{D}f(c, x)\) is regarded mainly as a function of the second variable \(x\!\), giving the relative change in \(f\!\) at various distances \(x\!\) from the center \(c\!\).
\[\operatorname{D}f : X \times X \to Y,\]
\[\operatorname{D}f(x, h) = f(x + h) - f(x).\]
Here, \(h\!\) is either a constant (usually 1), in discrete contexts, or a variably "small" amount (near to 0) over which a limit is being taken, as in continuous contexts. \(\operatorname{D}f(x, h)\) is regarded mainly as a function of the first variable \(x\!\), in effect, giving the differences in the value of \(f\!\) between \(x\!\) and a neighbor that is a distance of \(h\!\) away, all the while that \(x\!\) itself ranges over its various possible locations.
\[\operatorname{D}f : X \times X \to Y,\]
\[\operatorname{D}f(x, \operatorname{d}x) = f(x + \operatorname{d}x) - f(x).\]
This is yet another variant of the previous form, with \(\operatorname{d}x\) denoting small changes contemplated in \(x\!\).
That's the basic idea. The next order of business is to develop the logical side of the analogy a bit more fully, and to take up the elaboration of some moderately simple applications of these ideas to a selection of relatively concrete examples.
Example 1. A Polymorphous Concept
I start with an example that is simple enough that it will allow us to compare the representations of propositions by venn diagrams, truth tables, and my own favorite version of the syntax for propositional calculus all in a relatively short space. To enliven the exercise, I borrow an example from a book with several independent dimensions of interest, Topobiology by Gerald Edelman. One finds discussed there the notion of a "polymorphous set". Such a set is defined in a universe of discourse whose elements can be described in terms of a fixed number \(k\!\) of logical features. A "polymorphous set" is one that can be defined in terms of sets whose elements have a fixed number \(j\!\) of the \(k\!\) features.
As a rule in the following discussion, I will use upper case letters as names for concepts and sets, lower case letters as names for features and functions.
The example that Edelman gives (1988, Fig. 10.5, p. 194) involves sets of stimulus patterns that can be described in terms of the three features "round" \(u\!\), "doubly outlined" \(v\!\), and "centrally dark" \(w\!\). We may regard these simple features as logical propositions \(u, v, w : X \to \mathbb{B}.\) The target concept \(\mathcal{Q}\) is one whose extension is a polymorphous set \(Q\!\), the subset \(Q\!\) of the universe \(X\!\) where the complex feature \(q : X \to \mathbb{B}\) holds true. The \(Q\!\) in question is defined by the requirement: "Having at least 2 of the 3 features in the set \(\{ u, v, w \}\!\)".
Taking the symbols \(u\!\) = "round", \(v\!\) = "doubly outlined", \(w\!\) = "centrally dark", and using the corresponding capital letters to label the circles of a venn diagram, we get a picture of the target set \(Q\!\) as the shaded region in Figure 1. Using these symbols as "sentence letters" in a truth table, let the truth function \(q\!\) mean the very same thing as the expression "(\(u\!\) and \(v\!\)) or (\(u\!\) and \(w\!\)) or (\(v\!\) and \(w\!\))".
o-----------------------------------------------------------o | X . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . .o-------------o. . . . . . . . . . . | | . . . . . . . . . . / . . . . . . . \ . . . . . . . . . . | | . . . . . . . . . ./. . . . . . . . .\. . . . . . . . . . | | . . . . . . . . . / . . . . . . . . . \ . . . . . . . . . | | . . . . . . . . ./. . . . . . . . . . .\. . . . . . . . . | | . . . . . . . . / . . . . . . . . . . . \ . . . . . . . . | | . . . . . . . .o. . . . . . . . . . . . .o. . . . . . . . | | . . . . . . . .|. . . . . . U . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . o--o----------o . o----------o--o . . . . . . | | . . . . . ./. . \%%%%%%%%%%\./%%%%%%%%%%/ . .\. . . . . . | | . . . . . / . . .\%%%%%%%%%%o%%%%%%%%%%/. . . \ . . . . . | | . . . . ./. . . . \%%%%%%%%/%\%%%%%%%%/ . . . .\. . . . . | | . . . . / . . . . .\%%%%%%/%%%\%%%%%%/. . . . . \ . . . . | | . . . ./. . . . . . \%%%%/%%%%%\%%%%/ . . . . . .\. . . . | | . . . o . . . . . . .o--o-------o--o. . . . . . . o . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . | . . . .V. . . . |%%%%%%%| . . . .W. . . . | . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . o . . . . . . . . o%%%%%%%o . . . . . . . . o . . . | | . . . .\. . . . . . . . .\%%%%%/. . . . . . . . ./. . . . | | . . . . \ . . . . . . . . \%%%/ . . . . . . . . / . . . . | | . . . . .\. . . . . . . . .\%/. . . . . . . . ./. . . . . | | . . . . . \ . . . . . . . . o . . . . . . . . / . . . . . | | . . . . . .\. . . . . . . ./.\. . . . . . . ./. . . . . . | | . . . . . . o-------------o . o-------------o . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | o-----------------------------------------------------------o Figure 1. Polymorphous Set Q
In other words, the proposition \(q\!\) is a truth-function of the 3 logical variables \(u\!\), \(v\!\), \(w\!\), and it may be evaluated according to the "truth table" scheme that is shown in Table 2. In this representation the polymorphous set \(Q\!\) appears in the guise of what some people call the "pre-image" or the "fiber of truth" under the function \(q\!\). More precisely, the 3-tuples for which \(q\!\) evaluates to true are in an obvious correspondence with the shaded cells of the venn diagram. No matter how we get down to the level of actual information, it's all pretty much the same stuff.
| u v w | u ∧ v | u ∧ w | v ∧ w | q |
|---|---|---|---|---|
| 0 0 0 | 0 | 0 | 0 | 0 |
| 0 0 1 | 0 | 0 | 0 | 0 |
| 0 1 0 | 0 | 0 | 0 | 0 |
| 0 1 1 | 0 | 0 | 1 | 1 |
| 1 0 0 | 0 | 0 | 0 | 0 |
| 1 0 1 | 0 | 1 | 0 | 1 |
| 1 1 0 | 1 | 0 | 0 | 1 |
| 1 1 1 | 1 | 1 | 1 | 1 |
With the pictures of the venn diagram and the truth table before us, we have come to the verge of seeing how the word "model" is used in logic, namely, to distinguish whatever things satisfy a description.
In the venn diagram presentation, to be a model of some conceptual description \(\mathcal{F}\) is to be a point \(x\!\) in the corresponding region \(F\!\) of the universe of discourse \(X\!\).
In the truth table representation, to be a model of a logical proposition \(f\!\) is to be a data-vector \(\mathbf{x}\!\) (a row of the table) on which a function \(f\!\) evaluates to true.
This manner of speaking makes sense to those who consider the ultimate meaning of a sentence to be not the logical proposition that it denotes but its truth value instead. From the point of view, one says that any data-vector of this type (\(k\!\)-tuples of truth values) may be regarded as an "interpretation" of the proposition with \(k\!\) variables. An interpretation that yields a value of true is then called a "model".
For the most threadbare kind of logical system that we find residing in propositional calculus, this notion of model is almost too simple to deserve the name, yet it can be of service to fashion some form of continuity between the simple and the complex.
The present is big with the future.
— Leibniz
Here I now delve into subject matters that are more specifically logical in the character of their interpretation.
Working Note. Need segue here to explain the use of Cactus Language.
Imagine that we are sitting in one of the cells of a venn diagram, contemplating the walls. There are \(k\!\) of them, one for each positive feature \(x_1, \ldots, x_k\) in our universe of discourse. Our particular cell is described by a concatenation of \(k\!\) signed assertions, positive or negative, regarding each of these features, and this description of our position amounts to what is called an "interpretation" of whatever proposition may rule the space, or reign on the universe of discourse. But are we locked into this interpretation?
With respect to each edge \(x\!\) of the cell we consider a test proposition \(\operatorname{d}x\) that determines our decision whether or not we will make a difference in how we stand regarding \(x\!\). If \(\operatorname{d}x\) is true then it marks our decision, intention, or plan to cross over the edge \(x\!\) at some point within the purview of the contemplated plan.
To reckon the effect of several such decisions on our current interpretation, or the value of the reigning proposition, we transform that position or that proposition by making the following array of substitutions everywhere in its expression:
\(1.\!\) Substitute "\((x_1, \operatorname{d}x_1)\)" for "\(x_1\!\)"
\(2.\!\) Substitute "\((x_2, \operatorname{d}x_2)\)" for "\(x_2\!\)"
\(3.\!\) Substitute "\((x_3, \operatorname{d}x_3)\)" for "\(x_3\!\)"
\(\ldots\)
\(k.\!\) Substitute "\((x_k, \operatorname{d}x_k)\)" for "\(x_k\!\)"
For concreteness, consider the polymorphous set \(Q\!\) of Example 1 and focus on the central cell, specifically, the cell described by the conjunction of logical features in the expression "\(u\ v\ w\)".
o-----------------------------------------------------------o | X . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . .o-------------o. . . . . . . . . . . | | . . . . . . . . . . / . . . . . . . \ . . . . . . . . . . | | . . . . . . . . . ./. . . . . . . . .\. . . . . . . . . . | | . . . . . . . . . / . . . . . . . . . \ . . . . . . . . . | | . . . . . . . . ./. . . . . . . . . . .\. . . . . . . . . | | . . . . . . . . / . . . . . . . . . . . \ . . . . . . . . | | . . . . . . . .o. . . . . . . . . . . . .o. . . . . . . . | | . . . . . . . .|. . . . . . U . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . o--o----------o . o----------o--o . . . . . . | | . . . . . ./. . \%%%%%%%%%%\./%%%%%%%%%%/ . .\. . . . . . | | . . . . . / . . .\%%%%%%%%%%o%%%%%%%%%%/. . . \ . . . . . | | . . . . ./. . . . \%%%%%%%%/%\%%%%%%%%/ . . . .\. . . . . | | . . . . / . . . . .\%%%%%%/%%%\%%%%%%/. . . . . \ . . . . | | . . . ./. . . . . . \%%%%/%%%%%\%%%%/ . . . . . .\. . . . | | . . . o . . . . . . .o--o-------o--o. . . . . . . o . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . | . . . .V. . . . |%%%%%%%| . . . .W. . . . | . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . o . . . . . . . . o%%%%%%%o . . . . . . . . o . . . | | . . . .\. . . . . . . . .\%%%%%/. . . . . . . . ./. . . . | | . . . . \ . . . . . . . . \%%%/ . . . . . . . . / . . . . | | . . . . .\. . . . . . . . .\%/. . . . . . . . ./. . . . . | | . . . . . \ . . . . . . . . o . . . . . . . . / . . . . . | | . . . . . .\. . . . . . . ./.\. . . . . . . ./. . . . . . | | . . . . . . o-------------o . o-------------o . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | o-----------------------------------------------------------o Figure 1. Polymorphous Set Q
The proposition or the truth-function \(q\!\) that describes \(Q\!\) is:
(( u v )( u w )( v w ))
Conjoining the query that specifies the center cell gives:
(( u v )( u w )( v w )) u v w
And we know the value of the interpretation by whether this last expression issues in a model.
Applying the enlargement operator \(\operatorname{E}\) to the initial proposition \(q\!\) yields:
(( ( u , du )( v , dv ) )( ( u , du )( w , dw ) )( ( v , dv )( w , dw ) ))
Conjoining a query on the center cell yields:
(( ( u , du )( v , dv ) )( ( u , du )( w , dw ) )( ( v , dv )( w , dw ) )) u v w
The models of this last expression tell us which combinations of feature changes among the set \(\{ \operatorname{d}u, \operatorname{d}v, \operatorname{d}w \}\) will take us from our present interpretation, the center cell expressed by "\(u\ v\ w\)", to a true value under the target proposition (( u v )( u w )( v w )) .
The result of applying the difference operator \(\operatorname{D}\) to the initial proposition \(\operatorname{q}\), conjoined with a query on the center cell, yields:
(
(( ( u , du )( v , dv )
)( ( u , du )( w , dw )
)( ( v , dv )( w , dw )
))
,
(( u v
)( u w
)( v w
))
)
u v w
The models of this last proposition are:
1. u v w du dv dw 2. u v w du dv (dw) 3. u v w du (dv) dw 4. u v w (du) dv dw
This tells us that changing any two or more of the features \(u, v, w\!\) will take us from the center cell to a cell outside the shaded region for the set \(Q.\!\)
It is one of the rules of my system of general harmony, that the present is big with the future, and that he who sees all sees in that which is that which shall be.
— Leibniz, Theodicy, ¶ 360, p. 341.
To round out the presentation of the Polymorphous Example 1, I will go through what has gone before and lay in the graphic forms of all of the propositional expressions. These graphs, whose official botanical designation makes them out to be a species of painted and rooted cacti (PARC's), are not too far from the actual graph-theoretic data-structures that result from parsing the cactus string expressions, the painted and rooted cactus expressions (PARCE's). Finally, I will add a couple of venn diagrams that will serve to illustrate the difference opus \(\operatorname{D}q\). If you apply an operator to an operand you must arrive at either an opus or an opera, no?
Consider the polymorphous set \(Q\!\) of Example 1 and focus on the central cell, described by the conjunction of logical features in the expression "\(u\ v\ w\!\)".
o-------------------------------------------------o | X . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . o-------------o . . . . . . . . | | . . . . . . . ./. . . . . . . .\. . . . . . . . | | . . . . . . . / . . . . . . . . \ . . . . . . . | | . . . . . . ./. . . . . . . . . .\. . . . . . . | | . . . . . . / . . . . . . . . . . \ . . . . . . | | . . . . . .o. . . . . .U. . . . . .o. . . . . . | | . . . . . .|. . . . . . . . . . . .|. . . . . . | | . . . . . .|. . . . . . . . . . . .|. . . . . . | | . . . . . .|. . . . . . . . . . . .|. . . . . . | | . . . .o---o---------o. .o---------o---o. . . . | | . . . / . . \%%%%%%%%%\ /%%%%%%%%%/ . . \ . . . | | . . ./. . . .\%%%%%%%%%o%%%%%%%%%/. . . .\. . . | | . . / . . . . \%%%%%%%/%\%%%%%%%/ . . . . \ . . | | . ./. . . . . .\%%%%%/%%%\%%%%%/. . . . . .\. . | | . o . . . . . . o---o-----o---o . . . . . . o . | | . | . . . . . . . . |%%%%%| . . . . . . . . | . | | . | . . . .V. . . . |%%%%%| . . . .W. . . . | . | | . | . . . . . . . . |%%%%%| . . . . . . . . | . | | . o . . . . . . . . o%%%%%o . . . . . . . . o . | | . .\. . . . . . . . .\%%%/. . . . . . . . ./. . | | . . \ . . . . . . . . \%/ . . . . . . . . / . . | | . . .\. . . . . . . . .o. . . . . . . . ./. . . | | . . . \ . . . . . . . / \ . . . . . . . / . . . | | . . . .o-------------o. .o-------------o. . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o Figure 1. Polymorphous Set Q
The proposition or truth-function \(q : X \to \mathbb{B}\) that describes \(Q\!\) is represented by the following graph and text expressions:
o-------------------------------------------------o | q . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . u v . u w . v w . . . . . . . . | | . . . . . . . . . .o. .o. .o. . . . . . . . . . | | . . . . . . . . . . \ .|. / . . . . . . . . . . | | . . . . . . . . . . .\.|./. . . . . . . . . . . | | . . . . . . . . . . . \|/ . . . . . . . . . . . | | . . . . . . . . . . . .o. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .@. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . (( u v )( u w )( v w )) . . . . . . | o-------------------------------------------------o
Conjoining the query that specifies the center cell gives:
o-------------------------------------------------o | q.uvw . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . u v . u w . v w . . . . . . . . | | . . . . . . . . . .o. .o. .o. . . . . . . . . . | | . . . . . . . . . . \ .|. / . . . . . . . . . . | | . . . . . . . . . . .\.|./. . . . . . . . . . . | | . . . . . . . . . . . \|/ . . . . . . . . . . . | | . . . . . . . . . . . .o. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .@ u v w. . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . (( u v )( u w )( v w )) u v w . . . | o-------------------------------------------------o
And we know the value of the interpretation by whether this last expression issues in a model.
Applying the enlargement operator \(\operatorname{E}\) to the initial proposition \(q\!\) yields:
o-------------------------------------------------o | Eq. . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . .u. du v. dv. u .du w .dw .v. dv w. dw. . . | | . . .o---o o---o. o---o o---o .o---o o---o. . . | | . . . \ .| |. / . .\. | | ./. . \ .| |. / . . . | | . . . .\.| |./. . . \ | | / . . .\.| |./. . . . | | . . . . \| |/ . . . .\| |/. . . . \| |/ . . . . | | . . . . .o=o. . . . . o=o . . . . .o=o. . . . . | | . . . . . . \ . . . . .|. . . . . / . . . . . . | | . . . . . . .\. . . . .|. . . . ./. . . . . . . | | . . . . . . . \ . . . .|. . . . / . . . . . . . | | . . . . . . . .\. . . .|. . . ./. . . . . . . . | | . . . . . . . . \ . . .|. . . / . . . . . . . . | | . . . . . . . . .\. . .|. . ./. . . . . . . . . | | . . . . . . . . . \ . .|. . / . . . . . . . . . | | . . . . . . . . . .\. .|. ./. . . . . . . . . . | | . . . . . . . . . . \ .|. / . . . . . . . . . . | | . . . . . . . . . . .\.|./. . . . . . . . . . . | | . . . . . . . . . . . \|/ . . . . . . . . . . . | | . . . . . . . . . . . .o. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .@. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . (( ( u , du ) ( v , dv ). . . . . . . | | . . . . . )( ( u , du ) ( w , dw ). . . . . . . | | . . . . . )( ( v , dv ) ( w , dw ). . . . . . . | | . . . . . )). . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o
Conjoining a query on the center cell yields:
o-------------------------------------------------o | Eq.uvw. . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . .u. du v. dv. u .du w .dw .v. dv w. dw. . . | | . . .o---o o---o. o---o o---o .o---o o---o. . . | | . . . \ .| |. / . .\. | | ./. . \ .| |. / . . . | | . . . .\.| |./. . . \ | | / . . .\.| |./. . . . | | . . . . \| |/ . . . .\| |/. . . . \| |/ . . . . | | . . . . .o=o. . . . . o=o . . . . .o=o. . . . . | | . . . . . . \ . . . . .|. . . . . / . . . . . . | | . . . . . . .\. . . . .|. . . . ./. . . . . . . | | . . . . . . . \ . . . .|. . . . / . . . . . . . | | . . . . . . . .\. . . .|. . . ./. . . . . . . . | | . . . . . . . . \ . . .|. . . / . . . . . . . . | | . . . . . . . . .\. . .|. . ./. . . . . . . . . | | . . . . . . . . . \ . .|. . / . . . . . . . . . | | . . . . . . . . . .\. .|. ./. . . . . . . . . . | | . . . . . . . . . . \ .|. / . . . . . . . . . . | | . . . . . . . . . . .\.|./. . . . . . . . . . . | | . . . . . . . . . . . \|/ . . . . . . . . . . . | | . . . . . . . . . . . .o. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .@ u v w. . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . (( ( u , du ) ( v , dv ). . . . . . . | | . . . . . )( ( u , du ) ( w , dw ). . . . . . . | | . . . . . )( ( v , dv ) ( w , dw ). . . . . . . | | . . . . . )). . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . u v w . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o
The models of this last expression tell us which combinations of feature changes among the set \(\{ \operatorname{d}u, \operatorname{d}v, \operatorname{d}w \}\) will take us from our present interpretation, the center cell expressed by "\(u\ v\ w\)", to a true value under the target proposition (( u v )( u w )( v w )) .
The result of applying the difference operator \(\operatorname{D}\) to the initial proposition \(q\!\), conjoined with a query on the center cell, yields:
o-------------------------------------------------o | Dq.uvw. . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . .u. du v. dv. u .du w .dw .v. dv w. dw. . . . | | . .o---o o---o. o---o o---o .o---o o---o. . . . | | . . \ .| |. / . .\. | | ./. . \ .| |. / . . . . | | . . .\.| |./. . . \ | | / . . .\.| |./. . . . . | | . . . \| |/ . . . .\| |/. . . . \| |/ . . . . . | | . . . .o=o. . . . . o=o . . . . .o=o. . . . . . | | . . . . . \ . . . . .|. . . . . / . . . . . . . | | . . . . . .\. . . . .|. . . . ./. . . . . . . . | | . . . . . . \ . . . .|. . . . / . . . . . . . . | | . . . . . . .\. . . .|. . . ./. . . . . . . . . | | . . . . . . . \ . . .|. . . / . . . . . . . . . | | . . . . . . . .\. . .|. . ./. . . . . . . . . . | | . . . . . . . . \ . .|. . / . .u v. u w .v w. . | | . . . . . . . . .\. .|. ./. . . .o. .o. .o. . . | | . . . . . . . . . \ .|. / . . . . \ .|. / . . . | | . . . . . . . . . .\.|./. . . . . .\.|./. . . . | | . . . . . . . . . . \|/ . . . . . . \|/ . . . . | | . . . . . . . . . . .o. . . . . . . .o. . . . . | | . . . . . . . . . . .|. . . . . . . .|. . . . . | | . . . . . . . . . . .|. . . . . . . .|. . . . . | | . . . . . . . . . . .|. . . . . . . .|. . . . . | | . . . . . . . . . . .o---------------o. . . . . | | . . . . . . . . . . . \ . . . . . . / . . . . . | | . . . . . . . . . . . .\. . . . . ./. . . . . . | | . . . . . . . . . . . . \ . . . . / . . . . . . | | . . . . . . . . . . . . .\. . . ./. . . . . . . | | . . . . . . . . . . . . . \ . . / . . . . . . . | | . . . . . . . . . . . . . .\. ./. . . . . . . . | | . . . . . . . . . . . . . . \ / . . . . . . . . | | . . . . . . . . . . . . . . .@ u v w. . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . ( . . . . . . . . . . . . . . . . . . . | | . . . . . (( ( u , du ) ( v , dv ). . . . . . . | | . . . . . )( ( u , du ) ( w , dw ). . . . . . . | | . . . . . )( ( v , dv ) ( w , dw ). . . . . . . | | . . . . . )). . . . . . . . . . . . . . . . . . | | . . . . , . . . . . . . . . . . . . . . . . . . | | . . . . . (( u v. . . . . . . . . . . . . . . . | | . . . . . )( u w. . . . . . . . . . . . . . . . | | . . . . . )( v w. . . . . . . . . . . . . . . . | | . . . . . )) . . . . . . . . . . . . . . . . . | | . . . . ) . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . u v w . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o
The models of this last proposition are:
1. u v w du dv dw
2. u v w du dv (dw)
3. u v w du (dv) dw
4. u v w (du) dv dw
This tells us that changing any two or more of the features \(u, v, w\!\) will take us from the center cell, as described by the conjunctive expression "\(u\ v\ w\)", to a cell outside the shaded region for the set \(Q\!\).
o-------------------------------------------------o
| X . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . . . o-------------o . . . . . . . . |
| . . . . . . . ./. . . . . . . .\. . . . . . . . |
| . . . . . . . / . . . .U. . . . \ . . . . . . . |
| . . . . . . ./. . . . . . . . . .\. . . . . . . |
| . . . . . . / . . . . . . . . . . \ . . . . . . |
| . . . . . .o. . . . . . . . . @ . .o. . . . . . |
| . . . . . .|. . . . . . . . . ^ . .|. . . . . . |
| . . . . . .|. . . . . . . . . |dw .|. . . . . . |
| . . . . . .|. . . . . . . . . | . .|. . . . @. |
| . . . .o---o---------o. .o----|----o---o. . ^ . |
| . . . / . . \%%%%%%%%%\ /%%%%%|%%%/ . . \ ./dw. |
| . . ./. . du \%%%%%dw%%o%%dv%%|%%/. . . .\/ . . |
| . . / .@<-----\-o<----/+\---->o%/ . . . ./\ . . |
| . ./. . . . . .\%%%%%/%|%\%%%%%/. . . . / .\. . |
| . o . . . . . . o---o--|--o---o . . . ./. . o . |
| . | . . . . . . . . |%%|%%| . . . . . / . . | . |
| . | .V. . . . . . . |%du%%| . . . . ./. .W. | . |
| . | . . . . . . . . |% |%%| . . . . / . . . | . |
| . o . . . . . . . . o%%v%%o . dv. ./. . . . o . |
| . .\. . . . . . . . .\%o-/------->@ . . . ./. . |
| . . \ . . . . . . . . \%/ . . . . . . . . / . . |
| . . .\. . . . . . . . .o. . . . . . . . ./. . . |
| . . . \ . . . . . . . / \ . . . . . . . / . . . |
| . . . .o-------------o. .o-------------o. . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . |
o-------------------------------------------------o
Figure 3. Effect of the Difference Operator D
Acting on a Polymorphous Function q
Figure 3 shows one way to picture this kind of a situation, by superimposing the paths of indicated feature changes on the venn diagram of the underlying proposition. Here, the models, or the satisfying interpretations, of the relevant difference proposition \(\operatorname{D}q\) are marked with "@" signs, and the boundary crossings along each path are marked with the corresponding differential features among the collection \(\{ \operatorname{d}u, \operatorname{d}v, \operatorname{d}w \}\). In sum, starting from the cell \(uvw\!\), we have the following four paths:
1. du dv dw => Change u, v, w. 2. du dv (dw) => Change u and v. 3. du (dv) dw => Change u and w. 4. (du) dv dw => Change v and w.
Next I will discuss several applications of logical differentials, developing along the way their logical and practical implications.
We have come to the point of making a connection, at a very primitive level, between propositional logic and the classes of mathematical structures that are employed in mathematical systems theory to model dynamical systems of very general sorts.
Recapitulation
Here is a flash montage of what has gone before, retrospectively touching on just the highpoints, and highlighting mostly just Figures and Tables, all directed toward the aim of ending up with a novel style of pictorial diagram, one that will serve us well in the future, as I have found it readily adaptable and steadily more trustworthy in my previous investigations, whenever we have to illustrate these very basic sorts of dynamic scenarios to ourselves, to others, to computers.
We typically start out with a proposition of interest, for example, the proposition \(q : X \to \mathbb{B}\) depicted here:
o-------------------------------------------------o | q . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . u v . u w . v w . . . . . . . . | | . . . . . . . . . .o. .o. .o. . . . . . . . . . | | . . . . . . . . . . \ .|. / . . . . . . . . . . | | . . . . . . . . . . .\.|./. . . . . . . . . . . | | . . . . . . . . . . . \|/ . . . . . . . . . . . | | . . . . . . . . . . . .o. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .@. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . (( u v )( u w )( v w )) . . . . . . | o-------------------------------------------------o
The proposition \(q\!\) is properly considered as an abstract object, in some acceptation of those very bedevilled and egging-on terms, but it enjoys an interpretation as a function of a suitable type, and all we have to do in order to enjoy the utility of this type of representation is to observe a decent respect for what befits.
I will skip over the details of how to do this for right now. .I started to write them out in full, and it all became even more tedious than my usual standard, and besides, I think that everyone more or less knows how to do this already.
Once we have survived the big leap of re-interpreting these abstract names as the names of relatively concrete dimensions of variation, we can begin to lay out all of the familiar sorts of mathematical models and pictorial diagrams that go with these modest dimensions, the functions that can be formed on them, and the transformations that can be entertained among this whole crew.
Here is the venn diagram for the proposition \(q\!\).
o-----------------------------------------------------------o | X . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . .o-------------o. . . . . . . . . . . | | . . . . . . . . . . / . . . . . . . \ . . . . . . . . . . | | . . . . . . . . . ./. . . . . . . . .\. . . . . . . . . . | | . . . . . . . . . / . . . . . . . . . \ . . . . . . . . . | | . . . . . . . . ./. . . . . . . . . . .\. . . . . . . . . | | . . . . . . . . / . . . . . . . . . . . \ . . . . . . . . | | . . . . . . . .o. . . . . . . . . . . . .o. . . . . . . . | | . . . . . . . .|. . . . . . U . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . o--o----------o . o----------o--o . . . . . . | | . . . . . ./. . \%%%%%%%%%%\./%%%%%%%%%%/ . .\. . . . . . | | . . . . . / . . .\%%%%%%%%%%o%%%%%%%%%%/. . . \ . . . . . | | . . . . ./. . . . \%%%%%%%%/%\%%%%%%%%/ . . . .\. . . . . | | . . . . / . . . . .\%%%%%%/%%%\%%%%%%/. . . . . \ . . . . | | . . . ./. . . . . . \%%%%/%%%%%\%%%%/ . . . . . .\. . . . | | . . . o . . . . . . .o--o-------o--o. . . . . . . o . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . | . . . .V. . . . |%%%%%%%| . . . .W. . . . | . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . o . . . . . . . . o%%%%%%%o . . . . . . . . o . . . | | . . . .\. . . . . . . . .\%%%%%/. . . . . . . . ./. . . . | | . . . . \ . . . . . . . . \%%%/ . . . . . . . . / . . . . | | . . . . .\. . . . . . . . .\%/. . . . . . . . ./. . . . . | | . . . . . \ . . . . . . . . o . . . . . . . . / . . . . . | | . . . . . .\. . . . . . . ./.\. . . . . . . ./. . . . . . | | . . . . . . o-------------o . o-------------o . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | o-----------------------------------------------------------o Figure 1. Venn Diagram for the Proposition q
By way of excuse, if not yet a full justification, I probably ought to give an account of the reasons why I continue to hang onto these primitive styles of depiction, even though I can hardly recommend that anybody actually try to draw them, at least, not once the number of variables climbs much higher than three or four or five at the utmost. . One of the reasons would have to be this: .that in the relationship between their continuous aspect and their discrete aspect, venn diagrams constitute a form of "iconic" reminder of a very important fact about all finite information depictions (FID's) of the larger world of reality, and that is the hard fact that we deceive ourselves to a degree if we imagine that the lines and the distinctions that we draw in our imagination are all there is to reality, and thus, that as we practice to categorize, we also manage to discretize, and thus, to distort, to reduce, and to truncate the richness of what there is to the poverty of what we can sieve and sift through our senses, or what we can draw in the tangled webs of our own very tenuous and tinctured distinctions.
Another common scheme for description and evaluation of a proposition is the so-called truth table or the semantic tableau, for example:
| u v w | u ∧ v | u ∧ w | v ∧ w | q |
|---|---|---|---|---|
| 0 0 0 | 0 | 0 | 0 | 0 |
| 0 0 1 | 0 | 0 | 0 | 0 |
| 0 1 0 | 0 | 0 | 0 | 0 |
| 0 1 1 | 0 | 0 | 1 | 1 |
| 1 0 0 | 0 | 0 | 0 | 0 |
| 1 0 1 | 0 | 1 | 0 | 1 |
| 1 1 0 | 1 | 0 | 0 | 1 |
| 1 1 1 | 1 | 1 | 1 | 1 |
Reading off the shaded cells of the venn diagram or the rows of the truth table that have a "1" in the q column, we see that the models, or satisfying interpretations, of the proposition \(q\!\) are the four that can be expressed, in either the additive or the multiplicative manner, as follows:
- The points of the space \(X\!\) that are assigned the coordinates:
\((u, v, w)\!\) = \((0, 1, 1)\!\) or \((1, 0, 1)\!\) or \((1, 1, 0)\!\) or \((1, 1, 1)\!\). - The points of the space \(X\!\) that have the conjunctive descriptions:
(u) v woru (v) woru v (w)oru v w, where "(x)" is "notx".
The next thing that one typically does is to consider the effects of various operators on the proposition of interest, which may be called the operand or the source proposition, leaving the corresponding terms opus or target as names for the result.
In our initial consideration of the proposition \(q\!\), we naturally interpret it as a function of the three variables that it wears on its sleeve, as it were, namely, those that we find contained in the basis \(\{ u, v, w \}\). As we begin to regard this proposition from the standpoint of a differential analysis, however, we may need to regard it as tacitly embedded in any number of higher dimensional spaces. Just by way of starting out, our immediate interest is with the first order differential analysis (FODA), and this requires us to regard all of the propositions in sight as functions of the variables in the first order extended basis, specifically, those in the set \(\{ u, v, w, \operatorname{d}u, \operatorname{d}v, \operatorname{d}w \}\). Now this does not change the expression of any proposition, like \(q\!\), that does not mention the extra variables, only changing how it gets interpreted as a function. A level of interpretive flexibility of this order is very useful, and it is quite common throughout mathematics. In this discussion, I will invoke its application under the name of the tacit extension of a proposition to any universe of discourse based on a superset of its original basis.
I think that we finally have enough of the preliminary set-ups and warm-ups out of the way that we can begin to tackle the differential analysis proper of the sample proposition, the truth-function \(q(u, v, w)\!\) that is given by the following expression:
(( u v )( u w )( v w ))
When \(X\!\) is the type of space that is generated by \(\{ u, v, w \}\!\), let \(\operatorname{d}X\) be the type of space that is generated by \(\{ \operatorname{d}u, \operatorname{d}v, \operatorname{d}w \}\), and let \(X \times \operatorname{d}X\) be the type of space that is generated by the extended set of boolean basis elements \(\{ u, v, w, \operatorname{d}u, \operatorname{d}v, \operatorname{d}w \}\). For convenience, define a notation "\(\operatorname{E}X\)" so that \(\operatorname{E}X = X \times \operatorname{d}X\). Even though the differential variables are in some abstract sense no different than other boolean variables, it usually helps to mark their distinctive roles and their differential interpretation by means of the distinguishing domain name "\(\operatorname{d}\mathbb{B}\)". Using these designations of logical spaces, the propositions over them can be assigned both abstract and concrete types.
For instance, consider the proposition \(q(u, v, w)\!\), as before, and then consider its tacit extension \(q(u, v, w, \operatorname{d}u, \operatorname{d}v, \operatorname{d}w)\!\), the latter of which may be indicated more explicitly as "\(\operatorname{e}q\!\)".
Proposition \(q\!\) is abstractly typed as \(q : \mathbb{B}^3 \to \mathbb{B}.\)
Proposition \(q\!\) is concretely typed as \(q : X \to \mathbb{B}.\)
Proposition \(\operatorname{e}q\!\) is abstractly typed as \(\operatorname{e}q : \mathbb{B}^3 \times \operatorname{d}\mathbb{B}^3 \to \mathbb{B}.\)
Proposition \(\operatorname{e}q\!\) is concretely typed as \(\operatorname{e}q : X \times \operatorname{d}X \to \mathbb{B}.\)
Succinctly, \(\operatorname{e}q : \operatorname{E}X \to \mathbb{B}.\)
We now return to our consideration of the effects of various differential operators on propositions. This time around we have enough exact terminology that we shall be able to explain what is actually going on here in a rather more articulate fashion.
The first transformation of the source proposition \(q\!\) that we may wish to stop and examine, though it is not unusual to skip right over this stage of analysis, frequently regarding it as a purely intermediary stage, holding scarcely even so much as the passing interest, is the work of the enlargement or shift operator \(\operatorname{E}.\)
Applying the operator \(\operatorname{E}\) to the operand proposition \(q\!\) yields:
o-------------------------------------------------o | Eq. . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . .u. du v. dv. u .du w .dw .v. dv w. dw. . . | | . . .o---o o---o. o---o o---o .o---o o---o. . . | | . . . \ .| |. / . .\. | | ./. . \ .| |. / . . . | | . . . .\.| |./. . . \ | | / . . .\.| |./. . . . | | . . . . \| |/ . . . .\| |/. . . . \| |/ . . . . | | . . . . .o=o. . . . . o=o . . . . .o=o. . . . . | | . . . . . . \ . . . . .|. . . . . / . . . . . . | | . . . . . . .\. . . . .|. . . . ./. . . . . . . | | . . . . . . . \ . . . .|. . . . / . . . . . . . | | . . . . . . . .\. . . .|. . . ./. . . . . . . . | | . . . . . . . . \ . . .|. . . / . . . . . . . . | | . . . . . . . . .\. . .|. . ./. . . . . . . . . | | . . . . . . . . . \ . .|. . / . . . . . . . . . | | . . . . . . . . . .\. .|. ./. . . . . . . . . . | | . . . . . . . . . . \ .|. / . . . . . . . . . . | | . . . . . . . . . . .\.|./. . . . . . . . . . . | | . . . . . . . . . . . \|/ . . . . . . . . . . . | | . . . . . . . . . . . .o. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .@. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . (( ( u , du ) ( v , dv ). . . . . . . | | . . . . . )( ( u , du ) ( w , dw ). . . . . . . | | . . . . . )( ( v , dv ) ( w , dw ). . . . . . . | | . . . . . )). . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o
The enlarged proposition \(\operatorname{E}q\) is minimally interpretable as a function on the six variables of \(\{ u, v, w, \operatorname{d}u, \operatorname{d}v, \operatorname{d}w \}.\) .In other words, \(\operatorname{E}q : \operatorname{E}X \to \mathbb{B},\) or \(\operatorname{E}q : X \times \operatorname{d}X \to \mathbb{B}.\)
Conjoining a query on the center cell, \(c = u\ v\ w\!\), yields:
o-------------------------------------------------o | Eq.c. . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . .u. du v. dv. u .du w .dw .v. dv w. dw. . . | | . . .o---o o---o. o---o o---o .o---o o---o. . . | | . . . \ .| |. / . .\. | | ./. . \ .| |. / . . . | | . . . .\.| |./. . . \ | | / . . .\.| |./. . . . | | . . . . \| |/ . . . .\| |/. . . . \| |/ . . . . | | . . . . .o=o. . . . . o=o . . . . .o=o. . . . . | | . . . . . . \ . . . . .|. . . . . / . . . . . . | | . . . . . . .\. . . . .|. . . . ./. . . . . . . | | . . . . . . . \ . . . .|. . . . / . . . . . . . | | . . . . . . . .\. . . .|. . . ./. . . . . . . . | | . . . . . . . . \ . . .|. . . / . . . . . . . . | | . . . . . . . . .\. . .|. . ./. . . . . . . . . | | . . . . . . . . . \ . .|. . / . . . . . . . . . | | . . . . . . . . . .\. .|. ./. . . . . . . . . . | | . . . . . . . . . . \ .|. / . . . . . . . . . . | | . . . . . . . . . . .\.|./. . . . . . . . . . . | | . . . . . . . . . . . \|/ . . . . . . . . . . . | | . . . . . . . . . . . .o. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .@ u v w. . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . (( ( u , du ) ( v , dv ). . . . . . . | | . . . . . )( ( u , du ) ( w , dw ). . . . . . . | | . . . . . )( ( v , dv ) ( w , dw ). . . . . . . | | . . . . . )). . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . u v w . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o
The models of this last expression tell us which combinations of feature changes among the set \(\{ \operatorname{d}u, \operatorname{d}v, \operatorname{d}w \}\) will take us from our present interpretation, the center cell expressed by "u v w", to a true value under the given proposition (( u v )( u w )( v w )).
The models of \(\operatorname{E}q \cdot c\) can be described in the usual ways as follows:
- The points of the space \(\operatorname{E}X\) that have the following coordinate descriptions:
<u, v, w, du, dv, dw> =
<1, 1, 1, 0, 0, 0>,
<1, 1, 1, 0, 0, 1>,
<1, 1, 1, 0, 1, 0>,
<1, 1, 1, 1, 0, 0>.
- The points of the space \(\operatorname{E}X\) that have the following conjunctive expressions:
u v w (du)(dv)(dw),
u v w (du)(dv) dw ,
u v w (du) dv (dw),
u v w du (dv)(dw).
In summary, \(\operatorname{E}q \cdot c\) informs us that we can get from \(c\!\) to a model of \(q\!\) by changing our position with respect to \(u, v, w\!\) according to the following description:
Change none or just one among \(\{ u, v, w \}.\!\)
I think that it would be worth our time to diagram the models of the enlarged or shifted proposition, \(\operatorname{E}q,\) at least, the selection of them that we find issuing from the center cell \(c.\!\)
Figure 4 is an extended venn diagram for the proposition \(\operatorname{E}q \cdot c,\) where the shaded area gives the models of \(q\!\) and the "@" signs mark the terminal points of the requisite feature alterations.
o-------------------------------------------------o
| X . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . . . o-------------o . . . . . . . . |
| . . . . . . . ./. . . . . . . .\. . . . . . . . |
| . . . . . . . / . . . . . . . . \ . . . . . . . |
| . . . . . . ./. . . . . . . . . .\. . . . . . . |
| . . . . . . / . . . . . . . . . . \ . . . . . . |
| . . . . . .o. . . . . .U. . . . . .o. . . . . . |
| . . . . . .|. . . . . . . . . . . .|. . . . . . |
| . . . . . .|. . . . . . . . . . . .|. . . . . . |
| . . . . . .|. . . . . . . . . . . .|. . . . . . |
| . . . .o---o---------o. .o---------o---o. . . . |
| . . . / . . \%%%%%%%%%\ /%%%%%%%%%/ . . \ . . . |
| . . ./. . . .\%%%%%dw%%o%%dv%%%%%/. . . .\. . . |
| . . / . . . . \%@<----/@\---->@%/ . . . . \ . . |
| . ./. . . . . .\%%%%%/%|%\%%%%%/. . . . . .\. . |
| . o . . . . . . o---o--|--o---o . . . . . . o . |
| . | . . . . . . . . |%%|%%| . . . . . . . . | . |
| . | . . . .V. . . . |%du%%| . . . .W. . . . | . |
| . | . . . . . . . . |% |%%| . . . . . . . . | . |
| . o . . . . . . . . o%%v%%o . . . . . . . . o . |
| . .\. . . . . . . . .\%@%/. . . . . . . . ./. . |
| . . \ . . . . . . . . \%/ . . . . . . . . / . . |
| . . .\. . . . . . . . .o. . . . . . . . ./. . . |
| . . . \ . . . . . . . / \ . . . . . . . / . . . |
| . . . .o-------------o. .o-------------o. . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . |
o-------------------------------------------------o
Figure 4. Effect of the Enlargement Operator E
On the Proposition q, Evaluated at c
One more piece of notation will save us a few bytes in the length of many of our schematic formulations.
Let \(\mathcal{X} = \{ x_1, \ldots, x_k \}\) be a finite set of variables, regarded as a formal alphabet of formal symbols but listed here without quotation marks. Starting from this initial alphabet, the following items may then be defined:
The "(first order) differential alphabet",
\(\operatorname{d}\mathcal{X} = \{ \operatorname{d}x_1, \ldots, \operatorname{d}x_k \}.\)
The "(first order) extended alphabet",
\(\operatorname{E}\mathcal{X} = \mathcal{X} \cup \operatorname{d}\mathcal{X},\)
\(\operatorname{E}\mathcal{X} = \{ x_1, \dots, x_k, \operatorname{d}x_1, \ldots, \operatorname{d}x_k \}.\)
Before we continue with the differential analysis of the source proposition \(q\!\), we need to pause and take another look at just how it shapes up in the light of the extended universe \(\operatorname{E}X,\) in other words, to examine in detail its tacit extension \(\operatorname{e}q.\!\)
The models of \(\operatorname{e}q\!\) in \(\operatorname{E}X\!\) can be comprehended as follows:
Working in the summary coefficient form of representation, if the coordinate list \(\mathbf{x}\!\) is a model of \(q\!\) in \(X,\!\) then one can construct a coordinate list \(\operatorname{e}\mathbf{x}\!\) as a model for \(\operatorname{e}q\!\) in \(\operatorname{E}X\!\) just by appending any combination of values for the differential variables in \(\operatorname{d}\mathcal{X}.\)
For example, to focus once again on the center cell \(c,\!\) which happens to be a model of the proposition \(q\!\) in \(X,\!\) one can extend \(c\!\) in eight different ways into \(\operatorname{E}X,\!\) and thus get eight models of the tacit extension \(\operatorname{e}q\!\) in \(\operatorname{E}X.\!\)
It is a trivial exercise to write these out, but it is useful to do so at least once in order to see the patterns of data involved.
The tacit extensions of \(c\!\) that are models of \(\operatorname{e}q\!\) in \(\operatorname{E}X\!\) are as follows:
<u, v, w, du, dv, dw> =
<1, 1, 1, 0, 0, 0>,
<1, 1, 1, 0, 0, 1>,
<1, 1, 1, 0, 1, 0>,
<1, 1, 1, 0, 1, 1>,
<1, 1, 1, 1, 0, 0>,
<1, 1, 1, 1, 0, 1>,
<1, 1, 1, 1, 1, 0>,
<1, 1, 1, 1, 1, 1>.
Working in the conjunctive product form of representation, if the conjunctive proposition \(x\!\) is a model of \(q\!\) in \(X,\!\) then one can construct a conjunctive proposition \(\operatorname{e}x\!\) as a model for \(\operatorname{e}q\!\) in \(\operatorname{E}X\!\) just by appending any combination of values for the differential variables in \(\operatorname{d}\mathcal{X}.\)
The tacit extensions of \(c\!\) that are models of \(\operatorname{e}q\!\) in \(\operatorname{E}X\!\) are as follows:
u v w (du)(dv)(dw),
u v w (du)(dv) dw ,
u v w (du) dv (dw),
u v w (du) dv dw ,
u v w du (dv)(dw),
u v w du (dv) dw ,
u v w du dv (dw),
u v w du dv dw .
In short, \(\operatorname{e}q \cdot c\) just enumerates all of the possible changes in \(\operatorname{E}X\!\) that derive from, issue from, or stem from the cell \(c\!\) in \(X.\!\)
That was pretty tedious, and I know that it all appears to be totally trivial, which is precisely why we usually just leave it "tacit" in the first place, but hard experience, and a real acquaintance with the confusion that can beset us when we do not render these implicit grounds explicit, have taught me that it will ultimately be necessary to get clear about it, and by this clear to say marked, not merely transparent.
Before going on, it would probably be a good idea to remind ourselves of just why we are going through with this exercise. It is to unify the world of change, for which aspect or regime of the world I occasionally evoke the eponymous figures of Prometheus and Heraclitus, and the world of logic, for which facet or realm of the world I periodically recur to the prototypical shades of Epimetheus and Parmenides, at least, that is, to state it more carefully, to encompass the antics and the escapades of these all too manifestly strife-born twins within the scopes of our thoughts and within the charts of our theories, as it is most likely the only places where ever they will, for the moment and as long as it lasts, be seen or be heard together.
With that intermezzo, with all of its echoes of the opening overture, over and done, let us now return to that droller drama, already fast in progress, the differential disentanglements, hopefully toward the end of a grandly enlightening denouement, of the ever-polymorphous \(Q.\!\)
The next transformation of the source proposition \(q,\!\) that we are typically aiming to contemplate in the process of carrying out a differential analysis of its dynamic effects or implications, is the yield of the so-called difference or delta operator \(\operatorname{D}.\) The resultant difference proposition \(\operatorname{D}q\) is defined in terms of the source proposition \(q\!\) and the shifted proposition \(\operatorname{E}q\) thusly:
\[\operatorname{D}q = \operatorname{E}q - q = \operatorname{E}q - \operatorname{e}q.\]
- Since "+" and "-" signify the same operation over \(\mathbb{B},\) we have:
\[\operatorname{D}q = \operatorname{E}q + q = \operatorname{E}q + \operatorname{e}q.\]
- Since "+" = "exclusive-or", cactus syntax expresses this as:
Eq q Eq eq
o---o o---o
\ / \ /
Dq = @ = @
Dq = ( Eq , q ) = ( Eq , eq ).
Recall that a \(k\)-place bracket "\((x_1, x_2, \ldots, x_k)\!\)" is interpreted (in the existential interpretation) to mean "Exactly one of the \(x_j\!\) is false", thus the two-place bracket is equivalent to the exclusive-or.
The result of applying the difference operator \(\operatorname{D}\) to the source proposition \(q,\!\) conjoined with a query on the center cell \(c,\!\) is:
o-------------------------------------------------o | Dq.uvw. . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . .u. du v. dv. u .du w .dw .v. dv w. dw. . . . | | . .o---o o---o. o---o o---o .o---o o---o. . . . | | . . \ .| |. / . .\. | | ./. . \ .| |. / . . . . | | . . .\.| |./. . . \ | | / . . .\.| |./. . . . . | | . . . \| |/ . . . .\| |/. . . . \| |/ . . . . . | | . . . .o=o. . . . . o=o . . . . .o=o. . . . . . | | . . . . . \ . . . . .|. . . . . / . . . . . . . | | . . . . . .\. . . . .|. . . . ./. . . . . . . . | | . . . . . . \ . . . .|. . . . / . . . . . . . . | | . . . . . . .\. . . .|. . . ./. . . . . . . . . | | . . . . . . . \ . . .|. . . / . . . . . . . . . | | . . . . . . . .\. . .|. . ./. . . . . . . . . . | | . . . . . . . . \ . .|. . / . .u v. u w .v w. . | | . . . . . . . . .\. .|. ./. . . .o. .o. .o. . . | | . . . . . . . . . \ .|. / . . . . \ .|. / . . . | | . . . . . . . . . .\.|./. . . . . .\.|./. . . . | | . . . . . . . . . . \|/ . . . . . . \|/ . . . . | | . . . . . . . . . . .o. . . . . . . .o. . . . . | | . . . . . . . . . . .|. . . . . . . .|. . . . . | | . . . . . . . . . . .|. . . . . . . .|. . . . . | | . . . . . . . . . . .|. . . . . . . .|. . . . . | | . . . . . . . . . . .o---------------o. . . . . | | . . . . . . . . . . . \ . . . . . . / . . . . . | | . . . . . . . . . . . .\. . . . . ./. . . . . . | | . . . . . . . . . . . . \ . . . . / . . . . . . | | . . . . . . . . . . . . .\. . . ./. . . . . . . | | . . . . . . . . . . . . . \ . . / . . . . . . . | | . . . . . . . . . . . . . .\. ./. . . . . . . . | | . . . . . . . . . . . . . . \ / . . . . . . . . | | . . . . . . . . . . . . . . .@ u v w. . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . ( . . . . . . . . . . . . . . . . . . . | | . . . . . (( ( u , du ) ( v , dv ). . . . . . . | | . . . . . )( ( u , du ) ( w , dw ). . . . . . . | | . . . . . )( ( v , dv ) ( w , dw ). . . . . . . | | . . . . . )). . . . . . . . . . . . . . . . . . | | . . . . , . . . . . . . . . . . . . . . . . . . | | . . . . . (( u v. . . . . . . . . . . . . . . . | | . . . . . )( u w. . . . . . . . . . . . . . . . | | . . . . . )( v w. . . . . . . . . . . . . . . . | | . . . . . )) . . . . . . . . . . . . . . . . . | | . . . . ) . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . u v w . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o
The models of the difference proposition \(\operatorname{D}q \cdot uvw\!\) are:
1. u v w du dv dw 2. u v w du dv (dw) 3. u v w du (dv) dw 4. u v w (du) dv dw
This tells us that changing any two or more of the features \(u, v, w\!\) will take us from the center cell that is marked by the conjunctive expression "\(u\ v\ w\)" to a cell outside the shaded region for the area \(Q.\!\)
o-------------------------------------------------o
| X . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . . . o-------------o . . . . . . . . |
| . . . . . . . ./. . . . . . . .\. . . . . . . . |
| . . . . . . . / . . . .U. . . . \ . . . . . . . |
| . . . . . . ./. . . . . . . . . .\. . . . . . . |
| . . . . . . / . . . . . . . . . . \ . . . . . . |
| . . . . . .o. . . . . . . . . @ . .o. . . . . . |
| . . . . . .|. . . . . . . . . ^ . .|. . . . . . |
| . . . . . .|. . . . . . . . . |dw .|. . . . . . |
| . . . . . .|. . . . . . . . . | . .|. . . . .@. |
| . . . .o---o---------o. .o----|----o---o. . ^ . |
| . . . / . . \%%%%%%%%%\ /%%%%%|%%%/ . . \ ./dw. |
| . . ./. . du \%%%%%dw%%o%%dv%%|%%/. . . .\/ . . |
| . . / .@<-----\-o<----/+\---->o%/ . . . ./\ . . |
| . ./. . . . . .\%%%%%/%|%\%%%%%/. . . . / .\. . |
| . o . . . . . . o---o--|--o---o . . . ./. . o . |
| . | . . . . . . . . |%%|%%| . . . . . / . . | . |
| . | .V. . . . . . . |%du%%| . . . . ./. .W. | . |
| . | . . . . . . . . |% |%%| . . . . / . . . | . |
| . o . . . . . . . . o%%v%%o . dv. ./. . . . o . |
| . .\. . . . . . . . .\%o-/------->@ . . . ./. . |
| . . \ . . . . . . . . \%/ . . . . . . . . / . . |
| . . .\. . . . . . . . .o. . . . . . . . ./. . . |
| . . . \ . . . . . . . / \ . . . . . . . / . . . |
| . . . .o-------------o. .o-------------o. . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . |
| . . . . . . . . . . . . . . . . . . . . . . . . |
o-------------------------------------------------o
Figure 3. Effect of the Difference Operator D
Acting on a Polymorphous Function q
Figure 3 shows one way to picture this kind of a situation, by superimposing the paths of indicated feature changes on the venn diagram of the underlying proposition. Here, the models, or the satisfying interpretations, of the relevant difference proposition \(\operatorname{D}q\) are marked with "@" signs, and the boundary crossings along each path are marked with the corresponding differential features among the collection \(\{ \operatorname{d}u, \operatorname{d}v, \operatorname{d}w \}\). In sum, starting from the cell \(u\ v\ w,\) we have the following four paths:
1. du dv dw = Change u, v, w. 2. du dv (dw) = Change u and v. 3. du (dv) dw = Change u and w. 4. (du) dv dw = Change v and w.
That sums up, but rather more carefully, the material that I ran through just a bit too quickly the first time around. Next time, I will begin to develop an alternative style of diagram for depicting these types of differential settings.
Another way of looking at this situation is by letting the (first order) differential features \(\operatorname{d}u, \operatorname{d}v, \operatorname{d}w\) be viewed as the features of another universe of discourse, called the tangent universe to \(X\!\) with respect to the interpretation \(c\!\) and represented as \(\operatorname{d}X \cdot c\) . In this setting, \(\operatorname{D}q \cdot c\) , the difference proposition of \(q\!\) at the interpretation \(c\!\) , where \(c = u\ v\ w\) , is marked by the shaded region in Figure 4.
o-----------------------------------------------------------o | dX.c. . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . .o-------------o. . . . . . . . . . . | | . . . . . . . . . . / . . . . . . . \ . . . . . . . . . . | | . . . . . . . . . ./. . . . . . . . .\. . . . . . . . . . | | . . . . . . . . . / . . . . . . . . . \ . . . . . . . . . | | . . . . . . . . ./. . . . . . . . . . .\. . . . . . . . . | | . . . . . . . . / . . . . . . . . . . . \ . . . . . . . . | | . . . . . . . .o. . . . . . . . . . . . .o. . . . . . . . | | . . . . . . . .|. . . . . .dU . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . o--o----------o . o----------o--o . . . . . . | | . . . . . ./. . \%%%%%%%%%%\./%%%%%%%%%%/ . .\. . . . . . | | . . . . . / . . .\%%% 2 %%%%o%%%% 3 %%%/. . . \ . . . . . | | . . . . ./. . . . \%%%%%%%%/%\%%%%%%%%/ . . . .\. . . . . | | . . . . / . . . . .\%%%%%%/%%%\%%%%%%/. . . . . \ . . . . | | . . . ./. . . . . . \%%%%/% 1 %\%%%%/ . . . . . .\. . . . | | . . . o . . . . . . .o--o-------o--o. . . . . . . o . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . | . . . dV. . . . |%% 4 %%| . . . dW. . . . | . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . o . . . . . . . . o%%%%%%%o . . . . . . . . o . . . | | . . . .\. . . . . . . . .\%%%%%/. . . . . . . . ./. . . . | | . . . . \ . . . . . . . . \%%%/ . . . . . . . . / . . . . | | . . . . .\. . . . . . . . .\%/. . . . . . . . ./. . . . . | | . . . . . \ . . . . . . . . o . . . . . . . . / . . . . . | | . . . . . .\. . . . . . . ./.\. . . . . . . ./. . . . . . | | . . . . . . o-------------o . o-------------o . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | o-----------------------------------------------------------o Figure 4. Tangent Venn Diagram for Dq.c
Taken in the context of the tangent universe to \(X\!\) at \(c = u\ v\ w\) , written \(\operatorname{d}X \cdot c\) or \(\operatorname{d}X \cdot u\ v\ w\) , the shaded area of Figure 4 indicates the models of the difference proposition \(\operatorname{d}q \cdot u\ v\ w\) , specifically:
1. u v w du dv dw 2. u v w du dv (dw) 3. u v w du (dv) dw 4. u v w (du) dv dw
Example 2. Jets and Sharks
Reference. Awbrey, J., and Awbrey, S. (1989), "Theme One : A Program of Inquiry", unpublished manuscript, 09 Aug 1989.
The propositional calculus that is based on the boundary operator can be interpreted in a way that resembles the logic of activation states and competition constraints in certain neural network models. One way to do this is by interpreting the blank or unmarked state as the resting state of a neural pool, the bound or marked state as its activated state, and by representing a mutually inhibitory pool of neurons \(A, B, C\!\) in the expression "\((A, B, C)\!\)". To illustrate this possibility, we transcribe a well-known example from the parallel distributed processing literature (McClelland and Rumelhart, 1988) and work through two of the associated exercises as portrayed in Existential Graph format.
File "jas.log". Jets and Sharks Example o-----------------------------------------------------------o | | | (( art ),( al ),( sam ),( clyde ),( mike ), | | ( jim ),( greg ),( john ),( doug ),( lance ), | | ( george ),( pete ),( fred ),( gene ),( ralph ), | | ( phil ),( ike ),( nick ),( don ),( ned ), | | ( karl ),( ken ),( earl ),( rick ),( ol ), | | ( neal ),( dave )) | | | | ( jets , sharks ) | | | | ( jets , | | ( art ),( al ),( sam ),( clyde ),( mike ), | | ( jim ),( greg ),( john ),( doug ),( lance ), | | ( george ),( pete ),( fred ),( gene ),( ralph )) | | | | ( sharks , | | ( phil ),( ike ),( nick ),( don ),( ned ),( karl ), | | ( ken ),( earl ),( rick ),( ol ),( neal ),( dave )) | | | | (( 20's ),( 30's ),( 40's )) | | | | ( 20's , | | ( sam ),( jim ),( greg ),( john ),( lance ), | | ( george ),( pete ),( fred ),( gene ),( ken )) | | | | ( 30's , | | ( al ),( mike ),( doug ),( ralph ),( phil ), | | ( ike ),( nick ),( don ),( ned ),( rick ), | | ( ol ),( neal ),( dave )) | | | | ( 40's , | | ( art ),( clyde ),( karl ),( earl )) | | | | (( junior_high ),( high_school ),( college )) | | | | ( junior_high , | | ( art ),( al ),( clyde ),( mike ),( jim ), | | ( john ),( lance ),( george ),( ralph ),( ike )) | | | | ( high_school , | | ( greg ),( doug ),( pete ),( fred ), | | ( nick ),( karl ),( ken ),( earl ), | | ( rick ),( neal ),( dave )) | | | | ( college , | | ( sam ),( gene ),( phil ),( don ),( ned ),( ol )) | | | | (( single ),( married ),( divorced )) | | | | ( single , | | ( art ),( sam ),( clyde ),( mike ),( doug ), | | ( pete ),( fred ),( gene ),( ralph ),( ike ), | | ( nick ),( ken ),( neal )) | | | | ( married , | | ( al ),( greg ),( john ),( lance ),( phil ), | | ( don ),( ned ),( karl ),( earl ),( ol )) | | | | ( divorced , | | ( jim ),( george ),( rick ),( dave )) | | | | (( bookie ),( burglar ),( pusher )) | | | | ( bookie , | | ( sam ),( clyde ),( mike ),( doug ), | | ( pete ),( ike ),( ned ),( karl ),( neal )) | | | | ( burglar , | | ( al ),( jim ),( john ),( lance ), | | ( george ),( don ),( ken ),( earl ),( rick )) | | | | ( pusher , | | ( art ),( greg ),( fred ),( gene ), | | ( ralph ),( phil ),( nick ),( ol ),( dave )) | | | o-----------------------------------------------------------o
We now apply the Study tool to the proposition defining the Jets and Sharks data base.
With a query on the name "ken" we obtain all of the propositional features associated with Ken, as shown in the following output.
File "ken.sen". Output of Query on "ken" o-----------------------------------------------------------o | | | ken | | sharks | | 20's | | high_school | | single | | burglar | | | o-----------------------------------------------------------o
With a query on the two features "college" and "sharks" we obtain the following outline of all features satisfying these constraints.
File "cos.sen". Output of Query on "college" and "sharks" o-----------------------------------------------------------o | | | college | | sharks | | 30's | | married | | bookie | | ned | | burglar | | don | | pusher | | phil | | ol | | | o-----------------------------------------------------------o
From this we discover that all college Sharks are 30-something and married. Further, we have a complete listing of their names broken down by occupation, as no doubt all of them will be, eventually.
Those who already know the tune,
Be at liberty to sing out of it.
Interlude
"The burden of genius is undeliverable"
From a poster, as I once misread it,
Marlboro, Vermont, c. 1976
How does Cosmo, and by this I mean my pet personification of cosmic order in the universe, not to be too tautologous about it, preserve a memory like that, a goodly fraction of a century later, whether localized to this body that's kept going by this heart, and whether by common assumption still more localized to the spongey fibres of this brain, or not?
It strikes me, as it has struck others, that it's terribly unlikely to be stored in persistent patterns of activation, for activation and persistent are nigh a contradiction in terms, as even the author, Cosmo, of the I Ching knew.
But that was then, this is now, so let me try to say it planar.
Notes on Cactus Language
I happened on the graphical syntax for propositional calculus that I now call the cactus language while exploring the confluence of three streams of thought. There was C.S. Peirce's use of operator variables in logical forms and the operational representations of logical concepts, there was George Spencer Brown's explanation of a variable as the contemplated presence or absence of a constant, and then there was the graph theory and group theory that I had been picking up, bit by bit, since I first encountered them in tandem in Frank Harary's foundations of math course, c. 1970.
More on that later, as the memories unthaw, but for the moment I want very much to take care of some long-unfinished business, and give a more detailed explanation of how I used this syntax to represent a popular exercise from the PDP literature of the late 1980's, McClelland's and Rumelhart's "Jets and Sharks".
The knowledge base of the case can be expressed as a single proposition. The following display presents it in the corresponding text file format.
File "jas.log". Jets and Sharks Example o-----------------------------------------------------------o | | | (( art ),( al ),( sam ),( clyde ),( mike ), | | ( jim ),( greg ),( john ),( doug ),( lance ), | | ( george ),( pete ),( fred ),( gene ),( ralph ), | | ( phil ),( ike ),( nick ),( don ),( ned ), | | ( karl ),( ken ),( earl ),( rick ),( ol ), | | ( neal ),( dave )) | | | | ( jets , sharks ) | | | | ( jets , | | ( art ),( al ),( sam ),( clyde ),( mike ), | | ( jim ),( greg ),( john ),( doug ),( lance ), | | ( george ),( pete ),( fred ),( gene ),( ralph )) | | | | ( sharks , | | ( phil ),( ike ),( nick ),( don ),( ned ),( karl ), | | ( ken ),( earl ),( rick ),( ol ),( neal ),( dave )) | | | | (( 20's ),( 30's ),( 40's )) | | | | ( 20's , | | ( sam ),( jim ),( greg ),( john ),( lance ), | | ( george ),( pete ),( fred ),( gene ),( ken )) | | | | ( 30's , | | ( al ),( mike ),( doug ),( ralph ),( phil ), | | ( ike ),( nick ),( don ),( ned ),( rick ), | | ( ol ),( neal ),( dave )) | | | | ( 40's , | | ( art ),( clyde ),( karl ),( earl )) | | | | (( junior_high ),( high_school ),( college )) | | | | ( junior_high , | | ( art ),( al ),( clyde ),( mike ),( jim ), | | ( john ),( lance ),( george ),( ralph ),( ike )) | | | | ( high_school , | | ( greg ),( doug ),( pete ),( fred ), | | ( nick ),( karl ),( ken ),( earl ), | | ( rick ),( neal ),( dave )) | | | | ( college , | | ( sam ),( gene ),( phil ),( don ),( ned ),( ol )) | | | | (( single ),( married ),( divorced )) | | | | ( single , | | ( art ),( sam ),( clyde ),( mike ),( doug ), | | ( pete ),( fred ),( gene ),( ralph ),( ike ), | | ( nick ),( ken ),( neal )) | | | | ( married , | | ( al ),( greg ),( john ),( lance ),( phil ), | | ( don ),( ned ),( karl ),( earl ),( ol )) | | | | ( divorced , | | ( jim ),( george ),( rick ),( dave )) | | | | (( bookie ),( burglar ),( pusher )) | | | | ( bookie , | | ( sam ),( clyde ),( mike ),( doug ), | | ( pete ),( ike ),( ned ),( karl ),( neal )) | | | | ( burglar , | | ( al ),( jim ),( john ),( lance ), | | ( george ),( don ),( ken ),( earl ),( rick )) | | | | ( pusher , | | ( art ),( greg ),( fred ),( gene ), | | ( ralph ),( phil ),( nick ),( ol ),( dave )) | | | o-----------------------------------------------------------o
Let's start with the simplest clause of the conjoint proposition:
( jets , sharks )
Drawn as the corresponding cactus graph, we have:
jets sharks
o-----o
\ /
\ /
@
According to my earlier, if somewhat sketchy interpretive suggestions, we are supposed to picture a quasi-neural pool that contains a couple of quasi-neural agents or units, that between the two of them stand for the logical variables jets and sharks, respectively. Further, we imagine these agents to be mutually inhibitory, so that settlement of the dynamic between them achieves equilibrium when just one of the two is active or changing and the other is stableor enduring.
We were focussing on a particular figure of syntax, presented here in both graph and string renditions:
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . x . . y . . . . . . . . . . | | . . . . . . . . . . o-----o . . . . . . . . . . | | . . . . . . . . . . .\. ./. . . . . . . . . . . | | . . . . . . . . . . . \ / . . . . . . . . . . . | | . . . . . . . . . . . .@. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . .( x , y ). . . . . . . . . . | o-------------------------------------------------o
In traversing the cactus graph, in this case a cactus of one rooted lobe, one starts at the root, reads off a left parenthesis "(" on the ascent up the left side of the lobe, reads off the variable "x", counts off a comma "," as one transits the interior expanse of the lobe, reads off the variable "y", and then sounds out a right parenthesiss ")" on the descent down the last slope that closes out the clause of this cactus lobe.
According to the current story about how the abstract logical situation is embodied in the concrete physical situation, the whole pool of units that corresponds to this expression comes to its resting condition when just one of the two units in {x, y} is resting and the other is charged. We may think of the state of the whole pool as associated with the root node of the cactus, here distinguished by an "amphora" or "at" sign "@", but the root of the cactus is not represented by an individual agent of the system, at least, not yet. We may summarize these facts in tabular form, as shown in Table 5. Simply by way of a common term, let's count a single unit as a "pool of one".
Table 5. Dynamics of (x , y) o---------o---------o---------o | x | y | (x , y) | o=========o=========o=========o | charged | charged | charged | o---------o---------o---------o | charged | resting | resting | o---------o---------o---------o | resting | charged | resting | o---------o---------o---------o | resting | resting | charged | o---------o---------o---------o
I'm going to let that settle a while.
Table 5 sums up the facts of the physical situation at equilibrium. If we let \(\mathbf{B} = \{ \mathrm{charged}, \mathrm{resting} \} = \{ \mathrm{moving}, \mathrm{steady} \} = \{ \mathrm{note}, \mathrm{rest} \},\) or whatever candidates you pick for the 2-membered set in question, the Table shows a function \(f : \mathbf{B} \times \mathbf{B} \to \mathbf{B},\) where \(f(x, y) = (x, y) = \operatorname{XOR}(x, y).\!\)
Table 5. Dynamics of (x , y) o---------o---------o---------o | x | y | (x , y) | o=========o=========o=========o | charged | charged | charged | o---------o---------o---------o | charged | resting | resting | o---------o---------o---------o | resting | charged | resting | o---------o---------o---------o | resting | resting | charged | o---------o---------o---------o
There are two ways that this physical function might be taken to represent a logical function:
If we make the identifications:
\(\mathrm{charged} = \mathrm{true}\ (= \mathrm{indicated}),\!\)
\(\mathrm{resting} = \mathrm{false}\ (= \mathrm{otherwise}),\!\)
then the physical function \(f : \mathbf{B} \times \mathbf{B} \to \mathbf{B}\) is tantamount to the logical function that is commonly known as logical equivalence, or just plain equality:
Table 6. Equality Function
o---------o---------o---------o
| x | y | (x , y) |
o=========o=========o=========o
| true | true | true |
o---------o---------o---------o
| true | false | false |
o---------o---------o---------o
| false | true | false |
o---------o---------o---------o
| false | false | true |
o---------o---------o---------o
If we make the identifications:
\(\mathrm{resting} = \mathrm{true}\ (= \mathrm{indicated}),\!\)
\(\mathrm{charged} = \mathrm{false}\ (= \mathrm{otherwise}),\!\)
then the physical function \(f : \mathbf{B} \times \mathbf{B} \to \mathbf{B}\) is tantamount to the logical function that is commonly known as logical difference, or exclusive disjunction:
Table 7. Difference Function
o---------o---------o---------o
| x | y | (x , y) |
o=========o=========o=========o
| false | false | false |
o---------o---------o---------o
| false | true | true |
o---------o---------o---------o
| true | false | true |
o---------o---------o---------o
| true | true | false |
o---------o---------o---------o
Although the syntax of the cactus language modifies the syntax of Peirce's graphical formalisms to some extent, the first interpretation corresponds to what he called the entitative graphs and the second interpretation corresponds to what he called the existential graphs. In working through the present example, I have chosen the existential interpretation of cactus expressions, and so the form "(jets , sharks)" is interpreted as saying that everything in the universe of discourse is either a Jet or a Shark, but never both at once.
Before we tangle with the rest of the Jets and Sharks example, let's look at a cactus expression that's next in the series we just considered, this time a lobe with three variables. For instance, let's analyze the cactus form whose graph and string expressions are shown in the next display.
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . x .y. z . . . . . . . . . . | | . . . . . . . . . . o--o--o . . . . . . . . . . | | . . . . . . . . . . .\. ./. . . . . . . . . . . | | . . . . . . . . . . . \ / . . . . . . . . . . . | | . . . . . . . . . . . .@. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . .(x, y, z). . . . . . . . . . | o-------------------------------------------------o
As always in this competitive paradigm, we assume that the units \(x, y, z\!\) are mutually inhibitory, so that the only states that are possible at equilibrium are those with exactly one unit charged and all the rest at rest. Table 8 gives the lobal dynamics of the form \((x, y, z).\!\)
Table 8. Lobal Dynamics of the Form (x, y, z) o-----------o-----------o-----------o-----------o | x | y | z | (x, y, z) | o-----------o-----------o-----------o-----------o | | | | | | charged | charged | charged | charged | | | | | | | charged | charged | resting | charged | | | | | | | charged | resting | charged | charged | | | | | | | charged | resting | resting | resting | | | | | | | resting | charged | charged | charged | | | | | | | resting | charged | resting | resting | | | | | | | resting | resting | charged | resting | | | | | | | resting | resting | resting | charged | | | | | | o-----------o-----------o-----------o-----------o
Given \(\mathbb{B} = \{ \mathrm{charged}, \mathrm{resting} \},\) the Table presents the appearance of a function \(f : \mathbb{B} \times \mathbb{B} \times \mathbb{B} \to \mathbb{B},\) where \(f(x, y, z) = (x, y, z).\!\)
If we make the identifications, \(\mathrm{charged} = \mathrm{false},\ \mathrm{resting} = \mathrm{true},\!\) in accord with the so-called existential interpretation, then the physical function \(f : \mathbb{B}^3 \to \mathbb{B}\!\) is tantamount to the logical function that is suggested by the phrase "just 1 of 3 is false". Table 9 is the truth table for the logical function that we get, this time using 0 for false and 1 for true in the customary way.
Table 9. Existential Interpretation of (x, y, z) o-----------o-----------o-----------o-----------o | x | y | z | (x, y, z) | o-----------o-----------o-----------o-----------o | | | | 0 0 0 | 0 | | | | | 0 0 1 | 0 | | | | | 0 1 0 | 0 | | | | | 0 1 1 | 1 | | | | | 1 0 0 | 0 | | | | | 1 0 1 | 1 | | | | | 1 1 0 | 1 | | | | | 1 1 1 | 0 | | | | o-----------------------------------o-----------o
The cactus lobe operators \((\ ), (x_1), (x_1, x_2), (x_1, x_2, x_3), \ldots, (x_1, \ldots, x_k)\!\) are often referred to as boundary operators and one of the reasons for this can be seen most easily in the venn diagram for the \(k\!\)-argument boundary operator \((x_1, \ldots, x_k).\!\) Figure 10 shows the venn diagram for the 3-fold boundary form \((x, y, z).\!\)
o-----------------------------------------------------------o | U . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . .o-------------o. . . . . . . . . . . | | . . . . . . . . . . / . . . . . . . \ . . . . . . . . . . | | . . . . . . . . . ./. . . . . . . . .\. . . . . . . . . . | | . . . . . . . . . / . . . . . . . . . \ . . . . . . . . . | | . . . . . . . . ./. . . . . . . . . . .\. . . . . . . . . | | . . . . . . . . / . . . . . . . . . . . \ . . . . . . . . | | . . . . . . . .o. . . . . . . . . . . . .o. . . . . . . . | | . . . . . . . .|. . . . . . X . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . . .|. . . . . . . . . . . . .|. . . . . . . . | | . . . . . . o--o----------o . o----------o--o . . . . . . | | . . . . . ./. . \%%%%%%%%%%\./%%%%%%%%%%/ . .\. . . . . . | | . . . . . / . . .\%%%%%%%%%%o%%%%%%%%%%/. . . \ . . . . . | | . . . . ./. . . . \%%%%%%%%/.\%%%%%%%%/ . . . .\. . . . . | | . . . . / . . . . .\%%%%%%/ . \%%%%%%/. . . . . \ . . . . | | . . . ./. . . . . . \%%%%/. . .\%%%%/ . . . . . .\. . . . | | . . . o . . . . . . .o--o-------o--o. . . . . . . o . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . | . . . .Y. . . . |%%%%%%%| . . . .Z. . . . | . . . | | . . . | . . . . . . . . |%%%%%%%| . . . . . . . . | . . . | | . . . o . . . . . . . . o%%%%%%%o . . . . . . . . o . . . | | . . . .\. . . . . . . . .\%%%%%/. . . . . . . . ./. . . . | | . . . . \ . . . . . . . . \%%%/ . . . . . . . . / . . . . | | . . . . .\. . . . . . . . .\%/. . . . . . . . ./. . . . . | | . . . . . \ . . . . . . . . o . . . . . . . . / . . . . . | | . . . . . .\. . . . . . . ./.\. . . . . . . ./. . . . . . | | . . . . . . o-------------o . o-------------o . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | o-----------------------------------------------------------o Figure 10. Venn Diagram for (x, y, z)
In this picture, the "oval" (actually, octangular) regions that are customarily said to be indicated by the basic propositions \(x, y, z : \mathbb{B}^3 \to \mathbb{B},\) that is, where the simple arguments \(x, y, z,\!\) respectively, evaluate to true, are marked with the corresponding capital letters \(X, Y, Z,\!\) respectively. The proposition \((x, y, z)\!\) comes out true in the region that is shaded with per cent signs. Invoking various idioms of general usage, one may refer to this region as the indicated region, truth set, or fiber of truth of the proposition in question.
It is useful to consider the truth set of the proposition \((x, y, z)\!\) in relation to the logical conjunction \(x\ y\ z\) of its arguments \(x, y, z.\!\)
In relation to the central cell indicated by the conjunction \(x\ y\ z,\) the region indicated by "\((x, y, z)\!\)" is composed of the adjacent or the bordering cells. Thus they are the cells that are just across the boundary of the center cell, arrived at by taking all of Leibniz's minimal changes from the given point of departure.
Any cell in a venn diagram has a well-defined set of nearest neighbors, and so we can apply a boundary operator of the appropriate rank to the list of signed features that conjoined would indicate the cell in view.
For example, having computed the boundary, or what is more properly called the point omitted neighborhood (PON) of the center cell in a 3-dimensional universe of discourse, what is the PON of the cell that is furthest from it, namely, the origin cell indicated by the proposition \((x)(y)(z)\!\)?
The region bordering the origin cell, \((x)(y)(z),\!\) can be computed by placing its three signed conjuncts in a 3-place bracket like \((\ldots,\ldots,\ldots),\!\) arriving at the cactus expression that is shown in both graph and string forms below.
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . x .y. z . . . . . . . . . . | | . . . . . . . . . . o .o. o . . . . . . . . . . | | . . . . . . . . . . | .|. | . . . . . . . . . . | | . . . . . . . . . . o--o--o . . . . . . . . . . | | . . . . . . . . . . .\. ./. . . . . . . . . . . | | . . . . . . . . . . . \ / . . . . . . . . . . . | | . . . . . . . . . . . .@. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . .((x),(y),(z)). . . . . . . . . | o-------------------------------------------------o
Figure 11 shows the venn diagram of this expression, whose meaning is adequately suggested by the phrase "just 1 of 3 is true".
o-----------------------------------------------------------o | U . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . .o-------------o. . . . . . . . . . . | | . . . . . . . . . . /%%%%%%%%%%%%%%%\ . . . . . . . . . . | | . . . . . . . . . ./%%%%%%%%%%%%%%%%%\. . . . . . . . . . | | . . . . . . . . . /%%%%%%%%%%%%%%%%%%%\ . . . . . . . . . | | . . . . . . . . ./%%%%%%%%%%%%%%%%%%%%%\. . . . . . . . . | | . . . . . . . . /%%%%%%%%%%%%%%%%%%%%%%%\ . . . . . . . . | | . . . . . . . .o%%%%%%%%%%%%%%%%%%%%%%%%%o. . . . . . . . | | . . . . . . . .|%%%%%%%%%%% X %%%%%%%%%%%|. . . . . . . . | | . . . . . . . .|%%%%%%%%%%%%%%%%%%%%%%%%%|. . . . . . . . | | . . . . . . . .|%%%%%%%%%%%%%%%%%%%%%%%%%|. . . . . . . . | | . . . . . . . .|%%%%%%%%%%%%%%%%%%%%%%%%%|. . . . . . . . | | . . . . . . . .|%%%%%%%%%%%%%%%%%%%%%%%%%|. . . . . . . . | | . . . . . . o--o----------o%%%o----------o--o . . . . . . | | . . . . . ./%%%%\ . . . . .\%/. . . . . /%%%%\. . . . . . | | . . . . . /%%%%%%\. . . . . o . . . . ./%%%%%%\ . . . . . | | . . . . ./%%%%%%%%\ . . . ./.\. . . . /%%%%%%%%\. . . . . | | . . . . /%%%%%%%%%%\. . . / . \ . . ./%%%%%%%%%%\ . . . . | | . . . ./%%%%%%%%%%%%\ . ./. . .\. . /%%%%%%%%%%%%\. . . . | | . . . o%%%%%%%%%%%%%%o--o-------o--o%%%%%%%%%%%%%%o . . . | | . . . |%%%%%%%%%%%%%%%%%| . . . |%%%%%%%%%%%%%%%%%| . . . | | . . . |%%%%%%%%%%%%%%%%%| . . . |%%%%%%%%%%%%%%%%%| . . . | | . . . |%%%%%%%%%%%%%%%%%| . . . |%%%%%%%%%%%%%%%%%| . . . | | . . . |%%%%%%% Y %%%%%%%| . . . |%%%%%% Z %%%%%%%%| . . . | | . . . |%%%%%%%%%%%%%%%%%| . . . |%%%%%%%%%%%%%%%%%| . . . | | . . . o%%%%%%%%%%%%%%%%%o . . . o%%%%%%%%%%%%%%%%%o . . . | | . . . .\%%%%%%%%%%%%%%%%%\. . ./%%%%%%%%%%%%%%%%%/. . . . | | . . . . \%%%%%%%%%%%%%%%%%\ . /%%%%%%%%%%%%%%%%%/ . . . . | | . . . . .\%%%%%%%%%%%%%%%%%\./%%%%%%%%%%%%%%%%%/. . . . . | | . . . . . \%%%%%%%%%%%%%%%%%o%%%%%%%%%%%%%%%%%/ . . . . . | | . . . . . .\%%%%%%%%%%%%%%%/.\%%%%%%%%%%%%%%%/. . . . . . | | . . . . . . o-------------o . o-------------o . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | o-----------------------------------------------------------o Figure 11. Venn Diagram for ((x),(y),(z))
Given the foregoing explanation of the k-fold boundary operator, along with its use to express such forms of logical constraints as "just 1 of k is false" and "just 1 of k is true", there will be no trouble interpreting an expression of the following shape from the Jets and Sharks example:
(( art ),( al ),( sam ),( clyde ),( mike ),
( jim ),( greg ),( john ),( doug ),( lance ),
( george ),( pete ),( fred ),( gene ),( ralph ),
( phil ),( ike ),( nick ),( don ),( ned ),
( karl ),( ken ),( earl ),( rick ),( ol ),
( neal ),( dave ))
This expression says that everything in the universe of discourse is either Art, or Al, or …, or Neal, or Dave, but never any two of them at once. In effect, I've exploited the circumstance that the universe contains but finitely many ostensible individuals to dedicate its own predicate to each one of them, imposing only the requirement that these predicates must be disjoint and exhaustive.
Likewise, each of the following clauses has the effect of partitioning the universe of discourse among the factions or features that are enumerated in the clause in question.
( jets , sharks ) (( 20's ),( 30's ),( 40's )) (( junior_high ),( high_school ),( college )) (( single ),( married ),( divorced )) (( bookie ),( burglar ),( pusher ))
We may note in passing that \((x, y) = ((x),(y)),\!\) but a rule of this form holds only in the case of the 2-fold boundary operator.
Let's collect the various ways of representing the structure of a universe of discourse that is described by the following cactus form, verbalized as "just 1 of \(x, y , z\!\) is true".
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . x .y. z . . . . . . . . . . | | . . . . . . . . . . o .o. o . . . . . . . . . . | | . . . . . . . . . . | .|. | . . . . . . . . . . | | . . . . . . . . . . o--o--o . . . . . . . . . . | | . . . . . . . . . . .\. ./. . . . . . . . . . . | | . . . . . . . . . . . \ / . . . . . . . . . . . | | . . . . . . . . . . . .@. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . .((x),(y),(z)). . . . . . . . . | o-------------------------------------------------o
Table 12 shows the truth table for the existential interpretation of the cactus formula \(((x),(y),(z)).\!\)
Table 12. Existential Interpretation of ((x),(y),(z)) o-----------o-----------o-----------o-------------o | x | y | z | (x, y, z) | o-----------o-----------o-----------o-------------o | | | | 0 0 0 | 0 | | | | | 0 0 1 | 1 | | | | | 0 1 0 | 1 | | | | | 0 1 1 | 0 | | | | | 1 0 0 | 1 | | | | | 1 0 1 | 0 | | | | | 1 1 0 | 0 | | | | | 1 1 1 | 0 | | | | o-----------------------------------o-------------o
Figure 13 shows the same data as a 2-colored 3-cube, coloring a node with a hollow dot (o) for false or a star (*) for true.
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . x .y. z . . . . . . . . . . | | . . . . . . . . . . . .o. . . . . . . . . . . . | | . . . . . . . . . . . /|\ . . . . . . . . . . . | | . . . . . . . . . . ./.|.\. . . . . . . . . . . | | . . . . . . . . . . / .|. \ . . . . . . . . . . | | . . . . . . . . . ./. .|. .\. . . . . . . . . . | | . . . . . . . . . / . .|. . \ . . . . . . . . . | | . . . . . . . . ./. . .|. . .\. . . . . . . . . | | . . . . . . . . / . x (y) z . \ . . . . . . . . | | . . . x .y.(z) o. . . .o. . . .o (x).y. z . . . | | . . . . . . . .|\ . . / \ . . /|. . . . . . . . | | . . . . . . . .|.\. ./. .\. ./.|. . . . . . . . | | . . . . . . . .|. \ / . . \ / .|. . . . . . . . | | . . . . . . . .|. .\. . . ./. .|. . . . . . . . | | . . . . . . . .|. / \ . . / \ .|. . . . . . . . | | . . . . . . . .|./. .\. ./. .\.|. . . . . . . . | | . . . . . . . .|/ . . \ / . . \|. . . . . . . . | | . . . x (y)(z).*. . . .*. . . .*.(x)(y) z . . . | | . . . . . . . . \ .(x).y.(z). / . . . . . . . . | | . . . . . . . . .\. . .|. . ./. . . . . . . . . | | . . . . . . . . . \ . .|. . / . . . . . . . . . | | . . . . . . . . . .\. .|. ./. . . . . . . . . . | | . . . . . . . . . . \ .|. / . . . . . . . . . . | | . . . . . . . . . . .\.|./. . . . . . . . . . . | | . . . . . . . . . . . \|/ . . . . . . . . . . . | | . . . . . . . . . . . .o. . . . . . . . . . . . | | . . . . . . . . . .(x)(y)(z). . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o
Figure 14 repeats the venn diagram that we've already seen.
o-----------------------------------------------------------o | U . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . .o-------------o. . . . . . . . . . . | | . . . . . . . . . . /%%%%%%%%%%%%%%%\ . . . . . . . . . . | | . . . . . . . . . ./%%%%%%%%%%%%%%%%%\. . . . . . . . . . | | . . . . . . . . . /%%%%%%%%%%%%%%%%%%%\ . . . . . . . . . | | . . . . . . . . ./%%%%%%%%%%%%%%%%%%%%%\. . . . . . . . . | | . . . . . . . . /%%%%%%%%%%%%%%%%%%%%%%%\ . . . . . . . . | | . . . . . . . .o%%%%%%%%%%%%%%%%%%%%%%%%%o. . . . . . . . | | . . . . . . . .|%%%%%%%%%%% X %%%%%%%%%%%|. . . . . . . . | | . . . . . . . .|%%%%%%%%%%%%%%%%%%%%%%%%%|. . . . . . . . | | . . . . . . . .|%%%%%%%%%%%%%%%%%%%%%%%%%|. . . . . . . . | | . . . . . . . .|%%%%%%%%%%%%%%%%%%%%%%%%%|. . . . . . . . | | . . . . . . . .|%%%%%%%%%%%%%%%%%%%%%%%%%|. . . . . . . . | | . . . . . . o--o----------o%%%o----------o--o . . . . . . | | . . . . . ./%%%%\ . . . . .\%/. . . . . /%%%%\. . . . . . | | . . . . . /%%%%%%\. . . . . o . . . . ./%%%%%%\ . . . . . | | . . . . ./%%%%%%%%\ . . . ./.\. . . . /%%%%%%%%\. . . . . | | . . . . /%%%%%%%%%%\. . . / . \ . . ./%%%%%%%%%%\ . . . . | | . . . ./%%%%%%%%%%%%\ . ./. . .\. . /%%%%%%%%%%%%\. . . . | | . . . o%%%%%%%%%%%%%%o--o-------o--o%%%%%%%%%%%%%%o . . . | | . . . |%%%%%%%%%%%%%%%%%| . . . |%%%%%%%%%%%%%%%%%| . . . | | . . . |%%%%%%%%%%%%%%%%%| . . . |%%%%%%%%%%%%%%%%%| . . . | | . . . |%%%%%%%%%%%%%%%%%| . . . |%%%%%%%%%%%%%%%%%| . . . | | . . . |%%%%%%% Y %%%%%%%| . . . |%%%%%% Z %%%%%%%%| . . . | | . . . |%%%%%%%%%%%%%%%%%| . . . |%%%%%%%%%%%%%%%%%| . . . | | . . . o%%%%%%%%%%%%%%%%%o . . . o%%%%%%%%%%%%%%%%%o . . . | | . . . .\%%%%%%%%%%%%%%%%%\. . ./%%%%%%%%%%%%%%%%%/. . . . | | . . . . \%%%%%%%%%%%%%%%%%\ . /%%%%%%%%%%%%%%%%%/ . . . . | | . . . . .\%%%%%%%%%%%%%%%%%\./%%%%%%%%%%%%%%%%%/. . . . . | | . . . . . \%%%%%%%%%%%%%%%%%o%%%%%%%%%%%%%%%%%/ . . . . . | | . . . . . .\%%%%%%%%%%%%%%%/.\%%%%%%%%%%%%%%%/. . . . . . | | . . . . . . o-------------o . o-------------o . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . . . . . . | o-----------------------------------------------------------o Figure 14. Venn Diagram for ((x),(y),(z))
Figure 15 shows an alternate form of venn diagram for the same proposition, where we collapse to a nullity all of the regions on which the proposition in question evaluates to false. This leaves a structure that partitions the universe into precisely three parts. In mathematics, operations that identify diverse elements are called quotient operations. In this case, many regions of the universe are being identified with the null set, leaving only this 3-fold partition as the quotient structure.
o-----------------------------------------------------------o | \ / | | \ / | | \ / | | \ / | | \ / | | \ X / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | \ / | | o | | | | | | | | | | | | | | Y | Z | | | | | | | | | | | | | | | | | | | | | | | | | | | | o-----------------------------o-----------------------------o Figure 15. Quotient Structure Venn Diagram for ((x),(y),(z))
Let's now look at the last type of clause that we find in my transcription of the Jets and Sharks data base, for instance, as exemplified by the following couple of lobal expressions:
( jets ,
( art ),( al ),( sam ),( clyde ),( mike ),
( jim ),( greg ),( john ),( doug ),( lance ),
( george ),( pete ),( fred ),( gene ),( ralph ))
( sharks ,
( phil ),( ike ),( nick ),( don ),( ned ),( karl ),
( ken ),( earl ),( rick ),( ol ),( neal ),( dave ))
Each of these clauses exhibits a generic pattern whose logical properties may be studied well enough in the form of the following schematic example.
o-------------------------------------------------o | | | y z | | o o | | x | | | | o--o--o | | \ / | | \ / | | @ | | | o-------------------------------------------------o | ( x ,(y),(z)) | o-------------------------------------------------o
The proposition \((u, v, w)\!\) evaluates to true if and only if just one of \(u, v, w\!\) is false. In the same way, the proposition \((x,(y),(z))\!\) evaluates to true if and only if exactly one of \(x, (y), (z)\!\) is false. Taking it by cases, let us first suppose that \(x\!\) is true. Then it has to be that just one of \((y)\!\) or \((z)\!\) is false, which is tantamount to the proposition \(((y),(z)),\!\) which is equivalent to the proposition \((y, z).\!\) On the other hand, let us suppose that \(x\!\) is the false one. Then both \((y)\!\) and \((z)\!\) must be true, which is to say that \(y\!\) is false and \(z\!\) is false.
What we have just said here is that the region where \(x\!\) is true is partitioned into the regions where \(y\!\) and \(z\!\) are true, respectively, while the region where \(x\!\) is false has both \(y\!\) and \(z\!\) false. In other words, we have a pie-chart structure, where the genus \(X\!\) is divided into the disjoint and \(X\!\)-haustive couple of species \(Y\!\) and \(Z.\!\)
The same analysis applies to the generic form \((x, (x_1), \ldots, (x_k)),\!\) specifying a pie-chart with a genus \(X\!\) and the \(k\!\) species \(X_1, \ldots, X_k.\!\)
Differential Logic : Graphical Exposition
Differential Propositions
One of the first things that you can do, once you have a really decent calculus for boolean functions or propositional logic, whatever you want to call it, is to compute the differentials of these functions or propositions.
Now there are many ways to dance around this idea, and I feel like I have tried them all, before one gets down to acting on it, and there many issues of interpretation and justification that we will have to clear up after the fact, that is, before we can be sure that it all really makes any sense, but I think this time I'll just jump in, and show you the form in which this idea first came to me.
Start with a proposition of the form "\(x\ \operatorname{and}\ y\)". This is graphed as two labels attached to a root node:
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . x y . . . . . . . . . . . | | . . . . . . . . . . . .@. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . x and y . . . . . . . . . . | o-------------------------------------------------o
Written as a string, this is just the concatenation "\(xy\!\)".
The proposition \(xy\!\) may be taken as a boolean function \(f(x, y)\!\) having the abstract type \(f : \mathbb{B} \times \mathbb{B} \to \mathbb{B},\) where \(\mathbb{B} = \{ 0, 1 \}\) is read in such a way that 0 means \(false\) and 1 means \(true.\)
In this style of graphical representation, the value \(true\) looks like a blank label and the value \(false\) looks like an edge.
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . .@. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . .true . . . . . . . . . . . | o-------------------------------------------------o
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . .o. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .@. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . .false . . . . . . . . . . .| o-------------------------------------------------o
Back to the proposition \(xy.\!\) Imagine yourself standing in a fixed cell of the corresponding venn diagram, say, the cell where the proposition \(xy\!\) is true, as pictured:
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . .o-----------o. .o-----------o. . . . . | | . . . . / . . . . . . \ / . . . . . . \ . . . . | | . . . ./. . . . . . . .o. . . . . . . .\. . . . | | . . . / . . . . . . . /%\ . . . . . . . \ . . . | | . . ./. . . . . . . ./%%%\. . . . . . . .\. . . | | . . o . . . . . . . o%%%%%o . . . . . . . o . . | | . . | . . . . . . . |%%%%%| . . . . . . . | . . | | . . | . . . . . . . |%%%%%| . . . . . . . | . . | | . . | . . . x . . . |%%%%%| . . . y . . . | . . | | . . | . . . . . . . |%%%%%| . . . . . . . | . . | | . . | . . . . . . . |%%%%%| . . . . . . . | . . | | . . o . . . . . . . o%%%%%o . . . . . . . o . . | | . . .\. . . . . . . .\%%%/. . . . . . . ./. . . | | . . . \ . . . . . . . \%/ . . . . . . . / . . . | | . . . .\. . . . . . . .o. . . . . . . ./. . . . | | . . . . \ . . . . . . / \ . . . . . . / . . . . | | . . . . .o-----------o. .o-----------o. . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o
Now ask yourself: What is the value of the proposition \(xy\!\) at a distance of \(\operatorname{d}x\) and \(\operatorname{d}y\) from the cell \(xy\!\) where you are standing?
Don't think about it — just compute:
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . dx o. .o dy . . . . . . . . . | | . . . . . . . . . . / \ / \ . . . . . . . . . . | | . . . . . . . . .x o---@---o y. . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . .(x + dx) and (y + dy). . . . . . . | o-------------------------------------------------o
To make future graphs easier to draw in Ascii land, I will use devices like @=@=@ and o=o=o to identify several nodes into one, as in this next redrawing:
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . x .dx y .dy . . . . . . . . . | | . . . . . . . . . o---o o---o . . . . . . . . . | | . . . . . . . . . .\. | | ./. . . . . . . . . . | | . . . . . . . . . . \ | | / . . . . . . . . . . | | . . . . . . . . . . .\| |/. . . . . . . . . . . | | . . . . . . . . . . . @=@ . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . .(x + dx) and (y + dy). . . . . . . | o-------------------------------------------------o
However you draw it, these expressions follow because the expression \(x + \operatorname{d}x,\) where the plus sign indicates (mod 2) addition in \(\mathbb{B},\) and thus corresponds to an exclusive-or in logic, parses to a graph of the following form:
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . x . .dx . . . . . . . . . . | | . . . . . . . . . . .o---o. . . . . . . . . . . | | . . . . . . . . . . . \ / . . . . . . . . . . . | | . . . . . . . . . . . .@. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . .x + dx . . . . . . . . . . | o-------------------------------------------------o
Next question: What is the difference between the value of the proposition \(xy\!\) "over there" and the value of the proposition \(xy\!\) where you are, all expressed as general formula, of course? Here it is:
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . x .dx y .dy . . . . . . . . . . . . | | . . . . . . o---o o---o . . . . . . . . . . . . | | . . . . . . .\. | | ./. . . . . . . . . . . . . | | . . . . . . . \ | | / . . . . . . . . . . . . . | | . . . . . . . .\| |/. . . . .x y. . . . . . . . | | . . . . . . . . o=o-----------o . . . . . . . . | | . . . . . . . . .\. . . . . ./. . . . . . . . . | | . . . . . . . . . \ . . . . / . . . . . . . . . | | . . . . . . . . . .\. . . ./. . . . . . . . . . | | . . . . . . . . . . \ . . / . . . . . . . . . . | | . . . . . . . . . . .\. ./. . . . . . . . . . . | | . . . . . . . . . . . \ / . . . . . . . . . . . | | . . . . . . . . . . . .@. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . ((x + dx) & (y + dy)) - xy. . . . . . | o-------------------------------------------------o
Computed over \(\mathbb{B},\) plus and minus are the very same operation. This will make the relationship between the differential and the integral parts of the resulting calculus slightly stranger than usual, but never mind that now.
Last question, for now: What is the value of this expression from your current standpoint, that is, evaluated at the point where \(xy\!\) is true? Substituting 1 for \(x\!\) and 1 for \(y\!\) in the graph amounts to the same thing as erasing those labels:
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . .dx . .dy . . . . . . . . . . . . . . | | . . . . . . o---o o---o . . . . . . . . . . . . | | . . . . . . .\. | | ./. . . . . . . . . . . . . | | . . . . . . . \ | | / . . . . . . . . . . . . . | | . . . . . . . .\| |/. . . . . . . . . . . . . . | | . . . . . . . . o=o-----------o . . . . . . . . | | . . . . . . . . .\. . . . . ./. . . . . . . . . | | . . . . . . . . . \ . . . . / . . . . . . . . . | | . . . . . . . . . .\. . . ./. . . . . . . . . . | | . . . . . . . . . . \ . . / . . . . . . . . . . | | . . . . . . . . . . .\. ./. . . . . . . . . . . | | . . . . . . . . . . . \ / . . . . . . . . . . . | | . . . . . . . . . . . .@. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . ((1 + dx) & (1 + dy)) - 1&1 . . . . . | o-------------------------------------------------o
And this is equivalent to the following graph:
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . dx. .dy . . . . . . . . . . | | . . . . . . . . . . .o. .o. . . . . . . . . . . | | . . . . . . . . . . . \ / . . . . . . . . . . . | | . . . . . . . . . . . .o. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .@. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . .dx or dy . . . . . . . . . . | o-------------------------------------------------o
We have just met with the fact that the differential of the \(\operatorname{and}\) is the \(\operatorname{or}\) of the differentials. Briefly summarized:
\(x\ \operatorname{and}\ y\ \xrightarrow{\operatorname{Diff}}\ \operatorname{d}x \ \operatorname{or}\ \operatorname{d}y\)
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . .dx . dy. . . | | . . . . . . . . . . . . . . . . . . o . o . . . | | . . . . . . . . . . . . . . . . . . .\ /. . . . | | . . . . . . . . . . . . . . . . . . . o . . . . | | . . . .x y. . . . . . . . . . . . . . | . . . . | | . . . . @ . . . . .--Diff-->. . . . . @ . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . .x y. . . . .--Diff-->. . .((dx) (dy)). . | o-------------------------------------------------o
It will be necessary to develop a more refined analysis of this statement directly, but that is roughly the nub of it.
If the form of the above statement reminds you of De Morgan's rule, it is no accident, as differentiation and negation turn out to be closely related operations. Indeed, one can find discussions of logical difference calculus in the Boole–De Morgan correspondence and C.S. Peirce also made use of differential operators in a logical context, but the exploration of these ideas has been hampered by a number of factors, not the least of which being a syntax adequate to handle the complexity of expressions that evolve.
For my part, it was definitely a case of the calculus being smarter than the calculator thereof. The graphical pictures were catalytic in their power over my thinking process, leading me so quickly past so many obstructions that I did not have time to think about all of the difficulties that would otherwise have inhibited the derivation. .It did eventually became necessary to write all this up in a linear script, and to deal with the various problems of interpretation and justification that I could imagine, but that took another 120 pages, and so, if you don't like this intuitive approach, then let that be your sufficient notice.
Let us run through the initial example again, this time attempting to interpret the formulas that develop at each stage along the way.
We begin with a proposition or a boolean function \(f(x, y) = xy.\!\)
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . .o-----------o. .o-----------o. . . . . | | . . . . / . . . . . . \ / . . . . . . \ . . . . | | . . . ./. . . . . . . .o. . . . . . . .\. . . . | | . . . / . . . . . . . /%\ . . . . . . . \ . . . | | . . ./. . . . . . . ./%%%\. . . . . . . .\. . . | | . . o . . . . . . . o%%%%%o . . . . . . . o . . | | . . | . . . . . . . |%%%%%| . . . . . . . | . . | | . . | . . . . . . . |%%%%%| . . . . . . . | . . | | . . | . . . x . . . |%%f%%| . . . y . . . | . . | | . . | . . . . . . . |%%%%%| . . . . . . . | . . | | . . | . . . . . . . |%%%%%| . . . . . . . | . . | | . . o . . . . . . . o%%%%%o . . . . . . . o . . | | . . .\. . . . . . . .\%%%/. . . . . . . ./. . . | | . . . \ . . . . . . . \%/ . . . . . . . / . . . | | . . . .\. . . . . . . .o. . . . . . . ./. . . . | | . . . . \ . . . . . . / \ . . . . . . / . . . . | | . . . . .o-----------o. .o-----------o. . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . x y . . . . . . . . . . . | | . . . . . . . . . . . .@. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | f = . . . . . . . . . x y . . . . . . . . . . . | o-------------------------------------------------o
A function like this has an abstract type and a concrete type. The abstract type is what we invoke when we write things like \(f : \mathbb{B} \times \mathbb{B} \to \mathbb{B}\) or \(f : \mathbb{B}^2 \to \mathbb{B}.\) The concrete type takes into account the qualitative dimensions or the "units" of the case, which can be explained as follows.
- Let \(X\!\) be the set of values \(\{ (\!|x|\!), x \} = \{ \operatorname{not}\ x, x \}.\)
- Let \(Y\!\) be the set of values \(\{ (\!|y|\!), y \} = \{ \operatorname{not}\ y, y \}.\)
Then interpret the usual propositions about \(x, y\!\) as functions of the concrete type \(f : X \times Y \to \mathbb{B}.\)
We are going to consider various operators on these functions. Here, an operator \(\operatorname{F}\) is a function that takes one function \(f\!\) into another function \(\operatorname{F}f.\)
The first couple of operators that we need to consider are logical analogues of those that occur in the classical finite difference calculus, namely:
- The difference operator \(\Delta,\!\) written here as \(\operatorname{D}.\)
- The enlargement operator \(\Epsilon,\!\) written here as \(\operatorname{E}.\)
These days, \(\operatorname{E}\) is more often called the shift operator.
In order to describe the universe in which these operators operate, it will be necessary to enlarge our original universe of discourse. We mount up from the space \(U = X \times Y\) to its differential extension:
\(\operatorname{E}U = U \times \operatorname{d}U = X \times Y \times \operatorname{d}X \times \operatorname{d}Y\)
\(\operatorname{d}X = \{ (\!|\operatorname{d}x|\!), \operatorname{d}x \}\)
\(\operatorname{d}Y = \{ (\!|\operatorname{d}y|\!), \operatorname{d}y \}\)
The interpretations of these new symbols can be diverse, but the easiest for now is just to say that \(\operatorname{d}x\) means "change \(x\!\) " and \(\operatorname{d}y\) means "change \(y\!\) ".
To draw the differential extension \(\operatorname{E}U\) of our present universe \(U = X \times Y\) as a venn diagram, it would take us four logical dimensions \(X, Y, \operatorname{d}X, \operatorname{d}Y,\) but we can project a suggestion of what it's about on the universe \(X \times Y\) by drawing arrows that cross designated borders, labeling the arrows as \(\operatorname{d}x\) when crossing the border between \(x\!\) and \((\!|x|\!)\) and as \(\operatorname{d}y\) when crossing the border between \(y\!\) and \((\!|y|\!),\) in either direction, in either case.
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . .o-----------o. .o-----------o. . . . . | | . . . . / . . . . . . \ / . . . . . . \ . . . . | | . . . ./. . . .x. . . .o. . . .y. . . .\. . . . | | . . . / . . . . . . . /%\ . . . . . . . \ . . . | | . . ./. . . . . . . ./%%%\. . . . . . . .\. . . | | . . o . . . . . . . o%%%%%o . . . . . . . o . . | | . . | . . . . . . . |%%%%%| . . . . . . . | . . | | . . | . . . . dy. . |%%%%%| . .dx . . . . | . . | | . . | . . <---------|--o--|---------> . . | . . | | . . | . . . . . . . |%%%%%| . . . . . . . | . . | | . . | . . . . . . . |%%%%%| . . . . . . . | . . | | . . o . . . . . . . o%%%%%o . . . . . . . o . . | | . . .\. . . . . . . .\%%%/. . . . . . . ./. . . | | . . . \ . . . . . . . \%/ . . . . . . . / . . . | | . . . .\. . . . . . . .o. . . . . . . ./. . . . | | . . . . \ . . . . . . / \ . . . . . . / . . . . | | . . . . .o-----------o. .o-----------o. . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o
We can form propositions from these differential variables in the same way that we would any other logical variables, for instance, interpreting the proposition \((\!| \operatorname{d}x\ (\!| \operatorname{d}y |\!) |\!)\) to say "\(\operatorname{d}x \Rightarrow \operatorname{d}y\) ", in other words, however you wish to take it, whether indicatively or injunctively, as saying something to the effect that there is "no change in \(x\!\) without a change in \(y\!\) ".
Given the proposition \(f(x, y)\!\) in \(U = X \times Y\!, \) the (first order) enlargement of \(f\!\) is the proposition \(\operatorname{E}f\) in \(\operatorname{E}U\) that is defined by the formula \(\operatorname{E}f(x, y, \operatorname{d}x, \operatorname{d}y) = f(x + \operatorname{d}x, y + \operatorname{d}y).\)
In the example \(f(x, y) = xy,\!\) we obtain:
\(\operatorname{E}f(x, y, \operatorname{d}x, \operatorname{d}y) = (x + \operatorname{d}x)(y + \operatorname{d}y).\)
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . x .dx y .dy . . . . . . . . . | | . . . . . . . . . o---o o---o . . . . . . . . . | | . . . . . . . . . .\. | | ./. . . . . . . . . . | | . . . . . . . . . . \ | | / . . . . . . . . . . | | . . . . . . . . . . .\| |/. . . . . . . . . . . | | . . . . . . . . . . . @=@ . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | Ef = . . . . . .(x, dx) (y, dy) . . . . . . . . | o-------------------------------------------------o
Given the proposition \(f(x, y)\!\) in \(U = X \times Y,\) the (first order) difference of \(f\!\) is the proposition \(\operatorname{D}f\) in \(\operatorname{E}U\) that is defined by the formula \(\operatorname{D}f = \operatorname{E}f - f,\) or, written out in full, \(\operatorname{D}f(x, y, \operatorname{d}x, \operatorname{d}y) = f(x + \operatorname{d}x, y + \operatorname{d}y) - f(x, y).\)
In the example \(f(x, y) = xy,\!\) the result is:
\(\operatorname{D}f(x, y, \operatorname{d}x, \operatorname{d}y) = (x + \operatorname{d}x)(y + \operatorname{d}y) - xy.\)
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . x .dx y .dy . . . . . . . . . . . . | | . . . . . . o---o o---o . . . . . . . . . . . . | | . . . . . . .\. | | ./. . . . . . . . . . . . . | | . . . . . . . \ | | / . . . . . . . . . . . . . | | . . . . . . . .\| |/. . . . .x y. . . . . . . . | | . . . . . . . . o=o-----------o . . . . . . . . | | . . . . . . . . .\. . . . . ./. . . . . . . . . | | . . . . . . . . . \ . . . . / . . . . . . . . . | | . . . . . . . . . .\. . . ./. . . . . . . . . . | | . . . . . . . . . . \ . . / . . . . . . . . . . | | . . . . . . . . . . .\. ./. . . . . . . . . . . | | . . . . . . . . . . . \ / . . . . . . . . . . . | | . . . . . . . . . . . .@. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | Df = . . . . . ((x, dx)(y, dy), xy) . . . . . . | o-------------------------------------------------o
We did not yet go through the trouble to interpret this (first order) difference of conjunction fully, but were happy simply to evaluate it with respect to a single location in the universe of discourse, namely, at the point picked out by the singular proposition \(xy,\!\) in as much as if to say, at the place where \(x = 1\!\) and \(y = 1.\!\) This evaluation is written in the form \(\operatorname{D}f|_{xy}\) or \(\operatorname{D}f|_{(1, 1)},\) and we arrived at the locally applicable law that states that:
\(f = xy = x\ \operatorname{and}\ y \Rightarrow \operatorname{D}f|_{xy} = (\!|(\!| \operatorname{d}x |\!)(\!| \operatorname{d}y |\!)|\!) = \operatorname{d}x\ \operatorname{or}\ \operatorname{d}y.\)
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . .o-----------o. .o-----------o. . . . . | | . . . . / . . . . . . \ / . . . . . . \ . . . . | | . . . ./. . . .x. . . .o. . . .y. . . .\. . . . | | . . . / . . . . . . . /%\ . . . . . . . \ . . . | | . . ./. . . . . . . ./%%%\. . . . . . . .\. . . | | . . o . . . . . . . o%%%%%o . . . . . . . o . . | | . . | . . . . . . . |%%%%%| . . . . . . . | . . | | . . | . . .dy (dx). |%%%%%| .dx (dy). . . | . . | | . . | . o<----------|--o--|---------->o . | . . | | . . | . . . . . . . |%%|%%| . . . . . . . | . . | | . . | . . . . . . . |%%|%%| . . . . . . . | . . | | . . o . . . . . . . o%%|%%o . . . . . . . o . . | | . . .\. . . . . . . .\%|%/. . . . . . . ./. . . | | . . . \ . . . . . . . \|/ . . . . . . . / . . . | | . . . .\. . . . . . . .|. . . . . . . ./. . . . | | . . . . \ . . . . . . /|\ . . . . . . / . . . . | | . . . . .o-----------o | o-----------o. . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . .dx|dy. . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .v. . . . . . . . . . . . | | . . . . . . . . . . . .o. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . dx. .dy . . . . . . . . . . | | . . . . . . . . . . .o. .o. . . . . . . . . . . | | . . . . . . . . . . . \ / . . . . . . . . . . . | | . . . . . . . . . . . .o. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .@. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | Df|xy = . . . . . ((dx) (dy)) . . . . . . . . . | o-------------------------------------------------o
The picture illustrates the analysis of the inclusive disjunction \((\!|(\!| \operatorname{d}x |\!)(\!| \operatorname{d}y |\!)|\!)\) into the following exclusive disjunction:
\(\operatorname{d}x\ (\!| \operatorname{d}y |\!) + \operatorname{d}y\ (\!| \operatorname{d}x |\!) + \operatorname{d}x\ \operatorname{d}y.\)
The latter proposition may be interpreted as saying "change \(x\!\) or change \(y\!\) or both". And this can be recognized as just what you need to do if you happen to find yourself in the center cell and desire a detailed description of ways to depart it.
We have just computed what will variously be called the difference map, the difference proposition, or the local proposition \(\operatorname{D}f_p\) for the proposition \(f(x, y) = xy\!\) at the point \(p\!\) where \(x = 1\!\) and \(y = 1.\!\)
In the universe \(U = X \times Y\) the four propositions \(xy,\ x (\!| y |\!),\ (\!| x |\!) y,\ (\!| x |\!)(\!| y |\!)\) that indicate the cells, or the smallest regions of the venn diagram, are called singular propositions. These serve as an alternative notation for naming the points \((1, 1),\ (1, 0),\ (0, 1),\ (0, 0),\) respectively.
Thus, we can write \(\operatorname{D}f_p = \operatorname{D}f|_p = \operatorname{D}f|_{(1, 1)} = \operatorname{D}f|_{xy},\) so long as we know the frame of reference in force.
Sticking with the example \(f(x, y) = xy,\!\) let us compute the value of the difference proposition \(\operatorname{D}f\) at all of the points.
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . x .dx y .dy . . . . . . . . . . . . | | . . . . . . o---o o---o . . . . . . . . . . . . | | . . . . . . .\. | | ./. . . . . . . . . . . . . | | . . . . . . . \ | | / . . . . . . . . . . . . . | | . . . . . . . .\| |/. . . . .x y. . . . . . . . | | . . . . . . . . o=o-----------o . . . . . . . . | | . . . . . . . . .\. . . . . ./. . . . . . . . . | | . . . . . . . . . \ . . . . / . . . . . . . . . | | . . . . . . . . . .\. . . ./. . . . . . . . . . | | . . . . . . . . . . \ . . / . . . . . . . . . . | | . . . . . . . . . . .\. ./. . . . . . . . . . . | | . . . . . . . . . . . \ / . . . . . . . . . . . | | . . . . . . . . . . . .@. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | Df = . . . .((x, dx)(y, dy), xy). . . . . . . . | o-------------------------------------------------o
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . .dx . .dy . . . . . . . . . . . . | | . . . . . . o---o o---o . . . . . . . . . . . . | | . . . . . . .\. | | ./. . . . . . . . . . . . . | | . . . . . . . \ | | / . . . . . . . . . . . . . | | . . . . . . . .\| |/. . . . . . . . . . . . . . | | . . . . . . . . o=o-----------o . . . . . . . . | | . . . . . . . . .\. . . . . ./. . . . . . . . . | | . . . . . . . . . \ . . . . / . . . . . . . . . | | . . . . . . . . . .\. . . ./. . . . . . . . . . | | . . . . . . . . . . \ . . / . . . . . . . . . . | | . . . . . . . . . . .\. ./. . . . . . . . . . . | | . . . . . . . . . . . \ / . . . . . . . . . . . | | . . . . . . . . . . . .@. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | Df|xy = . . . . . ((dx) (dy)) . . . . . . . . . | o-------------------------------------------------o
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . o . . . . . . . . . . . . . . | | . . . . . . . .dx | .dy . . . . . . . . . . . . | | . . . . . . o---o o---o . . . . . . . . . . . . | | . . . . . . .\. | | ./. . . . . . . . . . . . . | | . . . . . . . \ | | / . . . . o . . . . . . . . | | . . . . . . . .\| |/. . . . . | . . . . . . . . | | . . . . . . . . o=o-----------o . . . . . . . . | | . . . . . . . . .\. . . . . ./. . . . . . . . . | | . . . . . . . . . \ . . . . / . . . . . . . . . | | . . . . . . . . . .\. . . ./. . . . . . . . . . | | . . . . . . . . . . \ . . / . . . . . . . . . . | | . . . . . . . . . . .\. ./. . . . . . . . . . . | | . . . . . . . . . . . \ / . . . . . . . . . . . | | . . . . . . . . . . . .@. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | Df|x(y) = . . . . .(dx) dy. . . . . . . . . . . | o-------------------------------------------------o
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . o . . . . . . . . . . . . . . . . . | | . . . . . . | .dx . .dy . . . . . . . . . . . . | | . . . . . . o---o o---o . . . . . . . . . . . . | | . . . . . . .\. | | ./. . . . . . . . . . . . . | | . . . . . . . \ | | / . . . . o . . . . . . . . | | . . . . . . . .\| |/. . . . . | . . . . . . . . | | . . . . . . . . o=o-----------o . . . . . . . . | | . . . . . . . . .\. . . . . ./. . . . . . . . . | | . . . . . . . . . \ . . . . / . . . . . . . . . | | . . . . . . . . . .\. . . ./. . . . . . . . . . | | . . . . . . . . . . \ . . / . . . . . . . . . . | | . . . . . . . . . . .\. ./. . . . . . . . . . . | | . . . . . . . . . . . \ / . . . . . . . . . . . | | . . . . . . . . . . . .@. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | Df|(x)y = . . . . . .dx (dy). . . . . . . . . . | o-------------------------------------------------o
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . o . . o . . . . . . . . . . . . . . | | . . . . . . | .dx | .dy . . . . . . . . . . . . | | . . . . . . o---o o---o . . . . . . . . . . . . | | . . . . . . .\. | | ./. . . . . . . . . . . . . | | . . . . . . . \ | | / . . . o . o . . . . . . . | | . . . . . . . .\| |/. . . . .\./. . . . . . . . | | . . . . . . . . o=o-----------o . . . . . . . . | | . . . . . . . . .\. . . . . ./. . . . . . . . . | | . . . . . . . . . \ . . . . / . . . . . . . . . | | . . . . . . . . . .\. . . ./. . . . . . . . . . | | . . . . . . . . . . \ . . / . . . . . . . . . . | | . . . . . . . . . . .\. ./. . . . . . . . . . . | | . . . . . . . . . . . \ / . . . . . . . . . . . | | . . . . . . . . . . . .@. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | Df|(x)(y) = . . . . .dx dy. . . . . . . . . . . | o-------------------------------------------------o
The easy way to visualize the values of these graphical expressions is just to notice the following equivalents:
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | .x. . . . . . . . . . . . . . . . . . . . . . . | | .o-o-o-...-o-o-o. . . . . . . . . . . . . . . . | | . \ . . . . . / . . . . . . . . . . . . . . . . | | . .\. . . . ./. . . . . . . . . . . . . . . . . | | . . \ . . . / . . . . . . . . . . . . . . . . . | | . . .\. . ./. . . . . . . . . . . . . x . . . . | | . . . \ . / . . . . . . . . . . . . . o . . . . | | . . . .\./. . . . . . . . . . . . . . | . . . . | | . . . . @ . . . . . . .=. . . . . . . @ . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | .(x, , ... , , ). . . .=. . . . . . .(x). . . . | o-------------------------------------------------o
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . .o. . . . . . . . . . . . . . . . | | x_1 x_2 . x_k .|. . . . . . . . . . . . . . . . | | .o---o-...-o---o. . . . . . . . . . . . . . . . | | . \ . . . . . / . . . . . . . . . . . . . . . . | | . .\. . . . ./. . . . . . . . . . . . . . . . . | | . . \ . . . / . . . . . . . . . . . . . . . . . | | . . .\. . ./. . . . . . . . . . . . . . . . . . | | . . . \ . / . . . . . . . . . . . . . . . . . . | | . . . .\./. . . . . . . . . . . .x_1 ... x_k. . | | . . . . @ . . . . . . .=. . . . . . . @ . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | .(x_1, ..., x_k, ()). .=. . . . .x_1 ... x_k. . | o-------------------------------------------------o
Laying out the arrows on the augmented venn diagram, one gets a picture of a differential vector field.
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . .o. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . .dx|dy. . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . .o-----------o.|.o-----------o. . . . . | | . . . . / . . . . . . \|/ . . . . . . \ . . . . | | . . . ./. . . .x. . . .|. . . .y. . . .\. . . . | | . . . / . . . . . . . /|\ . . . . . . . \ . . . | | . . ./. . . . . . . ./%|%\. . . . . . . .\. . . | | . . o . . . . . . . o%%|%%o . . . . . . . o . . | | . . | . . .dy (dx). |%%v%%| .dx (dy). . . | . . | | . . | . o-----------|->o<-|-----------o . | . . | | . . | . . . . . . . |%%%%%| . . . . . . . | . . | | . . | . o<----------|--o--|---------->o . | . . | | . . | . . .dy (dx). |%%|%%| .dx (dy). . . | . . | | . . o . . . . . . . o%%|%%o . . . . . . . o . . | | . . .\. . . . . . . .\%|%/. . . . . . . ./. . . | | . . . \ . . . . . . . \|/ . . . . . . . / . . . | | . . . .\. . . . . . . .|. . . . . . . ./. . . . | | . . . . \ . . . . . . /|\ . . . . . . / . . . . | | . . . . .o-----------o.|.o-----------o. . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . .dx|dy. . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .v. . . . . . . . . . . . | | . . . . . . . . . . . .o. . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o
This really just constitutes a depiction of the interpretations in \(\operatorname{E}U = X \times Y \times \operatorname{d}X \times \operatorname{d}Y\) that satisfy the difference proposition \(\operatorname{D}f,\) namely, these:
1. x y dx dy 2. x y dx (dy) 3. x y (dx) dy 4. x (y)(dx) dy 5. (x) y dx (dy) 6. (x)(y) dx dy
By inspection, it is fairly easy to understand \(\operatorname{D}f\) as telling you what you have to do from each point of \(U\!\) in order to change the value borne by \(f(x, y).\!\)
We have been studying the action of the difference operator \(\operatorname{D},\) also known as the localization operator, on the proposition \(f : X \times Y \to \mathbb{B}\) that is commonly known as the conjunction \(xy.\!\) We described \(\operatorname{D}f\) as a (first order) differential proposition, that is, a proposition of the type \(\operatorname{D}f : X \times Y \times \operatorname{d}X \times \operatorname{d}Y \to \mathbb{B}.\) Abstracting from the augmented venn diagram that illustrates how the models, or the satisfying interpretations, of \(\operatorname{D}f\) distribute within the extended universe \(\operatorname{E}U = X \times Y \times \operatorname{d}X \times \operatorname{d}Y,\) we can depict \(\operatorname{D}f\) in the form of a digraph or directed graph, one whose points are labeled with the elements of \(U = X \times Y\) and whose arrows are labeled with the elements of \(\operatorname{d}U = \operatorname{d}X \times \operatorname{d}Y.\)
o-------------------------------------------------o | f = . . . . . . . . . x y . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | Df =. . . . . . . x .y. ((dx)(dy)). . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . + . . . x (y) .(dx) dy. . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . + . . .(x) y. . dx (dy) . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . + . . .(x)(y) . dx .dy. . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . x y . . . . . . . . . . . | | .x (y) o<------------->o<------------->o (x) y. | | . . . . . . (dx) dy . .^. . dx (dy) . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . dx | dy . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .v. . . . . . . . . . . . | | . . . . . . . . . . . .o. . . . . . . . . . . . | | . . . . . . . . . . (x) (y) . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o
Any proposition worth its salt has many equivalent ways to view it, any one of which may reveal some unsuspected aspect of its meaning. We will encounter more and more of these variant readings as we go.
The enlargement operator \(\operatorname{E},\) also known as the shift operator, has many interesting and very useful properties in its own right, so let us not fail to observe a few of the more salient features that play out on the surface of our simple example, \(f(x, y) = xy.\!\)
Introduce a suitably generic definition of the extended universe of discourse:
- For \(U = X_1 \times \ldots \times X_k\),
- let \(\operatorname{E}U = U \times \operatorname{d}U = X_1 \times \ldots \times X_k \times \operatorname{d}X_1 \times \ldots \times \operatorname{d}X_k.\)
For a proposition \(f : X_1 \times \ldots \times X_k \to \mathbb{B},\) the (first order) enlargement of \(f\!\) is the proposition \(\operatorname{E}f : \operatorname{E}U \to \mathbb{B}\) that is defined by:
\(\operatorname{E}f(x_1, \ldots x_k, \operatorname{d}x_1, \ldots, \operatorname{d}x_k) = f(x_1 + \operatorname{d}x_1, \ldots, x_k + \operatorname{d}x_k).\)
It should be noted that the so-called differential variables \(\operatorname{d}x_j\) are really just the same kind of boolean variables as the other \(x_j.\!\) It is conventional to give the additional variables these brands of inflected names, but whatever extra connotations we might choose to attach to these syntactic conveniences are wholly external to their purely algebraic meanings.
For the example \(f(x, y) = xy,\!\) we obtain:
\(\operatorname{E}f(x, y, \operatorname{d}x, \operatorname{d}y) = (x + \operatorname{d}x)(y + \operatorname{d}y).\)
Given that this expression uses nothing more than the boolean ring operations of addition \((+)\!\) and multiplication \((\cdot),\) it is permissible to multiply things out in the usual manner to arrive at the result:
\(\operatorname{E}f(x, y, \operatorname{d}x, \operatorname{d}y) = xy + x\ \operatorname{d}y + y\ \operatorname{d}x + \operatorname{d}x\ \operatorname{d}y.\)
To understand what this means in logical terms, for instance, as expressed in a boolean expansion or a disjunctive normal form (DNF), it is perhaps a little better to go back and analyze the expression the same way that we did for \(\operatorname{D}f.\) Thus, let us compute the value of the enlarged proposition \(\operatorname{E}f\) at each of the points in the universe of discourse \(U = X \times Y.\)
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . x .dx y .dy . . . . . . . . . | | . . . . . . . . . o---o o---o . . . . . . . . . | | . . . . . . . . . .\. | | ./. . . . . . . . . . | | . . . . . . . . . . \ | | / . . . . . . . . . . | | . . . . . . . . . . .\| |/. . . . . . . . . . . | | . . . . . . . . . . . @=@ . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | Ef = . . . . . .(x, dx) (y, dy) . . . . . . . . | o-------------------------------------------------o
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . .dx . .dy . . . . . . . . . | | . . . . . . . . . o---o o---o . . . . . . . . . | | . . . . . . . . . .\. | | ./. . . . . . . . . . | | . . . . . . . . . . \ | | / . . . . . . . . . . | | . . . . . . . . . . .\| |/. . . . . . . . . . . | | . . . . . . . . . . . @=@ . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | Ef|xy = . . . . . .(dx) (dy). . . . . . . . . . | o-------------------------------------------------o
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . . . . o . . . . . . . . . . . | | . . . . . . . . . . .dx | .dy . . . . . . . . . | | . . . . . . . . . o---o o---o . . . . . . . . . | | . . . . . . . . . .\. | | ./. . . . . . . . . . | | . . . . . . . . . . \ | | / . . . . . . . . . . | | . . . . . . . . . . .\| |/. . . . . . . . . . . | | . . . . . . . . . . . @=@ . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | Ef|x(y) = . . . . .(dx) .dy . . . . . . . . . . | o-------------------------------------------------o
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . o . . . . . . . . . . . . . . | | . . . . . . . . . | .dx . .dy . . . . . . . . . | | . . . . . . . . . o---o o---o . . . . . . . . . | | . . . . . . . . . .\. | | ./. . . . . . . . . . | | . . . . . . . . . . \ | | / . . . . . . . . . . | | . . . . . . . . . . .\| |/. . . . . . . . . . . | | . . . . . . . . . . . @=@ . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | Ef|(x)y = . . . . . dx .(dy). . . . . . . . . . | o-------------------------------------------------o
o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . o . . o . . . . . . . . . . . | | . . . . . . . . . | .dx | .dy . . . . . . . . . | | . . . . . . . . . o---o o---o . . . . . . . . . | | . . . . . . . . . .\. | | ./. . . . . . . . . . | | . . . . . . . . . . \ | | / . . . . . . . . . . | | . . . . . . . . . . .\| |/. . . . . . . . . . . | | . . . . . . . . . . . @=@ . . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | Ef|(x)(y) = . . . . dx . dy . . . . . . . . . . | o-------------------------------------------------o
Given the sort of data that arises from this form of analysis, we can now fold the disjoined ingredients back into a boolean expansion or a DNF that is equivalent to the proposition \(\operatorname{E}f.\)
\(\operatorname{E}f = xy\ \operatorname{E}f_{x y} + x (\!| y |\!)\ \operatorname{E}f_{x (\!| y |\!)} + (\!| x |\!) y\ \operatorname{E}f_{(\!| x |\!) y} + (\!| x |\!)(\!| y |\!)\ \operatorname{E}f_{(\!| x |\!)(\!| y |\!)}.\)
Here is a summary of the result, illustrated by means of a digraph picture, where the no change element \((\!| \operatorname{d}x |\!)(\!| \operatorname{d}y |\!)\) is drawn as a loop at the point \(xy.\!\)
o-------------------------------------------------o | f = . . . . . . . . . x y . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | Ef =. . . . . . . x .y. .(dx)(dy) . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . + . . . x (y) .(dx) dy. . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . + . . .(x) y. . dx (dy) . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . + . . .(x)(y) . dx .dy. . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o | . . . . . . . . . . . . . . . . . . . . . . . . | | . . . . . . . . . .(dx) (dy). . . . . . . . . . | | . . . . . . . . . . --->--- . . . . . . . . . . | | . . . . . . . . . . \ . . / . . . . . . . . . . | | . . . . . . . . . . .\x y/. . . . . . . . . . . | | . . . . . . . . . . . \ / . . . . . . . . . . . | | .x (y) o-------------->o<--------------o (x) y. | | . . . . . . (dx) dy . .^. . dx (dy) . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . dx | dy . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .|. . . . . . . . . . . . | | . . . . . . . . . . . .o. . . . . . . . . . . . | | . . . . . . . . . . (x) (y) . . . . . . . . . . | | . . . . . . . . . . . . . . . . . . . . . . . . | o-------------------------------------------------o
We may understand the enlarged proposition \(\operatorname{E}f\) as telling us all the different ways to reach a model of \(f\!\) from any point of the universe \(U.\!\)
Propositional Forms on Two Variables
To broaden our experience with simple examples, let us now contemplate the sixteen functions of concrete type \(X \times Y \to \mathbb{B}\) and abstract type \(\mathbb{B} \times \mathbb{B} \to \mathbb{B}.\) For future reference, I will set here a few Tables that detail the actions of \(\operatorname{E}\) and \(\operatorname{D}\) on each of these functions, allowing us to view the results in several different ways.
By way of initial orientation, Table 1 lists equivalent expressions for the sixteen functions in a number of different languages for zeroth order logic.
| \(\mathcal{L}_1\) | \(\mathcal{L}_2\) | \(\mathcal{L}_3\) | \(\mathcal{L}_4\) | \(\mathcal{L}_5\) | \(\mathcal{L}_6\) | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Table 2 exhibits the same information in a different order, grouping the sixteen functions into seven natural classes.
| \(\mathcal{L}_1\) | \(\mathcal{L}_2\) | \(\mathcal{L}_3\) | \(\mathcal{L}_4\) | \(\mathcal{L}_5\) | \(\mathcal{L}_6\) | ||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
\(f_{0}\!\) |
\(f_{0000}\!\) |
0 0 0 0 |
\((~)\!\) |
\(\operatorname{false}\) |
\(0\!\) | ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
\(f_{15}\!\) |
\(f_{1111}\!\) |
1 1 1 1 |
\(((~))\!\) |
\(\operatorname{true}\) |
\(1\!\) |
The next four Tables expand the expressions of \(\operatorname{E}f\) and \(\operatorname{D}f\) in two different ways, for each of the sixteen functions. Notice that the functions are given in a different order, here being collected into a set of seven natural classes.
| \(f\!\) |
|
|
|
| |||||||||||||||||||||||||
| \(f_{0}\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
| \(f_{15}\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) | ||||||||||||||||||||||||
| Fixed Point Total : | \(4\!\) | \(4\!\) | \(4\!\) | \(16\!\) | |||||||||||||||||||||||||
| \(f\!\) | \(\operatorname{D}f|_{\operatorname{d}x\ \operatorname{d}y}\) | \(\operatorname{D}f|_{\operatorname{d}x(\operatorname{d}y)}\) | \(\operatorname{D}f|_{(\operatorname{d}x)\operatorname{d}y}\) | \(\operatorname{D}f|_{(\operatorname{d}x)(\operatorname{d}y)}\) | |||||||||||||||||||||||||
| \(f_{0}\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
| \(f_{15}\!\) | \(((~))\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) |
| \(f\!\) | \(\operatorname{E}f|_{xy}\) | \(\operatorname{E}f|_{x(y)}\) | \(\operatorname{E}f|_{(x)y}\) | \(\operatorname{E}f|_{(x)(y)}\) | |||||||||||||||||||||||||
| \(f_{0}\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
| \(f_{15}\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) |
| \(f\!\) | \(\operatorname{D}f|_{xy}\) | \(\operatorname{D}f|_{x(y)}\) | \(\operatorname{D}f|_{(x)y}\) | \(\operatorname{D}f|_{(x)(y)}\) | |||||||||||||||||||||||||
| \(f_{0}\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
| \(f_{15}\!\) | \(((~))\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) |
If the medium truly is the message, the blank slate is the innate idea.
If you think that I linger in the realm of logical difference calculus out of sheer vacillation about getting down to the differential proper, it is probably out of a prior expectation that you derive from the art or the long-engrained practice of real analysis. But the fact is that ordinary calculus only rushes on to the sundry orders of approximation because the strain of comprehending the full import of E and D at once whelm over its discrete and finite powers to grasp them. But here, in the fully serene idylls of ZOL, we find ourselves fit with the compass of a wit that is all we'd ever wish to explore their effects with care.
So let us do just that.
I will first rationalize the novel grouping of propositional forms in the last set of Tables, as that will extend a gentle invitation to the mathematical subject of group theory, and demonstrate its relevance to differential logic in a strikingly apt and useful way. The data for that account is contained in Table 3.
The shift operator E can be understood as enacting a substitution operation on the proposition that is given as its argument. In our immediate example, we have the following data and definition:
- E : (U → B) → (EU → B),
- E : f(x, y) → Ef(x, y, dx, dy),
- Ef(x, y, dx, dy) = f(x + dx, y + dy).
Therefore, if we evaluate Ef at particular values of dx and dy, for example, dx = i and dy = j, where i, j are in B, we obtain:
- Eij : (U → B) → (U → B),
- Eij : f → : Eijf,
- Eijf = Ef|<dx = i, dy = j> = f(x + i, y + j).
The notation is a little bit awkward, but the data of the Table should make the sense clear. The important thing to observe is that Eij has the effect of transforming each proposition f : U → B into some other proposition f´ : U → B. As it happens, the action is one-to-one and onto for each Eij, so the gang of four operators {Eij : i, j in B} is an example of what is called a transformation group on the set of sixteen propositions. Bowing to a longstanding local and linear tradition, I will therefore redub the four elements of this group as T00, T01, T10, T11, to bear in mind their transformative character, or nature, as the case may be. Abstractly viewed, this group of order four has the following operation table:
o----------o----------o----------o----------o----------o | % | | | | | * % T_00 | T_01 | T_10 | T_11 | | % | | | | o==========o==========o==========o==========o==========o | % | | | | | T_00 % T_00 | T_01 | T_10 | T_11 | | % | | | | o----------o----------o----------o----------o----------o | % | | | | | T_01 % T_01 | T_00 | T_11 | T_10 | | % | | | | o----------o----------o----------o----------o----------o | % | | | | | T_10 % T_10 | T_11 | T_00 | T_01 | | % | | | | o----------o----------o----------o----------o----------o | % | | | | | T_11 % T_11 | T_10 | T_01 | T_00 | | % | | | | o----------o----------o----------o----------o----------o
It happens that there are just two possible groups of 4 elements. One is the cyclic group Z4 (German Zyklus), which this is not. The other is Klein's four-group V4 (German Vier), which it is.
More concretely viewed, the group as a whole pushes the set of sixteen propositions around in such a way that they fall into seven natural classes, called orbits. One says that the orbits are preserved by the action of the group. There is an Orbit Lemma of immense utility to "those who count" which, depending on your upbringing, you may associate with the names of Burnside, Cauchy, Frobenius, or some subset or superset of these three, vouching that the number of orbits is equal to the mean number of fixed points, in other words, the total number of points (in our case, propositions) that are left unmoved by the separate operations, divided by the order of the group. In this instance, T00 operates as the group identity, fixing all 16 propositions, while the other three group elements fix 4 propositions each, and so we get:
- Number of orbits = (4 + 4 + 4 + 16) ÷ 4 = 7.
Amazing!
We have been contemplating functions of the type f : U → B, studying the action of the operators E and D on this family. These functions, that we may identify for our present aims with propositions, inasmuch as they capture their abstract forms, are logical analogues of scalar potential fields. These are the sorts of fields that are so picturesquely presented in elementary calculus and physics textbooks by images of snow-covered hills and parties of skiers who trek down their slopes like least action heroes. The analogous scene in propositional logic presents us with forms more reminiscent of plateaunic idylls, being all plains at one of two levels, the mesas of verity and falsity, as it were, with nary a niche to inhabit between them, restricting our options for a sporting gradient of downhill dynamics to just one of two, standing still on level ground or falling off a bluff.
We are still working well within the logical analogue of the classical finite difference calculus, taking in the novelties that the logical transmutation of familiar elements is able to bring to light. Soon we will take up several different notions of approximation relationships that may be seen to organize the space of propositions, and these will allow us to define several different forms of differential analysis applying to propositions. In time we will find reason to consider more general types of maps, having concrete types of the form X1 × … × Xk → Y1 × … × Yn and abstract types Bk → Bn. We will think of these mappings as transforming universes of discourse into themselves or into others, in short, as transformations of discourse.
Before we continue with this intinerary, however, I would like to highlight another sort of differential aspect that concerns the boundary operator or the marked connective that serves as one of the two basic connectives in the cactus language for ZOL.
For example, consider the proposition f of concrete type f : X × Y × Z → B and abstract type f : B3 → B that is written (x, y, z) in cactus syntax. Taken as an assertion in what Peirce called the existential interpretation, (x, y, z) says that just one of x, y, z is false. It is useful to consider this assertion in relation to the conjunction xyz of the features that are engaged as its arguments. A venn diagram of (x, y, z) looks like this:
o-----------------------------------------------------------o | U | | | | o-------------o | | / \ | | / \ | | / \ | | / \ | | / \ | | o x o | | | | | | | | | | | | | | | | | | | | | | o--o----------o o----------o--o | | / \%%%%%%%%%%\ /%%%%%%%%%%/ \ | | / \%%%%%%%%%%o%%%%%%%%%%/ \ | | / \%%%%%%%%/ \%%%%%%%%/ \ | | / \%%%%%%/ \%%%%%%/ \ | | / \%%%%/ \%%%%/ \ | | o o--o-------o--o o | | | |%%%%%%%| | | | | |%%%%%%%| | | | | |%%%%%%%| | | | | |%%%%%%%| | | | | |%%%%%%%| | | | o y o%%%%%%%o z o | | \ \%%%%%/ / | | \ \%%%/ / | | \ \%/ / | | \ o / | | \ / \ / | | o-------------o o-------------o | | | | | o-----------------------------------------------------------o
In relation to the center cell indicated by the conjunction xyz, the region indicated by (x, y, z) is comprised of the adjacent or the bordering cells. Thus they are the cells that are just across the boundary of the center cell, as if reached by way of Leibniz's minimal changes from the point of origin, here, xyz.
The same form of boundary relationship is exhibited for any cell of origin that one might elect to indicate, say, by means of the conjunction of positive and negative basis features u1 … uk, where uj = xj or uj = (xj), for j = 1 to k. The proposition (u1, …, uk) indicates the disjunctive region consisting of the cells that are "just next door" to the cell u1 … uk.
The Pragmatic Maxim
Consider what effects that might conceivably have practical bearings you conceive the objects of your conception to have. Then, your conception of those effects is the whole of your conception of the object.
Charles Sanders Peirce, "The Maxim of Pragmatism, CP 5.438.
One other subject that it would be opportune to mention at this point, while we have an object example of a mathematical group fresh in mind, is the relationship between the pragmatic maxim and what are commonly known in mathematics as representation principles. As it turns out, with regard to its formal characteristics, the pragmatic maxim unites the aspects of a representation principle with the attributes of what would ordinarily be known as a closure principle. We will consider the form of closure that is invoked by the pragmatic maxim on another occasion, focusing here and now on the topic of group representations.
Let us return to the example of the so-called four-group V4. We encountered this group in one of its concrete representations, namely, as a transformation group that acts on a set of objects, in this particular case a set of sixteen functions or propositions. Forgetting about the set of objects that the group transforms among themselves, we may take the abstract view of the group's operational structure, say, in the form of the group operation table copied here:
o---------o---------o---------o---------o---------o | % | | | | | . % e | f | g | h | | % | | | | o=========o=========o=========o=========o=========o | % | | | | | e % e | f | g | h | | % | | | | o---------o---------o---------o---------o---------o | % | | | | | f % f | e | h | g | | % | | | | o---------o---------o---------o---------o---------o | % | | | | | g % g | h | e | f | | % | | | | o---------o---------o---------o---------o---------o | % | | | | | h % h | g | f | e | | % | | | | o---------o---------o---------o---------o---------o
This table is abstractly the same as, or isomorphic to, the versions with the Eij operators and the Tij transformations that we discussed earlier. That is to say, the story is the same — only the names have been changed. An abstract group can have a multitude of significantly and superficially different representations. Even after we have long forgotten the details of the particular representation that we may have come in with, there are species of concrete representations, called the regular representations, that are always readily available, as they can be generated from the mere data of the abstract operation table itself.
For example, select a group element from the top margin of the Table, and "consider its effects" on each of the group elements as they are listed along the left margin. We may record these effects as Peirce usually did, as a logical "aggregate" of elementary dyadic relatives, that is to say, a disjunction or a logical sum whose terms represent the ordered pairs of <input : output> transactions that are produced by each group element in turn. This yields what is usually known as one of the regular representations of the group, specifically, the first, the post-, or the right regular representation. It has long been conventional to organize the terms in the form of a matrix:
Reading "+" as a logical disjunction:
G = e + f + g + h,
And so, by expanding effects, we get:
G = e:e + f:f + g:g + h:h
+ e:f + f:e + g:h + h:g
+ e:g + f:h + g:e + h:f
+ e:h + f:g + g:f + h:e
More on the pragmatic maxim as a representation principle later.
Consider what effects that might conceivably have practical bearings you conceive the objects of your conception to have. Then, your conception of those effects is the whole of your conception of the object.
Peirce, "Maxim of Pragmaticism", Collected Papers, CP 5.438.
The genealogy of this conception of pragmatic representation is very intricate. I will delineate some details that I presently fancy I remember clearly enough, subject to later correction. Without checking historical accounts, I will not be able to pin down anything like a real chronology, but most of these notions were standard furnishings of the 19th Century mathematical study, and only the last few items date as late as the 1920's.
The idea about the regular representations of a group is universally known as Cayley's Theorem, usually in the form: "Every group is isomorphic to a subgroup of Aut(X), the group of automorphisms of an appropriate set X". There is a considerable generalization of these regular representations to a broad class of relational algebraic systems in Peirce's earliest papers. The crux of the whole idea is this:
Contemplate the effects of the symbol whose meaning you wish to investigate as they play out on all the stages of conduct on which you have the ability to imagine that symbol playing a role.
This idea of contextual definition is basically the same as Jeremy Bentham's notion of paraphrasis, a "method of accounting for fictions by explaining various purported terms away" (Quine, in Van Heijenoort, p. 216). Today we'd call these constructions term models. This, again, is the big idea behind Schönfinkel's combinators {S, K, I}, and hence of lambda calculus, and I reckon you know where that leads.
Let me return to Peirce's early papers on the algebra of relatives to pick up the conventions that he used there, and then rewrite my account of regular representations in a way that conforms to those.
Peirce expresses the action of an "elementary dual relative" like so:
[Let] A:B be taken to denote the elementary relative which multiplied into B gives A. (Peirce, CP 3.123).
And though he is well aware that it is not at all necessary to arrange elementary relatives into arrays, matrices, or tables, when he does so he tends to prefer organizing dyadic relations in the following manner:
[ A:A A:B A:C | | | | B:A B:B B:C | | | | C:A C:B C:C ]
That conforms to the way that the last school of thought I matriculated into stipulated that we tabulate material:
[ e_11 e_12 e_13 | | | | e_21 e_22 e_23 | | | | e_31 e_32 e_33 ]
So, for example, let us suppose that we have the small universe {A, B, C}, and the 2-adic relation m = mover of that is represented by this matrix:
m = [ m_AA (A:A) m_AB (A:B) m_AC (A:C) | | | | m_BA (B:A) m_BB (B:B) m_BC (B:C) | | | | m_CA (C:A) m_CB (C:B) m_CC (C:C) ]
Also, let m be such that:
A is a mover of A and B, B is a mover of B and C, C is a mover of C and A.
In sum:
m = [ 1 * (A:A) 1 * (A:B) 0 * (A:C) | | | | 0 * (B:A) 1 * (B:B) 1 * (B:C) | | | | 1 * (C:A) 0 * (C:B) 1 * (C:C) ]
For the sake of orientation and motivation, compare with Peirce's notation in CP 3.329.
I think that will serve to fix notation and set up the remainder of the account.
It is common in algebra to switch around between different conventions of display, as the momentary fancy happens to strike, and I see that Peirce is no different in this sort of shiftiness than anyone else. A changeover appears to occur especially whenever he shifts from logical contexts to algebraic contexts of application.
In the paper "On the Relative Forms of Quaternions" (CP 3.323), we observe Peirce providing the following sorts of explanation:
If X, Y, Z denote the three rectangular components of a vector, and W' denote numerical unity (or a fourth rectangular component, involving space of four dimensions), and (Y:Z) denote the operation of converting the Y component of a vector into its Z component, then
1 = (W:W) + (X:X) + (Y:Y) + (Z:Z) i = (X:W) - (W:X) - (Y:Z) + (Z:Y) j = (Y:W) - (W:Y) - (Z:X) + (X:Z) k = (Z:W) - (W:Z) - (X:Y) + (Y:X)In the language of logic (Y:Z) is a relative term whose relate is a Y component, and whose correlate is a Z component. The law of multiplication is plainly (Y:Z)(Z:X) = (Y:X), (Y:Z)(X:W) = 0, and the application of these rules to the above values of 1, i, j, k gives the quaternion relations
i^2 = j^2 = k^2 = -1, ijk = -1, etc.The symbol a(Y:Z) denotes the changing of Y to Z and the multiplication of the result by a'. If the relatives be arranged in a block
W:W W:X W:Y W:Z X:W X:X X:Y X:Z Y:W Y:X Y:Y Y:Z Z:W Z:X Z:Y Z:Zthen the quaternion w + xi + yj + zk is represented by the matrix of numbers
w -x -y -z x w -z y y z w -x z -y x wThe multiplication of such matrices follows the same laws as the multiplication of quaternions. The determinant of the matrix = the fourth power of the tensor of the quaternion.
The imaginary x + y(-1)^(1/2) may likewise be represented by the matrix
x y -y xand the determinant of the matrix = the square of the modulus.
C.S. Peirce, Collected Papers, CP 3.323, (1882). Johns Hopkins University Circulars, No. 13, p. 179.
This way of talking is the mark of a person who opts to multiply his matrices "on the right", as they say. Yet Peirce still continues to call the first element of the ordered pair (i:j) its "relate" while calling the second element of the pair (i:j) its "correlate". That doesn't comport very well, so far as I can tell, with his customary reading of relative terms, suited more to the multiplication of matrices "on the left".
So I still have a few wrinkles to iron out before I can give this story a smooth enough consistency.
Let us make up the model universe $1$ = A + B + C and the 2-adic relation n = "noter of", as when "X is a data record that contains a pointer to Y". That interpretation is not important, it's just for the sake of intuition. In general terms, the 2-adic relation n can be represented by this matrix:
n = [ n_AA (A:A) n_AB (A:B) n_AC (A:C) | | | | n_BA (B:A) n_BB (B:B) n_BC (B:C) | | | | n_CA (C:A) n_CB (C:B) n_CC (C:C) ]
Also, let n be such that:
A is a noter of A and B, B is a noter of B and C, C is a noter of C and A.
Filling in the instantial values of the "coefficients" nij, as the indices i and j range over the universe of discourse:
n = [ 1 * (A:A) 1 * (A:B) 0 * (A:C) | | | | 0 * (B:A) 1 * (B:B) 1 * (B:C) | | | | 1 * (C:A) 0 * (C:B) 1 * (C:C) ]
In Peirce's time, and even in some circles of mathematics today, the information indicated by the elementary relatives (i:j), as i, j range over the universe of discourse, would be referred to as the "umbral elements" of the algebraic operation represented by the matrix, though I seem to recall that Peirce preferred to call these terms the "ingredients". When this ordered basis is understood well enough, one will tend to drop any mention of it from the matrix itself, leaving us nothing but these bare bones:
n = [ 1 1 0 | | | | 0 1 1 | | | | 1 0 1 ]
However the specification may come to be written, this is all just convenient schematics for stipulating that:
- n = A:A + B:B + C:C'+ A:B + B:C + C:A
Recognizing !1! = A:A + B:B + C:C to be the identity transformation, the 2-adic relation n = "noter of" may be represented by an element !1! + A:B + B:C + C:A of the so-called "group ring", all of which just makes this element a special sort of linear transformation.
Up to this point, we are still reading the elementary relatives of the form i:j in the way that Peirce reads them in logical contexts: i is the relate, j is the correlate, and in our current example we read i:j, or more exactly, nij = 1, to say that i is a noter of j. This is the mode of reading that we call "multiplying on the left".
In the algebraic, permutational, or transformational contexts of application, however, Peirce converts to the alternative mode of reading, although still calling i the relate and j the correlate, the elementary relative i:j now means that i gets changed into j. In this scheme of reading, the transformation A:B + B:C + C:A is a permutation of the aggregate $1$ = A + B + C, or what we would now call the set {A, B, C}, in particular, it is the permutation that is otherwise notated as:
( A B C ) < > ( B C A )
This is consistent with the convention that Peirce uses in the paper "On a Class of Multiple Algebras" (CP 3.324–327).
We have been contemplating the virtues and the utilities of the pragmatic maxim as a standard heuristic in hermeneutics, that is, as a principle of interpretation that guides us in finding clarifying representations for a problematic corpus of symbols by means of their actions on other symbols or in terms of their effects on the syntactic contexts wherein we discover them or where we might conceive to distribute them.
I began this excursion by taking off from the moving platform of differential logic and passing by way of the corresponding transformation groups, as they act on propositions, and on to an exercise in applying the pragmatic maxim, by contemplating the regular representations of groups as giving us one of the simplest conceivable, relatively concrete applications of the general principle of representation in question.
There are a few problems of implementation that have to be worked out in practice, most of which are cleared up by keeping in mind which of several possible conventions we have chosen to follow at a given time.
But there does appear to remain this rather more substantial question: Are the effects we seek relates or correlates, or does it even matter?
I will have to leave that question as it is for now, in hopes that a solution will evolve itself in time.
Obstacles to Applying the Pragmatic Maxim
No sooner do you get a good idea and try to apply it than you find that a motley array of obstacles arise.
It would be good if we could in practice more consistently apply the pragmatic maxim to the purpose for which it was purportedly intended by its author. That aim would be the clarification of concepts, that is, intellectual symbols or mental signs, to the point where their inherent senses, or their lacks thereof, would be rendered manifest to suitable interpreters.
There are big obstacles and little obstacles to applying the pragmatic maxim. In good subgoaling fashion, I will merely mention a few of the bigger blocks, as if in passing, but not really getting past them, and then I will get down to the details of the problems that more immediately obstruct our advance.
Obstacle 1. People do not always read the instructions very carefully. There is a tendency in readers of particular prior persuasions to blow the problem all out of proportion, to think that the maxim is meant to reveal the absolutely positive and the totally unique meaning of every preconception to which they might deign or elect to apply it. Reading the maxim with an even minimal attention, you can see that it promises no such finality of unindexed sense, but ties what you conceive to you. I have lately come to wonder at the tenacity of this misinterpretation. Perhaps people reckon that nothing less would be worth their attention. I am not sure. I can only say the achievement of more modest goals is the sort of thing on which our daily life depends, and there can be no final end to inquiry nor any ultimate community without a continuation of life, and that means life on a day to day basis. All of which only brings me back to the point of persisting with local meantime examples, because if we can't apply the maxim there, we can't apply it anywhere.
Obstacle 2. Applying the pragmatic maxim, even with a moderate aim, can be hard. I think that my present example, deliberately impoverished as it is, affords us with an embarassing richness of evidence of just how complex the simple can be.
All the better reason for me to see if I can finish it up before moving on.
Expressed most simply, the idea is to replace the question of "what it is", which modest people know is far too difficult for them to answer right off, with the question of "what it does", which most of us know a modicum about.
In the case of regular representations of groups we found a non-plussing surplus of answers to sort our way through. So let us track back one more time to see if we can learn any lessons that might carry over to more realistic cases.
Here is is the operation table of V4 once again:
Table 1. Klein Four-Group V_4 o---------o---------o---------o---------o---------o | % | | | | | . % e | f | g | h | | % | | | | o=========o=========o=========o=========o=========o | % | | | | | e % e | f | g | h | | % | | | | o---------o---------o---------o---------o---------o | % | | | | | f % f | e | h | g | | % | | | | o---------o---------o---------o---------o---------o | % | | | | | g % g | h | e | f | | % | | | | o---------o---------o---------o---------o---------o | % | | | | | h % h | g | f | e | | % | | | | o---------o---------o---------o---------o---------o
A group operation table is really just a device for recording a certain 3-adic relation, to be specific, the set of triples of the form (x, y, z) satisfying the equation x\(\cdot\)y = z, where "\(\cdot\)" signifies the group operation, usually omitted as understood in context.
In the case of V4 = (G, \(\cdot\)), where G is the "underlying set" {e, f, g, h}, we have the 3-adic relation L(V4) ⊆ G × G × G whose triples are listed below:
<e, e, e> <e, f, f> <e, g, g> <e, h, h> <f, e, f> <f, f, e> <f, g, h> <f, h, g> <g, e, g> <g, f, h> <g, g, e> <g, h, f> <h, e, h> <h, f, g> <h, g, f> <h, h, e>
It is part of the definition of a group that the 3-adic relation L ⊆ G3 is actually a function L : G × G → G. It is from this functional perspective that we can see an easy way to derive the two regular representations. Since we have a function of the type L : G × G → G, we can define a couple of substitution operators:
- Sub(x, (_, y)) puts any specified x into the empty slot of the rheme (_, y), with the effect of producing the saturated rheme (x, y) that evaluates to xy.
- Sub(x, (y, _)) puts any specified x into the empty slot of the rheme (y, _), with the effect of producing the saturated rheme (y, x) that evaluates to yx.
In (1), we consider the effects of each x in its practical bearing on contexts of the form (_, y), as y ranges over G, and the effects are such that x takes (_, y) into xy, for y in G, all of which is summarily notated as x = {(y : xy) : y in G}. The pairs (y : xy) can be found by picking an x from the left margin of the group operation table and considering its effects on each y in turn as these run across the top margin. This aspect of pragmatic definition we recognize as the regular ante-representation:
e = e:e + f:f + g:g + h:h f = e:f + f:e + g:h + h:g g = e:g + f:h + g:e + h:f h = e:h + f:g + g:f + h:e
In (2), we consider the effects of each x in its practical bearing on contexts of the form (y, _), as y ranges over G, and the effects are such that x takes (y, _) into yx, for y in G, all of which is summarily notated as x = {(y : yx) : y in G}. The pairs (y : yx) can be found by picking an x from the top margin of the group operation table and considering its effects on each y in turn as these run down the left margin. This aspect of pragmatic definition we recognize as the regular post-representation:
e = e:e + f:f + g:g + h:h f = e:f + f:e + g:h + h:g g = e:g + f:h + g:e + h:f h = e:h + f:g + g:f + h:e
If the ante-rep looks the same as the post-rep, now that I'm writing them in the same dialect, that is because V4 is abelian (commutative), and so the two representations have the very same effects on each point of their bearing.
So long as we're in the neighborhood, we might as well take in some more of the sights, for instance, the smallest example of a non-abelian (non-commutative) group. This is a group of six elements, say, G = {e, f, g, h, i, j}, with no relation to any other employment of these six symbols being implied, of course, and it can be most easily represented as the permutation group on a set of three letters, say, X = {A, B, C}, usually notated as G = Sym(X) or more abstractly and briefly, as Sym(3) or S3. Here are the permutation (= substitution) operations in Sym(X):
Table 1. Permutations or Substitutions in Sym_{A, B, C}
o---------o---------o---------o---------o---------o---------o
| | | | | | |
| e | f | g | h | i | j |
| | | | | | |
o=========o=========o=========o=========o=========o=========o
| | | | | | |
| A B C | A B C | A B C | A B C | A B C | A B C |
| | | | | | |
| | | | | | | | | | | | | | | | | | | | | | | | |
| v v v | v v v | v v v | v v v | v v v | v v v |
| | | | | | |
| A B C | C A B | B C A | A C B | C B A | B A C |
| | | | | | |
o---------o---------o---------o---------o---------o---------o
Here is the operation table for S3, given in abstract fashion:
Table 2. Symmetric Group S_3 | ^ | e / \ e | / \ | / e \ | f / \ / \ f | / \ / \ | / f \ f \ | g / \ / \ / \ g | / \ / \ / \ | / g \ g \ g \ | h / \ / \ / \ / \ h | / \ / \ / \ / \ | / h \ e \ e \ h \ | i / \ / \ / \ / \ / \ i | / \ / \ / \ / \ / \ | / i \ i \ f \ j \ i \ | j / \ / \ / \ / \ / \ / \ j | / \ / \ / \ / \ / \ / \ | ( j \ j \ j \ i \ h \ j ) | \ / \ / \ / \ / \ / \ / | \ / \ / \ / \ / \ / \ / | \ h \ h \ e \ j \ i / | \ / \ / \ / \ / \ / | \ / \ / \ / \ / \ / | \ i \ g \ f \ h / | \ / \ / \ / \ / | \ / \ / \ / \ / | \ f \ e \ g / | \ / \ / \ / | \ / \ / \ / | \ g \ f / | \ / \ / | \ / \ / | \ e / | \ / | \ / | v
By the way, we will meet with the symmetric group S3 again when we return to take up the study of Peirce's early paper "On a Class of Multiple Algebras" (CP 3.324–327), and also his late unpublished work "The Simplest Mathematics" (1902) (CP 4.227–323), with particular reference to the section that treats of "Trichotomic Mathematics" (CP 4.307–323).
By way of collecting a short-term pay-off for all the work that we did on the regular representations of the Klein 4-group V4, let us write out as quickly as possible in "relative form" a minimal budget of representations for the symmetric group on three letters, Sym(3). After doing the usual bit of compare and contrast among the various representations, we will have enough concrete material beneath our abstract belts to tackle a few of the presently obscur'd details of Peirce's early "Algebra + Logic" papers.
Table 1. Permutations or Substitutions in Sym {A, B, C}
o---------o---------o---------o---------o---------o---------o
| | | | | | |
| e | f | g | h | i | j |
| | | | | | |
o=========o=========o=========o=========o=========o=========o
| | | | | | |
| A B C | A B C | A B C | A B C | A B C | A B C |
| | | | | | |
| | | | | | | | | | | | | | | | | | | | | | | | |
| v v v | v v v | v v v | v v v | v v v | v v v |
| | | | | | |
| A B C | C A B | B C A | A C B | C B A | B A C |
| | | | | | |
o---------o---------o---------o---------o---------o---------o
Writing this table in relative form generates the following "natural representation" of S3.
e = A:A + B:B + C:C f = A:C + B:A + C:B g = A:B + B:C + C:A h = A:A + B:C + C:B i = A:C + B:B + C:A j = A:B + B:A + C:C
I have without stopping to think about it written out this natural representation of S3 in the style that comes most naturally to me, to wit, the "right" way, whereby an ordered pair configured as X:Y constitutes the turning of X into Y. It is possible that the next time we check in with CSP that we will have to adjust our sense of direction, but that will be an easy enough bridge to cross when we come to it.
To construct the regular representations of S3, we pick up from the data of its operation table:
Table 1. Symmetric Group S_3 | ^ | e / \ e | / \ | / e \ | f / \ / \ f | / \ / \ | / f \ f \ | g / \ / \ / \ g | / \ / \ / \ | / g \ g \ g \ | h / \ / \ / \ / \ h | / \ / \ / \ / \ | / h \ e \ e \ h \ | i / \ / \ / \ / \ / \ i | / \ / \ / \ / \ / \ | / i \ i \ f \ j \ i \ | j / \ / \ / \ / \ / \ / \ j | / \ / \ / \ / \ / \ / \ | ( j \ j \ j \ i \ h \ j ) | \ / \ / \ / \ / \ / \ / | \ / \ / \ / \ / \ / \ / | \ h \ h \ e \ j \ i / | \ / \ / \ / \ / \ / | \ / \ / \ / \ / \ / | \ i \ g \ f \ h / | \ / \ / \ / \ / | \ / \ / \ / \ / | \ f \ e \ g / | \ / \ / \ / | \ / \ / \ / | \ g \ f / | \ / \ / | \ / \ / | \ e / | \ / | \ / | v
Just by way of staying clear about what we are doing, let's return to the recipe that we worked out before:
It is part of the definition of a group that the 3-adic relation L ⊆ G3 is actually a function L : G × G → G. It is from this functional perspective that we can see an easy way to derive the two regular representations.
Since we have a function of the type L : G × G → G, we can define a couple of substitution operators:
- Sub(x, «_, y») puts any specified x into the empty slot of the rheme «_, y», with the effect of producing the saturated rheme «x, y» that evaluates to xy.
- Sub(x, «y, _») puts any specified x into the empty slot of the rheme «y, _», with the effect of producing the saturated rheme «y, x» that evaluates to yx.
In (1), we consider the effects of each x in its practical bearing on contexts of the form «_, y», as y ranges over G, and the effects are such that x takes «_, y» into xy, for y in G, all of which is summarily notated as x = {(y : xy) : y in G}. The pairs (y : xy) can be found by picking an x from the left margin of the group operation table and considering its effects on each y in turn as these run along the right margin. This produces the regular ante-representation of S3, like so:
e = e:e + f:f + g:g + h:h + i:i + j:j f = e:f + f:g + g:e + h:j + i:h + j:i g = e:g + f:e + g:f + h:i + i:j + j:h h = e:h + f:i + g:j + h:e + i:f + j:g i = e:i + f:j + g:h + h:g + i:e + j:f j = e:j + f:h + g:i + h:f + i:g + j:e
In (2), we consider the effects of each x in its practical bearing on contexts of the form «y, _», as y ranges over G, and the effects are such that x takes «y, _» into yx, for y in G, all of which is summarily notated as x = {(y : yx) : y in G}. The pairs (y : yx) can be found by picking an x on the right margin of the group operation table and considering its effects on each y in turn as these run along the left margin. This generates the regular post-representation of S3, like so:
e = e:e + f:f + g:g + h:h + i:i + j:j f = e:f + f:g + g:e + h:i + i:j + j:h g = e:g + f:e + g:f + h:j + i:h + j:i h = e:h + f:j + g:i + h:e + i:g + j:f i = e:i + f:h + g:j + h:f + i:e + j:g j = e:j + f:i + g:h + h:g + i:f + j:e
If the ante-rep looks different from the post-rep, it is just as it should be, as S3 is non-abelian (non-commutative), and so the two representations differ in the details of their practical effects, though, of course, being representations of the same abstract group, they must be isomorphic.
the way of heaven and earth
is to be long continued
in their operation
without stoppingi ching, hexagram 32
You may be wondering what happened to the announced subject of "Differential Logic". If you think that we have been taking a slight excursion my reply to the charge of a scenic rout would be both "yes and no". What happened was this. We chanced to make the observation that the shift operators Eij form a transformation group that acts on the set of propositions of the form f : B2 → B. Group theory is a very attractive subject, but it did not have the effect of drawing us so far off our initial course as one might at first think. For one thing, groups, in particular, the special family of groups that have come to be named after the Norwegian mathematician Marius Sophus Lie, turn out to be of critical importance in the solution of differential equations. For another thing, group operations afford us examples of 3-adic relations that have been extremely well-studied over the years, and thus they supply us with no small bit of guidance in the study of sign relations, another class of 3-adic relations that have significance for logical studies, in our brief acquaintance with which we have scarcely even begun to break the ice. Finally, I could not resist taking up the connection between group representations, which constitute a very generic class of logical models, and the all-important pragmatic maxim.
Biographical Data for Marius Sophus Lie (1842–1899)
We've seen a couple of groups, V4 and S3, represented in various ways, and we've seen their representations presented in a variety of different manners. Let us look at one other stylistic variant for presenting a representation that is frequently seen, the so-called "matrix representation" of a group.
Recalling the manner of our acquaintance with the symmetric group S3, we began with the "bigraph" (bipartite graph) picture of its natural representation as the set of all permutations or substitutions on the set X = {A, B, C}.
Table 1. Permutations or Substitutions in Sym {A, B, C}
o---------o---------o---------o---------o---------o---------o
| | | | | | |
| e | f | g | h | i | j |
| | | | | | |
o=========o=========o=========o=========o=========o=========o
| | | | | | |
| A B C | A B C | A B C | A B C | A B C | A B C |
| | | | | | |
| | | | | | | | | | | | | | | | | | | | | | | | |
| v v v | v v v | v v v | v v v | v v v | v v v |
| | | | | | |
| A B C | C A B | B C A | A C B | C B A | B A C |
| | | | | | |
o---------o---------o---------o---------o---------o---------o
Then we rewrote these permutations — since they are functions f : X → X they can also be recognized as 2-adic relations f ⊆ X × X — in "relative form", in effect, in the manner to which Peirce would have made us accustomed had he been given a relative half-a-chance:
e = A:A + B:B + C:C f = A:C + B:A + C:B g = A:B + B:C + C:A h = A:A + B:C + C:B i = A:C + B:B + C:A j = A:B + B:A + C:C
These days one is much more likely to encounter the natural representation of S3 in the form of a "linear representation", that is, as a family of linear transformations that map the elements of a suitable vector space into each other, all of which would in turn usually be represented by a set of matrices like these:
Table 2. Matrix Representations of the Permutations in Sym(3) o---------o---------o---------o---------o---------o---------o | | | | | | | | e | f | g | h | i | j | | | | | | | | o=========o=========o=========o=========o=========o=========o | | | | | | | | 1 0 0 | 0 0 1 | 0 1 0 | 1 0 0 | 0 0 1 | 0 1 0 | | 0 1 0 | 1 0 0 | 0 0 1 | 0 0 1 | 0 1 0 | 1 0 0 | | 0 0 1 | 0 1 0 | 1 0 0 | 0 1 0 | 1 0 0 | 0 0 1 | | | | | | | | o---------o---------o---------o---------o---------o---------o
The key to the mysteries of these matrices is revealed by noting that their coefficient entries are arrayed and overlayed on a place mat marked like so:
[ A:A A:B A:C | | B:A B:B B:C | | C:A C:B C:C ]
Of course, the place-settings of convenience at different symposia may vary.
Differential Logic : Brief Recap
It would be good to summarize, in rough but intuitive terms, the outlook on differential logic that we have reached so far.
We have been considering a class of operators on universes of discourse, each of which takes us from considering one universe of discourse, \(X,\!\) to considering a larger universe of discourse, \(\operatorname{E}X.\!\)
Each of these operators, in general terms having the form \(\operatorname{F} : X \to \operatorname{E}X,\!\) acts on each proposition \(p : X \to \mathbb{B}\!\) of the source universe \(X\!\) to produce a proposition \(\operatorname{F}p : \operatorname{E}X \to \mathbb{B}\!\) of the target universe \(\operatorname{E}X.\!\)
The two main operators that we have worked with up to this point are the enlargement operator \(\operatorname{E} : X \to \operatorname{E}X\!\) and the difference operator \(\operatorname{D} : X \to \operatorname{E}X.\!\)
\(\operatorname{E}\!\) and \(\operatorname{D}\!\) take a proposition in \(X,\!\) that is, a proposition \(p : X \mathbb{B}\!\) that is said to be about the subject matter of \(X,\!\) and produce the extended propositions \(\operatorname{E}p, \operatorname{D}p : \operatorname{E}X \to \mathbb{B},\!\) which may be interpreted as being about specified collections of changes that might occur in \(X.\!\)
Here we have need of visual representations, some array of concrete pictures to anchor our more earthy intuitions and to help us keep our wits about us before we try to climb any higher into the ever more rarefied air of abstractions.
One good picture comes to us by way of the field concept. Given a space \(X,\!\) a field of a specified type \(\mathcal{T}\!\) over \(X\!\) is formed by assigning to each point of \(X\!\) an object of type \(\mathcal{T}.\!\) If that sounds like the same thing as a function from \(X\!\) to the space of things of type \(\mathcal{T},\!\) it is, but it does seems to help to vary the mental pictures and the figures of speech that naturally spring to mind within these fertile fields.
In the field picture a proposition \(p : X \to \mathbb{B}\!\) becomes a scalar field, that is, a field of values in \(\mathbb{B},\!\) or a field of true-false indications.
Let us take a moment to view an old proposition in this new light, for example, the conjunction \(uv : X \to \mathbb{B}\!\) that is depicted in Figure 1.
o-------------------------------------------------o | X | | | | o-------------o o-------------o | | / \ / \ | | / o \ | | / /%\ \ | | / /%%%\ \ | | o o%%%%%o o | | | |%%%%%| | | | | U |%%%%%| V | | | | |%%%%%| | | | o o%%%%%o o | | \ \%%%/ / | | \ \%/ / | | \ o / | | \ / \ / | | o-------------o o-------------o | | | | | o-------------------------------------------------o | f = u v | o-------------------------------------------------o Figure 1. Conjunction uv : X -> B
Each of the operators \(\operatorname{E}, \operatorname{D} : X \to \operatorname{E}X\!\) takes us from considering propositions \(p : X \to \mathbb{B},\!\) here viewed as scalar fields over \(X,\!\) to considering the corresponding differential fields over \(X,\!\) analogous to what are usually called vector fields \(X.\!\)
The structure of these differential fields can be described this way. To each point of \(X\!\) there is attached an object of the following type, a proposition about changes in \(X,\!\) that is, a proposition \(g : \operatorname{d}X \to \mathbb{B}.\!\) In this setting, if \(X\!\) is the universe that is generated by the set of coordinate propositions \(\{ u, v \},\!\) then \(\operatorname{d}X\!\) is the differential universe that is generated by the set of differential propositions \(\{ \operatorname{d}u, \operatorname{d}v \}.\!\) These differential propositions may be interpreted as indicating "change in \(u\!\)" and "change in \(v\!\)", respectively.
A differential operator \(\operatorname{F},\!\) of the first order sort that we have been considering, takes a proposition \(p : X \to \mathbb{B}\!\) and gives back a differential proposition \(\operatorname{F}p : \operatorname{E}X \to \mathbb{B}.\!\)
In the field view, we see the proposition \(p : X \to \mathbb{B}\!\) as a scalar field and we see the differential proposition \(\operatorname{F}p : \operatorname{E}X \to \mathbb{B}\!\) as a vector field, specifically, a field of propositions about contemplated changes in \(X.\!\)
The field of changes produced by \(\operatorname{E}\!\) on \(uv\!\) is shown in Figure 2.
o-------------------------------------------------o | X | | | | o-------------o o-------------o | | / \ / \ | | / U o V \ | | / /%\ \ | | / /%%%\ \ | | o o.->-.o o | | | u(v)(du)dv |%\%/%| (u)v du(dv) | | | | o---------------|->o<-|---------------o | | | | |%%^%%| | | | o o%%|%%o o | | \ \%|%/ / | | \ \|/ / | | \ o / | | \ /|\ / | | o-------------o | o-------------o | | | | | | | | | | | o | | (u)(v) du dv | | | o-------------------------------------------------o | f = u v | o-------------------------------------------------o | | | Ef = u v (du)(dv) | | | | + u (v) (du) dv | | | | + (u) v du (dv) | | | | + (u)(v) du dv | | | o-------------------------------------------------o Figure 2. Enlargement E[uv] : EX -> B
The differential field \(\operatorname{E}[uv]\!\) specifies the changes that need to be made from each point of \(X\!\) in order to reach one of the models of the proposition \(uv,\!\) that is, in order to satisfy the proposition \(uv.\!\)
The field of changes produced by \(\operatorname{D}\!\) on \(uv\!\) is shown in Figure 3.
o-------------------------------------------------o | X | | | | o-------------o o-------------o | | / \ / \ | | / U o V \ | | / /%\ \ | | / /%%%\ \ | | o o%%%%%o o | | | (du)dv |%%%%%| du(dv) | | | | o<--------------|->o<-|-------------->o | | | | |%%^%%| | | | o o%%|%%o o | | \ \%|%/ / | | \ \|/ / | | \ o / | | \ /|\ / | | o-------------o | o-------------o | | | | | | | | v | | o | | du dv | | | o-------------------------------------------------o | f = u v | o-------------------------------------------------o | | | Df = u v ((du)(dv)) | | | | + u (v) (du) dv | | | | + (u) v du (dv) | | | | + (u)(v) du dv | | | o-------------------------------------------------o Figure 3. Difference D[uv] : EX -> B
The differential field \(\operatorname{D}[uv]\!\) specifies the changes that need to be made from each point of \(X\!\) in order to change the value of the proposition \(uv.\!\)
Appendices
Appendix 1
Propositional Forms on Two Variables
Table A1. Propositional Forms on Two Variables
| \(\mathcal{L}_1\) | \(\mathcal{L}_2\) | \(\mathcal{L}_3\) | \(\mathcal{L}_4\) | \(\mathcal{L}_5\) | \(\mathcal{L}_6\) | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Table A2. Propositional Forms on Two Variables
| \(\mathcal{L}_1\) | \(\mathcal{L}_2\) | \(\mathcal{L}_3\) | \(\mathcal{L}_4\) | \(\mathcal{L}_5\) | \(\mathcal{L}_6\) | ||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
\(f_{0}\!\) |
\(f_{0000}\!\) |
0 0 0 0 |
\((~)\!\) |
\(\operatorname{false}\) |
\(1\!\) | ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
\(f_{15}\!\) |
\(f_{1111}\!\) |
1 1 1 1 |
\(((~))\!\) |
\(\operatorname{true}\) |
\(1\!\) |
Table A3. Ef Expanded Over Differential Features
| \(f\!\) |
|
|
|
| |||||||||||||||||||||||||
| \(f_{0}\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
| \(f_{15}\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) | ||||||||||||||||||||||||
| Fixed Point Total : | \(4\!\) | \(4\!\) | \(4\!\) | \(16\!\) | |||||||||||||||||||||||||
Table A4. Df Expanded Over Differential Features
| \(f\!\) | \(\operatorname{D}f|_{\operatorname{d}x\ \operatorname{d}y}\) | \(\operatorname{D}f|_{\operatorname{d}x(\operatorname{d}y)}\) | \(\operatorname{D}f|_{(\operatorname{d}x)\operatorname{d}y}\) | \(\operatorname{D}f|_{(\operatorname{d}x)(\operatorname{d}y)}\) | |||||||||||||||||||||||||
| \(f_{0}\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
| \(f_{15}\!\) | \(((~))\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) |
Table A5. Ef Expanded Over Ordinary Features
| \(f\!\) | \(\operatorname{E}f|_{xy}\) | \(\operatorname{E}f|_{x(y)}\) | \(\operatorname{E}f|_{(x)y}\) | \(\operatorname{E}f|_{(x)(y)}\) | |||||||||||||||||||||||||
| \(f_{0}\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
| \(f_{15}\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) | \(((~))\!\) |
Table A6. Df Expanded Over Ordinary Features
| \(f\!\) | \(\operatorname{D}f|_{xy}\) | \(\operatorname{D}f|_{x(y)}\) | \(\operatorname{D}f|_{(x)y}\) | \(\operatorname{D}f|_{(x)(y)}\) | |||||||||||||||||||||||||
| \(f_{0}\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
|
|
|
|
|
| ||||||||||||||||||||||||
| \(f_{15}\!\) | \(((~))\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) | \((~)\!\) |
Appendix 2
Differential Forms
The actions of the difference operator \(\operatorname{D}\) and the tangent operator \(\operatorname{d}\) on the 16 propositional forms in two variables are shown in the Tables below.
Table A7 expands the resulting differential forms over a logical basis:
\(\{ (\operatorname{d}x)(\operatorname{d}y),\ \operatorname{d}x\,(\operatorname{d}y),\ (\operatorname{d}x)\,\operatorname{d}y,\ \operatorname{d}x\,\operatorname{d}y \}.\)
This set consists of the singular propositions in the first order differential variables, indicating mutually exclusive and exhaustive cells of the tangent universe of discourse. Accordingly, this set of differential propositions may also be referred to as the cell-basis, point-basis, or singular differential basis. In this setting it is frequently convenient to use the following abbreviations:
\(\partial x = \operatorname{d}x\,(\operatorname{d}y)\) and \(\partial y = (\operatorname{d}x)\,\operatorname{d}y.\)
Table A8 expands the resulting differential forms over an algebraic basis:
\(\{ 1,\ \operatorname{d}x,\ \operatorname{d}y,\ \operatorname{d}x\,\operatorname{d}y \}.\)
This set consists of the positive propositions in the first order differential variables, indicating overlapping positive regions of the tangent universe of discourse. Accordingly, this set of differential propositions may also be referred to as the positive differential basis.
Table A7. Differential Forms Expanded on a Logical Basis
| \(f\!\) | \(\operatorname{D}f\) | \(\operatorname{d}f\) | |||||
| \(f_{0}\!\) | \((~)\!\) | \(0\!\) | \(0\!\) | ||||
|
|
|
| ||||
|
|
|
| ||||
|
|
|
| ||||
|
|
|
| ||||
|
|
|
| ||||
| \(f_{15}\!\) | \(((~))\!\) | \(0\!\) | \(0\!\) |
Table A8. Differential Forms Expanded on an Algebraic Basis
| \(f\!\) | \(\operatorname{D}f\) | \(\operatorname{d}f\) | |||||
| \(f_{0}\!\) | \((~)\!\) | \(0\!\) | \(0\!\) | ||||
|
|
|
| ||||
|
|
|
| ||||
|
|
|
| ||||
|
|
|
| ||||
|
|
|
| ||||
| \(f_{15}\!\) | \(((~))\!\) | \(0\!\) | \(0\!\) |
Appendix 3
Table A9. Taylor Series Expansion
|
\(\operatorname{d}f = \) \(\partial_x f \cdot \operatorname{d}x\ +\ \partial_y f \cdot \operatorname{d}y\) |
\(\operatorname{d}^2 f = \) \(\partial_{xy} f \cdot \operatorname{d}x\, \operatorname{d}y\) |
\(\operatorname{d}f|_{x\, y}\!\) | \(\operatorname{d}f|_{x\, (y)}\!\) | \(\operatorname{d}f|_{(x)\, y}\!\) | \(\operatorname{d}f|_{(x)(y)}\!\) | ||||||||
| \(f_0\!\) | \(0\!\) | \(0\!\) | \(0\!\) | \(0\!\) | \(0\!\) | \(0\!\) | |||||||
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
| |||||||
| \(f_{15}\!\) | \(0\!\) | \(0\!\) | \(0\!\) | \(0\!\) | \(0\!\) | \(0\!\) |
Table A10. Partial Differentials and Relative Differentials
| \(f\!\) | \(\frac{\partial f}{\partial x}\) | \(\frac{\partial f}{\partial y}\) |
\(\operatorname{d}f =\) \(\partial_x f \cdot \operatorname{d}x\ +\ \partial_y f \cdot \operatorname{d}y\) |
\(\left. \frac{\partial x}{\partial y} \right| f\) | \(\left. \frac{\partial y}{\partial x} \right| f\) | ||||||||
| \(f_0\!\) | \((~)\!\) | \(0\!\) | \(0\!\) | \(0\!\) | \(0\!\) | \(0\!\) | |||||||
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
| |||||||
| \(f_{15}\!\) | \(((~))\!\) | \(0\!\) | \(0\!\) | \(0\!\) | \(0\!\) | \(0\!\) |
Appendix 4
Table A11. Detail of Calculation for the Difference Map
|
\(\begin{array}{cr} & \operatorname{E}f|_{\operatorname{d}x\ \operatorname{d}y} \\ + & f|_{\operatorname{d}x\ \operatorname{d}y} \\ = & \operatorname{D}f|_{\operatorname{d}x\ \operatorname{d}y} \\ \end{array}\) |
\(\begin{array}{cr} & \operatorname{E}f|_{\operatorname{d}x\ (\operatorname{d}y)} \\ + & f|_{\operatorname{d}x\ (\operatorname{d}y)} \\ = & \operatorname{D}f|_{\operatorname{d}x\ (\operatorname{d}y)} \\ \end{array}\) |
\(\begin{array}{cr} & \operatorname{E}f|_{(\operatorname{d}x)\ \operatorname{d}y} \\ + & f|_{(\operatorname{d}x)\ \operatorname{d}y} \\ = & \operatorname{D}f|_{(\operatorname{d}x)\ \operatorname{d}y} \\ \end{array}\) |
\(\begin{array}{cr} & \operatorname{E}f|_{(\operatorname{d}x)(\operatorname{d}y)} \\ + & f|_{(\operatorname{d}x)(\operatorname{d}y)} \\ = & \operatorname{D}f|_{(\operatorname{d}x)(\operatorname{d}y)} \\ \end{array}\) | |||||||||||||||||||||
| \(f_{0}\!\) | \(0 + 0 = 0\!\) | \(0 + 0 = 0\!\) | \(0 + 0 = 0\!\) | \(0 + 0 = 0\!\) | ||||||||||||||||||||
|
|
|
|
| ||||||||||||||||||||
|
|
|
|
| ||||||||||||||||||||
|
|
|
|
| ||||||||||||||||||||
|
|
|
|
| ||||||||||||||||||||
|
|
|
|
| ||||||||||||||||||||
| \(f_{15}\!\) | \(1 + 1 = 0\!\) | \(1 + 1 = 0\!\) | \(1 + 1 = 0\!\) | \(1 + 1 = 0\!\) |
References
- Ashby, William Ross (1956/1964), An Introduction to Cybernetics, Chapman and Hall, London, UK, 1956. Reprinted, Methuen and Company, London, UK, 1964.
- Awbrey, J., and Awbrey, S. (1989), "Theme One : A Program of Inquiry", Unpublished Manuscript, 09 Aug 1989. Microsoft Word Document.
- Edelman, Gerald M. (1988), Topobiology : An Introduction to Molecular Embryology, Basic Books, New York, NY.
- Leibniz, Gottfried Wilhelm, Freiherr von, Theodicy : Essays on the Goodness of God, The Freedom of Man, and The Origin of Evil, Austin Farrer (ed.), E.M. Huggard (trans.), based on C.J. Gerhardt (ed.), Collected Philosophical Works, 1875–1890, Routledge and Kegan Paul, London, UK, 1951. Reprinted, Open Court, La Salle, IL, 1985.
- McClelland, James L., and Rumelhart, David E. (1988), Explorations in Parallel Distributed Processing : A Handbook of Models, Programs, and Exercises, MIT Press, Cambridge, MA.
- Adaptive Systems
- Artificial Intelligence
- Combinatorics
- Computer Science
- Cybernetics
- Differential Logic
- Discrete Systems
- Dynamical Systems
- Formal Languages
- Formal Sciences
- Formal Systems
- Graph Theory
- Group Theory
- Inquiry
- Linguistics
- Logic
- Mathematics
- Mathematical Systems Theory
- Science
- Semiotics
- Philosophy
- Systems Science
- Visualization