Difference between revisions of "Directory:Jon Awbrey/Papers/Differential Analytic Turing Automata"
Jon Awbrey (talk | contribs) (update) |
Jon Awbrey (talk | contribs) (update) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 117: | Line 117: | ||
3 & 1 & 0 & 0 \\ | 3 & 1 & 0 & 0 \\ | ||
4 & 1 & 0 & 0 \\ | 4 & 1 & 0 & 0 \\ | ||
| − | 5 & {}^ | + | 5 & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel |
\end{array}</math> | \end{array}</math> | ||
|} | |} | ||
| Line 134: | Line 134: | ||
3 & 1 & 0 & 0 \\ | 3 & 1 & 0 & 0 \\ | ||
4 & 1 & 0 & 0 \\ | 4 & 1 & 0 & 0 \\ | ||
| − | 5 & {}^ | + | 5 & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel |
\end{array}</math> | \end{array}</math> | ||
|} | |} | ||
| Line 247: | Line 247: | ||
|+ style="height:30px" | <math>\text{Table 1.} ~~ \text{Syntax and Semantics of a Calculus for Propositional Logic}\!</math> | |+ style="height:30px" | <math>\text{Table 1.} ~~ \text{Syntax and Semantics of a Calculus for Propositional Logic}\!</math> | ||
|- style="height:40px; background:ghostwhite" | |- style="height:40px; background:ghostwhite" | ||
| + | | <math>\text{Graph}\!</math> | ||
| <math>\text{Expression}~\!</math> | | <math>\text{Expression}~\!</math> | ||
| <math>\text{Interpretation}\!</math> | | <math>\text{Interpretation}\!</math> | ||
| <math>\text{Other Notations}\!</math> | | <math>\text{Other Notations}\!</math> | ||
|- | |- | ||
| − | | | + | | height="100px" | [[Image:Cactus Node Big Fat.jpg|20px]] |
| − | | <math>\ | + | | <math>~</math> |
| + | | <math>\operatorname{true}</math> | ||
| <math>1\!</math> | | <math>1\!</math> | ||
|- | |- | ||
| − | | <math>\texttt{(~)} | + | | height="100px" | [[Image:Cactus Spike Big Fat.jpg|20px]] |
| − | | <math>\ | + | | <math>\texttt{(~)}</math> |
| + | | <math>\operatorname{false}</math> | ||
| <math>0\!</math> | | <math>0\!</math> | ||
|- | |- | ||
| − | | <math> | + | | height="100px" | [[Image:Cactus A Big.jpg|20px]] |
| − | | <math> | + | | <math>a\!</math> |
| − | | <math> | + | | <math>a\!</math> |
| + | | <math>a\!</math> | ||
|- | |- | ||
| − | | <math>\texttt{(} | + | | height="120px" | [[Image:Cactus (A) Big.jpg|20px]] |
| − | | <math>\ | + | | <math>\texttt{(} a \texttt{)}~</math> |
| − | | | + | | <math>\operatorname{not}~ a</math> |
| − | <math>\ | + | | <math>\lnot a \quad \bar{a} \quad \tilde{a} \quad a^\prime</math> |
| − | |||
| − | |||
| − | \tilde{ | ||
| − | \\ | ||
| − | |||
| − | |||
|- | |- | ||
| − | | <math> | + | | height="100px" | [[Image:Cactus ABC Big.jpg|50px]] |
| − | | <math> | + | | <math>a ~ b ~ c</math> |
| − | | <math> | + | | <math>a ~\operatorname{and}~ b ~\operatorname{and}~ c</math> |
| + | | <math>a \land b \land c</math> | ||
|- | |- | ||
| − | | <math>\texttt{((} | + | | height="160px" | [[Image:Cactus ((A)(B)(C)) Big.jpg|65px]] |
| − | | <math> | + | | <math>\texttt{((} a \texttt{)(} b \texttt{)(} c \texttt{))}</math> |
| − | | <math> | + | | <math>a ~\operatorname{or}~ b ~\operatorname{or}~ c</math> |
| + | | <math>a \lor b \lor c</math> | ||
|- | |- | ||
| − | | <math>\texttt{(} | + | | height="120px" | [[Image:Cactus (A(B)) Big.jpg|60px]] |
| + | | <math>\texttt{(} a \texttt{(} b \texttt{))}</math> | ||
| | | | ||
<math>\begin{matrix} | <math>\begin{matrix} | ||
| − | + | a ~\operatorname{implies}~ b | |
| − | \\ | + | \\[6pt] |
| − | \ | + | \operatorname{if}~ a ~\operatorname{then}~ b |
\end{matrix}</math> | \end{matrix}</math> | ||
| − | | <math> | + | | <math>a \Rightarrow b</math> |
|- | |- | ||
| − | | <math>\texttt{(} | + | | height="120px" | [[Image:Cactus (A,B) Big ISW.jpg|65px]] |
| + | | <math>\texttt{(} a \texttt{,} b \texttt{)}</math> | ||
| | | | ||
<math>\begin{matrix} | <math>\begin{matrix} | ||
| − | + | a ~\operatorname{not~equal~to}~ b | |
| − | \\ | + | \\[6pt] |
| − | + | a ~\operatorname{exclusive~or}~ b | |
\end{matrix}</math> | \end{matrix}</math> | ||
| | | | ||
<math>\begin{matrix} | <math>\begin{matrix} | ||
| − | + | a \neq b | |
| − | \\ | + | \\[6pt] |
| − | + | a + b | |
\end{matrix}</math> | \end{matrix}</math> | ||
|- | |- | ||
| − | | <math>\texttt{((} | + | | height="160px" | [[Image:Cactus ((A,B)) Big.jpg|65px]] |
| + | | <math>\texttt{((} a \texttt{,} b \texttt{))}</math> | ||
| | | | ||
<math>\begin{matrix} | <math>\begin{matrix} | ||
| − | + | a ~\operatorname{is~equal~to}~ b | |
| − | \\ | + | \\[6pt] |
| − | + | a ~\operatorname{if~and~only~if}~ b | |
\end{matrix}</math> | \end{matrix}</math> | ||
| | | | ||
<math>\begin{matrix} | <math>\begin{matrix} | ||
| − | + | a = b | |
| − | \\ | + | \\[6pt] |
| − | + | a \Leftrightarrow b | |
\end{matrix}</math> | \end{matrix}</math> | ||
|- | |- | ||
| − | | <math>\texttt{(} | + | | height="120px" | [[Image:Cactus (A,B,C) Big.jpg|65px]] |
| + | | <math>\texttt{(} a \texttt{,} b \texttt{,} c \texttt{)}</math> | ||
| | | | ||
<math>\begin{matrix} | <math>\begin{matrix} | ||
| − | \ | + | \operatorname{just~one~of} |
\\ | \\ | ||
| − | + | a, b, c | |
\\ | \\ | ||
| − | \ | + | \operatorname{is~false}. |
\end{matrix}</math> | \end{matrix}</math> | ||
| | | | ||
<math>\begin{matrix} | <math>\begin{matrix} | ||
| − | + | & \bar{a} ~ b ~ c | |
\\ | \\ | ||
| − | + | \lor & a ~ \bar{b} ~ c | |
\\ | \\ | ||
| − | + | \lor & a ~ b ~ \bar{c} | |
\end{matrix}</math> | \end{matrix}</math> | ||
|- | |- | ||
| − | | <math>\texttt{((} | + | | height="160px" | [[Image:Cactus ((A),(B),(C)) Big.jpg|65px]] |
| + | | <math>\texttt{((} a \texttt{),(} b \texttt{),(} c \texttt{))}</math> | ||
| | | | ||
<math>\begin{matrix} | <math>\begin{matrix} | ||
| − | \ | + | \operatorname{just~one~of} |
\\ | \\ | ||
| − | + | a, b, c | |
\\ | \\ | ||
| − | \ | + | \operatorname{is~true}. |
| − | \\ | + | \\[6pt] |
| − | + | \operatorname{partition~all} | |
| − | |||
| − | \ | ||
\\ | \\ | ||
| − | \ | + | \operatorname{into}~ a, b, c. |
\end{matrix}</math> | \end{matrix}</math> | ||
| | | | ||
<math>\begin{matrix} | <math>\begin{matrix} | ||
| − | + | & a ~ \bar{b} ~ \bar{c} | |
\\ | \\ | ||
| − | + | \lor & \bar{a} ~ b ~ \bar{c} | |
\\ | \\ | ||
| − | + | \lor & \bar{a} ~ \bar{b} ~ c | |
\end{matrix}</math> | \end{matrix}</math> | ||
|- | |- | ||
| + | | height="160px" | [[Image:Cactus (A,(B,C)) Big.jpg|90px]] | ||
| + | | <math>\texttt{(} a \texttt{,(} b \texttt{,} c \texttt{))}</math> | ||
| | | | ||
<math>\begin{matrix} | <math>\begin{matrix} | ||
| − | \ | + | \operatorname{oddly~many~of} |
\\ | \\ | ||
| − | + | a, b, c | |
\\ | \\ | ||
| − | \ | + | \operatorname{are~true}. |
| − | \end{matrix} | + | \end{matrix}</math> |
| | | | ||
| − | + | <p><math>a + b + c\!</math></p> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | <p><math> | ||
<br> | <br> | ||
<p><math>\begin{matrix} | <p><math>\begin{matrix} | ||
| − | + | & a ~ b ~ c | |
\\ | \\ | ||
| − | + | \lor & a ~ \bar{b} ~ \bar{c} | |
\\ | \\ | ||
| − | + | \lor & \bar{a} ~ b ~ \bar{c} | |
\\ | \\ | ||
| − | + | \lor & \bar{a} ~ \bar{b} ~ c | |
| − | \end{matrix} | + | \end{matrix}</math></p> |
|- | |- | ||
| − | | <math>\texttt{(} | + | | height="160px" | [[Image:Cactus (X,(A),(B),(C)) Big.jpg|90px]] |
| + | | <math>\texttt{(} x \texttt{,(} a \texttt{),(} b \texttt{),(} c \texttt{))}</math> | ||
| | | | ||
<math>\begin{matrix} | <math>\begin{matrix} | ||
| − | \ | + | \operatorname{partition}~ x |
\\ | \\ | ||
| − | \ | + | \operatorname{into}~ a, b, c. |
| − | \\ | + | \\[6pt] |
| − | + | \operatorname{genus}~ x ~\operatorname{comprises} | |
\\ | \\ | ||
| − | \ | + | \operatorname{species}~ a, b, c. |
| − | |||
| − | |||
\end{matrix}</math> | \end{matrix}</math> | ||
| | | | ||
<math>\begin{matrix} | <math>\begin{matrix} | ||
| − | + | & \bar{x} ~ \bar{a} ~ \bar{b} ~ \bar{c} | |
\\ | \\ | ||
| − | + | \lor & x ~ a ~ \bar{b} ~ \bar{c} | |
\\ | \\ | ||
| − | + | \lor & x ~ \bar{a} ~ b ~ \bar{c} | |
\\ | \\ | ||
| − | + | \lor & x ~ \bar{a} ~ \bar{b} ~ c | |
\end{matrix}</math> | \end{matrix}</math> | ||
|} | |} | ||
| Line 763: | Line 759: | ||
A sketch of this work is presented in the following series of Figures, where each logical proposition is expanded over the basic cells <math>uv, u \texttt{(} v \texttt{)}, \texttt{(} u \texttt{)} v, \texttt{(} u \texttt{)(} v \texttt{)}\!</math> of the 2-dimensional universe of discourse <math>U^\bullet = [u, v].\!</math> | A sketch of this work is presented in the following series of Figures, where each logical proposition is expanded over the basic cells <math>uv, u \texttt{(} v \texttt{)}, \texttt{(} u \texttt{)} v, \texttt{(} u \texttt{)(} v \texttt{)}\!</math> of the 2-dimensional universe of discourse <math>U^\bullet = [u, v].\!</math> | ||
| − | ===Computation Summary | + | ===Computation Summary for Logical Disjunction=== |
| − | The venn diagram in Figure 1.1 shows how the proposition <math>f = \texttt{((u)(v))}</math> can be expanded over the universe of discourse <math>[u, v]\!</math> to produce a logically equivalent exclusive disjunction, namely, <math>\texttt{ | + | The venn diagram in Figure 1.1 shows how the proposition <math>f = \texttt{((} u \texttt{)(} v \texttt{))}\!</math> can be expanded over the universe of discourse <math>[u, v]\!</math> to produce a logically equivalent exclusive disjunction, namely, <math>uv + u \texttt{(} v \texttt{)} + \texttt{(} u \texttt{)} v.\!</math> |
{| align="center" border="0" cellpadding="10" | {| align="center" border="0" cellpadding="10" | ||
| Line 811: | Line 807: | ||
|} | |} | ||
| − | Figure 1.2 expands <math>\mathrm{E}f = \texttt{((u + | + | Figure 1.2 expands <math>\mathrm{E}f = \texttt{((} u + \mathrm{d}u \texttt{)(} v + \mathrm{d}v \texttt{))}\!</math> over <math>[u, v]\!</math> to give: |
| − | {| align="center" cellpadding="8" | + | {| align="center" cellpadding="8" style="text-align:center; width:100%" |
| − | | <math>\texttt{uv | + | | |
| + | <math>\begin{matrix} | ||
| + | \mathrm{E}\texttt{((} u \texttt{)(} v \texttt{))} | ||
| + | & = & uv \cdot \texttt{(} \mathrm{d}u ~ \mathrm{d}v \texttt{)} | ||
| + | & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{))} | ||
| + | & + & \texttt{(} u \texttt{)} v \cdot \texttt{((} \mathrm{d}u \texttt{)} \mathrm{d}v \texttt{)} | ||
| + | & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} | ||
| + | \end{matrix}</math> | ||
|} | |} | ||
| Line 861: | Line 864: | ||
|} | |} | ||
| − | Figure 1.3 expands <math>\mathrm{D}f = f + \mathrm{E}f</math> over <math>[u, v]\!</math> to produce: | + | Figure 1.3 expands <math>\mathrm{D}f = f + \mathrm{E}f\!</math> over <math>[u, v]\!</math> to produce: |
| − | {| align="center" cellpadding="8" | + | {| align="center" cellpadding="8" style="text-align:center; width:100%" |
| − | | <math>\texttt{uv~ | + | | |
| + | <math>\begin{matrix} | ||
| + | \mathrm{D}\texttt{((} u \texttt{)(} v \texttt{))} | ||
| + | & = & uv \cdot \mathrm{d}u ~ \mathrm{d}v | ||
| + | & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} | ||
| + | & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v | ||
| + | & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} | ||
| + | \end{matrix}</math> | ||
|} | |} | ||
| Line 913: | Line 923: | ||
I'll break this here in case anyone wants to try and do the work for <math>g\!</math> on their own. | I'll break this here in case anyone wants to try and do the work for <math>g\!</math> on their own. | ||
| − | ===Computation Summary | + | ===Computation Summary for Logical Equality=== |
| − | The venn diagram in Figure 2.1 shows how the proposition <math>g = \texttt{((u,~v))}</math> can be expanded over the universe of discourse <math>[u, v]\!</math> to produce a logically equivalent exclusive disjunction, namely, <math>\texttt{ | + | The venn diagram in Figure 2.1 shows how the proposition <math>g = \texttt{((} u \texttt{,~} v \texttt{))}\!</math> can be expanded over the universe of discourse <math>[u, v]\!</math> to produce a logically equivalent exclusive disjunction, namely, <math>uv + \texttt{(} u \texttt{)(} v \texttt{)}.\!</math> |
{| align="center" border="0" cellpadding="10" | {| align="center" border="0" cellpadding="10" | ||
| Line 961: | Line 971: | ||
|} | |} | ||
| − | Figure 2.2 expands <math>\mathrm{E}g = \texttt{((u + | + | Figure 2.2 expands <math>\mathrm{E}g = \texttt{((} u + \mathrm{d}u \texttt{,~} v + \mathrm{d}v \texttt{))}\!</math> over <math>[u, v]\!</math> to give: |
| − | {| align="center" cellpadding="8" | + | {| align="center" cellpadding="8" style="text-align:center; width:100%" |
| − | | <math>\texttt{uv | + | | |
| + | <math>\begin{matrix} | ||
| + | \mathrm{E}\texttt{((} u \texttt{,~} v \texttt{))} | ||
| + | & = & uv \cdot \texttt{((} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{))} | ||
| + | & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} | ||
| + | & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} | ||
| + | & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{))} | ||
| + | \end{matrix}</math> | ||
|} | |} | ||
| Line 1,011: | Line 1,028: | ||
|} | |} | ||
| − | Figure 2.3 expands <math>\mathrm{D}g = g + \mathrm{E}g</math> over <math>[u, v]\!</math> to yield the form: | + | Figure 2.3 expands <math>\mathrm{D}g = g + \mathrm{E}g\!</math> over <math>[u, v]\!</math> to yield the form: |
| − | {| align="center" cellpadding="8" | + | {| align="center" cellpadding="8" style="text-align:center; width:100%" |
| − | | <math>\texttt{uv | + | | |
| + | <math>\begin{matrix} | ||
| + | \mathrm{D}\texttt{((} u \texttt{,~} v \texttt{))} | ||
| + | & = & uv \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} | ||
| + | & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} | ||
| + | & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} | ||
| + | & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} | ||
| + | \end{matrix}</math> | ||
|} | |} | ||
| Line 1,082: | Line 1,106: | ||
| | | | ||
<math>\begin{array}{lllll} | <math>\begin{array}{lllll} | ||
| − | F & = & (f, g) & = & ( ~\texttt{((u)(v))}~ , ~\texttt{((u,~v))}~ ) | + | F |
| + | & = & (f, g) | ||
| + | & = & ( ~ \texttt{((} u \texttt{)(} v \texttt{))} ~,~ \texttt{((} u \texttt{,~} v \texttt{))} ~ ) | ||
\end{array}</math> | \end{array}</math> | ||
|} | |} | ||
| Line 1,088: | Line 1,114: | ||
To speed things along, I will skip a mass of motivating discussion and just exhibit the simplest form of a differential <math>\mathrm{d}F\!</math> for the current example of a logical transformation <math>F,\!</math> after which the majority of the easiest questions will have been answered in visually intuitive terms. | To speed things along, I will skip a mass of motivating discussion and just exhibit the simplest form of a differential <math>\mathrm{d}F\!</math> for the current example of a logical transformation <math>F,\!</math> after which the majority of the easiest questions will have been answered in visually intuitive terms. | ||
| − | For <math>F = (f, g)\!</math> we have <math>\mathrm{d}F = (\mathrm{d}f, \mathrm{d}g),</math> and so we can proceed componentwise, patching the pieces back together at the end. | + | For <math>F = (f, g)\!</math> we have <math>\mathrm{d}F = (\mathrm{d}f, \mathrm{d}g),\!</math> and so we can proceed componentwise, patching the pieces back together at the end. |
We have prepared the ground already by computing these terms: | We have prepared the ground already by computing these terms: | ||
| Line 1,095: | Line 1,121: | ||
| | | | ||
<math>\begin{array}{lll} | <math>\begin{array}{lll} | ||
| − | \mathrm{E}f & = & \texttt{(( u + | + | \mathrm{E}f & = & \texttt{((} u + \mathrm{d}u \texttt{)(} v + \mathrm{d}v \texttt{))} |
| − | \\ | + | \\[8pt] |
| − | \mathrm{E}g & = & \texttt{(( u + | + | \mathrm{E}g & = & \texttt{((} u + \mathrm{d}u \texttt{,~} v + \mathrm{d}v \texttt{))} |
| − | \\ | + | \\[8pt] |
| − | \mathrm{D}f & = & \texttt{((u)(v)) ~+~ (( u + | + | \mathrm{D}f & = & \texttt{((} u \texttt{)(} v \texttt{))} ~+~ \texttt{((} u + \mathrm{d}u \texttt{)(} v + \mathrm{d}v \texttt{))} |
| − | \\ | + | \\[8pt] |
| − | \mathrm{D}g & = & \texttt{((u,~v)) ~+~ (( u + | + | \mathrm{D}g & = & \texttt{((} u \texttt{,~} v \texttt{))} ~+~ \texttt{((} u + \mathrm{d}u \texttt{,~} v + \mathrm{d}v \texttt{))} |
| − | \end{array} | + | \end{array}</math> |
|} | |} | ||
| − | As a matter of fact, computing the symmetric differences <math>\mathrm{D}f = f + \mathrm{E}f</math> and <math>\mathrm{D}g = g + \mathrm{E}g</math> has already taken care of the ''localizing'' part of the task by subtracting out the forms of <math>f\!</math> and <math>g\!</math> from the forms of <math>\mathrm{E}f</math> and <math>\mathrm{E}g,</math> respectively. Thus all we have left to do is to decide what linear propositions best approximate the difference maps <math>\mathrm{D}f</math> and <math>\mathrm{D}g,</math> respectively. | + | As a matter of fact, computing the symmetric differences <math>\mathrm{D}f = f + \mathrm{E}f\!</math> and <math>\mathrm{D}g = g + \mathrm{E}g\!</math> has already taken care of the ''localizing'' part of the task by subtracting out the forms of <math>f\!</math> and <math>g\!</math> from the forms of <math>\mathrm{E}f\!</math> and <math>\mathrm{E}g,\!</math> respectively. Thus all we have left to do is to decide what linear propositions best approximate the difference maps <math>{\mathrm{D}f}\!</math> and <math>{\mathrm{D}g},\!</math> respectively. |
This raises the question: What is a linear proposition? | This raises the question: What is a linear proposition? | ||
| − | The answer that makes the most sense in this context is this: A proposition is just a boolean-valued function, so a linear proposition is a linear function into the boolean space <math>\mathbb{B}.</math> | + | The answer that makes the most sense in this context is this: A proposition is just a boolean-valued function, so a linear proposition is a linear function into the boolean space <math>\mathbb{B}.\!</math> |
| − | In particular, the linear functions that we want will be linear functions in the differential variables <math> | + | In particular, the linear functions that we want will be linear functions in the differential variables <math>\mathrm{d}u\!</math> and <math>\mathrm{d}v.\!</math> |
| − | As it turns out, there are just four linear propositions in the associated ''differential universe'' <math>\mathrm{d}U^\bullet = [ | + | As it turns out, there are just four linear propositions in the associated ''differential universe'' <math>\mathrm{d}U^\bullet = [\mathrm{d}u, \mathrm{d}v].\!</math> These are the propositions that are commonly denoted: <math>{0, ~\mathrm{d}u, ~\mathrm{d}v, ~\mathrm{d}u + \mathrm{d}v},\!</math> in other words: <math>\texttt{(~)}, ~\mathrm{d}u, ~\mathrm{d}v, ~\texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)}.\!</math> |
==Notions of Approximation== | ==Notions of Approximation== | ||
| Line 1,140: | Line 1,166: | ||
Justifying a notion of approximation is a little more involved in general, and especially in these discrete logical spaces, than it would be expedient for people in a hurry to tangle with right now. I will just say that there are ''naive'' or ''obvious'' notions and there are ''sophisticated'' or ''subtle'' notions that we might choose among. The later would engage us in trying to construct proper logical analogues of Lie derivatives, and so let's save that for when we have become subtle or sophisticated or both. Against or toward that day, as you wish, let's begin with an option in plain view. | Justifying a notion of approximation is a little more involved in general, and especially in these discrete logical spaces, than it would be expedient for people in a hurry to tangle with right now. I will just say that there are ''naive'' or ''obvious'' notions and there are ''sophisticated'' or ''subtle'' notions that we might choose among. The later would engage us in trying to construct proper logical analogues of Lie derivatives, and so let's save that for when we have become subtle or sophisticated or both. Against or toward that day, as you wish, let's begin with an option in plain view. | ||
| − | Figure 1.4 illustrates one way of ranging over the cells of the underlying universe <math>U^\bullet = [u, v]\!</math> and selecting at each cell the linear proposition in <math>\mathrm{d}U^\bullet = [ | + | Figure 1.4 illustrates one way of ranging over the cells of the underlying universe <math>U^\bullet = [u, v]\!</math> and selecting at each cell the linear proposition in <math>\mathrm{d}U^\bullet = [\mathrm{d}u, \mathrm{d}v]\!</math> that best approximates the patch of the difference map <math>{\mathrm{D}f}\!</math> that is located there, yielding the following formula for the differential <math>\mathrm{d}f.\!</math> |
| − | {| align="center" cellpadding="8" | + | {| align="center" cellpadding="8" style="text-align:center; width:100%" |
| − | | <math>\mathrm{d}f | + | | |
| + | <math>\begin{array}{*{11}{c}} | ||
| + | \mathrm{d}f | ||
| + | & = & \mathrm{d}\texttt{((} u \texttt{)(} v \texttt{))} | ||
| + | & = & uv \cdot 0 | ||
| + | & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u | ||
| + | & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}v | ||
| + | & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} | ||
| + | \end{array}</math> | ||
|} | |} | ||
| Line 1,190: | Line 1,224: | ||
|} | |} | ||
| − | Figure 2.4 illustrates one way of ranging over the cells of the underlying universe <math>U^\bullet = [u, v]\!</math> and selecting at each cell the linear proposition in <math>\mathrm{d}U^\bullet = [du, dv]</math> that best approximates the patch of the difference map <math>\mathrm{D}g</math> that is located there, yielding the following formula for the differential <math>\mathrm{d}g.\!</math> | + | Figure 2.4 illustrates one way of ranging over the cells of the underlying universe <math>U^\bullet = [u, v]\!</math> and selecting at each cell the linear proposition in <math>\mathrm{d}U^\bullet = [du, dv]\!</math> that best approximates the patch of the difference map <math>\mathrm{D}g\!</math> that is located there, yielding the following formula for the differential <math>\mathrm{d}g.\!</math> |
| − | {| align="center" cellpadding="8" | + | {| align="center" cellpadding="8" style="text-align:center; width:100%" |
| − | | <math>\mathrm{d}g | + | | |
| + | <math>\begin{array}{*{11}{c}} | ||
| + | \mathrm{d}g | ||
| + | & = & \mathrm{d}\texttt{((} u \texttt{,} v \texttt{))} | ||
| + | & = & uv \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} | ||
| + | & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} | ||
| + | & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} | ||
| + | & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,} \mathrm{d}v \texttt{)} | ||
| + | \end{array}</math> | ||
|} | |} | ||
| Line 1,240: | Line 1,282: | ||
|} | |} | ||
| − | Well, <math>g,\!</math> that was easy, seeing as how <math>\mathrm{D}g</math> is already linear at each locus, <math>\mathrm{d}g = \mathrm{D}g.</math> | + | Well, <math>g,\!</math> that was easy, seeing as how <math>\mathrm{D}g\!</math> is already linear at each locus, <math>\mathrm{d}g = \mathrm{D}g.\!</math> |
==Analytic Series== | ==Analytic Series== | ||
| − | We have been conducting the differential analysis of the logical transformation <math>F : [u, v] \mapsto [u, v]</math> defined as <math>F : (u, v) \mapsto ( ~\texttt{((u)(v))}~, ~\texttt{((u, v))}~ ),</math> and this means starting with the extended transformation <math>\mathrm{E}F : [u, v, | + | We have been conducting the differential analysis of the logical transformation <math>F : [u, v] \mapsto [u, v]\!</math> defined as <math>F : (u, v) \mapsto ( ~ \texttt{((} u \texttt{)(} v \texttt{))} ~,~ \texttt{((} u \texttt{,~} v \texttt{))} ~ ),\!</math> and this means starting with the extended transformation <math>\mathrm{E}F : [u, v, \mathrm{d}u, \mathrm{d}v] \to [u, v, \mathrm{d}u, \mathrm{d}v]\!</math> and breaking it into an analytic series, <math>\mathrm{E}F = F + \mathrm{d}F + \mathrm{d}^2 F + \ldots,\!</math> and so on until there is nothing left to analyze any further. |
| − | so on until there is nothing left to analyze any further. | ||
As a general rule, one proceeds by way of the following stages: | As a general rule, one proceeds by way of the following stages: | ||
| Line 1,251: | Line 1,292: | ||
{| align="center" cellpadding="8" width="90%" | {| align="center" cellpadding="8" width="90%" | ||
| | | | ||
| − | <math>\begin{array}{ | + | <math>\begin{array}{*{6}{l}} |
| − | 1. & \mathrm{E}F | + | 1. & \mathrm{E}F |
| + | & = & \mathrm{d}^0 F | ||
| + | & + & \mathrm{r}^0 F | ||
\\ | \\ | ||
| − | 2. & \mathrm{r}^0 F & = & \mathrm{d}^1 F & + & \mathrm{r}^1 F | + | 2. & \mathrm{r}^0 F |
| + | & = & \mathrm{d}^1 F | ||
| + | & + & \mathrm{r}^1 F | ||
\\ | \\ | ||
| − | 3. & \mathrm{r}^1 F & = & \mathrm{d}^2 F & + & \mathrm{r}^2 F | + | 3. & \mathrm{r}^1 F |
| + | & = & \mathrm{d}^2 F | ||
| + | & + & \mathrm{r}^2 F | ||
\\ | \\ | ||
4. & \ldots | 4. & \ldots | ||
| Line 1,262: | Line 1,309: | ||
|} | |} | ||
| − | In our analysis of the transformation <math>F,\!</math> we carried out Step 1 in the more familiar form <math>\mathrm{E}F = F + \mathrm{D}F | + | In our analysis of the transformation <math>F,\!</math> we carried out Step 1 in the more familiar form <math>\mathrm{E}F = F + \mathrm{D}F\!</math> and we have just reached Step 2 in the form <math>\mathrm{D}F = \mathrm{d}F + \mathrm{r}F,\!</math> where <math>\mathrm{r}F\!</math> is the residual term that remains for us to examine next. |
| − | ''' | + | '''Note.''' I'm am trying to give quick overview here, and this forces me to omit many picky details. The picky reader may wish to consult the more detailed presentation of this material at the following locations: |
| − | + | :* [[Differential Logic and Dynamic Systems 2.0|Differential Logic and Dynamic Systems]] | |
| − | : [[Differential Logic and Dynamic Systems 2.0#The Secant Operator : E|The Secant Operator]] | + | ::* [[Differential Logic and Dynamic Systems 2.0#The Secant Operator : E|The Secant Operator]] |
| − | : [[Differential Logic and Dynamic Systems 2.0#Taking Aim at Higher Dimensional Targets|Higher Dimensional Targets]] | + | ::* [[Differential Logic and Dynamic Systems 2.0#Taking Aim at Higher Dimensional Targets|Higher Dimensional Targets]] |
Let's push on with the analysis of the transformation: | Let's push on with the analysis of the transformation: | ||
| Line 1,275: | Line 1,322: | ||
| | | | ||
<math>\begin{matrix} | <math>\begin{matrix} | ||
| − | F & : & (u, v) & \mapsto & (f(u, v), | + | F & : & (u, v) & \mapsto & (f(u, v), g(u, v)) |
| + | & = & ( ~ \texttt{((} u \texttt{)(} v \texttt{))} ~,~ \texttt{((} u \texttt{,~} v \texttt{))} ~) | ||
| + | \end{matrix}</math> | ||
|} | |} | ||
For ease of comparison and computation, I will collect the Figures that we need for the remainder of the work together on one page. | For ease of comparison and computation, I will collect the Figures that we need for the remainder of the work together on one page. | ||
| − | ===Computation Summary | + | ===Computation Summary for Logical Disjunction=== |
| − | Figure 1.1 shows the expansion of <math>f = \texttt{((u)(v))}</math> over <math>[u, v]\!</math> to produce the expression: | + | Figure 1.1 shows the expansion of <math>f = \texttt{((} u \texttt{)(} v \texttt{))}\!</math> over <math>[u, v]\!</math> to produce the expression: |
{| align="center" cellpadding="8" width="90%" | {| align="center" cellpadding="8" width="90%" | ||
| − | | <math>\ | + | | |
| + | <math>\begin{matrix} | ||
| + | uv & + & u \texttt{(} v \texttt{)} & + & \texttt{(} u \texttt{)} v | ||
| + | \end{matrix}</math> | ||
|} | |} | ||
| − | Figure 1.2 shows the expansion of <math>\mathrm{E}f = \texttt{((u + | + | Figure 1.2 shows the expansion of <math>\mathrm{E}f = \texttt{((} u + \mathrm{d}u \texttt{)(} v + \mathrm{d}v \texttt{))}\!</math> over <math>[u, v]\!</math> to produce the expression: |
{| align="center" cellpadding="8" width="90%" | {| align="center" cellpadding="8" width="90%" | ||
| − | | <math>\ | + | | |
| + | <math>\begin{matrix} | ||
| + | uv \cdot \texttt{(} \mathrm{d}u ~ \mathrm{d}v \texttt{)} & + & | ||
| + | u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{))} & + & | ||
| + | \texttt{(} u \texttt{)} v \cdot \texttt{((} \mathrm{d}u \texttt{)} \mathrm{d}v \texttt{)} & + & | ||
| + | \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} | ||
| + | \end{matrix}</math> | ||
|} | |} | ||
| − | <math>\mathrm{E}f</math> tells you what you would have to do, from | + | In general, <math>\mathrm{E}f\!</math> tells you what you would have to do, from wherever you are in the universe <math>[u, v],\!</math> if you want to end up in a place where <math>f\!</math> is true. In this case, where the prevailing proposition <math>f\!</math> is <math>\texttt{((} u \texttt{)(} v \texttt{))},\!</math> the indication <math>uv \cdot \texttt{(} \mathrm{d}u ~ \mathrm{d}v \texttt{)}\!</math> of <math>\mathrm{E}f\!</math> tells you this: If <math>u\!</math> and <math>v\!</math> are both true where you are, then just don't change both <math>u\!</math> and <math>v\!</math> at once, and you will end up in a place where <math>\texttt{((} u \texttt{)(} v \texttt{))}\!</math> is true. |
Figure 1.3 shows the expansion of <math>\mathrm{D}f</math> over <math>[u, v]\!</math> to produce the expression: | Figure 1.3 shows the expansion of <math>\mathrm{D}f</math> over <math>[u, v]\!</math> to produce the expression: | ||
{| align="center" cellpadding="8" width="90%" | {| align="center" cellpadding="8" width="90%" | ||
| − | | <math>\ | + | | |
| + | <math>\begin{matrix} | ||
| + | uv \cdot \mathrm{d}u ~ \mathrm{d}v & + & | ||
| + | u \texttt{(} v \texttt{)} \cdot \mathrm{d}u \texttt{(} \mathrm{d}v \texttt{)} & + & | ||
| + | \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{)} \mathrm{d}v & + & | ||
| + | \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{))} | ||
| + | \end{matrix}</math> | ||
|} | |} | ||
| − | <math>\mathrm{D}f</math> tells you what you would have to do, from | + | In general, <math>{\mathrm{D}f}\!</math> tells you what you would have to do, from wherever you are in the universe <math>[u, v],\!</math> if you want to bring about a change in the value of <math>f,\!</math> that is, if you want to get to a place where the value of <math>f\!</math> is different from what it is where you are. In the present case, where the reigning proposition <math>f\!</math> is <math>\texttt{((} u \texttt{)(} v \texttt{))},\!</math> the term <math>uv \cdot \mathrm{d}u ~ \mathrm{d}v\!</math> of <math>{\mathrm{D}f}\!</math> tells you this: If <math>u\!</math> and <math>v\!</math> are both true where you are, then you would have to change both <math>u\!</math> and <math>v\!</math> in order to reach a place where the value of <math>f\!</math> is different from what it is where you are. |
| − | Figure 1.4 approximates <math>\mathrm{D}f</math> by the linear form <math>\mathrm{d}f</math> that expands over <math>[u, v]\!</math> as follows: | + | Figure 1.4 approximates <math>{\mathrm{D}f}\!</math> by the linear form <math>\mathrm{d}f\!</math> that expands over <math>[u, v]\!</math> as follows: |
{| align="center" cellpadding="8" width="90%" | {| align="center" cellpadding="8" width="90%" | ||
| Line 1,310: | Line 1,374: | ||
<math>\begin{matrix} | <math>\begin{matrix} | ||
\mathrm{d}f | \mathrm{d}f | ||
| − | & = & | + | & = & uv \cdot 0 |
| − | \\ | + | & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u |
| − | & = & & & \texttt{ | + | & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}v |
| + | & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} | ||
| + | \\[8pt] | ||
| + | & = &&& u \texttt{(} v \texttt{)} \cdot \mathrm{d}u | ||
| + | & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}v | ||
| + | & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} | ||
\end{matrix}</math> | \end{matrix}</math> | ||
|} | |} | ||
| − | Figure 1.5 shows what remains of the difference map <math>\mathrm{D}f</math> when the first order linear contribution <math>\mathrm{d}f</math> is removed, namely: | + | Figure 1.5 shows what remains of the difference map <math>{\mathrm{D}f}\!</math> when the first order linear contribution <math>\mathrm{d}f\!</math> is removed, namely: |
{| align="center" cellpadding="8" width="90%" | {| align="center" cellpadding="8" width="90%" | ||
| | | | ||
| − | <math>\begin{ | + | <math>\begin{array}{*{9}{l}} |
\mathrm{r}f | \mathrm{r}f | ||
| − | & = & | + | & = & uv \cdot \mathrm{d}u ~ \mathrm{d}v |
| − | \\ | + | & + & u \texttt{(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v |
| − | & = & \ | + | & + & \texttt{(} u \texttt{)} v \cdot \mathrm{d}u ~ \mathrm{d}v |
| − | \end{ | + | & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \mathrm{d}u ~ \mathrm{d}v |
| + | \\[8pt] | ||
| + | & = & \mathrm{d}u ~ \mathrm{d}v | ||
| + | \end{array}</math> | ||
|} | |} | ||
| Line 1,371: | Line 1,443: | ||
</pre> | </pre> | ||
|} | |} | ||
| − | |||
| − | |||
{| align="center" border="0" cellpadding="10" | {| align="center" border="0" cellpadding="10" | ||
| Line 1,417: | Line 1,487: | ||
</pre> | </pre> | ||
|} | |} | ||
| − | |||
| − | |||
{| align="center" border="0" cellpadding="10" | {| align="center" border="0" cellpadding="10" | ||
| Line 1,463: | Line 1,531: | ||
</pre> | </pre> | ||
|} | |} | ||
| − | |||
| − | |||
{| align="center" border="0" cellpadding="10" | {| align="center" border="0" cellpadding="10" | ||
| Line 1,509: | Line 1,575: | ||
</pre> | </pre> | ||
|} | |} | ||
| − | |||
| − | |||
{| align="center" border="0" cellpadding="10" | {| align="center" border="0" cellpadding="10" | ||
| Line 1,556: | Line 1,620: | ||
|} | |} | ||
| − | ===Computation Summary | + | ===Computation Summary for Logical Equality=== |
| − | Figure 2.1 shows the expansion of <math>g = \texttt{((u, v))}</math> over <math>[u, v]\!</math> to produce the expression: | + | Figure 2.1 shows the expansion of <math>g = \texttt{((} u \texttt{,~} v \texttt{))}\!</math> over <math>[u, v]\!</math> to produce the expression: |
{| align="center" cellpadding="8" width="90%" | {| align="center" cellpadding="8" width="90%" | ||
| − | | <math>\ | + | | |
| + | <math>\begin{matrix} | ||
| + | uv & + & \texttt{(} u \texttt{)(} v \texttt{)} | ||
| + | \end{matrix}</math> | ||
|} | |} | ||
| − | Figure 2.2 shows the expansion of <math>\mathrm{E}g = \texttt{((u + | + | Figure 2.2 shows the expansion of <math>\mathrm{E}g = \texttt{((} u + \mathrm{d}u \texttt{,~} v + \mathrm{d}v \texttt{))}\!</math> over <math>[u, v]\!</math> to produce the expression: |
| − | {| align="center" cellpadding="8" width="90%" | + | {| align="center" cellpadding="8" width="90%" |
| − | | <math>\ | + | | |
| + | <math>\begin{matrix} | ||
| + | uv \cdot \texttt{((} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{))} & + & | ||
| + | u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} & + & | ||
| + | \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} & + & | ||
| + | \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{((} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{))} | ||
| + | \end{matrix}</math> | ||
|} | |} | ||
| − | <math>\mathrm{E}g</math> tells you what you would have to do, from | + | In general, <math>\mathrm{E}g\!</math> tells you what you would have to do, from wherever you are in the universe <math>[u, v],\!</math> if you want to end up in a place where <math>g\!</math> is true. In this case, where the prevailing proposition <math>g\!</math> is <math>\texttt{((} u \texttt{,~} v \texttt{))},\!</math> the component <math>uv \cdot \texttt{((} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{))}\!</math> of <math>\mathrm{E}g\!</math> tells you this: If <math>u\!</math> and <math>v\!</math> are both true where you are, then change either both or neither of <math>u\!</math> and <math>v\!</math> at the same time, and you will attain a place where <math>\texttt{((} u \texttt{,~} v \texttt{))}\!</math> is true. |
| − | Figure 2.3 shows the expansion of <math>\mathrm{D}g</math> over <math>[u, v]\!</math> to produce the expression: | + | Figure 2.3 shows the expansion of <math>\mathrm{D}g\!</math> over <math>[u, v]\!</math> to produce the expression: |
| − | {| align="center" cellpadding="8" width="90%" | + | {| align="center" cellpadding="8" width="90%" |
| − | | <math>\ | + | | |
| + | <math>\begin{matrix} | ||
| + | uv \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} & + & | ||
| + | u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} & + & | ||
| + | \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} & + & | ||
| + | \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} | ||
| + | \end{matrix}</math> | ||
|} | |} | ||
| − | <math>\mathrm{D}g</math> tells you what you would have to do, from | + | In general, <math>\mathrm{D}g\!</math> tells you what you would have to do, from wherever you are in the universe <math>[u, v],\!</math> if you want to bring about a change in the value of <math>g,\!</math> that is, if you want to get to a place where the value of <math>g\!</math> is different from what it is where you are. In the present case, where the ruling proposition <math>g\!</math> is <math>\texttt{((} u \texttt{,~} v \texttt{))},\!</math> the term <math>uv \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)}\!</math> of <math>\mathrm{D}g\!</math> tells you this: If <math>u\!</math> and <math>v\!</math> are both true where you are, then you would have to change one or the other but not both <math>u\!</math> and <math>v\!</math> in order to reach a place where the value of <math>g\!</math> is different from what it is where you are. |
| − | Figure 2.4 approximates <math>\mathrm{D}g</math> by the linear form <math>\mathrm{d}g</math> that expands over <math>[u, v]\!</math> as follows: | + | Figure 2.4 approximates <math>\mathrm{D}g\!</math> by the linear form <math>{\mathrm{d}g}\!</math> that expands over <math>[u, v]\!</math> as follows: |
{| align="center" cellpadding="8" width="90%" | {| align="center" cellpadding="8" width="90%" | ||
| | | | ||
| − | <math>\begin{array}{ | + | <math>\begin{array}{*{9}{l}} |
\mathrm{d}g | \mathrm{d}g | ||
| − | & = & \texttt{ | + | & = & uv \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} |
| − | \\ | + | & + & u \texttt{(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} |
| − | & = & \texttt{( | + | & + & \texttt{(} u \texttt{)} v \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} |
| + | & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} | ||
| + | \\[8pt] | ||
| + | & = & \texttt{(} \mathrm{d}u \texttt{,~} \mathrm{d}v \texttt{)} | ||
\end{array}</math> | \end{array}</math> | ||
|} | |} | ||
| − | Figure 2.5 shows what remains of the difference map <math>\mathrm{D}g</math> when the first order linear contribution <math>\mathrm{d}g</math> is removed, namely: | + | Figure 2.5 shows what remains of the difference map <math>\mathrm{D}g\!</math> when the first order linear contribution <math>{\mathrm{d}g}\!</math> is removed, namely: |
{| align="center" cellpadding="8" width="90%" | {| align="center" cellpadding="8" width="90%" | ||
| | | | ||
| − | <math>\begin{ | + | <math>\begin{array}{*{9}{l}} |
\mathrm{r}g | \mathrm{r}g | ||
| − | & = & | + | & = & uv \cdot 0 |
| − | \\ | + | & + & u \texttt{(} v \texttt{)} \cdot 0 |
| − | & = & | + | & + & \texttt{(} u \texttt{)} v \cdot 0 |
| − | \end{ | + | & + & \texttt{(} u \texttt{)(} v \texttt{)} \cdot 0 |
| + | \\[8pt] | ||
| + | & = & 0 | ||
| + | \end{array}</math> | ||
|} | |} | ||
| Line 1,647: | Line 1,732: | ||
</pre> | </pre> | ||
|} | |} | ||
| − | |||
| − | |||
{| align="center" border="0" cellpadding="10" | {| align="center" border="0" cellpadding="10" | ||
| Line 1,693: | Line 1,776: | ||
</pre> | </pre> | ||
|} | |} | ||
| − | |||
| − | |||
{| align="center" border="0" cellpadding="10" | {| align="center" border="0" cellpadding="10" | ||
| Line 1,739: | Line 1,820: | ||
</pre> | </pre> | ||
|} | |} | ||
| − | |||
| − | |||
{| align="center" border="0" cellpadding="10" | {| align="center" border="0" cellpadding="10" | ||
| Line 1,785: | Line 1,864: | ||
</pre> | </pre> | ||
|} | |} | ||
| − | |||
| − | |||
{| align="center" border="0" cellpadding="10" | {| align="center" border="0" cellpadding="10" | ||
| Line 1,843: | Line 1,920: | ||
==Visualization== | ==Visualization== | ||
| − | In my work on [[Differential Logic and Dynamic Systems 2.0|Differential Logic and Dynamic Systems]], I found it useful to develop several different ways of visualizing logical transformations, indeed, I devised four distinct styles of picture for the job. Thus far in our work on the mapping <math>F : [u, v] \to [u, v],\!</math> we've been making use of what I call the ''areal view'' of the extended universe of discourse, <math>[u, v, | + | In my work on [[Differential Logic and Dynamic Systems 2.0|Differential Logic and Dynamic Systems]], I found it useful to develop several different ways of visualizing logical transformations, indeed, I devised four distinct styles of picture for the job. Thus far in our work on the mapping <math>F : [u, v] \to [u, v],\!</math> we've been making use of what I call the ''areal view'' of the extended universe of discourse, <math>[u, v, \mathrm{d}u, \mathrm{d}v],\!</math> but as the number of dimensions climbs beyond four, it's time to bid this genre adieu and look for a style that can scale a little better. At any rate, before we proceed any further, let's first assemble the information that we have gathered about <math>F\!</math> from several different angles, and see if it can be fitted into a coherent picture of the transformation <math>F : (u, v) \mapsto ( ~ \texttt{((} u \texttt{)(} v \texttt{))} ~,~ \texttt{((} u \texttt{,~} v \texttt{))} ~ ).\!</math> |
In our first crack at the transformation <math>F,\!</math> we simply plotted the state transitions and applied the utterly stock technique of calculating the finite differences. | In our first crack at the transformation <math>F,\!</math> we simply plotted the state transitions and applied the utterly stock technique of calculating the finite differences. | ||
| Line 1,852: | Line 1,929: | ||
| | | | ||
<math>\begin{array}{c|cc|cc|} | <math>\begin{array}{c|cc|cc|} | ||
| − | t & | + | t & u & v & \mathrm{d}u & \mathrm{d}v \\[8pt] |
| − | 0 & | + | 0 & 1 & 1 & 0 & 0 \\ |
| − | 1 & | + | 1 & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel |
\end{array}</math> | \end{array}</math> | ||
|} | |} | ||
| − | A quick inspection of the first Table suggests a rule to cover the case when <math> | + | A quick inspection of the first Table suggests a rule to cover the case when <math>u = v = 1,\!</math> namely, <math>\mathrm{d}u = \mathrm{d}v = 0.\!</math> To put it another way, the Table characterizes Orbit 1 by means of the data: <math>(u, v, \mathrm{d}u, \mathrm{d}v) = (1, 1, 0, 0).\!</math> Another way to convey the same information is by means of the extended proposition: <math>u v \texttt{(} \mathrm{d}u \texttt{)(} \mathrm{d}v \texttt{)}.\!</math> |
{| align="center" cellpadding="8" style="text-align:center" | {| align="center" cellpadding="8" style="text-align:center" | ||
| Line 1,865: | Line 1,942: | ||
| | | | ||
<math>\begin{array}{c|cc|cc|cc|} | <math>\begin{array}{c|cc|cc|cc|} | ||
| − | t & | + | t & u & v & \mathrm{d}u & \mathrm{d}v & \mathrm{d}^2 u & \mathrm{d}^2 v \\[8pt] |
| − | 0 & | + | 0 & 0 & 0 & 0 & 1 & 1 & 0 \\ |
| − | 1 & | + | 1 & 0 & 1 & 1 & 1 & 1 & 1 \\ |
| − | 2 & | + | 2 & 1 & 0 & 0 & 0 & 0 & 0 \\ |
| − | 3 & | + | 3 & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel & {}^\shortparallel |
\end{array}</math> | \end{array}</math> | ||
|} | |} | ||
| − | A more fine combing of the second Table brings to mind a rule that partly covers the remaining cases, that is, <math>\ | + | A more fine combing of the second Table brings to mind a rule that partly covers the remaining cases, that is, <math>\mathrm{d}u = v, ~ \mathrm{d}v = \texttt{(} u \texttt{)}.\!</math> This much information about Orbit 2 is also encapsulated by the extended proposition <math>\texttt{(} uv \texttt{)((} \mathrm{d}u \texttt{,} v \texttt{))(} \mathrm{d}v, u \texttt{)},\!</math> which says that <math>u\!</math> and <math>v\!</math> are not both true at the same time, while <math>\mathrm{d}u\!</math> is equal in value to <math>v\!</math> and <math>\mathrm{d}v\!</math> is opposite in value to <math>u.\!</math> |
==Turing Machine Example== | ==Turing Machine Example== | ||
| + | |||
| + | <font size="3">☞</font> See [[Theme One Program]] for documentation of the cactus graph syntax and the propositional modeling program used below. | ||
By way of providing a simple illustration of Cook's Theorem, namely, that “Propositional Satisfiability is NP-Complete”, I will describe one way to translate finite approximations of turing machines into propositional expressions, using the cactus language syntax for propositional calculus that I will describe in more detail as we proceed. | By way of providing a simple illustration of Cook's Theorem, namely, that “Propositional Satisfiability is NP-Complete”, I will describe one way to translate finite approximations of turing machines into propositional expressions, using the cactus language syntax for propositional calculus that I will describe in more detail as we proceed. | ||
| Line 1,891: | Line 1,970: | ||
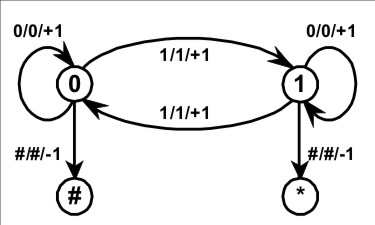
A turing machine for computing the parity of a bit string is described by means of the following Figure and Table. | A turing machine for computing the parity of a bit string is described by means of the following Figure and Table. | ||
| − | + | {| align="center" border="0" cellspacing="10" style="text-align:center; width:100%" | |
| − | + | | [[Image:Parity_Machine.jpg|400px]] | |
| − | {| align="center" border="0" | + | |- |
| − | + | | height="20px" valign="top" | <math>\text{Figure 3.} ~~ \text{Parity Machine}\!</math> | |
| − | |||
| − | |||
| − | | | ||
| − | | | ||
| − | |||
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | Figure | ||
| − | </ | ||
|} | |} | ||
| Line 1,919: | Line 1,981: | ||
| | | | ||
<pre> | <pre> | ||
| − | Table | + | Table 4. Parity Machine |
o-------o--------o-------------o---------o------------o | o-------o--------o-------------o---------o------------o | ||
| State | Symbol | Next Symbol | Ratchet | Next State | | | State | Symbol | Next Symbol | Ratchet | Next State | | ||
| Line 2,817: | Line 2,879: | ||
The output of <math>\mathrm{Stunt}(2)</math> being the symbol that rests under the tape head <math>\mathrm{H}</math> when and if the machine <math>\mathrm{M}</math> reaches one of its resting states, we get the result that <math>\mathrm{Parity}(1) = 1.</math> | The output of <math>\mathrm{Stunt}(2)</math> being the symbol that rests under the tape head <math>\mathrm{H}</math> when and if the machine <math>\mathrm{M}</math> reaches one of its resting states, we get the result that <math>\mathrm{Parity}(1) = 1.</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Document History== | ==Document History== | ||
| Line 2,992: | Line 2,910: | ||
* http://forum.wolframscience.com/archive/topic/228-1.html | * http://forum.wolframscience.com/archive/topic/228-1.html | ||
* http://forum.wolframscience.com/showthread.php?threadid=228 | * http://forum.wolframscience.com/showthread.php?threadid=228 | ||
| − | * http://forum.wolframscience.com/printthread.php?threadid=228&perpage= | + | * http://forum.wolframscience.com/printthread.php?threadid=228&perpage=50 |
# http://forum.wolframscience.com/showthread.php?postid=664#post664 | # http://forum.wolframscience.com/showthread.php?postid=664#post664 | ||
# http://forum.wolframscience.com/showthread.php?postid=666#post666 | # http://forum.wolframscience.com/showthread.php?postid=666#post666 | ||
Latest revision as of 15:30, 11 October 2013
Author: Jon Awbrey
The task ahead is to chart a course from general ideas about transformational equivalence classes of graphs to a notion of differential analytic turing automata (DATA). It may be a while before we get within sight of that goal, but it will provide a better measure of motivation to name the thread after the envisioned end rather than the more homely starting place.
The basic idea is as follows. One has a set \(\mathcal{G}\) of graphs and a set \(\mathcal{T}\) of transformation rules, and each rule \(\mathrm{t} \in \mathcal{T}\) has the effect of transforming graphs into graphs, \(\mathrm{t} : \mathcal{G} \to \mathcal{G}.\) In the cases that we shall be studying, this set of transformation rules partitions the set of graphs into transformational equivalence classes (TECs).
There are many interesting excursions to be had here, but I will focus mainly on logical applications, and and so the TECs I talk about will almost always have the character of logical equivalence classes (LECs).
An example that will figure heavily in the sequel is given by rooted trees as the species of graphs and a pair of equational transformation rules that derive from the graphical calculi of C.S. Peirce, as revived and extended by George Spencer Brown.
Here are the fundamental transformation rules, also referred to as the arithmetic axioms, more precisely, the arithmetic initials.
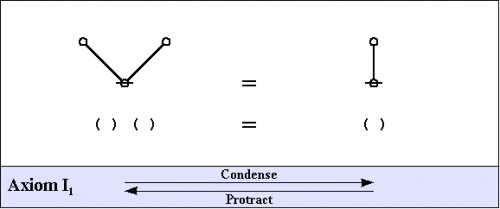 |
(1) |
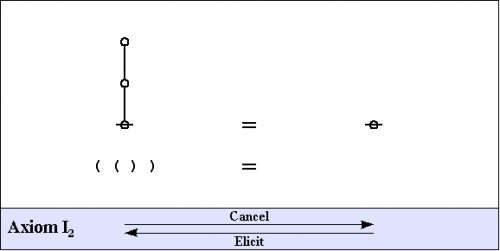 |
(2) |
That should be enough to get started.
Cactus Language
I will be making use of the cactus language extension of Peirce's Alpha Graphs, so called because it uses a species of graphs that are usually called "cacti" in graph theory. The last exposition of the cactus syntax that I've written can be found here:
The representational and computational efficiency of the cactus language for the tasks that are usually associated with boolean algebra and propositional calculus makes it possible to entertain a further extension, to what we may call differential logic, because it develops this basic level of logic in the same way that differential calculus augments analytic geometry to handle change and diversity. There are several different introductions to differential logic that I have written and distributed across the Internet. You might start with the following couple of treatments:
I will draw on those previously advertised resources of notation and theory as needed, but right now I sense the need for some concrete examples.
Example 1
Let's say we have a system that is known by the name of its state space \(X\!\) and we have a boolean state variable \(x : X \to \mathbb{B},\!\) where \(\mathbb{B} = \{ 0, 1 \}.\!\)
We observe \(X\!\) for a while, relative to a discrete time frame, and we write down the following sequence of values for \(x.\!\)
|
\(\begin{array}{c|c} t & x \'"`UNIQ-MathJax1-QINU`"' in other words'"`UNIQ-MathJax2-QINU`"' =='"`UNIQ--h-10--QINU`"'Notions of Approximation== {| cellpadding="2" cellspacing="2" width="100%" | width="60%" | | width="40%" | for equalities are so weighed<br> that curiosity in neither can<br> make choice of either's moiety. |- | height="50px" | | valign="top" | — ''King Lear'', Sc.1.5–7 (Quarto) |- | | for qualities are so weighed<br> that curiosity in neither can<br> make choice of either's moiety.<br> |- | height="50px" | | valign="top" | — ''King Lear'', 1.1.5–6 (Folio) |} Justifying a notion of approximation is a little more involved in general, and especially in these discrete logical spaces, than it would be expedient for people in a hurry to tangle with right now. I will just say that there are ''naive'' or ''obvious'' notions and there are ''sophisticated'' or ''subtle'' notions that we might choose among. The later would engage us in trying to construct proper logical analogues of Lie derivatives, and so let's save that for when we have become subtle or sophisticated or both. Against or toward that day, as you wish, let's begin with an option in plain view. Figure 1.4 illustrates one way of ranging over the cells of the underlying universe \(U^\bullet = [u, v]\!\) and selecting at each cell the linear proposition in \(\mathrm{d}U^\bullet = [\mathrm{d}u, \mathrm{d}v]\!\) that best approximates the patch of the difference map \({\mathrm{D}f}\!\) that is located there, yielding the following formula for the differential \(\mathrm{d}f.\!\)
Figure 2.4 illustrates one way of ranging over the cells of the underlying universe \(U^\bullet = [u, v]\!\) and selecting at each cell the linear proposition in \(\mathrm{d}U^\bullet = [du, dv]\!\) that best approximates the patch of the difference map \(\mathrm{D}g\!\) that is located there, yielding the following formula for the differential \(\mathrm{d}g.\!\)
Well, \(g,\!\) that was easy, seeing as how \(\mathrm{D}g\!\) is already linear at each locus, \(\mathrm{d}g = \mathrm{D}g.\!\) Analytic SeriesWe have been conducting the differential analysis of the logical transformation \(F : [u, v] \mapsto [u, v]\!\) defined as \(F : (u, v) \mapsto ( ~ \texttt{((} u \texttt{)(} v \texttt{))} ~,~ \texttt{((} u \texttt{,~} v \texttt{))} ~ ),\!\) and this means starting with the extended transformation \(\mathrm{E}F : [u, v, \mathrm{d}u, \mathrm{d}v] \to [u, v, \mathrm{d}u, \mathrm{d}v]\!\) and breaking it into an analytic series, \(\mathrm{E}F = F + \mathrm{d}F + \mathrm{d}^2 F + \ldots,\!\) and so on until there is nothing left to analyze any further. As a general rule, one proceeds by way of the following stages:
In our analysis of the transformation \(F,\!\) we carried out Step 1 in the more familiar form \(\mathrm{E}F = F + \mathrm{D}F\!\) and we have just reached Step 2 in the form \(\mathrm{D}F = \mathrm{d}F + \mathrm{r}F,\!\) where \(\mathrm{r}F\!\) is the residual term that remains for us to examine next. Note. I'm am trying to give quick overview here, and this forces me to omit many picky details. The picky reader may wish to consult the more detailed presentation of this material at the following locations: Let's push on with the analysis of the transformation:
For ease of comparison and computation, I will collect the Figures that we need for the remainder of the work together on one page. Computation Summary for Logical DisjunctionFigure 1.1 shows the expansion of \(f = \texttt{((} u \texttt{)(} v \texttt{))}\!\) over \([u, v]\!\) to produce the expression:
Figure 1.2 shows the expansion of \(\mathrm{E}f = \texttt{((} u + \mathrm{d}u \texttt{)(} v + \mathrm{d}v \texttt{))}\!\) over \([u, v]\!\) to produce the expression:
In general, \(\mathrm{E}f\!\) tells you what you would have to do, from wherever you are in the universe \([u, v],\!\) if you want to end up in a place where \(f\!\) is true. In this case, where the prevailing proposition \(f\!\) is \(\texttt{((} u \texttt{)(} v \texttt{))},\!\) the indication \(uv \cdot \texttt{(} \mathrm{d}u ~ \mathrm{d}v \texttt{)}\!\) of \(\mathrm{E}f\!\) tells you this: If \(u\!\) and \(v\!\) are both true where you are, then just don't change both \(u\!\) and \(v\!\) at once, and you will end up in a place where \(\texttt{((} u \texttt{)(} v \texttt{))}\!\) is true. Figure 1.3 shows the expansion of \(\mathrm{D}f\) over \([u, v]\!\) to produce the expression:
In general, \({\mathrm{D}f}\!\) tells you what you would have to do, from wherever you are in the universe \([u, v],\!\) if you want to bring about a change in the value of \(f,\!\) that is, if you want to get to a place where the value of \(f\!\) is different from what it is where you are. In the present case, where the reigning proposition \(f\!\) is \(\texttt{((} u \texttt{)(} v \texttt{))},\!\) the term \(uv \cdot \mathrm{d}u ~ \mathrm{d}v\!\) of \({\mathrm{D}f}\!\) tells you this: If \(u\!\) and \(v\!\) are both true where you are, then you would have to change both \(u\!\) and \(v\!\) in order to reach a place where the value of \(f\!\) is different from what it is where you are. Figure 1.4 approximates \({\mathrm{D}f}\!\) by the linear form \(\mathrm{d}f\!\) that expands over \([u, v]\!\) as follows:
A more fine combing of the second Table brings to mind a rule that partly covers the remaining cases, that is, \(\mathrm{d}u = v, ~ \mathrm{d}v = \texttt{(} u \texttt{)}.\!\) This much information about Orbit 2 is also encapsulated by the extended proposition \(\texttt{(} uv \texttt{)((} \mathrm{d}u \texttt{,} v \texttt{))(} \mathrm{d}v, u \texttt{)},\!\) which says that \(u\!\) and \(v\!\) are not both true at the same time, while \(\mathrm{d}u\!\) is equal in value to \(v\!\) and \(\mathrm{d}v\!\) is opposite in value to \(u.\!\) Turing Machine Example☞ See Theme One Program for documentation of the cactus graph syntax and the propositional modeling program used below. By way of providing a simple illustration of Cook's Theorem, namely, that “Propositional Satisfiability is NP-Complete”, I will describe one way to translate finite approximations of turing machines into propositional expressions, using the cactus language syntax for propositional calculus that I will describe in more detail as we proceed.
I will follow the pattern of discussion in Herbert Wilf (1986), Algorithms and Complexity, pp. 188–201, but translate his logical formalism into cactus language, which is more efficient in regard to the number of propositional clauses that are required. A turing machine for computing the parity of a bit string is described by means of the following Figure and Table.
The TM has a finite automaton (FA) as one component. Let us refer to this particular FA by the name of \(\mathrm{M}.\) The tape head (that is, the read unit) will be called \(\mathrm{H}.\) The registers are also called tape cells or tape squares. Finite ApproximationsTo see how each finite approximation to a given turing machine can be given a purely propositional description, one fixes the parameter \(k\!\) and limits the rest of the discussion to describing \(\mathrm{Stilt}(k),\!\) which is not really a full-fledged TM anymore but just a finite automaton in disguise. In this example, for the sake of a minimal illustration, we choose \(k = 2,\!\) and discuss \(\mathrm{Stunt}(2).\) Since the zeroth tape cell and the last tape cell are both occupied by the character \(^{\backprime\backprime}\texttt{\#}^{\prime\prime}\) that is used for both the beginning of file \((\mathrm{bof})\) and the end of file \((\mathrm{eof})\) markers, this allows for only one digit of significant computation. To translate \(\mathrm{Stunt}(2)\) into propositional form we use the following collection of basic propositions, boolean variables, or logical features, depending on what one prefers to call them: The basic propositions for describing the present state function \(\mathrm{QF} : P \to Q\) are these:
The proposition of the form \(\texttt{pi\_qj}\) says:
The basic propositions for describing the present register function \(\mathrm{RF} : P \to R\) are these:
The proposition of the form \(\texttt{pi\_rj}\) says:
The basic propositions for describing the present symbol function \(\mathrm{SF} : P \to (R \to S)\) are these:
The proposition of the form \(\texttt{pi\_rj\_sk}\) says:
Initial ConditionsGiven but a single free square on the tape, there are just two different sets of initial conditions for \(\mathrm{Stunt}(2),\) the finite approximation to the parity turing machine that we are presently considering. Initial Conditions for Tape Input "0"The following conjunction of 5 basic propositions describes the initial conditions when \(\mathrm{Stunt}(2)\) is started with an input of "0" in its free square:
This conjunction of basic propositions may be read as follows:
Initial Conditions for Tape Input "1"The following conjunction of 5 basic propositions describes the initial conditions when \(\mathrm{Stunt}(2)\) is started with an input of "1" in its free square:
This conjunction of basic propositions may be read as follows:
Propositional ProgramA complete description of \(\mathrm{Stunt}(2)\) in propositional form is obtained by conjoining one of the above choices for initial conditions with all of the following sets of propositions, that serve in effect as a simple type of declarative program, telling us all that we need to know about the anatomy and behavior of the truncated TM in question. Mediate Conditions
Terminal Conditions
State Partition
Register Partition
Symbol Partition
Interaction Conditions
Transition Relations
Interpretation of the Propositional ProgramLet us now run through the propositional specification of \(\mathrm{Stunt}(2),\) our truncated TM, and paraphrase what it says in ordinary language. Mediate Conditions
In the interpretation of the cactus language for propositional logic that we are using here, an expression of the form \(\texttt{(p(q))}\) expresses a conditional, an implication, or an if-then proposition, commonly read in one of the following ways:
A text string expression of the form \(\texttt{(p(q))}\) corresponds to a graph-theoretic data-structure of the following form:
Taken together, the Mediate Conditions state the following:
Terminal Conditions
In cactus syntax, an expression of the form \(\texttt{((p)(q))}\) expresses the disjunction \(p ~\mathrm{or}~ q.\) The corresponding cactus graph, here just a tree, has the following shape:
In effect, the Terminal Conditions state the following:
State Partition
In cactus syntax, an expression of the form \(\texttt{((} e_1 \texttt{),(} e_2 \texttt{),(} \ldots \texttt{),(} e_k \texttt{))}\!\) expresses a statement to the effect that exactly one of the expressions \(e_j\!\) is true, for \(j = 1 ~\mathit{to}~ k.\) Expressions of this form are called universal partition expressions, and the corresponding painted and rooted cactus (PARC) has the following shape:
The State Partition segment of the propositional program consists of three universal partition expressions, taken in conjunction expressing the condition that \(\mathrm{M}\) has to be in one and only one of its states at each point in time under consideration. In short, we have the constraint:
Register Partition
The Register Partition segment of the propositional program consists of three universal partition expressions, taken in conjunction saying that the read head \(\mathrm{H}\) must be reading one and only one of the registers or tape cells available to it at each of the points in time under consideration. In sum:
Symbol Partition
The Symbol Partition segment of the propositional program for \(\mathrm{Stunt}(2)\) consists of nine universal partition expressions, taken in conjunction stipulating that there has to be one and only one symbol in each of the registers at each point in time under consideration. In short, we have:
Interaction Conditions
In briefest terms, the Interaction Conditions simply express the circumstance that the mark on a tape cell cannot change between two points in time unless the tape head is over the cell in question at the initial one of those points in time. All that we have to do is to see how they manage to say this. Consider a cactus expression of the following form:
This expression has the corresponding cactus graph:
A propositional expression of this form can be read as follows:
The eighteen clauses of the Interaction Conditions simply impose one such constraint on symbol changes for each combination of the times \(p_0, p_1,\!\) registers \(r_0, r_1, r_2,\!\) and symbols \(s_0, s_1, s_\#.\!\) Transition Relations
The Transition Relation segment of the propositional program for \(\mathrm{Stunt}(2)\) consists of sixteen implication statements with complex antecedents and consequents. Taken together, these give propositional expression to the TM Figure and Table that were given at the outset. Just by way of a single example, consider the clause:
This complex implication statement can be read to say:
ComputationThe propositional program for \(\mathrm{Stunt}(2)\) uses the following set of \(9 + 12 + 36 = 57\!\) basic propositions or boolean variables:
This means that the propositional program itself is nothing but a single proposition or boolean function of the form \(p : \mathbb{B}^{57} \to \mathbb{B}.\) An assignment of boolean values to the above set of boolean variables is called an interpretation of the proposition \(p,\!\) and any interpretation of \(p\!\) that makes the proposition \(p : \mathbb{B}^{57} \to \mathbb{B}\) evaluate to \(1\!\) is referred to as a satisfying interpretation of the proposition \(p.\!\) Another way to specify interpretations, instead of giving them as bit vectors in \(\mathbb{B}^{57}\) and trying to remember some arbitrary ordering of variables, is to give them in the form of singular propositions, that is, a conjunction of the form \(e_1 \cdot \ldots \cdot e_{57}\) where each \(e_j\!\) is either \(v_j\!\) or \(\texttt{(} v_j \texttt{)},\) that is, either the assertion or the negation of the boolean variable \({v_j},\!\) as \(j\!\) runs from 1 to 57. Even more briefly, the same information can be communicated simply by giving the conjunction of the asserted variables, with the understanding that each of the others is negated. A satisfying interpretation of the proposition \(p\!\) supplies us with all the information of a complete execution history for the corresponding program, and so all we have to do in order to get the output of the program \(p\!\) is to read off the proper part of the data from the expression of this interpretation. OutputOne component of the \(\begin{smallmatrix}\mathrm{Theme~One}\end{smallmatrix}\) program that I wrote some years ago finds all the satisfying interpretations of propositions expressed in cactus syntax. It's not a polynomial time algorithm, as you may guess, but it was just barely efficient enough to do this example in the 500 K of spare memory that I had on an old 286 PC in about 1989, so I will give you the actual outputs from those trials. Output Conditions for Tape Input "0"Let \(p_0\!\) be the proposition that we get by conjoining the proposition that describes the initial conditions for tape input "0" with the proposition that describes the truncated turing machine \(\mathrm{Stunt}(2).\) As it turns out, \(p_0\!\) has a single satisfying interpretation. This interpretation is expressible in the form of a singular proposition, which can in turn be indicated by its positive logical features, as shown in the following display:
The Output Conditions for Tape Input "0" can be read as follows:
The output of \(\mathrm{Stunt}(2)\) being the symbol that rests under the tape head \(\mathrm{H}\) if and when the machine \(\mathrm{M}\) reaches one of its resting states, we get the result that \(\mathrm{Parity}(0) = 0.\) Output Conditions for Tape Input "1"Let \(p_1\!\) be the proposition that we get by conjoining the proposition that describes the initial conditions for tape input "1" with the proposition that describes the truncated turing machine \(\mathrm{Stunt}(2).\) As it turns out, \(p_1\!\) has a single satisfying interpretation. This interpretation is expressible in the form of a singular proposition, which can in turn be indicated by its positive logical features, as shown in the following display:
The Output Conditions for Tape Input "1" can be read as follows:
The output of \(\mathrm{Stunt}(2)\) being the symbol that rests under the tape head \(\mathrm{H}\) when and if the machine \(\mathrm{M}\) reaches one of its resting states, we get the result that \(\mathrm{Parity}(1) = 1.\) Document HistoryOntology List : Feb–Mar 2004
NKS Forum : Feb–Jun 2004
Inquiry List : Feb–Jun 2004
|