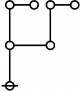
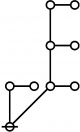
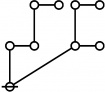
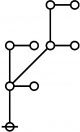
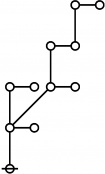
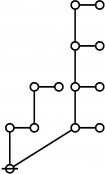
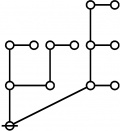
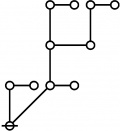
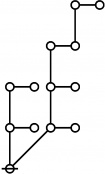
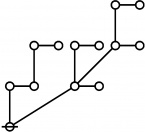
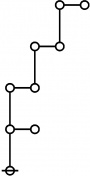
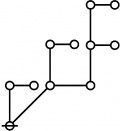
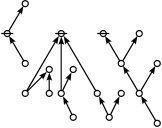
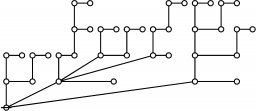
Riffs and Rotes
Idea
Let \(\text{p}_i\!\) be the \(i^\text{th}\!\) prime, where the positive integer \(i\!\) is called the index of the prime \(\text{p}_i\!\) and the indices are taken in such a way that \(\text{p}_1 = 2.\!\) Thus the sequence of primes begins as follows:
|
\(\begin{matrix} \text{p}_1 = 2, & \text{p}_2 = 3, & \text{p}_3 = 5, & \text{p}_4 = 7, & \text{p}_5 = 11, & \text{p}_6 = 13, & \text{p}_7 = 17, & \text{p}_8 = 19, & \ldots \end{matrix}\) |
The prime factorization of a positive integer \(n\!\) can be written in the following form:
| \(n ~=~ \prod_{k = 1}^{\ell} \text{p}_{i(k)}^{j(k)},\!\) |
where \(\text{p}_{i(k)}^{j(k)}\!\) is the \(k^\text{th}\!\) prime power in the factorization and \(\ell\!\) is the number of distinct prime factors dividing \(n.\!\) The factorization of \(1\!\) is defined as \(1\!\) in accord with the convention that an empty product is equal to \(1.\!\)
Let \(I(n)\!\) be the set of indices of primes that divide \(n\!\) and let \(j(i, n)\!\) be the number of times that \(\text{p}_i\!\) divides \(n.\!\) Then the prime factorization of \(n\!\) can be written in the following alternative form:
| \(n ~=~ \prod_{i \in I(n)} \text{p}_{i}^{j(i, n)}.\!\) |
For example:
|
\(\begin{matrix} 123456789 & = & 3^2 \cdot 3607 \cdot 3803 & = & \text{p}_2^2 \text{p}_{504}^1 \text{p}_{529}^1. \end{matrix}\) |
Each index \(i\!\) and exponent \(j\!\) appearing in the prime factorization of a positive integer \(n\!\) is itself a positive integer, and thus has a prime factorization of its own.
Continuing with the same example, the index \(504\!\) has the factorization \(2^3 \cdot 3^2 \cdot 7 = \text{p}_1^3 \text{p}_2^2 \text{p}_4^1\!\) and the index \(529\!\) has the factorization \({23}^2 = \text{p}_9^2.\!\) Taking this information together with previously known factorizations allows the following replacements to be made in the expression above:
|
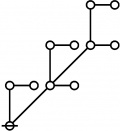
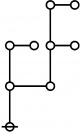
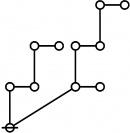
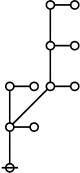
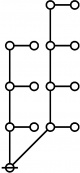
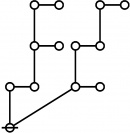
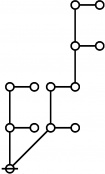
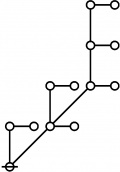
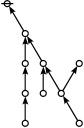
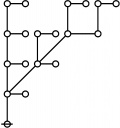
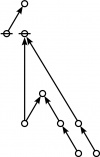
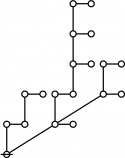
\(\begin{array}{rcl} 2 & \mapsto & \text{p}_1^1 \'"`UNIQ-MathJax1-QINU`"' '"`UNIQ-MathJax2-QINU`"' '"`UNIQ-MathJax3-QINU`"' '"`UNIQ-MathJax4-QINU`"' :{| border="1" cellpadding="20" | [[Image:Rote 802701 Big.jpg|330px]] |} '"`UNIQ-MathJax5-QINU`"' <br> {| align="center" border="1" cellpadding="6" |+ style="height:25px" | \(a(n) = \text{Rote Height of}~ n\) |
\(1\!\) \(a(1) ~=~ 0\) |
\(\text{p}\!\) \(a(2) ~=~ 1\) |
\(\text{p}_\text{p}\!\) \(a(3) ~=~ 2\) |
\(\text{p}^\text{p}\!\) \(a(4) ~=~ 2\) |
\(\text{p}_{\text{p}_\text{p}}\!\) \(a(5) ~=~ 3\) |
|
\(\text{p} \text{p}_\text{p}\!\) \(a(6) ~=~ 2\) |
\(\text{p}_{\text{p}^\text{p}}\!\) \(a(7) ~=~ 3\) |
\(\text{p}^{\text{p}_\text{p}}\!\) \(a(8) ~=~ 3\) |
\(\text{p}_\text{p}^\text{p}\!\) \(a(9) ~=~ 2\) |
\(\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(10) ~=~ 3\) | |
|
\(\text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(a(11) ~=~ 4\) |
\(\text{p}^\text{p} \text{p}_\text{p}\!\) \(a(12) ~=~ 2\) |
\(\text{p}_{\text{p} \text{p}_\text{p}}\!\) \(a(13) ~=~ 3\) |
\(\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(a(14) ~=~ 3\) |
\(\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(15) ~=~ 3\) | |
|
\(\text{p}^{\text{p}^\text{p}}\!\) \(a(16) ~=~ 3\) |
\(\text{p}_{\text{p}_{\text{p}^\text{p}}}\!\) \(a(17) ~=~ 4\) |
\(\text{p} \text{p}_\text{p}^\text{p}\!\) \(a(18) ~=~ 2\) |
\(\text{p}_{\text{p}^{\text{p}_\text{p}}}\!\) \(a(19) ~=~ 4\) |
\(\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(20) ~=~ 3\) | |
|
\(\text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(a(21) ~=~ 3\) |
\(\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(a(22) ~=~ 4\) |
\(\text{p}_{\text{p}_\text{p}^\text{p}}\!\) \(a(23) ~=~ 3\) |
\(\text{p}^{\text{p}_\text{p}} \text{p}_\text{p}\!\) \(a(24) ~=~ 3\) |
\(\text{p}_{\text{p}_\text{p}}^\text{p}\!\) \(a(25) ~=~ 3\) | |
|
\(\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(a(26) ~=~ 3\) |
\(\text{p}_\text{p}^{\text{p}_\text{p}}\!\) \(a(27) ~=~ 3\) |
\(\text{p}^\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(a(28) ~=~ 3\) |
\(\text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(a(29) ~=~ 4\) |
\(\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(30) ~=~ 3\) | |
|
\(\text{p}_{\text{p}_{\text{p}_{\text{p}_\text{p}}}}\!\) \(a(31) ~=~ 5\) |
\(\text{p}^{\text{p}_{\text{p}_\text{p}}}\!\) \(a(32) ~=~ 4\) |
\(\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(a(33) ~=~ 4\) |
\(\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!\) \(a(34) ~=~ 4\) |
\(\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!\) \(a(35) ~=~ 3\) | |
|
\(\text{p}^\text{p} \text{p}_\text{p}^\text{p}\!\) \(a(36) ~=~ 2\) |
\(\text{p}_{\text{p}^\text{p} \text{p}_\text{p}}\!\) \(a(37) ~=~ 3\) |
\(\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!\) \(a(38) ~=~ 4\) |
\(\text{p}_\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(a(39) ~=~ 3\) |
\(\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}_\text{p}}\!\) \(a(40) ~=~ 3\) | |
|
\(\text{p}_{\text{p}_{\text{p} \text{p}_\text{p}}}\!\) \(a(41) ~=~ 4\) |
\(\text{p} \text{p}_\text{p} \text{p}_{\text{p}^\text{p}}\!\) \(a(42) ~=~ 3\) |
\(\text{p}_{\text{p} \text{p}_{\text{p}^\text{p}}}\!\) \(a(43) ~=~ 4\) |
\(\text{p}^\text{p} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(a(44) ~=~ 4\) |
\(\text{p}_\text{p}^\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(45) ~=~ 3\) | |
|
\(\text{p} \text{p}_{\text{p}_\text{p}^\text{p}}\!\) \(a(46) ~=~ 3\) |
\(\text{p}_{\text{p}_\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(a(47) ~=~ 4\) |
\(\text{p}^{\text{p}^\text{p}} \text{p}_\text{p}\!\) \(a(48) ~=~ 3\) |
\(\text{p}_{\text{p}^\text{p}}^\text{p}\!\) \(a(49) ~=~ 3\) |
\(\text{p} \text{p}_{\text{p}_\text{p}}^\text{p}\!\) \(a(50) ~=~ 3\) | |
|
\(\text{p}_\text{p} \text{p}_{\text{p}_{\text{p}^\text{p}}}\!\) \(a(51) ~=~ 4\) |
\(\text{p}^\text{p} \text{p}_{\text{p} \text{p}_\text{p}}\!\) \(a(52) ~=~ 3\) |
\(\text{p}_{\text{p}^{\text{p}^\text{p}}}\!\) \(a(53) ~=~ 4\) |
\(\text{p} \text{p}_\text{p}^{\text{p}_\text{p}}\!\) \(a(54) ~=~ 3\) |
\(\text{p}_{\text{p}_\text{p}} \text{p}_{\text{p}_{\text{p}_\text{p}}}\!\) \(a(55) ~=~ 4\) | |
|
\(\text{p}^{\text{p}_\text{p}} \text{p}_{\text{p}^\text{p}}\!\) \(a(56) ~=~ 3\) |
\(\text{p}_\text{p} \text{p}_{\text{p}^{\text{p}_\text{p}}}\!\) \(a(57) ~=~ 4\) |
\(\text{p} \text{p}_{\text{p} \text{p}_{\text{p}_\text{p}}}\!\) \(a(58) ~=~ 4\) |
\(\text{p}_{\text{p}_{\text{p}_{\text{p}^\text{p}}}}\!\) \(a(59) ~=~ 5\) |
\(\text{p}^\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!\) \(a(60) ~=~ 3\) |
Miscellaneous Examples
| |||||||||||||||||||||||||||||||||
|