Hypostatic abstraction

Hypostatic abstraction is a formal operation that takes an element of information, as expressed in a proposition \(X\ \operatorname{is}\ Y,\) and conceives its information to consist in the relation between that subject and another subject, as expressed in the proposition \(X\ \operatorname{has}\ Y\!\operatorname{-ness}.\) The existence of the abstract subject \(Y\!\operatorname{-ness}\) consists solely in the truth of those propositions that contain the concrete predicate \(Y.\!\) Hypostatic abstraction is known under many names, for example, hypostasis, objectification, reification, and subjectal abstraction. The object of discussion or thought thus introduced is termed a hypostatic object.

The above definition is adapted from the one given by Charles Sanders Peirce (CP 4.235, "The Simplest Mathematics" (1902), in Collected Papers, CP 4.227–323).

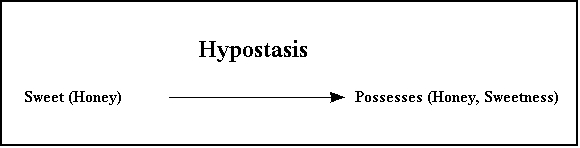
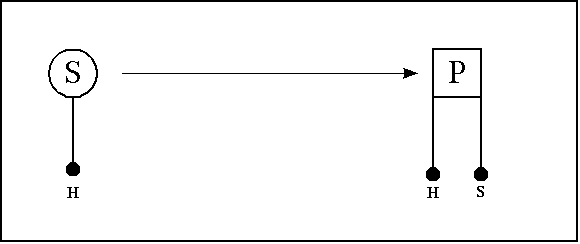
The way that Peirce describes it, the main thing about the formal operation of hypostatic abstraction, insofar as it can be observed to operate on formal linguistic expressions, is that it converts an adjective or some part of a predicate into an extra subject, upping the arity, also called the adicity, of the main predicate in the process.

For example, a typical case of hypostatic abstraction occurs in the transformation from "honey is sweet" to "honey possesses sweetness", which transformation can be viewed in the following variety of ways:

The grammatical trace of this hypostatic transformation tells of a process that abstracts the adjective "sweet" from the main predicate "is sweet", thus arriving at a new, increased-arity predicate "possesses", and as a by-product of the reaction, as it were, precipitating out the substantive "sweetness" as a new second subject of the new predicate, "possesses".

References

• Peirce, C.S., Collected Papers of Charles Sanders Peirce, vols. 1–6, Charles Hartshorne and Paul Weiss (eds.), vols. 7–8, Arthur W. Burks (ed.), Harvard University Press, Cambridge, MA, 1931–1935, 1958.

See also

Template:Col-break

• Abstraction
• Abstraction in computing
• Abstraction in mathematics
• Analogy
• Category theory

Template:Col-break

• Continuous predicate
• Hypostatic object
• Prescisive abstraction
• Reification
• E-prime

Template:Col-end

External links

• Hypostatic Abstraction → ThoughtMesh

• J. Jay Zeman, Peirce on Abstraction

Aficionados

• See Talk:Hypostatic abstraction for discussions/comments regarding this article.
• See Hypostatic abstraction/Aficionados for those who have listed Hypostatic abstraction as an interest.
• See Talk:Hypostatic abstraction/Aficionados for discussions regarding this interest.

---

<sharethis />