Difference between revisions of "Directory:Jon Awbrey/Notes/Factorization And Reification"
Jon Awbrey (talk | contribs) (→Nominalism and Realism: adjust notation) |
Jon Awbrey (talk | contribs) (mdasher, mdancer ...) |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 9: | Line 9: | ||
|} | |} | ||
| − | The question is: What sort of thing is a connotation? Is it a sign? | + | The question is: What sort of thing is a connotation? Is it a sign? — that is to say, yet another term? Or is it something like an abstract attribute — a character, intension, property, or quality? And while we're asking, does it really even matter? |
| − | "No" is one answer worth considering. But then: Why does it not matter? What reason | + | "No" is one answer worth considering. But then: Why does it not matter? What reason could be given to excuse the indifference? |
| − | This is a question that has exercised me since my earliest studies of Peirce. I can remember discussing it with my philosophy mentor at the time and I distinctly recall having arrived at some conclusion or other | + | This is a question that has exercised me since my earliest studies of Peirce. I can remember discussing it with my philosophy mentor at the time and I distinctly recall having arrived at some conclusion or other — alas, I haven't the foggiest notion what exactly my revelation amounted to. |
These days, I usually try to finesse the trick under the trumped up rubric of a factorization. So let me excavate my last attempts to explain this business and see if I can improve on them. | These days, I usually try to finesse the trick under the trumped up rubric of a factorization. So let me excavate my last attempts to explain this business and see if I can improve on them. | ||
| Line 69: | Line 69: | ||
What does all of this have to do with reification and so on? | What does all of this have to do with reification and so on? | ||
| − | + | To begin answering that question, suppose that the source domain <math>X\!</math> is a set of ''objects'', that the target domain <math>Y\!</math> is a set of ''signs'', and suppose that the function <math>f : X \to Y</math> indicates the effect of a classification, conceptualization, discrimination, perception, or some other type of sorting operation, distributing the elements of the set <math>X\!</math> of objects and into a set of sorting bins that are labeled with the elements of the set <math>Y,\!</math> regarded as a set of classifiers, concepts, descriptors, percepts, or just plain signs, whether these signs are regarded as being in the mind, as with concepts, or whether they happen to be inscribed more publicly in another medium. | |
| − | In general, if we | + | In general, if we use the signs in the target domain <math>Y\!</math> to denote or describe the objects in the source domain <math>X,\!</math> then we are engaged in a form of ''general denotation'' or ''plural reference'' with regard to those objects, that is, each sign may refer to each of many objects, in a way that would normally be called ''ambiguous'' or ''equivocal''. |
Notice what I did not say here, that one sign denotes a ''set'' of objects, because I am for the moment conducting myself as such a dyed-in-the-wool nominal thinker that I hesitate even to admit so much as the existence of this thing we call a ''set'' into the graces of my formal ontology, though, of course, my casual speech is rife with the use of the word ''set'', and in a way that the nominal thinker, true-blue to the end, would probably be inclined or duty-bound to insist is a purely dispensable convenience. | Notice what I did not say here, that one sign denotes a ''set'' of objects, because I am for the moment conducting myself as such a dyed-in-the-wool nominal thinker that I hesitate even to admit so much as the existence of this thing we call a ''set'' into the graces of my formal ontology, though, of course, my casual speech is rife with the use of the word ''set'', and in a way that the nominal thinker, true-blue to the end, would probably be inclined or duty-bound to insist is a purely dispensable convenience. | ||
| Line 119: | Line 119: | ||
|} | |} | ||
| − | + | It may be difficult at first to see how anything of significance could follow from an observation so facile as the fact that an arbitrary function factors into a surjective function followed by an injective function. What it means is that there is no loss of generality in assuming that there is a domain of intermediate entities under which the objects of a general denotation or plural reference can be marshaled, just as if they had something more essential and more substantial in common than the shared attachment to a coincidental name. So the problematic status of a hypostatic entity like <math>o\!</math> is reduced from a question of its nominal existence to a matter of its local habitation. Is it more like an object or more like a sign? One wonders why there has to be only these two categories, and why not just form up another, but that does not seem like playing the game to propose it. At any rate, I will defer for now one other obvious possibility — obvious from the standpoint of the pragmatic theory of signs — the option of assigning the new concept, or mental symbol, to the role of an interpretant sign. | |
| − | |||
| − | What it means is that | ||
If we force the factored annotation function, initially extracted from the sign relation <math>L,\!</math> back into the frame from whence it came, we get the augmented sign relation <math>L^\prime,\!</math> shown in the next Figure: | If we force the factored annotation function, initially extracted from the sign relation <math>L,\!</math> back into the frame from whence it came, we get the augmented sign relation <math>L^\prime,\!</math> shown in the next Figure: | ||
Latest revision as of 02:42, 27 June 2009
|
It is important to distinguish between the two functions of a word: 1st to denote something — to stand for something, and 2nd to mean something — or as Mr. Mill phrases it — to connote something. What it denotes is called its Sphere. What it connotes is called its Content. Thus the sphere of the word man is for me every man I know; and for each of you it is every man you know. The content of man is all that we know of all men, as being two-legged, having souls, having language, &c., &c. (Peirce 1866, Lowell Lecture 7, CE 1, 459). |
The question is: What sort of thing is a connotation? Is it a sign? — that is to say, yet another term? Or is it something like an abstract attribute — a character, intension, property, or quality? And while we're asking, does it really even matter?
"No" is one answer worth considering. But then: Why does it not matter? What reason could be given to excuse the indifference?
This is a question that has exercised me since my earliest studies of Peirce. I can remember discussing it with my philosophy mentor at the time and I distinctly recall having arrived at some conclusion or other — alas, I haven't the foggiest notion what exactly my revelation amounted to.
These days, I usually try to finesse the trick under the trumped up rubric of a factorization. So let me excavate my last attempts to explain this business and see if I can improve on them.
Factoring Functions
|
Things are equivocally named, when they have the name only in common, the definition (or statement of essence) corresponding with the name being different. For instance, while a man and a portrait can properly both be called "animals" [since the Greek zõon applies to both], these are equivocally named. For they have the name only in common, the definitions (or statements of essence) corresponding with the name being different. For if you are asked to define what the being an animal means in the case of the man and the portrait, you give in either case a definition appropriate to that case alone. (Categories, p. 13). Aristotle, "The Categories", in Aristotle, Volume 1, H.P. Cooke and H. Tredennick (trans.), Loeb Classics, William Heinemann Ltd, London, UK, 1938. |
I would like to introduce a concept that I find to be of use in discussing the problems of hypostatic abstraction, reification, the reality of universals, and the questions of choosing among nominalism, conceptualism, and realism, generally.
I will take this up first in the simplest possible setting, where it has to do with the special sorts of relations that are commonly called functions, and after the basic idea is made as clear as possible in this easiest case I will deal with the notion of factorization as it affects more generic types of relations.
Picture an arbitrary function from a source or domain to a target or codomain. Here is a picture of such a function, \(f : X \to Y,\) as generic as it needs to be for our present purposes:
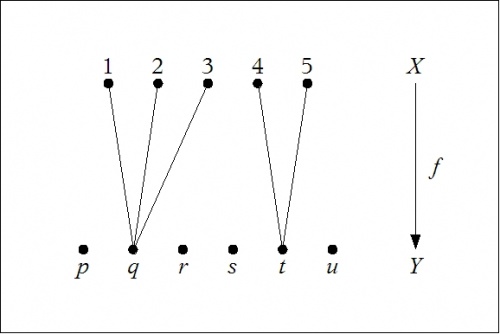
|
| \(\text{Figure 1. Function}~ f : X \to Y\) |
It is a fact that any old function that you might pick factors into a composition of two other functions, a surjective ("onto") function and an injective ("one-to-one") function, in the present example as pictured below:
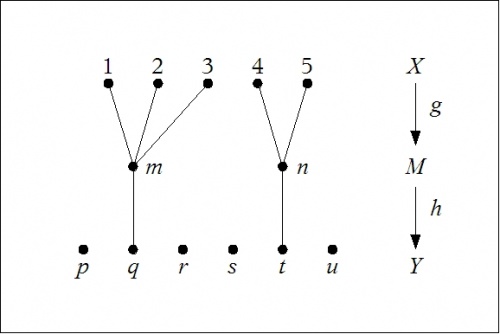
|
| \(\text{Figure 2. Factorization}~ f = g \circ h\) |
Writing functional compositions \(f = g \circ h\) "on the right", we have the following data about the situation:
|
\(\begin{array}{ccl} X & = & \{ 1, 2, 3, 4, 5 \} \\[4pt] M & = & \{ m, n \} \\[4pt] Y & = & \{ p, q, r, s, t, u \} \\[8pt] f & : & X \to Y, ~\text{arbitrary} \\[4pt] g & : & X \to M, ~\text{surjective} \\[4pt] h & : & M \to Y, ~\text{injective} \\[8pt] f & = & g \circ h \end{array}\) |
What does all of this have to do with reification and so on?
To begin answering that question, suppose that the source domain \(X\!\) is a set of objects, that the target domain \(Y\!\) is a set of signs, and suppose that the function \(f : X \to Y\) indicates the effect of a classification, conceptualization, discrimination, perception, or some other type of sorting operation, distributing the elements of the set \(X\!\) of objects and into a set of sorting bins that are labeled with the elements of the set \(Y,\!\) regarded as a set of classifiers, concepts, descriptors, percepts, or just plain signs, whether these signs are regarded as being in the mind, as with concepts, or whether they happen to be inscribed more publicly in another medium.
In general, if we use the signs in the target domain \(Y\!\) to denote or describe the objects in the source domain \(X,\!\) then we are engaged in a form of general denotation or plural reference with regard to those objects, that is, each sign may refer to each of many objects, in a way that would normally be called ambiguous or equivocal.
Notice what I did not say here, that one sign denotes a set of objects, because I am for the moment conducting myself as such a dyed-in-the-wool nominal thinker that I hesitate even to admit so much as the existence of this thing we call a set into the graces of my formal ontology, though, of course, my casual speech is rife with the use of the word set, and in a way that the nominal thinker, true-blue to the end, would probably be inclined or duty-bound to insist is a purely dispensable convenience.
In fact, the invocation of a new order of entities, whether you regard its typical enlistee as a class, a concept, a form, a general, an idea, an interpretant, a property, a set, a universal, or whatever you elect to call it, is tantamount exactly to taking this step that I just now called the factoring of the classification function into surjective and injective factors.
Observe, however, that this is where all the battles begin to break out, for not all factorizations are regarded with equal equanimity by folks who have divergent philosophical attitudes toward the creation of new entities, especially when they get around to asking: In what domain or estate shall the multiplicity of newborn entities be lodged or yet come to reside on a permanent basis? Some factorizations enfold new orders of entities within the Object domain of a fundamental ontology, and some factorizations invoke new orders of entities within the Sign domains of concepts, data, interpretants, language, meaning, percepts, and sense in general. Now, opting for the object choice of habitation would usually be taken as symptomatic of realist leanings, while opting out of the factorization altogether, or weakly conceding the purely expedient convenience of the sign choice for the status of the intermediate entities, would probably be taken as evidence of a nominalist persuasion.
Factoring Sign Relations
Let us now apply the concepts of factorization and reification, as they are developed above, to the analysis of sign relations.
Suppose we have a sign relation \(L \subseteq O \times S \times I,\) where \(O\!\) is the object domain, \(S\!\) is the sign domain, and \(I\!\) is the interpretant domain of the sign relation \(L.\!\)
Now suppose that the situation with respect to the denotative component of \(L,\!\) in other words, the projection of \(L\!\) on the subspace \(O \times S,\) can be pictured in the following manner:

|
| \(\text{Figure 3. Denotative Component of Sign Relation}~ L\) |
The Figure depicts a situation where each of the three objects, \(o_1, o_2, o_3,\!\) has a proper name that denotes it alone, namely, the three proper names \(s_1, s_2, s_3,\!\) respectively. Over and above the objects denoted by their proper names, there is the general sign \(s,\!\) which denotes any and all of the objects \(o_1, o_2, o_3.\!\) This kind of sign is described as a general name or a plural term, and its relation to its objects is a general reference or a plural denotation.
If you now ask, Is the object of the sign \(s\!\) one or many?, the answer has to be many. That is, there is not one \(o\!\) that \(s\!\) denotes, but only the three \(o\!\)'s in the object space. Nominal thinkers would ask: Granted this, what need do we have really of more excess? The maxim of the nominal thinker is never read a general name as a name of a general, meaning that we should never jump from the accidental circumstance of a plural sign \(s\!\) to the abnominal fact that a unit \(o\!\) exists.
In actual practice this would be just one segment of a much larger sign relation, but let us continue to focus on just this one piece. The association of objects with signs is not in general a function, no matter which way, from \(O\!\) to \(S\!\) or from \(S\!\) to \(O,\!\) that we might try to read it, but very often one will choose to focus on a selection of links that do make up a function in one direction or the other.
In general, but in this context especially, it is convenient to have a name for the converse of the denotation relation, or for any selection from it. I have been toying with the idea of calling this annotation, or maybe ennotation.
For example, the assignment of the general term \(s\!\) to each of the objects \(o_1, o_2, o_3\!\) is one such functional patch, piece, segment, or selection. So this patch can be pictured according to the pattern that was previously observed, and thus transformed by means of a canonical factorization.
In our example of a sign relation, we had a functional subset of the following shape:
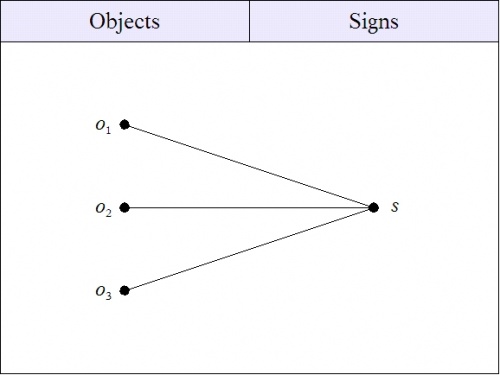
|
| \(\text{Figure 4. One Part of Sign Relation}~ L\) |
The function \(f : O \to S\) factors into a composition \(g \circ h,\!\) where \(g : O \to M,\) and \(h : M \to S,\) as shown here:
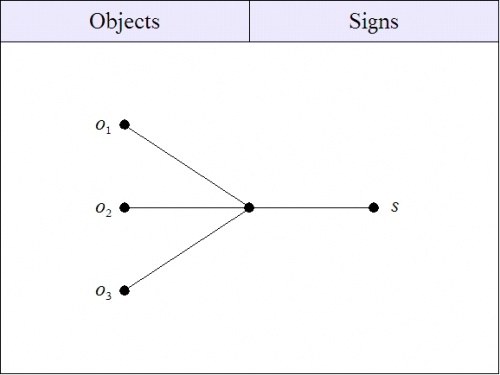
|
| \(\text{Figure 5. Factored Part of Sign Relation}~ L\) |
It may be difficult at first to see how anything of significance could follow from an observation so facile as the fact that an arbitrary function factors into a surjective function followed by an injective function. What it means is that there is no loss of generality in assuming that there is a domain of intermediate entities under which the objects of a general denotation or plural reference can be marshaled, just as if they had something more essential and more substantial in common than the shared attachment to a coincidental name. So the problematic status of a hypostatic entity like \(o\!\) is reduced from a question of its nominal existence to a matter of its local habitation. Is it more like an object or more like a sign? One wonders why there has to be only these two categories, and why not just form up another, but that does not seem like playing the game to propose it. At any rate, I will defer for now one other obvious possibility — obvious from the standpoint of the pragmatic theory of signs — the option of assigning the new concept, or mental symbol, to the role of an interpretant sign.
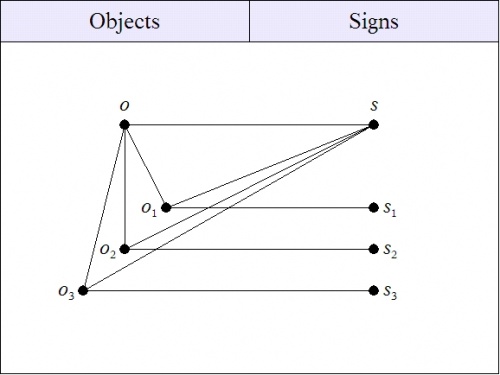
If we force the factored annotation function, initially extracted from the sign relation \(L,\!\) back into the frame from whence it came, we get the augmented sign relation \(L^\prime,\!\) shown in the next Figure:
|
| \(\text{Figure 6. Denotative Component of Sign Relation}~ L^\prime\) |
This amounts to the creation of a hypostatic object \(o,\!\) which affords us a singular denotation for the sign \(s.\!\)
By way of terminology, it would be convenient to have a general name for the transformation that converts a bare, nominal sign relation like \(L\!\) into a new, improved hypostatically augmented or extended sign relation like \(L^\prime.\) Let us call this kind of transformation an objective extension or an outward extension of the underlying sign relation.
This naturally raises the question of whether there is also an augmentation of sign relations that might be called an interpretive extension or an inward extension of the underlying sign relation, and this is the topic that I will take up next.
Nominalism and Realism
Let me now illustrate what I think that a lot of our controversies about nominalism versus realism actually boil down to in practice. From a semiotic or a sign-theoretic point of view, it all begins with a case of plural reference, which occurs when a sign \(s\!\) is taken to denote each object \(o_j\!\) in a collection of objects \(\{ o_1, \ldots, o_k, \ldots \},\) a situation whose general pattern is suggested by a sign-relational table of the following form:
| ||||||
|
For example, consider the sign relation \(L\!\) whose sign relational triples are precisely as shown in Table 8.
| ||||||
|
For the moment, it does not matter what the interpretants are.
I would like to diagram this somewhat after the following fashion, here detailing just the denotative component of the sign relation, that is, the 2-adic relation that is obtained by "projecting out" the Object and Sign columns of the table.

|
| \(\text{Figure 9. Denotative Component of Sign Relation}~ L\) |
Notice the subtle distinction between these two cases:
- A sign denotes each object in a set of objects.
- A sign denotes a set of objects.
The first option uses the notion of a set in a casual, informal, or metalinguistic way, and does not really commit us to the existence of sets in any formal way. This is the more razoresque choice, much less risky, ontologically speaking, and so we may adopt it as our "nominal" starting position.
In this plural denotative component of the sign relation, we are looking at what may be seen as a functional relationship, in the sense that we have a piece of some function \(f : O \to S,\) such that \(f(o_1) =\!\) \(f(o_2) =\!\) \(f(o_3) = s,\!\) for example. A function always admits of being factored into an "onto" (surjective) map followed by a "one-to-one" (injective) map, as discussed earlier.
But where do the intermediate entities go? We could lodge them in a brand new space all their own, but Ockham the Innkeeper is right up there with Old Procrustes when it comes to the amenity of his accommodations, and so we feel compelled to at least try shoving them into one or another of the spaces already reserved.
In the rest of this discussion, let us assign the label \({}^{\backprime\backprime} i \, {}^{\prime\prime}\) to the intermediate entity between the objects \(o_j\!\) and the sign \(s.\!\)
Now, should you annex \(i\!\) to the object domain \(O\!\) you will have instantly given yourself away as having realist tendencies, and you might as well go ahead and call it an intension or even an Idea of the grossly subtlest Platonic brand, since you are about to booted from Ockham's Establishment, and you might as well have the comforts of your ideals in your exile.
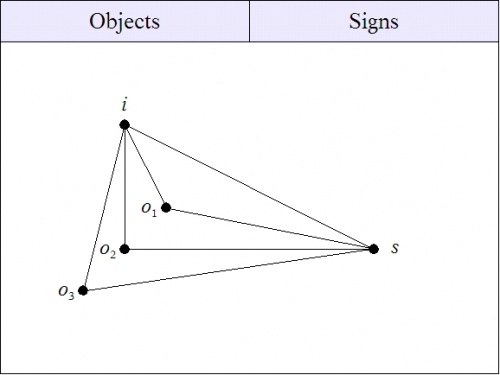
|
| \(\text{Figure 10. Denotative Component of Sign Relation}~ L^\prime\) |
But if you assimilate \(i\!\) to the realm of signs \(S,\!\) you will be showing your inclination to remain within the straight and narrow of conceptualist or even nominalist dogmas, and you may regard the intermediate entity \(i\!\) as an intelligible concept, or an idea of the safely decapitalized, mental impression variety.
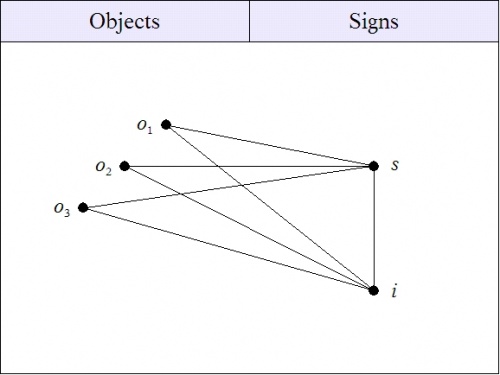
|
| \(\text{Figure 11. Denotative Component of Sign Relation}~ L^{\prime\prime}\) |
But if you dare to be truly liberal, you might just find that you can easily afford to accommodate both intellectual inclinations, and after a while you begin to wonder how all that mental or ontological downsizing got started in the first place.
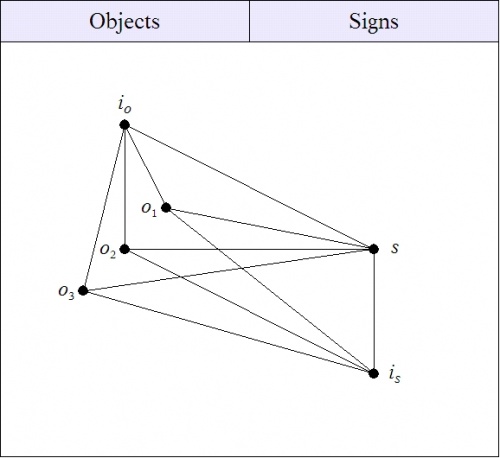
|
| \(\text{Figure 12. Denotative Component of Sign Relation}~ L^{\prime\prime\prime}\) |
To sum up, we have recognized the perfectly innocuous utility of admitting the abstract intermediate object \(i_o,\!\) that may be interpreted as an intension, a property, or a quality that is held in common by all of the initial objects \(o_j\!\) that are plurally denoted by the sign \(s.\!\) Further, it appears to be equally unexceptionable to allow the use of the sign \({}^{\backprime\backprime} s \, {}^{\prime\prime}\) to denote this shared intension \(i_o.\!\) Finally, all of this flexibility arises from a universally available construction, a type of compositional factorization, common to the functional parts of the 2-adic components of any relation.
Document History
Nov 2000 — Factorization Issues
Standard Upper Ontology
- http://suo.ieee.org/email/msg02332.html
- http://suo.ieee.org/email/msg02334.html
- http://suo.ieee.org/email/msg02338.html
- http://suo.ieee.org/email/msg02340.html
- http://suo.ieee.org/email/msg02345.html
- http://suo.ieee.org/email/msg02349.html
- http://suo.ieee.org/email/msg02355.html
- http://suo.ieee.org/email/msg02396.html
- http://suo.ieee.org/email/msg02400.html
- http://suo.ieee.org/email/msg02430.html
- http://suo.ieee.org/email/msg02448.html
Ontology List
- http://suo.ieee.org/ontology/msg00007.html
- http://suo.ieee.org/ontology/msg00025.html
- http://suo.ieee.org/ontology/msg00032.html
Mar 2001 — Factorization Flip-Flop
Ontology List
Standard Upper Ontology
Apr 2001 — Factorization Flip-Flop
Sep 2001 — Descartes' Factorization
Arisbe List
Ontology List
Nov 2001 — Factorization Issues
- http://suo.ieee.org/email/msg07143.html
- http://suo.ieee.org/email/msg07166.html
- http://suo.ieee.org/email/msg07182.html
- http://suo.ieee.org/email/msg07185.html
- http://suo.ieee.org/email/msg07186.html
Mar 2005 — Factorization Issues
- http://stderr.org/pipermail/inquiry/2005-March/002495.html
- http://stderr.org/pipermail/inquiry/2005-March/002496.html
May 2005 — Factorization And Reification
- http://stderr.org/pipermail/inquiry/2005-May/002747.html
- http://stderr.org/pipermail/inquiry/2005-May/002748.html
- http://stderr.org/pipermail/inquiry/2005-May/002749.html
- http://stderr.org/pipermail/inquiry/2005-May/002751.html