12,080
edits
Changes
Directory:Jon Awbrey/Papers/Riffs and Rotes (view source)
Revision as of 22:00, 30 January 2016
, 22:00, 30 January 2016update
{{DISPLAYTITLE:Riffs and Rotes}}
{{DISPLAYTITLE:Riffs and Rotes}}
__TOC__
<div class="nonumtoc">__TOC__</div>
==Idea==
==Idea==
Each index <math>i\!</math> and exponent <math>j\!</math> appearing in the prime factorization of a positive integer <math>n\!</math> is itself a positive integer, and thus has a prime factorization of its own.
Each index <math>i\!</math> and exponent <math>j\!</math> appearing in the prime factorization of a positive integer <math>n\!</math> is itself a positive integer, and thus has a prime factorization of its own.
Continuing with the same example, the index <math>504\!</math> has the factorization <math>2^3 \cdot 3^2 \cdot 7 = \text{p}_1^3 \text{p}_2^2 \text{p}_4^1\!</math> and the index <math>529\!</math> has the factorization <math>{23}^2 = \text{p}_9^2.\!</math> Taking this information together with previously known factorizations allows the following replacements to be made in the above expression:
Continuing with the same example, the index <math>504\!</math> has the factorization <math>2^3 \cdot 3^2 \cdot 7 = \text{p}_1^3 \text{p}_2^2 \text{p}_4^1\!</math> and the index <math>529\!</math> has the factorization <math>{23}^2 = \text{p}_9^2.\!</math> Taking this information together with previously known factorizations allows the following replacements to be made in the expression above:
{| align="center" cellpadding="6" width="90%"
{| align="center" cellpadding="6" width="90%"
|}
|}
The pattern of indices and exponents exhibited in this example is called a ''doubly recursive factorization'', or ''DRF''. Applying the same procedure to any positive integer <math>n\!</math> produces an expression called the DRF of <math>n.\!</math> If <math>\mathbb{M}</math> is the set of positive integers, <math>\mathcal{L}</math> is the set of DRF expressions, and the mapping defined by the factorization process is denoted <math>\operatorname{drf} : \mathbb{M} \to \mathcal{L},</math> then the doubly recursive factorization of <math>n\!</math> is denoted <math>\operatorname{drf}(n).\!</math>
The pattern of indices and exponents illustrated here is called a ''doubly recursive factorization'', or ''DRF''. Applying the same procedure to any positive integer <math>n\!</math> produces an expression called the DRF of <math>n.\!</math> If <math>\mathbb{M}</math> is the set of positive integers, <math>\mathcal{L}</math> is the set of DRF expressions, and the mapping defined by the factorization process is denoted <math>\operatorname{drf} : \mathbb{M} \to \mathcal{L},</math> then the doubly recursive factorization of <math>n\!</math> is denoted <math>\operatorname{drf}(n).\!</math>
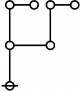
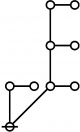
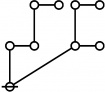
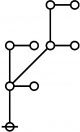
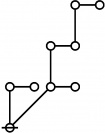
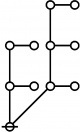
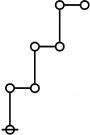
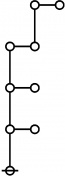
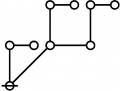
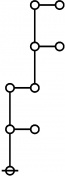
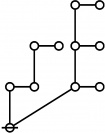
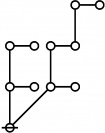
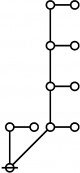
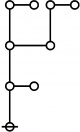
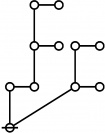
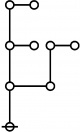
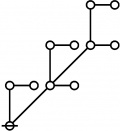
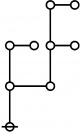
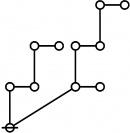
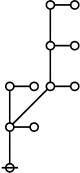
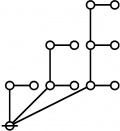
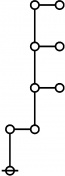
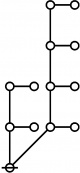
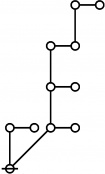
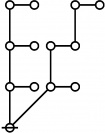
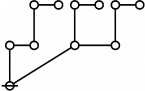
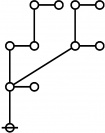
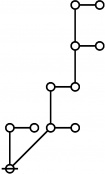
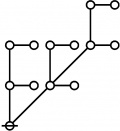
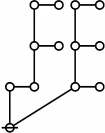
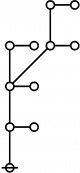
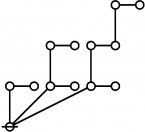
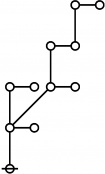
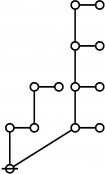
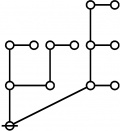
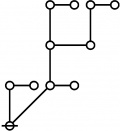
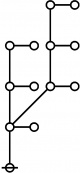
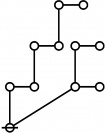
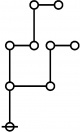
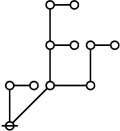
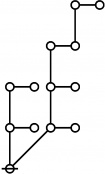
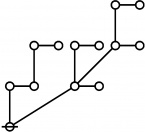
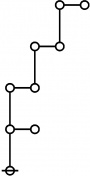
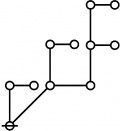
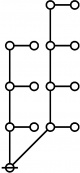
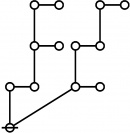
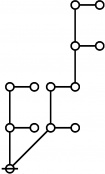
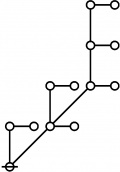
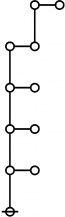
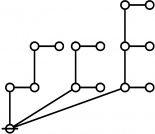
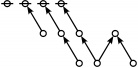
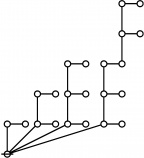
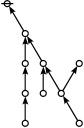
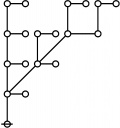
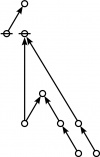
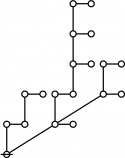
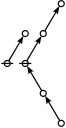
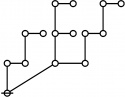
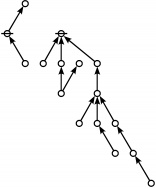
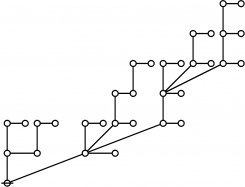
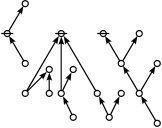
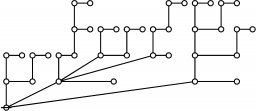
The forms of DRF expressions can be mapped into either one of two classes of graph-theoretical structures, called ''riffs'' and ''rotes'', respectively.
The forms of DRF expressions can be mapped into either one of two classes of graph-theoretical structures, called ''riffs'' and ''rotes'', respectively.
==Riffs in Numerical Order==
==Riffs in Numerical Order==
{| align="center" border="1" cellpadding="10"
{| align="center" border="1" cellpadding="12"
|+ style="height:25px" | <math>\text{Riffs in Numerical Order}\!</math>
|+ style="height:25px" | <math>\text{Riffs in Numerical Order}\!</math>
| valign="bottom" |
| valign="bottom" |
{| align="center" border="1" cellpadding="6"
{| align="center" border="1" cellpadding="6"
|+ style="height:25px" | <math>\text{Rotes in Numerical Order}\!</math>
| valign="bottom" |
| valign="bottom" |
<p>[[Image:Rote 1 Big.jpg|20px]]</p><br>
<p>[[Image:Rote 1 Big.jpg|20px]]</p><br>
<p><math>\text{p}^\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br>
<p><math>\text{p}^\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br>
<p><math>\begin{array}{l} 1\!:\!2 ~~ 2\!:\!1 ~~ 3\!:\!1 \\ 60 \end{array}</math></p>
<p><math>\begin{array}{l} 1\!:\!2 ~~ 2\!:\!1 ~~ 3\!:\!1 \\ 60 \end{array}</math></p>
|}
==Prime Animations==
===Riffs 1 to 60===
{| align="center"
| [[Image:Animation Riff 60 x 0.16.gif]]
|}
===Rotes 1 to 60===
{| align="center"
| [[Image:Animation Rote 60 x 0.16.gif]]
|}
|}
* '''Number of "rooted odd trees with only exponent symmetries" (Rotes) on 2n+1 nodes.'''
* '''Number of "rooted odd trees with only exponent symmetries" (Rotes) on 2n+1 nodes.'''
* [http://oeis.org/wiki/A061396 OEIS Wiki Entry for A061396].
* [http://oeis.org/A061396 OEIS Entry for A061396].
{| align="center" border="1" width="96%"
{| align="center" border="1" width="96%"
* '''Triangle in which k-th row lists natural number values for the collection of riffs with k nodes.'''
* '''Triangle in which k-th row lists natural number values for the collection of riffs with k nodes.'''
* [http://oeis.org/wiki/A062504 OEIS Wiki Entry for A062504].
* [http://oeis.org/A062504 OEIS Entry for A062504].
{| align="center"
{| align="center"
* '''Nodes in riff (rooted index-functional forest) for n.'''
* '''Nodes in riff (rooted index-functional forest) for n.'''
* [http://oeis.org/wiki/A062537 OEIS Wiki Entry for A062537].
* [http://oeis.org/A062537 OEIS Entry for A062537].
{| align="center" border="1" cellpadding="10"
{| align="center" border="1" cellpadding="10"
* '''Smallest j with n nodes in its riff (rooted index-functional forest).'''
* '''Smallest j with n nodes in its riff (rooted index-functional forest).'''
* [http://oeis.org/wiki/A062860 OEIS Wiki Entry for A062860].
* [http://oeis.org/A062860 OEIS Entry for A062860].
{| align="center" border="1" cellpadding="10"
{| align="center" border="1" cellpadding="10"
* '''a(n) = rhig(n) = rote height in gammas of n, where the "rote" corresponding to a positive integer n is a graph derived from the primes factorization of n, as illustrated in the comments.'''
* '''a(n) = rhig(n) = rote height in gammas of n, where the "rote" corresponding to a positive integer n is a graph derived from the primes factorization of n, as illustrated in the comments.'''
* [http://oeis.org/wiki/A109301 OEIS Wiki Entry for A109301].
* [http://oeis.org/A109301 OEIS Entry for A109301].
; Example
; Example
<p><math>\text{p}^\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br>
<p><math>\text{p}^\text{p} \text{p}_\text{p} \text{p}_{\text{p}_\text{p}}\!</math></p><br>
<p><math>a(60) ~=~ 3</math></p>
<p><math>a(60) ~=~ 3</math></p>
|}
==Miscellaneous Examples==
{| align="center" border="1" width="96%"
|+ style="height:24px" | <math>\text{Integers, Riffs, Rotes}\!</math>
|- style="height:50px; background:#f0f0ff"
|
{| cellpadding="12" style="background:#f0f0ff; text-align:center; width:100%"
| width="10%" | <math>\text{Integer}\!</math>
| width="45%" | <math>\text{Riff}\!</math>
| width="45%" | <math>\text{Rote}\!</math>
|}
|-
|
{| cellpadding="12" style="text-align:center; width:100%"
| width="10%" | <math>1\!</math>
| width="45%" |
| width="45%" | [[Image:Rote 1 Big.jpg|15px]]
|-
| <math>2\!</math>
| [[Image:Riff 2 Big.jpg|15px]]
| [[Image:Rote 2 Big.jpg|30px]]
|-
| <math>3\!</math>
| [[Image:Riff 3 Big.jpg|30px]]
| [[Image:Rote 3 Big.jpg|30px]]
|-
| <math>4\!</math>
| [[Image:Riff 4 Big.jpg|30px]]
| [[Image:Rote 4 Big.jpg|48px]]
|-
| <math>360\!</math>
| [[Image:Riff 360 Big.jpg|120px]]
| [[Image:Rote 360 Big.jpg|135px]]
|-
| <math>2010\!</math>
| [[Image:Riff 2010 Big.jpg|138px]]
| [[Image:Rote 2010 Big.jpg|144px]]
|-
| <math>2011\!</math>
| [[Image:Riff 2011 Big.jpg|84px]]
| [[Image:Rote 2011 Big.jpg|120px]]
|-
| <math>2012\!</math>
| [[Image:Riff 2012 Big.jpg|100px]]
| [[Image:Rote 2012 Big.jpg|125px]]
|-
| <math>2500\!</math>
| [[Image:Riff 2500 Big.jpg|66px]]
| [[Image:Rote 2500 Big.jpg|125px]]
|-
| <math>802701\!</math>
| [[Image:Riff 802701 Big.jpg|156px]]
| [[Image:Rote 802701 Big.jpg|245px]]
|-
| <math>123456789\!</math>
| [[Image:Riff 123456789 Big.jpg|162px]]
| [[Image:Rote 123456789 Big.jpg|256px]]
|}
|}
|}